Estimating Effect Sizes in Genome-Wide Association Studies

Abstract

Knowledge about the proportion of markers without effects (p₀) and the effect sizes in large scale genetic studies is important to understand the basic properties of the data and for applications such as the control of false discoveries and designing adequately powered replication studies. Many p₀ estimators have been proposed. However, high dimensional data sets typically comprise a large range of effect sizes and it is unclear whether the estimated p₀ is related to the whole range, including markers with very small effects, or just the markers with large effects. In this article we develop an estimation procedure that can be used in all scenarios where the test statistic distribution under the alternative can be characterized by a single parameter (e.g. non-centrality parameter of the non-central chi-square or F distribution). The estimation procedure starts with estimating the largest effect in the data set, then the second largest effect, then the third largest effect, etc. We stop when the effect sizes become so small that they cannot be estimated precisely anymore for the given sample size. Once the individual effect sizes are estimated, they can be used to calculate an interpretable estimate of p₀. Thus, our method results in both an interpretable estimate of p₀ as well as estimates of the effect sizes present in the whole marker set by repeatedly estimating a single parameter. Simulations suggest that the effects are estimated precisely with only a small upward bias. The R codes that compute the effect estimates are freely downloadable from the website: http://www.people.vcu.edu/~jbukszar/.

Introduction

Genome-wide association studies offer great promise to expedite the discovery of genetic variants affecting susceptibility to common diseases. A first challenge in the analyses is to understand the basic properties of these massive data sets, containing millions of (imputed) markers, such as the proportion of markers without effects (p₀) and the effect sizes (ε) of markers with effects. These basic properties provide a direct indication of the relevance of the genotyped markers for the disease. In addition, this information is crucial for a wide variety of applications such as the control of false discoveries and designing follow-up studies that have adequate power to replicate the initial findings.

High dimensional data sets typically comprise a large range of effect sizes. This presents a problem for the wide variety of existing estimators for p₀ (Allison et al. 2002; Benjamini and Hochberg 2000; Dalmasso et al. 2005; Efron et al. 2001; Hsueh et al. 2003; Meinshausen and Rice 2006; Mosig et al. 2001; Pounds and Cheng 2004; Pounds and Morris 2003; Schweder and Spjøtvoll 1982; Storey 2002; Turkheimer et al. 2001). That is, it is unclear whether the m × (1 – p₀) estimated effects pertain to the whole range of effect sizes, including markers with very small effects, or just the markers with large effects. To solve the unclear interpretation, we would need to know the effect sizes of the markers with effects. These effect sizes are commonly estimated by focusing on the significant markers in the sample that has also been used for testing. However, this approach typically yields estimates with considerable upward bias (Goring et al. 2001; Ioannidis et al. 2001). The reason is that markers that due to sampling fluctuations appear to have a large effect size are more likely to be declared significant. In an independent sample, however, the effect size estimates will “shrink” towards the true effect size or be close to zero because the marker was a false positive. Alternative methods have been proposed to obtain less biased effect size estimates. Zollner and Pritchard (2007), for example, present a likelihood function based on a model with population frequency, penetrance and population prevalence parameters. They use a sophisticated optimization method to find the parameter values that maximize the likelihood given that the marker is significant. Based on the conditional likelihood function of the statistic of a single marker given that the marker is selected, Zhong and Prentice (2008) propose the ML and the median estimator of the effect size. Moreover, in order to avoid overcorrection, they present a weighted estimator, which is a suitably chosen linear combination of the former two. In their work published at the same time as that of Zhong and Prentice (2008), Ghosh et al. (2008) present the conditional likelihood estimator that is essentially the same as Zhong and Prentice’ ML corrected estimator. A significant disadvantage of all these methods is that the effect size estimate they provide for a selected marker is dependent on the selection criterion, e.g. the significance threshold. That is, the effect size estimate varies for different selection criteria. Another drawback is that we will not obtain any information for markers that are not selected but have effect. Also selected null markers will be assigned with estimated effects.

In this article we propose a novel method that yields both an interpretable estimate for the proportion of markers without effects plus the effect sizes of markers with effects by repeatedly estimating a single parameter. Our estimates are obtained using information from the entire set of tested markers and not just those markers that are declared significant. Therefore, unlike existing approaches that estimate effect sizes of only the significant markers in the same sample that has been used for testing, it cannot suffer from the upward bias associated with this approach (Goring et al. 2001; Ioannidis et al. 2001). Furthermore, as we do not select markers, we obtain information for all GWAS markers.

We prefer a more general definition of what is typically referred to in the literature as an “effect size”. More specifically, our method estimates the detectability of a marker is defined as $\sqrt{n}\epsilon$, where n is the sample size and ε an effect size that is a function of the allele frequency plus a genetic effect such as the odds ratio. One reason for this more general definition is that whether we can estimate the “effect sizes” precisely depends not only on the effect size but also on the sample size. For example, a marker with a certain effect size may be detectable, or estimated precisely, in a study with a large sample but not in a study with a small sample. Note that there is a direct correspondence with statistical power that is also determined by both effect size and sample size. Other advantages of using this more general definition is that because detectability incorporates the samples size, by estimating the detectability parameter rather than the effect size we can also handle missing data conveniently.

Instead of the widely used mixture model likelihood function, we used the more realistic real maximum likelihood function to estimate the detectibility. The major difference between the two is that, as in reality, in our model the number of true alternatives is a constant rather than a binomially distributed random variable as in the mixture model. As a result of modeling the true scenario where the number of alternatives is constant, the test statistic distribution of all GWAS markers become dependent, which results in a likelihood function that is much more complex than the one from the mixture model. However, we show that the complexity of optimizing the real maximum likelihood is justified by the much better precision. Our method starts with estimating the largest detectability in the data set, then the second largest detectability, then the third largest detectability, etc. We stop when the detectabilities become so small that they cannot be estimated precisely anymore with the current sample size (i.e. are not “detectable”). Once the individual detectabilities and effect sizes are estimated, they can be used to calculate an interpretable estimate of p₀. Thus, we can calculate p₀ at any step k of the estimation sequence as p_0(k) = 1 – k/m, where m denotes the total number of markers. The calculated p_0(i) has a clear interpretation, it is the estimated proportion of markers whose effect sizes are smaller than the (estimated) k largest effect size. For example, in a study with m = 500,000 markers where the k = 3rd largest effect is estimated as ε₍₃₎ = 0.07, we know that the p₀₍₃₎ of 0.999994 (= 1 – 3/500,000) refers to the three markers with effect sizes 0.07 or larger. In a sense, our method avoids estimating p₀ altogether and solves the unclear interpretation by estimating the effect sizes above a threshold instead.

We implemented our method with two key adaptations that improve the precision of the estimates and evade numerical problems. First, we will need to specify the distribution of test statistic under the alternative hypothesis so that the estimator “recognizes” how observed test statistic values are related to effect sizes. A complication is that the asymptotic equivalent for the distribution of the test statistic may depend on multiple parameters (Bukszár and Van den Oord 2005). To avoid estimating all these parameters for each marker, we propose to use approximations of the asymptotic equivalent that rely on a single parameter only. Fortunately, good and commonly used single value approximations exist for the vast majority of tests performed in statistical genetics. For example, categorical tests, quantitative tests, case–control tests, and tests used in the context of family based designs typically have either a non-central Chi-square or non-central F distributions under the alternative that depend on a single (non-centrality) parameter only. Second, although it is possible to directly estimate the individual effect sizes, it turned out to be more precise to repeatedly estimate average effect size Δ and then calculate the individual effect sizes ε from them. Thus, we first estimate the largest effect by assuming m₁ = 1, then estimate the mean of the two largest effects by estimating Δ while assuming m₁ = 2 and obtain the effect size of the second largest effect by subtraction, etc. Thus, we are essentially estimating the largest individual effect sizes by repeatedly estimating a single parameter.

There are two additional points that may be important to note. First, although our method makes certain simplifying assumptions when estimating average effect size Δ, no assumptions are made about the distribution of the individual effect sizes ε that are simply obtained by subtraction. This is important as in genetic association studies it will be almost impossible to justify parametric assumptions about the effect size distribution. Second, statistics used to test for interactions or more complex models also typically have single value approximations under the alternative (e.g. Wald test for the significance of the interaction effect or likelihood ratio tests obtained by fitting multiple/logistic regression models with and without the interaction effects). Thus, our method is not limited to testing for “main” effects.

Method and results

Estimating individual effect sizes

Maximum likelihood estimator

To estimate the individual effect sizes, ε₁, ε₂,…, first we estimate the average of the k-th largest effect sizes, Δ_k, for k = 1, 2,…, where our effect size parameter is a function of the allele frequency plus a genetic effect such as the odds ratio. We initially make the crude assumption that all individual effect size parameters are identical, and as a result they will be identical with the average effect size, Δ. In the next section we show how this crude assumption of identical effect size parameters can be “overwritten” when the actual individual effect sizes are calculated without making any assumption about their distribution.

Suppose m identical hypothesis tests H₁,…, H_m are performed with statistics T₁,…, T_m. Exactly m₀ of the m statistics follow the null distribution characterized by density function f₀ and the rest of the m₁ = m – m₀ statistics follow an alternative distribution characterized by density function f_Δ that depends on average effect size Δ that is unknown. Let H_i = 0 when null hypothesis i is true, and H_i = 1 otherwise. Note that vector H = (H₁,…, H_m) has m₀ 0 and m₁ 1 components. We assume that H = (H₁,…, H_m) is a random variable whose possible outcomes, the 0–1 vectors of length m with exactly m₁ 1′s, are taken with the same probability, ${\left(\begin{array}{c}\hfill m\hfill \\ \hfill m_1\hfill \end{array}\right)}^{-1}$. Note that H₁,…, H_m are not independent. The likelihood function on the test statistic values t₁,…, t_m is

$$\begin{array}{cc}\hfill L=(m_1,\Delta )& =\frac{1}{\left(\begin{array}{c}\hfill m\hfill \\ \hfill m_1\hfill \end{array}\right)}\sum _H{f}_{H_1\cdot \Delta }\left(t_1\right)\dots f_{H_m\cdot \Delta }\left(t_m\right)\hfill \\ \hfill & =\frac{1}{\left(\begin{array}{c}\hfill m\hfill \\ \hfill m_1\hfill \end{array}\right)}\left(\prod _{i=1}^m{f}_0\left(t_i\right)\right)\sum _{\left\{i_{1,\dots ,i_{m_1}}\right\}\subseteq \{1,\dots ,m\}}\frac{f_{\Delta }\left(t_{i_1}\right)}{f_0\left(t_{i_1}\right)}\times \dots \times \frac{f_{\Delta }\left(t_{i_{m_1}}\right)}{f_0\left(t_{i_{m_1}}\right)}.\hfill \end{array}$$ (1)

where H_i·Δ = Δ if H_i = 1 and H_i·Δ = 0 if H_i = , furthermore, the sum in the upper line is on all possible outcomes of random variable H, and f_Δ (f₀) is the density function of T_i when H_i = 1 (H_i = 0). Thus, the maximum likelihood (ML) estimator of p₀ and the (average) effect size will be ${\widehat{p}}_0=1-{\widehat{m}}_1∕m$ and $\widehat{\Delta }$, respectively, where ${\widehat{m}}_1$ and $\widehat{\Delta }$ maximize function L. In the second line of (1) we also indicated the sample size in subscript of the density function to account for the fact that sample sizes may differ across markers as a result of missing values. This will be discussed later, now we assume equal samples for the sake of simplicity. Note that the density function does not depend on the sample size under the null hypothesis. We stress out that our model differs from the mixture model, where H₁,…, H_m are independent Bernoulli random variables causing the number of true alternatives to be a binomially distributed random variable, M₁ ~ b(((m₁)/m);m), whereas it is a constant in our model, as in reality. It is interesting to remark, that the 1-D marginal distributions are the same for the two likelihoods, but they are dependent for the real likelihood and independent for the mixture model likelihood.

Due to enormous number of terms in the sum, the likelihood cannot be evaluated directly. For example, with a total number of tests m = 100,000 of which m₁ = 5 markers have an effect, there are 8.33 × 10²² terms. We therefore developed the method below that is based on recursive series to calculate the real likelihood. Define S(n) as

$$S\left(n\right)=\sum _{\{i_1,\dots ,i_n\}\subseteq \{1,\dots ,m\}}{a}_{i_1}\dots a_{i_n}$$ (2)

for n = 1,…, m, and S(0) = 1, where $a_i=\frac{f_{\Delta }\left(t_i\right)}{f_0\left(t_i\right)}$ for i = 1,…, m. Then the maximum likelihood function can be re-written as

$$L(m_1,\Delta )=\frac{1}{\left(\begin{array}{c}\hfill m\hfill \\ \hfill m_1\hfill \end{array}\right)}\left(\prod _{i=1}^m{f}_0\left(t_i\right)\right)S\left(m_1\right).$$

One can verify the following sieve-formula

$$S\left(n\right)=\frac{1}{n}\sum _{i=1}^n{(-1)}^{i+1}R\left(i\right)S(n-i),$$

where $R\left(i\right)={\sum }_{j=1}^m{a}_j^i$. By this formula we can calculate S(m₁) in the real likelihood function in a recursive way starting from S(0) and S(1). The large spectrum of a_i’s in combination with the recursive use of them, will cause numerical problems when evaluating S(n). A major technique involved partitioning the set of a_i’s. That is, the distribution of a_i’s is such that the vast majority of markers have values with small range. For this set we can use the recursive formula. For the remaining markers that have a very large range of a_i’s, we created bins of 10 markers. Because there are only 10 markers in each bin, we don’t need the recursive formula for which a large range is problematic. Instead, we calculated S(n) directly using (2). The S(n)’s of all bins were then combined to calculate the S(n) for all markers.

Technically, it would also be possible to maximize L(m₁|Δ = c) to estimate the number of markers ${\widehat{m}}_1$ that together have average effect c. However, the use of L(Δ|m₁ = k) is more sensible. First, the average of the m₁ = k largest effect sizes will always exist although for large values of k the effects are probably very small. However, Δ = c may not exist, for instance the specified c can be larger than the largest effects size, so that there is the risk of trying to estimate something that is not present in the data. Second, even if the specified Δ = c is in an existing range, it will be specified with error because it is real valued whereas m₁ is an integer.

Obtaining the individual effect sizes

It will be hard to justify parametric assumptions about the distribution of the effect sizes. We therefore avoid such assumptions. Rather than estimating m₁ and Δ simultaneously we condition on a pre-specified number m₁ = k of markers with effect and then maximize the function L(Δ|m₁ = k) to estimate their average effect size ${\widehat{\Delta }}_k$. From these average effect sizes we can calculate the effect sizes of the individual markers, ε-s. Thus, for k = 1 we can directly calculate ${\widehat{\epsilon }}_1={\widehat{\Delta }}_1$ and for k > 1 we have

$${\widehat{\epsilon }}_k=k{\widehat{\Delta }}_k-(k-1){\widehat{\Delta }}_{k-1}.$$ (3)

For example, the third largest effect can be obtained as ${\widehat{\epsilon }}_3=3{\widehat{\Delta }}_3-2{\widehat{\Delta }}_2$, where the average effect of the top 3 $\left({\widehat{\Delta }}_3\right)$ and top 2 markers $\left({\widehat{\Delta }}_2\right)$ are estimated by maximizing L(Δ|m₁ = 3) and L(Δ|m₁ = 2) respectively. As we will see we obtain a precise estimate of the average of the highest effect sizes by maximizing L(Δ|m₁ = k). Intuitively, it is so because the ML estimator conditioned on m₁ “does not see” or “barely sees” the effect sizes smaller than the highest m₁ ones. For instance, if we consider k = 3, the estimator will estimate the mean of the three biggest effects and will not be substantially affected by smaller effects. Thus, in the presence of higher effect sizes, the lower effects remain not or just a bit visible for the estimator.

We need a stopping rule to determine the value of the highest k, where the recursion given in (3) stops. Based on extensive simulations, we selected the stopping rule $k={\widehat{m}}_1+1$, where ${\widehat{m}}_1$ is either our conservative estimator with fine-tuning parameter 1 (Kuo et al. 2007) or the Meinshausen–Rice estimator with linear bounding function and fine-tuning parameter 0.5 (Meinshausen and Rice 2006) of the number of individual effect sizes.

In principle we can estimate the m₁ effect sizes directly by the maximum likelihood method. However, even with m₁ = 2, it turned out the variance of the two effect size estimators was large and that it was much more precise to repeatedly estimate average effect size Δ and then obtain the individual effect sizes ε by subtraction.

Detectability

A certain effect size of a causal marker may be estimated precisely (or may be detectable), in a study with a large sample but not in a study with a small sample. How precisely an effect can be estimated depends on both the effect size, ε and the sample size, n, through the quantity $\sqrt{n}\epsilon$, which we will refer to as detectability. For instance, suppose that in experiment B the effect size of a causal marker is half of the effect size of a causal marker in experiment A, i.e. ${\epsilon }^B={\epsilon }^A∕2$, then in experiment B we need four times as many samples as we had in experiment A because $\sqrt{n^B}{\epsilon }^B=\sqrt{4n^A}\left({\epsilon }^A∕2\right)$.

The concept of detectability is convenient to use in simulation studies as well, because with a certain detectability choice we cover infinite selections of effect sizes and sample sizes. In such a simulation we estimate detectabilities rather than effect sizes for convenience, detectabilities and effect sizes can easily be calculated from each other after all. To further illustrate the interpretation of the concept detectability, in Fig. 1 we show all combinations of odds ratios and sample sizes that result in the same detectability $\sqrt{n}\epsilon =3.79$ for fixed minor allele frequency 0.2 (solid line) and 0.5 (dashed line). For example, in an experiment with sample size 980 a marker with odds ratio 1.5 has the same detectability (3.79) as the marker with odds ratio 1.2 in an experiment with sample size 5,128 assuming MAF is 0.2.

Fig. 1.

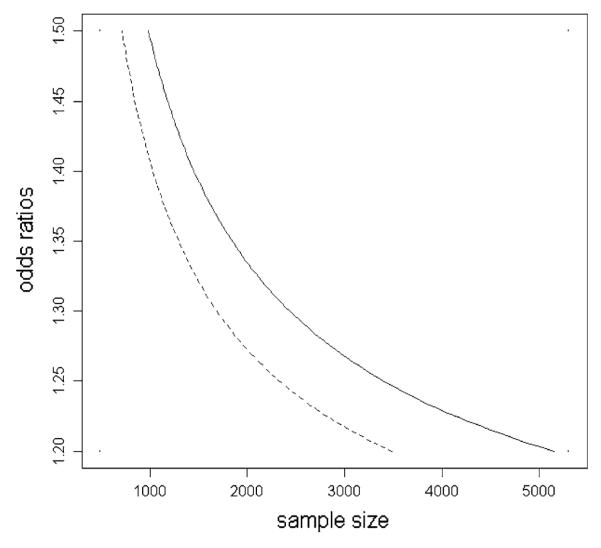
All combinations of odds ratios and sample sizes that result in the same detectability $\sqrt{n}\epsilon =3.79$ for fixed minor allele frequency 0.2 (solid line) and 0.5 (dashed line)

Handling missing values

If there is no missing observations, optimization of (1) is not affected by sample size as it is a constant, thus, we can estimate the effect sizes without considering the sample size. However, if there is missing data, each individual density under the alternative would need to have the marker specific sample size included. Rather than doing this, it is more convenient from a numerical perspective to estimate the detectability parameter $\sqrt{n_i}\epsilon$ instead of the effect size. Recall that the estimated effect sizes or detectabilities are the attributes of the whole set of markers and not some individual markers.

Testing the estimator

Our maximum likelihood estimator requires an approximating density function under the null f₀ and alternative f_Δ. This is because effect sizes are estimated on the basis of (the distribution of) all observed test statistics, which depend on the effect sizes under the alternative. By choosing different functions for f₀ and f_Δ, the method can be applied to a wide variety of studies. Here we will give single value approximation for case–control studies with SNPs.

The distribution of Pearson’s statistic is often approximated with a non-central chi-square distribution with ν – 1 degrees of freedom and non-centrality parameter nε² (Agresti 1990; Cohen 1988; Weir 1996), where n is the total sample size. This approximation depends on only the single value ε, given in (4) below, apart from the known parameter n. However, this approximation can sometimes be inaccurate (Bukszár and Van den Oord 2005). To be able to evaluate the precision of our estimator across a wide variety of scenarios with any potential confounding effect of inaccuracies of the standard approximation, we derived a slightly different single value approximation that was more accurate across a wide variety if scenarios. In particular, define

$$\epsilon =\sqrt{{\gamma }^{\delta }{\sum }_{j=1}^v\frac{{(p_j-q_j)}^2}{\gamma p_j+\delta q_j}}.$$ (4)

where p_i (i = 1,…, ν) is the probability that a randomly chosen case falls into category i, and q_i (i = 1,…, ν) is the probability that a randomly chosen control falls into category i, moreover, γ and δ = 1 – γ are the proportions of cases and controls in the total sample size n. We showed that Pearson’s test statistic is well approximated by

$${\chi }_{v-2}+(1-{\epsilon }^2){\chi }_1\left(\frac{n{\epsilon }^2}{1-{\epsilon }^2}\right),$$ (5)

where χ_ν–2 is a (central) chi-square random variable with ν – 2 degrees of freedom and ${\chi }_1\left(\frac{n{\epsilon }^2}{1-{\epsilon }^2}\right)$ is a chi-square random variable with 1 degree of freedom and non-centrality parameter $\frac{n{\epsilon }^2}{1-{\epsilon }^2}$ (see supplemental material at http://www.people.vcu.edu/~jbukszar/ for the proof). Note that for ε = 0, which happens if and only if the null hypothesis is true, i.e. p_i = q_i for every i, the term in (5) is a central chi-square random variable with ν – 1 degrees of freedom.

The single scalar ε can be interpreted as an effect size. For 2 × 2 tables, for example, we have

$$\epsilon =\frac{\sqrt{{\gamma }^{\delta }}\sqrt{q_1(1-q_1)}(o-1)}{\sqrt{\left(\right(o-1\left)\right(\gamma +\delta q_1)+1)\left(\right(o-1)\delta q_1+1)}},$$ (6)

where o = (p₁(1 – q₁))/(q₁(1 – p₁)) is the odds ratio and p₁ (q₁) the allele frequency in the cases (controls). The fact that an approximation that depends on only a single parameter exists is of great importance because it means that we only have to estimate a single parameter to characterize the effect sizes.

Simulations

We performed simulations to test our method. We first generated a distribution of individual effect sizes ε as defined in (6). To determine the allele frequencies q₁ we downloaded genotype calls for the Affymetrix Mapping 500 K chip set on the 270 HapMap samples (http://www.affymetrix.com/support/technical/sample_data/500k_hapmap_genotype_data.affx). The distribution of the randomly generated odds ratios o comprised two components. The first component represented the five “detectible” odds ratios that were assumed to have the shape of an exponential distribution for which there is some empirical evidence (Hayes and Goddard 2001). For our simulation we used a rate parameter of one where outcomes were linearly transformed to odds ratios. As the second component we also added 37 markers with very small odds ratios that arise due to phenomena such as genotyping errors, selection, and ascertainment differences between cases and controls. For this purpose we used a gamma distribution (shape parameter = 7, rate parameter = 30) and then linearly transformed the outcomes to an odds ratio scale whose minimum was one. The exponential/gamma distributions are just used to create a “skewed” scenario where there are many more small effects compared to big effects.

The effect sizes are probably the most important feature of the simulations. Rather than studying a very limited number of conditions making it hard to generalize results to other scenarios, we created 1,000 conditions with different effect sizes and estimated effect sizes within each condition. Specifically, odds ratios were randomly drawn from the basic skewed distribution in such a way that there were five effect sizes greater than 0.06. As doing many simulations within each condition but that would have been problematic in terms of computer time, for each of the 1,000 conditions we simulated a single sample of 1,000 cases and 1,000 controls. Because the total sample size is 4,000, (1,000 cases + 1,000 controls) × 2 alleles, the 0.06 threshold for effect sizes is equivalent with the threshold $0.06\times \sqrt{4,000}=3.79$ for detectabilities.

Simulation results

We first examine how existing p₀ estimators handled the above situation comprising a broad range of effect sizes. Meinshausen and Rice (2006) gave an estimator that is an upper bound for p₀ with a pre-specified probability α. Their estimator was included (using α = 0.1) because it is specifically designed for applications such as the one considered in this article where the proportion of true null hypotheses is very close to one. In addition, we included our conservative estimator with fine-tuning parameter 1 (Kuo et al. 2007) that performed relatively well in the context of genetic studies. Two studies (Dalmasso et al. 2005; Hsueh et al. 2003) compared additional multiple and non-overlapping sets of estimators. In these studies the Lowest slope and Location based estimator (LBE) showed the most favorable properties and were therefore included here. In addition, an estimator developed Storey (Storey 2002) was included because they may be among the most commonly used estimators. For Storey’s estimator we used the grid he suggested in his article (0, 0.05,…, 0.95) plus a second grid (38 points from 0.00 to 10⁻⁴) that worked better in this specific application where p₀ is known to be very close to 1.

For each of the 1,000 conditions we generated a sample of 1,000 cases + 1,000 controls with the number of markers equal to m = 100,000. We realize that arrays with 500,000 to 1 M markers are now commonly used. However, when this many markers are tested, further increasing the number of markers has a marginal effect on the precision of the estimates so that we preferred m = 100,000 to reduce CPU time. Since the number of detectable effects was 5 in each simulation, the detectable p₀ was 0.99995. Table 1 shows the results. Storey’s estimator using the standard grid and LBE did not perform well in this specific application. They underestimate p₀ considerably, have (very) large standard errors of the estimates, and very often suggest p₀ = 1. The performance of the other estimators was comparable (lowest slope, Meinshausen–Rice, and Storey* with the tailored grid). All p₀ estimators that performed satisfactory in our simulations overestimated p₀ considerably suggesting there were only 4–5 effects rather than about 42 effects that include also the ones that are obtained from the simulated very small odds ratios. This suggests that only the 4–5 biggest effect sizes are detectable for the p₀ estimators, hence we correctly call them detectable effect sizes based on our definition.

Table 1.

Estimating p0 = 0.99958 for effect sizes with mean = 0.0262 (standard deviation = 0.00235)

	Meinshausen & Rice	Conservative	Lowest slope	Storey	Storey*	LBE
# p0 = 1	0	0	118	219	10	472
Mean	0.999969	0.999961	0.999972	0.994538	0.999945	0.988834
Standard deviation	0.000013	0.000015	0.000020	0.007160	0.000058	0.015589

Each of the 1,000 simulations comprised 1,000 cases + 1,000 controls, and the number of markers was m = 100,000. The 42 sample effect sizes were randomly drawn

^*For Storey we used the 38 point grid from 0 to 10⁻⁴

In Table 2 the mean of the actual and the estimated detectabilities across the 1,000 conditions are obtained by maximizing the conditional likelihood L(. |m₁ = k) with k = 1…10. To facilitate the evaluation, we also reported the ratios of the estimated versus real means plus standard deviations in the final two rows of the first part of Table 2. Results show that the detectabilities greater than 3.79, which correspond to effect sizes higher than 0.06, are estimated precisely with only a small upwards bias and standard deviation is only slightly higher than the real standard deviation of the effect sizes. However, for detectabilities smaller than 3.79 the upward bias is more severe and the standard deviation is smaller.

Table 2.

Means and standard deviations of 10 largest real and estimated detectabilities

	k
	1 p0(k)	2	3	4	5	6	7	8	9	10
	0.99999	0.99998	0.99997	0.99996	0.99995	0.99994	0.99993	0.99992	0.99991	0.9999
Five detectabilities greater than 3.79
Real effects
Mean	8.26872	6.51113	5.47011	4.71179	4.13689	3.23375	2.9036	2.58295	2.29898	2.06054
Standard deviation	1.85562	1.35219	0.96892	0.71088	0.44968	0.33963	0.4598	0.49585	0.48826	0.47181
Estimated effects
Mean	8.47427	6.64015	5.58838	4.78895	4.2716	3.97182	3.79473	3.65876	3.54808	3.46143
Standard deviation	1.93911	1.4167	1.08972	0.80322	0.573	0.40477	0.35481	0.34342	0.32002	0.29536
Ratio estimated:real
Mean	1.025	1.020	1.022	1.016	1.033	1.228	1.307	1.417	1.543	1.680
Standard deviation	1.045	1.048	1.125	1.130	1.274	1.192	0.772	0.693	0.655	0.626
No detectabilities greater than 3.79
Real effects
Mean	3.27738	2.98393	2.69869	2.44444	2.22182	2.01121	1.8278	1.6817	1.55521	1.44643
Standard deviation	0.30105	0.42248	0.46106	0.47244	0.45347	0.43323	0.40161	0.35354	0.32382	0.2846
Estimated effects
Mean	3.36024	2.80241	2.52287	2.36032	2.24142	2.14592	2.07066	2.00362	1.94607	1.49386
Standard deviation	1.24783	1.0056	0.92275	0.89556	0.87722	0.86963	0.84749	0.8399	0.83294	1.16245
Ratio estimated:real
Mean	1.025	0.939	0.935	0.966	1.009	1.067	1.133	1.191	1.251	1.033
Standard deviation	4.142	2.381	2.001	1.896	1.934	2.007	2.112	2.375	2.572	4.085

Each of the 1,000 simulations comprised 1,000 cases + 1,000 controls, and the number of markers was m = 100,000. The 42 sample effect sizes were randomly drawn and we ensured that there were five (upper part) or zero (lower part) detectabilities greater than 3.79

Above we proposed the stopping rule k = m₁ + 1. Table 1 shows average estimates of p₀ of 0.999969 and 0.999961 for the Meinshausen and Rice and our conservative estimator, respectively. Because m₁ = m(1 – p₀), the rule would suggest to stop at k = 4.2 when using Meinshausen–Rice and k = 4.9 when using the conservative estimator. As shown in Table 2, the first five effects can be estimated relatively precise, indicating that the stopping rule works reasonably well. Table 2 also shows that as one goes beyond the stopping rule, i.e. beyond the 4th or 5th column, then the effect size will become too small to be precisely estimated, indeed. We did extensive simulations that led to the same conclusion, notably that the precision of the effect size estimate drops when the simulation goes beyond the stopping rule.

To study the method under the complete “null” hypotheses, we analyzed 1,000 conditions where there were no detectabilities higher than 3.79, i.e. all effect sizes were smaller than 0.06. Results are reported in the second part of Table 2. Surprisingly the estimates of the low (<3.79) detectabilities were considerably less biased than the estimates of the similar low (<3.79) detectabilities in the presence of detectabilities higher than 3.79. The reduction in bias seemed, however, accompanied by larger standard deviation of the estimates. The results are encouraging because if there are no big effects then the estimator gives us small effect size estimates, even more precisely in terms of bias, so we will be precisely informed by the estimator about the absence of the big effects.

The simulations that included effects higher than 0.06 were repeated in a number of possibly less favorable conditions. First, we re-ran the simulations assuming dependent rather than independent markers, which could possible impact the precision of the estimates. The dependency among markers in the human genome can be characterized by a block structure where within block correlations are high and between block correlations are low. To simulate the data, we assumed blocks of five markers with statistical association R² = 0.5 as geneticists generally do not genotype markers with correlation higher than R² = 0.5 to avoid redundancy (Carlson et al. 2004). Next, we increased the number of markers to 500,000, but kept the number of effects identical. Possibly it could be more difficult to estimate the effect size because of the much larger number and proportion of null markers, which results in p₀ = 0.99999. Finally, we reduced the sample size to 500 cases and 500 controls. Results in Figs. 2 and 3 show that the simulations assuming dependency between markers and the presence of a larger number of null markers produce results very similar to those reported in Table 2 for the baseline condition in the upper part of the table. Thus, whether or not markers are dependent or the effects need to be detected among a much larger set of null markers hardly affected the precision of the effect size estimates. Note that by varying the total number of markers, we varied p0, which has hardly affects the results. Reducing the sample size does have an impact, most notably on the standard deviation of the effect size estimates. Note that reducing the sample size also reduces detectability. In addition, increasing the proportion of null markers by almost a factor 5 (500,000 rather than 100,000 markers where the number of effects was kept the same) had only a marginal effect. In a final set of simulations we examined extreme conditions. First, we lowered sample sizes to 250 cases/250 controls and 100 cases/100 controls. The estimates still behaved reasonably with sample sizes of 250/250. However, with sample sizes of 100/100 the method broke down and even the largest effect size were severely biased with very large standard deviation. In addition, we performed simulations assuming blocks of five markers with statistical association as high as R² = 0.8. Except for a somewhat higher standard error the bias remained very similar and this high correlation did not appear to affect the estimation a lot.

Fig. 2.

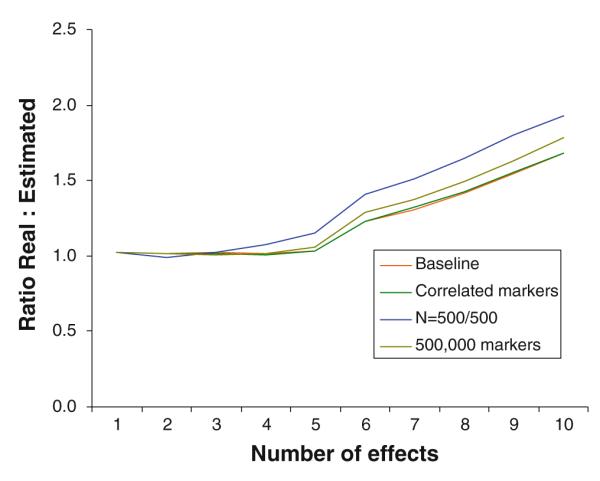
Ratio of estimated versus real mean of effect sizes in a variety of conditions (labels have the same order as ratios for marker 10)

Fig. 3.

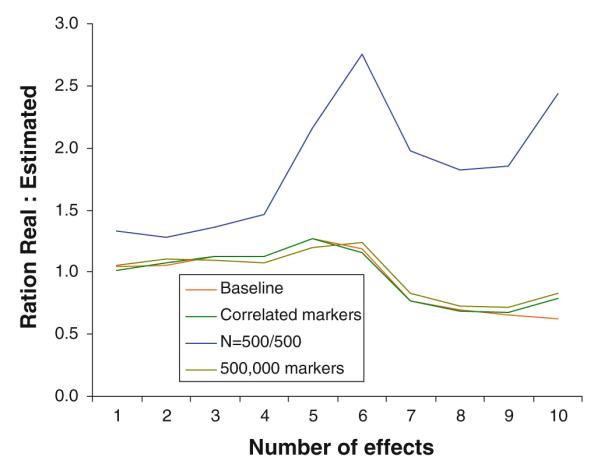
Ratio of estimated versus real standard deviation of effect sizes in a variety of conditions (labels have the same order as ratios for marker 10)

Application to empirical GWAS data

A total of 420,287 genetic markers were tested for their association with neuroticism in a genome-wide association study (GWAS, for details see (van den Oord et al. 2008). In short, the 1,227 subjects came from the “control” sample in the NIMH Genetics repository and were originally part of a large schizophrenia study. We used a multi-dimensional scaling (MDS) approach to correct for potential confounding effects of substructure. Input data for the MDS approach were the genome-wide average proportion of alleles shared identical by state (IBS) between any two individuals. We found that the first 3-D captured the vast majority of genetic substructure in the sample. These three covariates together with genotype data of an SNP formed the four predictors in the linear regression model we used to compute the test statistic value corresponding to an SNP. The response variable was the factor score of the subjects. We used these three covariates together with genotype data of an SNP to compute the test statistic value corresponding to the SNP by linear regression. It is well-known that the distribution of the test statistic is a t-distribution. The expected value of the test statistic is

$$\sqrt{\frac{n-4}{2}}\frac{\Gamma \left(\right(n-5)∕2)}{\Gamma \left(\right(n-4)∕2)}\times \frac{\beta }{\sqrt{{\sigma }^2{\left[{\left(X^{T}X\right)}^{-1}\right]}_{11}}},$$

where X is a n × 4 matrix whose first column contains the genotype data of the SNP and the last three columns contain the factor score of the covariates, and σ² is the variance of the observational error. The absolute value of the expectation of the test statistic can be regarded as the detectability, which divided by $\sqrt{n}$ can be regarded as the effect size. This (single value) detectability is zero if and only if the SNP is independent of the response variables, otherwise it is positive. This enables us to use our method. According to Meinshausen–Rice estimator (with linear bounding function and fine-tuning parameter 0.5), the number causal markers is 4, thus, we stop at 5. The 5 highest estimated individual detectabilities are 4.338, 4.265, 4.191, 4.117 and 4.046. There are about five causal markers with about the estimated detectabilities.

Discussion

Knowledge about the proportion of markers without effects (p₀) and the effect sizes (ε) in large scale genetic studies is important to understand the basic properties of the data and for applications such as the control of false discoveries and designing adequately powered replication studies. Many p₀ estimators have been proposed but the estimates are difficult to interpret as it is unclear whether they are related to the whole range of effect sizes, including markers with very small effects, or just the markers with large effects. Furthermore, current approaches for estimating effect sizes tend to focus on significant findings only, often producing estimates with considerable upward bias. In this article we proposed a method that can be used to obtain an interpretable estimate of p ₀ as well as the individual effect sizes as present in the whole marker set by repeatedly estimating a single parameter. Our results suggested that detectible effect sizes are estimated precisely with only a small upward bias.

It should be stressed that the inability of our method to estimate effects below a certain threshold is not a specific shortcoming. For example, in association testing some effect sizes will have very low statistical power to be declared significant and are essentially also not “detectable”. Furthermore, all existing p₀ estimators are affected by the same phenomenon. For example, the estimators that performed satisfactory in our simulations all overestimated p₀ considerably suggesting there were only 4–5 effects rather than about 42 effects we simulated. The advantage of our method compared to existing methods, however, is that we know how to interpret the p₀ estimates in all these situations. For example, if we would double the sample size in a study, the traditional p₀ estimators would suddenly “see” more effects. However, our estimator is not subject to such misinterpretations because our p₀ estimate is tied to a specific effect size.

Very small effect size may still be very interesting from a substantive and statistical perspective. As estimating individual effect sizes in the “undetectable” range may be impossible for fundamental reasons, very different procedures may need to be developed. One option would be to avoid estimating the small effects altogether and develop a method that estimates the average of all remaining effect sizes rather than each small effect size individually.

Our effect size estimates are obtained using information from the entire set of tested markers and not just those markers that are declared significant. This avoids the upward bias compared to approaches that estimate effect sizes of only the significant markers in the same sample that has been used for testing. The flip side is that our method does not assign effect size estimates to individual markers but estimates the effect sizes present in the whole marker set. However, this may not necessarily limit the practical use of our method. For example, for any set of markers declared significant, we can still calculate the individual effect sizes on this set of significant markers as a whole and design adequately powered replication studies. In addition, we can calculate the posterior probability that the effect size of a marker equals ε_i. As the posterior probability that a marker has a certain effect size can be expressed by a mathematical formula that incorporates only the effect sizes, the test statistic values and the pdf of the statistics, we can estimate the posterior probability by plugging the individual effect size estimates in this formula. Thus, by selecting the effect size with the highest posterior probability we can still assign effect sizes to individual markers. Of more practical importance, by this method one can estimate the probability that a marker has no effects, i.e. the local FDR.

As an alternative approach we explored to avoid the enormous number of terms in (1) is to use the log-likelihood function of the frequently used mixture model. In the mixture model p₀ (or equivalently m₁) is a variable rather than a fixed number. Thus, whereas the likelihood in (1) estimates the number of markers in the selected set of markers, the mixture model approach estimates the proportion of null markers in the population of all possible markers by drawing markers from a large number of markers. It could be argued that in a study one is typically interested in the properties of the markers that have been genotyped rather than the properties of the (fictitious) population of all possible markers. In addition to being less appealing from a theoretical perspective, a simulation study (see supplementary material) showed that the mixture model likelihood estimates of the average effect sizes were very similar regardless of the number of effect sizes in the condition. Consequently, estimates of the individual effect sizes that are obtained by subtraction were very poor.

A wide variety of applications are conceivable using the estimated effect sizes. For example, it may sometimes (e.g. screening studies) be more important to ensure that a desired proportion of markers with effect are detected rather than controlling false discoveries. For this purpose, authors have proposed indices termed a false negative rate, false non-discovery rate, or miss rate in the literature (Delongchamp et al. 2004; Genovese and Wasserman 2002, 2004; Sarkar 2002, 2004; Taylor et al. 2005), which are defined as the proportion of true positives among the markers that are not significant. However, these indices are affected by the proportion of markers without effect p₀, which is irrelevant for the purpose of avoiding that too many true effects are eliminated. Thus, in two studies that achieve the same miss rate, the proportion of true effects that are detected can be very different depending on the value of p₀. In contrast, the availability of an estimate of the average effect size will allow us to calculate the P-value threshold ensuring that a desired proportion of markers with detectable effects are detected.