Integrating beat rate variability: From single cells to hearts

Introduction

The timescales of variations in cardiac pacemaker rhythmicity expressed as heart rate variability (HRV) are similar in nature to those of other biological processes driven by ultradian, circadian, and infradian clocks.¹ To this end, pacemakers have been defined as “that part of the circadian system … conferring … the ability to persist in rhythmicity without rhythmic environmental input. Without rhythmic input the period of the rhythm expressed by the system will reflect thus its physical-chemico properties.”²

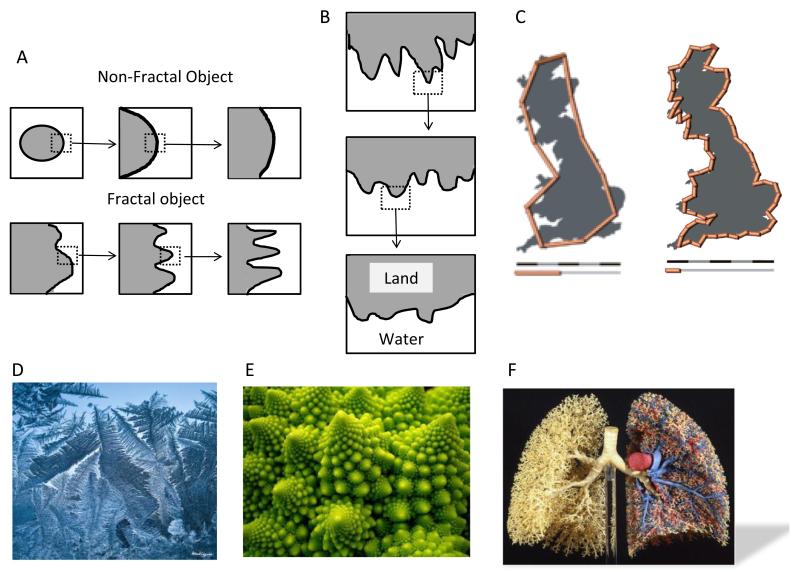
Consideration of the origins of HRV requires a discussion of fractality, self-similarity, and power-law relations. Fractals are “objects or processes whose small pieces resemble the whole”³; that is, a fractal is an object or quantity displaying the property of self-similarity on all scales. Self-similarity means that an object or a time series is composed of subunits and sub-sub-units on multiple levels that (statistically) resemble the structure of the whole object. The object need not exhibit exactly the same structure at all scales, but the same “types” of structures must appear. Whereas magnification of a nonfractal object reveals no new features (Figure 1A, upper row), as a fractal object is magnified, ever-finer features are seen whose shapes resemble those of the larger features thus demonstrating the concept of self-similarity (Figure 1A lower row, Figure 1B). Prototypical examples of fractals exhibiting self-similarity are listed as follows:

1. The coastline: In Figure 1C the length of a Great Britain coastline is measured with different length rulers; the shorter the ruler, the greater the length measured.³ Furthermore, a double logarithmic plot of the length of the ruler vs the measured length of the coastline provides a straight line whose slope (a number between 1 and 2) describes the power law.

2. Natural phenomena with fractal features: Frost crystals forming on cold glass (Figure 1D), Romanesco cauliflower (Figure 1E), and lung airways (Figure 1F).

Figure 1.

Presentation of the basic concept of fractality and selfsimilarity. A: A schematic illustration depicting the difference between a fractal and a nonfractal object. B: A schematic illustration depicting the concept of selfsimilarity. Both illustrations are adopted from Reference 3 by permission of Oxford University Press, USA. C: An example of the coastline paradox. If the coastline of Great Britain is measured by using fractal units 100 km (62 mi) long, then the length of the coastline is approximately 2800 km (1700 mi). With 50 km (31 mi) units, the total length is approximately 3400 km (2100 mi), approximately 600 km (370 mi) longer (http://en.wikipedia.org/wiki/Coastline_paradox). Natural phenomena with fractal features: frost crystals formed naturally on cold glass (http://www.flickr.com/photos/monteregina/6635078819) (D), Romanesco broccoli (E) (http://www.flickr.com/photos/sasha_kopf/2063282413), and lung airways (F).

Heart rate variability and beat rate variability

The power spectral density of HRV incorporates several power bands: The high-frequency band is mainly associated with parasympathetic activity, the low-frequency band with sympathetic activity, and the very low and ultralow frequencies are associated with slow oscillations influenced by thermoregulation, hormonal activity, and other less-defined factors. The very low and ultralow bands in the human heart manifest a property—the power-law behavior—which is common to many representations in nature, such as scale of hurricanes and earthquakes, volcanic eruptions and floods, meteorites size, physiologic measurements, and heart rate fluctuations. Specifically, applying a line-fitting algorithm to the measures of log power on log very low and ultralow frequencies of the power spectrum provides a line with a slope denoted by β. A β of 1 is also known as 1/f, or power-law relation. Different slopes can be distinguished in settings such as myocardial infarction, heart transplant, and aging.^4,5

Consistent with the behavior of the in situ heart, our recent findings indicated that “human embryonic stem cell-derived cardiomyocytes (hESC-CM) and induced pluripotent stem cell-derived cardiomyocytes (iPSC-CM) exhibit beat rate variability (BRV) and power-law behavior,” resembling HRV in the human sinoatrial node (SAN).⁶ Specifically, hESC-CM and iPSC-CM exhibit self-similar long-range oscillations having fractal-like features of the beat rate time series as does the SAN.^7,8 Although hESC-CM and iPSC-CM grow in culture devoid of neural and humoral inputs, both share the feature of fractal behavior with the in situ SAN, suggesting that the origin of this power-law behavior is an intrinsic feature of pacemaker cells. These findings are consistent with previous studies, showing that the rhythmicity of spontaneously beating cardiomyocytes in culture^9-11 and the rhythmicity of other excitable cells (eg, single presynaptic neurons in feline rostral ventrolateral medulla) exhibit self-similarity and fractality.¹²

An important issue raised by these findings is whether BRV and HRV have the same mechanism and origin. A robust body of research shows that “steady-state” characteristics of biological systems result from the integration of oscillations, rhythms, and clocks, which are essential for the regulated function of an organism.¹ Hence, the sources for HRV of the in situ heart might be considered in terms of the non-steady-state firing patterns of individual cardiac pacemakers, the interactions among neighboring pacemakers in a cluster, and the external environment’s influences on all these.

Relating HRV to BRV

While relating HRV to BRV, we first consider the fractal behavior of hESC-CM and iPSC-CM and use the SAN as a model for comparison. In the normal heart, HRV reflects the modulation of the SAN pacemaker function mainly by the autonomic nervous system activity. However, in hearts lacking direct autonomic neural input, cardiac rhythm dynamics are sufficiently altered to suggest roles for other intrinsic cardiac regulatory mechanisms and for circulating neurohumors.⁴

Hence, we asked whether HRV is simply the in situ manifestation of BRV, with the impact of the sympathetic and parasympathetic nervous systems and of extracardiac inputs added to it. This simple question requires us to dissect a complex subject—the origin of the oscillatory activity and pacemaker activity in the heart. Oscillatory activity is a property of a variety of cells, both excitable and inexcitable, seen as a perturbation in membrane voltage varying around a baseline membrane potential. Such an activity can be synchronous or dyssynchronous in cell networks.¹³ Oscillations are related not only to Ca²⁺ movement intracellularly but also to the function of organelles such as mitochondria.¹⁴ As discussed below, this may reflect oscillations in other systems as well, such as cyclic adenosine monophosphate levels and phosphorylation processes.

Pacemaker ion currents, such as the funny current, differ from oscillations in that they displace membrane potential from a negative to a more positive voltage. Yet, regardless of the source of membrane potential displacement, once the net membrane current is inward, bringing the cell membrane to threshold potential, an action potential will occur. In considering pacemaker function, we are confronting interrelated yet mechanistically diverse events contributing to the expression of rhythm and rate.

We can further explore the relationships and feedback between BRV and HRV by hypothesizing 3 levels of interaction. The first level is the single pacemaker cell; the second is a cluster of interconnected pacemaker cells; the third is the SAN in the in situ heart. The hypothesis implies that the overall activity of the cell cluster (ie, its BRV) is determined by integrated interactions among different oscillators residing in each of its cells. The activity of individual cells, in turn, depends on oscillations in organelles and pathways within those cells. In other words, every cell in a cluster is an independent dynamic oscillator whose activity depends on interdependent and simultaneous regulatory processes expressed as variations—oscillations—in membrane potential and in intracellular Ca²⁺ movements, which generate BRV.

The first level: The single cell

The concept is that BRV and fractality are fundamental properties of a single pacemaker cell, resulting from a variety of nonlinear dynamic processes such as ion-channel gating, intracellular Ca²⁺ cycling, mitochondrial function, and variations in intracellular processes such as cyclic adenosine monophosphate production and protein phosphorylation/dephosphorylation. Previous research supports this notion,¹¹ but the intracellular mechanisms underlying BRV at the single cell level largely remain to be elucidated. To address this issue, we will consider fractalilty at different subcellular levels, which together can account for the fractal behavior of the single cell firing pattern.

Ion channels

Several studies, heavily vested in computer simulation, have proposed that fractal behavior is a property of single ion channels contributing to the overall fractal firing properties of a single pacemaker cell.^15-18 Fractal analysis of ion channels assumes that the single channel current has memory. Here, single ion-channel fluctuations are treated as arising from movement through a large number of substates, where switching between substates may vary with time.¹⁹ French and Stockbridge¹⁵ examined kinetic behavior in 2 types of channels from human and avian fibroblasts: for both channels, openings showed mixed fractal and Markovian behavior while closings mainly gave fractal kinetics. A Markovian process can be thought of as stochastic and having no short-term or long-term memory. In contrast, fractal processes are basically deterministic in nature, which means that every step in the process is determined (or dependent) by the previous step.

Lowen et al¹⁸ investigated the causal relationship between ion-channel gating and neuronal spiking by using the Fitzhugh-Nagumo and Hodgkin-Huxley neuronal models. They concluded that fractal ion-channel gating activity is sufficient to account for the fractal-rate firing behavior. By extension, we can hypothesize that fractal gating properties of the ion currents contributing to automaticity (eg, the funny current and the L-type Ca²⁺ current) can contribute to BRV at the single cell level.

Circadian rhythms come into play in ion-channel modulation as follows: While the general consensus is that circadian variations in cardiac physiology are due to physiological responses to autonomic stimuli, there are intrinsic circadian changes in cardiac metabolism and expression of circadian clock genes^20-25 independent of autonomic inputs. For example, Ko et al²⁶ described circadian regulation of the L-type calcium channels in embryonic chick hearts. Specifically, the protein expression of both α1C and α1D subunits were high during the “night” and low during the “day.” This was paralleled by significantly higher Ca²⁺ current densities recorded during the “night” than “day.” Furthermore, the phosphorylation patterns of key signaling molecules, including Erk, p38, Akt, and GSK, were shown to be circadian. However, whether these different circadian pathways are synchronized via diffusion of these molecules through gap junctions or via paracrine/juxtacrine mechanisms is yet to be determined. More studies are needed on circadian-related clocks and BRV in single cells and on whether possible disease-related changes in these clocks contribute to the altered HRV properties observed in a variety of cardiac pathologies such as congestive heart failure.^4,27

Mitochondria and calcium clock as sources for BRV

Because of the key role of mitochondria in the maintenance of intracellular homeostasis in cardiomyocytes, scale invariant processes in mitochondrial energetics are likely contributors to pacemaker fractality. Recent studies have shown that mitochondria can behave as individual pacemakers whose dynamics can obey collective network features.^1,14,28 Aon and coworkers demonstrated in guinea pig cardiomyocytes that the mitochondrial membrane potential (ΔΦ_m) and reactive oxygen species (which couples the individual mitochondria) dynamic exhibit power-law behavior spanning at least 3 orders of magnitude, thus corresponding to fractal behavior.^14,28 Under pathological conditions such as ischemia and reperfusion injury, mitochondrial coordination strengthens and the frequency spectrum narrows dramatically to low-frequency/high-amplitude oscillations.^14,29 Since under a variety of cardiac pathologies HRV diminishes,^4,27 these derangements in mitochondrial dynamics should be considered as possible contributory mechanisms.

The experimental evidence for an association between mitochondrial fractal dynamics and BRV is as follows: Mitochondria can accumulate large quantities of Ca²⁺, which enters the mitochondria through the Ca²⁺ uniporter^29,30 in a manner dependent on ΔΦ_m (which exhibits fractal behavior). Ca²⁺ is extruded from mitochondria via the mitochondrial Na⁺/Ca²⁺ exchanger.^31-33 Consequently, mitochondrial Ca²⁺ uptake and release participate in regulating the amplitude and spatiotemporal pattern of intracellular Ca²⁺ signals in various cells, including cardiomyocytes. It is likely that mitochondria-related Ca²⁺ release/uptake machinery interacts with the sarcoplasmic reticulum (SR) Ca²⁺ cycling, which constitutes the “Ca²⁺ clock,” thus contributing to normal automaticity of cardiac pacemaker cells.^34,35 Supporting this notion, Yaniv et al³⁶ demonstrated mitochondrial-SR Ca²⁺ cross-talk, modulating the basal coupled-clock system automaticity in rabbit SAN cells.

The second level: A cluster of pacemaker cells

A pacemaker cell cluster represents the isolated/detached SAN devoid of extracardiac influences. In this interconnected network of spontaneously oscillating pacemakers, individual cells can fire at different rates but the ensemble network displays a “collective phenomenon.”³⁷ Here, the influences of intercellular coupling are such that the entire cluster can fire at a rate which is not necessarily that of the pacemaker cell with the fastest rate.

While it is thought that key determinants/modulators of HRV in the heart in situ are the autonomic nervous system, thermoregulation, and humoral factors, little is known about mechanisms generating the firing fluctuations in a cardiac network composed of many coupled excitable elements. Computer modeling has been used to decipher the putative determinants of the network fractal behavior. Soen and Braun⁹ generated simulations to study the effect of intercellular coupling on the network firing patterns. Yoneyama and Kawahara³⁷ found that the formation of strong heterogeneous coupling among the 3 oscillators in their model is a key determinant of the complexity in the interval series as well as in the scaling behavior. More recently, Ponard et al³⁸ reported a mathematical model of pacemaker cell network in which stochastic fluctuations in transmembrane currents and stochastic gating of Ca²⁺ release channels could not reproduce the spatiotemporal patterns observed in vitro. In contrast, long-term correlations produced by the turnover of ion channels induced variability patterns with a power-law behavior similar to those observed experimentally. In view of the diverse observations and interpretations of the contribution of intercellular coupling to the putative differences in BRV properties of single cells vs the network, the effect of gap junction uncoupling on BRV properties of iPSC-CM networks should be investigated. On the basis of the experimental evidence to date, we propose that the ΔΦ_m (exhibiting fractal dynamics)-driven uniporter-mediated mitochondrial Ca²⁺ extrusion triggers a concomitant (fractal) SR Ca²⁺ cycle, which thus initiates automaticity manifesting BRV and fractality.

The third level: The in situ heart—integration of all 3 levels

SAN rhythmicity is characterized by HRV, which follows power-law behavior and results from extracardiac modulation of pacemaker automaticity. The inherent pacemaker firing pattern is continuously exposed to a variety of rate- and rhythm-modifying effectors, such as the autonomic system, humoral factors such as epinephrine, and thermoregulatory and circadian inputs. Collectively, these factors, some of which have synergistic and other antagonistic effects on heart rate, operate in concert to determine the actual heart rate.

A 3-level hypothesis may partly explain the multiscale origin of HRV. As multiple “clocks” are involved within the 3 levels in initiating and integrating the momentary heart rate, their different frequencies that operate at different timescales may constitute the origin of the multiscale pattern of HRV. This complex process is repeated over and over again for each heartbeat, from the cell and its intrinsic components and processes up to the SAN. However, because the initial conditions at every level may change for every beat (eg, due to brief physical stress, chemical changes, or altered ion concentrations), the complex integration of the summated changes translated through multiple levels may increase or decrease a change in the target organ—the heart. While it is established that scaling invariance of HRV/BRV arises from nonlinear interactions between processes operating at different timescales, the novel concept presented here is that the integration at 3 different spatial scales (cells/clusters/organs) contributes to HRV/BRV properties. Nonetheless, whether integration/interaction at multiple temporal scales is more important than multiple spatial scales is yet to be determined.

Conclusions: BRV as the cellular determinant of HRV

On the basis of above arguments and evidence, it seems likely that HRV is continuously determined and modulated by different molecular, genetic, metabolic, and neural influences initiated at the single molecule and single cell level, augmented and modified at the network level, and further integrated and changed at the level of the in situ heart. Thus, the BRV of the single cell or a cluster of cells, after proceeding through the different levels (and sublevels) and gathering along the way stimuli from different sources (eg, hormonal and neural), ends up in HRV, which is universal in the healthy heart.

Furthermore, deviations from behavior in the healthy heart can also be explained through this mechanism. Loss of fractality, quasi-deterministic HRV, alterations in power-law behavior, and diminution of the phase space are the hallmarks of the diseased heart.^5,27,39,40 As there are many different inputs to the system, it is possible that at any stage—from the organelle to the cell to the intact heart—these different inputs may alter the final output.

Aging in humans has been shown to diminish variability and reduce the fractal behavior of heart rate, signifying that the system receives fewer inputs, causing it to be less complex. Similar decomplexification of the cardiovascular system has been reported during certain illnesses and pain reactions.^39-41 In all these settings, the 3-level approach can be used to explain the link between BRV and HRV, as well as between the healthy and the diseased heart, with regard to HRV.

ABBREVIATIONS

BRV

beat rate variability

hESC-CM

human embryonic stem cell-derived cardiomyocytes

HRV

heart rate variability

iPSC-CM

induced pluripotent stem cell-derived cardiomyocytes

SAN

sinoatrial node

SR

sarcoplasmic reticulum