Modeling anterograde and retrograde transport of short mobile microtubules from the site of axonal branch formation

Abstract

This theoretical research is motivated by a recent model of microtubule (MT) transport put forward by Baas and Mozgova (Cytoskeleton 69:416–425, 2012). According to their model, in an axon all plus-end-distal mobile MTs move anterogradely while all minus-end-distal mobile MTs move retrogradely. Retrograde MT transport thus represents a mechanism by which minus-end-distal MTs are removed from the axon. We suggested equations that implement Baas and Mozgova’s model. We employed these equations to simulate transport of short mobile MTs from a region (such as the site of axonal branch formation) where MT severing activity results in generation of a large number of short MTs of both orientations. We obtained the exact and approximate transient solutions of these equations utilizing the Laplace transform technique. We applied the obtained solutions to calculate the average rates of anterograde and retrograde transport of short MTs.

Introduction

Microtubules (MTs) are major tracks for transport of organelles and cytoskeletal elements in axons. However, short mobile MTs themselves are transported as part of a slow component “a”, moving with an average velocity of 0.002–0.1 μm/s in both anterograde and retrograde directions [2–4]. Mobile MTs are short; they do not exceed 7–10 μm in length [1]. It was established by Anthony Brown and colleagues that MTs move intermittently and asynchronously, alternating between short runs and long pauses. During the runs, mobile MTs move with velocities on the order of 1 μm/s, which is the velocity of known molecular motors, such as kinesin and dynein [2, 5]. However, it was not clear whether MTs are transported by the sliding filament mechanism or by the cargo mechanism. In the sliding filament mechanism, the motor is stationary and the mobile MT interacts with the motor domain. In the cargo mechanism, a mobile MT interacts with the cargo domain of the motor while the motor domain “walks” on a stationary track, such as a long stationary MT [1].

There has also been no agreement on what specific kinesin motors move MTs and what the role of dynein is. Gelfand and colleagues [6] recently presented results that suggest that conventional kinesin (kinesin-1) might be the motor that slides microtubules in axons. Their conclusion is based on an experimental investigation of MT transport in Drosophila neurons.

In contrast to Gelfand’s hypothesis [6], Baas and Mozgova [1] recently suggested a different model of MT transport. According to their model, short mobile MTs always move with their plus-ends leading. The role of dynein motors in axonal transport of MTs has been elucidated in many publications, including He et al. [7] and Ahmad et al. [8]. Baas and Mozgova [1] suggested that dynein may be the main motor responsible for MT transport. They assumed that the dynein motors that drive MTs are immobilized because the dynein cargo domains interact with either long stationary MTs or the actin cytoskeleton [9, 10]. The dynein motor domains then interact with short mobile MTs, causing their sliding, in accordance with the sliding filament mechanism. For this reason, all plus-end-distal mobile MTs move anterogradely while all minus-end-distal mobile MTs move retrogradely.

According to the hypothesis put forward in Baas and Mozgova [1], the above mechanism represents the error correction mechanism by which axons clear themselves of short minus-end-distal MTs before these MTs had a chance to elongate and become stationary. This enables axons to maintain the plus-end-distal MT polarity orientation. Baas and Mozgova’s hypothesis is consistent with experimental findings of Zheng et al. [11], who established that the number of minus-end-distal MTs increases in dynein mutant axons of Drosophila neurons, in which dynein function is suppressed.

Although long stationary MTs in axons are oriented plus-end-distally, short mobile MTs with both plus-end-distal and minus-end-distal orientations can be produced by first severing these long stationary MTs and then flipping some of the short MTs (see Fig. 5 in Baas and Mozgova [1]). Such severing events can occur, for example, at the site of axonal branch formation [12–14].

Fig. 5.

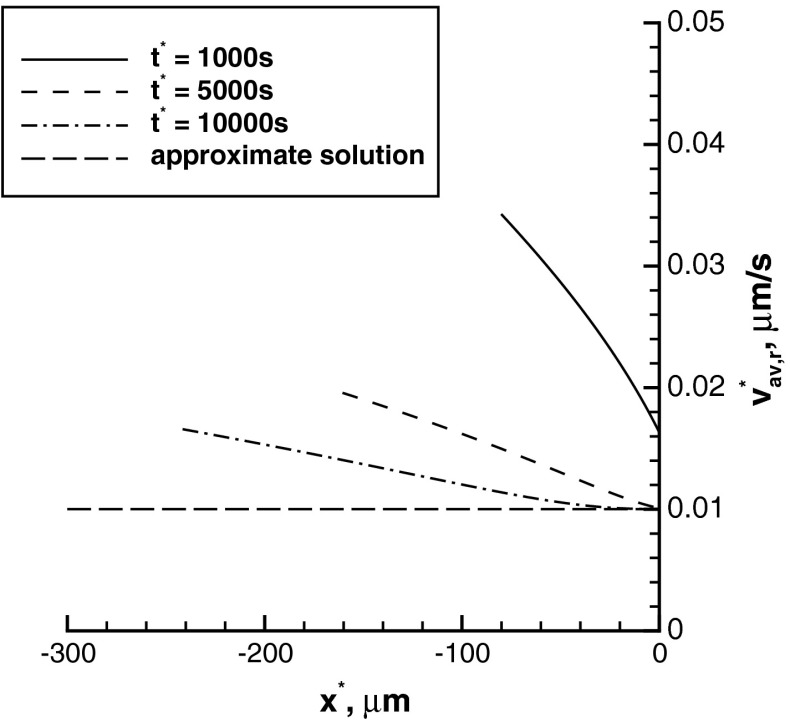
Average velocity of retrogradely moving short MTs

In this paper, we put the model of Baas and Mozgova [1] in the form of mathematical equations. We investigated transport of short mobile MTs generated by the above mechanism at the site of axonal branch formation. We then analytically solved these equations and investigated how concentration waves propagate from the site of branch formation. We also investigated the average velocities of anterograde and retrograde MT transport. The goal was to model the concept of the dynein-driven scenario proposed by Baas and Mozgova and to check whether Baas’s model stands up as a mechanistically feasible mechanism of MT transport in axons. By mechanistically feasible we mean that the model can be used to write self-consistent transport equations for short MTs and that the model predictions, in particular for the average velocity of short MTs, are reasonable. Demonstrating the feasibility of Baas’s model [1] is important in light of the alternate idea suggested by Gelfand [6].

Methods and models

Mathematical model of anterograde and retrograde transport of mobile MTs

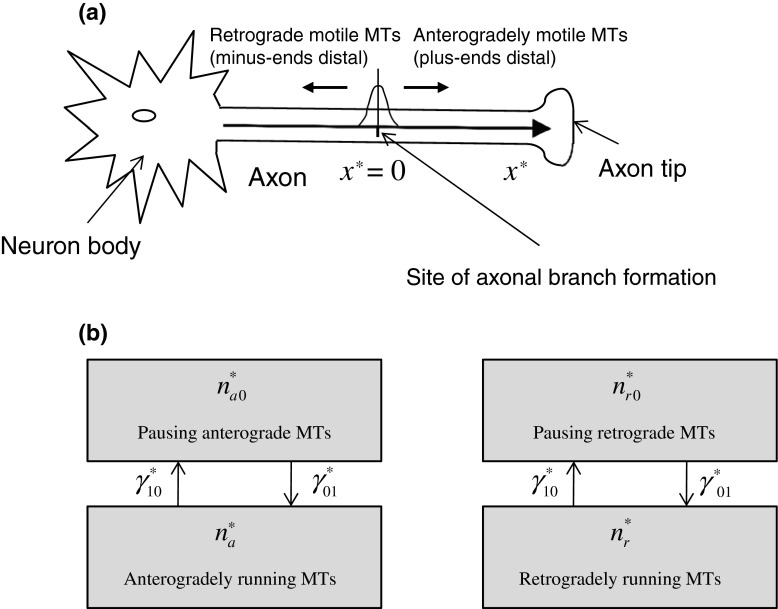
A sketch of a neuron and a coordinate system in the axon are shown in Fig. 1a. The origination point of the coordinate system is located at the site of axonal branch formation. We assumed that at x^∗ = 0 plus-end-distal and minus-end-distal mobile MTs are being produced. In developing transport equations for MTs, we relied on Jung and Brown’s stop-and-go model and their equations describing transport of neurofilaments (Eq. (7) in Jung and Brown [15], see also Li et al. [16]). Concentrations of mobile MTs in a particular kinetic state were characterized by the linear number density of MTs, which is the number of mobile MTs residing in that particular kinetic state per unit axon length (μm^− 1). The governing equations for the plus-end-distal mobile MTs that move anterogradely are:

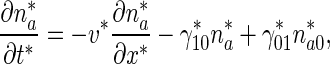1

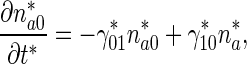2

where 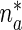is the concentration of mobile MTs in the anterograde running state (μm^− 1), 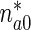is the concentration of anterograde mobile MTs in the pausing state (μm^− 1), 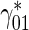is a first-order rate constant describing the probability of transition of mobile MTs from the pausing to the running state (s^− 1), 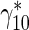is a first-order rate constant describing the probability of transition of mobile MTs from the running to the pausing state (see Fig. 1b) (s^− 1), v^∗ is the average velocity of dynein motors (μm/s), x^∗ is the linear coordinate along the axon (μm), and t^∗ is the time (s). Asterisks denote dimensional quantities.

Fig. 1.

a Sketch of the problem showing a neuron body and an axon with a branch formation site, which is located at x ^∗ = 0. MT severing at the axonal branch formation site results in a mixture of plus-end-distal and minus-end-distal mobile MTs. The plus-end-distal MTs move anterogradely and the minus-end-distal MTs move retrogradely. b Kinetic diagrams showing running and pausing MTs that are transported anterogradely (plus-end-distal MTs) and retrogradely (minus-end-distal MTs)

The governing equations for the minus-end-distal mobile MTs that move retrogradely are:

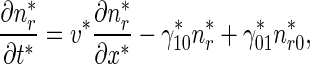3

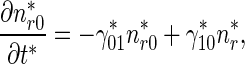4

where 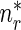is the concentration of mobile MTs in the retrograde running state (μm^− 1) and 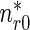is the concentration of retrograde mobile MTs in the pausing state (μm^− 1).

Note that the signs before 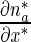and 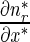in (1) and (3) are different.

Equation (1) is a first-order partial differential equation (PDE) while (2) is an ordinary differential equation (ODE). Only one boundary condition can be imposed for the system (1), (2), and this is the boundary condition on :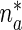

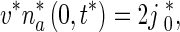5

The value of 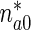at x^∗ = 0 can then be determined by solving (1), (2), and (5).

Similarly, the boundary condition for the system (3), (4) is

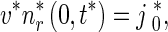6

and the value of 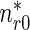at x^∗ = 0 can then be determined by solving (3), (4), and (6).

In (5) and (6), 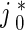is the flux of retrogradely transported mobile MTs generated at the site where an axonal branch is being formed (see Fig. 5 of Baas and Mozgova [1]). Based on Wang and Brown [2], He et al. [7], Myers and Baas [17], we assumed that the flux of anterogradely transported mobile MTs is .

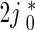The initial conditions for (1)–(4) are

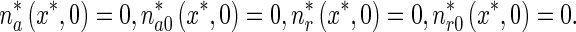7

Non-dimensionalization

In order to reduce the number of parameters involved in the model, the model was recast into a dimensionless form. Dimensionless quantities were defined as follows:

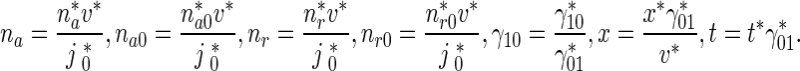8

Dimensionless anterograde equations are

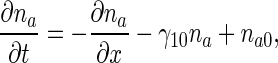9

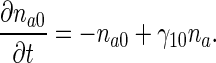10

Dimensionless retrograde equations are

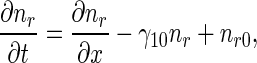11

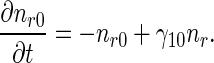12

Dimensionless boundary conditions are

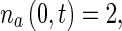13

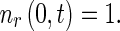14

Results

Analytical solution by the Laplace transform method

Equations (9)–(12) for mobile MTs in the anterograde and retrograde pausing and running states were solved by the Laplace transform technique. Utilizing zero initial conditions, the subsidiary equations for the Laplace transforms of functions n_a , n_a0, n_r, and n_r0 are

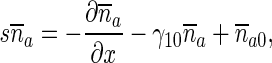15

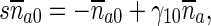16

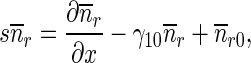17

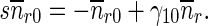18

The Laplace transforms of boundary conditions (13) and (14) are

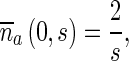19

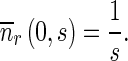20

The solutions of the subsidiary equations are

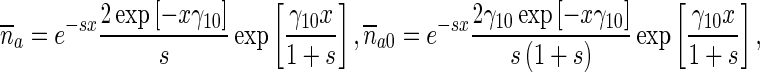21

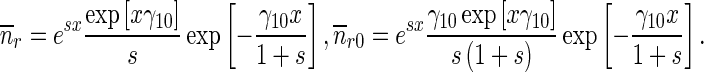22

Calculating the inverse Laplace transform of the right-hand sides of (21), the solutions for the MT concentrations in the anterograde running and pausing states were obtained as, respectively:

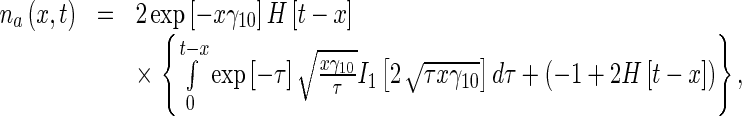23

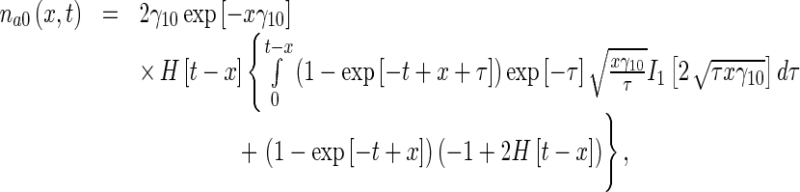24

where I₁(η) is the modified Bessel function of the first kind of order 1 and H(η) is the Heaviside step function.

The total concentration of anterograde MTs is then found as follows:

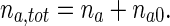25

Next, calculating the inverse Laplace transform of the right-hand sides of (22), the solutions for the MT concentrations in the retrograde running and pausing states were obtained as, respectively:

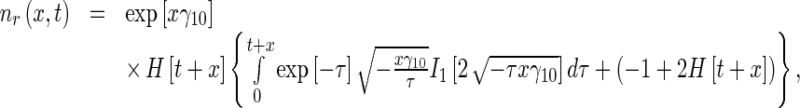26

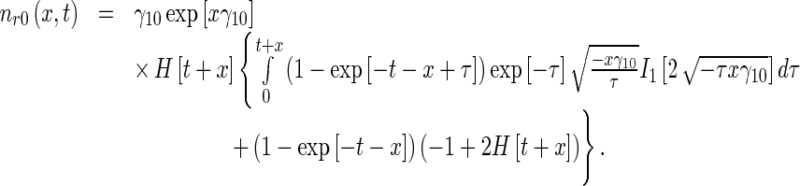27

The total concentration of retrograde MTs is then found as follows:

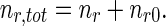28

The average velocity of anterogradely moving MTs was calculated by dividing the total flux of anterograde MTs, 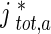, at a certain location x^∗, by the total concentration of anterograde MTs, 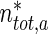, in this location:

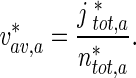29

Here, 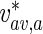depends on the location in the axon.

Similarly, the average velocity of retrogradely moving MTs was calculated as:

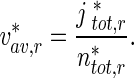30

Since

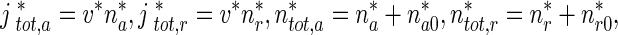31

the average velocities of anterogradely and retrogradely moving MTs were obtained as, respectively:

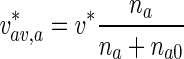32

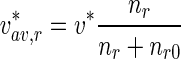33

Approximate solution based on the equilibrium assumption

Much simpler approximate solutions of (9) and (10) can be obtained if one assumes that anterograde pausing and running MTs are in equilibrium. This assumption leads to

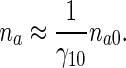34

By adding (9) and (10) and using (34), one obtains:

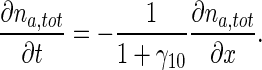35

The boundary condition for (35) is obtained from (13) and (34), as:

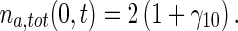36

Solving (35) and (36) by the Laplace transform technique, one obtains

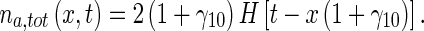37

From the approximate solution given by (37), the average velocity of anterogradely moving MTs is

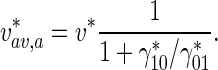38

Equation (38) shows that the larger the ratio of the transition rate of short MTs to the pausing state to their transition rate to the running state, 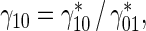, the slower MT transport occurs.

Similarly, if one assumes that retrograde pausing and running MTs are in equilibrium:

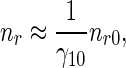39

then an approximate analytical solution of (11) and (12), subject to boundary condition (14), can be obtained as:

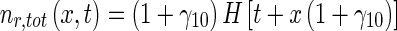40

From (40), the average velocity of retrogradely moving MTs is again

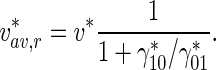41

Estimation of parameter values

Estimated values of parameters involved in the problem are summarized in Table 1.

Table 1.

Estimated values of dimensional parameters involved in the model

Parameter	Notation	Dimension	Value	Reference
Average velocity of dynein motors	v  ∗	μm/s	1	King and Schroer [18], Toba et al. [19]
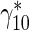
Rate constant describing the probability of transition of mobile MTs from the running to the pausing state		s − 1	0.093a	Jung and Brown [15]
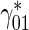
Rate constant describing the probability of transition of mobile MTs from the pausing to the running state		s − 1	0.00094b	see the explanation below Table 1

^aThis estimate is based on the value reported in Jung and Brown [15] for slow neurofilament transport in the axon of a rat superior cervical ganglion neuron

^bIf equilibrium between running and pausing kinetic states is assumed, the residence time of a mobile MT in the running state is proportional to 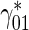while the residence time of a mobile MT in the pausing state is proportional to 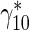. Since MTs in the running state move with a velocity v ^∗ and in the pausing state the MTs do not move, the average velocity of MT transport was estimated as 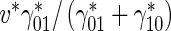(this reasoning was used to estimate the average velocity of NF transport in Kuznetsov [20, 21]). According to Tytell et al. [22], tubulin is transported within the axon with an average velocity of 0.002...0.01 μm/s. Based on measurements in a squid giant axon, Galbraith et al. [23] reported a slightly larger average tubulin velocity of 0.025 μm/s. Using the value of 0.01 μm/s for the average tubulin velocity, the value of 1 μm/s for dynein velocity, and the value of 0.093 s^− 1 for 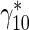, we estimated 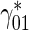to be 0.00094 s^− 1

Data reported in Table 1 were used to estimate the value of the dimensionless parameter, γ₁₀2.

Table 2.

Estimated value of the dimensionless parameter involved in the model

Dimensionless parameter	Notation	Definition	Value
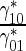
Ratio of the rate of MT transitions from the running to pausing state to the rate of the backward transitions	γ 10		98.9

Numerical results

The effort required for coding the analytical solution is significantly less than the effort that would be required for numerical solution of the system of partial differential (1)–(4) by using a finite difference method. We implemented (23), (24) and (26), (27) using the software package Mathematica 9.0 (Wolfram Research, Champaign, IL). Numerical integration was implemented via the built-in function NIntegrate. Numerical results are then obtained within a few seconds on a standard laptop PC.

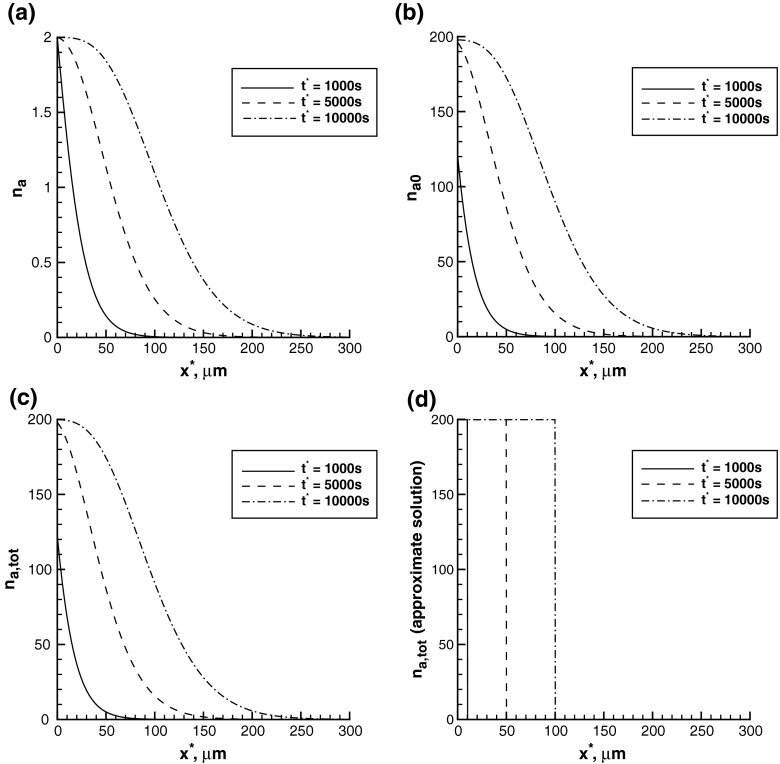
The concentration of running plus-end-distal mobile MTs, n_a, gradually advances from the site of axonal branch formation (Fig. 2a). It should be noted that the model expressed by (1) and (2) does not contain any diffusion; n_a decreases as x^∗ increases due to MT transport in the running kinetic state and MT transitions between the running and pausing kinetic states (see Fig. 1b). At x^∗ = 0, the dimensionless concentration of anterogradely running MTs is equal to 2, which is a consequence of (13). Physically, Eq. (13) posits a constant flux of short plus-end-distal MTs at the site of axonal branch formation. This flux is caused by severing of long MTs by MT-severing enzymes [24].

Fig. 2.

Concentrations of plus-end-distal mobile MTs in the a running and b pausing kinetic states. c Total concentration of plus-end-distal mobile MTs obtained from the exact solution. d Total concentration of plus-end-distal mobile MTs obtained from the approximate solution. Plus-end-distal mobile MTs move anterogradely

The concentration of pausing plus-end-distal mobile MTs, n_a0, behaves similarly to n_a, but is about 100 times larger (Fig. 2b). This is because 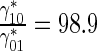. This ratio of the kinetic constants reflects the fact that in order to move with an average velocity of 0.01 μm/s, which is 100 times smaller than the dynein velocity of 1 μm/s, mobile MTs have to spend approximately 100 times more time in the pausing state than in the running state (see Fig. 1b).

The total concentration of plus-end-distal mobile MTs (the sum of n_a and n_a0) displayed in Fig. 2c is only slightly larger than the concentration of plus-end-distal pausing MTs and has a similar shape. However, the approximate solution for the total concentration of anterogradely moving MTs (given by (37)) (Fig. 2d) is quite different from the total concentration based on the exact solution (Fig. 2c). This is because the approximate solution is based on the assumption that the running and pausing plus-end-distal MTs are in equilibrium at all times, which results in a constant average velocity of their transport and the total concentration exhibiting a sharp front (Fig. 2d).

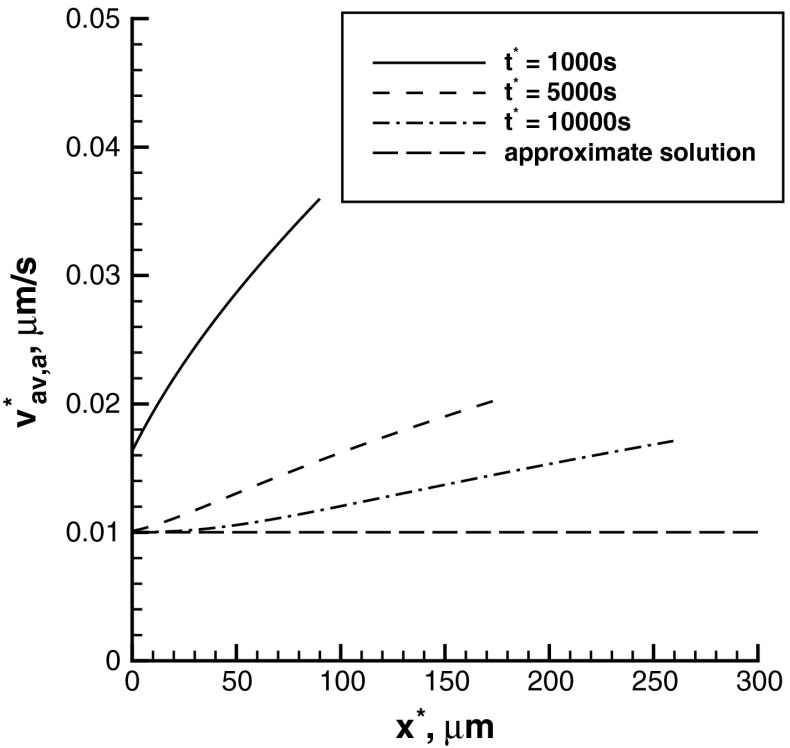
The average velocity of anterogradely moving MTs increases as the distance from the branch formation site increases (Fig. 3). This is because at the tip of the wave the portion of running MTs is larger (the ratio of running-to-pausing MTs is farther from equilibrium). Since MTs in the running kinetic state are the ones that are moving, at the wave’s tip their concentration must be larger. Apparently, it takes some time to reach equilibrium between the pausing and running states. For example, at x^∗ = 0 at times t^∗ = 5000 s and 10000 s the equilibrium is reached, but at t^∗ = 1000 s there are still less MTs in the pausing state than there are at equilibrium (Fig. 2b). For this reason, at x^∗ = 0 at time t^∗ = 1000 s the average velocity of MTs is approximately 1.6 times larger than the equilibrium value of 0.01 μm/s. Such a slow establishment of equilibrium is because of a constant supply of new mobile MTs at x^∗ = 0 due to severing of long MTs. In our model, we assumed that at the boundary there is a constant flux of newly produced mobile MTs in the running kinetic state (see (5)). The lines in Fig. 3 interrupt at the tip of the concentration wave, n_a (Fig. 2a). The approximate solution, which is based on the equilibrium assumption, predicts a constant average velocity of transport of plus-end-distal MTs (Fig. 3). This reconfirms our conjecture that the increase of the average velocity is caused by the deviation from equilibrium.

Fig. 3.

Average velocity of anterogradely moving short MTs

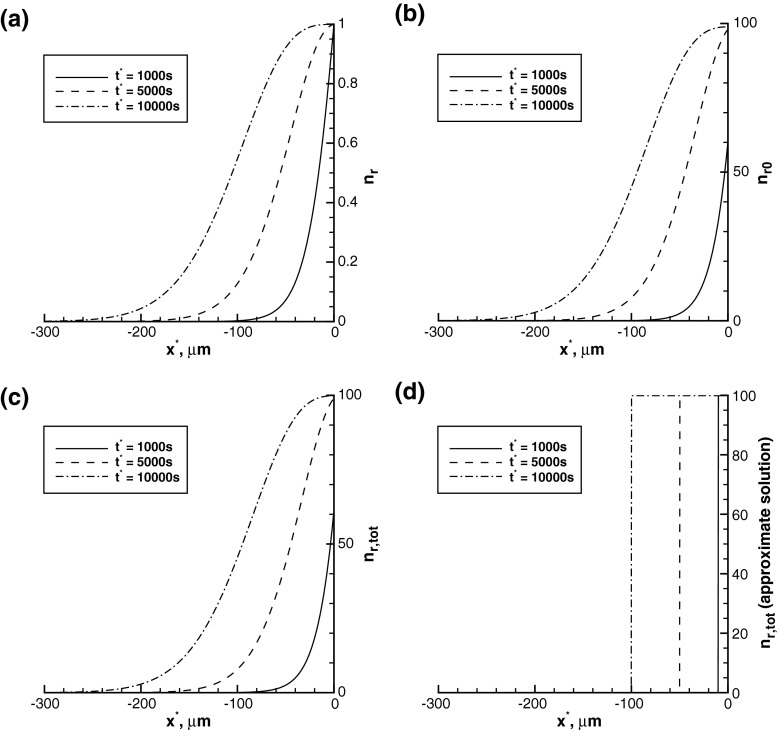
The concentrations of minus-end-distal mobile MTs in the running and pausing kinetic states as well as the total concentration of minus-end-distal mobile MTs (Fig. 4a, b, c) are similar to the concentrations in their plus-end-distal counterpart states (Fig. 2a, b, c), but the concentrations displayed in Fig. 4a, b, c are two times smaller. This is because we assumed that out of all newly generated mobile MTs at x^∗ = 0, two-thirds are plus-end-distal and only one-third is minus-end-distal (compare (13) and (14)). This is in agreement with reports of Wang and Brown [2], He et al. [7], Myers and Baas [17] that two-thirds of the short mobile MTs transit in the anterograde direction and only one-third transit in the retrograde direction. The total concentration of minus-end-distal MTs predicted by the approximate solution (40) is also two times smaller than the corresponding concentration of plus-end-distal MTs (compare Figs. 4d and 2d).

Fig. 4.

Concentrations of minus-end-distal mobile MTs in the a running and b pausing kinetic states. c Total concentration of minus-end-distal mobile MTs obtained from the exact solution. d Total concentration of minus-end-distal mobile MTs obtained from the approximate solution. Minus-end-distal mobile MTs move retrogradely

The absolute values of velocities of retrogradely moving MTs (Fig. 5) are similar to velocities of anterogradely moving MTs (Fig. 3). This is because, in accordance with [1], we assumed that all anterograde and retrograde motions of MTs are propelled by the same dynein motors.

Discussion and conclusions

We developed a continuum model for investigating transport of short mobile MTs. The model is based on a recent hypothesis put forward in Baas and Mozgova [1]. According to this hypothesis, plus-end-distal mobile MTs are always transported anterogradely while minus-end-distal mobile MTs are always transported retrogradely, and dynein motors propel both anterograde and retrograde MT transport by the sliding filament mechanism. Relying on the stop-and-go model of Jung and Brown [15], Li et al. [16], we developed governing equations for simulating MT transport from a site where short mobile MTs are produced by MT severing events, such as the site of axonal branch formation.

Although there is no MT diffusion in the model, the concentrations of anterogradely and retrogradely moving mobile MTs decrease with the increase of the distance from the branch formation site; the concentrations advance as time increases. This behavior is due to MT transitions between the running and pausing kinetic states and MT transport in the running states.

Our model predicts that the average velocity of anterogradely and retrogradely moving MTs increases as the distance from the branch formation site increases. This is because only MTs in the running kinetic state are moving, and since the tip of the wave should contain the fastest MTs, the concentration of running MTs at the wave’s tip must be largest. The equilibrium between running and pausing MTs is established first at the branch formation site, but it still takes more than a 1000 s to establish the equilibrium at this location. This is because new mobile MTs are constantly produced at the branch formation site (by severing of long MTs), and in the model we attributed these newly produced MTs to the running kinetic state.

The obtained results suggest that Baas’s model [1] is mechanistically feasible. More insight can be gained in the future by directly comparing the predictions of Baas’s [1] and Gelfand’s [6] models, but in order to do that, more details need to be provided for Gelfand’s model, so that it could also be written in terms of transport equations.

In this research, we assumed that all mobile MTs are transported as part of slow comportment “a”. However, a portion of tubulin, at least in some neurons, moves in slow component “b” (that is 5-10 times faster) [2, 25–27]. Future models should account for both populations of mobile MTs, those moving in slow component “a” and those moving in slow component “b”.