Testing optimal foraging theory in a penguin–krill system

Abstract

Food is heterogeneously distributed in nature, and understanding how animals search for and exploit food patches is a fundamental challenge in ecology. The classic marginal value theorem (MVT) formulates optimal patch residence time in response to patch quality. The MVT was generally proved in controlled animal experiments; however, owing to the technical difficulties in recording foraging behaviour in the wild, it has been inadequately examined in natural predator–prey systems, especially those in the three-dimensional marine environment. Using animal-borne accelerometers and video cameras, we collected a rare dataset in which the behaviour of a marine predator (penguin) was recorded simultaneously with the capture timings of mobile, patchily distributed prey (krill). We provide qualitative support for the MVT by showing that (i) krill capture rate diminished with time in each dive, as assumed in the MVT, and (ii) dive duration (or patch residence time, controlled for dive depth) increased with short-term, dive-scale krill capture rate, but decreased with long-term, bout-scale krill capture rate, as predicted from the MVT. Our results demonstrate that a single environmental factor (i.e. patch quality) can have opposite effects on animal behaviour depending on the time scale, emphasizing the importance of multi-scale approaches in understanding complex foraging strategies.

1. Introduction

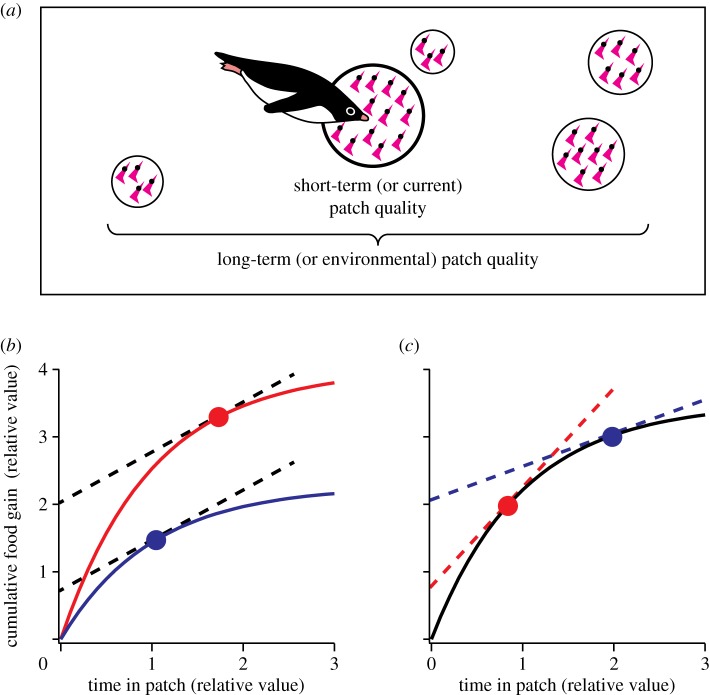
In nature, food is often heterogeneously distributed because of physical (e.g. landscape structure) and biological (e.g. inter- and intraspecific interactions) reasons [1]. Therefore, understanding how animals effectively search for and exploit food patches has long been a fundamental objective in ecology [2]. A series of optimal foraging theories have been developed in line with this objective [3]. By assuming that animal activities are optimized to maximize the rate of net energy gain, optimal foraging theories provide testable hypotheses as well as bases for interpreting complex animal behaviour [3,4]. The marginal value theorem (MVT) [5] is central to these theories and has been very influential. It assumes that, as animals forage in a patch, the availability of food in the patch diminishes, and the expected, instantaneous rate of food gain also diminishes. Under this ‘diminishing return’ assumption, the MVT states that individuals should move from one patch to another when the instantaneous rate of food gain drops to the long-term rate of food gain across many patches in the environment (figure 1a). This statement leads to a remarkable prediction: animal behaviour is affected by both short- and long-term food availabilities (‘patch quality’) in opposite directions. Short-term patch quality positively affects patch residence time (figure 1b), whereas long-term patch quality negatively affects patch residence time (figure 1c).

Figure 1.

Illustration and schematic diagram showing how optimal patch residence time will change in response to patch quality according to the MVT. (a) Consider an animal foraging in an environment where prey patches are heterogeneously distributed. The theorem states that animals should leave a patch when the instantaneous food gain rate in the patch (the gradient of gain function curves in (b,c)) drops to the long-term food gain rate across many patches in the environment (the slope of dotted lines in (b,c)). Two main predictions arise from the theorem. (b) Consider two patches in which short-term quality varies (high, red curve; low, blue curve) but long-term quality is constant (dashed line). In this case, animals are predicted to stay longer in the patch with higher short-term quality. (c) Consider two patches in which short-term quality is constant (solid curve) but long-term quality varies (high, red dashed line; low, blue dashed line). In this case, animals are predicted to stay more briefly in the patch with higher long-term quality. In dynamic patch systems such as krill swarms, both short- and long-term patch quality are rarely constant, and what we would expect to observe in the penguin–krill system is a combination of (b) and (c).

A number of studies empirically tested the effect of patch quality on animal behaviour, mostly by providing animals (in captivity or in the field) with artificial food patches of variable quality or location [3,6]. These studies provided good support for the predictions of the MVT, although some studies reported deviations from the predictions. The next logical step is to examine if, and to what extent, the behaviour of wild animals feeding on natural prey is consistent with the MVT. Unfortunately, the progress of this step has been slow owing to technical difficulties in monitoring foraging behaviour under natural conditions. The foraging behaviour of some terrestrial animals (e.g. lizards [7], land birds [8,9] and primates [10]) can be observed visually, and these species have provided some support for the MVT. However, this is not the case for marine animals, whose three-dimensional movements are difficult to observe directly. Although their swimming and diving patterns can now be recorded by a range of electronic tags [11,12], monitoring their foraging behaviour, as well as the patch quality they encounter, remains a major challenge. Previous attempts at testing the MVT with marine predators [13,14] did not collect direct information about what and when they ate, and instead used indirect information about their relative foraging success based on dive duration or changes in buoyancy. Furthermore, those studies only assessed the effect of long-term patch quality (figure 1c), because the low temporal resolution of their estimates of foraging success precluded examining the effect of short-term patch quality (figure 1b). As a result, direct evidence is lacking for the hypothesis that marine predators flexibly change their behaviour in response to patch quality at multiple time scales.

Recently, we developed a method to record individual prey capture events in Adélie penguins Pygoscelis adeliae [15], a top marine predator in the Southern Ocean. In our study area, this species feeds on krill, including Euphausia superba (Antarctic krill, a major component of the Southern Ocean food web) and Euphausia crystallorophias, as well as some fishes. Our method uses acceleration of the penguin's head relative to the body (measured by two accelerometers attached to the head and the back) as a signal of prey capture events. When calibrated using simultaneously recorded movies from animal-borne video cameras, the method was found to have high detection rates (83–88%) and low false discovery rates (10–15%). This technical innovation provides a unique opportunity to examine how marine predators (penguins) respond to mobile, patchily distributed prey (krill). We are now able to plot the gain function (i.e. the cumulative number of krill captures over time) directly to examine whether the ‘diminishing return’ assumption is met in a natural predator–prey system. The shape of the gain function is expected to represent the nature of the system (e.g. the hunting skills of the predator, and the mobility, density and ephemerality of the prey patch), and is an important concept in foraging ecology [3]. If the assumption is met, we will then be able to measure the patch quality experienced by the penguins at multiple time scales, and examine whether penguins’ diving behaviour is affected by those patch qualities as predicted from the MVT.

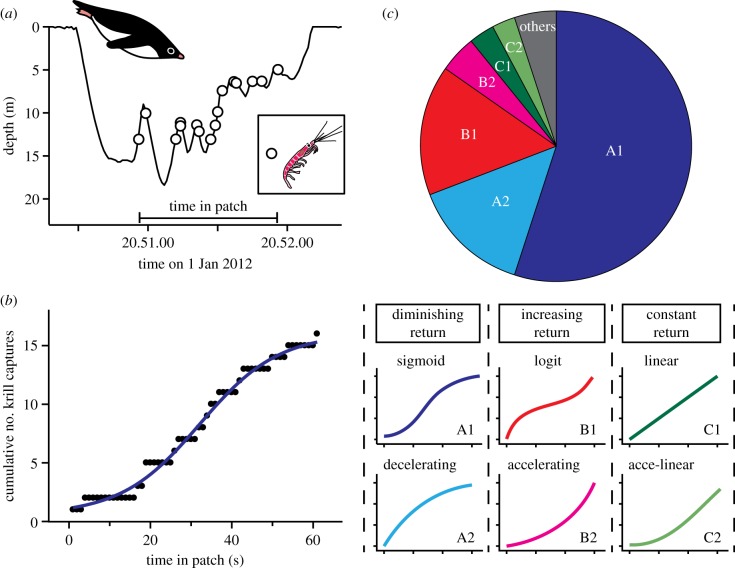
The penguin–krill system is an excellent predator–prey model in marine ecosystems for several reasons. First, the spatial distribution of Antarctic krill has ecologically attractive characteristics. It is not only highly heterogeneous, but also hierarchically structured, where high-density patches at small scales are nested within low-density patches at larger scales [16,17]. Second, penguins dive exclusively to forage, and their foraging effort can be quantified accurately by their diving activities. Third, the foraging behaviour of penguins can be viewed from two well-defined time scales: (i) a single dive and (ii) a succession of dives, called a dive bout (figure 2). This hierarchical structure of diving behaviour allows us to define short-term (i.e. dive scale) and long-term (i.e. bout scale) time windows, objectively.

Figure 2.

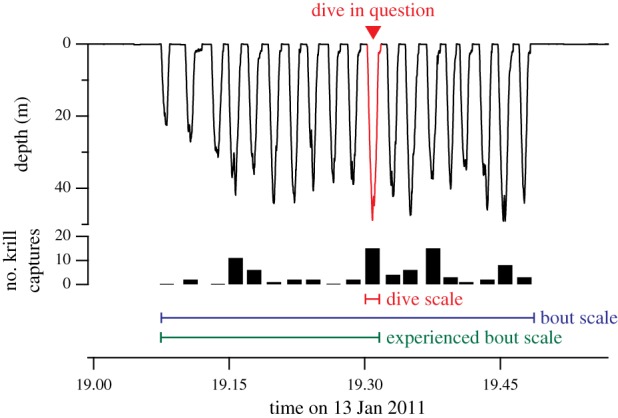
An example of successive diving activities, called a ‘dive bout’, of an Adélie penguin with the number of krill capture events in each dive. For each dive, dive-scale (red horizontal bar) and bout-scale (blue horizontal bar) krill capture rates are calculated and used for the analysis. Note that a dive is a part of a bout, and dive-scale and bout-scale krill capture rates share some information, posing the risk of collinearity in the modelling analysis. Bout-scale krill capture rates include information that will be known by the penguin in the future. Therefore, the experienced bout-scale (green horizontal bar) krill capture rate, which is based only on the experienced portion of the bout (i.e. excluding dives subsequent to the dive in question), is also examined.

In this study, we measured the diving behaviour as well as the timings of krill captures from free-ranging Adélie penguins, and tested the MVT by regarding an individual dive as the exploration of a krill patch. Our working hypotheses were that (i) the gain functions of the penguins within dives show diminishing returns, as assumed in the MVT, and that (ii) dive durations increase with short-term, dive-scale patch quality, but decrease with long-term, bout-scale patch quality, as predicted by the MVT.

2. Material and methods

(a). Fieldwork

We conducted fieldwork at the Hukuro Cove colony (69°13′ S, 39°39′ E) in Lützow-Holm Bay, Antarctica, over two consecutive seasons, from late December 2010 to early February 2011 and from late December 2011 to early February 2012. All of the experimental procedures were approved by The Ministry of the Environment, Japan. Data collected in the first season (for 14 birds) were published previously [15], in which the method for detecting prey capture events from acceleration records was developed. By adding the new data from the second season, data for 22 individual birds were collected.

All study birds, rearing one or two chicks, were captured using a dip net when leaving for a foraging trip. They were equipped with two accelerometers (ORI400-D3GT; 12 mm diameter, 45 mm length, 9 g weight; Little Leonardo Co.), one on the back and the other on the head, using tape. The accelerometers recorded triaxial acceleration at 1/20 s intervals, as well as depth and temperature at 1 s intervals for approximately 50 h. In addition to the two accelerometers, all birds were equipped with either a video camera (33 or 41 g depending on the model, for 13 birds) or global positioning system (GPS) logger (88 g, for nine birds) on the back; the data from these devices were not used in this study. The total weight of the instruments attached to each bird (two accelerometers plus a video camera or a GPS logger) was 51–106 g, which accounted for 1.2–2.6% of the average weight of the instrumented birds (4.1 kg). In a previous study [18], the attachment of an 80 g tag did not alter the foraging trip duration, stomach content mass or breeding success of Adélie penguins in our study area, and hence the behaviour recorded in this study were assumed to be normal. All handling procedures, including the measurements of body morphology and the attachment of the instruments, were completed within 15 min. The instruments were recovered by recapturing the birds when they returned from the trip, typically 1–2 days after release.

(b). Dive analysis

From the whole diving records obtained, we extracted diving bouts composed of only krill-feeding dives, which are readily distinguished from fish-feeding dives by the characteristic depth profile with repeated up-and-down movements [15]. Diving bouts were defined as successive diving activities interrupted by surfacing periods of less than 250 s (figure 2). Among the krill-feeding diving bouts extracted, only bouts composed of greater than or equal to 10 dives were used in further analyses. This is because during shorter bouts the short-term (i.e. dive-scale) and long-term (i.e. bout-scale) patch quality share more information, so that statistical collinearity could be an issue (see below for the test of collinearity). From the extracted datasets, the timing of krill captures were detected by analysing acceleration records of the head and body of the birds [15].

(c). Gain function

The gain function was plotted for each dive extracted, with the x-axis as the time (s) from the first krill capture to the last krill capture in the dive, and the y-axis as the cumulative number of krill caught during the dive (figure 3a,b). When only a small number of krill were captured in a dive, the resolution for the shape of the gain function was too low to be fitted by simple mathematical models. Therefore, only dives with at least 15 krill capture events were used in this particular analysis.

Figure 3.

Gain function analyses. (a) Example of a time-series depth record with the timings of krill capture events (open circles) during a dive from an Adélie penguin. Time in patch (horizontal bar) represents the time from the first krill capture to the last krill capture. (b) The cumulative numbers of krill captures plotted against time in patch, called gain function, of the dive in (a). A sigmoid curve (blue) was the most parsimonious model to express its shape in this case. (c) The proportions of gain functions (n = 263 dives from 22 birds), each of which is categorized by the shape at the end of the fitted model as ‘diminishing return’ (blue and light blue), ‘increasing return’ (red and pink), ‘constant return’ (green and light green) or ‘others’ (grey).

A series of simple models with up to four parameters were fitted to the plot using the least-squares method, and the most parsimonious model was determined based on the Akaike information criterion (AIC). The fitted models included polynomial (y = a + b⋅x + c⋅x² + d⋅x³), sigmoidal (y = a + b/(1 + exp(−(x − d)/c)), exponential growth (y = a + b⋅exp(c⋅x)) and exponential rise to max (y = a + b⋅(1 − exp(−c⋅x))). For polynomial models, linear (y = a + b⋅x), quadratic (y = a + b⋅x + c⋅x²) and cubic models (y = a + b⋅x + c⋅x² + d⋅x³) were fitted separately. For sigmoidal, exponential growth and exponential rise to max models, the equations with and without the intercept (the parameter a) were fitted separately. These models can express a range of shapes that may occur in gain functions, including decelerating curves (diminishing return), accelerating curves (increasing return), linear (constant return), sigmoid (increasing return followed by diminishing return) and logit (diminishing return followed by increasing return) (figure 3c). Occasionally, even the best model selected by AIC was a poor fit (as evaluated visually), and such dives were categorized as ‘other’.

(d). Patch quality and modelling

The predictions from the MVT were tested using linear mixed models with dive duration (s) as a response variable and bird ID as a random factor. Dive duration, rather than bottom duration (i.e. time spent at the bottom phase of dives), was used because the penguins’ dive profiles varied from dive to dive, and defining the bottom phase for each dive was necessarily subjective. To control for the effect of descent and ascent duration (which are not related to foraging), dive depth (m) was included as a predictor variable. The other predictor variables were dive-scale patch quality and bout-scale patch quality. Dive-scale patch quality was defined as the number of krill captured during the dive in question (figure 2), standardized for a 100 s dive duration by dividing it by the duration of the dive (s) and multiplying by 100. Bout-scale patch quality was defined as the number of krill captured in the bout that included the dive in question (figure 2). It was standardized for a 1000 s bout duration by dividing it by the bout duration (s) and multiplying by 1000. All dives in the extracted datasets were used in the modelling analysis, regardless of whether the dive met the criteria for gain function analysis (i.e. greater than or equal to 15 krill capture events). An underlying assumption of using bout-scale patch quality as long-term patch quality is that penguins know the total krill capture rate in the bout before they actually finish the bout (figure 2). This assumption may not be reasonable, although foraging animals may asymptotically predict the total prey capture rate in the future from past experiences [19]. Therefore, we also defined another long-term patch quality metric that was based only on the penguins’ past experiences. Experienced bout-scale patch quality (figure 2) was defined as the number of krill caught in the bout so far (i.e. excluding dives subsequent to the dive in question), standardized for a 1000 s duration by dividing it by the duration (s) and multiplying by 1000. According to this definition, each past foraging dive in the bout has the same influence on the calculation of prey capture rates, regardless of how recently the dive occurred. This is the simplest form for how animals may process past experiences to predict the total, long-term prey capture rate in the future [19]. We repeated the modelling analysis (described below) after replacing bout-scale patch quality with experienced bout-scale patch quality.

The null model was (dive duration = dive depth), and the full model was (dive duration = dive depth + dive-scale patch quality + bout-scale patch quality). Modelling with the raw data resulted in a violation of homogeneity of variance (which is assumed in linear mixed models), whereas modelling with the log-transformed response variable resulted in a violation of normality of error. Therefore, we transformed all predictors using log₁₀(X + 1), and, in this case, both assumptions were reasonably met. Moreover, to compare the relative strength of the effect among predictors, all log-transformed predictors were standardized to have a mean of zero and standard deviation of one.

A dive is a part of a bout (figure 2), and dive-scale and bout-scale patch quality share some information, posing a risk of collinearity in the full model. To address this possibility, we examined the tolerance value for each predictor ((1 − r²), where r² is from the least-squares multiple regression of the predictor against the remaining predictors), which can be used to detect collinearity [20]. The most parsimonious model was chosen among the null, full and intermediate models based on AIC and Akaike weight. All statistical analyses were performed with the software R.

3. Results

Sixty-one krill-feeding diving bouts, comprising 1385 individual dives (mean ± s.d., 22.7 ± 13.4 dives per bout) and 10 284 krill capture events (mean ± s.d., 7.4 ± 9.8 events per dive), were extracted from the dataset for the 22 birds. Of the 1385 dives, 263 dives included at least 15 krill capture events, thereby meeting the criteria for gain function analysis (figure 3). Sixty-nine per cent of the dives showed diminishing return, either at the end of (sigmoid curve, 55%) or throughout the period (decelerating curve, 14%); 20% of the dives showed increasing return, either at the end of (logit curve, 15.5%) or throughout the period (accelerating curve, 4.5%); and 6% of the dives showed constant return, either at the end of (accelerating-linear curve, 3%) or throughout the period (linear, 3%). Five per cent of the dives were categorized as ‘other’. The mean (±s.d.) instantaneous krill capture rate (individuals per second) at the end of the foraging period, calculated as the gradient at the end of the fitted model, was 0.22 ± 0.24 (n = 182 dives), 1.04 ± 0.95 (n = 53 dives) and 0.79 ± 0.56 (n = 15 dives) for dives showing diminishing return, increasing return and constant return, respectively.

Durations of the 1385 krill-feeding dives were best explained by the full model (Akaike weight, 0.9997), with dive depth, dive-scale patch quality and bout-scale patch quality included as predictors (table 1). In the full model, the tolerance values for dive depth, dive-scale patch quality and bout-scale patch quality were 0.99, 0.49 and 0.49, respectively. These values were well above 0.1, a ‘rule of thumb’ below which collinearity can be a serious issue [20]. The estimated coefficients in the full model, representing the direction and relative strength of the effect, were +20.8, +2.9 and −8.4 for dive depth, dive-scale patch quality and bout-scale patch quality, respectively. Partial regression plots showed considerable variations around the regression lines both for dive-scale (Pearson's r, 0.13) and bout-scale patch quality (Pearson's r, −0.21) (figure 4). Replacing bout-scale patch quality by experienced bout-scale patch quality (figure 2) did not alter the overall results; however, the fit of the full model became poorer (i.e. AIC increased; table 1), and the effect of patch quality on dive duration became weaker (coefficient; +21.5, +1.9 and −4.3 for dive depth, dive-scale patch quality and experienced dive-scale patch quality, respectively).

Table 1.

Fitting of linear mixed models. PQ, patch quality; AIC, Akaike information criterion; wAIC, Akaike weight. Bird ID was included as a random factor in all models.

model	AIC	wAIC
dive duration = dive depth + dive-scale PQ + bout-scale PQ	11 968	0.9997
dive duration = dive depth + bout-scale PQ	11 984	0.0003
dive duration = dive depth + dive-scale PQ	12 062	<0.0001
dive duration = dive depth	12 063	<0.0001
dive duration = dive depth + dive-scale PQ + experienced bout-scale PQ	12 039	0.8176
dive duration = dive depth + experienced bout-scale PQ	12 042	0.1824
dive duration = dive depth + dive-scale PQ	12 062	<0.0001
dive duration = dive depth	12 063	<0.0001

Figure 4.

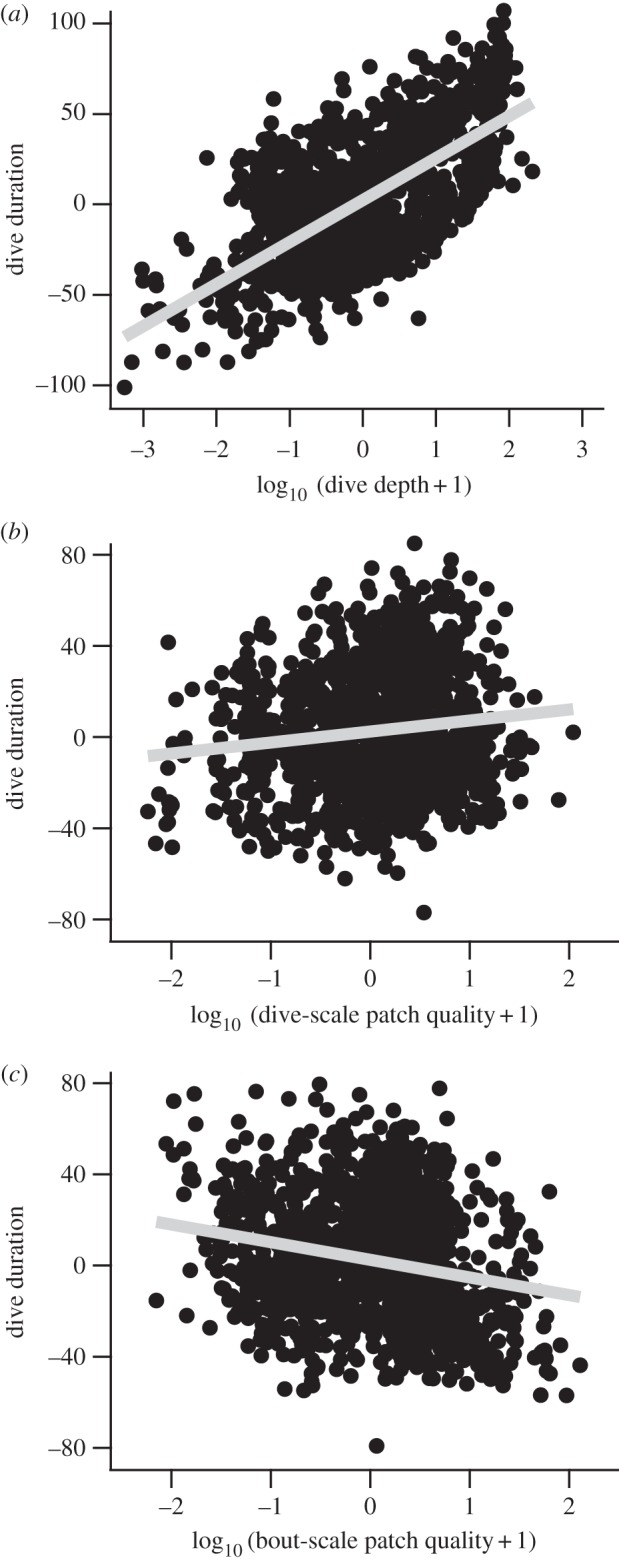
Partial regression plots (i.e. the relationship between the response variable and a predictor, with the other predictors held constant [20]) from a linear mixed model (dive duration = dive depth + dive-scale patch quality + bout-scale patch quality) with bird ID as a random factor. For example, the x-axis in (a) is the residuals from a linear mixed model of dive depth against the other predators. The y-axis in (a) is the residuals from a linear mixed model of dive duration against all predictors excluding dive depth. Grey lines represent least-squares regression lines. All predictors were log-transformed and then standardized to have a mean of zero and standard deviation of 1.

4. Discussion

A number of previous studies have tested the predictions of the MVT [3,6]. However, the present study is rare in that (i) we studied a marine predator–prey system under natural conditions; (ii) we directly measured the gain function and determined its shape using a model-fitting technique; and (iii) we detected opposing effects of short- and long-term patch quality on foraging behaviour from a single dataset.

The majority (69%) of gain functions examined in this study showed diminishing return near the end of the foraging periods. This result demonstrates that the assumption of the MVT is actually met, at least when a large number of krill were captured in a dive. Diminishing returns are presumably a result of krill escaping, as well as krill being captured by the penguins. When encountering predators, Antarctic krill exhibit burst, backward swimming modes with a maximum speed of about 0.6 m s⁻¹ [21], which is much slower than the routine and burst swim speed of Adélie penguins (about 2 and 3 m s⁻¹, respectively [22]). Therefore, a flight response of individually detected krill may have little chance of success (see electronic supplementary material, movie S2 in [15]). Nevertheless, the krill that are not directly targeted by penguins may be able to swim 36 m during a 60 s foraging period, which could allow the krill to escape from the penguins.

However, most (80%) of the gain functions showing diminishing returns were not simple decelerating curves, as hypothesized by the MVT, but sigmoid curves, in which an increasing return is followed by a diminishing return. Penguins must search for a krill aggregation that is escaping from the penguins at the beginning of the foraging period, presumably resulting in a low krill capture rate. Low krill capture rates at the beginning and end of the foraging period may also be due to hierarchical, spatial structures of krill swarms, with high internal density often surrounded by aggregations of lower density [17]. The penguins may start foraging at the edge of the swarm, where gain rate is low, and proceed to the core of the swarm, where gain rate is high, and then come to the edge of the swarm again before returning to the surface. These two explanations (i.e. the escape behaviour of individual krill and the spatial structure of krill swarms) are not mutually exclusive, because the escape behaviour of individual krill is a major driving force shaping the three-dimensional structure of krill swarms [23]. A sigmoidal gain function was previously hypothesized for mobile predator–prey systems, in which prey can avoid predators at first, but later a cluster of prey is found by the predator [3]. We provide the empirical evidence for the existence and dominance of the sigmoidal gain function.

As predicted from the MVT, dive-scale and bout-scale patch quality had opposite effects (positive effect for dive-scale and negative effect for bout-scale) on dive duration. Together with the confirmation of the diminishing return assumption, our study provides qualitative support for the MVT from a natural predator–prey system. The variations in dive duration explained by patch quality were relatively small (figure 4b,c); however, this is not surprising, given that we focused on simple ecological factors without considering any physiological factors. In breath-hold divers, dive duration is basically regulated by physiology, notably via oxygen store management [24]. Therefore, parameters such as inhaled air volume, blood flow and workload of locomotory muscles [24–26] might explain some of the observed residuals (figure 4b,c). According to AIC (table 1) and coefficients in the full model, bout-scale patch quality had a stronger effect than dive-scale patch quality on dive duration. This result suggests that penguins place more importance on the information integrated over multiple dives, compared with the information from a single dive.

A major criticism of the MVT is that predators are implicitly assumed to know the total prey capture rates in the environment (i.e. bout-scale patch quality in our case; figure 2) before they finish exploring it [19,27]. However, replacing bout-scale patch quality by the experienced bout-scale patch quality metric (which does not require the assumption) provided essentially the same result, indicating that our main finding―long- and short-term patch quality have a negative and positive effect, respectively, on patch residence time―is robust. Interestingly, the fit of the full model became poorer and the effect of patch quality on dive duration became weaker when the predictor was replaced. Our results suggest that penguins may have some knowledge of the overall foraging success of an ongoing bout, and that how penguins process past experience to anticipate the future is more sophisticated than assumed in our definition of the experienced bout-scale patch quality (i.e. placing equal weight on all previous dives). Although a similar result was reported for baboons feeding on plants [10], our result is more surprising, because Adélie penguins feed within a mobile, complex patch system, where dive-to-dive variations in foraging success are large [15]. Generally, animal behaviour can be considered a compromise among various requirements across various time scales [28,29]. We demonstrated that a single environmental factor (i.e. patch quality) can have contrasting effects on animal behaviour depending on the time scale, emphasizing the importance of multi-scale approaches for understanding the complexity of foraging strategies.

An increasing number of studies use the diving behaviour of marine predators as a proxy of prey availability [13,30]. This approach has implications for the monitoring and management of marine resources, because their below-sea density and distribution cannot be examined by satellite-based remote-sensing technologies. In addition, the approach using diving animals can examine polar oceans, where shipboard research as well as satellite remote sensing is limited due to extensive sea ice [31]. A longer dive duration (or bottom-time duration) is often considered indicative of a more successful dive made in a richer patch [13], although some studies have argued the opposite [14]. We showed here that relating dive duration to patch quality is more complex than previously thought. Longer dive durations can represent high short-term patch quality, low long-term patch quality or both. Disentangling the opposing effects would be difficult without information of actual foraging success. Fortunately, recording prey capture signals by accelerometery over months is now becoming possible due to the on-board data-processing technique [32]. We suggest that this technique, together with the relationship between dive duration and patch quality shown in this study, will be a complementary tool to oceanographic sampling for monitoring the dynamics of marine resources.

In conclusion, we showed that: (i) the gain function within a dive is mostly sigmoidal, which is inconsistent with the simple deceleration curve hypothesized in the MVT but still meeting the assumption of diminishing return; (ii) dive duration of penguins increased with short-term, dive-scale krill capture rates, but decreased with long-term, bout-scale krill capture rates, a result predicted under the MVT; and (iii) dive duration can be explained by the classic, simple MVT better than an alternative model based on past experiences. The penguin–krill system continues to provide an attractive model for ecologists to investigate how marine predators behave flexibly in response to dynamic prey patches in their three-dimensional search space.

Data accessibility

Data used for the linear mixed model analysis are available in the electronic supplementary file.

Funding statement

This work was funded by JARE and Grants-in-Aids for Scientific Research from the Japan Society for the Promotion of Science (21681002 and 25850138 to Y.Y.W. and 20310016 to A.T.). The production of this paper was supported by an NIPR publication subsidy.