Generalized Polynomial Chaos Based Uncertainty Quantification for Planning MRgLITT Procedures

Abstract

Purpose

A generalized polynomial chaos (gPC) method is used to incorporate constitutive parameter uncertainties within the Pennes representation of bioheat transfer phenomena. The stochastic temperature predictions of the mathematical model are critically evaluated against MR thermometry data for planning MR-guided Laser Induced Thermal Therapies (MRgLITT).

Methods

Pennes bioheat transfer model coupled with a diffusion theory approximation of laser tissue interaction was implemented as the underlying deterministic kernel. A probabilistic sensitivity study was used to identify parameters that provide the most variance in temperature output. Confidence intervals of the temperature predictions are compared to MR temperature imaging (MRTI) obtained during phantom and in vivo canine (n=4) MRgLITT experiments. The gPC predictions were quantitatively compared to MRTI data using probabilistic linear and temporal profiles as well as 2-D 60 °C isotherms.

Results

Within the range of physically meaningful constitutive values relevant to the ablative temperature regime of MRgLITT, the sensitivity study indicated that the optical parameters, particularly the anisotropy factor, created the most variance in the stochastic model's output temperature prediction. Further, within the statistical sense considered, a nonlinear model of the temperature and damage dependent perfusion, absorption, and scattering is captured within the confidence intervals of the linear gPC method. Multivariate stochastic model predictions using parameters with the dominant sensitivities show good agreement with experimental MRTI data.

Conclusions

Given parameter uncertainties and mathematical modeling approximations of the Pennes bioheat model, the statistical framework demonstrates conservative estimates of the therapeutic heating and has potential for use as a computational prediction tool for thermal therapy planning.

Introduction

Magnetic resonance-guided laser induced thermal therapy (MRgLITT) is a minimally invasive ablative procedure that can rapidly (<180s) deliver heat to treat focal cancerous lesions or radiation necrosis in the brain [1,2]. The optical fiber is placed through a burr hole into the target disease via stereotaxy, analogous to an image-guided stereotactic biopsy [1,3]. MRgLITT for patient-specific treatment of focal cancerous lesions in brain presents an attractive treatment option with significantly less impact on the patient compared to conventional surgical procedures. For many anatomical sites of interest, MRI guidance provides a means for planning, targeting, monitoring and verifying the delivery of these therapies in a single, closed-loop session. To this end, several FDA-cleared MRgLITT systems (Monteris www.monteris.com, Visualase www.visualaseinc.com) have become commercially available. These systems facilitate MRgLITT procedures on any modern clinical MRI scanner and are currently in post-market studies at multiple institutions [1,3–9]. The goal of the therapy is to treat a targeted tissue volume, <3cm in diameter, in such a highly controlled manner so as not to incur damage to nearby normal tissue structures which would result in complications.

Proton resonance frequency based thermometry or magnetic resonance temperature imaging (MRTI) provides a means to real-time monitor the heat distribution during the therapy [10,11]. MRTI's temperature information improves the safety and efficacy of MRgLITT by allowing the physician to avoid overheating, tissue vaporization, and charring near the laser and prevent treating tissue beyond disease extent. However, in the current paradigm, visual assessment of multiple structures in multiple planes, even with the aid of user assigned critical monitoring points, presents a delivery paradigm that is inherently difficult to manage. Integration of mathematical modeling and computational science techniques with the clinical imaging information available may prove useful for MRgLITT before and during the procedure, either by predicting the result of a treatment before the surgery, or during surgery to improve MRTI and robustly estimate lost information due to data corrupting motion, low signal-to-noise-ratio (SNR), excessive heating, and catheter induced signal voids [12–15]. These enhanced real-time monitoring approaches may further assist in more safely and accurately controlling therapy delivery for increased efficacy of the procedure [16,17]. The availability of increasingly powerful high performance and portable computing resources, such as Nvidia® graphics processing units (GPUs)[18] and Intel® many integrated core (MIC) architecture [19] indicate that the presence of computational science is likely to continue escalating in these image-guided thermal therapy procedures.

The development of computational tools for planning hyperthermia and ablation therapies has received significant attention for improving therapy outcomes [10,20–24]. With predictive modeling, the laser fiber placement can be planned in a virtual environment to improve the likelihood of a successful and short treatment. A common method for predictive modeling of the distribution of induced heating in blood perfused tissue is the Pennes bioheat transfer equation (BHTE) [25] solved with a finite element method (FEM) [26–28]. A difficulty in obtaining accurate results from the BHTE is the uncertainty incurred by using homogeneous literature values of biothermal and optical constitutive values for patient specific planning. Uncertainty is further increased with incorporating the additional complexity of investigating the nonlinear effects of temperature- or thermal dose-dependent constitutive parameters

Truly predictive prospective computer modeling requires substantial validation efforts and novel computer modeling techniques that incorporate the inherent uncertainties of the computer model into the predicted solution [29–31]. A deterministic simulation uses a single set of input parameters and yields a single solution for the temperature field. In light of myriad uncertainties, it is difficult to know when to trust a deterministic solution, especially for predictive purposes. A possible solution is to use uncertainty quantification (UQ) in the model. Monte Carlo modeling is the quintessential example of a UQ method. While a Monte Carlo approach would provide the necessary probabilistic outputs, the computational cost required to simulate a sufficient number of realizations is large. There exist methods to improve the convergence of Monte Carlo through the quasi-Monte Carlo method, Latin hypercube sampling, and the Markov Chain Monte Carlo method [32–36].

Another successful technique to accelerate UQ is generalized polynomial chaos (gPC) expansion, a means of providing the model with UQ prodigiously faster than Monte Carlo for computations using few random input variables, i.e. <10 variables. gPC is originally based on the work of Wiener [37]. This method used a high order Hermite polynomial as a spectral approximation for model outputs. Nearly 50 years later, Ghanem and Spanos identified the spectral approximation as a viable tool in FEM modeling of stochastic differential equations [38]. Xiu and Karniadakis demonstrated that the convergence of spectral methods for solutions to differential equations were optimized by matching certain input functions' distributions with corresponding output polynomials, known as the Wiener-Askey scheme [39]. For similar diffusive type equations, gPC's convergence to a mean solution, N < 10 realizations, compares exceptionally favorably, pointwise error < 1. E-2, when compared with Monte Carlo's N = 20000 realizations [39,40]. gPC has already been applied to an eclectic list of studies. gPC The topics include radiation oncology, combustion modeling, nuclear reactor design, and robotic dynamics on rugged terrain [41–44].

Here we investigate the use of a stochastic form of the BHTE coupled to a diffusion theory approximation of light transport in tissue for improving the decision-making utility of thermal modeling. Temperature dependent constitutive values are mathematically characterized via an assumed probability distribution providing the ability to perform UQ via gPC and provide quantitative confidence levels in the computer model predicted temperature for each spatial location at each time point.

Methods

Mathematical Model of Uncertainty

Ignoring discretization errors, computer implementations of mathematical models fundamentally have uncertainty in their representation and predictions of physical phenomena [45] due to two dominant sources of inherent variability. 1-Simplifications are needed to make the algorithm practical. For example, in this work we implore a Pennes bioheat transfer equation (1) with a perfusion term that represents the manifestation of a complex and tortuous microvasculature on the bulk continuum scale heat transfer. 2-The computer model parameters are not known precisely. In this application, optical and biothermal parameters are taken from literature values and are empirical representations of nonlinear temperature and damage dependent phenomena. Further, the parameters fail to incorporate patient and tissue specific variability resulting from heterogeneities.

This investigation aims to manage model parameter uncertainty associated with a stochastic form of Pennes bioheat transfer equation for blood perfused tissues (1). The motivating idea is that the Pennes' representation of the physics of the bioheat transfer phenomena coupled with statistical methods of uncertainty quantification may synergistically provide a reliable prediction model regardless of constitutive parameter uncertainties and mathematical modeling approximations.

$$\begin{array}{l}\rho c_p\frac{\partial u}{\partial t}(\mathbf{x},t,\overrightarrow{Z})-\nabla ·(k(\overrightarrow{Z})\nabla u)+\omega (\overrightarrow{Z})c_{\mathit{\text{blood}}}(u-u_a)={\mu }_a{q}_{\text{laser}}(\mathbf{x},t,\overrightarrow{Z})\\ q_{\text{laser}}(x,t,\overrightarrow{Z})={\int }_{u_{\mathit{\text{tip}}}}\frac{P(t)}{\text{Vol}(U_{\mathit{\text{tip}}})}\frac{3{\mu }_{tr}exp(-{\mu }_{\mathit{\text{eff}}}\Vert x-\xi \Vert )}{4\pi \Vert x-\xi \Vert }d\xi x\in U\backslash U_{\mathit{\text{tip}}}\\ {\mu }_{tr}={\mu }_a(\overrightarrow{Z})+{\mu }_s(\overrightarrow{Z})(1-g(\overrightarrow{Z})){\mu }_{\mathit{\text{eff}}}=\sqrt{3{\mu }_a(\overrightarrow{Z}){\mu }_{tr}}\mathrm{\Omega }(t)={\int }_0^{t}A{e}^{\frac{-E_A}{Ru(\tau )}\mathrm{d}\tau }-k(\overrightarrow{Z})\nabla u\cdot \mathbf{n}=0\text{on}\partial Uu(\mathbf{x},0,\overrightarrow{Z})=u^0\text{in}U\\ \overrightarrow{Z}\equiv (Z_k,Z_{{\omega }^{\text{native}}},Z_{{\omega }^{\text{coag}}},Z_g,Z_{{\mu }_a^{\text{native}}},Z_{{\mu }_a^{\text{coag}}},Z_{{\mu }_s^{\text{native}}},Z_{{\mu }_s^{\text{coag}}})\end{array}$$ (1)

Here, ρ is the tissue density, c_p is the specific heat of tissue, k, is the tissue conductivity; ω is the tissue microperfusion primarily due to capillaries, c_blood is the specific heat of blood, and u_a denotes the arterial core blood temperature. The laser source term, q_laser, is modeled using a standard diffusion approximation [28]. Power is denoted, P, the volume of applicator is denoted, U_tip, and the volume of the biological domain is denoted U. Optical parameters include the absorption, scattering, and anisotropy factor, denoted μ_a, μ_s, and g, respectively. Arrhenius damage model, Ω, parameters are denoted, A, E_A, and R. The objective of this work is to use this mathematical model to predict the 4D temperature field, u, as a function of a random vector, Z⃑, with a known probability distribution that mathematically represents our uncertainty the optical parameters, perfusion, and conduction, $\overrightarrow{Z}=(Z_k,Z_{{\omega }^{\text{native}}},Z_{{\omega }^{\text{coag}}},Z_g,Z_{{\mu }_a^{\text{native}}},Z_{{\mu }_a^{\text{coag}}},Z_{{\mu }_s^{\text{native}}},Z_{{\mu }_s^{\text{coag}}})$.

Statistical methods provided by UQ techniques, such as gPC, provide novel methodologies for modeling the complex bioheat transfer phenomena. In particular, it is well known that the constitutive parameters behave nonlinearly with temperature increase and tissue damage. Constitutive parameters that account for damage dependent nonlinearities of the perfusion, thermal conductivity, and optical parameters [46] are generally more scarce than the linear counterparts and the variability of the mathematical form of the constitutive nonlinearities seen within the literature suggests a potentially higher degree of uncertainty within the nonlinear parameters [10,23,27,47,48]. Here we will consider the uncertainty associated with both linear and nonlinear constitutive forms of the perfusion, absorption, and scattering. A goal of our work is to investigate if a relatively simple linear model with physically meaningful bounds on constitutive values can be coupled with stochastic methods to produce useful predictions. Stochastic parameters associated with linear forms of the BHTE are chosen by the following expressions that are spatially homogenous and constant in time.

$$k(\overrightarrow{Z})=Z_k\omega (\overrightarrow{Z})=Z_{{\omega }^{\text{native}}}g(\overrightarrow{Z})=Z_g{\mu }_a(\overrightarrow{Z})=Z_{{\mu }_a^{\text{native}}}{\mu }_s(\overrightarrow{Z})=Z_{{\mu }_s^{\text{native}}}$$ (2)

While several empirical models of nonlinearites are available, for feasibility, a common form of the constitutive nonlinearities (3) was considered for absorption, scattering, and perfusion as a function of Arrhenius thermal damage, Ω. As seen in Figure 1, for this particular analytical form chosen [27], undamaged constitutive values transition to coagulated values between the temperature range of 51-61 °C. Similar to previous studies [49] of the time temperature histories relevant to MRgLITT, the tissue is fully damaged at approximately a 61 °C threshold.

Figure 1.

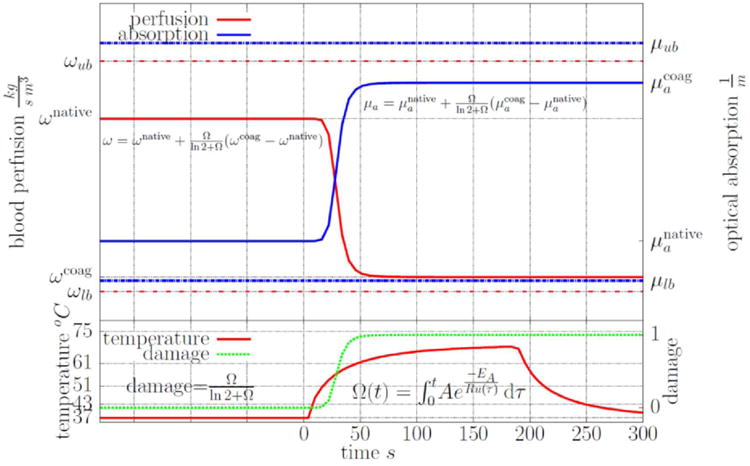
A graphical illustration of the nonlinear constitutive model [27] used for the perfusion and optical absorption is shown. The scattering behaves similar to the absorption. Damage, perfusion, and absorption are plotted as a function of a time-temperature history representative of those observed in MRgLITT procedures. As shown, the native undamaged constitutive values transition to coagulated constitutive values between the temperature range of approximately 51-61 °C. Similar to previous results [49], the tissue is fully damaged at a 61 °C threshold.

$${\mu }_a(\overrightarrow{Z})=Z_{{\mu }_a^{\text{native}}}+\frac{\mathrm{\Omega }}{ln2+\mathrm{\Omega }}(Z_{{\mu }_a^{\text{coag}}}-Z_{{\mu }_a^{\text{native}}}){\mu }_s(\overrightarrow{Z})=Z_{{\mu }_s^{\text{native}}}+\frac{\mathrm{\Omega }}{ln2+\mathrm{\Omega }}(Z_{{\mu }_s^{\text{coag}}}-Z_{{\mu }_s^{\text{native}}})\omega (\overrightarrow{Z})=Z_{{\omega }^{\text{native}}}+\frac{\mathrm{\Omega }}{ln2+\mathrm{\Omega }}(Z_{{\omega }^{\text{coag}}}-Z_{{\omega }^{\text{native}}}$$ (3)

The native conduction, Z_k, perfusion, Z_ω^native, optical scattering, $Z_{{\mu }_s^{\mathit{\text{native}}}}$, optical absorption, $Z_{{\mu }_a^{\mathit{\text{native}}}}$, and the optical anisotropy, Z_g as well as the coagulated values of the absorption, $Z_{{\mu }_a^{\mathit{\text{coag}}}}$, scattering, $Z_{{\mu }_s^{\mathit{\text{coag}}}}$, and perfusion, Z_ω^coag, are understood mathematically as uniform random variables with quantitative bounds given in Table 1. As seen in Figure 1, the uncertainty range of constitutive nonlinearities is considered as a subset of the uncertainty within the linear UQ problem.

Table 1.

Literature based constitutive values [46,50–52,54,55,77–80] A table of the constitutive values used for perfusion, conduction, absorption, and scattering is shown. Uniform distributions are denoted U(a,b). Deterministic values are otherwise used. Values for density, specific heat, and Arrhenius parameters are as follows: ρ=1045 [kg/m³], c_blood =3840 [kg/J/K], c_p= 3600 [J/kg/K], A = 3.1E98 [1/s], E_A = 6.28E5 [J/mol], R = 8.314 [J/mol/K].

Figure	ω [kg/(m̂3 * s)]	k [W/(m * K)]	μa[1/m]	μs[1/m]	g [Unity]
2A	U(3, 9)	0.527	500	14000	0.88
2A	6	U(0.490, 0.527)	500	14000	0.88
2A	6	0.527	U(400, 600)	14000	0.88
2A	6	0.527	500	U(11200, 16800)	0.88
2A	6	0.527	500	14000	U(0.85, 0.99)
2B	6	0.527	Linear-U(50, 600)	14000	0.88
2B	6	0.527	Native-U(50, 300); Coag-U(300-660)	14000	0.88
2B	6	0.527	500	Linear-U(5000, 50000)	0.88
2B	6	0.527	500	Native-U(5000, 30000); Coag-U(30000-50000)	0.88
2C	Linear-U(0, 9)	0.527	500	14000	0.88
2C	Native-U(3, 9); Coag-U(0-3)	0.527	500	14000	0.88
2D	U(3, 9)	U(0.490, 0.527)	U(400, 600)	U(11200, 16800)	0.88
3	0	0.527	U(4, 200)	14000	U(0.85, 0.95)
4, 5 and 6	6	0.527	U(400, 600)	U(11200, 16800)	U(0.88, 0.95)
5A (White Matter)	U(3,9)	0.527	320	46900	0.88

Constitutive data

Constitutive parameter values [46,50–55] used in simulating the bioheat transfer for the in vivo brain data and ex vivo phantom setup are provided in Table 1. Variability in the model parameters [46,55,56] was input into the gPC model as uniformly distributed random variables using the bounds shown in Table 1. For the linear simulations, the parameter values were varied over a range that covers all conceivable healthy values, but does not include thermal dose effects. For examples, see Table 1 and the constitutive values for Figures 2A, 4, 5, and 6. The nonlinear simulations and the contrasting linear simulations include thermal dose effects. For examples, see Table 1 and the parameter values for Figures 2B and 2C. The values for the Arrhenius dose parameters listed in Table 1 are from Henriques and Moritz' classic work [57]. The choice of dose parameters is dependent on what endpoint is sought. Here the threshold is tissue death by any heating effects shortly (< 20 minutes) after treatment. The dose analysis for the four canines, is described by Yung et al. [49], demonstrates that an Arrhenius dose module using Henriques' dose values lead to agreement with post-treatment, postcontrast T1-weighted MRI.

Figure 2.

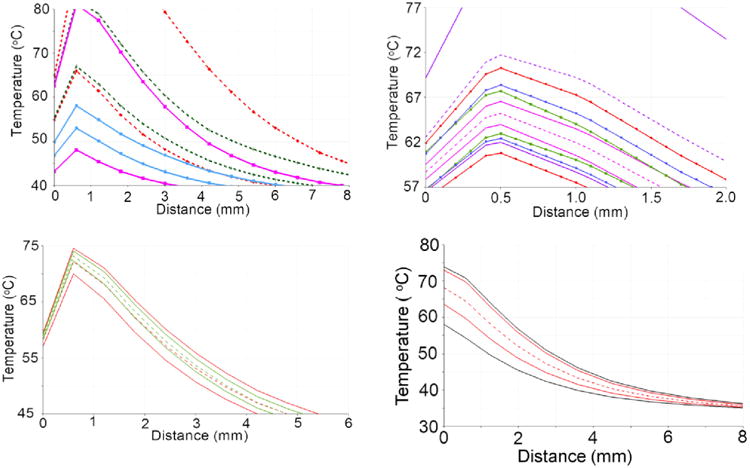
These plots are spatial profiles that demonstrate the properties of a stochastic BHTE, with inputs listed in Table 1. Except for D), the solid lines represent the CDF = 2.3 and 97.7%; the enclosed region is the central 95% confidence interval. A) is a linear sensitivity study; each color represents data from a univariate model, i.e., one parameter is varied while all others are constant. A) has the following plots, listed from low to high variance at peak heating: perfusion (fuchsia), conductivity (green), optical scattering (blue), optical absorption (red), and optical anisotropy (violet). A) is dramatically zoomed in so the five variables' plots are more distinguishable. Except for the optical anisotropy model, all univariate models in A) have very similar means, plotted as dashed lines for A). To simplify the plot, only the mean of the perfusion and the anisotropy univariate models are presented. The parameters' relative sensitivities can be seen in this figure. E.g., perfusion is proportionally varied more than the optical absorption and scattering parameters, but the optical parameters still have a greater temperature variance. The BHTE is most sensitive to the anisotropy factor in this study. B) and C) are a sensitivity study comparing linear and nonlinear perfusion parameters; B) has optical absorption (red and green with dashed lines) and scattering (fuchsia and blue with solid lines) while C) has perfusion. The linear cases' inputs vary the concerned parameter over a range that includes both the native and coagulated states of the nonlinear case. The plots demonstrate coagulation is affecting the temperature distributions. D) simultaneously varies optical scattering, optical absorption, conductivity, and perfusion. The difference between the worst case scenarios (black) and CDF = 1% and 99% (red) is shown.

Figure 4.

These images are MRTI from the four canine normal brain MRgLITT ablations. All images are from a slice that intersects the longitudinal axis of the laser applicator. Images A), B), C), and D) respectively correspond to canines 1, 2, 3, and 4 near maximum heating times t = 432 s, 222 s, 120 s, and 135 s. The superimposed green lines represent where the linear profiles for the four canines are plotted for the subsequent figures. Green diamonds indicate the location of temporal profiles in canine Figure 5. The black rectangles in each image are where the laser fibers were. The concentric red contours correspond to the 60 °C isotherm contours with probabilities CDF = 2.3% and 97.7%. The areas between the red contours represent the central 95% of the model's temperature distribution. According to the model, the CDF = 2.3% contour has a high probability of occurring, i.e., 97.7%. The dark blue and light blue contours respectively are the 60 °C isotherms from the MRTI temperature ± 2σ of MRTI noise.

Figure 5.

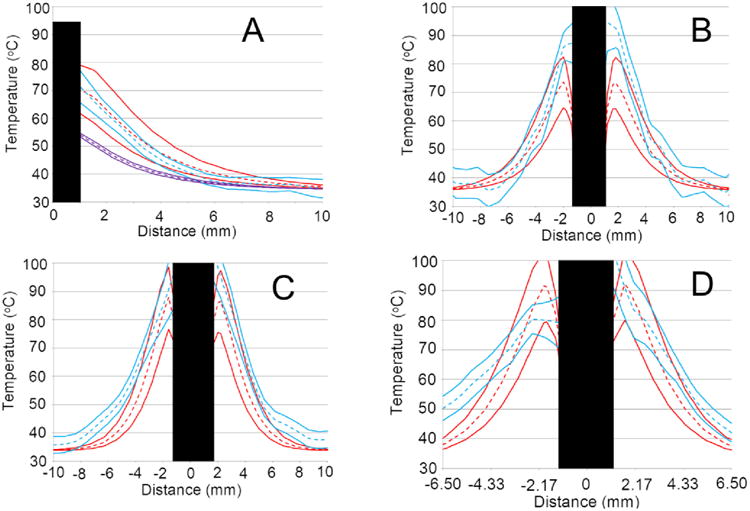
All plots are from simulations that vary the three optical parameters (red), i.e., the trivariate model, and are compared to MRTI (blue). Means are dashed lines and solid lines enclose the central 95% confidence interval. Plots A) through D) correspond to canines 1 through 4 at the same time points described in Figure 4. A) also contains a perfusion univariate model that uses optical scattering and absorption from white matter tissue (violet). The black rectangles obfuscate the portions of the linear profiles that are on the laser fibers because those regions provide invalid comparisons. A) suggests that white matter optical scattering and absorption parameters produce profoundly colder temperatures. In plots A) and B) the trivariate model tends to overlap the MRTI well. Plots C) and D) show some agreement near the fiber (∼±3 mm), but diverge at farther distances.

Figure 6.

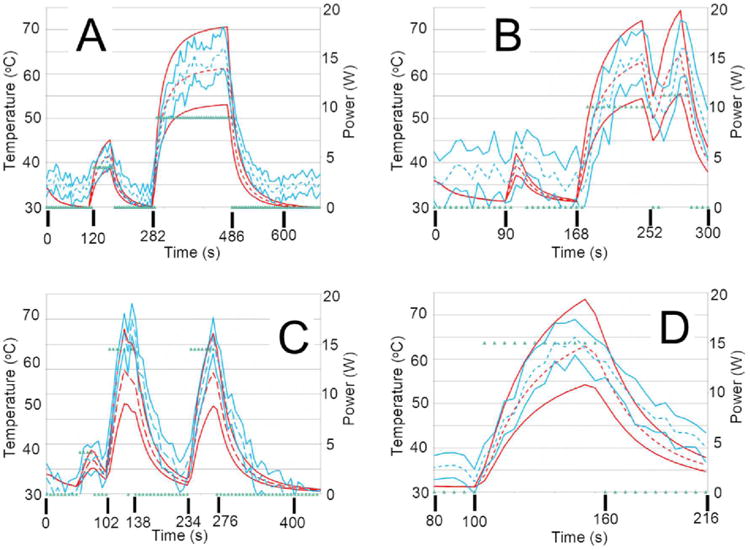
These temporal profiles, A) through D), are temporal profiles from canines 1 through 4, respectively. The red and blue dashed and solid lines represent the same as in Figure 5. The green points represent the power history. The spatial locations of the temporal profiles are shown in Figure 4 via the green diamonds. A) and D) show the best agreement of the four plots. B) is more successful at the beginning of the imaging sequence but the model is much colder at later time points. C) tends to be somewhat cooler, but significant overlap remains between the MRTI and model distributions.

Optical Parameter Uncertainty

Relatively large variability maybe seen in optical parameter values reported in the literature, Table 1. These differences may be associated with different techniques for in vivo and in vitro measurements, different radiative transport models, and differences in preparation of tissue specimens [58,59]. The nonlinear behavior of optical parameters is well known [27,46,60–62] and further increases the uncertainties in optical properties. For example, a 10% increase in the absorption coefficient and a 2-4 fold increase in the scattering coefficient was seen between native and coagulated brain tissue [46,61]. Further, the blood content of the tissue has been seen to affect the optical properties [63]. Significant changes in the optical properties of the blood can be expected with varying concentrations of haematocrit and oxygen concentration. There is also great uncertainty in the tumor type to use for the optical parameter values as well as blood content of the tumor. This may particularly contribute to the uncertainty in the optical parameters when irradiating heterogeneous tumors where the patient specific blood content and the amount of cerebral spinal fluid (CSF) present may vary significantly.

Gray matter optical parameter values—μ_a, μ_s, and g—were used in simulating MRgLITT in normal canine brain tissue. For nonlinear simulations, the values of absorption and scattering were set to represent the native state and transition to a coagulated state (3). The range of optical values used in the linear simulation for comparison against the nonlinear simulation is a superset of the range of the native and coagulated transition, listed in Table 1 Figures 2B and 2C.

Multiplanar magnetic resonance thermal imaging in phantom and animal models

Simulations were compared to MRTI data obtained from a safety and feasibility study of MRgLITT conducted in the brains of four clinically normal mixed breed hounds (20-25 kg) [28,49]. MRTI data was also obtained from an MRgLITT heating experiment in a perfusion-less ex vivo tissue phantom [17] constructed from an excised canine prostate embedded within 1% agar, Figure 3. MRTI data was acquired on a 1.5 T MRI (ExciteHD®, GE Healthcare Technologies, Waukesha, WI) with an 8-channel, receive-only phased-array head coil (MRI Devices, Gainesville, FL) and a 2D multi-slice 8-shot EPI sequence [64] (FA = 60°, FOV = 20 × 20 cm, slice thickness 4 mm, TR/TE = 544/20 ms, encoding matrix of 256 × 128, with 5-6 s per update). The procedures were conducted under institutional protocol. The canines were anesthetized with ketamine/midazolam (Versed) solution (ketamine, 10 mg/kg; midazolam, 0.5 mg/kg; and glycolpyrrolate, 0.01 mg/kg), incubated, and aspirated with a mixture of 2% isoflurane/oxygen. Once the dogs were anesthetized, a burr hole was introduced in the right parietal bone of each animal. In each case, the laser applicator was percutaneously placed through the burr hole and into the clinically normal brain. The silica applicator was 400 μm diameter with a 1 cm axial length for laser diffusion. The laser wavelength was 980 nm with a maximum power of 15 W (Photex 15, BioTex, Houston, TX). The applicator was water-cooled with a maximum flow of 15 mL/min. Power histories are shown in Figures 3 and 6. Flouroptic probes were not included to attempt to avoid susceptibility artifact.

Figure 3.

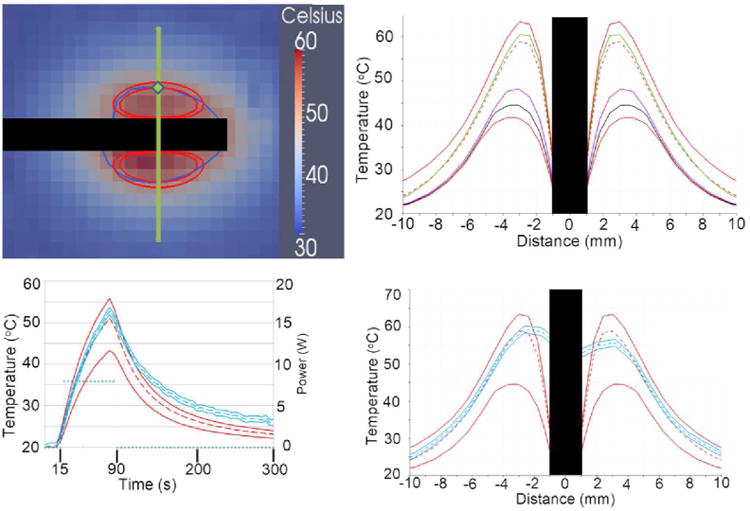
The trivariate joint uncertainty of the optical absorption, scattering, anisotropy are input for the gPC simulations. Model parameters are listed in Table 1. A) is the MRTI of the phantom study at t = 90 s. The inner red contour is the 50 °C isotherm for the model's mean and the outer red contour is for the CDF = 97.3%; CDF = 2.3% never reaches 50 °C. The dark blue contour is the MRTI's 50 °C isotherm. Only one MRTI isotherm is displayed because the MRTI variance is very small; ±2σ of MRTI noise is ∼2 °C. The black rectangles in A), B), and D) occlude where the laser fiber was. The superimposed green line represents the location for linear profiles, B) and D). A green diamond indicates the location of temporal profile in C). D) compares the linear profile of the central 95% confidence intervals of the model and MRTI. In plot D), the model's mean tracks very well with the MRTI, particularly near the laser fiber (∼±6 mm). D) also dramatically shows the potential for non-Gaussian distributions to arise in the temperature model, further illustrated in B). B) shows various CDF values tracked in the gPC computer package, DAKOTA. The top red is CDF = 99%, green is the median (50%), red dashed line is the mean, violet is 5%, black is 2.3%, bottom red is 1%. Note the extreme skewness of the model's temperature output near the fiber, as evidenced by the mean and median being much nearer the higher % CDFs than the lower % CDFs. The power (green points) is provided units on the right vertical axis.

Computational methods

A hexahedral finite element mesh that conforms to the geometric details of the water cooled laser applicator [28,65] was created in CUBIT [66]. A 21 °C Dirichlet boundary condition representing the water-cooled catheter was applied to the domain of the applicator. Simulations at several mesh spatial resolutions were run at quarter symmetry to ensure numerical convergence; 13968/47368/169680 element meshes with 15770/50898/177549 corresponding nodes were evaluated. The DAKOTA software [67] was used to implement the generalized polynomial chaos expansion. Similar to ensuring convergence of the mesh resolution, the number of polynomial chaos basis functions used in the gPC expansion was increased until the truncation error of the gPC expansion was negligible [68]. This was achieved by computing the difference between a lower order and a higher order gPC expansion. When the maximum pointwise difference between a lower order and a higher order gPC expansion was < 0.001 °C, the gPC expansion was assumed converged. Using DAKOTA, the gPC expansion order is inferred from the quadrature order in probability space. A quadrature order of four was found to achieve truncation error convergence in the gPC expansion. For comparison to gPC, a worst case scenario approach was also run [69]. The worst case scenario approach provides the extreme upper and lower bound of the temperature distribution by considering the extrema of the input parameter variability.

Results

A sensitivity study of the thermal conduction, perfusion, absorption, scattering, and anisotropy is presented in Figure 2. The sensitivity study was performed by investigating the effect of the uncertainty range of each parameter individually on the mean and 95% confidence interval of the resulting temperature field. Here the 95% confidence intervals are reported as the output cumulative temperature distribution (CDF) between 2.5% and 97.5%. Representative profiles of the temperature field 95% confidence intervals resulting from considering the uncertainty in thermal conduction, perfusion, absorption, scattering, and anisotropy individually is shown in Figure 2A. Results in Figure 2A are shown for the linear heat transfer problem (1) near the maximum heating time point. Given the physically meaningful distributions found in the literature, Table 1, the resulting temperature field was found to be least sensitive to the perfusion and most sensitive to the anisotropy. The sensitivities in Figure 2A can be summarized by listing their peak standard deviations in °C: g, 3.51; μ_a, 2.94; μ_s, 1.84; k, 1.43; and ω, 0.94. The sensitivity of the absorption, scattering, and perfusion nonlinear parameters (2) on the resulting temperature distribution is shown in Figures 2B-2C. As seen in Figure 1, the uncertainty in the linear problem was assumed to bound the total nonlinear variations and the resulting linear temperature field bounds the nonlinear temperature field, Figure 2B and 2C. The effect of thermal coagulation is seen to shift the means of the output distributions for the nonlinear perfusion, absorption, and scattering (not shown). Figure 2D demonstrates the difference between UQ from multivariate gPC and worst case scenarios as an estimate for UQ.

Of the five univariate gPC expansions considered, the sensitivity of the final temperature distribution 95% confidence interval for the MRgLITT simulations is seen to be least sensitive to conduction and perfusion variability. Subsequent MRgLITT simulations consider the trivariate joint uncertainty of the optical parameters, absorption, scattering and anisotropy, for comparison to MR thermometry data. The thermometry data shown was generated using standard complex phase differencing techniques and SNR based estimates of the Gaussian uncertainty in the measured temperature value [28].

Figure 3, compares the 95% confidence interval of the gPC MRgLITT simulation to MRTI data acquired during an ex vivo heating of canine prostate tissue. The phantom provides a perfusion-less environment to compare theory to experiment. The trivariate joint uncertainty of the absorption, scattering and anisotropy are input into the gPC simulations. Model parameters used are provided in Table 1. Figure 3A shows a temperature map of the MRTI near a maximum time heating point. A plot of temperature over time comparing measured to predicted values of temperature is shown in 3C. The power history is provided on the right axis. A spatial profile of the experimental and simulation temperature values is shown in Figures 3B and 3D. The location of the spatial profiles and temporal profiles are provided in Figure 3A. During heating, good agreement is seen between the measured and predicted temperature values.

The trivariate joint uncertainty of the absorption, scattering and anisotropy are input into the gPC simulations and compared to MRTI data acquired during four canine MRgLITT experiments. The comparison is provided in Figures 4-6. MRTI from the four canine MRgLITT procedures is shown in Figure 4. Contours of the 60 °C isotherm of the MRTI are compared to the 95% confidence interval of the gPC predictions. Locations of spatial and temporal profiles used in Figures 5 and 6 are shown. An additional simulation varying perfusion only and using optics parameters from white matter is shown to compare the differences in input parameters from white matter to gray matter, Figure 5A. The white matter-based, ω-univariate simulation shown in Figure 5A is clearly much colder and led to the decision to use gray matter weighted optics parameters in the trivariate simulations, shown in Table 1. Spatial and temporal profiles, seen in Figures 5 and 6, show that canines 1 and 2 had a majority of overlapping regions between the MRTI and the simulations' 95% confidence intervals. It should be noted that canines 3 and 4's disagreement occurs relatively distant from the laser fiber.

Discussion

A generalized polynomial chaos (gPC) method was used to propagate the uncertainty in the biothermal and optical parameters. A finite element based stochastic form of the 3D Pennes bioheat transfer model was implemented for these purposes. The ability to accept plausible distributions of the biothermal and optical parameters and output realistic distributions of the temperature mean and variance is a novel aspect of gPC based simulation. In a probabilistic bioheat simulation, the challenge shifts from utilizing the most precise constitutive values to identifying an appropriate input distribution. However when using gPC, the model input distributions are limited to the Wiener-Askey scheme [39]. The two distributions considered were the Gaussian and uniform distributions. Because Gaussian distributions have been successfully and ubiquitously applied to probabilistic natural phenomena, Gaussian distributions were initially identified as an option. However, Gaussian distributions are positive from −∞ to +∞. In order to be physical, the constitutive values must be positive. If a Gaussian distribution was applied to the constitutive input distributions, the model would be influenced by nonphysical inputs. The uniform distribution was chosen for use in the constitutive value distributions because it is straightforward to restrict the distribution to physical values.

The sensitivity study, displayed in Figure 2, shows the output variance of the five univariate models. It is important to note the relative input variance, based on published literature values, to the output variance. E.g., ω is varied from 3 to 9 kg m^-3 s^-1, i.e., the variance is the mean ± 50%. When compared to the variance of μ_a (mean ± 20%), it is evident that the BHTE is much more sensitive to μ_a than ω. Namely, even though ω is proportionally varied more than μ_a, the output temperature variance due to ω is considerably less than μ_a. The parameters found to produce the greatest variances were the optical parameters. Further, for the parameter range considered, the confidence intervals of temperature simulations using nonlinear temperature and damage dependent perfusion, scattering, and absorption (3) is bounded by the linear temperature simulations. Within this statistical setting, linear problem with its associated uncertainty is used as a surrogate for the more complex nonlinear bioheat transfer phenomena. The linear form of the optical parameters, μ_a, μ_s, and g, were use in the trivariate gPC based MRgLITT simulations for comparison with the phantom experiments and canine ablations.

Comparison of worst case scenarios and gPC estimates, Figure 2D, demonstrate that the deterministic worst case scenarios do not adequately capture the bulk of the statistical information in multivariate simulations. This is particularly true as the joint uncertainty of progressively more parameters is expanded in probability space. It is conceivable that worst case scenarios could approximate gPC estimates in special cases, e.g., univariate simulations or parameters with low sensitivity yielding low output variance. However, these same special cases are less likely to require UQ estimation, which is the reason we used to legitimize our focus on the optics when comparing the trivariate models for the gPC based MRgLITT simulations.

A more exhaustive application of UQ to LITT would also examine the effect of other bioheat parameters, e.g. ρ, c_t, and u_a, and thermal dose parameters. For the bioheat parameters that are not ω or k, the authors did not vary them because the parameters have less uncertainty and sensitivity. As for possibly varying the dose parameters (either Arrhenius or cumulative effective minute (CEM) models) [70], the situation depends on the temporal length of the hyperthermia treatment. In the case of relatively temporally short, spatially small >60 °C ablations, thermal dose models predict the spatial transition between coagulative necrosis of tissue and survival is small. It is the expectation of the authors that the thermal dose parameters of either dose models would need to have variances that exceed the literature to create variances in the lethal threshold region that are comparable to the variance of lethal threshold regions created by varying bioheat and optical parameters. However, for sub-ablative hyperthermia where thermal dose is accumulated over greater time, variance in thermal dose parameters may lead to appreciable spatial variance in the lethal threshold region or other interesting thermal dose level. Future studies should investigate uncertainty in thermal dose parameters' effect on thermal dose uncertainty, especially for temporally longer hyperthermia treatments.

Regarding the MRTI for canine 1, Figures 4, 5 and 6, it should be noted that the canine's brain ventricle was punctured by the catheter. The ventricle leaked cerebral spinal fluid (CSF) into catheter's insertion tract and ultimately pooled near one side of the laser fiber. The effect of the CSF on the thermal ablation can be seen as reduced temperature for the lower side of the thermal lesion in Figure 1. The effect is most obvious in the MRTI's 60 °C isotherms. The model did not account for the presence of the CSF and therefore the regions affected by the CSF were excluded from analysis. Regarding the MRTI in general, the pixels imaging the laser fiber and very proximal regions affected by susceptibility artifact were not included in the linear profiles or isotherm contours. Further sources of discrepancy between simulation and MRTI during the cooling regime, Figures 3C and 6, are not seen in studies with external optical fibers [71] and are likely due to inaccuracies of the Dirichlet boundary condition to model the convective cooling of the catheter. Validation of physics based models [72,73] of the convective heat transfer of the cooling fluid through the laser applicator is a topic of future work.

Despite multivariate gPC expansions being more appropriate for thermal therapy simulation, univariate gPC expansions may be used in future investigations to identify which parameters create the greatest variance of the temperature output, and subsequently restrict the gPC expansion to parameters that affect the temperature output the greatest. Improving the input distributions for the constitutive values should be investigated. Ideally, the model's constitutive distributions would reflect the natural distributions of the constitutive parameters. The Wiener-Askey scheme includes gamma and beta distributions that are each a set of parameterized distributions. Both gamma and beta distributions include distributions that are not negative and resemble the Gaussian distribution's distinctive ‘bell curve’. While Gaussian-like distributions exist, there is presently no particular reason any single distribution should work best. It may be sufficient to attempt an array of distributions in order to discover distributions that minimize the difference between the model and MRTI. Future investigations should additionally explore further statistical metrics of the model's outcome. Possible tests include using spatio-temporal pixel-wise statistical tests for the difference or similarity between the model's mean and MRTI's temperature. The common example test for means is the Student's t-test, however, the model's polynomial expansion is not generally a Gaussian distribution so other tests should be sought.

This investigation took the natural step of comparing the model's confidence interval to the MRTI's confidence interval. In the case of gPC, the polynomial expansion probability distribution function was integrated to yield the polynomial expansion's CDF. The CDF in turn indicated the probability of a threshold temperature (e.g. the temperature is >60 °C) as a function of distance from the laser fiber. These probabilities have a clear use in planning for thermal ablations. A stochastic simulation with temperature UQ gives the surgeon a probabilistic measure of the temperature. There are at least two methods of clinically using temperature UQ. First, the physician can plan the ablation using the stochastic model's mean temperature prediction and the variance about the mean. E.g., if a physician observes a large variance about the mean, the simulation cannot be implicitly trusted. Alternatively, temperature UQ could aid ablation planning by displaying a isotherm that is very likely to occur. E.g., the physician could plan the ablation based on the CDF = 5% level. I.e., the model would display a treated region that has a 95% chance of occurring. While deterministic thermal predictions do not have a measure of their uncertainty, a stochastic simulation provides confidence intervals. An example would be a surface contour that demarks a volume that has at least a 95% probability of reaching 60 °C. Uncertainty quantification to create a ‘high probability of treatment’ contour is a highly desired goal. An accurate, high-probability-of-treatment contour would allow physicians to quantify a measure of the probability of success. Also, there is little risk of overtreatment if the contour exceeds the desired treatment region; MRgLITT's real-time MRTI provides the physician with feedback for ceasing treatment.

In conclusion, results demonstrate the utility of generalized polynomial chaos (gPC) expansion techniques to propagate parameter uncertainties through the computer model of bioheat transfer and quantify uncertainties in the resulting output temperature distributions. Given parameter uncertainties and mathematical modeling approximations of the Pennes bioheat model (1), the 95% confidence intervals within the statistical framework demonstrate conservative estimates of the thermal therapy outcome and have potential for use as a computational prediction tool for thermal treatment planning.