Tumor Burden Analysis on Computed Tomography by Automated Liver and Tumor Segmentation

Abstract

The paper presents the automated computation of hepatic tumor burden from abdominal CT images of diseased populations with images with inconsistent enhancement. The automated segmentation of livers is addressed first. A novel three-dimensional (3D) affine invariant shape parameterization is employed to compare local shape across organs. By generating a regular sampling of the organ's surface, this parameterization can be effectively used to compare features of a set of closed 3D surfaces point-to-point, while avoiding common problems with the parameterization of concave surfaces. From an initial segmentation of the livers, the areas of atypical local shape are determined using training sets. A geodesic active contour corrects locally the segmentations of the livers in abnormal images. Graph cuts segment the hepatic tumors using shape and enhancement constraints. Liver segmentation errors are reduced significantly and all tumors are detected. Finally, support vector machines and feature selection are employed to reduce the number of false tumor detections. The tumor detection true position fraction of 100% is achieved at 2.3 false positives/case and the tumor burden is estimated with 0.9% error. Results from the test data demonstrate the method's robustness to analyze livers from difficult clinical cases to allow the temporal monitoring of patients with hepatic cancer.

1 Introduction

According to the American Cancer Society, approximately 26,190 new cases of liver cancer are expected to occur in the US in 2011 and more than 80% of them to be hepatocellular carcinomas [1]. The majority of primary liver cancers have their origins in alcohol-related cirrhosis and fatty liver disease associated with obesity. Other major risk factors are hepatitis B and C viruses. The incidence of liver cancer has been increasing by more than 3% yearly. About 19,590 liver cancer deaths are expected in 2011 with incidence and mortality more than twice as high in men as in women [1]. Early stage liver cancer can sometimes be treated successfully with surgery and transplantation. Patients whose tumors cannot be removed surgically may benefit from ablation, embolization or targeted drug therapy. The overall 5-year survival rate for patients with liver cancer is 14%.

Liver metastases are hepatic cancers that have spread from another primary source in the body. The liver is a prime candidate for metastases from cancers in the breast, colon, prostate, lung, pancreas, stomach, esophagus, adrenal glands or skin (melanoma) [32]. A hepatic metastasis can be found at the time of the diagnosis of the primary cancer or appear later after the removal of the primary tumor. The treatment and prognosis of secondary liver cancers vary largely depending on its source and stage. Systemic chemotherapy is usually used to treat the metastases, but ablation and embolization are also common, while surgery is a rarer option [9,32]. Although secondary liver cancer is generally untreatable, treatments may improve life expectancy.

Computed tomography (CT) is commonly adopted for imaging abdominal organs for diagnosis and pre-operative planning. The three-dimensional (3D) analysis of volumes, shapes and enhancements of abdominal organs, such as the liver, are common indicators of disorders and important markers for diagnosis and treatment response evaluation of cancer [13,58,61]. Organ and tumor volume measurements have been found to be important in making surgical decisions involving organ transplantation [5,29]. Clinical cases can exhibit low contrast, imaging and motion artifacts and large pathologies, which change the intensity and shape of organs. But it is in these unusual clinical cases that potentially require surgical interventions that the current fully automated 3D segmentation techniques most often break down.

In traditional clinical practice, 3D organ analysis is performed via time-consuming manual measurements, or as an alternative the evaluation is incomplete, based on 2D projection images. There are several advantages that automated methods have over manual or interactive techniques. An important aspect is the reproducibility of results, which in automated algorithms are not subjected to user interaction. Moreover, automated techniques may be faster, readily available, and can run in the background without interrupting the clinical workflow (do not require human presence).

The automated computer-aided diagnosis (CAD) of livers from medical scans can provide quantitative data. The implementation of a robust and fully automated 3D segmentation technique for liver and its tumors would allow radiologists and surgeons to have easy and convenient access to organ measurements and 3D visualization. The proposed method for the automated segmentation of the liver, and detection, segmentation and classification of tumors can be employed as an assisting diagnostic tool robust to morphological changes from normal and pathological anatomical variability, as well as poor image quality or enhancement. The following sections of the manuscript present the state of the art in shape parameterization, liver segmentation and liver tumor analysis.

1.1 Shape Parameterization

Shape analysis is often performed via image-based registration [34,35] or landmark identification [36,65], which rely on image-based metrics and landmark repeatability. To identify subtle shape differences between two objects, a robust parameterization of their surfaces is required in combination with an invariant shape descriptor and a point-to-point correspondence.

Previous methods for 3D surface analysis have been proposed in medical applications [14], but a reliable parameterization of human organs remains challenging. In a more general sense, the parameterization of star-shaped objects [2,14] is restrictive for irregular shapes in the abdomen. To avoid this shortcoming, the method in [6] involves generating a bijective mapping from the 3D surface to the unit sphere as an explicit parametric representation and global description of surfaces of simply connected 3-D objects. A spherical harmonics-based parameterization was also presented in [25] by dividing a given surface into a set of basis functions. Spherical harmonics-based parameterizations for brain [16,60] and cardiac [23] application have been particularly popular. Spherical harmonics can introduce aliasing that results in an inaccurate representation of difficult data and induce computational complexity. For the liver, corresponding points were initialized by the user in [31] to be incorporated in statistical shape models [21].

1.2 Liver Segmentation

A variety of methods have been proposed to segment the liver in recent years. This increased interest in the field reflects the difficulty of liver segmentation for clinical applications. The following paragraphs detail some of the most relevant published techniques. A comprehensive review of CT-based liver segmentation techniques was done by Campadelli et al. [7], describing methods that employed live wire, gray-level analysis, neural networks, model fitting, level sets and probabilistic atlases. Campadelli et al. highlighted the advantages and drawbacks that limit the use of such techniques in the clinic.

For a straightforward comparison, in 2007 a liver segmentation competition from mainly pathological CT data was held in conjunction with the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) [22]. The Workshop on 3D Segmentation in the Clinic: A Grand Challenge provided a set-up for a segmentation competition for automatic and semi-automatic extraction of the whole liver from CT scans. All data in the competition were obtained using enhancement, as the use of contrast in CT acquisition helps differentiate the liver parenchyma from surrounding abdominal soft tissue. Besides training and testing data, the competition also provided ground truth and tools for the quantitative evaluation of results. A variety of techniques were presented and their performance evaluated through a combination of metrics, including volume overlap and error, root-mean square error, and average surface distance. Amongst the ten automatic and six interactive methods for liver segmentation, the interactive methods achieved some of the best segmentation results [3,10]. Statistical shape models were the best fully automated liver segmentation methods and performed competitively with the semi-automatic techniques. In particular, a combination of shape-constrained statistical deformable models based on a heuristic intensity model had the best performance among automated methods [28]. Other notable participations in the competition employed region growing [47], a technique sensitive to liver abnormalities, and a semantic formulation of knowledge and context [49], but with relatively low segmentation overlap.

Several other approaches to segment the liver should be mentioned. A model-based segmentation was also employed in a supervised segmentation using graph representation in [51]. A shape-constrained graph-cut approach segmented abdominal organs including the liver in [35], but mainly normal anatomy. The graph was initialized from training data statistics and constraints on shape, from Parzen windows, and location, from a probabilistic atlas, were used for segmentation. Shape densities and boundary appearance models were used in [63] with high accuracy. A fast hierarchical model using marginal space learning was introduced in [33], but segmentation outliers were excluded from validation. Finally, a multilevel statistical shape model (ML-SSM) and principal component analysis (PCA) were used in [42], but required heavy manual initialization.

1.3 Hepatic Tumor Analysis

In 2008, another segmentation competition followed in conjunction with MICCAI, this time addressing the segmentation of liver tumors from CT data [11]. CT images covered a range of pathologies and were acquired with contrast enhancement to allow the differentiation of tumors from healthy liver parenchyma. Data and evaluation tools were made available to the participants. One interactive, five semi-automatic and four automatic methods for tumor segmentation were evaluated. The evaluation of the techniques was performed using similar metrics to the liver segmentation competition. As in the case of the liver, the highest scoring technique was interactive, using classic graph cuts and the watershed algorithm to accurately segment tumors [59]. The most successful semi-automatic approaches scored similarly and employed adaptive thresholding and morphological processing [40], voxel classification and propagational learning [66], and a level set with fuzzy pixel classification [56]. Tumors were best automatically segmented via machine learning and classification techniques, namely using cognition network technology [50] and ensemble segmentation trained using AdaBoost [55].

Other recent notable approaches to segment hepatic lesions employed intensity distribution combined with hidden Markov fields in [20]. The method is interactive and the tumor volume estimation error was over 23%. The semi-automatic segmentation of tumors based on support vector machines and affinity constraint propagation was addressed in [15] with results comparable to the reports from the MICCAI competition. Machine learning was also used for the detection of liver cancers based on linear discriminant analysis [64].

CAD and surgical planning would benefit from fully automated 3D segmentation of both the liver and liver tumors, as well as the organ's vasculature [18,54]. Methods for the concurrent segmentations of liver structures are mainly interactive [45]. Exceptionally, both the liver and its tumors were automatically segmented with a combination of statistical models, active contours and expectation maximization in [38]; the method struggled with pathological cases. In an integrated approach, a technique that uses a combination of thresholding, mathematical morphology and distance maps to automatically delineate the liver and related structures was shown to be beneficial to radiologists when compared with traditional reading of the CT scan [57].

1.4 Tumor Burden

The tumor burden, the percentage of total tumor in the liver, is commonly used to monitor the evolution of disease in patients with hepatic cancer. The measure of tumor burden can be used for developing treatment protocols [27]. Tumor burden also provides meaningful comparison between different treatment regimens, and has been shown to be accurate as an assessment of prognosis. An accurate assessment allows both physicians and patients to make better therapeutic choices earlier [17].

The quantification of tumor burden with CT and magnetic resonance (MR) imaging is being used with increasing frequency to assess the effectiveness of cytotoxic anticancer drugs [46]. Tumor sizes are typically estimated from measuring the maximum tumor diameters in the transverse plane; often, the largest perpendicular tumor diameters are also taken into consideration [12]. Pretreatment and post-treatment cross products are compared to categorize treatment response. Considerable inter-observer variation among radiologists in CT linear tumor measurement has been reported [24], especially for ill-defined and irregular lesions common in hepatic cancers.

Computer-aided detection and segmentation techniques can supply precise tumor volumes. Automated volumetric measurements reduce the inter-observer variability in estimating the size of lesions that are confluent and irregular. Another advantage of volumetric measurements is the calculation of overall tumor burden in an organ, which eliminates the arbitrary guideline of measuring five indicator lesions per organ. For the liver, a CAD system should be sufficiently accurate to segment both the liver and liver tumors from typical variable clinical data to correctly estimate the tumor burden.

1.5 Our Approach

We first present a novel automated technique to segment diseased livers from everyday CT data with inconsistent contrast-enhancement and imaging artifacts. A robust parameterization of 3D surfaces, like those of abdominal organs, is proposed for the comparison of objects by point-to-point correspondence. 3D objects are represented by parallel planes that intersect the surface of objects in closed planar curves. This spatial representation avoids common problems with the surface parameterization of concave objects. To compare local shape features of two organs we employ a shape descriptor invariant under rotation and scale and robust to noise. Once shape ambiguities are detected on an initial segmentation of the liver, a shape-driven geodesic active contour improves the segmentation significantly even in severe cases.

From the segmented liver, graph cuts are employed to detect and segment hepatic tumors using shape and enhancement constraints. Features are extracted for the tumor candidates and classification is performed using support vector machines. The segmentation techniques are evaluated using several databases, some public, for an adequate comparison with the exiting literature. The liver tumor burden is computed from the segmented liver and tumors. The automated liver analysis technique allows monitoring and diagnosing patients with abnormal livers under poor image quality and inconsistent enhancement, and provides assessments for treatment and disease evolution.

2 Methods and Materials

A schematic showing the pipeline of the technique is illustrated in Figure 1. The study included 101 CT scans from 68 patients from a variety of public and clinical sources. The acquisition and analysis of clinical data at the National Institutes of Health was approved by the NIH Institutional Review Board and informed consent was waived. The use of the public cases was approved by the NIH Office of Human Subjects research. The groups of data are described in detail below.

Figure 1.

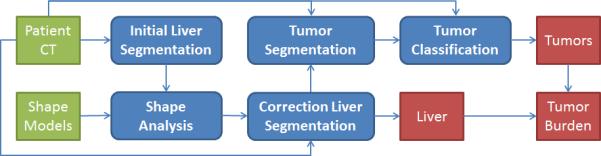
A schematic of the automated technique for tumor burden analysis. The green and red boxes show the input and output data, respectively. The blue boxes represent the modules of the algorithm starting with the initial liver segmentation (Section 2.1), continuing with shape analysis (Section 2.2) and the corrected liver segmentation (Section 2.3), and the segmentation and classification of tumors (Sections 2.4 and 2.5).

The main clinical test set consisted of 50 abdominal CT scans collected from 17 patients with prostate cancer at single/multiple time-points on five different scanners at our institution. Image resolution was 0.63 to 0.92 mm in the axial view with 5 mm slice thickness. Images were acquired prior to and following intravenous contrast administration; contrast data were obtained at varying enhancement times from early-arterial to late portal venous phases. Additional to the inconsistent enhancement, cases with imaging and movement artifacts were present in the database. The volumes of the 50 test livers were available from clinical reports (estimated by image processing technologists supervised by experienced radiologists). These manual measurements were performed on enhanced and non-contrast data (though only a few latter cases were present in the clinical test set) independently from this study and no segmentation results were available with the exception of the numerical value of the volume. The liver volume ranged from 1.07 L to 4.08 L, including cases with mild and severe hepatomegaly. Twenty-two of the 50 clinical test cases presented tumors of highly variable size. Tumors were manually segmented in 14 of the clinical cases (79 tumors) with metastatic liver cancer by a research fellow supervised by an experienced radiologist. The tumor size varied from 10.0 to 206.4 mm in the largest diameter. All manually segmented tumors were analyzed on contrast-enhanced images, as tumors are poorly visible (or even invisible to the eye) without enhancement.

The liver shape training set consisted of 27 scans from 27 patients acquired clinically at our institution at high resolution (1 mm slice thickness and sub-millimeter axial resolution). This dataset consisted of normal and hepatomegaly (enlarged liver) cases. The livers were manually segmented in the 27 CT data by three research fellows supervised by an experienced radiologist.

Additionally, 10 anonymized public cases (10 patients), mainly pathological, with manual liver segmentations from the MICCAI liver segmentation challenge held in 2007 [22] were used for testing the automated segmentation of livers. The MICCAI cases were acquired on a variety of scanners, had contrast enhancement and no imaging artifacts. Images had 1-5 mm slice thickness and 0.5-0.8 mm axial resolution. The ground truth data was available only to the organizers of the competition (www.sliver07.org).

Four more anonymized public pathological cases with manual segmentations of ten hepatic tumors from the MICCAI liver tumor segmentation challenge held in 2008 [11] (http://lts08.bigr.nl/) were used to test the automated segmentation of liver tumors. Cases were obtained using three scanners and a contrast-enhanced imaging protocol with slice thickness of 1-1.5mm and in-plane resolution of 0.6-0.9mm. There was no ground truth available for the segmentation of livers in these four cases.

2.1 Initial Liver Segmentation

All test CT images were automatically cropped at the first slice containing the liver. For that purpose the lungs were segmented through histogram analysis and image parsing in the cranio-caudal direction identified the liver dome. Livers were automatically segmented from the 74 test CT cases using a technique previously designed for the analysis of hepatic artifact-free CT data acquired at portal-venous enhancement and applied to patient data with less severe liver diseases [34]. The segmentation technique was based on a probabilistic atlas of the liver constructed from training data. For the coarse estimation of organs, an average model of the liver was registered to the patient's contrast-enhanced CT image. This estimation was improved by a geodesic active contour. Subsequently, the patient specific intensity statistics inside the liver were estimated and used to discard tissue areas that did not satisfy the intensity constraints. Finally, location corrections from the normalized probabilistic atlas were performed [34]. While the probabilistic analysis ensured some level of compliance with the pathologies in the test data, unsurprisingly, there were large segmentation errors on difficult clinical cases. Notably, after this preliminary liver segmentation, 19 of the 50 clinical test cases had severe liver segmentation errors (>10% volume error) and the other 31 livers exhibited small to moderate errors (<10% volume error).

2.2 Shape Analysis and Surface Parameterization

To detect shape ambiguities, a 3D-analogue of a curvature-feature [37] was used as shape feature S for comparing closed planar curves [62]. Specifically, at a given point p on a planar curve, S is the area of intersection of the interior of the curve and a ‘seed’ (a sphere centered at p). S of a curve C can be used for both local (at every corresponding point on two matched curves) and global comparison of two curves, given an adequate simultaneous parameterization of the two curves (Figure 2).

$$S\left(p\right)=\frac{{\int }_C{V}_r(p,x)dx}{{\int }_{{\Re }^3}{V}_r(p,x)dx};$$

V_r(p) is an indicator function on the interior of the spherical seed centered at p. S is then the normalized volume of the intersection of C and the seed sphere of radius r centered at a point p. A compensation function accounted for the pixelation of digital objects. The shape descriptor is rotation and scale invariant by design and robust to noise [37].

Figure 2.

An illustration of the shape descriptor on 2D closed curves. The seed is a circle that intersects the objects (here a square and a larger circle). Given a correct parameterization of the two closed curves, their point-to-point local difference can be assessed.

To allow point-to-point comparisons across multiple surfaces, our method uses the structure of a general class of objects we call ‘planar-convex’. We assume that livers fall under this category. We define a planar-convex object O in ${\Re }^n$ to be a closed surface for which a set of parallel hyper-planes P exists, such that every intersection of a plane in P with O results in a singular closed planar curve. We call each set of parallel hyper-planes which intersects with O in this way ‘convexity planes’ [62]. Some 2D examples are shown in Figure 3.

Figure 3.

Objects represented in the planar-convex space. Objects include the simpler ‘V’ shape (left), a non-star shape domain such as the ‘S’ shape (middle), and the more irregular ‘ink blot’ shape (right). Convexity planes are colored blue, while their intersections with the respective objects are shown in red.

To find convexity planes, we could search over all sets of parallel planes with normal-vectors lying on the top unit-hemisphere. An approximation to doing this is to search over a uniformly spaced sampling on the top-half of the unit sphere. Such a uniform sampling is provided by the vertices of a dodecahedron. We choose a dodecahedron with 32 vertices for ease of computation and sufficient sampling power. Thus, to match two objects, we align their principal components and then orient about the object's largest principal component a set of symmetric points comprising the vertices of a dodecahedron for sampling. Each intersection of the planes with the liver is then analyzed and the average number of connected components is found. The minimum sum of average components across the corresponding axes/planes of the two compared objects is then computed. This defines the set of matched convexity planes P (as defined above) between the two compared objects. The number of convexity planes could be varied with the surface size, but it was kept constant to eight in our application.

The surface of each convexity plane is uniformly sampled by a user-defined number of partitions, with points at these partitions being projected onto the object surface (Figure 4). Figure 4 also shows an example of liver parameterization. These projections or ‘parameterization points’ have point-to-point correspondence between the compared objects/livers.

Figure 4.

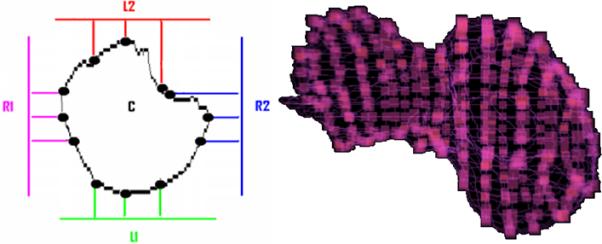
Parameterization points. Left - Uniformly spaced points are projected onto the object in the convexity plane shown in different colors. Right – the parameterization points are highlighted as small cubes on the surface of a liver with irregular shape, when 13 convexity planes were used. These points allow point-to-point correspondence between two shapes.

2.3 Correction of Liver Segmentation

At each parameterization point we compute the shape feature S on both matched objects’ surfaces to allow the visualization of results. The dissimilarity between two matched shapes (a training and a test shape) at p is computed as the absolute difference of their shape features S at p: a large value indicates high dissimilarity, while zero is the perfect match. The dissimilarity at p is then averaged as the mean value between dissimilarities with all training shapes at p. By using the average, we avoid similarity to a single shape in the reference database that may be itself unusual. I_s is the shape image obtained from extrapolating the dissimilarity values on the surface of the test liver, normalized between 0 and 1.

From the initial liver segmentation, the shape analysis on matched surface points with training data identifies areas on the surface of the liver that have ambiguous shape. To allow some level of intra-patient variability, I_s is thresholded at 0.5 and component analysis used to assign individual labels to each ambiguous area. As livers were primarily undersegmented by the initial method [34], seeds are placed at the centroid of these labels and a fast marching level set [53] employed to “grow” the segmentation based on the sigmoid of the gradient of the CT image. A geodesic active contour [8] refines the segmentation. Our formulation of the geodesic active contour (I_g) includes I_s as shape condition.

$$\frac{d{I}_g}{dt}=(I_e+I_s)(c+k)\mid \nabla I_g\mid +\nabla I_e\nabla I_g,$$

where I_e is the sigmoid of the gradient of image I with parameters α=−0.5 and β=3.5 [25], c=1 is the speed parameter and k=1 the curvature. The stopping condition of the adaptation of the active contour is that I_s < 0.5 or the volume change between iterations becomes insignificant.

2.4 Liver Tumor Segmentation

With the liver segmented, a graph-cut approach [4] is applied to find hepatic tumors. In the basic form, graph cuts suffer from the shrinking bias problem, particularly for segmenting elongated and small structures, such as the blood vessels and certain types of tumors [30]. Graph-cuts were shown to improve the segmentation of abdominal organs in [35] using training shapes, but tumors are highly variable between cases. However, tumors are generally round.

The graph cuts method for image segmentation operates by finding a globally optimal cut through the graph based on the input data. Let A = (A₁, A₂, ..., A_p, ...) be a binary vector with components A_p that can be either objects of interest (tumors) denoted by O or background B (healthy liver parenchyma), where $B\cap O=\varnothing$. Typical graphs perform data labeling (t-links), via log-likelihoods based solely on interactive histogram fitting, and penalize neighborhood changes (n-links) through likelihoods from the image gradients [4]. In our application, seed points were generated automatically for the tumors by finding adaptive thresholds in the data. Multiple intensity threshold values are tried and the number of remaining voxels inside the liver is plotted against the threshold value. The resulting curve is then approximated by pairs of fitted lines as in [52] and the optimal threshold is the one that generates the pair of lines with the highest sum of correlation coefficients. Additionally, the object seed points were further constrained to have non-zero Hessian-based shape response, as described below.

Background seeds were obtained from the inverted binary image of the foreground seeds followed by morphological erosion.

The cost function of the graph E in our application can be written as

$$E\left(A\right)=E_{data}\left(A\right)+E_{enhance}\left(A\right)+E_{shape}\left(A\right)+E_{boundary}\left(A\right)$$

$$E_{data}\left(A\right)=-\sum _{p\in O}\ln \left(\frac{\sqrt{P(I_p\mid O)}}{\sqrt{P(I_p\mid O)}+\sqrt{P(I_p\mid B)}}\right)-\sum _{p\in B}\ln \left(\frac{\sqrt{P(I_p\mid B)}}{\sqrt{P(I_p\mid O)}+\sqrt{P(I_p\mid B)}}\right)$$

with

$$E_{boundary}\left(A\right)=\sum _{\{p,q\}\in N_p}\exp \left(-\frac{{(I_p-I_q)}^2}{2{\sigma }^2}\right)\frac{1}{d(p,q)}.$$

and I_p is the voxel intensity at p, P(I_p|O) the probability of I_p to be object (O), N_p a local neighborhood of p, d(p,q) the Euclidean distance between two voxels p and q, and σ the standard deviations of image noise [4].

The new terms in the formulation are E_enhance and E_shape. E_enhance is the regional term that penalizes voxels that do not follow the difference in the enhancement distribution between the tumor and healthy liver parenchyma models, as determined from training. With our database, E_enhance encourages darker regions inside the liver to be labeled as tumors, as the healthy liver is brighter than the cancerous tissue. This relation between the healthy (background) and unhealthy (object) liver changes during training for other types of liver cancers.

$$E_{enhance}\left(A\right)=\sum _{\{p,q\}\in N_p}\frac{1}{1+{\left(\frac{{\left(I_O^p-I_B^q\right)}^2}{2{\sigma }^2}\right)}^2}$$

where $I_O^p$ is the intensity value at p given that p is an object (O) and $I_B^p$ the intensity value at the background (B).

E_shape is a Hessian-based shape condition to emphasize rounder tumors at multiple scales σ. The eigenvalues of the Hessian (λ₁ > λ₂ > λ₃) at point p define unique shape constraints to optimize the segmentation of tumors and reduce tumor false positives [48]. The following energy terms are incorporated in the graph-cut definition

$$E_{shape}=-\ln \underset{\sigma }{\max }\left(w\right);\text{with}{\lambda }_3>0;\text{and}w=e^{-\left(\frac{{\lambda }_1}{{\lambda }_3}1\right)}.$$

The method does not intend to segment the hepatic vasculature, as the enhancement in our cases is irregular. To account for the slight undersegmentation of tumors, a classic geodesic active contour [8] was employed to refine their segmentation with a speed propagation parameter of 5 and a curvature parameter of 2.5. The total volume of tumors was computed for each patient and normalized by the total liver volume to compute tumor burden and monitor cases with metastatic hepatic cancer. The tumor burden error is estimated as the absolute difference between manually and automatically measured tumor burdens. To study the reproducibility of the estimation of tumor burden under image noise and patient position variation, artificial Gaussian noise and body rotations in the axial plane were induced in one dataset and the tumor burden recorded and compared to the ground truth.

2.5 Tumor Features and Classification

For each tumor candidate a set of 157 features were automatically computed to characterize the detection. They include size, enhancement, 3D shape, 3D texture and statistics of these measures, as shown in Table 1. Due to the large number of features used for classification, feature selection was used to retain the optimal combination of features for the separation of true positive (TP) from false positive (FP) detections. Since these features can be redundant and correlated, identifying the most informative and independent features is keypoint to the success of the classifier. Otherwise the discriminant information hidden in these features may be contaminated or affected by noisy features when we calculate similarities between training samples which in turn will lead to poor classification accuracy. To address this issue, we conducted experiments on feature selection using the minimum redundancy and maximum relevance feature selection method (mRMR) [44]. mRMR is a state-of-the-art feature selection method popular in biomedical data analysis. It selects good features according to the maximal statistical dependency criterion based on mutual information and minimizes the redundancy among features simultaneously.

Table 1.

One hundred and fifty-seven automated tumor features were computed for the tumor candidates. Edge refers to the two pixel-wide band of liver tissue surrounding the tumor.

3D Features	Descriptor	Explanation
Tumor Volume	Size	Volumetric size.
Tumor Diameter	Size	Linear size
Tumor Size Region Ratio	Shape	Ratio of the size of the object bounding box and the real size of the object
Tumor Binary Elongation	Shape	Ratio of the largest principal moment by the smallest principal moment
Tumor Roundness	Shape	Sphericity
Tumor Hessian Eigenvalues	Shape	Local extrema and stationary points
Tumor Blobness Measures	Shape	Roundness from the Hessian eigenvalues
Tumor Intensity*	Enhancement	Enhancement of tumor
Edge Intensity*	Enhancement	Enhancement of healthy parenchyma
Tumor Cluster Prominence*	Texture	Skewness / asymmetry
Edge Cluster Prominence*	Texture	Skewness / asymmetry
Tumor Cluster Shade*	Texture	Skewness / asymmetry
Edge Cluster Shade*	Texture	Skewness / asymmetry
Tumor Correlation*	Texture	Correlation / complexity
Edge Correlation*	Texture	Correlation / complexity
Tumor Energy*	Texture	Uniformity
Edge Energy*	Texture	Uniformity
Tumor Entropy*	Texture	Randomness
Edge Entropy*	Texture	Randomness
Tumor Haralick Correlation*	Texture	Linear dependence between the voxels relative to each other.
Edge Haralick Correlation*	Texture	Linear dependence between the voxels relative to each other.
Tumor Inertia*	Texture	Local heterogeneity
Edge Inertia*	Texture	Local heterogeneity
Tumor Inverse Difference Moment*	Texture	Local homogeneity
Edge Inverse Difference Moment*	Texture	Local homogeneity

^*indicates that the min, max, mean, standard deviation, variance, median, kurtosis and skewness were computed for the feature. For definitions of the texture features computed from the co-occurrence matrix please refer to [19].

Support vector machines (SVM) are a set of kernel-based supervised learning methods used for classification and regression. Kernel refers to a matrix that encodes the similarities between samples (evaluated by a certain kernel function, which is a weighting function in the integral equation used to calculate similarities between samples). SVM minimize the empirical classification error and maximize the geometric margin simultaneously on a training set, which leads to a high generalization ability on the test samples. Through feature selection, SVM optimize the similarity between samples to maximize the margin between the two classes of samples (TP and FP). For training and testing purposes, a leave-one-patient-out strategy was employed.

The receiver operating characteristic (ROC) curves for the hepatic tumor detection were generated with and without feature selection to record the effects of classification and feature selection on the reduction of false detections. The performances of the two classifiers (with and without feature selection) were compared using ROCKIT [39]. ROCKIT uses maximum likelihood estimation to fit binormal ROC curves and calculates the statistical differences between ROC with regard to the difference in the areas under the curve (AUC).

3 Results

The livers were shown to be planar-convex. In other words, for each organ there exists a set of parallel planes such that every intersection of a plane and the organ is a closed planar curve. Planes were found uniquely for each pair of compared livers or shapes. The planar convexity attribute was valid for every combination of livers paired between the training and testing set, and allowed to identify local shape discrepancies.

The preliminary segmentation technique was less accurate than previously reported [34] due to the presence of tumors and artifacts in our data, and an inconsistent acquisition of contrast-enhanced images. Quantitative results from applying our method to the automated segmentation of the liver are shown in Table 2 before and after the segmentation correction. The use of liver-to-liver shape parameterization coupled with geodesic active contours reduced the percentage of volume error significantly for both cases of severe segmentation failure and cases in need of only minor/moderate adjustments.

Table 2.

Volume Error (VER) for liver segmentation from the clinical test data (5mm slice thickness). The initial automatic segmentation results are compared to results following shape analysis and corrected (final) segmentation; p-values were calculated via the Wilcoxon rank sum test. Variability in initial VER ranged from <2% to >50%; cases were separated into severe errors (VER>10%) and small/moderate errors (VER<10%). Cases with small errors, large errors and hepatic tumors are shown separately. Additionally, the last row presents the results on the MICCAI dataset (slice thickness 1-5mm).

Group/VER (%)	Initial Segmentation	Final Segmentation	p-value
Small Error (n=31)	5.3±2.4	2.9±2.2	<0.001
Severe Error (n=19)	28.9±14.3	6.6±7.3	<0.001
Tumors (n=22)	17.0±15.8	5.2±6.9	<0.001
All clinical cases (n=50)	9.3±13.5	3.8±5.3	<0.001
MICCAI (n=10)	-	2.2±2.3	-

Our technique improved significantly the segmentation of cases with large tumors and segmentation errors (p<0.001), while avoiding the generation of errors in well-segmented livers (Table 2). Additionally, a t-test was performed between the results (volume errors) of liver segmentation on the clinical test set and the MICCAI set (shown in Table 2); the p-value was 0.07. Figure 5 presents an example of segmentation from a case with artifacts and without contrast-enhancement, a moderately inaccurate segmentation, and a severe segmentation failure with their corresponding shape images and final corrected outputs.

Figure 5.

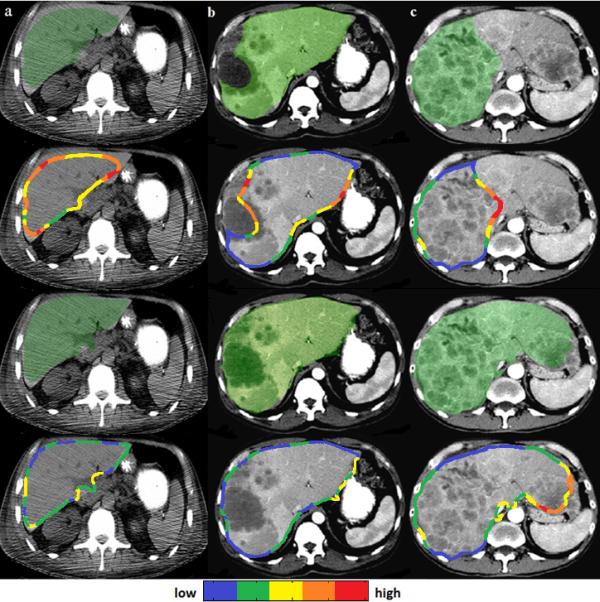
Examples of liver segmentation (overlaid in green on axial views of 3D CT data) of a case without contrast enhancement and with motion artifacts (a), a moderately inaccurate segmentation (b), and a severe segmentation failure (c). Initial segmentations are shown in the top row and their corresponding shape images in the second row. Shape ambiguities are depicted in a cold (low) to hot (high) colormap. The corrected liver segmentations are shown in the third row and their corresponding shape images in the bottom row.

More quantitative results were obtained on the segmentation of livers from the MICCAI liver data. The volume overlaps between manual and automated segmentations were 93.6±1.4% (Jaccard Index) with 2.2±2.3% volume error, 1.0±0.3 mm average surface distance and 1.9±0.5 mm root-mean-square distance. The average score obtained with the evaluation software offered by the organizers of the MICCAI liver competition was 76.2; for details please refer to [22].

The volume error was used to estimate the sensitivity of the method to the number of training liver shapes. The error becomes stable at approximately 14 training shapes, though not at the optimal value, which is reached when about 23 training shapes are employed, as shown in Figure 6. Our method uses 27 training cases to ensure that sufficient inter-patient variability is captured.

Figure 6.

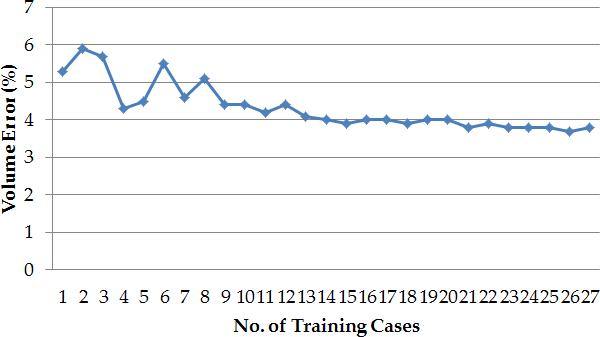
The variation of the volume error (estimated over the 50 clinical cases) with the number of training liver shapes.

The results of the detection and segmentation of hepatic tumors are presented in Table 3. All 79 tumors in the clinical test set were correctly identified. False positives occurred generally near the porta hepatis and coronary ligaments, where there is lack of enhancement and high curvatures. There was no significant difference between the manual and automatic measurements of tumor burden (p>0.6 from the Wilcoxon rank sum test).

Table 3.

True Positives Fraction (TPF) and false positives (FP)/case are reported for the detection of hepatic tumors. Automated and manual segmentations of tumors were compared and we present Dice Overlaps (DC), Jaccard Index (JI), Volume Errors (VER) and Average Surface Distances (ASD). The Tumor Burden Error (TBE) is the difference between manually and automatically measured tumor burdens.

Group	TPF (%)	FP/case	DC (%)	JI (%)	VER (%)	ASD (mm)	TBE (%)
79 tumors (n=14 )	100.0	3.1	74.1±16.9	70.9±17.7	12.4±12.0	1.6±1.5	0.9±1.0
10 MICCAI tumors (n=4)	--	--	75.4±9.0	72.6±9.3	13.9±12.6	1.3±0.5	--

Table 3 also presents quantitative results for the segmentation of the ten tumors in the MICCAI liver tumor dataset with similar results to those obtained on the clinical test set. The TP, FP fraction and tumor burden could not be calculated for this dataset, as there was no ground truth available for the total number of tumors and the volumes of the livers. The errors in estimating tumor burden under variations in image noise and patient position are presented in Table 4. The range of tumor burden errors is [0.96% 1.57%].

Table 4.

Tumor burden error under variations in image noise and patient position. The columns show the level of artificial Gaussian noise in the image and the rows the induced degree of axial rotation of the patient body.

Noise/Rotation	0%	5%	10%	20%
0°	1.12%	1.10%	1.21%	1.32%
5°	0.96%	1.09%	1.19%	1.27%
10°	1.17%	1.15%	1.24%	1.39%
20°	1.37%	1.42%	1.47%	1.57%

Figure 7 illustrates the manual and automatic segmentation of hepatic tumors for two patients, each at two time points. Manual, automatic, and false positive segmentations are presented for comparison. In Figure 8, the change over time in liver volume is presented for several patients. Figure 9 shows quantitatively the change in tumor burden in the five patients with multiple scans at different time points and manual measurement of the tumor burden.

Figure 7.

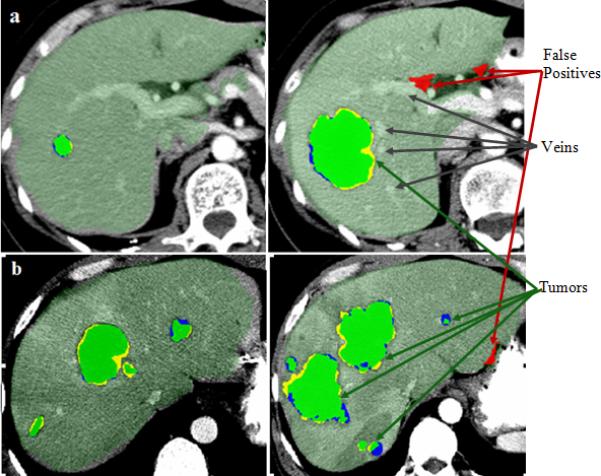
Examples of hepatic tumor segmentation: manual (blue), automated (yellow) and their overlaps in green overlaid on axial views of 3D CT of two patients (a) and (b), each at two time points (different CT scans of the same patient). False positives from the automated segmentation are displayed in red. The two cases also illustrate the difference in the enhancement protocols with well-enhanced portal and hepatic veins in (a), which are not visible in (b).

Figure 8.

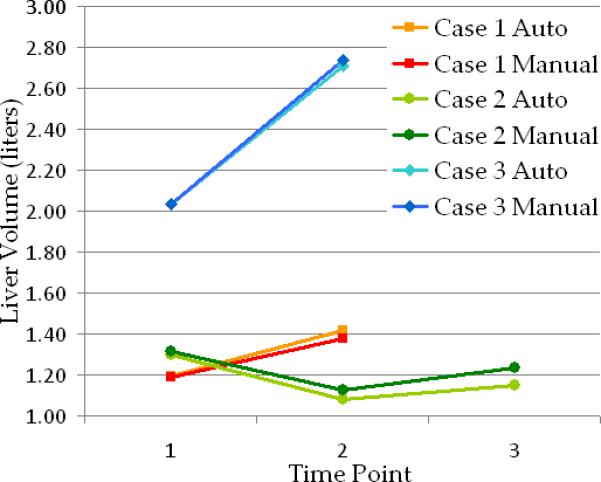
Examples of change over time in liver volume for three cases from the clinical data with small (case 1- red), moderate (case 2- green) and large (case 3- blue) metastatic liver tumors. Manual and automated estimations are presented for comparison. Image data for cases 1 and 3 are shown in Figure 7.a and 7.b respectively.

Figure 9.

The change in tumor burden in five patients with two (cases 2, 3 and 5) and three (cases 1 and 4) scans obtained at different time points. The automated measures are compared with the manual estimates of tumor burden at each time point.

The SVM classifier was employed after extracting 157 features for each true and false tumor candidate. Without feature selection, the AUC of the classifier was 0.62. The maximum AUC of 0.85 was achieved for a combination of eight tumor candidate features. The eight selected features were a combination of intensity, shape and texture inside and outside the tumor candidates. Namely, the eight selected tumor features were: the median intensity, roundness, mean λ₁, mean λ₃, and minimum value of the Haralick correlation. Additionally, the following features computed around the edge of the tumor were retained for classification: the median of the energy, and kurtosis and variance of the inverse difference moment.

The SVM classifier with eight features achieved a sensitivity of 100% TP at 2.3 FP/case (or 94% TP at 1.6 FP/case). There was a significant difference (p<0.001) between the SVM classifiers with and without feature selection. Feature selection resulted in 24% sensitivity increase at 1.6 FP/case, as shown in the free-response ROC curves in Figure 10.

Figure 10.

The top figure shows the variation of AUC with the number of features used in the SVM classification. The maximum AUC was achieved using eight features. The bottom figure shows comparative free-response ROC curves using eight (SVM 8) and all 157 (SVM 157) features for classification. The difference between the two classifiers was significant (p<0.001).

4 Discussion

The focus of this manuscript is on the computer-assisted analysis of diseased livers from noisy data with highly variable pathology, as existing techniques often fail when the liver is abnormal and imaging conditions are not ideal. CT data were acquired from a cohort of patients with metastatic liver cancer with highly variable contrast enhancement. Imaging and movement artifacts were also present in the database. It can be noted both visually from Figure 5 and Figure 7 and from the results in Table 2 that the livers in our clinical test set originate from patients with very complex diseases and images difficult to process.

First, we introduce a technique for shape parameterization with promising results for point-to-point matching of abdominal organs with complex anatomy. The parameterization, combined with an invariant shape feature allows comparing local shape across abdominal organs, such as the liver. While the shape parameterization is intuitively robust, it is difficult to judge the accuracy of point correspondences, which is dependent on the type of data and application. We hope to have achieved a simpler and more intuitive way to represent abdominal organs. The level set representation in [43] could be an alternative and it was shown to work with a variety of shapes. Besides the relative simplicity of our parameterization, we avoid using nonlinear registration in the absence of anatomical landmarks to control it. Importantly, the proposed shape parameterization scheme allows the identification of local shape incongruities between one object and a shape training set to guide the segmentation of difficult or usual data.

Our confidence in claiming that planar convexity occurs generally with organ-surfaces is based on the results of our tests comparing local shape of 101 livers and our intuition based on experience with radiological data outside of this project. In our liver database, the assumption of planar-convexity was valid in 100% of cases. Perhaps offering some examples of curves/surfaces that are not planar-convex, such as curves/surfaces with a hole or large-scale concave indentation, can provide some helpful clarification. Finding a set of convexity planes for the surface is equally essential for the parameterization. The planar convexity assumption is used to find a uniformly spaced set of points on the surface of the liver. Thus, a set of convexity planes helps to cover the surface fully with the sampling of points. Additionally, this uniform sampling allows dimensionality reduction for shape analysis, which is time-consuming.

Once shape differences are identified, the preliminary segmentation of the liver, which was obtained using probabilistic atlases and level sets, is corrected through active contours governed by image and shape information. Comparative results before and after shape correction show significant improvements (p<0.001) on the accuracy of liver segmentation in even the most difficult cancerous cases. Cases with severe segmentation errors had their volume error improved from 28.9% to 6.6%, while cases with tumors went from 17.0% to 5.2% volume error.

The tumor detection and segmentation is achieved using graphs constrained by shape and enhancement models. This allows to segment tumors of variable sizes with a reduced number of false positives. The method does not specifically address the heterogeneity of some liver tumors. The combination of enhancement and shape constraints in the segmentation of tumors is generally robust to heterogeneous patterns, as illustrated by results, but may struggle with unusual cases. Additionally, we propose an extensive set of appearance, shape and texture features (see Table 1) to be computed for each tumor candidate (inside and outside the tumor) and demonstrate that the number of false detections is reduced significantly through feature selection and classification using support vector machines. Interestingly, the selected tumor features describe the intensity/enhancement, shape/roundness and the linear dependence of voxels inside the tumor, while the features computed on the tissue around the edge of the tumor represent measures of the uniformity and local homogeneity of the normal liver parenchyma. For both segmentation and classification, information is used from a single enhancement phase, preferably the portal venous phase.

All tumors were correctly detected at 2.3 false positives/case. The segmentation of tumors resulted in 74% volume overlap between manual and automatic segmentations and 1.6 mm average surface distance and allowed to compute the liver tumor burden, which was estimated with an error of 0.9% (the difference between manually and automatically measured tumor burdens). The results of our method on the MICCAI liver tumor data [11] are comparable to those achieved by the best automated method presented at the competition [55]. Namely, the overlap error, volume error and average surface distance were 27.4%, 13.9% and 1.3 mm for our method compared to 28.9%, 18.2% and 1.8 mm in [55]. The MICCAI liver tumor competition data represented a range of pathologies with variable enhancement, including hepato-cellular carcinoma, hemangioma and metastases. The clinical test set consisted of metastatic prostate cancers. These tumors tend to enhance less, though heterogeneously, than the healthy liver parenchyma.

A similar comparison was performed with the results of the MICCAI liver segmentation competition [22]. The MICCAI liver competition used mainly pathological cases, including primary tumors, metastases and cysts, but the types of pathologies were not available for consultation. Our results on the MICCAI liver data are comparable to those achieved by the best two automated liver segmentation method presented at the competition [28,63]. Namely, the overlap error, volume error, average surface distance, root-mean-square distance and score were 6.3%, 2.2%, 1.0 mm, 1.9 mm and 76.2 for our method compared to 6.0%, −2.8%, 0.9 mm, 1.8 mm and 77.3 for the technique in [28], and 6.4%, 1.0%, 1.0 mm, 2.0 mm and 76.8 for the algorithm in [63]. More details can be found at www.sliver07.org.

As reviewed at the beginning of the manuscript, different methods in the literature model the image information to segment the liver and tumors. In particular, statistical shape models were successful to segment the liver [28] and machine learning methods were effective to analyze tumors [55]. Our approach combines anatomical (shape) and physiological (appearance/enhancement) modeling for both liver and tumor analysis. Additionally, probabilistic location information is used to segment the liver and an extensive set of tumor and healthy parenchyma features are employed via machine learning techniques for tumor analysis.

In our approach, level sets were used to correct segmentations given detected objects, while the initializations were performed by probabilistic atlases and graph-cuts for the liver and tumors respectively. Hence, discrete approaches were used for an initial estimation of the object of interest and the segmentation was refined by continuous formulations. In this scenario, histogram fitting and enhancement and location constraints were employed to both detect the objects and initiate their segmentation. Please note that the level sets in our approach were designed to grow the segmented object from their initial segmentation and correct where the intensity model was insufficiently supple.

The running time for one case was between 50-60 min, including about 30-35 min for the initial liver segmentation, 20-25 min for liver segmentation correction and a couple of additional minutes for tumor analysis. The most expensive computation part of the algorithm was the registration.

The low rate of false positives in the detection of hepatic tumors and the very small error in the tumor burden by the proposed technique suggest the high clinical utility of the computer-assisted tool for liver analysis. False positives are generally small, easily identifiable by radiologists and do not add substantially to the tumor burden, which is performed at each time-point independently when a patient has multiple CT scans. Another potential application of the method would be tumor grading, a highly important area in radiology and diagnosis and a subject of future work.

The method proposed in this paper is designed for general liver image analysis, but due to the availability of data, was applied to metastatic liver cancer. Future developments of the technique aim to constitute a computer-aided system for the fully automated integrated analysis of the liver. Importantly, this study brings together the automated segmentation of the liver with the detection, segmentation and classification of hepatic tumors from typical clinical radiological data with variability in imaging acquisition parameters.