Geometric Control of Capillary Architecture via Cell-Matrix Mechanical Interactions

Abstract

Capillary morphogenesis is a multistage, multicellular activity that plays a pivotal role in various developmental and pathological situations. In-depth understanding of the regulatory mechanism along with the capability of controlling the morphogenic process will have direct implications on tissue engineering and therapeutic angiogenesis. Extensive research has been devoted to elucidate the biochemical factors that regulate capillary morphogenesis. The roles of geometric confinement and cell-matrix mechanical interactions on the capillary architecture, nevertheless, remain largely unknown. Here, we show geometric control of endothelial network topology by creating physical confinements with microfabricated fences and wells. Decreasing the thickness of the matrix also results in comparable modulation of the network architecture, supporting the boundary effect is mediated mechanically. The regulatory role of cell-matrix mechanical interaction on the network topology is further supported by alternating the matrix stiffness by a cell-inert PEG-dextran hydrogel. Furthermore, reducing the cell traction force with a Rho-associated protein kinase inhibitor diminishes the boundary effect. Computational biomechanical analysis delineates the relationship between geometric confinement and cell-matrix mechanical interaction. Collectively, these results reveal a mechanoregulation scheme of endothelial cells to regulate the capillary network architecture via cell-matrix mechanical interactions.

1. Introduction

Tissue engineering, a rapidly emerging field in regenerative medicine, holds great potential for providing solutions to numerous diseases by creating replacement tissues to restore, maintain, or improve tissue function [1, 2]. A critical challenge in building any tissue, however, is the requirement of microvasculature for sufficient oxygen and nutrient transport to support cell growth and function [3]. The generation of a functional microvasculature within the tissue construct is essential toward the overall goal of tissue engineering. Furthermore, the formation of new blood vessels is critical in numerous malignant, ischemic, inflammatory, infectious and immune disorders [4]. An in-depth understanding of capillary morphogenesis and the capability of controlling the process, therefore, will have important implications on repair or replacement of defective tissues and other novel approaches of disease therapeutics.

Capillary morphogenesis is a multistage, multicellular activity that plays essential roles in various developmental and pathological processes [5]. During capillary morphogenesis, cells migrate, elongate and self-organize into capillary structures. For instance, vasculogenesis is the de novo formation of primary capillary plexus from angioblasts during embryonic development [6]. Organs of ectodermal origin, such as brain and kidney, are vascularized by angiogenesis – the outgrowth of new capillaries from existing vasculature [7]. Angiogenesis is also responsible for new blood vessel growth at later developmental stages and in tissue repair. Within the context of tissue engineering, studies have been demonstrated to create pre-vascularized tissue constructs for integrating with the host vasculature [8, 9]. In these situations, capillary formation occurs in micro- or nanoengineered structures or materials with various confinements and physical properties. Nevertheless, the roles of these physical factors, such as geometric confinements and matrix mechanical properties, on the capillary architectures are poorly understood.

Intensive effort has been devoted to studying the effects of soluble chemical factors and fluid shear stress on angiogenesis [10–12]. Notch signaling, VEGF signaling, and matrix metalloproteinase activities are some of the key regulatory mechanisms in capillary morphogenesis [13–15]. Recently, emerging evidence has suggested that angiogenesis is controlled by the cell-matrix interaction that alters the cell shape and cytoskeletal structure. For example, the Rho inhibitor (p190RhoGAP) is demonstrated to control retinal angiogenesis in vivo by adjusting the balance between two transcription factors that regulate the expression of VEGF receptors [16]. Tissue contractility and deformation are also shown to induce the formation of VEGF gradients, which may contribute to the long-range patterning of the vascular system [17]. While mechanical factors are known to play essential roles in various cellular processes, such as tubulogenesis, elongation, and alignment, and directly influence scaffold design and material selection for tissue engineering [18–20], the effects of geometric confinement and cell-matrix mechanical interactions on the microvascular architecture have not been investigated systematically.

Here we study the effects of geometric confinement and cell-matrix mechanical interactions on capillary-like structures formed by human endothelial umbilical vein endothelial cells (HUVEC) on matrigel (Fig. 1A). This in vitro assay, which captures the migration, aggregation, and elongation steps observed in early angiogenic development, has been applied to investigate various aspects of microvasculature assembly [21–23]. We investigate the effects of geometric confinement on the network topology and mean cord length of the capillary architecture by creating microfabricated PDMS wells and fences. To clarify the roles of cell-matrix mechanical interaction on the boundary mediated network modulation, the thickness of the extracellular matrix is adjusted and the matrix stiffness is controlled by incorporating a cell-inert PEG-dextran hydrogel into the matrigel. The cell-matrix interaction is also modulated by reducing the cell traction force with a Rho-associated protein kinase inhibitor, Y-27632. Computational biomechanical analysis is also performed to qualitatively illustrate the interrelationship between geometric confinement and cell-matrix mechanical interaction, and facilitate the interpretation on the mechanoregulation of the capillary architectures.

Figure 1.

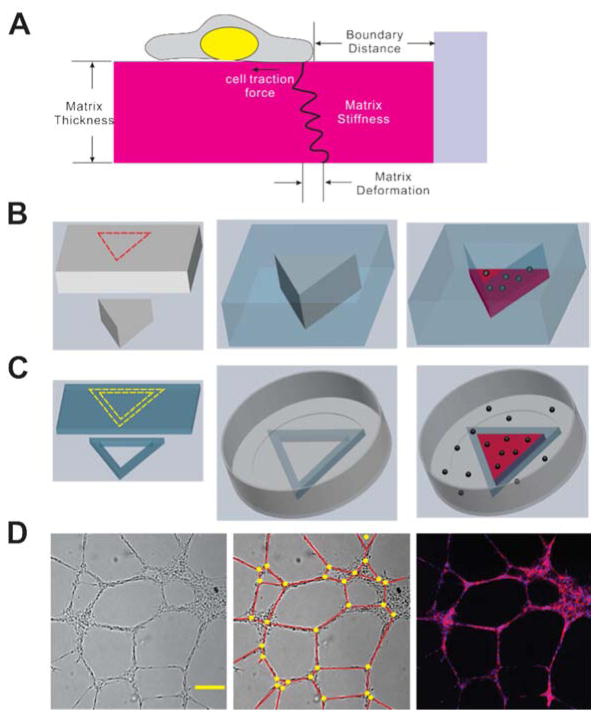
(A) Schematics of cell-matrix mechanical interactions and related physical factors, (B) Schematics of PDMS microwells fabrication (Grey: poly acrylic plate and mold; Blue: PDMS; Red dash lines: laser cut). (C) Schematics of PDMS microfences fabrication (Grey: Petri-dish; Blue: PDMS; Red: matrigel; Black spheres: endothelial cells; Yellow dashed lines: scalpel cut). (D) Bright field image (left) and fluorescent image (right) of capillary-like structures (Red: F-actin; Blue: nucleus). Scale bar: 200 μm. To quantify the cord length and network density, we defined node (Yellow circle) and cord (Red line) of capillary-like structures as was shown in (D, mid).

2. Materials and methods

2.1. Cell culture

HUVEC were obtained from BD Bioscience (Bedford, MA). The cells were cultured in Medium 200 with the addition of low serum growth supplement (Invitrogen, Carlsbad, CA) at 37°C, 5% CO₂. HUVEC were used from passages three to six in the experiments.

2.2. PDMS well and fence fabrication

A reverse molding process was developed to create geometric confinement in microwells (Fig. 1B). Briefly, positive molds with arbitrary shapes (e.g., circle, triangle, rectangle and star) were created from poly acrylic plates (6 mm in thickness) using a laser machining system (VersaLaser). Polydimethylsiloxane (PDMS; Sylgard 184, Dow Corning) at a 10:1 (base: curing agent) ratio was casted onto the mold, which was fixed to a petri dish with double-sided tapes. After incubation for 4 hours at 70°C, the molds surrounded by PDMS were cut and detached from the petri dish, and the PDMS wells were formed after removing the poly acrylic molds. The boundary lengths of the triangle, rectangle and five-pointed star were 10 mm, 10 mm and 5 mm respectively and the diameter of the circle was 10 mm. To fabricate the PDMS fences (Fig. 1C), 3.5 g PDMS was poured uniformly in a petri dish with 100 mm diameter to create a thin sheet (~600 μm thickness). Then, desired geometries were cut from the PDMS sheet to form the fences. Even after plasma treatment, PDMS did not bind strongly with polystyrene under standard dry condition. In order to attach the PDMS fence to the polystyrene petri dish (35 mm in diameter), they were both treated with air plasma followed by the bonding procedure in the presence of water and elevated temperature (70°C) overnight.

2.3. Measurement of gel thickness and stiffness

To control the thickness of matrigel (BD Bioscience, Bedford, MA), 60 μL matrigel was added to the well in a 96-well plate followed by aspiration of 30 μL or 50 μL matrigel with a precooled pipette. This approach allows the formation of relatively uniform matrigel layers with small thickness. The thickness of matrigel was measured by focusing at the gel surface and the well surface using an epi-fluorescence microscope (Nikon TE2000-U) with a 10× objective. To adjust the stiffness of the matrigel-based extracellular matrix while maintaining the ligand density for cell adhesion, 30 μL PEG-dextran hydrogel (3-D Life Hydrogel, pH 7.0, Cellendes, Reutlingen, Germany) obtained from different concentrations of Mal-Dextran and PEG-Link (0, 1 or 3 mM) was mixed with a fixed amount of matrigel (120 μL). The stiffness of the PEG-dextran hydrogel increased with the concentration of Mal-Dextran and PEG-Link. The stiffness of the final mixture was estimated based on weight induced compression of the matrix and calculated according to the equation below [24]: $E=\frac{\mathit{FLo}}{Ao\mathrm{\Delta }L}$, where E is the Young’s modulus, F is the force exerted on the gel, A_o is the original cross-sectional area through which the force is applied, ΔL is the change in the thickness of the gel, L_o is the initial thickness of the gel. To create the load, a 0.1–0.2 g PDMS block with a cross-sectional area of 0.2 cm² was placed on top of the gel (~600 μm thick). The thicknesses of the matrigel before and after force loading were determined microscopically.

2.4. Capillary-like structure formation assay

Matrigel was thawed overnight with ice at 4°C. The matrigel or matrigel-hydrogel mixtures were added into 96-well plates, PDMS wells or PDMS fences. The fences were filled completely with gel to test the effects of accumulation of cell derived growth factors near the boundary. At least 30 min was incubated to allow complete gelation at 37°C. Cells were seeded (250 cells/mm ²) on top of the gel, and images were taken 8 hours after cell seeding with a CCD camera (Cooke SensiCam) using a 4× or 2× objective.

2.5. Data analysis

The topography of the network was analyzed from bright-field images (Fig. 1D). The cord length of the capillary-like structures in the image was measured and analyzed using ImageJ. In this study, the area 1 mm from the wall of the PDMS wells and fences was considered as the boundary region including the corner region and the “side” region (i.e., not near the corner), and a 2 mm by 2 mm area was considered as the center region.

2.6. Computational simulation

As a simplified model, a 2D finite element model is developed using ANSYS 13 to qualitatively study the displacement of the extracellular matrix resulting from a contractile cell. In this model, the cell was simulated as a homogenous, linear elastic, isotropic material with Young’s modulus of 1 kPa [25] and Poisson’s ratio of 0.45 [26]. Three factors, namely gel thickness, gel stiffness, and cell position in regards to gel boundary were considered in the analysis. It was assumed that the cell was firmly attached to the matrix and the displacement of the matrix was confined on the gel-plate interface. For the sake of consistency, similar meshing technique was employed in all simulations using a 1 μm (approximately) element size. Finally, the normalized deformation of cell along the gel surface, as well as gel deformation contour, was calculated.

3. Results

3.1. Geometric control of the capillary network topography

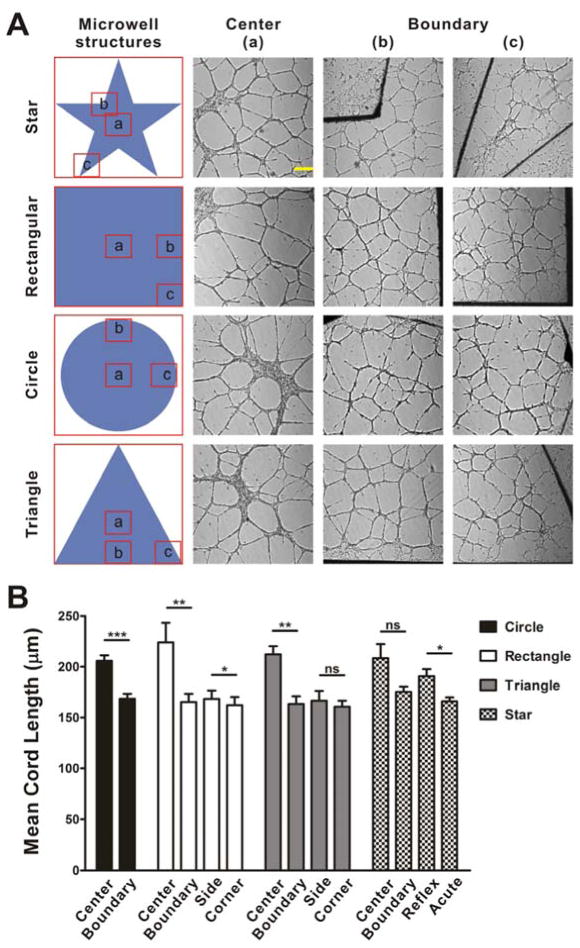
PDMS wells were first applied to study the effects of geometric confinement on capillary-like structures formation (Fig. 1B). Remarkably, the HUVEC network near the boundary has significantly higher densities and shorter mean cord length compared to the center region (Fig. S1). To avoid the potential effects of meniscus formation that may cause the cells to roll down to the center region, and accumulation or absorption of cell derived growth factors near the boundary that may modulate the chemical gradient, PDMS fences were employed and the experiments were repeated (Fig. 1C). In particular, the matrigel was controlled to have the same height as the PDMS fences by carefully adjusting the gel volume. Flat matrix surfaces (i.e., no slope for cell rolling) near the boundary and uniform initial cell distributions were confirmed by microscopic inspections. Dense networks and short mean cord lengths were observed near the boundary in the PDMS fence for all geometries, similar to the microwell experiments (Fig. 2). The modulation of the network structures are, therefore, unlikely to be originated by accumulation or absorption of diffusible factors. We further analyzed the network near the corners with various angles and near the boundaries. For triangular and rectangular fences, the mean cord lengths near the boundaries were similar to the values near the corners, and there was no statistical significant difference between them. On the other hand, the mean cord length near reflex angle corners was significantly higher than that near acute angle corners in the star structures (Fig. 2B). This observation further supports that the geometric effects on the network topography is mediated mechanically.

Figure 2.

The effect of extracellular matrix geometry on capillary-like structure formation using PDMS fences. (A) Bright field images of capillary-like structures on matrigel with various geometries. Scale bar, 300 μm. (B) Statistical analysis of the mean cord length of capillary-like structures at the center region and boundary region of matrigel (ns, not significant; *, P<0.05; **, P<0.01; ***, P<0.001). Results represent mean±SE from three independent experiments.

3.2. Modulation of the cell network by matrix thickness

The microwell and fence experiments suggest geometric confinement may modulate the network topology mechanically. If the boundary exerts its effect mechanically, the thickness of the extracellular matrix, which connects to the solid substrate, should have similar effects on the network. To test this hypothesis, we controlled the matrix thickness by adjusting the final volume of matrigel. The thickness of matrigel in the center region of the 96-well plate was adjusted to 50 μm, 150 μm or 600 μm. The networks in the center region of the well were analyzed (Fig. 3A). Capillary-like structures were formed in all thicknesses tested. Consistent with the hypothesis, the network topology can be modulated by the matrix thickness. As the gel thickness decreased, the mean cord length of the network decreased and the network was significantly denser (Fig. 3B). The matrix thickness dependency has previously been reported using bovine aortic endothelial cells (BAEC), supporting the effects of physical boundary on capillary network architectures [27]. Since the boundary effect was observed consistently in the microwell, fence and thickness experiments, the geometric effects are likely mediated mechanically, such as matrix physical properties or cell-matrix mechanical interactions.

Figure 3.

The effect of extracellular matrix thickness on capillary-like structure formation. (A) Bright field images of capillary-like structures on matrigel with increasing thickness (50 μm, 150 μm and 600 μm). Scale bar, 200 μm. (B) Statistical analysis, n=5 (*, P<0.05; **, P<0.01).

3.3. The effects of matrix stiffness

The cell-matrix mechanical interaction was then modulated by changing the matrix stiffness with mixtures of matrigel and a cell-inert PEG-dextran hydrogel. We observed diluted matrigel with lower matrix stiffness modulated the network topology (data not shown). However, diluting matrigel may also reduce the ligand density for cell adhesion. The gel mixture approach allowed the matrix stiffness to be controlled independently while maintaining a constant ligand density for cell adhesion. As the final concentration of PEG-dextran hydrogel increased from 0 to 0.2 mM and 0.6 mM, the stiffness of the gel mixture increased from 444 Pa to 809 Pa and 1331 Pa respectively. The stiffness of 100% matrigel was previously measured to be around 500 Pa by AFM nano-indentation [28] and the value was in reasonable agreement with our results using 80% matrigel. In our experiment, capillary-like structures did not form on the stiffest substrate (1331 Pa). Similar observation was reported in studies using BAEC on type I collagen and polyacrylamide as the substrate, which showed capillary-like structures were formed only on compliant substrates (E=200–1000 Pa) [29]. To minimize the uncertainty due to ligand density, we applied PEG-dextran hydrogel as an alternative cell-inert crosslinking gel of polyacrylamide. Capillary-like structure formations were observed on compliant gel (444 Pa to 809 Pa). A dense network with a small mean cord length was observed in the stiff substrate with hydrogel (Fig. 4). The stiffness dependency is consistent with our hypothesis that the capillary formation process can be modulated by cell-matrix mechanical interactions.

Figure 4.

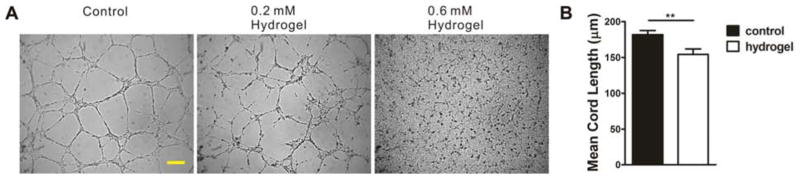
The effect of extracellular matrix stiffness on capillary-like structure formation. (A) Bright field images of capillary-like structures on matrigel (control) and matrigel-hydrogel mix with increased hydrogel concentrations (0.2 mM and 0.6 mM, final). Scale bar, 200 μm. (B) Statistical analysis of mean cord length of capillary-like structures on matrigel and matrigel-hydrogel mix (0.2 mM hydrogel), n=8 (**, P<0.01).

3.4. Modulation of the cell traction force

The effects of the cell-matrix mechanical interactions were further investigated by modulating the cell traction force pharmacologically. To evaluate the effect of cell traction forces on the capillary network formation, an inhibitor of Rho-associated protein kinase (ROCK), Y-27632, was added to the cell suspension with a final concentration of 15 μM. With the ROCK inhibitor, the mean cord length of the network was significantly reduced compared to control (Fig. 5). The experiments were also performed in rectangular PDMS fences to test the combined effects of geometric confinement and cell traction force. The geometric effects near the boundary was observed in both experiments (i.e., with and without the ROCK inhibitor). Cell networks near the boundary of the rectangular PDMS fence displayed a higher network density than those at the center statistically. Nevertheless, the reduction in mean cord length was much smaller with the treatment of Y-27632. It indicated that the boundary effect was suppressed with the decrease of the cell traction force, suggesting the geometric effect was mediated by the cell traction force.

Figure 5.

The effect of cell traction forces and extracellular matrix boundary on capillary-like structure formation. (A) Bright field images of capillary-like structures on matrigel with rectangle PDMS fences. Scale bar, 200 μm. (B) Statistical analysis of the mean cord length of capillary-like structures on the center region and boundary region of matrigel at the presence of Y-27632 or not, n=3 (ns, not significant; *, P<0.05).

3.5. Computational simulation

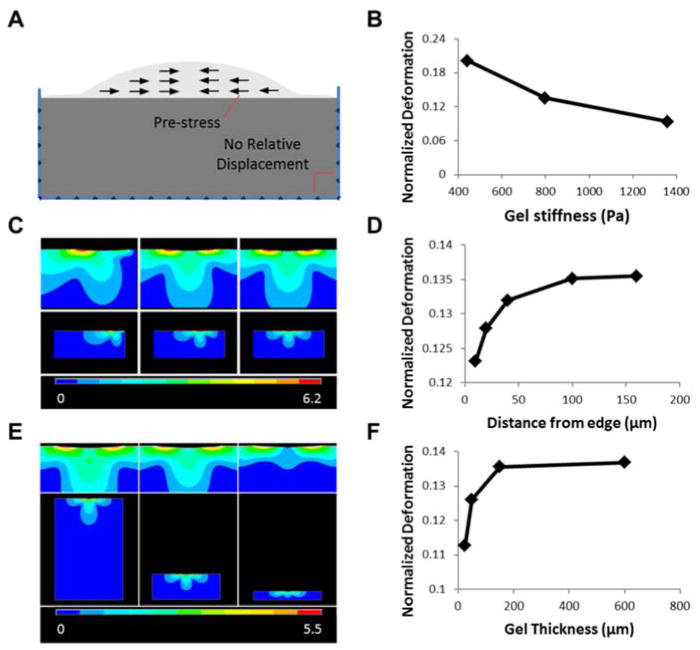
Our experimental data indicate the characteristics of the microenvironment, such as the geometry and matrix stiffness, can modulate the cell-matrix interaction and the network topography. To study the effects of geometric confinement on the cell-matrix mechanical interactions, a finite element model of a contractile cell on top of an elastic substrate was developed. In this simplified model, a pre-stress was exerted on the cell, from the edge to the center, to mimic the cell traction force (Fig. 6A). Similar approach was previously introduced for studying cell-matrix mechanical interactions and in particular, in assessment of the range of sense of touch of cells [30]. In this study, the physical deformation of the cell and the matrix, resulting from the cell contraction, was estimated with various matrix stiffness values, cell positions, and matrix thicknesses. As anticipated, the resistance of the matrix increased with its stiffness and subsequently the cell deformation decreased with the matrix stiffness (Fig. 6B). Next, the simulation was repeated for cells positioned at different distances from the physical boundary to illustrate the effect of geometric confinement on cell-matrix interaction (Fig. 6C). Near the boundary, the rigid wall significantly modulated the cell-matrix interaction. In particular, the effective resistance of the matrix near the wall increased due to the boundary condition, resulting in an asymmetric deformation contour. The deformation of the cell and the matrix reduced near the boundary. At a large distance, the boundary effect disappeared and the value saturated (Fig. 6D). Similarly, the effects of the matrix thickness were investigated. As the matrix thickness decreased, both the amplitude of gel deformation and the size of deformed area reduced (Fig. 6E). This result indicated a large resistance to deformation in thin gels. Analyzing the cell deformation revealed that under the same cell traction force, the normalized deformation of cell along the matrix surface increased with the gel thickness (Fig. 6F). With a large thickness, the value saturated and the boundary effect disappeared.

Figure 6.

Finite element analysis of the cell-matrix interactions. (A) Schematic of the 2D model. (B), (D), (F) Normalized cell deformation along the gel surface in regards to different gel stiffness, cell position, and gel thickness, respectively. (C), (E) Gel displacement vector sum (μm) for varying cell position and gel thickness, respectively.

4. Discussion

In this study, we develop an approach that combines microfabrication, hydrogel processing, and computational analysis to study the mechanoregulation of multicellular self-organization. Mechanical cues, such as matrix stiffness and geometry, are known to be important regulatory factors in various biological processes [31]. The microfabricated PDMS wells and fences presented in this study represent an effective approach to adjust the physical boundary condition for studying geometric control of cell behaviors. Understanding the geometric effects on cell behaviors may be useful in controlling the morphogenic processes in tissue constructs for regenerative medicine applications. For instance, microengineered hydrogel microwells have been applied for studying the size dependency of the embryoid bodies and directing stem cell fate [32]. In our platform, the matrix stiffness and cell traction force can be modulated independently to elucidate the effects of cell-matrix mechanical interaction. We also demonstrated hydrogel processing for controlling the matrix stiffness. The effect of extracellular matrix stiffness on capillary formation was originally investigated by using fibrin gel of various concentrations [33]. In fact, the network topology could be modulated by the changing the concentration of the matrix gel. However, adjusting the matrix concentration also changes the ligand density that may modulate the cell attachment and the signal transduction. We demonstrated a cell-inert PEG-dextran hydrogel to adjust the stiffness of the matrix with constant ligand densities for cell adhesion. Since geometric confinements and matrix properties are commonly encountered in various physiological conditions, our techniques should have broad applicability in various biological studies in the future.

Our study provides evidence that geometric confinement modulates the capillary topology, including the mean cord length and the network density, via cell-matrix mechanical interactions. Current models of capillary morphogenesis delineate the roles of biochemical factors (e.g., VEGF), Notch signaling, and extracellular matrix remodeling (e.g. matrix metalloproteinase) [13–15]. The boundary effect was shown to induce spread endothelial networks with large lumens in collagen gels [18]. Geometric boundary also directed cell alignment and elongation in tissue-engineered constructs and adipose tissue derived microvessel systems [19, 20]. Nevertheless, the effects of geometry on capillary network topology and the processes by which endothelial cells interact with the physical boundary remain poorly understood. In our study, dense networks with short mean cord length were observed near the boundary. The PDMS wells, PDMS fences, and matrix thickness experiments collectively supported the boundary effect was medicated mechanically. Cells near rigid boundaries displayed high network density under all conditions. Interestingly, cell networks near an acute angle displayed shorter mean cord lengths than networks near a reflex angle in the star pattern. These observations cannot be explained solely by local gradients of diffusible factors. On the other hand, the resistance of the matrix to be deformed was correlated with the capillary network density. The importance of the matrix deformability was further observed using a hydrogel based approach to module the matrix stiffness. Pharmacological perturbation of the cell traction force provided additional evidence on the importance of the cell-matrix mechanical interaction. In particular, the boundary effect was significant reduced with the treatment of Y-27632, suggesting the boundary effect is related to the cell traction force.

A computational model was developed to illustrate the relationship between geometric boundary, matrix thickness, and matrix stiffness. Despite its simplicity, the simulation data were in general agreement with the experiments and illustrated the effects of geometric confinement on cell-matrix mechanical interactions. In particular, rigid walls or substrates introduce a rigid boundary condition, which prevents the matrix from being deformed easily. Furthermore, increasing the matrix stiffness also reduced the deformability of the matrix. These results are in agreement with the experiment and provide a conceivable mechanism on the geometric control of the capillary network. Nevertheless, the exact processes by which the endothelial cells sense and interpret the cell-matrix mechanical interaction remain unclear. The matrix deformation resulting from cell traction forces could induce matrix remodeling (redistribution of fibers) for guiding cell migration and capillary morphogenesis [34, 35]. A stiff matrix is known to induce a large cell traction force representing an adaptive response of the cells [36, 37]. The intracellular stress and matrix deformation could also modulate the formation of VEGF gradients and the tip-stalk organization during capillary formation. Physiologically, it is tempting to hypothesize that a high network density can facilitate gas and nutrient transport in confined regions or stiff environments, which often has low diffusivity. It may represent an ability of the cells to adapt to different environments. Furthermore, the in vitro capillary formation assay only represents some early events of capillary morphogenesis and does not fully capture all aspects of the complex morphogenic process. Future investigation is warranted to clarify these aspects. Microengineered or 3D tissue engineering constructs and in vivo models should be incorporated.

5. Conclusions

In summary, we revealed geometric control of capillary morphogenesis using a combination of microfabrication, hydrogel matrix, and computation analysis. In particular, human endothelial cells form dense networks near the physical boundary. Our observations suggest that cell-matrix mechanical interactions play a key role in the geometric control of the capillary architecture. These findings will have significant implications for designing exogenous extracellular matrix and tissue scaffolds and should be considered in tissue engineering studies in the future.