Measurement of insulin-mediated glucose uptake: Direct comparison of the modified insulin suppression test and the euglycemic, hyperinsulinemic clamp

Abstract

Background

Two direct measurements of peripheral insulin sensitivity are the M value derived from the euglycemic, hyperinsulinemic clamp (EC) and the steady-state plasma glucose (SSPG) concentration derived from the insulin suppression test (IST). Prior work suggests that these measures are highly correlated, but the agreement between them is unknown. To determine the agreement between SSPG and M and to develop transformation equations to convert SSPG to M and vice versa, we directly compared these two measurements in the same individuals.

Methods

A total of 15 nondiabetic subjects (9 women and 6 men) underwent both an EC and a modified version of the IST within a median interval of 5 days. We performed standard correlation metrics of the two measures and developed transformation regression equations for the two measures.

Results

The mean ± SD age of the subjects was 57 ± 7 years and body mass index, 27.7 ± 3.9 kg/m². The median (interquartile range) SSPG concentration was 6.7 (5.1, 9.8) mmol/L and M value, 49.6 (28.9, 64.2) μmol/min/kg-LBM. There was a highly significant correlation between SSPG and M (r = −0.87, P <0.001). The relationship was best fit by regression models with exponential/logarithmic functions (R² = 0.85). Bland-Altman plots demonstrated an excellent agreement between these measures of insulin action.

Conclusion

The SSPG and M are highly related measures of insulin sensitivity and the results provide the means to directly compare the two measurements.

Introduction

Insulin-mediated glucose disposal varies several-fold (1, 2) in apparently healthy individuals, whether measured by the euglycemic, hyperinsulinemic clamp (EC) technique or the insulin suppression test (IST). Approximately one-third of these individuals are sufficiently insulin resistant to be at increased risk to develop a number of adverse clinical syndromes (3, 4), including type 2 diabetes, coronary heart disease, nonalcoholic fatty liver disease, and polycystic ovary syndrome (5-7). Given the importance of insulin resistance as a predictor of several clinical syndromes, it seems important to specifically and quantitatively measure this variable.

We have previously shown (8) that estimates of insulin-mediated glucose disposal as determined by the EC, defined by the M value, and the IST, defined by the steady-state plasma glucose (SSPG) concentration, are highly correlated with each other in nondiabetic individuals and in patients with type 2 diabetes. In that study, the IST was performed using propranolol and epinephrine to suppress endogenous insulin secretion (8, 9). However, since the publication of these findings in 1981, a modified version of the IST in which endogenous insulin secretion is more simply suppressed with octreotide acetate has been adopted by our research group and other investigators (10). Using the modified IST, Mimura and colleagues showed that the SSPG concentrations were highly inversely correlated (r = −0.91) with the M values measured by the EC in patients with type 1 diabetes (11).

We initiated the current study to ensure that estimates of insulin-mediated glucose disposal (SSPG concentration) obtained with the modified IST were still closely related to M values derived from the EC. Furthermore, we believed the results of this comparison would provide the opportunity to establish equivalence between the two methods. We therefore sought to provide transformation equations that allow for the derivation of M value from SSPG concentration and vice versa. Establishing such equivalence will be important in justifying the pooling or meta-analyses of studies that have measured peripheral insulin sensitivity using either of the two methods.

Methods

Study subjects

Our study included 15 subjects (9 women and 6 men) whose age ranged from 42 to 69 years and body mass index from 20.4 to 32.8 kg/m² (Table 1). The participants were recruited from communities surrounding Stanford University by placing newspaper advertisements. All individuals reported the absence of clinically significant cardiovascular disease and had normal hematocrit and liver and kidney functions. Furthermore, none of the subjects had diabetes by the oral glucose tolerance test; and of the 15 individuals, four had normal fasting glucose (NFG) and normal glucose tolerance (NGT), 10 had impaired fasting glucose (IFG) and NGT, and one had IFG and impaired glucose tolerance by the American Diabetes Association criteria (12).

Table 1.

Clinical characteristics of the 15 study subjects

Variable	Mean ± SD or n
Age (years)	57 ± 7
Women/Men (n)	9/6
Caucasian/African American (n)	12/3
Body mass index (kg/m2)	27.7 ± 3.9
Waist circumference (cm)	97 ± 11
Fasting glucose (mmol/L)	5.7 ± 0.5
Fasting insulin (pmol/L)	110 ± 36

To convert fasting glucose from mmol/L to mg/dL, divide by 0.05551; and to convert fasting insulin from pmol/L to μU/mL, divide by 6.

Stanford University's Human Subjects Committee approved the study protocol, and the study participants signed an informed consent before admission to the Clinical and Translational Research Unit for testing. Each subject underwent an IST and an EC. The median time interval between the tests was 5 days, during which the subjects maintained their body weight and physical activity level.

Insulin suppression test

We performed a modified version (10) of the insulin suppression test that has been described and validated by our research group (8, 9). After an overnight fast, an intravenous catheter was placed in the antecubital vein of each arm; one arm vein was used for drawing blood samples and the other for giving a simultaneous, continuous infusion of octreotide acetate (0.27 μg/m²/min), insulin (32 mU/ m²/min), and glucose (267 mg/m²/min) for 180 min. Blood samples were drawn every 30 min until 150 min to monitor plasma glucose concentrations and then every 10 min until 180 min to measure plasma glucose and insulin concentrations. The plasma glucose and insulin concentration values during the last 30 min of the infusion were averaged to determine the SSPG and steady-state plasma insulin (SSPI) concentrations, respectively. Because all individuals had comparable SSPI concentrations and received comparable glucose loads, the magnitude of the SSPG concentration provided a direct measure of peripheral insulin sensitivity. In other words, individuals with higher SSPG concentration were more insulin resistant than those with lower SSPG concentration.

Euglycemic, hyperinsulinemic clamp

We performed EC using a well-established methodology that has been previously described (13) and used in the multi-national European Group for the Study of Insulin Resistance/Relationship between Insulin Sensitivity and Cardiovascular Disease (EGIR/RISC) study (14). The only exception to the clamp method was that we conducted the EC using mixed venous blood samples and did not attempt to “arterialize” blood sampled by using the “hot hand” technique. This decision was based on the results of a previous study showing that use of mixed venous blood to perform EC yielded M values that were essentially identical to those obtained with “arterialized” blood (15).

After an overnight fast, an intravenous catheter was placed in the antecubital vein of each arm; one arm vein was used for drawing blood samples and the other for infusing insulin and glucose for 120 min. We gave each subject a priming dose of insulin (160 mU/m²/min for the first 4 minutes and 80 mU/m²/min for the next 4 min) followed by a continuous infusion of insulin at 40 mU/m²/min. The plasma glucose target for the clamp was between 4.5 and 5.5 mmol/L. Plasma glucose concentrations were measured every 5 minutes during the study on a bedside Beckman glucose analyzer, and the glucose infusion rate titrated to ‘clamp’ the plasma glucose concentration within 15% of the target glucose value. The steady-state period for the calculation of insulin sensitivity (M value) and SSPI was between 80 and 120 min.

We calculated the M values according to the protocol used in EGIR/RISC study. During the steady-state phase of the clamp, the time course of the glucose infusion consisted of periods of constant glucose infusion. We integrated these periods using the piecewise constant function to determine the integral of the glucose infusion rate (GIR). Next, we calculated the mean GIR by dividing the integral of the GIR by the time interval (minutes) between the start and the end of the steady-state period. Using the Watson formula for estimating total body water (16), we then determined each subject's lean body mass (LBM) and used the LBM value to convert the mean GIR from mg/min/kg-body weight to mg/min/kg-LBM. After that, for each clamp, we calculated the glucose space correction (GSC) value, which quantified the variation in glucose pool size during the steady-state period. We determined the GSC value by the following formula: GSC = [V × (G₁₂₀ - G₈₀)/40], where V represented the glucose distribution volume (290 ml/kg-LBM); G₁₂₀ and G₈₀, the glucose values (mg/mL) at 80 min and 120 min, respectively; and 40, the time interval (minutes) between the two samples. Finally, we calculated the M value (mg/min/kg-LBM) by subtracting the GSC value from the mean GIR. A single operator (F.A.) performed all 15 clamps.

One of the authors (A.N.) independently evaluated the clamps for quality using the same criteria as in the EGIR/RISC study. The evaluation entailed examination of the coefficient of variation (CV) of plasma glucose concentration, the distance between the mean glucose concentration and the target, the stability of the GIR, and the relationship between the GIR and plasma glucose concentration. In addition, A.N. scored all clamps using a 0 to 3 point system on the basis of the overall quality of the clamps. A score of 0 indicated that there were no concerns; 1, minor concerns; 2, some concerns; and 3, major concerns.

Plasma insulin concentrations were measured by radioimmuno assay using kits by Millipore (parent company of Linco), catalog # HI-14K. The insulin assay had an inter-assay CV of 5.2%.

Statistical analysis

We first plotted M and SSPG in a scatter diagram and calculated Pearson correlation coefficient between the two measures of insulin action. Next, to express the relationship between M and SSPG in the form of an equation, we performed various regression analyses including linear, power, exponential, logarithmic, and hyperbolic models. Using the equations of the best fit regression models, we predicted SSPG concentrations (SSPG_predicted) from the measured M values (M_observed) and predicted M values (M_predicted) from the measured SSPG concentrations (SSPG_observed).

We then employed Bland-Altman statistics and plots to determine by how much the observed and predicted values of peripheral insulin sensitivity differed from each other (17). To quantify the differences, we first computed the agreement (mean difference) between SSPG_observed and SSPG_predicted and between M_observed and M_predicted. Next, we calculated the upper and lower limits [mean difference ± (1.96 × SD)] of the two agreements and determined the precision (95% confidence interval) of each agreement and of its upper and lower limits.

To inspect the differences between the measured and predicted values of peripheral insulin sensitivity, we drew two Bland Altman plots. In the first plot, we graphed the individual differences between SSPG_observed and SSPG_predicted (on the y-axis) against their means (on the x-axis). Similarly, in the second plot, we graphed the individual differences between M_observed and M_predicted against their means. In each plot, the differences were visualized in reference to horizontal lines representing the mean difference (agreement) and the upper and lower limits of the agreement.

Finally, we performed a cross-validation analysis employing the leave-one-observation-out approach. Specifically, we excluded one observation from the dataset in turn and used the remaining observations to estimate the best fit regression equations to predict M from SSPG and vice versa. We then used the Bland-Altman statistics and plots to quantify and inspect the agreement between the observed and thus predicted values of SSPG concentration and M.

The summary statistics are mean ± SD unless otherwise noted. We analyzed the data with Microsoft Excel 2010 and the statistical software R (version 2.13.0) by The R Foundation for Statistical Computing.

Results

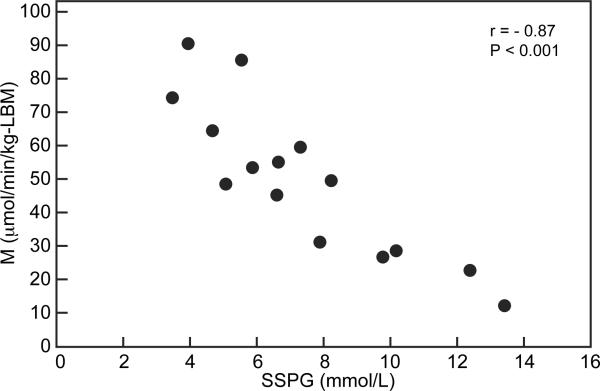
Fig. 1 displays the relationship between SSPG concentration and M in our study sample. It can be seen that there was a highly significant inverse correlation between the two measures of insulin sensitivity (r = −0.87, P <0.001), and this occurred over a several-fold variations in both SSPG concentration and M values. The median (interquartile range) SSPG concentration was 6.7 (5.1, 9.8) mmol/L; M adjusted for LBM, 49.6 (28.9, 64.2) μmol/min/kg-LBM; and M unadjusted for LBM, 32.9 (22.0, 41.5) μmol/min/kg.

Figure 1.

Relationship between M and SSPG concentration.

Footnote: r indicates the Pearson's correlation coefficient. To convert SSPG from mmol/L to mg/dL, divide by 0.05551; and to convert M from μmol/min/kg-LBM to mg/min/kg-LBM, divide by 5.551.

None of the clamps was adjudicated to have a major problem when assessed for quality based on the scoring system. Plasma glucose concentration during the steady-state phase of the EC was 5.5 ± 0.5 mmol/L with a CV of 7.9 ± 3.1%. The SSPI concentration during the EC was somewhat higher (792 ± 95 pmol/L) than that during the IST (549 ± 102 pmol/L).

The best fit for the data was provided by a logarithmic model that predicted SSPG from the M values (R² = 0.85) and by an exponential model that predicted M from the SSPG concentration (R² = 0.85). Table 2 gives the transformation equations and the agreement between the two measures of peripheral insulin sensitivity. The observed means of each measure closely matched the means predicted by the transformation equations. For the SSPG concentration, the observed mean (measured by the IST) was 7.4 ± 3.0 mmol/L while the predicted mean (derived from the corresponding M values and the transformation equation) was 7.4 ± 2.7 mmol/L. For the M values, the observed mean (measured by the EC) was 49.8 ± 22.9 μmol/min/kg-LBM while the predicted mean (calculated from the corresponding SSPG values and the transformation equation) was 48.9 ± 21.3 μmol/min/kg-LBM.

Table 2.

Agreement between measurements of peripheral insulin sensitivity by the insulin suppression test (SSPG) and the euglycemic, hyperinsulinemic clamp (M)

Measure of Peripheral Insulin Sensitivity			Agreement Mean difference (95% CI)	Limits of Agreement		Transformation Equation
	Observed	Predicted		Lower mean difference - 2SD (95% CI)	Upper mean difference + 2SD (95% CI)
SSPG (mmol/L)	7.4 ± 3.0	7.4 ± 2.7	−0.001 (−0.6 – 0.6)	−2.3 (−3.4 – −1.8)	2.3 (1.2 – 3.4)	aSSPGpredicted = 26.24-4.97*ln(Mobserved)
M (μmol/min/kg-LBM)	49.8 ± 22.9	48.9 ± 21.3	0.9 (−5.3 – 7.0)	−21.3 (−32.0 – −10.7)	23.1 (12.5 − 33.8)	bMpredicted = 157.17*exp (–0.17* SSPGobserved)

Observed and predicted values are mean ± SD. To convert SSPG from mmol/L to mg/dL, divide by 0.05551; and to convert M from μmol/min/kg-LBM to mg/min/kg-LBM, divide by 5.551.

^aLogarithmic regression model equation (R² = 0.85); ln indicates natural logarithm.

^bExponential regression model equation (R²= 0.85); exp indicates exponential function.

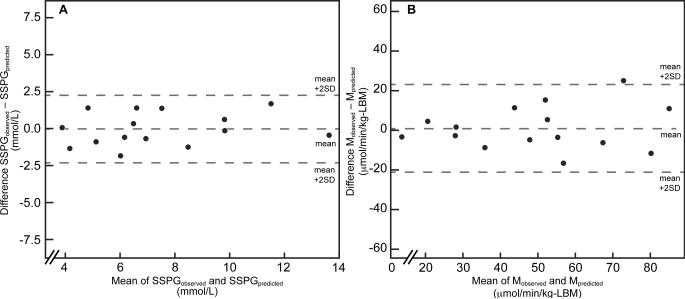
Fig. 2 displays the Bland-Altman plots depicting the agreement between the two measures of peripheral insulin sensitivity. Panel A shows the individual differences between SSPG_observed and SSPG_predicted across a wide range of SSPG concentrations (3.9 – 13.7 mmol/L). The differences are normally distributed and span from -1.8 to 1.7 mmol/L. Similarly, panel B shows individual differences between M_observed and M_predicted over a range of M values (13.8 – 85.0 μmol/min/kg-LBM). The differences are also normally distributed and span from −16.9 to 24.8 μmol/min/kg-LBM.

Figure 2.

Bland-Altman plots depicting the agreement between insulin sensitivity measurements by the insulin suppression test (IST) and the euglycemic, hyperinsulinemic clamp (EC).

Footnote: SSPG_observed and M_observed were measured during the IST and EC, respectively. SSPG_predicted = 26.24-4.97*ln(M_observed); and M_predicted = 157.17*exp (−0.17* SSPG_observed). The mean indicates the mean difference between the observed and predicted values. To convert SSPG from mmol/L to mg/dL, divide by 0.05551; and to convert M from μmol/min/kg-LBM to mg/min/kg-LBM, divide by 5.551.

The results of the cross-validation analysis, in which we left one observation out in turn and used the remaining observations to predict SSPG from M and vice versa, showed that the observed and predicted values of SSPG concentration were essentially similar to each other; and the same was true of the observed and predicted M values. Specifically, the mean (95% confidence interval) difference between SSPG_observed and SSPG_predicted was −0.002 (−0.7 – 0.7) mmol/L and that between M_observed and M_predicted was 0.71 (−6.2 – 7.6) μmol/min/kg-LBM. Furthermore, Bland-Altman showed an excellent agreement between the observed and predicted values of SSPG concentration and M.

Discussion

The results of this study provide additional evidence that measurements of whole body insulin-mediated glucose disposal obtained with the EC and the IST are highly correlated, regardless of the method used to suppress endogenous insulin secretion, i.e., epinephrine/propranolol or octreotide (8-10). The finding is perhaps not surprising given the goals of either of the two tests. Both the EC and IST quantify the ability of a steady-state of physiological hyperinsulinemia to stimulate glucose disposal. They differ in that the measure of insulin action derived from the EC is the amount of glucose infused (M) in order to maintain basal plasma glucose concentration, whereas the IST quantifies insulin action by determining the ability of the hyperinsulinemia to limit the height of the ensuing plasma glucose (SSPG) concentration in response to the fixed-load of infused glucose.

During both the EC and IST, the hepatic glucose production (HGP) is suppressed by the combination of physiological hyperinsulinemia and the infusion of glucose. However, it has been argued that the extent to which the HGP is inhibited depends on the degree of hyperinsulinemia achieved. In this regard, Conte and colleagues have recently reported that HGP was suppressed to 90% of the baseline value in response to mean steady-state insulin concentration of 595 pmol/L in obese individuals with normal glucose tolerance (18). Regarding the influence of infusion of glucose on HGP, our research group has shown that HGP was decreased to approximately half of the original value in response to glucose infusion rate of 200 μmol/m²/min (36 mg/m²/min) under conditions in which the ambient insulin concentrations ranged from 60 to 70 pmol/L (19). In the present study, as we did not perform the measurements of HGP, we cannot comment regarding the extent to which the physiological hyperinsulinemia and the glucose infusion suppressed the HGP. However, in light of the published evidence, we believe that the degree of hyperinsulinemia achieved during both the EC (792 ± 95 pmol/L) and IST (549 ± 102 pmol/L), as well as the infusion of glucose, was sufficient to suppress HGP in all individuals and that the residual HGP contributed marginally, if at all, to the quantification of insulin resistance.

In the present study, the measurements of insulin action were performed in subjects whose clinical and metabolic characteristics were rather heterogeneous (Table 1). There were an approximately 4-fold variability in SSPG concentration and an 8-fold variability in M values (Figure 1). However, the M value of the study participants (49.8 ± 22.9 μmol/min/kg-LBM) was similar to that observed in a cohort of 1146 individuals (49.7 ± 18.0 μmol/min/kg-LBM) in the EGIR study (20). Likewise, the SSPG concentration of our participants (7.4 ± 3.0 mmol/L) was comparable to that noted by us (8.4 ± 4.4 mmol/L) in a group of 490 healthy individuals (2). These similarities in the distributions of M values and SSPG concentration support our belief that the measurements of insulin sensitivity in the present study were representative of the population at large. Furthermore, we would like to point out that our original description of a highly significant relationship between M and SSPG was also observed in a group of individuals with heterogeneous characteristics (8). On the other hand, it can be argued that different mathematical relationships between SSPG concentration and M values would emerge if these measures of peripheral insulin action are compared in homogenous populations, especially those enriched with insulin resistant or insulin sensitive individuals. Our study, however, did not have sufficient number of individuals to address this issue, but we believe that it can be addressed by others in the future.

A high correlation between two measurements does not necessarily guarantee successful derivation of one measure from the other at the individual level. However, our Bland-Altman plots using our optimized transformation equations suggest very good agreement at the individual level regardless of the direction of transformation. Nevertheless, investigators employing the conversion equations should be mindful of the following issues. First, we conducted the EC at the insulin infusion rate of 40 mU/m²/min and the IST at the insulin infusion rate of 32 mU/m²/min. Second, we used mixed venous blood instead of arterialized blood to perform both tests. Although these factors might not have affected the relationship between the M values and the SSPG concentration, it can be argued that they influenced the coefficients of the transformation equations.

In conclusion, the observations made in our study have important implications for association studies focused on identifying novel determinants of insulin-mediated glucose disposal, including studies trying to identify the genetic basis of insulin sensitivity using high-density genotyping or high throughput sequencing platforms, given the challenges of quantifying insulin action using the IST or the EC in large numbers. Our findings suggest that cohorts with insulin sensitivity measurements with either method can be combined analytically with no major concerns. The ability to increase sample size in this manner is likely to translate to substantially increased power to identify novel determinants of this important physiologic parameter with the hope that such discoveries can then be leveraged to develop new therapeutic options that will reduce the risk of the myriad of adverse health effects associated with insulin resistance.

Abbreviations

CV

Coefficient of variation

EC

Euglycemic, hyperinsulinemic clamp

GIR

Glucose infusion rate

GSC

Glucose space correction

IST

Insulin suppression test

LBM

Lean body mass

SD

Standard deviation

SSPG

Steady-state plasma glucose