Abstract
The passive properties of skeletal muscle play an important role in muscle function. While the passive quasi-static elastic properties of muscle fibers have been well characterized, the dynamic visco-elastic passive behavior of fibers has garnered less attention. In particular, it is unclear how the visco-elastic properties are influenced by lengthening velocity, in particular for the range of physiologically relevant velocities. The goals of this work were to: (i) measure the effects of lengthening velocity on the peak stresses within single muscle fibers to determine how passive behavior changes over a range of physiologically relevant lengthening rates (0.1–10 Lo/s), and (ii) develop a mathematical model of fiber viscoelasticity based on these measurements. We found that passive properties depend on strain rate, in particular at the low loading rates (0.1–3 Lo/s), and that the measured behavior can be predicted across a range of loading rates and time histories with a quasi-linear viscoelastic model. In the future, these results can be used to determine the impact of viscoelastic behavior on intramuscular stresses and forces during a variety of dynamic movements.
Keywords: muscle fiber mechanics, viscoelasticity, QLV model
1. INTRODUCTION
The passive properties of skeletal muscle determine an important component of total force generated within a muscle fiber (Proske and Morgan, 1999). Like most biological soft tissues, the passive properties of skeletal muscle are known to be viscoelastic (Best et al., 1994). However, to date, most studies of passive muscle properties have focused on quantifying the stress-strain behaviors during quasti-static loading conditions. Furthermore, most computational models designed to study muscle function assume that muscle tissue behaves purely elastically during passive lengthening (Blemker et al., 2005; Zajac, 1989). This assumption implies that the passive properties of muscle are independent of velocity and therefore that the transient stress response within the tissue is independent of strain rate. While these assumptions allow for the accurate description of intramuscular stresses during static loading, it is unclear how the viscoelastic properties of muscle may impact transient stresses over a physiologic range of lengthening velocities.
The protein titin is known to contribute significantly to the passive properties of muscle fibers while undergoing tensile deformation (Maruyama et al., 1985; Toursel et al., 2002; Wang et al., 1993). Furthermore, many studies have shown that titin does in fact behave viscoelastically and displays force hysteresis secondary to folding and refolding of Ig domains (Kellermayer et al, 1997). This happens at a length beyond the elastic-viscoelastic transition point, which can be altered by manipulating the folding and unfolding mechanics of the protein (Bartoo et al., 1997; Minajeva et al., 2001; Wang et al., 1993; Kellermayer et al., 1998). Recent work at the level of the myofibril has found that this property does in fact scale beyond the level of a single titin protein, although a region of pure elasticity is not identifiable (Herzog et al., 2012). Therefore, the transient passive stresses within whole muscle fibers are also likely dependent on the rate of loading.
Several studies have shown that muscle in fact does behave viscoelastically when subjected to tensile and compressive deformation. This behavior has primarily been evaluated in whole muscle preparations (Anderson et al., 2002; Best et al., 1994; Van Loocke et al., 2008, Takaza et al. 2013) and fiber bundles (Mutungi and Ranatunga, 1996). While some studies have observed viscoelastic behavior in single muscle fiber preparations (Meyer et al., 2011; Toursel et al., 2002), the dependence of passive properties on lengthening velocities in the physiologic range (0.1–10 Lo/s) has not been thoroughly evaluated within single muscle fibers. This information is likely important to consider when predicting muscle forces during dynamic loading processes.
The goals of this work were to: (i) measure the effects of lengthening velocity on the peak stresses within single muscle fibers to determine how passive behavior changes over a range of physiologically relevant lengthening rates, and (ii) develop a mathematical model of fiber viscoelasticity based on these measurements. This was accomplished by measuring both the quasi-static and dynamic passive properties of single fibers from mouse tibialis anterior (TA) muscles that were subjected to a spectrum of loading conditions and loading rates. These measurements were used as the foundation for the development of a mathematical model that was able to predict the stress behavior in response to a variety of loading conditions. The viscoelastic model was further validated in order to determine the range of effectiveness in predicting intramuscular stresses during dynamic loading.
2. METHODS
A total of ten tibialis anterior (TA) muscles were dissected from two-month-old male C57/B6 wild-type mice after euthanization by carbon dioxide induced narcosis in accordance with the guidelines set out by the Animal Care and Use Committee at the University of Virginia. Immediately following dissection, muscle tissues were placed in room temperature relaxing solution (Hellam and Podolsky, 1969). This solution prevented depolarization across potentially damaged regions of the membrane as well as preventing proteolytic degradation. All muscles were stored for less than two weeks in a 50% glycerol storage solution at −20°C (Einarsson et al., 2008).
One muscle fiber was manually dissected from each TA muscle while immersed in relaxing solution. Skinned fibers were secured on each end to a thin gauge wire using two 10-0 nylon sutures. One wire was attached to a high-speed length controller (Aurora Scientific Inc., Aurora, CA, model no. 322C) and the other was secured to an ultrasensitive force transducer (Aurora Scientific Inc., Aurora, CA, model no. 405A, 1.0mN/volt). The entire experimental apparatus was mounted on the stage of an inverted microscope so that fibers could be imaged during the course of the experiments (Fig 1A). All mechanical tests were conducted while the fiber was immersed in relaxing solution at 37°C.
Figure 1.

Experimental Setup. Skinned fibers were secured between two thin gauge wires with one end attached to a high-speed length controller and the other secured to an ultrasensitive force transducer. The setup was mounted on the stage of an inverted microscope (Fig 1A). All fibers were imaged at 40× magnification in order to monitor sarcomere lengths and detect fiber damage (Fig. 1B). From these images, sarcomere length was calculated using a Fast Fourier Transform/Autocorrelation algorithm that was implemented in MATLAB.
Initial fiber length was set to the length at which the fiber began to resist passive extension by closely monitoring the force output during slow passive extension. All fibers were imaged at 10× magnification in order to measure initial fiber length (Lo). Fibers were then imaged at 40× magnification throughout the course of the experiments in order to monitor sarcomere lengths and detect fiber damage (Fig. 1B). Sarcomere length was measured from 40× images using a Fast Fourier Transform/Autocorrelation algorithm implemented in MATLAB (Mathworks, Inc, Natick, MA). This algorithm detected the fundamental frequency along a line perpendicular to the z-line and calculated sarcomere length based on calibration data. Average initial sarcomere length was 2.5µm. Throughout the course of the experiments, fiber stretch was defined as:
| (Eq. 1) |
where L is equal to the current fiber length and Lo is the initial fiber length. Stretch was also calculated based on sarcomere length measurements and compared to the value calculated on the fiber level. Differences in these two values indicated movement of the fiber relative to the experimental apparatus. Data were discarded if the two stretch calculations were not in agreement.
Preconditioning
In order to evaluate the structural integrity of each specimen and to provide a consistent initial configuration for all experiments, each fiber underwent a thorough preconditioning protocol. Initially each fiber was subjected to 40 cycles of a 2Hz sinusoidal length change with maximum and minimum amplitudes of 1.5Lo and 1.1Lo respectively (Fig. 2A). Next, the frequency was increased to 10Hz and the cycle was repeated (Fig. 2A). The hysteresis loops began to overlap after 25–30 cycles, indicating that the fibers were effectively preconditioned at both loading rates and range of stretches.
Figure 2.
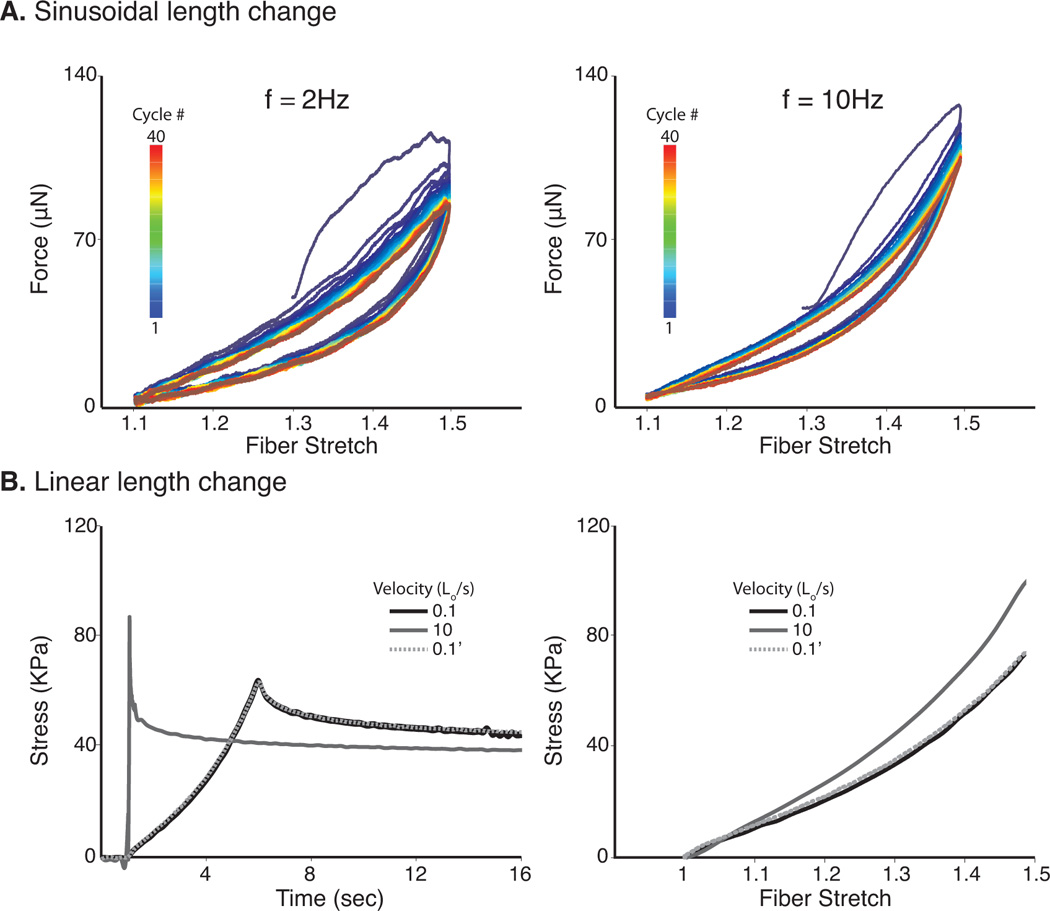
Fiber Preconditioning. Each fiber underwent 40 cycles of a 2Hz sinusoidal length change with maximum and minimum amplitudes of 1.5Lo and 1.1Lo respectively (Fig. 2A). The frequency was increased to 10Hz and the cycle was repeated. A third round of preconditioning was performed by a) applying a ramp hold test to 1.5 Lo at a lengthening rate of 0.1 L․o/s, b) increasing the lengthening rate to 10 Lo/s and lengthening to 1.5 Lo, and c) repeating step a) (0.1’) (Fig. 2B). Discordant measurements between steps a) and c) indicated structural compromise of the fiber and the specimen was discarded and data was not included in the final analysis.
The third round of preconditioning assessed the repeatability of the measurements by subjecting each fiber to three independent steps: 1) applying a ramp hold test to 1.5 Lo at a lengthening rate of 0.1 Lo/s, 2) increasing the lengthening rate to 10 Lo/s and lengthening to 1.5 Lo, and 3) repeating the first step (Fig. 2B). Each fiber rested for two minutes between individual tests at length Lo. If steps 1 and 3 were not repeatable, the fiber was discarded and the data was excluded from analysis.
Measuring Quasi-static response
Each fiber was lengthened by applying a ramp-hold test at a rate of 1 Lo/s (Fig 3A). The fiber stretch was held for 30 seconds and the force response was measured. This test was repeated for stretch values of 1.1, 1.2, 1.3, 1.4, and 1.5. Average sarcomere length at maximal stretch was 3.7µm. The fiber rested for 2 minutes between each experiment. Fiber cross-sectional areas were calculated by assuming a cylindrical shape and volume preservation throughout the experiment. Stress was calculated by dividing measured force by cross-sectional area. The steady state stress was estimated as the fiber stress at the end of 30 seconds of relaxation. This response was then fit with an exponential function.
Figure 3.
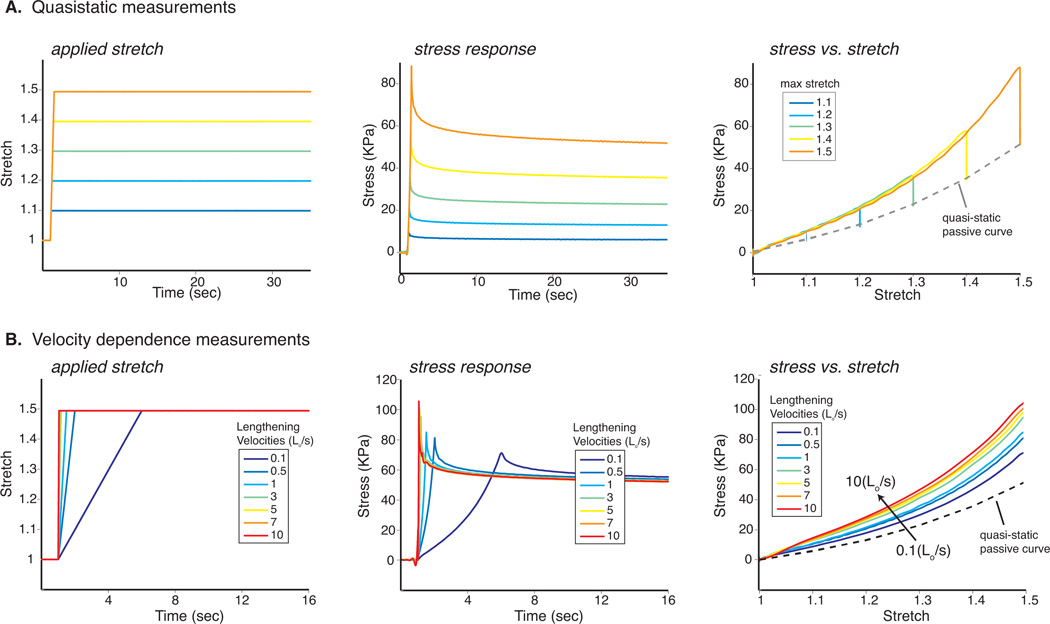
Quasi-static and Velocity Dependent Responses. A ramp-hold test at a rate of 1 Lo/s was applied to each fiber. The force response was measured while holding the fiber stretch for 30 seconds. This protocol was repeated for stretch values of 1.1, 1.2, 1.3, 1.4, and 1.5 (Fig 3A). Stress was calculated from force and cross-sectional area and steady state was estimated at the end of 30 seconds. Ramp hold tests were conducted by stretching fibers to 1.5Lo at 13 different lengthening velocities ranging from 0.1 to 10 fiber lengths per second (Lo/s) (Fig 3B). Sarcomere lengths and fiber diameters were measured at 1Lo and 1.5Lo and were used to calculate stress. Stress responses for all fibers were averaged for each individual loading rate and subsequently plotted vs. time and stretch.
Effect of Velocity on Transient Stresses
To examine the effect of lengthening velocity on the transient stresses observed within the fibers, ramp hold tests were conducted by stretching fibers to 1.5Lo at 13 different lengthening velocities ranging from 0.1 to 10 fiber lengths per second (Lo/s) (Fig 3B). Two minutes were allowed to elapse between each consecutive test in order to ensure full relaxation of the fiber. 40× images were acquired at fiber lengths Lo and 1.5Lo for each ramp hold test in order to measure sarcomere lengths and fiber diameters. The stress vs. stretch response was plotted for the loading phase of each lengthening velocity. Data were further analyzed by averaging the entire stress/time response for all fibers at each loading rate. Peak stress was determined as the maximum stress measured during the ramp phase of the individual test. Peak stresses for all fibers were averaged at each respective lengthening velocity.
Modeling the Viscoelastic Response
We developed a quasi-linear viscoelastic model (QVL) (Fung, 1993) based on the experimental data. The QLV formulation states that the stress at a given time is dependent on the past loading history and is given by the following hereditary integral:
| (Eq. 2) |
where σ(t) is the stress in the fiber, G(t) is the reduced relaxation function, and σ(e)(λ) is the elastic response. The QLV formulation makes two main assumptions: (i) the nonlinear instantaneous elastic response can be separated from the time dependent relaxation response, and (ii) the relaxation response is independent of the amount of fiber stretch. The reduced relaxation function was represented as a three term Prony series of decaying exponentials (Kent et al., 2009):
| (Eq. 3) |
where βi are time constants and G∞ is the steady state response. Furthermore, the elastic response was modeled as an exponential taking the form:
| (Eq. 4) |
This form of the convolution can be solved numerically. The transient component of stress is calculated as:
| (Eq. 5) |
and the steady-state component of stress is given by:
| (Eq. 6) |
The total stress at each time point can be calculated by:
| (Eq. 7) |
Six weighting parameters (Gi), five time constants (βi), and two instantaneous elastic coefficients (A and B) were determined simultaneously in MATLAB. Initial estimates for all model coefficients were calculated using a least squares optimization algorithm that minimized the error between the average data from the ramp-hold tests (Lo/s = 1/s) and the model predictions. This model was refined by fitting the average data for each of the studied velocities simultaneously. Lastly, the optimization algorithm was modified by more heavily weighting error calculations during the periods of loading and the first 100ms of relaxation. This method allowed for a better approximation of the time constants associated with a wide spectrum of loading protocols.
To determine the predictive power of the model, two additional loading protocols were studied. The first protocol consisted of four consecutive ramp inputs of 10% stretch. An average data set was calculated for all fibers and used as the basis for comparison to the viscoelastic model. The stretch history was input and the model was used to predict the stress response of the fiber (Fig. 5A). The second more complex protocol (“arbitrary stretch input”) consisted of various levels and velocities of ramp and sinusoidal stretch inputs. Once again, the loading history was used as an input to the model and the model was used to predict the fiber stress (Fig. 5B).
Figure 5.
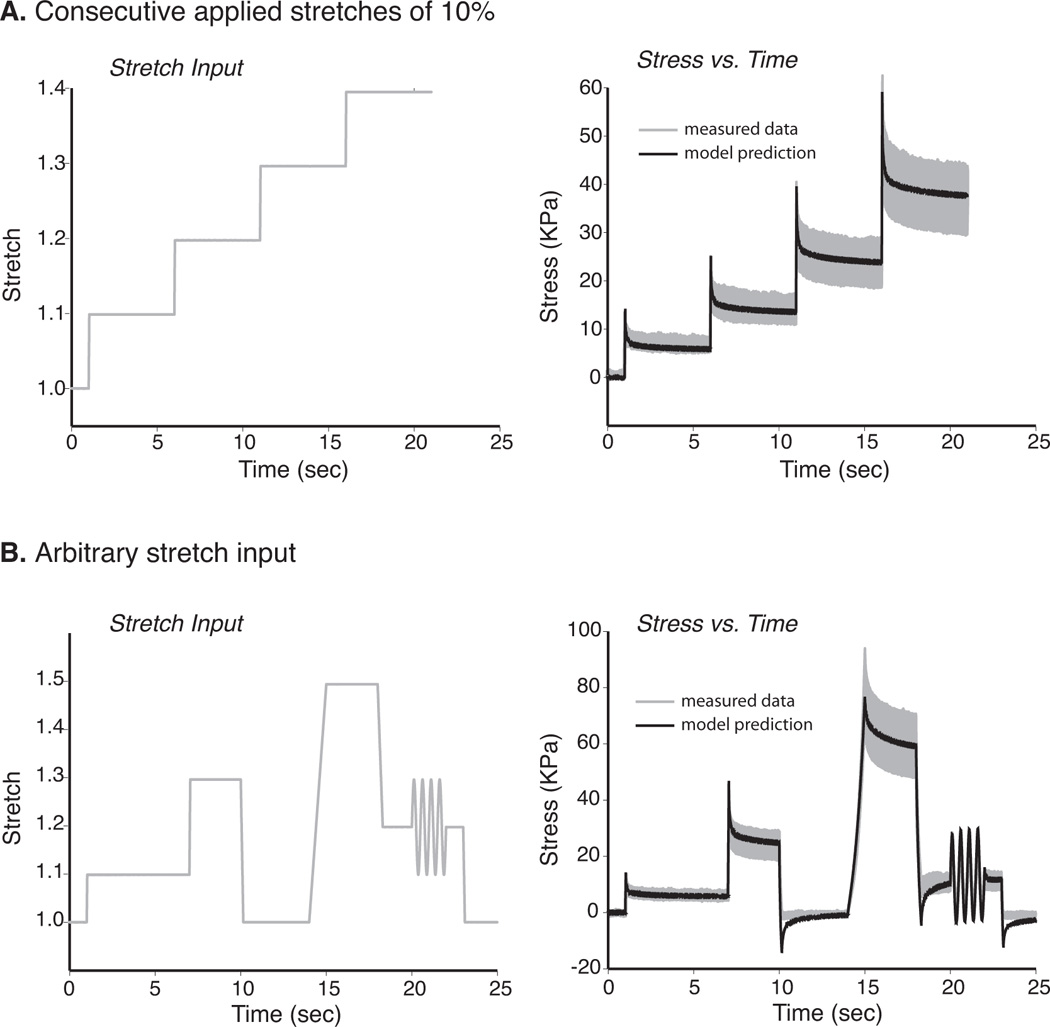
Evaluation of Model Predictive Capacity Given Variable Loading Histories. Two different loading protocols were considered in order to evaluate the predictive power of the model. 1) Four consecutive ramp inputs of 10% stretch were applied to all fibers. This stretch history was input into the viscoelastic model and used to predict stress and compared to the average stress response as calculated for the set of all fibers (Fig. 5A (shaded region = ±1 std) 2) A second more complex protocol (“arbitrary stretch input”) consisted of various levels and velocities of ramp and sinusoidal stretch inputs. This loading history was input into the model and compared to measured data (Fig. 5B). For both loading protocols, the model closely predicted the experimental measurements.
3. RESULTS
The quasi-static stress vs. stretch relationship was nonlinear (Fig. 4A), and was predicted well by an exponential relationship. Across a range of velocities, peak fiber stress increased with lengthening velocity (Fig 4B). This was particularly evident at slower rates where small increases in velocity corresponded to larger changes in peak stress. For example, when stretched to 1.5 Lo the maximum average steady state stress (Lo/s = 0) was 52.6 ± 10.2 KPa. At lengthening velocities 0.1 and 0.5 the peak transient stresses were 70.8 ± 12.2 KPa and 80.9 ± 12.9 KPa respectively. Using a single factor ANOVA test, there was a significant difference in the peak stress between all velocities (p< 0.0001). Thus, peak transient stress increases significantly with lengthening velocity. Additionally, as indicated by a 1-tailed student t-test, peak stresses measured for the 0.1, 0.5, and 1 Lo/s loading conditions differed significantly from all other peak stresses (p<0.05). However, the peak values measured at faster lengthening rates (i.e. 3, 5, 7, 10) did not differ significantly from one another. This result suggests that the peak transient stress begins approaching an asymptotic limit at lengthening velocities above 3 Lo/s when stretched to a length of 1.5Lo (Fig 4B).
Figure 4.
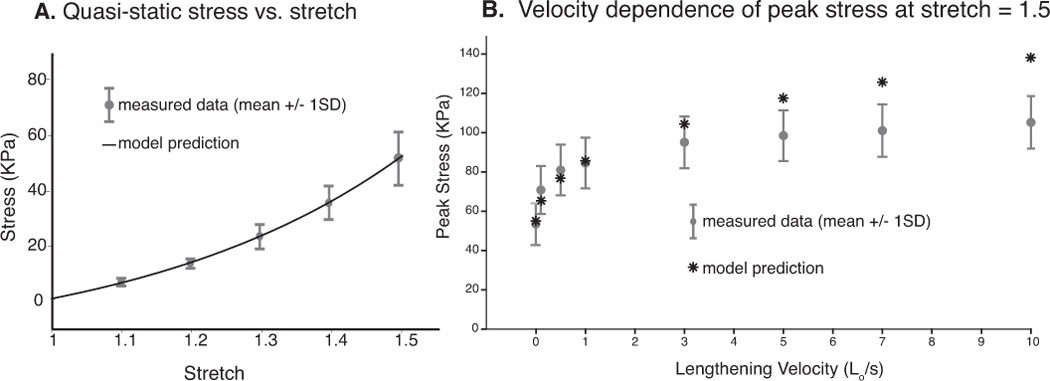
Model Predictions of Quasi-static and Velocity Dependent Responses. An exponential relationship predicted the quasi-static stress vs. stretch relationship (Fig. 4A). Peak fiber stress increased with lengthening velocity across a wide range of lengthening velocities and was found to be particularly sensitive to small changes in velocity at the slower rates (Fig 4B). Model predictions were plotted vs. measured data.
The QLV model generally showed excellent agreement with the experimental data for both the instantaneous elastic response (Fig 5A) and the relaxation response at all levels of stretch up to 1.5Lo (data presented correspond to a lengthening velocity of 1Lo/s). At lower lengthening velocities (0.1, 0.5, 1, and 3), the model performed well in predicting the peak fiber stress (Fig 4B). However, as lengthening velocity increased above 3Lo/s, the peak stresses predicted by the model were slightly higher than the measured data. The model compared favorably with the two predictive tests. The difference between the average experimental data and the model predictions was well within the standard deviation of the experimental data.
4. DISCUSSION
Previous studies have found that the passive properties of single muscle fibers are viscoelastic (Anderson et al., 2002; Bensamoun et al., 2006; Meyer et al., 2011; Toursel et al., 2002). Furthermore, the viscoelasticity displayed during tensile loading is likely due to the passive properties of the protein titin (Bartoo et al., 1997; Wang et al., 1993). While this material behavior has been observed in many previous studies, few have attempted to measure the effects of loading rate on fiber stress across such a broad range of lengthening velocities, especially in the low, physiologic range (0.1–10 Lo/s) (Anderson et al., 2002; Best et al., 1994; Meyer et al., 2011). The goal of this work was to measure the dependence of passive properties on lengthening velocity and to develop a mathematical model that is capable of predicting this response across a physiologic range of loading rates. The results of the tensile tests as presented in this study explicitly show the dependence of passive properties on strain rate, in particular at the low loading rates. The measured behavior can be predicted across a range of loading rates and time histories with a quasi-linear viscoelastic model.
Most studies that have analyzed the viscoelastic effects of whole muscles and muscle fibers have focused on a relatively narrow range of loading rates. For example, Bensamoun et al. (2006) loaded fibers at 0.005 Lo/s and 10 Lo/s in order to measure the peak stress during a near instantaneous stretch and a very slow, quasi-static condition. This study found that loading velocity did impact peak transient stresses; however the authors did not attempt to elucidate the entirety of the relationship across a broader spectrum of rates. Numerous other studies have also passively lengthened muscle at a variety of rates ranging from 50%/s (Anderson et al., 2002) to 667%/s (Best et al., 1994). Meyer et al. (2011) reported the passive viscoelastic properties of single muscle fibers are well matched by a pseudoplastic model over a range of lengthening velocities, primarily between 2 and 200 Lo/s. The pseudoplastic model contains a viscosity term that depends inversely on strain rate and predicts less significant differences in peak stress at higher lengthening velocities. While these studies have provided useful insights into the viscoelastic behavior of the tissue, the variation of passive properties across a physiologic range of loading rates has not been described. A previous study that analyzed muscle tendon behavior during high speed sprinting found that the maximum muscle-tendon lengthening velocity in the hamstrings muscles approaches 2 Lo/s (Thelen et al., 2005). Because that study included the tendon in series with the muscles, it is likely that the actual fiber lengthening velocity is slightly less than this value. In the present study we found that the peak transient stress is sensitive to lengthening velocities in the range of 0.1 to 2 Lo/s. Above 2 Lo/s, increasing lengthening velocity did not significantly change the peak transient stress within the fiber (Fig 3B). Because 2 Lo/s is the maximum strain rate achieved during high speed sprinting, it is likely that fiber lengthening velocities range between 0 and 2 Lo/s during normal human locomotion. Within this realm of strain rates, the viscoelastic properties of the muscle fibers are important in determining peak passive stresses. This behavior may be particularly relevant in the context of strain injuries that are believed to result from regions of large stress and strain near the myotendinous junction (Best, 1995; Fiorentino et al., 2012; Rehorn and Blemker, 2010; Silder et al., 2008). Therefore, it is necessary to consider the viscoelastic behavior of the tissue when studying lengthening conditions.
In order to explore the impact of the passive viscoelastic behavior of muscle tissue on transient stresses during a variety of loading conditions, it is necessary to develop a mathematical model that can predict the behavior of the tissue across a broad range of conditions. This allows for the inclusion of these properties into computational models that are designed to study muscle function during a variety of movements. Previous investigators have modeled the passive viscoelastic behavior of muscle by applying a diverse range of mechanical models. Anderson et al. (Anderson et al., 2002) developed a model that represented the muscle as a modified 3-parameter solid consisting of multiple spring elements representing the structural proteins of the muscle. However, while this type of viscoelastic model is very useful in certain contexts, it relies on several key assumptions that can limit its range of application. First, in order to solve for the model coefficients, it is assumed that stretch is applied as an instantaneous heavy-side step function. Therefore, it is impossible to account for the initial relaxation that occurs during loading. Meyer et al. (2011) developed a pseudoplastic viscoelastic model which calculates viscosity as a function of lengthening velocity and time, but is independent of past loading history. This means that the model’s current state does not depend on previous loads, possibly contributing to the inadequacy of the QLV model to approximate the data in that study. Ultimately, this limitation weakens the utility of discrete models in predicting the response to a broader range of inputs.
In order to address this limitation, it is necessary to introduce a hereditary integral which allows one to consider the previous loading history in determining the current state of the system (Lakes, 1999). The QLV model incorporates the hereditary integral formulation and also allows one to model the non-linear stress/strain relationships that are characteristic of biological tissues (Fung, 1993). Best et al. (Best et al., 1994) applied the QLV formulation to study the viscoelastic behavior of the rabbit EDL and TA muscles. However, this model formulation described the muscle-tendon unit and did not specifically address the behavior of muscle fibers and it still relied on the assumption that stretch was applied instantaneously.
The QLV formulation discussed in the present study is the first to specifically model the behavior of muscle fibers throughout a broad range of lengthening velocities and loading histories. Additionally, the method used in the development of this model made it possible to account for the relaxation that occurs during lengthening. The current QLV formulation was able to predict the stress response to a variety of applied loads in addition to the simple ramp-hold tests. This formulation can be included in future modeling applications to study the impact of passive viscoelastic behaviors on stresses developed within muscles during movement which may be particularly important in studying dynamic loading conditions thought to be linked to tissue damage.
There are several limitations to this study. First, only TA muscle fibers were analyzed. Previous studies have shown that passive properties can vary between muscles (Best et al., 1994) and that titin isoforms may differ across mouse muscles (Ottenheijm et al., 2009). This implies that the viscoelastic properties may be different form one muscle to the next and that it may be necessary to develop muscle specific QLV models. However, the model formulation as described in this study can be adapted to fit the data for a specific muscle. Second, previous work showed that the mouse TA operates at sarcomere lengths ranging from 2.3–2.9µm when subjected to anatomic loading conditions, which correlated to a stretch of 0.92–1.16 (Lieber, 1997). This implies that a stretch of 1.5Lo may be supraphysiologic. However, it is known that stretch can be distributed nonuniformally across muscle fibers and therefore average fiber stretch likely underestimates maximal regional stretch (e.g., Rehorn and Blemker, 2010). Third, the proposed model over predicts peak stresses at lengthening velocities greater than 5 Lo/s (Fig 4B). Previous work has found that maximum lengthening strain rates during high speed sprinting are less than 2 Lo/s (Thelen et al., 2005) and that in vivo fascicle strain rates measured during landing maneuvers in wild turkeys do not exceed 2 Lo/s (Konow et al. 2011). Therefore, it is likely that the current model will be successful at predicting fiber stresses in most physiological applications. Inclusion of a strain-rate dependent viscosity term could improve these predictions at higher velocities.
While titin plays a critical role in determining the passive properties of muscle fibers, the present study may not recapitulate all the known properties of titin. For example, titin is known to interact directly with calcium and subsequently the stiffness of titin is altered during activation (Joumaa et al. 2008; Labeit et al. 2003). Therefore, it is likely that the viscoelastic behavior of the tissue changes during active lengthening due to the effects of calcium on the titin protein, which would not be reflected in our data since we studied the fibers only under passive conditions. Also, titin is known to behave elastically prior to the unfolding of Ig domains (Kellermayer et al., 1997). However, no transition point was identified in this study, which could be a result of (1) our preconditioning protocol and/or (2) the fact that fiber preparations test the amalgamation of many titin and other intracellular proteins, which may average out the effects of molecular-level phenomena like the Ig domain unfolding events.
The passive properties of muscle fibers are significantly affected by lengthening velocity. As lengthening rate increases, the peak transient stress within the muscle fiber also increases. Even at very slow velocities (e.g. 0.1 Lo/s), the peak stress is significantly larger than what is observed in a quasi-static condition (Fig 3B). The QLV formulation is appropriate to model this behavior because it can include the nonlinear instantaneous elastic behavior of the tissue in addition to accounting for previous loading histories. In the future, this behavior can be included in computational models to explore the impact of viscoelastic behavior on intramuscular stresses and strains during a variety of movements such as high speed running.
ACKNOWLEDGEMENTS
We would like to thank Richard Lieber, Samuel Ward, Shannon Bremmer, Geoff Handsfield and Bahar Sharafi for helpful discussions and assistance with preparing the experimental setup. This work was funded by National Institutes of Health R01 AR056201 and a grant from the National Skeletal Muscle Research Center at UC San Diego.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
CONFLICT OF INTEREST STATEMENT
We would like to declare that we do not have any conflict of interest to report in this research.
REFERENCES
- Anderson J, Li Z, Goubel F. Models of skeletal muscle to explain the increase in passive stiffness in desmin knockout muscle. J Biomech. 2002;35gg:1315–1324. doi: 10.1016/s0021-9290(02)00170-7. [DOI] [PubMed] [Google Scholar]
- Bartoo ML, Linke WA, Pollack GH. Basis of passive tension and stiffness in isolated rabbit myofibrils. Am J Physiol. 1997;273:C266–C276. doi: 10.1152/ajpcell.1997.273.1.C266. [DOI] [PubMed] [Google Scholar]
- Bensamoun S, Stevens L, Fleury MJ, Bellon G, Goubel F, Ho Ba Tho MC. Macroscopic-microscopic characterization of the passive mechanical properties in rat soleus muscle. J Biomech. 2006;39:568–578. doi: 10.1016/j.jbiomech.2004.04.036. [DOI] [PubMed] [Google Scholar]
- Best TM. Muscle-tendon injuries in young athletes. Clin Sports Med. 1995;14:669–686. [PubMed] [Google Scholar]
- Best TM, McElhaney J, Garrett WE, Jr, Myers BS. Characterization of the passive responses of live skeletal muscle using the quasi-linear theory of viscoelasticity. J Biomech. 1994;27:413–419. doi: 10.1016/0021-9290(94)90017-5. [DOI] [PubMed] [Google Scholar]
- Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J Biomech. 2005;38:657–665. doi: 10.1016/j.jbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Einarsson F, Runesson E, Friden J. Passive mechanical features of single fibers from human muscle biopsies--effects of storage. J Orthop Surg Res. 2008;3:22. doi: 10.1186/1749-799X-3-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiorentino NM, Epstein FH, Blemker SS. Activation and aponeurosis morphology affect in vivo muscle tissue strains near the myotendinous junction. J Biomech. 2012;45:647–652. doi: 10.1016/j.jbiomech.2011.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukushima H, Chung CS, Granzier H. Titin-isoform dependence of titin-actin interaction and its regulation by S100A1/Ca2+ in skinned myocardium. J Biomed Biotechnol. 2010;2010:727239. doi: 10.1155/2010/727239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York: Springer-Verlag; 1993. [Google Scholar]
- Hellam DC, Podolsky RJ. Force Measurements in Skinned Muscle Fibres. J Physiol. 1969;200:807–819. doi: 10.1113/jphysiol.1969.sp008723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herzog JA, Leonard TR, Jinha A, Herzog W. Are titin properties reflected in single myofibrils? J Biomech. 2012;45:1893–1899. doi: 10.1016/j.jbiomech.2012.05.021. [DOI] [PubMed] [Google Scholar]
- Joumaa V, Rassier DE, Leonard TR, Herzog W. The origin of passive force enhancement in skeletal muscle. Am J Physiol Cell Physiol. 2008;294:C74–C78. doi: 10.1152/ajpcell.00218.2007. [DOI] [PubMed] [Google Scholar]
- Kellermayer MSZ, Smith SB, Granzier HL, Bustamante C. Folding-unfolding in single titin molecules characterized with laster tweezers. Science. 1997;276:1112–1116. doi: 10.1126/science.276.5315.1112. [DOI] [PubMed] [Google Scholar]
- Kellermayer MSZ. Complete Unfolding of the Titin Molecule Under External Force. J Struct Biol. 1998;122:197–205. doi: 10.1006/jsbi.1998.3988. [DOI] [PubMed] [Google Scholar]
- Kent RW, Woods WA, Salzar RS, Damon AM, Bass CR. The transient relationship between pressure and volume in the pediatric pulmonary system. J Biomech. 2009;42:1656–1663. doi: 10.1016/j.jbiomech.2009.04.027. [DOI] [PubMed] [Google Scholar]
- Konow N, Azizi E, Roberts TJ. Muscle power attenuation by tendon during energy dissipation. Proc R Soc B. 2012;279:1108–1113. doi: 10.1098/rspb.2011.1435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labeit D, Watanabe K, Witt C, Fujita H, Wu Y, Lahmers S, Funck T, Labeit S, Granzier H. Calcium-dependent molecular spring elements in the giant protein titin. PNAS. 2003;100:13716–13721. doi: 10.1073/pnas.2235652100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakes R. Viscoelastic Solids. New York, NY: CRC Press; 1999. [Google Scholar]
- Lieber RL, Runesson E, Einarsson F, Friden J. Inferior mechanical properties of spastic muscle bundles due to hypertrophic but compromised extracellular matrix material. Muscle Nerve. 2003;28:464–471. doi: 10.1002/mus.10446. [DOI] [PubMed] [Google Scholar]
- Lieber RL. Muscle fiber length and moment arm coordination during dorsi- and plantarflexion in the mouse hindlimb. Acta Anat. 1997;159:84–89. doi: 10.1159/000147970. [DOI] [PubMed] [Google Scholar]
- Maruyama K, Yoshioka T, Higuchi H, Ohashi K, Kimura S, Natori R. Connectin filaments link thick filaments and Z lines in frog skeletal muscle as revealed by immunoelectron microscopy. J Cell Biol. 1985;101:2167–2172. doi: 10.1083/jcb.101.6.2167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer GA, McCulloch AD, Lieber RL. A nonlinear model of passive muscle viscosity. J Biomech Eng. 2011;133:091007. doi: 10.1115/1.4004993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minajeva A, Kulke M, Fernandez JM, Linke WA. Unfolding of titin domains explains the viscoelastic behavior of skeletal myofibrils. Biophys J. 2001;80:1442–1451. doi: 10.1016/S0006-3495(01)76116-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutungi G, Ranatunga KW. The viscous, viscoelastic and elastic characteristics of resting fast and slow mammalian (rat) muscle fibres. J Physiol. 1996;496(Pt 3):827–836. doi: 10.1113/jphysiol.1996.sp021730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottenheijm CA, Knottnerus AM, Buck D, Luo X, Greer K, Hoying A, Labeit S, Granzier H. Tuning passive mechanics through differential splicing of titin during skeletal muscle development. Biophys J. 2009;97:2277–2286. doi: 10.1016/j.bpj.2009.07.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proske U, Morgan DL. Do cross-bridges contribute to the tension during stretch of passive muscle? J Muscle Res Cell Motil. 1999;20:433–442. doi: 10.1023/a:1005573625675. [DOI] [PubMed] [Google Scholar]
- Rehorn MR, Blemker SS. The effects of aponeurosis geometry on strain injury susceptibility explored with a 3D muscle model. J Biomech. 2010;43:2574–2581. doi: 10.1016/j.jbiomech.2010.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silder A, Heiderscheit BC, Thelen DG, Enright T, Tuite MJ. MR observations of long-term musculotendon remodeling following a hamstring strain injury. Skeletal Radiol. 2008;37:1101–1109. doi: 10.1007/s00256-008-0546-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takaza M, Moerman KM, Simms CK. Passive skeletal muscle response to impact loading: experimental testing and inverse modeling. J Mech Behav Biomed Mater. 2013;27:214–225. doi: 10.1016/j.jmbbm.2013.04.016. [DOI] [PubMed] [Google Scholar]
- Thelen DG, Chumanov ES, Hoerth DM, Best TM, Swanson SC, Li L, Young M, Heiderscheit BC. Hamstring muscle kinematics during treadmill sprinting. Med Sci Sports Exerc. 2005;37:108–114. doi: 10.1249/01.mss.0000150078.79120.c8. [DOI] [PubMed] [Google Scholar]
- Toursel T, Stevens L, Granzier H, Mounier Y. Passive tension of rat skeletal soleus muscle fibers: effects of unloading conditions. J Appl Physiol. 2002;92:1465–1472. doi: 10.1152/japplphysiol.00621.2001. [DOI] [PubMed] [Google Scholar]
- Van Loocke M, Lyons CG, Simms CK. Viscoelastic properties of passive skeletal muscle in compression: stress-relaxation behaviour and constitutive modelling. J Biomech. 2008;41:1555–1566. doi: 10.1016/j.jbiomech.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Wang K, McCarter R, Wright J, Beverly J, Ramirez-Mitchell R. Viscoelasticity of the sarcomere matrix of skeletal muscles. The titin-myosin composite filament is a dual-stage molecular spring. Biophys J. 1993;64:1161–1177. doi: 10.1016/S0006-3495(93)81482-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17:359–411. [PubMed] [Google Scholar]


