The Bayesian Covariance Lasso

Abstract

Estimation of sparse covariance matrices and their inverse subject to positive definiteness constraints has drawn a lot of attention in recent years. The abundance of high-dimensional data, where the sample size (n) is less than the dimension (d), requires shrinkage estimation methods since the maximum likelihood estimator is not positive definite in this case. Furthermore, when n is larger than d but not sufficiently larger, shrinkage estimation is more stable than maximum likelihood as it reduces the condition number of the precision matrix. Frequentist methods have utilized penalized likelihood methods, whereas Bayesian approaches rely on matrix decompositions or Wishart priors for shrinkage. In this paper we propose a new method, called the Bayesian Covariance Lasso (BCLASSO), for the shrinkage estimation of a precision (covariance) matrix. We consider a class of priors for the precision matrix that leads to the popular frequentist penalties as special cases, develop a Bayes estimator for the precision matrix, and propose an efficient sampling scheme that does not precalculate boundaries for positive definiteness. The proposed method is permutation invariant and performs shrinkage and estimation simultaneously for non-full rank data. Simulations show that the proposed BCLASSO performs similarly as frequentist methods for non-full rank data.

1. INTRODUCTION

Shrinkage of a high-dimensional covariance matrix or its inverse, known as the precision or concentration matrix, particularly when the dimension of the matrix (d) is larger than the sample size (n), has drawn a lot of attention in recent years. The abundance of high-dimensional data in structural and functional magnetic resonance imaging where a few dozen subjects are scanned with each scan having thousands of voxels or hundreds of regions of interest [14], spectroscopy, climate studies and many other applications are just a few examples. Another motivation is due to the major use of precision matrices in statistical tools like principal component analysis, linear and quadratic discriminant analysis, inference on the mean parameters, analysis of independence and conditional independence in graphical models, and so on. They all require estimation of the covariance or precision matrix. The precision matrix has a partial correlation interpretation- off-diagonal elements represent the conditional covariances between the corresponding variables. The results can be summarized in a graph by linking conditionally dependent variables, thereby providing an understanding of how variables, such as the genes or regions of the brain, are related to each other. Hence it is suitable for network exploration.

In-depth theoretical studies of the sample (empirical) covariance matrix S have shown that without regularization, the sample covariance matrix performs poorly in high dimensional settings, hence stimulating research on alternative estimators. When the dimension of the matrix is large, the largest eigenvalue can be very large compared to the smallest eigenvalue, resulting in a large condition number and unstable estimators for the precision matrix S^–1. In practice, when n is relatively small compared to the dimension d, the S matrix approaches singularity, therefore leading to unreliable estimates for the precision matrix S^–1. In many cases, such a situation may lead to near-zero eigenvalues for S. The problem is even more serious for non-full rank data (when n < d). In this case, S has a maximum rank of n which is smaller than its dimension d, and therefore S is singular.

In the frequentist framework, significant work has been done on model selection and precision (covariance) matrix estimation in Gaussian models [1, 12, 11, 8, 31]. The original paper by Dempster [6] introduced the idea of shrinkage estimation which forces some elements of the precision matrix to be zero. In its infancy, the methods for shrinkage estimation involved two steps: (i) identify the “correct” model by determining which elements are zero; (ii) estimate the parameters for the non-zero elements. Edwards [9] has discussed some standard approaches for identifying the model, such as greedy stepwise forward-selection and backward-elimination procedures, achieved through hypothesis testing. Drton and Perlman [8] proposed a conservative simultaneous confidence interval to select a model in a single step as an improvement. [1] and [12] proposed the graphical (covariance) lassso (CLASSO) penalty to force some elements of the precision matrix to zero and simultaneously estimate the rest of the elements. [11] extended the CLASSO approach to the adaptive covariance lasso (ACLASSO) and the smoothly clipped absolute deviation penalty for covariance estimation (CSCAD). [31] and [22] used a penalty on the off-diagonal elements only and called their estimator the sparse permutation invariant covariance estimator (SPICE).

Among Bayesian shrinkage methods, [29] used reference priors on the eigenvalues of the covariance matrix to regularize the eigen structure. Smith and Kohn [27] decomposed the precision matrix Φ as Φ = BDB^T where B is a lower triangular matrix with 1's on the diagonal and D is a diagonal matrix. They introduced priors on the elements of B and D. [13] extended this idea and used a Cholesky decomposition on the covariance matrix V = CC^T, where C is a lower triangular matrix. They also discussed how the ordering of the data can change the zero patterns. These methods use priors on the Cholesky factors and therefore are not permutation invariant; they may not be rational choices when there is no natural ordering of the parameters in the matrix. [2] decomposed the covariance matrix as Σ = diag(s)R diag(s), where s is the d × 1 vector of standard deviations and R is the d × d matrix of correlation coefficients. They used priors on individual elements of these matrices. [28] extended this idea to the precision matrix Φ and decomposed Φ = TCT^T, where T = diag(T₁, . . . , T_d) is a diagonal matrix such that T_k are the inverses of the partial standard deviations and C is a correlation matrix with C_kk = 1 and C_kk′ = –ρ_kk′ for all k ≠ k′. The graphical methods of [21, 3] rely on hyper-inverse Wishart based sampling. These two-step methods need to exploit decombosibility structures of the graphs, which may not be the case for unstructured precision matrices. Moreover, they only use Wishart priors and are unable to exploit other types of penalties.

The single-step Bayesian methods primarily rely on priors on the elements arising from some sort of decomposition of the precision (covariance) matrix, which do not readily translate to any recognizable priors on the elements of the precision (covariance) matrix itself. Furthermore, most of these methods are based on sampling the elements of the matrix one at a time which is not efficient. Specifically, these methods pick a single element at a time, find an appropriate boundary that yields a positive definite matrix, and then draw a sample of this element. Drawing one element at a time is inefficient, and coupled with the additional computational complexities in computing boundaries for the elements, these methods are not suitable for high-dimensional matrices. The full posterior distribution of the elements of the precision and covariance matrices under lasso-type penalties have not been explored. The direct L₁ penalties on the elements of the covariance matrix have not been studied in the Bayesian framework. There appears to be a lack of a connection between the popular frequentist penalized approaches and their Bayesian competitors. Our goal is to build a bridge between the frequentist and Bayesian approaches to covariance estimation.

We propose generalized priors which include common frequentist penalties like the adaptive lasso penalty of [11], the lasso (L₁) penalty of [12], and the SPICE penalty of [22] as special cases. Then we introduce a new Bayesian approach for sampling from the posterior distribution of the precision matrix one whole column at a time and rely on multiple tries to achieve the desired acceptance rate. The proposed method is particularly attractive and efficient compared to the existing single-step methods as it updates the matrix one entire column at a time (on the order of d) instead of one element at a time (on the order of d²). Our sampling scheme rejects any sample that is not a positive definite matrix and is permutation invariant. In addition, the method is based on specifying priors directly on the elements of the precision matrix instead of priors on the elements of a matrix decomposition, and the proposed method performs shrinkage and estimation simultaneously. We also explore the posterior distribution of the elements under the lasso penalty and provide a Bayesian minimax estimator as an alternative to the popular frequentist posterior mode estimators under L₁ penalties.

To illustrate the proposed methodology, we consider data from functional connectivity Magnetic Resonance Imaging (fcMRI) from 90 regions of interest (ROI) of 30 2-year old children. All images were acquired on a 3 Tesla Magnetic Resonance (MR) scanner with a gradient echo-planar imaging sequence. The imaging sequence was repeated 150 times. The images of the first 10-20 time points were typically excluded from the data analysis to ensure that magnetization reaches the steady state. All subjects are healthy normal controls and imaged at sleep without sedation. In this study, the signals were obtained from the remaining 130 time points. Our primary purpose here is to build a network between regions when there is no prior information about the underlying structure of the network or graph.

2. THE GENERAL METHOD

Let Y_i ~ N_d(0, Φ^–1) for i = 1, . . . , n be n independent observations, where Φ = (θ_kk′) = Σ^–1 is a d × d precision matrix. Then the joint distribution of Y = (Y₁, . . . , Y_n)is given by

$$p(Y\mid ϴ)\propto {\left(\text{det}ϴ\right)}^{\frac{n}{2}}\text{exp}\left\{-\frac{1}{2}\sum _{i=1}^n{Y}_i^{\mathrm{T}}ϴY_i\right\}I(ϴ\succ 0),$$

where $I(ϴ\succ 0)$ is an indicator function of the event that Φ is positive definite. $S={\sum }_{i=1}^n{Y}_i{Y}_i^{\mathrm{T}}∕n$ is the maximum likelihood estimator of Σ.

2.1 Proposed Priors

We choose independent exponential priors for the diagonal elements; φ_kk ~ Exp(β_k) and Laplace priors for the off-diagonal elements φ_kk′ ~ Laplace(0, b_kk′) for k > k′ and k, k′ = 1, . . . , d. Then, the posterior distribution of Φ, p(Φ|Y), is given by

$${\left(\text{det}ϴ\right)}^{\frac{n}{2}}\prod _{k=1}^d\text{exp}\{-\frac{n}{2}tr\left(Sϴ\right)-\sum _{k=1}^d{\beta }_k{\theta }_{kk}-\sum _{k=2}^d\sum _{k^{\prime }=1}^{k-1}{b}_{k{k}^{\prime }}\mid {\theta }_{k{k}^{\prime }}\mid \},$$

where det(·) denotes the determinant of a matrix. The log-posterior function equals

$$\text{log}p(ϴ\mid Y)=\frac{n}{2}\text{log det}ϴ-\frac{n}{2}tr\left(Sϴ\right)-\sum _{k=1}^d{\beta }_k{\theta }_{kk}-\sum _{k=2}^d\sum _{k^{\prime }=1}^{k-1}{b}_{k{k}^{\prime }}\mid {\theta }_{k{k}^{\prime }}\mid +C,$$ (1)

where C is a constant independent of Φ. The popular frequentist penalized likelihoods including ACLASSO, CLASSO and SPICE can be derived from (1) as special cases as follows. If we choose β_k = ndλ_kk/2 and b_kk′ = ndλ_kk′ (for k > k′), then (1) reduces to

$$\frac{n}{2}\{\text{log det}ϴ-tr\left(Sϴ\right)-\sum _{k=1}^d\sum _{k^{\prime }=1}^{d}d{\lambda }_{k{k}^{\prime }}\mid {\theta }_{k{k}^{\prime }}\mid \}+C.$$ (2)

[11] optimized equation (2) as the objective function in the ACLASSO method, which can be interpreted as the posterior mode under Exp(ndλ_kk/2) priors for the diagonal elements and Laplace(ndλ_kk′) priors for the off-diagonal elements of the precision matrix.

If we set b_kk′ = 2β_k = nρ, the priors for φ_kk are i.i.d Exp(nρ/2) and the φ_kk′ are i.i.d Laplace(nρ) for k > k′. Then (1) reduces to

$$\text{log}p(ϴ\mid Y)=\frac{n}{2}\{\text{log det}ϴ-tr\left(Sϴ\right)-\rho {\Vert ϴ\Vert }_{l_1}\}+C,$$ (3)

where ${\Vert ϴ\Vert }_{l_1}={\sum }_{k=1}^d{\sum }_{k^{\prime }=1}^p\mid {\theta }_{k{k}^{\prime }}\mid$ is the l₁ norm of Φ. [1] optimized equation (3) in their covariance selection method (ignoring n/2), while [12] also optimized equation (3) in their CLASSO method, which is essentially the posterior mode under Exp(nρ/2) priors for the diagonal elements and Laplace(nρ) priors for the off-diagonal elements of Φ. [1] has shown that (3) is concave in Φ, which yields that the posterior distribution of Φ is uni-modal. Hence, we will use Exp(nρ/2) priors for the diagonal elements and Laplace(nρ) priors for the off-diagonal elements of Φ so that our log-posterior is the same as the objective function of CLASSO in (3).

If we choose not to penalize the diagonal elements of Φ, then we can let the hyperparameter β_k approach 0 (β_k → 0) or equivalently choose improper uniform priors on (0, ∞) for the diagonal elements of Φ. In that case, (3) further reduces to

$$\text{log}p(ϴ\mid Y)=\frac{n}{2}\{\text{log det}ϴ-tr\left(Sϴ\right)-\rho {\Vert {ϴ}^{-}\Vert }_{l_1}\}+C,$$ (4)

where Φ^– has the same off-diagonal elements as Φ but all the diagonal elements are zero. [31] and [22] used equation (4) as their objective function (ignoring n/2 and C) and calculated the posterior mode in their SPICE method.

2.2 Full Conditionals

For k = 1, . . . , d, we partition and rearrange the columns of Φ and S as follows:

$$ϴ=\left(\begin{array}{cc}\hfill {ϴ}_{-kk}\hfill & \hfill {\theta }_k\hfill \\ \hfill {\theta }_k^{\mathrm{T}}\hfill & \hfill {\theta }_{kk}\hfill \end{array}\right)\text{and}S=\left(\begin{array}{cc}\hfill S_{-kk}\hfill & \hfill {\mathit{s}}_k\hfill \\ \hfill {\mathit{s}}_k^{\mathrm{T}}\hfill & \hfill s_{kk}\hfill \end{array}\right),$$ (5)

where φ_kk is the kth diagonal element of Φ, φ_k = (φ_k1, . . . , φ_k,k–1, φ_k,k+1, . . . , φ_kd)^T is the vector of all off-diagonal elements of the kth column, and Φ_–kk is the (d – 1) × (d – 1) matrix of all the remaining elements, i.e., the matrix resulting from deleting the kth row and kth column from Φ. By using the Schur decomposition [25], we have det(Φ) = det(Φ_–kk)D_k, where D_k = (φ_kk – C_k) and $C_k={\theta }_k^T{ϴ}_{-kk}^{-1}{\theta }_k$ are scalar quantities. Similarly, s_kk is the kth diagonal element of S, s_k is the vector of all off-diagonal elements of the kth column of S, and S_–kk is the matrix of all remaining elements.

Our primary aim is to sample from the posterior distribution of the kth column of Φ for k = 1, . . . , d. It follows from (3) that the conditional densities for θ_kk and θ_k can be written as follows:

$$\begin{array}{cc}\hfill p({\theta }_{kk}\mid y,{\theta }_k,{ϴ}_{-kk},\rho )& \propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_{kk}+\rho ){\theta }_{kk}\},\hfill \\ \hfill p({\theta }_k\mid y,{\theta }_{kk},{ϴ}_{-kk},\rho )& \propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_k^{\mathrm{T}}{\theta }_k+\rho {\Vert {\theta }_k\Vert }_{l_1})\}\times I(D_k>0),\hfill \end{array}$$ (6)

where I(A) is the indicator function of the event A. The derivation of (6) is given in Appendix I. Under the SPICE penalty, the full conditional distribution for θ_k is the same while the full conditional distribution for θ_kk changes to $p({\theta }_{kk}\mid y,{\theta }_k,{ϴ}_{-kk},\rho )\propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}{s}_{kk}{\theta }_{kk}\}$.

Note that in (6), we could replace D_k by det(Φ) which is computed faster than D_k since ${\theta }_k^{\mathrm{T}}{ϴ}_{-kk}^{-1}{\theta }_k$ requires inverting a (d – 1) × (d – 1) matrix and then computing a quadratic form of the same order. However, we will need to compute ${\theta }_k^{\mathrm{T}}{ϴ}_{-kk}^{-1}{\theta }_k$ to sample the diagonal elements θ_kk and we will not require any additional computations when sampling the off-diagonals θ_k. We are led to the following theorem whose proof is given in Appendix I.

Theorem 1: Suppose we start with a positive definite current value of Φ and sample from $p({\theta }_{kk}\mid y,{\theta }_k,{ϴ}_{-kk})\propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_{kk}+\rho ){\theta }_{kk}\}$ and

$$p({\theta }_k\mid y,{\theta }_{kk},{ϴ}_{-kk})\propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}{({\mathit{s}}_k+\rho {\gamma }_k)}^{\mathrm{T}}{\theta }_k\}I(D_k>0),$$

where γ_k = (γ_k1, . . . , γ_kd)^T and γ_kj = sign(θ_kj) for j = 1, . . . , d. This sampling process guarantees that we sample positive definite values of Φ at all subsequent steps.

Theorem 1 ensures that the Bayesian covariance lasso (BCLASSO) can achieve positive-definiteness for any nonnegative penalty parameter ρ.

2.3 Proposed Sampling Scheme

Gibbs sampling for the diagonal elements is straightforward since their full conditionals are available in closed form. The full conditionals for the off-diagonals are not available in closed form and therefore we will use the standard Metropolis-Hastings algorithm within Gibbs to sample the off-diagonal elements. In many applications, the off-diagonal elements are nearly symmetric suggesting a normal proposal density as a suitable choice. The mean of the proposal density is chosen to be the current value of Φ and the choice of the variance of the proposal density is determined from the Hessian matrix. We can write

$$\text{log}p({\theta }_k\mid y,{\theta }_{kk},{ϴ}_{-kk})=0.5n\{\text{log}{D}_k-{({\mathit{s}}_k+\rho {\gamma }_k)}^{\mathrm{T}}{\theta }_k\}+C.$$

The first-order derivative of the logarithm of full conditional distribution with respect to θ_k is $0.5n\left\{D_k^{-1}{D}_k^{\left(1\right)}-({\mathit{s}}_k+\rho {\gamma }_k)\right\}$, where $D_k^{\left(1\right)}=-2{ϴ}_{-kk}^{-1}{\theta }_k$ is the first-order derivative of D_k with respect to θ_k. The second-order derivative matrix of the logarithm of the full conditional distribution with respect to θ_k equals $-0.5n\left\{D_k^{-1}(D_k^{-1}{D}_k^{\left(1\right)}{D}_k^{\left(1\right)\mathrm{T}}+D_k^{\left(2\right)})\right\}$, where $D_k^{\left(2\right)}=-2{ϴ}_{-kk}^{-1}$ is the second-order derivative of D_k with respect to θ_k. Therefore, the covariance matrix of the proposal density is $V_k=c{D}_k{(D_k^{-1}{D}_k^{\left(1\right)}{D}_k^{\left(1\right)\mathrm{T}}-D_k^{\left(2\right)})}^{-1}{\mid }_{ϴ=Q}$, where Q is a suitable estimate of Φ (such as S^–1, (S + aI)^–1, a > 0, etc.) and c > 0 is the variance tuning factor discussed below. Note that V_k is positive definite almost surely as long as Q is positive definite. Our proposal density is therefore taken as $q\left({\theta }_k\right)\equiv N_{d-1}({\theta }_k^t,V_k)$, where ${\theta }_k^t$ is the current value of the k-th off-diagonal column at iteration t. If x is the proposed value for ${\theta }_k^{t+1}$, then the Metropolis-Hastings acceptance probability is $\alpha =\text{min}\{1,p(x\mid y,{\theta }_{kk},{ϴ}_{-kk})∕p({\theta }_k^t\mid y,{\theta }_{kk},{ϴ}_{-kk})\}$. Therefore, we set ${\theta }_k^{t+1}=x$ with probability α and ${\theta }_k^{t+1}={\theta }_k^t$ with probability 1 – α.

There are several possible sampling strategies. We could sample Φ one element at a time, but that will be on the order of d², which is less efficient and ignores the possible correlations between the elements in the same column. We could also sample only the lower triangular off-diagonal elements, in which we would sample the d – 1 vector (θ₁₂, . . . , θ_1d) first, the d – 2 vector (θ₂₃, . . . , θ_2d) second, and so on. This would update all the elements of Φ by virtue of symmetry, which might be the most efficient way of sampling. However, this sampling procedure still ignores the correlations between the upper triangular elements and the lower triangular elements within the same column. We recommend sampling the whole off-diagonal column all at once, which yields an algorithm on the order of d. Updating the whole off-diagonal column has another advantage in that each θ_kk′ (k ≠ k′) has two chances to get updated. We update θ_kk′ when we update column k and again when we update column k′ due to θ_kk′ = θ_k′k. For each cycle, the latter updated value of θ_kk′ will replace the first updated value. Thus, this will result in one-step thinning to reduce autocorrelations between samples. Thus the actual replacement rates for the individual elements (θ_kk′'s) are higher than the acceptance rates of the columns θ_k. Our computations show that the replacement rate is roughly (1 – acceptance rate)², implying that the acceptance of column k and column k′ (k ≠ k′) are nearly independent. This implies that, if we target an average replacement rate of 36%, which is enough for an ideal sampling scheme, we will need an average acceptance rate for a column to be around 20%. Therefore, we can use fewer tries and/or a larger variance to obtain an ideal sampling scheme.

Variance tuning will, in most cases, result in shrinkage. We tune the variance in cases where the estimate Q of the parameter Φ leads to an unusually high variance of the proposal density. Such a situation can lead to too many draws of multiple try method, small acceptance rates, and high autocorrelations among sampled elements. This can also happen when we take Q = S^–1, where S^–1 is still positive definite but the sample size is small relative to the dimension, leading to an inflated V_k. For high-dimensional cases, when S is singular or close to singular, we can choose Q = (S + aI)^–1 for a suitable a > 0, that is we add a small constant to the diagonals to make Q positive definite. This can also help in making Q more stable when n is not sufficiently large compared to d, since for larger d/n the smaller eigenvalues approach zero to destabilize the inversion.

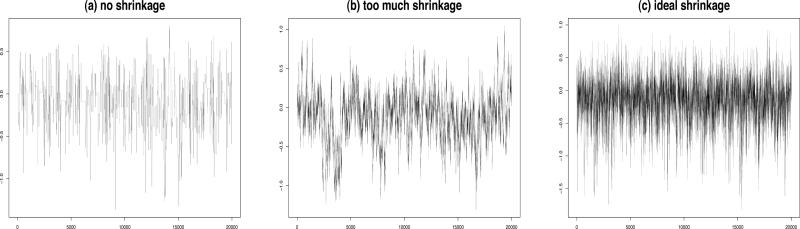
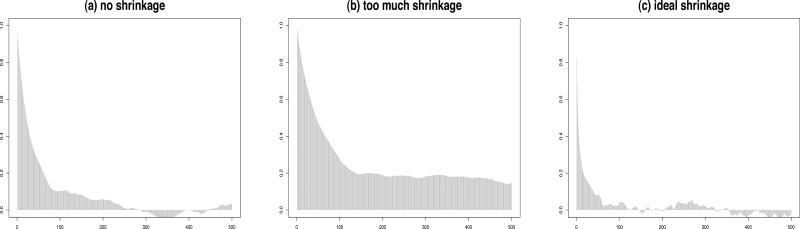
Shrinking the variance too much can lead to a failure in exploring the full range of values for θ_k and also result in high autocorrelations among the elements. Similar problems also arise when there is no shrinkage at all. Thus, in order to optimize the acceptance rates, we shrink the variance moderately and combine that with the multiple try method proposed by [17] with some modifications as discussed below. A combination of shrinkage and multiple tries is necessary since we have the positive definiteness constraint coupled with the high dimension d of Φ. Figures 1 and 2 show the trace plots and autocorrelations for 3 different choices of the proposal density variance. Ideal shrinkage will lead to nice looking trace plots and greatly reduce the autocorrelations among successive values. The use of multiple tries can lead to faster convergence requiring fewer burn-in samples. We can now formally state our algorithm for the k-th off-diagonal column as follows:

1. Draw m independent vectors, w₁, . . . , w_m from the symmetric proposal density $N_{d-1}({\theta }_k^t,V_k)$, where m is the number of tries; in our simulation we choose m = 5.

2. If $I({\theta }_{kk}-{\mathit{w}}_j^T{ϴ}_{-kk}^{-1}{\mathit{w}}_j>0)=0$ for all j = 1, . . , m then do not replace θ_k and stop; otherwise select w_j from w₁, . . . , w_m with probability proportional to p(w_j|θ_kk, Φ_–kk). Denote the selected vector as w.

3. Draw ${\mathit{x}}_1^{\ast },\dots ,{\mathit{x}}_{m-1}^{\ast }$ from N_d–1(w, V_k), and denote ${\mathit{x}}_m^{\ast }={\theta }_k^t$.

4. Replace ${\theta }_k^t$ by w with probability

   $$\text{min}\left\{1,\frac{p({\mathit{w}}_1\mid {\theta }_{kk},{ϴ}_{-kk})+\cdots +p({\mathit{w}}_m\mid {\theta }_{kk},{ϴ}_{-kk})}{p(x_m^{\ast }\mid {\theta }_{kk},{ϴ}_{-kk}+\cdots +p(x_m^{\ast }\mid {\theta }_{kk},{ϴ}_{-kk})}\right\},$$

   where $p\left({\mathit{x}}_j^{\ast }\right)\propto p({\mathit{x}}_j^{\ast }\mid {\theta }_{kk},{ϴ}_{-kk})$.

Note that, in the above scheme V_k remains constant for all MCMC samples; p(w_j|θ_kk, Φ_–kk) and $p({\mathit{x}}_j^{\ast }\mid {\theta }_{kk},{ϴ}_{-kk})$ are in the same form as (6) where θ_k is replaced by w_j and ${\mathit{x}}_j^{\ast }$, respectively.

Figure 1.

Trace plots of θ₁₂ for d = 5 and n = 10 showing the impact of variance tuning of the proposal density.

Figure 2.

Autocorrelation plots for θ₁₂ for d = 5 and n = 10 showing the impact of variance tuning of the proposal density.

For the BCLASSO method, we have several options for choosing the hyperparameter ρ. First, we can choose a conjugate gamma-type hyperprior for the penalty parameter. If we choose ρ ~ Gamma(α₀, β₀), then it could be sampled using the Gibbs sampler. The full conditional of ρ is ρ|α₀, β₀, Φ, Y ~ Gamma(α₀, β₀ + ||Φ||l₁). This choice requires choosing appropriate values of the hyperparameters α₀ and β₀; one could choose noninformative hyperpriors for large sample, however, for small sample the choice is not trivial as it has to be informative to impose penalty. An alternative is to choose the penalty parameter via cross-validation using the log-likelihood as a maximizer; we chose 5-fold cross-validation for the optimal choice of penalty parameters for each method.

We first compute BCLASSOm, which is the minimax estimator under the L₁-penalty [29]. Since BCLASSOm estimates all of the elements of Φ as non-zero, similar to posterior means, we also compute adhoc BCLASSOs estimators by forcing credible interval-based sparsity. That is, we construct the credible intervals and force an element of BCLASSOm to zero if the interval contains zero. Sparsity can be controlled by either the penalty parameter ρ or the width of the credible interval. A larger ρ or a prior with a larger mean will lead to a more sparse matrix when the width of the credible interval is fixed. A wider credible interval will also lead to a more sparse matrix when the penalty ρ or its prior mean is fixed. We found a credible interval or around 30% to be ideal. Forcing some elements to zero can theoretically result in non-positive definite matrices, however, they are positive definite with high probability given a small credible region is chooses (we suggest below 30%). Our simulation of 600 samples have all resulted in positive definite matrices as evidenced by the ability to compute finite L₁ losses for all cases, since any zero eigenvalue will result in infinite loss and negative eigenvalue would lead to an undefined loss. This credible- interval based thresholding has probabilistic interpretation and deserves further attention in other Bayesian estimation problems in which there is a need for sparsity. The threshholding also allows network exploration since forcing some zeros is the key in such network building.

2.4 Credible Regions

Suppose we have E MCMC samples Φ₁, . . . , Φ_E from the posterior distribution of the d dimensional precision matrix Φ and let Ψ_e = log(Φ_e) be the matrix logarithm of the e–th sample and Φ_e = exp(Ψ_e) be the matrix exponential of Φ_e. Note that, if λ₁, . . . , λ_d are the eigenvalues of Φ and γ₁, . . . , γ_d are the eigenvalues of Ψ, then γ_k = log(λ_k) for k = 1, . . . , d. Now, let $\stackrel{‒}{\Psi }$ is the posterior arithmetic mean of Ψ₁, . . . , Ψ_E then ${\stackrel{‒}{ϴ}}_G=\text{exp}\left(\overline{\Psi }\right)$ is the posterior geometric mean of Φ_e. We define the Euclidean distance between Ψ_e = (ψ_e,kk′) and the posterior mean $\stackrel{‒}{\Psi }=\left({\stackrel{‒}{\psi }}_{k{k}^{\prime }}\right)$ given by

$$d_{E,e}={\Vert {\Psi }_e-\stackrel{‒}{\Psi }\Vert }_2^2={\left\{\sum _{k,k^{\prime }=1}^d{({\psi }_{e,k{k}^{\prime }}-{\stackrel{‒}{\psi }}_{k{k}^{\prime }})}^{0.5}\right\}}^2.$$

Then, we sort the E samples according to the values of d_E,e and then use (d_E,α/2, d_E,1–α/2) as the (1 – α)100% credible region for Ψ. Finally, we obtain (exp(d_E,α/2), exp(d_E,1–α/2)) as the (1 – α)100% geometric confidence region for Φ.

3. SIMULATION STUDY

We used simulations to compare the performance of our BCLASSOm and BCLASSOs estimators with the three frequentist penalized likelihood methods namely, CLASSO [12], ACLASSO [11], and CSCAD [11]. Among the Bayesian methods, the [29] method uses shrinkage on the eigenvalues. This is infeasible in our non-full rank setting as some of the eigenvalues are zero since the dimension of Φ is larger than the sample size (hence the matrix is singular). In [27] and [28], an element-wise sampling was used and does not specify a recognizable prior on the precision (covariance) matrix. We restrict our comparison to permutation invariant methods that work for non-full rank data, use priors and l₁-type penalties directly on the elements of the precision matrix, and perform simultaneous shrinkage and estimation.

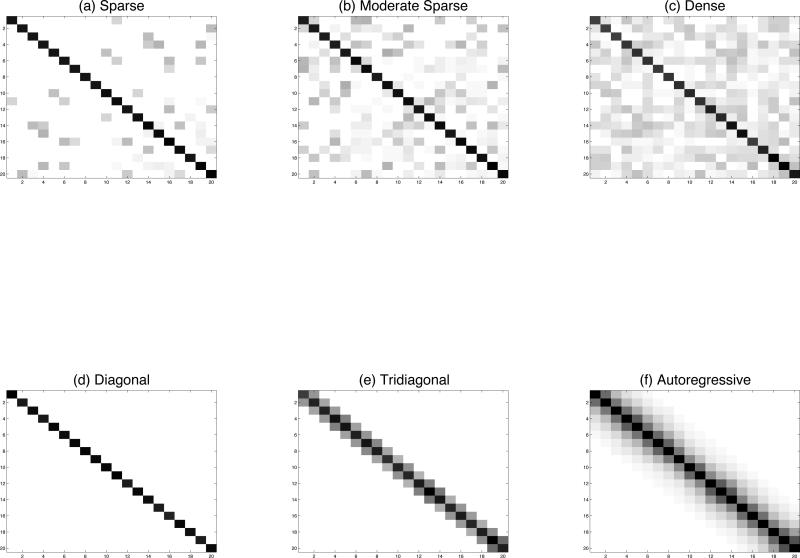
For the simulation, we fixed the dimensionality d and considered 3 unstructured and 3 structured matrix types. Among the unstructured types, the sparse matrix has at least 80% zeros on the off-diagonals, the moderately sparse one has at least 40% zeros on the off-diagonals, and the dense matrix has less than 5% zeros on the off-diagonals. The structured matrix types are tri-diagonal, autoregressive order one (i.e., AR(1)), and diagonal. In each case, we first generated a precision matrix. Then we generated 100 datasets for a non-full rank case where the sample size is less than the dimension (d = 20, n = 10) and compared the performance of each method based on those 100 samples.

We relied on a Cholesky decomposition to generate the 3 unstructured positive definite precision matrices of different sparsity levels. We generated a matrix A such that A_kk = 1, A_kk′ = U[–.5, .5] with probability p and A_kk′ = 0 with probability 1 – p for k < k′, and A_kk′ = 0 for k > k′. Then we computed Φ = AA^T and Σ = Φ^–1. The degree of sparsity was controlled by p, where a smaller p leads to a more sparse matrix. A tridiagonal precision matrix results in an AR(1) covariance matrix. In this case, the elements of the covariance matrix Σ are σ_kk′ = exp(–q|r_k – r_k′|), where r₁ < . . . < r_d for some q > 0. Here, we chose r_k – r_k–1 to be i.i.d from U[0.5, 1] for i = 2, . . . , d. An AR(1) precision matrix results in a tridiagonal covariance matrix and we generated the elements θ_kk′ = exp(–q|r_k – r_k′|) as above. A diagonal precision matrix results in a diagonal covariance matrix; in this case, we generated the diagonal elements of Σ where σ_kk are independently generated from U[1, 1.25] for k = 1, . . . , d. For the BCLASSOs estimators we used thresholding on the elements of BCLASSOm based on 30% credible intervals. This choice of the credible intervals is arbitrary and will depend on the choice of the penalty parameter ρ or the value of the hyperparameters on the prior of ρ.

3.1 Criteria for comparison

There are several loss measures proposed for evaluating the performance in estimation of the precision and covariance matrices as discussed in [29]. Among these, the entropy loss, denoted as L₁, and the quadratic loss, denoted as L₂, are the most commonly used. The L₁ and L₂ loss functions for Φ are defined as

$$\begin{array}{cc}\hfill L_1(ϴ,\widehat{ϴ})& =tr\left({ϴ}^{-1}\widehat{ϴ}\right)-\text{log det}\left({ϴ}^{-1}\widehat{ϴ}\right)-d,\hfill \\ \hfill L_2(ϴ,\widehat{ϴ})& =tr{({ϴ}^{-1}\widehat{ϴ}-I)}^2.\hfill \end{array}$$ (7)

where vec(A) = (a₁₁, · · · , a_1d) a_d1, · · · , a_dd)^T for any d × d matrix A = (a_ij). Similar loss functions for Σ will result in the Bayes estimators ${\widehat{\Sigma }}_{L_1}={\left\{E(ϴ\mid Y)\right\}}^{-1}$ and

$$\text{vec}\left({\widehat{\Sigma }}_{L_2}\right)={\left\{E(ϴ\otimes ϴ\mid Y)\right\}}^{-1}\text{vec}{\left\{E(ϴ\mid Y)\right\}}^{-1},$$

respectively. We use ${\widehat{ϴ}}_{L_1}={\left\{E(\Sigma \mid Y)\right\}}^{-1}\text{and}{\widehat{\Sigma }}_{L_1}={\left\{E(ϴ\mid Y)\right\}}^{-1}$ in our simulation studies as the BCLASSO estimators for Φ and Σ, respectively. Since ${\widehat{ϴ}}_{L_2}$ and ${\widehat{\Sigma }}_{L_2}$ are computationally less efficient, requiring inversion of a d² × d² matrix at each step of the Monte-Carlo sampling, we do not use them in our simulation. Our estimators ${\widehat{ϴ}}_{L_1}$ and ${\widehat{\Sigma }}_{L_1}$ in the simulation are Bayes under the L₁ loss, but not under the L₂ loss. Nevertheless, we were able to achieve reasonable L₂ loss for ${\widehat{ϴ}}_{L_1}$ and ${\widehat{\Sigma }}_{L_1}$ in our non-full rank simulation cases. Moreover, using L₁-Bayes estimators is more intuitive since we are using an L₁ penalty. Another measure known as the matrix correlation was defined by [10] as $R(ϴ,\widehat{ϴ})=\mathrm{tr}\left(ϴ\widehat{ϴ}\right)∕{\left\{\mathrm{tr}\left(ϴϴ\right)\mathrm{tr}\left(\widehat{ϴ}\widehat{ϴ}\right)\right\}}^{1∕2}$. In this measure, the closer the estimator $\widehat{ϴ}$ is to Φ, the higher the value of $R(ϴ,\widehat{ϴ})$. We compared our estimates ${\widehat{ϴ}}_{L_1}$ and ${\widehat{\Sigma }}_{L_1}$ with the CLASSO, ACLASSO, and CSCAD methods for the L₁ loss, the L₂ loss, and the matrix correlation based on 6 different matrix types of dimension 20. For each of the 6 matrix types, we used 100 Markov chain Monte Carlo (MCMC) samples of size 10 each. For all cases we choose Q = (S + aI)^–1 with a = 0.1, the number of tries as m = 5, the value of c = 0.5 was chosen to get about 30% acceptance rate. We collected 10, 000 MCMC samples after 5, 000 burn-in, which gave us an average computation time of about 10 minutes for each simulation.

We can also define the L₁ and L₂ loss functions for in a similar fashion. The optimal estimators minimize these loss functions. [29] showed that the Bayes (hence minimax) estimators of Φ under L₁ and L₂ are, respectively, given by

$$\begin{array}{cc}\hfill & {\widehat{ϴ}}_{L_1}={\widehat{ϴ}}_{L_1}={\left\{E(\Sigma \mid Y)\right\}}^{-1}\hfill \\ \hfill & \text{vec}\left({\widehat{ϴ}}_{L_2}\right)={\left\{E(\Sigma \otimes \Sigma \mid Y)\right\}}^{-1}\text{vec}{\left\{E(\Sigma \mid Y)\right\}}^{-1}.\hfill \end{array}$$

3.2 Results

Table 1 summarizes the mean L₁ losses and their standard deviations for the six types of precision and covariance matrices. The CSCAD method performs poorly in terms of L₁ loss for small sample non-full rank cases for all types of structures in both the precision and covariance matrices. For both the precision and covariance matrices, CLASSO, SPICE, ACLASSO, BCLASSOm, and BCLASSOs perform similarly. Table 2 summarizes the mean L₂ losses and their standard deviations for these four methods. For all structures, except the diagonal case, CSCAD is worse than CLASSO, SPICE, ACLASSO, BCLASSOm and BCLASSOs, while these five methods perform somewhat similarly for all six structures compared. Only for the diagonal precision matrix does CSCAD perform the best among the 5 methods compared. Table 3 summarizes the mean matrix correlations and their standard deviations. In terms of the matrix correlation measure $R(ϴ,\widehat{ϴ})$, CLASSO, BCLASSOm and BCLASSOs perform somewhat similarly in both the precision and covariance matrices. The ACLASSO and SPICE methods perform similarly in the precision matrix, but they are worse than BCLASSO and CLASSO in the covariance matrix. The CSCAD method performs the worst among all the methods in both the precision and covariance matrices for all six types of structures considered. As evident from Tables 1 and 2, although there is minimal or no loss in credible interval based sparsity in the precision matrix, there are substantial gains in matrix loss for the covariance matrix. The SPICE estimator seems to improve on the covariance over CLASSO. Performance of both SPICE and CSCAD improves when sparsity increases. The poor performance of CSCAD is somewhat surprising due to small sample sizes.

Table 1.

Mean L₁ losses (and standard deviations) for the different methods

Type		CLASSO	SPICE	ACLASSO	CSCAD	BCLASSOm	BCLASSOs
Sparse	Θ	2.38(0.43)	4.18(1.91)	5.71(2.62)	14.27(12.18)	4.82 (1.11)	4.52 (0.87)
	Σ	4.03(1.03)	2.99(0.76)	5.65(1.42)	19.02(7.92)	13.65(1.70)	3.56 (0.67)
Moderately	Θ	3.29(0.52)	5.09(2.69)	6.07(2.74)	13.44(8.80)	6.09 (1.29)	5.79 (1.03)
Sparse	Σ	5.76(1.42)	4.17(0.77)	6.41(1.25)	22.84(9.61)	12.93(1.89)	5.10 (0.87)
Dense	Θ	4.90(0.53)	7.08(1.83)	7.65(2.46)	17.22(11.49)	6.87 (1.17)	6.39 (0.87)
	Σ	9.53(2.24)	6.35(1.04)	9.95(1.31)	31.91(27.49)	12.82(1.80)	6.04 (0.69)
AR(1)	Θ	5.44(0.57)	7.60(2.16)	8.12(2.14)	13.11(7.14)	7.02 (1.15)	7.00 (0.87)
	Σ	9.53(2.24)	7.48(1.29)	7.95(1.31)	31.91(27.49)	12.42(5.97)	5.97 (0.59)
Tridiagonal	Θ	5.70(0.57)	7.99(1.83)	7.80(2.32)	19.45(9.45)	10.43(1.42)	9.27 (0.95)
	Σ	11.37(2.65)	9.37(1.79)	9.19(1.48)	24.50(9.10)	12.79(1.82)	12.18(1.16)
Diagonal	Θ	2.41(2.75)	3.69(2.11)	7.00(3.79)	10.49(5.87)	4.31 (1.46)	3.98 (0.98)
	Σ	4.23(4.74)	2.43(0.79)	7.27(5.44)	18.47(9.72)	13.81(1.67)	4.47 (0.99)

Note: CLASSO = covariance lasso; ACLASSO = adaptive covariance lasso; SPICE = sparse permutation invariant covariance estimator; ACLASSO = adaptive covariance lasso; CSCAD = smoothly clipped absolute deviation for covariance; BCLASSOm = Bayesian covariance; lasso with L₁ minimax estimator; BCLASSOs = Bayesian covariance lasso with sparsity forced;

Table 2.

Mean L₂ losses (and standard deviations) for the different methods

Type		CLASSO	SPICE	ACLASSO	CSCAD	BCLASSOm	BCLASSOs
Sparse	Θ	15.26(13.94)	51.45(55.79)	96.16(111.92)	497.49(1,542.28)	50.97(19.84)	51.70(19.96)
	Σ	101.15(65.48)	52.58(55.77)	19.04(22.16)	1,027.38(966.93)	215.78(17.12)	50.63(19.98)
Moderately	Θ	18.11(18.66)	58.23(137.26)	87.90(144.86)	278.80(980.90)	62.54(22.77)	63.94(23.15)
Sparse	Σ	167.56(104.94)	62.20(142.07)	44.09(55.24)	1,457.29(1,194.27)	199.12(20.64)	59.43(22.78)
Dense	Θ	11.38(12.00)	60.61(66.64)	91.98(111.98)	549.42(1,293.01)	33.09(18.97)	36.60(20.44)
	Σ	244.69(146.12)	78.22(78.46)	66.76(63.69)	1,364.45(1,702.53)	177.33(23.33)	30.09(19.33)
AR(1)	Θ	13.85(16.27)	57.19(71.12)	86.76(92.51)	208.60(664.13)	50.10(21.85)	48.95(21.75)
	Σ	318.06(189.03)	810.42(429.57)	95.49(88.67)	3,152.38(4,734.21)	30.46(18.40)	10.45(13.93)
Tridiagonal	Θ	11.80(13.44)	55.39(65.98)	76.50(100.36)	580.22(1,058.43)	153.65(24.70)	24.61(34.17)
	Σ	394.00(236.01)	17.06(17.48)	109.96(100.93)	1,433.68(1,053.86)	159.86(25.95)	88.63(27.74)
Diagonal	Θ	4.16(52.40)	53.25(63.51)	101.06(11.52)	1.02(4.34)	51.20(20.13)	51.41(20.13)
	Σ	75.39(217.11)	13.54(26.94)	17.84(34.07)	898.15(312.30)	223.66(15.74)	84.89(22.54)

Table 3.

Mean matrix correlations (and standard deviations) for the different methods

Type		CLASSO	SPICE	ACLASSO	CSCAD	BCLASSOm	BCLASSOs
Sparse	Θ	0.92(0.01)	0.84(0.06)	0.87(0.02)	0.69(0.09)	0.85(0.02)	0.88(0.02)
	Σ	0.89(0.04)	0.84(0.06)	0.76(0.06)	0.80(0.09)	0.92(0.02)	0.91(0.02)
Moderately	Θ	0.90(0.01)	0.82(0.05)	0.86(0.02)	0.66(0.09)	0.83(0.02)	0.85(0.03)
Sparse	Σ	0.85(0.03)	0.80(0.05)	0.74(0.06)	0.79(0.07)	0.89(0.01)	0.86(0.02)
Dense	Θ	0.86(0.01)	0.80(0.05)	0.83(0.02)	0.64(0.10)	0.79(0.04)	0.81(0.02)
	Σ	0.79(0.04)	0.67(0.05)	0.72(0.05)	0.70(0.05)	0.80(0.02)	0.73(0.02)
AR(1)	Θ	0.79(0.02)	0.71(0.06)	0.78(0.02)	0.59(0.07)	0.80(0.02)	0.80(0.02)
	Σ	0.78(0.03)	0.66(0.05)	0.72(0.04)	0.69(0.05)	0.75(0.02)	0.73(0.02)
Tridiagonal	Θ	0.87(0.02)	0.80(0.05)	0.85(0.02)	0.66(0.09)	0.75(0.01)	0.78(0.03)
	Σ	0.81(0.03)	0.74(0.05)	0.72(0.04)	0.77(0.05)	0.85(0.01)	0.79(0.03)
Diagonal	Θ	0.92(0.95)	0.87(0.07)	0.85(0.89)	0.66(0.77)	0.88(0.02)	0.90(0.02)
	Σ	0.86(0.95)	0.86(0.06)	0.72(0.78)	0.85(0.86)	0.95(0.01)	0.94(0.02)

4. APPLICATION TO REAL DATA

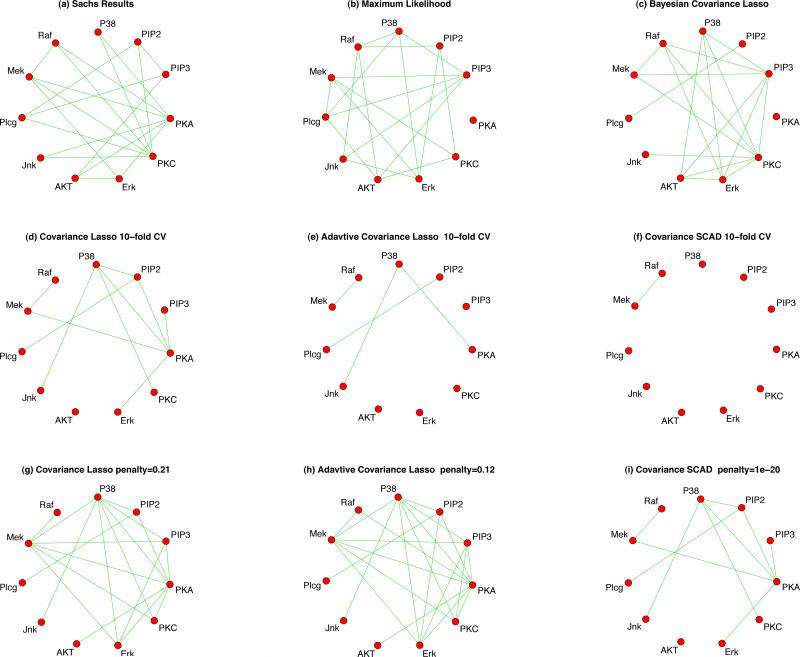
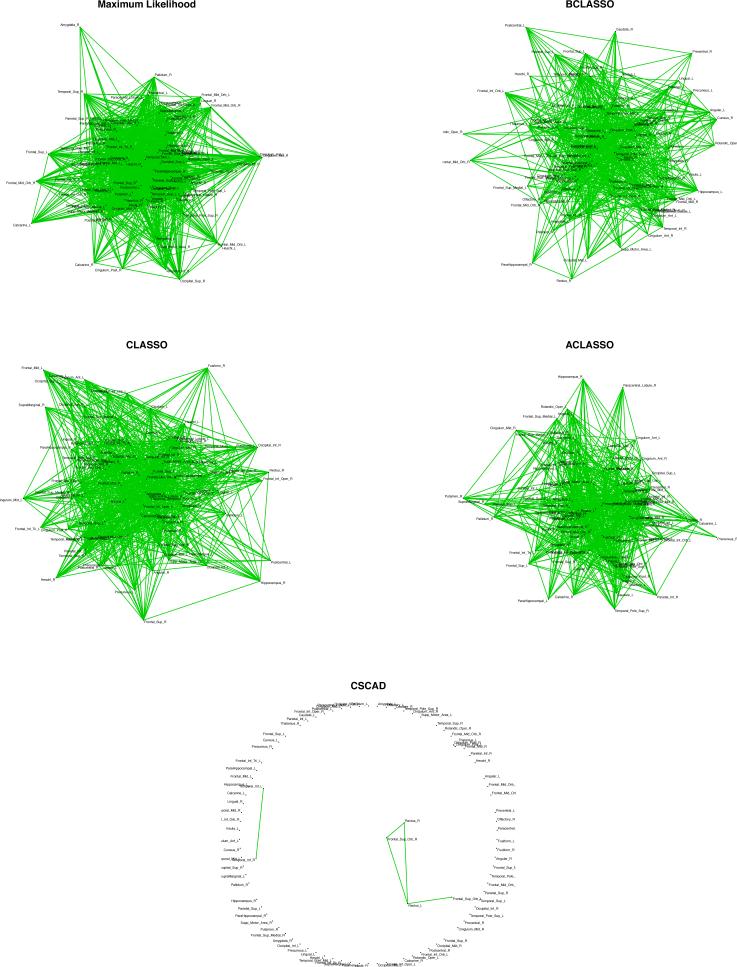
Example 1: The first dataset is flow cytometry data on d = 11 proteins on n = 7466 cells from [23]. In [23], a Bayesian network was developed and elucidated most of the signaling relationships reported traditionally and also predicted novel interpathway network causalities, which were verified through experiments. The data was also used by [12] for comparison of the agreements of CLASSO under different values of the penalty parameter. The data was generated from 9 simulations on 11 proteins. We adjusted the data for a random simulation effect as well as fixed effects of simulation and protein. Our purpose was to build a network between proteins via partial correlations (via Φ). For the maximum likelihood network in Figure 4(b), we used a hard-threshold that gives the same number of connections as those of [23]. The penalties for the CLASSO in Figure 4(d), ACLASSO in Figure 4(e) and CSCAD in Figure 4(f), were obtained through 10-fold cross validation. Since the penalties based on cross validation resulted in a more sparse network for these 3 frequentist methods than that of Sachs, we decided to fix the penalty manually to get the same number of connections. The results are shown in Figures 4 (g), 5(h) and 5(i), respectively. For CSCAD, no matter how small ρ is, the number of connections does not increase after a certain point. Finally, for BCLASSO, we used a gamma prior for the penalty parameter, ρ ~ Gamma(1, 1), and used 80,000 MCMC samples after 20,000 burn-ins to obtain posterior means and credible intervals. We constructed credible intervals of different widths for each element as shown in Table 4; the Bayesian network that has the closest number of connections to that of Sachs is shown on Figure 4. The level of agreement of each of these 4 methods to those of Sachs’ results were computed and reported in Table 4. The results indicate similar agreement between the networks of BCLASSO, ACLASSO and CLASSO and [23]'s network when the number of connections are similar.

Figure 4.

Networks for 11 proteins from Sachs et al. (2003)

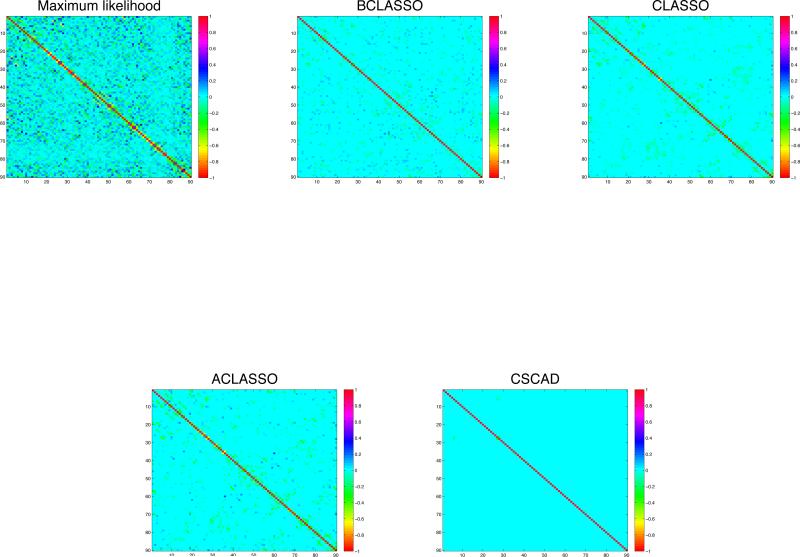
Figure 5.

Image plots of the partial correlation matrices for 90 regions of 2-year old children’ brains using the five different methods

Table 4.

Agreement of Methods with the Results from Sachs et al. (2003)

Method	No	Se	Sp	PPV	NPV
Sachs	19	1.00	1.00	1.00	1.00
Maximum Likelihood	20	0.37	0.64	0.35	0.66
BCLASSO 10%	30	0.58	0.47	0.37	0.68
BCLASSO 20%	21	0.47	0.67	0.43	0.71
BCLASSO 25%	18	0.42	0.72	0.44	0.70
BCLASSO 30%	13	0.32	0.81	0.46	0.69
BCLASSO 35%	13	0.32	0.83	0.46	0.72
BCLASSO 40%	8	0.26	0.92	0.63	0.70
BCLASSO 50%	8	0.26	0.92	0.63	0.70
CLASSO 10-fold CV	10	0.32	0.89	0.60	0.71
ACLASSO 10-fold CV	4	0.16	0.97	0.75	0.69
SCAD 10-fold CV	1	0.05	1.00	1.00	0.67
LASSO ρ = 0.21	19	0.47	0.72	0.47	0.72
ACLASSO ρ = 0.12	19	0.47	0.72	0.47	0.72
SCAD ρ = 10–3	10	0.32	0.89	0.60	0.71
SCAD ρ = 10–20	10	0.32	0.89	0.60	0.71

Note: CI = credible interval: No = Number of connections; Se = Sensitivity; Sp = Specificity; PPV = Positive predictive value; NPV = Negative predictive value.

Example 2: While it is well recognized that the human brain forms large scale networks of distributed and interconnected neuronal populations, the study of different brain networks has been hampered by the lack of non-invasive tools. Recently, the introduction of the resting functional connectivity MRI approach offers, potentially, a potent tool, to specifically alleviate this difficulty, allowing a direct investigation of a wide array of brain networks. Researchers are often interested in exploring the brain networks through partial correlations where the connection between two regions is explored after removing the effect of all other regions.

The data consists of average fcMRI signals from 90 brain regions (d = 90) of 30 2-year old children (N = 30). All images were acquired on a 3T MR scanner with a gradient echo-planar imaging sequence. The imaging sequence was repeated 150 times. The images of the first 10-20 time points were typically excluded from the data analysis to ensure that magnetization reaches the steady state. All subjects are healthy normal controls and imaged at sleep without sedation. In this study, the signals were obtained from the remaining 130 repeats (T = 130, so that n = NT = 3900). Our primary purpose here is to build a network between regions after adjusting for subject effects and region specific means. Let Y_ijk (i = 1, . . . , N; j = 1, . . . , T; k = 1, . . . d) represent the adjusted average fcMRI signal from subject i at repeat (time) j in region k. Then Y_ij is the d-dimensional vector of adjusted responses from subject i on repeat j and Y_ij ~ N_d(0, Σ). Let n = NT, the joint distribution of Y is given by

$$p(Y\mid ϴ)\propto {\left\{\text{det}\left(ϴ\right)\right\}}^{\frac{n}{2}}\text{exp}\left\{-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^T{Y}_{ij}^{\mathrm{T}}ϴY_{ij}\right\}I(ϴ\succ 0).$$

The posterior distribution of Φ under the lasso penalty can be written as in (3) and the full conditionals are given in (6). For the penalty parameter ρ, we take ρ ~ Gamma(1, 1). For thresholding, we construct credible intervals of different widths to control sparsity. For CLASSO, ACLASSO, and CSCAD, we used 10-fold cross validation to choose the optimal penalty. We report the resulting precision matrices in Figure 5 and the networks in Figure 6. The summary statistics of the number of connections along with the global efficiencies E_glob (a measure of how efficiently the regions communicate in the whole brain) and local efficiencies E_loc (a measure of how efficiently the regions in each local area communicate) are reported in Table 5.

Figure 6.

Networks for 90 regions of 2-year old children’ brains using the different methods

Table 5.

Regions With the Highest Number of Connections Picked by the Four Methods

Maximum Likelihood		Covariance Lasso		Adaptive Covariance Lasso		Bayesian Covariance Lasso
Temporal Pole Mid L	35	Rectus L	33	Temporal Inf L	27	Occipital Inf R	32
Frontal Mid L	31	Temporal Inf L	30	Temporal Inf R	24	Temporal Sup L	31
Precentral R	29	Temporal Inf R	28	Rectus L	23	Frontal Inf Oper R	30
Occipital Sup R	29	Cingulum Post L	28	Supp Motor Area L	23	Angular R	29
Fusiform L	28	Frontal Sup Orb R	27	Cingulum Post L	22	Temporal Mid R	29
Temporal Inf L	28	Heschl L	26	Heschl L	20	Amygdala L	28
Temporal Inf R	28	Supp Motor Area L	25	Frontal Sup Orb R	19	Frontal Mid Orb L	26
Temporal Pole Sup R	27	Frontal Mid Orb R	24	Paracentral Lobule L	19	Frontal Inf Tri L	26
Temporal Pole Mid R	27	Paracentral Lobule L	24	Precentral R	19	Cingulum Mid L	25
Precentral L	26	Olfactory L	24	Olfactory L	18	Parietal Inf L	25
Frontal Sup L	26	Parietal Sup R	23	Occipital Mid R	18	Occipital Sup L	25
Frontal Inf Orb R	26	Frontal Mid Orb R	22	Temporal Pole Mid L	18	Frontal Mid Orb L	24
Temporal Mid L	26	Amygdala L	22	Parietal Sup L	18	Occipital Sup R	24
Angular R	25	Pallidum R	22	Frontal Sup Orb L	18	Occipital Inf L	22
Frontal Sup Orb R	24	Precentral R	21	Frontal Mid Orb R	17	Calcarine L	22
Frontal Mid Orb R	24	Frontal Mid R	21	Parietal Sup R	17	Hippocampus L	22
Occipital Inf L	24	Occipital Mid R	21	Frontal Mid Orb R	17	ParaHippocampal L	21
Parietal Inf R	24	Frontal Mid Orb L	21	Amygdala L	17	Temporal Mid L	21
Frontal Sup Orb L	23	Caudate L	21	Pallidum R	17	Heschl L	20
Frontal Inf Tri R	23	Heschl R	21	Frontal Mid R	17	Caudate L	19
Rectus L	23	Insula L	21	Frontal Mid Orb L	17	Thalamus L	19
Postcentral L	23	Putamen L	21	Calcarine R	17	Precuneus R	19
Parietal Sup R	23	Temporal Pole Mid L	20	Temporal Pole Sup R	17	Olfactory L	18
Frontal Sup R	22	Occipital Inf R	20	Occipital Inf R	16	Frontal Sup L	18
Frontal Inf Orb L	22	Parietal Sup L	20	Cingulum Post R	16	Lingual R	18
Rolandic Oper L	22	Rolandic Oper R	20	Frontal Mid L	16	Temporal Inf L	17
Frontal Sup Medial R	22	Cingulum Post R	20	Frontal Sup R	16	Temporal Pole Mid L	17
Occipital Inf R	22	Calcarine R	20	ParaHippocampal L	16	Pallidum L	17
Frontal Inf Oper R	21	Caudate R	20	Angular R	16	Angular L	17
Occipital Sup L	21	Temporal Pole Sup R	19	Occipital Inf L	16	SupraMarginal L	17
SupraMarginal L	21	Frontal Sup Orb L	19	Frontal Mid Orb L	16	Frontal Mid R	17
Temporal Sup R	21	Cingulum Ant R	19	Olfactory R	15	Calcarine R	16
Frontal Mid R	20	Cingulum Mid R	19	Cingulum Mid L	15	Thalamus R	16
Supp Motor Area L	20	Putamen R	19	Putamen L	14	Fusiform L	16
Supp Motor Area R	20	Thalamus L	19	Caudate R	14	Frontal Inf Orb L	16
Parietal Inf L	20	Frontal Mid L	18	Frontal Sup L	14	Frontal Inf Orb R	16
Angular L	20	Frontal Sup L	18	Supp Motor Area R	14	Temporal Pole Sup L	16
Precuneus L	20	Frontal Sup R	18	Hippocampus R	14	Parietal Sup R	16
Frontal Inf Oper L	19	Supp Motor Area R	18	Amygdala R	14	Olfactory R	15
Frontal Inf Tri L	19	ParaHippocampal L	18	Fusiform L	14	Paracentral Lobule R	15
Cingulum Post L	19	Frontal Sup Medial L	18	Precuneus L	14	Insula R	15
Calcarine L	19	Lingual L	18	Caudate L	13	Temporal Sup R	15
Occipital Mid R	19	Hippocampus R	18	Heschl R	13	Cuneus L	15
Fusiform R	19	Amygdala R	18	Lingual L	13	Occipital Mid R	15
Parietal Sup L	19	Thalamus R	18	Precentral L	13	Frontal Mid L	14
SupraMarginal R	19	Precentral L	17	Parietal Inf R	13	Temporal Pole Mid R	14
Temporal Pole Sup L	19	Angular R	17	Rolandic Oper L	13	Occipital Mid L	14
ParaHippocampal L	18	Parietal Inf R	17	Temporal Pole Mid R	13	Postcentral R	14
Precuneus R	18	Rolandic Oper L	17	Calcarine L	13	Parietal Sup L	14
Temporal Sup L	18	Parietal Inf L	17	Insula R	13	Temporal Pole Sup R	13
Frontal Mid Orb L	17	Cingulum Ant L	17	Temporal Sup R	13	Cingulum Ant L	13
Rolandic OperR	17	Cuneus R	17	Cingulum Ant R	12	Frontal Inf Oper L	13
ParaHippocampal R	17	Hippocampus L	17	Cingulum Mid R	12	Temporal Inf R	13
Lingual R	17	Olfactory R	17	Putamen R	12	Cingulum Post R	12
Occipital Mid L	17	Cingulum Mid L	17	Thalamus R	12	Amygdala R	12
Temporal Mid R	17	Occipital Sup R	16	Cuneus R	12	Precentral L	12
Frontal Mid Orb R	16	Fusiform L	16	Frontal Inf Oper L	12	Cuneus R	12
Rectus R	16	Occipital Inf L	16	Fusiform R	12	Parietal Inf R	12
Cingulum Ant R	16	Precuneus L	16	ParaHippocampal R	12	Fusiform R	12
Cingulum Mid R	16	Frontal Inf Oper L	16	Frontal Inf Orb L	12	SupraMarginal R	12

The CSCAD method performs poorly compared to the other three methods and shows very few connections across the entire brain, leading to rather low global and local efficiencies. This result contradicts the well formed brain networks of 2 year olds, which has been reported in the literature using both imaging and behavioral approaches [14]. In contrast, CLASSO, ACLASSO, and BCLASSO appear to provide more similar results, demonstrating well connected brain networks. Although there are differences in the regions with the highest number of connections, some consistent patterns are observed from CLASSO, ACLASSO, and BCLASSO. The brain regions that exhibit the highest number of connections with other regions are consistently shown by these three methods in the temporal, frontal and occipital lobes. These results suggest that even at the age of 2 years, children develop well connected networks, particularly in the temporal and frontal areas. More studies are clearly needed to further determine how the proposed approach is capable of better delineating the development of brain networks across different age groups. The top regions picked up by the different methods are listed in Table 5. The BCLASSO results are based on thresholding with a 70% credible interval. This choice was made in order to closely align the total number of connections from BCLASSO to that of CLASSO and ACLASSO.

5. DISCUSSION

We have introduced a general class of priors for the precision matrix which yield the ACLASSO, CLASSO, and SPICE penalties as special cases. We have also developed a sampling scheme for the estimation of the precision and covariance matrices under a special case that corresponds to the lasso penalty, which can facilitate exploration of the full posterior distribution of the matrix under L₁ penalites. Although our proposed priors do not guarantee positive definiteness of Φ, we have developed a fast sampling scheme that guarantees positive definite MCMC samples of the precision matrix at each iteration regardless of the value of the penalty parameter. Our proposed method is the first Bayesian method that uses priors that directly translate into the L₁ penalty, the method works well for non-full rank data, and performs shrinkage and estimation simultaneously. Simulations show that BCLASSO performs similarly to CLASSO, SPICE and ACLASSO for non-full rank data when the sample size is small, while performing better than CSCAD. We will further develop an efficient algorithm to sample from p(θ_k|y, θ_kk, ρ). The proposed method can be easily extended to more complex models that account for subject-specific variation for building networks in longitudinal data. The priors can be generalized to independent gamma priors for the diagonal elements; θ_kk ~ gamma(α_k, β_k) and independent double gamma priors for the off-diagonal elements θ_kk′ ~ double gamma(0, a_kk′, b_kk′|) for k > k′; that is, p(θ_kk′) ∝ |θ_kk′|^a_kk′–1 exp(–b_kk′|θ_kk′|), where a_kk′ > 0 and b_kk′ > 0. Then, the posterior distribution of Φ is given by

$$\begin{array}{cc}\hfill p(ϴ\mid Y)\propto & {\left(\text{det}ϴ\right)}^{\frac{n}{2}}\prod _{k=1}^d{\theta }_{kk}^{{\alpha }_k-1}\prod _{k=2}^d\prod _{k^{\prime }=1}^{k-1}{\mid {\theta }_{k{k}^{\prime }}\mid }^{a_{k{k}^{\prime }}-1}\hfill \\ \hfill & \text{exp}\{-\frac{n}{2}tr\left(Sϴ\right)-\sum _{k=1}^d{\beta }_k{\theta }_{kk}-\sum _{k=2}^d\sum _{k^{\prime }=1}^{k-1}{b}_{k{k}^{\prime }}\mid {\theta }_{k{k}^{\prime }}\mid \},\hfill \end{array}$$

This is particularly attractive for Bayseian analysis since appropriate choice of shape and scale paramters can lead to an infinite spike of the prior at 0 and heavier tails leading to larger shrinkage of smaller parameters and smaller shrinkage of larger parameters compared to L₁-penalties.

Like many Bayesian methods, scalibility to larger dimensions is a challenge for BCLASSO. Nevertheless, the posterior estimators for dimensions up to 50 do well and networks dimension near 100 works similar to CLASSO and ACLASSO as evidenced by the brain imaging data example. The main advantage of a fully Bayesian approach is the ability to sample the whole posterior distribution instead of just estimating the posterior mode.

Figure 3.

Image plots of the six types of precision matrices (Φ) considered in the simulation study. The top 3 are unstructured and the bottom 3 are structured.

Appendix I

Proof of Theorem 1: Without loss of generality, we partition and rearrange the columns of current Φ^(t) as

$${ϴ}^{\left(t\right)}=\left(\begin{array}{cc}\hfill {ϴ}_{-kk}^{\left(t\right)}\hfill & \hfill {\theta }_k^{\left(t\right)}\hfill \\ \hfill {\theta }_k^{\mathrm{T}\left(t\right)}\hfill & \hfill {\theta }_{kk}^{\left(t\right)}\hfill \end{array}\right)\succ 0.$$

Since ${ϴ}_{-kk}^{\left(t\right)}\succ 0$, all of its diagonal elements are positive and all the leading determinants are positive. In particular, ${\left({ϴ}_{-kk}^{\left(t\right)}\right)}^{-1}\succ 0$ and so there exists an A_k such that ${\left({ϴ}_{-kk}^{\left(t\right)}\right)}^{-1}=A_k{A}_k^{\mathrm{T}}$ based on the Cholesky decomposition. We only need to show that after updating the first column (θ_kk and θ_k), the diagonal element ${\theta }_{kk}^{(t+1)}$ is positive and the last determinant is positive, i.e., $\text{det}{\left(ϴ\right)}^{(t+1)}=D_k^{(t+1)}\text{det}\left({ϴ}_{-kk}^{\left(t\right)}\right)>0$; this implies $D_k^{(t+1)}>0$ since ${ϴ}_{-kk}^{\left(t\right)}\succ 0$. When we update the last column (or equivalently row) we have

$$C_k^{\left(t\right)}={\left({\theta }_k^{\left(t\right)}\right)}^{\mathrm{T}}{\left({ϴ}_{-kk}^{\left(t\right)}\right)}^{-1}{\theta }_k^{\left(t\right)}={\left(A_k^T{\theta }_k^{\left(t\right)}\right)}^{\mathrm{T}}{A}_k^{\mathrm{T}}{\theta }_k^{\left(t\right)}={\eta }^{\mathrm{T}}\eta \ge 0.$$

Thus, we have

$${\theta }_{kk}^{(t+1)}=C_k^{\left(t\right)}+Gamma\left(\frac{n}{2}+1,\frac{n}{2}(s_{kk}+\rho )\right)>0.$$

Let x be the proposed value for ${\theta }_k^{(t+1)}$. Then $D_x=\left({\theta }_k^{(t+1)}\right)-x^{\mathrm{T}}{\left({ϴ}_{-kk}^{\left(t\right)}\right)}^{-1}x$. Thus, $p(x\mid Y,{\theta }_{kk}^{(t+1)},{ϴ}_{-kk}^{\left(t\right)})$ is proportional to

$$D_x^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}{({\mathit{s}}_k+\rho {\gamma }_k^t)}^{\mathrm{T}}{\theta }_k^t\}I(D_x>0).$$

However, $p(x\mid Y,{\theta }_{kk}^{(t+1)},{ϴ}_{-kk}^{\left(t\right)})=0$ whenever D_x ≤ 0, so that the Metropolis acceptance probability is

$$\alpha =\text{min}\left\{1,\frac{p(x\mid Y,{\theta }_{kk}^{(t+1)},{ϴ}_{-kk}^{\left(t\right)})}{p({\theta }_k^{\left(t\right)}\mid Y,{\theta }_{kk}^{(t+1)},{ϴ}_{-kk}^{\left(t\right)})}\right\}=0.$$

That is, we can only accept the proposed value when D_x > 0. Thus, ${\theta }_k^{(t+1)}=x\Rightarrow D_x>0$. This is true for any column of Φ that we update, therefore leading to positive definite values of Φ at any stage in the updating process. This completes the proof.

Derivation of (6): Let ρ ~ Gamma(α₀, 0.5nβ₀). Then the joint posterior of (Φ, ρ) becomes

$$\begin{array}{cc}\hfill p(ϴ,\rho \mid Y)=& p(ϴ,\rho \mid S)\propto \text{det}{\left(ϴ\right)}^{n∕2}{\rho }^{{\alpha }_0-1}\hfill \\ \hfill & \text{exp}\left(0.5n\{-\mathrm{tr}\left(Sϴ\right)-\rho {\Vert ϴ\Vert }_{l_1}-\rho {\beta }_0\}\right),\hfill \end{array}$$

which yields that

$$p(\rho \mid ϴ,Y)\propto {\rho }^{{\alpha }_0-1}\text{exp}\{-0.5n\rho ({\beta }_0+{\Vert ϴ\Vert }_{l_1})\},$$

which is the kernel of a Gamma(α₀, 0.5n(β₀ + ||Φ||l₁)) distribution. Now, using the partition in (5), we can write det(Φ) = det(Φ_–kk)D_k, where $D_k=({\theta }_{kk}-{\theta }_k^{\mathrm{T}}{ϴ}_{-kk}^{-1}{\theta }_k)$. Moreover, ||Φ||l₁ = ||Φ_–kk||l₁ + 2||θ_k||l₁ + θ_kk and tr(SΦ) is given by

$$\begin{array}{cc}\hfill \mathrm{tr}\left(Sϴ\right)& =tr\left\{\left(\begin{array}{cc}\hfill S_{-kk}\hfill & \hfill {\mathit{s}}_k\hfill \\ \hfill {\mathit{s}}_k^{\mathrm{T}}\hfill & \hfill s_{kk}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {ϴ}_{-kk}\hfill & \hfill {\theta }_k\hfill \\ \hfill {\theta }_k^{\mathrm{T}}\hfill & \hfill {\theta }_{kk}\hfill \end{array}\right)\right\}\hfill \\ \hfill & =\mathrm{tr}\left(\begin{array}{cc}\hfill S_{-kk}{ϴ}_{-kk}+{\mathit{s}}_k{\theta }_k^{\mathrm{T}},\hfill & \hfill S_{-kk}{\theta }_k+{\mathit{s}}_k{\theta }_{kk}\hfill \\ \hfill {\mathit{s}}_k^{\mathrm{T}}{ϴ}_{-kk}+s_{kk}{\theta }_k^{\mathrm{T}},\hfill & \hfill s_k^{\mathrm{T}}{\theta }_k+s_{kk}{\theta }_{kk}\hfill \end{array}\right)\hfill \\ \hfill & =tr\left(S_{-kk}{ϴ}_{-kk}\right)+2s_k^{\mathrm{T}}{\theta }_k+s_{kk}{\theta }_{kk}.\hfill \end{array}$$

Therefore, the joint posterior distribution of (Φ, ρ) can be written as

$$=p(ϴ,\rho \mid Y,\rho )=\text{det}{\left(ϴ\right)}^{n∕2}\text{exp}\left(0.5n\{-\mathrm{tr}\left(Sϴ\right)-\rho {\Vert ϴ\Vert }_{l_1}\}\right)=\text{det}{\left({ϴ}_{-kk}\right)}^{n∕2}{D}_k^{n∕2}\text{exp}\left(0.5n\{-\mathrm{tr}\left(S_{-kk}{ϴ}_{-kk}\right)-2s_k^{\mathrm{T}}{\theta }_k-s_{kk}{\theta }_{kk}-\rho ({\Vert {ϴ}_{-kk}\Vert }_{l_1}+2{\Vert {\theta }_k\Vert }_{l_1}+{\theta }_{kk})\}\right).$$

After dropping unnecessary constants, we have

$$\begin{array}{cc}\hfill p({\theta }_{kk}\mid Y,{\theta }_k,{ϴ}_{-kk},\rho )& \propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_{kk}+\rho ){\theta }_{kk}\},\hfill \\ \hfill p({\theta }_k\mid Y,{\theta }_{kk},{ϴ}_{-kk},\rho )& \propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_k^{\mathrm{T}}{\theta }_k+\rho {\Vert {\theta }_k\Vert }_{l_1})\}.\hfill \end{array}$$

To derive the full conditional distribution of θ_kk, we write

$$\begin{array}{cc}\hfill p({\theta }_{kk}\mid Y,{\theta }_k,{ϴ}_{-kk},\rho )& \propto D_k^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_{kk}+\rho ){\theta }_{kk}\}\hfill \\ \hfill & ={({\theta }_{kk}-C_k)}^{\frac{n}{2}}\text{exp}\{-n∕2(s_{kk}+\rho ){\theta }_{kk}\}\hfill \\ \hfill & \propto {({\theta }_{kk}-C_k)}^{\frac{n}{2}}\text{exp}\{-\frac{n}{2}(s_{kk}+\rho )({\theta }_{kk}-C_k)\}.\hfill \end{array}$$

Thus, θ_kk – C_k|Y, θ_k, Φ_–kk ~ Gamma(n/2 + 1, n/2(s_kk + ρ)) and this implies that θ_kk|Y, θ_k, Φ_–kk ~ C_k + Gamma(n/2 + 1, n/2(s_kk + ρ)).