Significance
One of the greatest challenges in addressing global environmental problems such as climate change, which involves public goods and common-pool resources, is achieving cooperation among peoples. There are great disparities in wealth among nations, and this heterogeneity can make agreements much more difficult to achieve (e.g., regarding implementation of climate change mitigation). This paper incorporates wealth inequality into a public goods dilemma, including an asymmetric distribution of wealth representative of existing inequalities among nations. Without homophily (imitation of like agents), inequality actually makes cooperation easier to achieve; homophily, however, can undercut this, leading to collapse because poor agents may contribute less. Understanding such effects may enhance the ability to achieve agreements on climate change and other issues.
Keywords: collective action, global warming, governance of the commons, environmental agreements, evolutionary game theory
Abstract
Taming the planet’s climate requires cooperation. Previous failures to reach consensus in climate summits have been attributed, among other factors, to conflicting policies between rich and poor countries, which disagree on the implementation of mitigation measures. Here we implement wealth inequality in a threshold public goods dilemma of cooperation in which players also face the risk of potential future losses. We consider a population exhibiting an asymmetric distribution of rich and poor players that reflects the present-day status of nations and study the behavioral interplay between rich and poor in time, regarding their willingness to cooperate. Individuals are also allowed to exhibit a variable degree of homophily, which acts to limit those that constitute one’s sphere of influence. Under the premises of our model, and in the absence of homophily, comparison between scenarios with wealth inequality and without wealth inequality shows that the former leads to more global cooperation than the latter. Furthermore, we find that the rich generally contribute more than the poor and will often compensate for the lower contribution of the latter. Contributions from the poor, which are crucial to overcome the climate change dilemma, are shown to be very sensitive to homophily, which, if prevalent, can lead to a collapse of their overall contribution. In such cases, however, we also find that obstinate cooperative behavior by a few poor may largely compensate for homophilic behavior.
Despite existing scientific consensus that anthropogenic greenhouse gas emissions (GHGE) perturb global climate patterns with negative consequences for many natural ecosystems (1–3), reaching a global agreement regarding reduction of GHGE remains one of the most challenging problems humans face (4). International climate negotiations have largely failed to reach consensus (5, 6), evidencing a conflict between rich and poor countries, which often do not agree on the urgency of emission reduction measures, given the scientific uncertainty regarding the impacts of climate change (7–10). Indeed, in the aftermath of the 15th Conference of Parties in Copenhagen/2009 one has observed a tendency of several governments to regard climate change as a problem of a distant future—2050—hence discounting (4) the actual risk of collective disaster—despite predictions that severe climate change consequences, such as increased occurrence of heat waves and droughts, for instance, may happen sooner (1).
The issue of reducing GHGE has been addressed recently, both experimentally and theoretically, by means of a threshold Public Goods Game (PGG) in which success requires overall cooperative collective action, and decisions must be made knowing that failure to cooperate implies a risk of overall collapse (10–18). Like many social dilemmas of collective action, any participant that curbs emissions pays a cost whereas the benefits are shared among everyone. Thus, the rational choice is to free ride on the benefits produced by others at their own expense (through abatement), leading to the well-known tragedy of the commons, where selfish behavior results in overexploitation of the public good (19, 20).
Both theory and experiment agree that risk perception plays a central role in escaping the tragedy of the commons (12, 13). Besides risk, the role of wealth inequality among participants has been recently investigated by means of economic experiments involving students from western, educated, industrialized, rich, and democratic (WEIRD) countries (a feature that may induce biases regarding behavior of subjects taking the role of poor countries) (10, 11). Games comprised groups of fixed size (N = 6) where participation was equally split between rich and poor individuals, whose different wealth resulted from two different start-up amounts of money made available to group participants. The insights provided by these experiments (10, 11) (using different methodologies and assumptions while using the same PGG) converge on the idea that resolution of the climate change policy problem stems from the rich compensating for the smaller contribution by the poor and, even when risk is very high (something that does not seem to apply to the present situation), there is still a very significant chance of failing to solve the climate change dilemma, a situation that is ameliorated whenever intermediate tasks are designated (11) or whenever individuals have the opportunity to pledge their contribution before actual action (10).
Here we address the issue of wealth inequality from a theoretical perspective. The model we extend here to deal with wealth inequality (13, 17) has been shown to lead to predictions that correlate nicely with previous economic experiments carried out in the absence of any wealth inequalities (10), with the added value of allowing a full exploration of how success in addressing the climate change dilemma depends on other important parameters, such as risk, group size, introduction of sanctioning institutions of global or local nature, etc. It is important to stress that, despite the limited number of scenarios realizable in the laboratory, data stemming from behavioral experiments have provided crucial insights, not only because they unravel human behavior when confronted with climate change issues, but also because they provide important guidelines that help in calibrating theoretical models, such as the one we use here. Indeed, here we model climate change negotiations in the framework of Evolutionary Game Theory, where individuals exhibit a well-defined behavior (C or D), as a result of which they accumulate a certain payoff resulting from the game group interactions. Regularly, every individual A compares her/his payoff with that of a randomly chosen individual B, imitating (or not) the behavior of B with a probability that is a growing function of the payoff difference between B and A. Naturally, the larger the payoff of individual B (randomly) selected as role model, the more likely it is that A imitates her/his behavior (see Methods for specific details of the update rule).
Let us consider a population of finite size Z of which ZR individuals are rich and ZP
= Z −
ZR individuals are poor. Individuals are randomly sampled from the population and organize into groups of size N. Each rich individual starts with an initial endowment bR whereas each “poor” individual starts with bP, with bR
> bP. These endowments may be used (or not) by an individual to contribute to reducing GHGE in her own group. We distinguish two types of behavior: (i) cooperators (Cs), who contribute a certain fraction c of their endowment to help solve the group task, and (ii) defectors (Ds) that do not contribute anything to solve the group task. Hence, the endowment is directly related to what each participant will lose if the next intermediate target is not met: Cs will lose 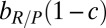 whereas Ds will lose the entire endowment
whereas Ds will lose the entire endowment 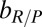 . If the overall amount of contributions in the group is above a certain threshold
. If the overall amount of contributions in the group is above a certain threshold 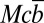 (where
(where 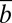 is the average endowment of the population), the target will be met. Otherwise, with a probability r—the perception of risk of collective disaster (10, 12, 13)—individuals in the group will lose whatever they have.
is the average endowment of the population), the target will be met. Otherwise, with a probability r—the perception of risk of collective disaster (10, 12, 13)—individuals in the group will lose whatever they have.
This framework creates an interdependent behavioral ecosystem, where each player in a group knows what all other members of the group will do and where decisions and achievements of others influence one’s own decisions (21–24). In particular, decisions taken by the poor can be potentially influenced by the actions and achievements of the rich (and vice versa), adding an additional coupling between these two subpopulations (details in Methods). In standard conditions, anyone in this population may influence and be influenced by anyone else. This, however, may not always be the case, in the sense that individuals may be more receptive to the behavior and decisions of those in the same wealth class, thus selecting preferentially those of their wealth class as peers. To this end we define a homophily parameter (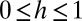 ), such that when
), such that when 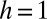 , individuals are restricted to influence (and be influenced) by those of the same wealth status, whereas when
, individuals are restricted to influence (and be influenced) by those of the same wealth status, whereas when 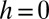 , no wealth discrimination takes place. Naturally, such influence dynamics occur in the presence of action errors (24) as well as other stochastic effects, such as random exploration of the strategy space, akin to behavioral mutations (25).
, no wealth discrimination takes place. Naturally, such influence dynamics occur in the presence of action errors (24) as well as other stochastic effects, such as random exploration of the strategy space, akin to behavioral mutations (25).
In SI Text, we show that in populations with a mixed composition of rich and poor (and for different combinations of Cs and Ds in each wealth group), the nature of the overall public goods dilemma faced by the rich subpopulation differs qualitatively from that faced by the poor subpopulation. In these limiting cases where a decoupling of the timescales associated with the dynamics of the rich and of the poor takes place, the rich generally face an N-person coordination dilemma between Cs and Ds, whereas (for most combinations of parameters) poor Cs and poor Ds engage in a coexistence dilemma. Such a diversity in the nature of the games played—due to, e.g., heterogeneous interaction patterns or resource distributions—will have strong implications on the emerging social dynamics, often promoting the chances of achieving cooperation in structured populations (13, 26, 27).
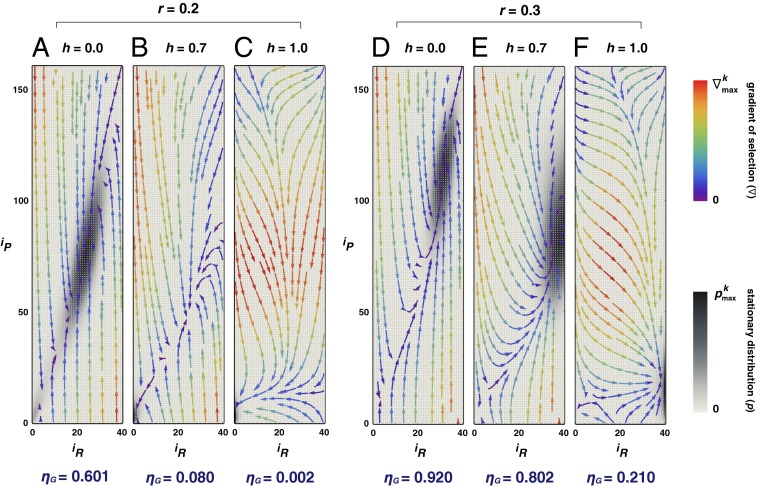
In practice, however, no reason other than mathematical simplicity may justify such extreme scenarios. When analyzing the fully coupled dynamics on the entire configuration space represented by a two-dimensional simplex (see, e.g., Fig. 2), in which the y axis (x axis) portrays the fraction of Cs among the poor (rich), it is natural to ask to which extent the existence of rich and poor alters the dynamics of the risky PGG at stake, compared with the standard model where no wealth inequality is explicitly considered. To answer this question, we start by recognizing that 20% of the world’s wealthier countries produce approximately the same gross domestic product as the remaining 80%. Thus, we break the population into two wealth classes, such that the poor comprise 80% of the population, whereas the rich constitute the remaining 20%. Concomitantly, we assume that poor countries contribute an amount proportional to their wealth (as reflected in their initial endowment) and similarly with the rich. As a result, different groups will exhibit, on average, different ratios of rich and poor, reflecting the intrinsic wealth asymmetry that one observes in the real world.
Fig. 2.
Stationary distribution and gradient of selection for different values of risk r and of the homophily parameter h. (A–F) Each panel contains all possible configurations of the population (in total ZR × ZP), each specified by the number of rich (iR) and poor (iP) it contains and represented by a gray-colored dot. Darker dots represent those configurations in which the population spends more time, thus providing a contour representation of the stationary distribution. The curved arrows show the so-called gradient of selection (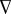 ), which provides the most likely direction of evolution from a given configuration. We use a color code in which red lines are associated with higher speed of transitions. The behavioral dynamics of the population depend on the homophily parameter h in a nonlinear way. For h ≤ 0.5, the results remain qualitatively similar to those depicted for h = 0, in which case everybody influences and is influenced by everybody else. In this case, the contribution of the rich is sizeable, which also leads the poor to contribute. For h > 0.5 the behavior changes abruptly, and one witnesses the rapid collapse of cooperation among the poor and, for low risk (r = 0.2, A–C), an ensuing disappearance of contributions to the overall PGG, with the population spending most of the time in full defection, leading to a dramatic impact on the overall group achievement ηG, indicated below each contour plot. However, a slight increase in overall risk perception (here r = 0.3, D–F) actually impels the rich to contribute, despite the fact that the poor still do not cooperate. Other parameters: Z = 200; ZR = 40; ZP = 160; c = 0.1; N = 6; M = 3c
), which provides the most likely direction of evolution from a given configuration. We use a color code in which red lines are associated with higher speed of transitions. The behavioral dynamics of the population depend on the homophily parameter h in a nonlinear way. For h ≤ 0.5, the results remain qualitatively similar to those depicted for h = 0, in which case everybody influences and is influenced by everybody else. In this case, the contribution of the rich is sizeable, which also leads the poor to contribute. For h > 0.5 the behavior changes abruptly, and one witnesses the rapid collapse of cooperation among the poor and, for low risk (r = 0.2, A–C), an ensuing disappearance of contributions to the overall PGG, with the population spending most of the time in full defection, leading to a dramatic impact on the overall group achievement ηG, indicated below each contour plot. However, a slight increase in overall risk perception (here r = 0.3, D–F) actually impels the rich to contribute, despite the fact that the poor still do not cooperate. Other parameters: Z = 200; ZR = 40; ZP = 160; c = 0.1; N = 6; M = 3c (
(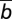 = 1); bP = 0.625; bR = 2.5;
= 1); bP = 0.625; bR = 2.5; 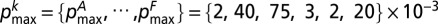 ; and
; and 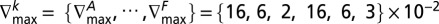 .
.
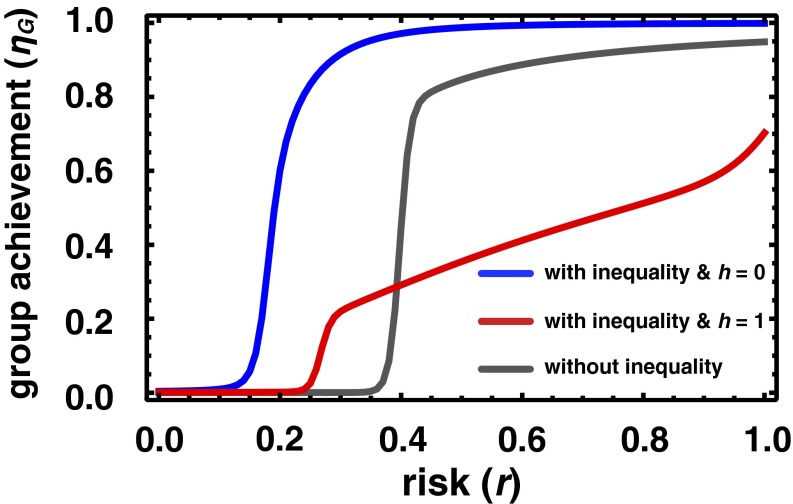
In Fig. 1 we compare the average group achievement (ηG), that is, the fraction of time a group succeeds in achieving 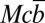 as a function of risk (Methods), in the cases when there is no wealth inequality (gray line) and in the presence of wealth inequality (blue and red lines). The results show unequivocally that wealth inequality may promote group success. This result, however, depends strongly on the level of homophily (h): Whenever the rich and poor are evenly influenced by anyone else (no homophily, h = 0, blue line), group achievement is enhanced for all values of risk (r). However, when the rich (poor) influence and are influenced by rich (poor) only (homophily h = 1, red line), the chances of success are generally below those attained in the absence of wealth inequality.
as a function of risk (Methods), in the cases when there is no wealth inequality (gray line) and in the presence of wealth inequality (blue and red lines). The results show unequivocally that wealth inequality may promote group success. This result, however, depends strongly on the level of homophily (h): Whenever the rich and poor are evenly influenced by anyone else (no homophily, h = 0, blue line), group achievement is enhanced for all values of risk (r). However, when the rich (poor) influence and are influenced by rich (poor) only (homophily h = 1, red line), the chances of success are generally below those attained in the absence of wealth inequality.
Fig. 1.
Average group achievement ηG as a function of risk. The gray line shows the average group achievement in the case of no wealth inequality; that is, all individuals have an initial endowment b =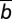 =1 and the cost of cooperation is 0.1b. The blue line shows results for wealth inequality with the homophily parameter h = 0, whereas the red line shows results for h = 1. We split the population of Z = 200 individuals into ZR = 40 rich (20%) and ZP = 160 poor (80%); initial endowments are bR = 2.5 and bP = 0.625, ensuring that the average endowment
=1 and the cost of cooperation is 0.1b. The blue line shows results for wealth inequality with the homophily parameter h = 0, whereas the red line shows results for h = 1. We split the population of Z = 200 individuals into ZR = 40 rich (20%) and ZP = 160 poor (80%); initial endowments are bR = 2.5 and bP = 0.625, ensuring that the average endowment 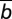 remains
remains 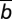 =1 (used to generate the gray line); the cost of cooperation also remains, on average, 0.1
=1 (used to generate the gray line); the cost of cooperation also remains, on average, 0.1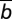 , which means cR = 0.1bR and cP = 0.1bP. The results show that wealth inequality significantly enhances the average chance of group success in the absence of homophily (h = 0), whereas under homophily (h = 1) the fact that only like influences like brings the overall chances of success to levels generally below those under wealth equality. Other parameters (Methods) are N = 6 and M = 3.
, which means cR = 0.1bR and cP = 0.1bP. The results show that wealth inequality significantly enhances the average chance of group success in the absence of homophily (h = 0), whereas under homophily (h = 1) the fact that only like influences like brings the overall chances of success to levels generally below those under wealth equality. Other parameters (Methods) are N = 6 and M = 3.
Fig. 1 also shows that ηG depends strongly on homophily, a feature that plays a central role in the overall dynamics, as is discussed in more detail below. However, it is also important to understand how the contributions are split between the rich and the poor, a feature that is not possible to grasp directly from ηG. To this end we now study in detail the stationary distributions associated with the dynamics of the two-subpopulation model. The results are shown in Fig. 2. Each (discrete) configuration is represented by a small circle, colored in gray tones. Darker circles indicate those configurations visited more often, providing a representation of the full stationary distribution (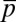 , Methods), i.e., the prevalence in time of each possible configuration of the population. Arrows in each simplex represent, in turn, the most probable direction of evolution starting from a given configuration (the gradient of selection
, Methods), i.e., the prevalence in time of each possible configuration of the population. Arrows in each simplex represent, in turn, the most probable direction of evolution starting from a given configuration (the gradient of selection 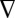 , Methods). For each arrow, we adopt a continuous color code associated with the likelihood of such a transition (brighter colors indicate more likely transitions).
, Methods). For each arrow, we adopt a continuous color code associated with the likelihood of such a transition (brighter colors indicate more likely transitions).
Fig. 2 shows that, even in the absence of significant homophily bias (h ≤ 0.5) a higher fraction of rich contribute (with average values of 57% for r = 0.2 and 78%, for r = 0.3), compared with the poor (with average values of 46% for r = 0.2 and 69% for r = 0.3), thus also protecting their greater wealth. This result does not depend on risk; however, for low risk, the overall contribution is limited, increasing significantly after a slight increase in overall risk perception. Indeed, in the absence of homophily, cooperation may prevail in a wealth-unequal world (e.g., Fig. 2D).
Qualitatively, one can now understand the results in Fig. 1 if one takes into account that, in most cases, the dynamics both among the rich and among the poor can become dominated by basins of attraction that lead to a coexistence between Cs and Ds (SI Text). Whenever the risk is moderate to high, there is an increase of the size of such basins, with a corresponding increase of the stationary fraction of cooperators, such that the feedback dynamics between the poor and the rich act to build up the cooperation levels among both subpopulations. In other words, the poor pave the way for the rich to cooperate, which, in turn, feeds back into the poor, also increasing their levels of cooperation. This feedback occurs because, perhaps counterintuitively, not only the poor imitate the rich, but also the rich imitate the poor. In fact, it is easy to prove that, for the model considered, the rich imitate the poor more often than the poor imitate the rich.
As also shown in Fig. 2, this positive feedback between the two subpopulations is interrupted whenever homophily becomes dominant (h ∼ 1). When rich and poor cease to be able to sway one another, we observe two distinct scenarios: At low risk (r = 0.2 in Fig. 2) overall cooperation collapses. With a slight increase in risk perception, however (r = 0.3), the rich contribute, despite the fact that the poor do not. Together with risk, a lack of homophily plays an important role: As soon as the homophily constraint is relaxed—by adopting h < 1—poor individuals start to be nudged by the successes of the rich, effectively inducing the poor players to contribute to the common good.
However, even in the absence of homophily (h = 0), this positive feedback between the two subpopulations does not always lead to an increase of cooperation—thus we obtain the coexistence dynamics shown in Fig. 2. Indeed, whenever most poor opt for cooperation, the dynamics drive rich countries toward less cooperation, given that they may now profit from the larger overall contributions stemming from the poor. Similar dynamics may also occur among the poor. This reduction, however, not only does not prevent the majority of rich from engaging in cooperation, but also does not compromise the overall group achievement values. As a result of these coupled dynamics, the population will stay most of the time nearby a coexistence equilibrium (interior attractor, Fig. 2 A, D, and E).
This said, we are all aware that some individuals may be more receptive than others to change their mind, based on the influence of their peers. In fact, some individuals—for various reasons, as witnessed in the world summits on climate change that have taken place to date—may maintain the same behavior irrespective of their sphere of influence. Given the small size of the overall population, such an obstinate behavior may lead to sizeable effects in the global dynamics. In the following we investigate how such obstinate behaviors (in both wealth classes) affect the overall dynamics. For simplicity, we assume that, in all cases, obstinate behavior amounts to 10% of individuals in one subpopulation—which corresponds to the same fixed contribution to the PGG, considering either rich or poor obstinate players—see SI Text for a more detailed analysis.
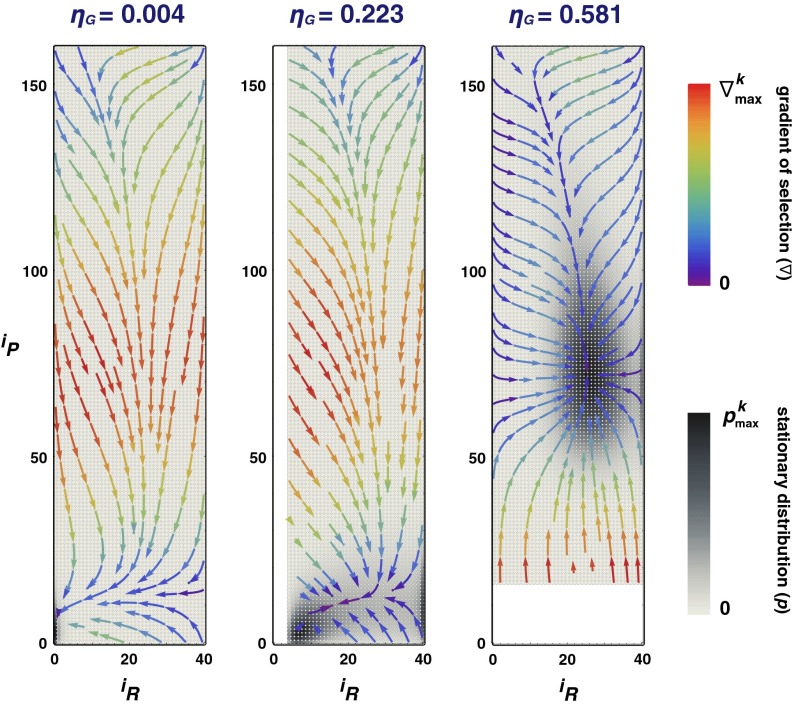
Fig. 3 shows that obstinate poor cooperators provide impressive improvements in the aggregate propensity of the population to achieve coordination (ηG = 0.581 compared with ηG = 0.004 in the absence of obstinate individuals), larger than obstinate rich cooperators, who lead to less pronounced enhancements (ηG = 0.223). This effect, which extends qualitatively to all values of h, is more pronounced when h = 1, as is the case in Fig. 3.
Fig. 3.
Stationary distribution and gradient of selection for populations comprising 10% of individuals exhibiting an obstinate cooperative behavior. Same notation as in Fig. 2 is used. Whenever 10% of individuals exhibit obstinate cooperative behavior (Center and Right contours), the number of configurations of the population in which the evolutionary dynamics proceed is correspondingly reduced (white areas in contours). The Left contour contains no obstinate individuals and is displayed for reference. In the Center contour, 10% of the rich individuals behave as obstinate cooperators; that is, they never change their behavior. In the Right contour, 10% of poor individuals exhibit such behavior. A small fraction of obstinate rich and obstinate poor cooperators lead to very different outcomes, also for the average group achievement ηG. Indeed, the chances of success are significantly enhanced whenever obstinate cooperator behavior occurs among the poor. The effect is most pronounced whenever individuals are homophilic, as is the case here (h = 1). Other parameters: Z = 200; ZR = 40; ZP = 160; c = 0.1; N = 6; M = 3c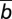 (
(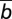 = 1); bP = 0.625; bR = 2.5; r = 0.2; β = 5.0;
= 1); bP = 0.625; bR = 2.5; r = 0.2; β = 5.0; 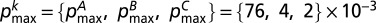 ; and
; and 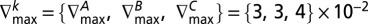 .
.
The trend shown in Fig. 3 is qualitatively inverted in the case of obstinate defectors who, in general, are detrimental to overall cooperation and group achievement (details in SI Text). These results are largely independent of the parameters chosen and highlight the important role that obstinate defectors among the rich and obstinate cooperators among the poor may play in the outcome of climate negotiations.
In summary, homophily generally impels the rich to compensate for the poor. Given that contributions from the poor are crucial to solving the climate change problem we face, it is then imperative that homophilic behavior is avoided (it is noteworthy that it is enough that overall behavior is not purely homophilic for homophily to be effectively avoided). Moreover, a small fraction of obstinate poor cooperators leads to sizable increases in the overall prospects for success, mostly when homophily rules. Perhaps unsurprisingly, when the contribution of the poor is widespread, the rich refrain from contributing. Certainly, David Hume would not be impressed by this feature that emerges from the game dynamics.
Conventional wisdom would lead one to believe that wealth inequality and homophily would constitute important obstacles regarding overall cooperation in climate change negotiations. Our results predict that, as long as (i) risk perception is high; (ii) climate negotiations are partitioned in smaller groups agreeing on local, short-term targets; and (iii) individuals are influenced by their more successful peers, whom they imitate—irrespective of their wealth class—and making errors while doing so, the prospects are not that grim. On the contrary we find that, under such conditions, cooperation may outcompete defection, benefiting from wealth inequality. Thus, hope remains that the problem may be overcome. Moreover, the qualitative nature of the results obtained here remains robust if we assume that, instead of proportional contributions, poor and rich contribute the same amount, when cooperating.
Our model, however, ignores an important factor: that the thresholds may be intrinsically uncertain. This uncertainty, if sizeable, can destroy cooperation, as sharply demonstrated recently, both theoretically and experimentally (9). Likely, to the extent that agreements aim at short-term targets involving smaller groups, it will also be easier to narrow down threshold uncertainties. Nonetheless, and in the absence of wealth inequality, introducing threshold uncertainty into our model leads to the same scenarios predicted (and confirmed) in ref. 9 (SI Text).
Finally, the recent report of the Intergovernmental Panel for Climate Change (28), besides emphasizing that climate change is real and humans are the main cause of it, urging countries to stop the warming of the planet, has also attempted to narrow down the threshold uncertainty. However, given that risk perception is low and that a bottom–up approach [as defended by the late Elinor Ostrom (29) and also, indirectly, by the results of the present model] has yet to spread globally, it is perhaps not surprising that today’s prospects remain gloomy. Clearly it is urgent that individuals become aware of the true risk that we face. Indeed, an increase in risk perception will surely promote the development of local initiatives that may foster overall cooperation by extending the bottom–up approach to all players of the global game.
Methods
We consider a population of Z individuals, ZR of which are considered rich (initial endowment 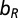 ) and ZP considered poor (initial endowment
) and ZP considered poor (initial endowment 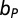 ) who, together, set up groups of size N, in which they engage in the climate change threshold PGG (12, 13). Each individual is capable of adopting one of the two strategies: C and D. Following the discussion in the main text, and given that rich Cs contribute
) who, together, set up groups of size N, in which they engage in the climate change threshold PGG (12, 13). Each individual is capable of adopting one of the two strategies: C and D. Following the discussion in the main text, and given that rich Cs contribute 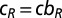 whereas poor Cs contribute
whereas poor Cs contribute 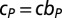 , the payoff of an individual playing in a group in which there are
, the payoff of an individual playing in a group in which there are 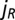 rich Cs,
rich Cs, 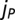 poor Cs, and
poor Cs, and 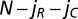 Ds, can be written as
Ds, can be written as 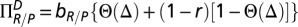 and
and 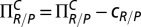 (
(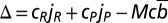 ), for rich/poor Ds and Cs, respectively. In the equations above,
), for rich/poor Ds and Cs, respectively. In the equations above, 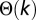 is the Heaviside function [that is,
is the Heaviside function [that is, 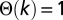 whenever
whenever 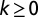 , being zero otherwise],
, being zero otherwise], 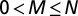 is a positive integer,
is a positive integer, 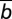 is the average endowment (
is the average endowment (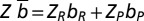 ), and r (the perception of risk) is a real parameter varying between 0 and 1; the parameters
), and r (the perception of risk) is a real parameter varying between 0 and 1; the parameters 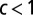 ,
, 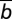 ,
, 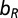 , and
, and 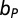 are all positive real numbers. Finally, the fitness
are all positive real numbers. Finally, the fitness 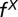 of an individual adopting a given strategy,
of an individual adopting a given strategy, 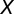 , will be associated with the average payoff of that strategy in the population. The average payoff can be computed for a given strategy in a configuration
, will be associated with the average payoff of that strategy in the population. The average payoff can be computed for a given strategy in a configuration 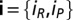 , using a multivariate hypergeometric sampling (without replacement) (details in SI Text). The number of individuals adopting a given strategy will evolve in time according to a stochastic birth–death process combined with the pairwise comparison rule (24, 30), which describes the social dynamics of rich Cs, poor Cs, rich Ds, and poor Ds in a finite population. Under pairwise comparison, each individual of strategy
, using a multivariate hypergeometric sampling (without replacement) (details in SI Text). The number of individuals adopting a given strategy will evolve in time according to a stochastic birth–death process combined with the pairwise comparison rule (24, 30), which describes the social dynamics of rich Cs, poor Cs, rich Ds, and poor Ds in a finite population. Under pairwise comparison, each individual of strategy 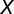 adopts the strategy
adopts the strategy 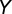 of another member of the population, with probability given by the Fermi function
of another member of the population, with probability given by the Fermi function 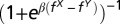 , where β controls the intensity of selection (β = 3 in Figs. 1 and 2, β = 5 in Fig. 3). In the absence of homophily, the strategy Y is chosen at random with uniform probability. For a finite value of the homophily parameter h, individuals of the same wealth class are chosen with probability 1 whereas individuals of the other wealth class are chosen with probability 1 − h; thus, when homophily is maximum, the choice occurs only among the individuals of the same wealth class (rich or poor) (details in SI Text). Additionally, we consider that, with a mutation probability μ (μ = 1/Z in Figs. 1–3), individuals adopt a randomly chosen strategy. As the evolution of the system depends only on its actual configuration, evolutionary dynamics can be described as a Markov process over a two-dimensional space. Its probability distribution function,
, where β controls the intensity of selection (β = 3 in Figs. 1 and 2, β = 5 in Fig. 3). In the absence of homophily, the strategy Y is chosen at random with uniform probability. For a finite value of the homophily parameter h, individuals of the same wealth class are chosen with probability 1 whereas individuals of the other wealth class are chosen with probability 1 − h; thus, when homophily is maximum, the choice occurs only among the individuals of the same wealth class (rich or poor) (details in SI Text). Additionally, we consider that, with a mutation probability μ (μ = 1/Z in Figs. 1–3), individuals adopt a randomly chosen strategy. As the evolution of the system depends only on its actual configuration, evolutionary dynamics can be described as a Markov process over a two-dimensional space. Its probability distribution function, 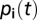 , which provides information on the prevalence of each configuration at time t, obeys a master equation (details in SI Text), a gain–loss equation involving the transition rates between all accessible configurations (24, 31, 32). The stationary distribution
, which provides information on the prevalence of each configuration at time t, obeys a master equation (details in SI Text), a gain–loss equation involving the transition rates between all accessible configurations (24, 31, 32). The stationary distribution 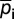 is then obtained by reducing the master equation to an eigenvector search problem (31) (details in SI Text). Another central quantity that portrays the overall evolutionary dynamics in the space of all possible configurations is the gradient of selection
is then obtained by reducing the master equation to an eigenvector search problem (31) (details in SI Text). Another central quantity that portrays the overall evolutionary dynamics in the space of all possible configurations is the gradient of selection 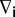 . For each configuration i, we compute the most likely path the population will follow, resorting to the probability to increase (decrease) the number of individuals adopting a strategy Sk,
. For each configuration i, we compute the most likely path the population will follow, resorting to the probability to increase (decrease) the number of individuals adopting a strategy Sk, 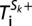 (
(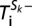 ) in each time step. Additionally, for each possible configuration i, we make use of multivariate hypergeometric sampling to compute the (average) fraction of groups that reach a total of Mc
) in each time step. Additionally, for each possible configuration i, we make use of multivariate hypergeometric sampling to compute the (average) fraction of groups that reach a total of Mc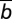 in contributions, that is, that successfully achieve the public good—which we designate by aG(i). Average group achievement—ηG—is then computed, averaging over all possible configurations i, each weighted with the corresponding stationary distribution
in contributions, that is, that successfully achieve the public good—which we designate by aG(i). Average group achievement—ηG—is then computed, averaging over all possible configurations i, each weighted with the corresponding stationary distribution 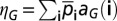 .
.
Supplementary Material
Acknowledgments
The authors thank Flávio L. Pinheiro for useful discussions. J.M.P. thanks all members of the Department of Ecology and Evolutionary Biology, Princeton University, for their support during his stay. This research was supported by Fundação para a Ciência e Tecnologia (FCT) through Grants SFRH/BD/86465/2012, PTDC/MAT/122897/2010, and EXPL/EEI-SII/2556/2013; by multiannual funding of CBMA and INESC-ID (under Projects PEst-C/BIA/UI4050/2011 and PEst-OE/EEI/LA0021/2013) provided by FCT, and by Fundação Calouste Gulbenkian through the “Stimulus to Research” program for young researchers. S.A.L. acknowledges financial support from National Science Foundation Grant EF-1137894.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1323479111/-/DCSupplemental.
References
- 1.Meehl GA, et al. Global climate projections. In: Solomon S, et al., editors. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. New York: Cambridge Univ Press; 2007. pp. 747–845. [Google Scholar]
- 2.Alley RB, et al. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. New York: Cambridge Univ Press; 2007. Summary for policy makers. [Google Scholar]
- 3.Stott PA, et al. Detection and attribution of climate change: A regional perspective. Wiley Interdiscip Rev Clim Change. 2010;1(2):192–211. [Google Scholar]
- 4.Levin SA. The trouble of discounting tomorrow. Solutions. 2012;4(3):20–24. [Google Scholar]
- 5.Barrett S. Environment and Statecraft: The Strategy of Environmental Treaty-Making. New York: Oxford Univ Press; 2005. [Google Scholar]
- 6.Barrett S. Why Cooperate? The Incentive to Supply Global Public Goods. New York: Oxford Univ Press; 2007. [Google Scholar]
- 7.O’Neill BC, Oppenheimer M. Climate change. Dangerous climate impacts and the Kyoto Protocol. Science. 2002;296(5575):1971–1972. doi: 10.1126/science.1071238. [DOI] [PubMed] [Google Scholar]
- 8.Oppenheimer M, Alley RB. Ice sheets, global warming, and Article 2 of the UNFCCC. Clim Change. 2005;68(3):257–267. [Google Scholar]
- 9.Barrett S, Dannenberg A. Climate negotiations under scientific uncertainty. Proc Natl Acad Sci USA. 2012;109(43):17372–17376. doi: 10.1073/pnas.1208417109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tavoni A, Dannenberg A, Kallis G, Löschel A. Inequality, communication, and the avoidance of disastrous climate change in a public goods game. Proc Natl Acad Sci USA. 2011;108(29):11825–11829. doi: 10.1073/pnas.1102493108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Milinski M, Röhl T, Marotzke J. Cooperative interaction of rich and poor can be catalyzed by intermediate climate targets. Clim Change. 2011;109:807–814. [Google Scholar]
- 12.Milinski M, Sommerfeld RD, Krambeck HJ, Reed FA, Marotzke J. The collective-risk social dilemma and the prevention of simulated dangerous climate change. Proc Natl Acad Sci USA. 2008;105(7):2291–2294. doi: 10.1073/pnas.0709546105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Santos FC, Pacheco JM. Risk of collective failure provides an escape from the tragedy of the commons. Proc Natl Acad Sci USA. 2011;108(26):10421–10425. doi: 10.1073/pnas.1015648108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang J, Fu F, Wu T, Wang L. Emergence of social cooperation in threshold public goods games with collective risk. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80(1 Pt 2):016101. doi: 10.1103/PhysRevE.80.016101. [DOI] [PubMed] [Google Scholar]
- 15.Abou Chakra M, Traulsen A. Evolutionary dynamics of strategic behavior in a collective-risk dilemma. PLoS Comput Biol. 2012;8(8):e1002652. doi: 10.1371/journal.pcbi.1002652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen X, Szolnoki A, Perc M. Risk-driven migration and the collective-risk social dilemma. Phys Rev E Stat Nonlin Soft Matter Phys. 2012;86(3 Pt 2):036101. doi: 10.1103/PhysRevE.86.036101. [DOI] [PubMed] [Google Scholar]
- 17.Vasconcelos VV, Santos FC, Pacheco JM. A bottom-up institutional approach to cooperative governance of risky commons. Nature Clim. Change. 2013;3(9):797–801. [Google Scholar]
- 18.Abou Chakra M, Traulsen A. Under high stakes and uncertainty the rich should lend the poor a helping hand. J Theor Biol. 2014;341:123–130. doi: 10.1016/j.jtbi.2013.10.004. [DOI] [PubMed] [Google Scholar]
- 19.Hardin G. The tragedy of the commons. Science. 1968;162(3859):1243–1248. [PubMed] [Google Scholar]
- 20.Ostrom E. Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge, UK: Cambridge Univ Press; 1990. [Google Scholar]
- 21.Fowler JH, Christakis NA. Cooperative behavior cascades in human social networks. Proc Natl Acad Sci USA. 2010;107(12):5334–5338. doi: 10.1073/pnas.0913149107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Carman KG. 2003. Social influences and the private provision of public goods: Evidence from charitable contributions in the workplace. Discussion paper 02–13 (Stanford Institute for Economic Policy Research, Stanford, CA)
- 23.Sigmund K. The Calculus of Selfishness. Princeton: Princeton Univ Press; 2010. [Google Scholar]
- 24.Traulsen A, Nowak MA, Pacheco JM. Stochastic dynamics of invasion and fixation. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74(1 Pt 1):011909. doi: 10.1103/PhysRevE.74.011909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Traulsen A, Hauert C, De Silva H, Nowak MA, Sigmund K. Exploration dynamics in evolutionary games. Proc Natl Acad Sci USA. 2009;106(3):709–712. doi: 10.1073/pnas.0808450106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Santos FC, Santos MD, Pacheco JM. Social diversity promotes the emergence of cooperation in public goods games. Nature. 2008;454(7201):213–216. doi: 10.1038/nature06940. [DOI] [PubMed] [Google Scholar]
- 27.Kun Á, Dieckmann U. Resource heterogeneity can facilitate cooperation. Nat Commun. 2013;4:2453. doi: 10.1038/ncomms3453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Intergovernmental Panel on Climate Change (2013) Climate Change 2013: The Physical Science Basis. Available at http://www.ipcc.ch/report/ar5/wg1/#.Us3i7fRdV8G. Accessed January 9, 2014.
- 29.Ostrom E. 2009. A polycentric approach for coping with climate change. Policy Research Working Paper, Background Paper to the 2010 World Development Report, WPS5095. Available at http://elibrary.worldbank.org/doi/book/10.1596/1813-9450-5095. Accessed January 9, 2014.
- 30.Szabó G, Toke C. Evolutionary prisoner’s dilemma game on a square lattice. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1998;58(1):69–73. doi: 10.1103/physreve.62.1095. [DOI] [PubMed] [Google Scholar]
- 31.Kampen NV. Stochastic Processes in Physics and Chemistry. Amsterdam: North-Holland; 2007. [Google Scholar]
- 32.Imhof LA, Fudenberg D, Nowak MA. Evolutionary cycles of cooperation and defection. Proc Natl Acad Sci USA. 2005;102(31):10797–10800. doi: 10.1073/pnas.0502589102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.