Anomalous diffusion and multifractality enhance mating encounters in the ocean

Significance

In the ocean, chemoreception plays a crucial role in increasing mate encounter rates in millimeter-scale crustaceans through pheromone trails that can be followed over hundreds of body lengths. Empirical evidence of trail following behavior is, however, limited to laboratory experiments conducted in still water. An important open question concerns what happens in the turbulent waters of the surface ocean where crustaceans instead experience background pheromone concentration. We show that both males and females of two key species react to background pheromone concentration, and their emerging behaviors depend on pheromone concentration, sex, species, and the level of reproductive experience of the individual tested, and are consistent with an adaptation to increase mate encounter rates.

Abstract

For millimeter-scale aquatic crustaceans such as copepods, ensuring reproductive success is a challenge as potential mates are often separated by hundreds of body lengths in a 3D environment. At the evolutionary scale, this led to the development of remote sensing abilities and behavioral strategies to locate, to track, and to capture a mate. Chemoreception plays a crucial role in increasing mate encounter rates through pheromone clouds and pheromone trails that can be followed over many body lengths. Empirical evidence of trail following behavior is, however, limited to laboratory experiments conducted in still water. An important open question concerns what happens in the turbulent waters of the surface ocean. We propose that copepods experience, and hence react to, a bulk-phase water pheromone concentration. Here we investigate the mating behavior of two key copepod species, Temora longicornis and Eurytemora affinis, to assess the role of background pheromone concentration and the relative roles played by males and females in mating encounters. We find that both males and females react to background pheromone concentration and exhibit both innate and acquired components in their mating strategies. The emerging swimming behaviors have stochastic properties that depend on pheromone concentration, sex, and species, are related to the level of reproductive experience of the individual tested, and significantly diverge from both the Lévy and Brownian models identified in predators searching for low- and high-density prey. Our results are consistent with an adaptation to increase mate encounter rates and hence to optimize reproductive fitness and success.

Animals constantly face the challenges of finding food, hosts, and mates while avoiding predators in spatially and temporally complex structured environments (1, 2). In particular, mating is an essential fitness and life history feature, and hence significant mate encounter rates are vital for population dynamics (3). Finding mates is, however, particularly challenging for copepods inhabiting the open waters of the ocean, as they typically rely on nonvisual senses for detecting, identifying, and locating mates (4). With concentrations of adult copepods as low as a few individuals per cubic meter or less in most natural populations, finding a mate is extremely difficult (5). Without the development of remote-sensing abilities and related behavioral strategies to locate, track, and capture a mate, copepods would be aimless wanderers in the pelagic realm of oceans.

Copepods are sensitive to hydrodynamic disturbance (6), and hydromechanical communication exists in mating copepods (7). However, the rapid decay of hydrodynamic signals makes them poorly informative; therefore, chemoreception is believed to be the main contributor to increase mate encounter rates (8). Furthermore, only one study showed that female copepods react to chemical exudates of male conspecifics with small hops, which increase encounter probability with potential mates (9); male copepods typically exhibit active mate searching behavior. Males search for chemical cues signaling the presence and position of the females. In some species, females leave a chemical trail in their wake, which males may detect and follow over many body lengths (10–12). In other species, pheromones are involved in the form of pheromone clouds (3, 13). Considerable research has been devoted to the assessment of how male copepods encounter females once they have detected their pheromone trail or cloud (3). The surface ocean is, however, mainly turbulent (14, 15), and turbulence stretches, twists, and breaks chemical trails (16). Chemical trails start to erode for turbulent intensities above a critical dissipation rate of 10⁻⁹ m²/s³ (13), leading to more diffuse pheromone distributions. In coastal and estuarine waters where copepods abound, turbulence intensities are typically in the range 10⁻⁶–10⁻⁴ m²/s³ (15, 17) so pheromone trails are homogenized by turbulent diffusion and trail following is unlikely. In a 3D turbulent environment, copepods do not form olfactory wakes but instead form clouds of chemical that engulf them. In this context, we show that the development of search strategies that optimize encounter rates under conditions of background pheromone concentrations may represent an evolutionary adaptation to life in turbulent conditions.

Specifically, we investigate under laboratory-controlled conditions the mating behavior of two key species of copepods in the coastal (Temora longicornis) and estuarine (Eurytemora affinis) waters of the Northern Hemisphere (SI Text). We assess the role of background pheromone concentration to condition both male and female swimming behaviors and theoretically investigate the consequences of the emerging stochastic properties on male-female encounter rates. Behavioral experiments involve exposing individual T. longicornis and E. affinis males and females to (i) control water (coastal or estuarine water filtered and autoclaved), (ii) male-conditioned control water that held 1, 5, 10, 20, 50, and 100 adult males per liter during 24 h, and (iii) female-conditioned control water that held 1, 5, 10, 20, 50, and 100 adult females per liter during 24 h. Furthermore, we investigate the behavior of virgin and nonvirgin males and females to infer the innate and acquired components of mating strategies (SI Text). We begin by introducing a numerical approach that may provide a unifying framework to unambiguously assess the nature of searching behavior, a critical prerequisite in behavioral ecology (18–20). This work is about the search component in mating behavior; it de facto differs from foraging, which characterizes the whole chain of events including search, taxis, capture, handling, digestion, and assimilation. We hence use the term searching instead of foraging, because a distinction between searching and foraging behavior is critically needed to make progress in animal movement studies (21, 22).

Intermittent Search Patterns and the Lévy Flight Foraging Hypothesis

An optimal search strategy, initially coined as the “Lévy flight foraging hypothesis” (23), which has been used to explain the strategies of organisms searching for food, predicts that predators should adopt Lévy search strategies for locating sparsely and randomly distributed prey and Brownian movement where prey is abundant (23) and probably more predictable (24, 25). Specifically, a Lévy flight is an intermittent search pattern characterized by displacements ranging from very likely small steps to rare and extremely long relocations. The move-step lengths l are drawn from a probability distribution with a power-law tail given by P(l) ∼ l^−μ, where 1 < μ ≤ 3, and the value μ = 2 corresponds to the lower extreme of superdiffusive processes that is a Lévy flight (26).

The Lévy flight search pattern (μ = 2) is optimal for the location of stationary targets when the searcher has no knowledge of target locations and when targets are not depleted or rejected once visited but instead can be repeatedly revisited and hence are remaining targets for future searches. Note that μ = 2 is not only optimal for the nondestructive case (which is quite restrictive to bees pollination and other processes alike), but is also optimal in predator–prey relationships (therefore with target depletion) when prey are patchily or aggregatedly distributed (27). For destructive searches of stationary prey (the prey is consumed on contact), the most efficient search strategy occurs for a ballistic motion (μ → 1), where the predator effectively makes straight-line paths between contacts with prey (23, 28, 29). The putative success of Lévy search patterns has been essentially demonstrated in model simulations (30). Lévy flight search patterns have nevertheless been reported for organisms preying on nonmotile targets such as frugivorous monkey (31), Ju/’hoansi hunter–gatherer (32), and fallow deer (29, 30, 33). Surprisingly, however, the Lévy flight search strategy has also been identified in a range of marine organisms such as reptiles, sharks, tuna, billfish, and seabirds preying on highly motile preys such as krill, squid, fish, and seal (24, 25, 34, 35), although heavily criticized (19, 36). This strategy is also consistent with evidence that the ballistic case μ → 1 and μ = 1.2 are, respectively, optimal when the prey is autonomously moving in a Brownian way (37) or advected by isotropic turbulence (38), suggesting that prey movements are likely to affect the Lévy exponent μ, or more generally the behavior of the searcher. In the turbulent ocean, male copepods have fundamentally no knowledge or information on the location of females but the presence and intensity of pheromone cues; a Lévy search strategy is hence a plausible candidate for optimal search of female copepods in a turbulent dilute 3D environment.

Lévy Flight, Lévy Walk, and a Family of Diffusive Search Patterns

The terms Lévy flight and Lévy walk are often used interchangeably in the biological and ecological literature (25, 34, 35, 39). A distinction is needed, however, as Lévy flights and walks fundamentally differ mathematically and physically. A Lévy flight is a discontinuous random jump process, where jumps are made in zero or vanishingly small time irrespective of their length and hence involve infinite velocities and are a mathematical abstraction (40). In contrast, a Lévy walk is a biologically plausible continuous random walk process, based on a finite velocity walk such that displacement is determined after a time t, reflecting a dynamical process such as movement (26, 40, 41). In this context, we examine the searching behaviors of T. longicornis and E. affinis for scale-free and anomalous diffusive characteristics and correspondence with Lévy walks previously identified in searching organisms (24, 25). A Lévy walk exhibits long-range correlations that have often been investigated based on the scaling behavior of the root-mean-square fluctuation of the displacement (24). This approach is, however, fundamentally limited to second-order moments, which is incompatible with the highly significantly (P < 0.001) non-Gaussian intermittent fluctuations perceptible in copepod velocity that ranges from very likely slow steps to rare and extremely rapid displacements (Fig. 1, Inset and Fig. S1). Here we use a more general approach, based on the analysis of qth-order long-range correlations in copepod displacements. Specifically, the norm ||ΔX_τ|| of copepod 3D displacements is defined from X_t = (x_t, y_t, z_t) coordinates as [(x_t+τ − x_t)² + (y_t+τ − y_t)² + (z_t+τ − z_t)²]^1/2, where τ is the temporal increment, and (x_t, y_t, z_t) and (x_t+τ, y_t+τ, z_t+τ) are, respectively, the positions of a copepod at time t and t + τ. ||ΔX_τ|| is a nonstationary process with stationary increments; its statistics do not depend on time, t, but on the temporal increment τ. The moments of order q (q > 0) of the norm of 3D displacements ||ΔX_τ|| depend on the temporal increment τ as

The exponents ζ(q) were estimated as the slope of the linear trend of 〈||ΔX_τ||^q〉 vs. τ in log-log plots (SI Text and Fig. S2). Low and high orders of moment, q, characterize, respectively, smaller and more frequent displacements and larger and less frequent displacements. The moment function ζ(q) characterizes the statistics of the random walk ||ΔX_τ|| of T. longicornis and E. affinis regardless of the scale and intensity (42) and the related diffusive properties (Fig. 1 and SI Text).

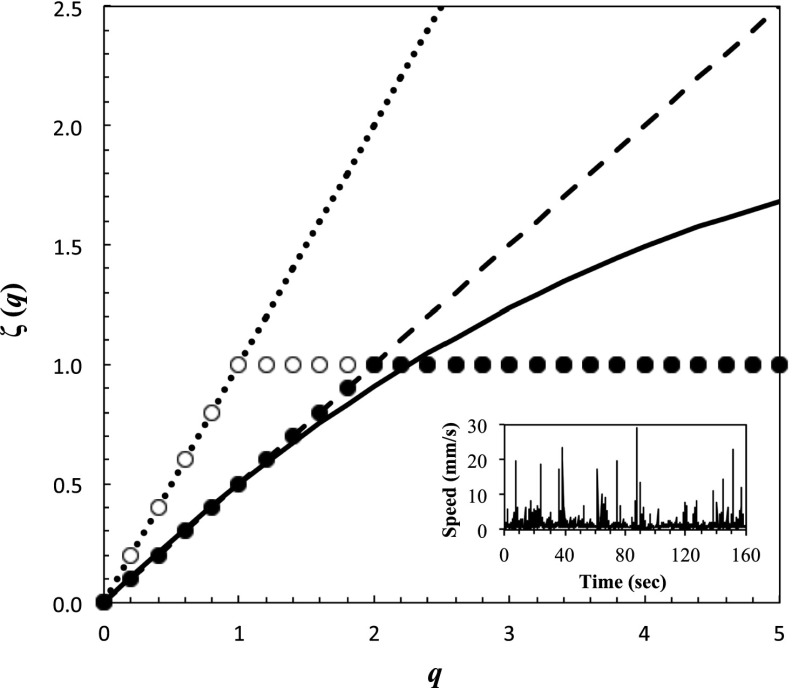
Fig. 1.

Identification of a model of searching from intermittent behavioral data (Inset) using the empirical function ζ(q). ζ(q) is a continuous function of the statistical order of moment q. The function ζ(q) is linear for fractional Brownian motion [ζ(q) = qH], with the limit ζ(q) = q (dotted line) corresponding to ballistic motion. For Brownian motion, ζ(q) = q/2 (dashed line). When 0 < H < 0.5, the motion is subdiffusive, whereas when 0.5 < H < 1, it is superdiffusive. For Lévy flights, ζ(q) = q/(μ − 1) for q < μ − 1 and ζ(q) = 1 for q ≥ μ − 1; μ (1 < μ ≤ 3) describes the tail of the probability distribution function of successive displacements l [P(l) = kl^−μ] with μ = 2 (open dots) characterizing optimal Lévy flights. The limit μ = 3 is shown by black dots. For a multifractal random walk, the function ζ(q) is nonlinear and convex (continuous line). See SI Text for further developments.

Results

We measured and analyzed nearly 95,000,000 displacements for T. longicornis and E. affinis (SI Text). Males were consistently swimming faster than females in control and conditioned waters (Wilcoxon–Mann–Whitney U test, P < 0.05). We observed no significant differences in the mean swimming speed of males and females between control water and conditioned water nor between the intensities of cues in male- and female-conditioned water treatments for both species (Kruskal–Wallis test, P > 0.05). This observation may suggest an absence of responsiveness of both T. longicornis and E. affinis to background pheromone concentrations but contradicts the trail-following behaviors exhibited by males of both species toward conspecific females (10, 43). The shape of the scaling exponents illustrates the departure of T. longicornis and E. affinis searching behavior from normal diffusion and ballistic motion for the different treatments, and appears to be both species and sex dependent (Figs. 1–3 and Fig. S3).

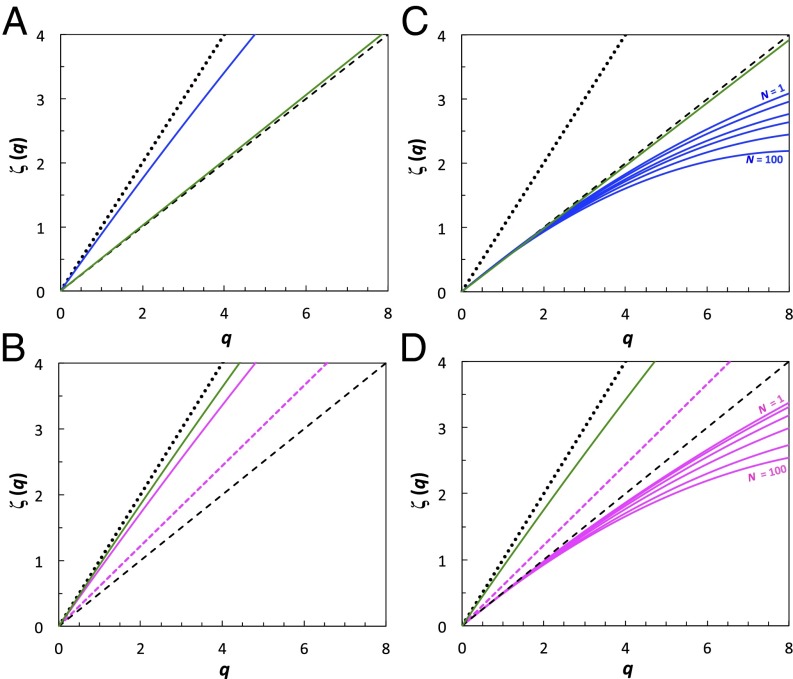
Fig. 3.

Effects of water conditioning on the search strategy of E. affinis males (blue; A and C) and females (nonovigerous females: continuous pink line, and ovigerous females: dashed pink line; B and D). Male and female diffusive properties are shown in the absence of any chemical cues in control estuarine water (A and B), and under conditions of increasing cue concentrations from nonovigerous females (C) and males (D) obtained using control water that, respectively, held n = 1, 5, 10, 20, 50, and 100 nonovigerous females and males per liter during 24 h. Virgin males (A and C) and virgin females (B and D) are shown in green. The linear functions expected for ballistic motion [ζ(q) = q; dotted line] and Brownian motion [ζ(q) = q/2; dashed line] are shown for comparison.

In the absence of chemical cues, copepods fundamentally move in a featureless and uniform environment. They are therefore naively not expected to exhibit any kind of optimal search pattern. This behavior is, however, not always the case and depends on both the reproductive stage and the reproductive experience of the individuals tested (Figs. 2 A and B and 3 A and B and Table S1). Under control water conditions, T. longicornis and E. affinis males and females exhibit superdiffusive swimming behaviors; the functions ζ(q) are slightly nonlinear and convex, revealing the multifractal nature of spontaneous search patterns, but are very close to the ballistic limit, ζ(q) = q (Figs. 2 A and B and 3 A and B), in particular for moments q ≤ 3.0. This result is consistent with the theoretical expectations for organisms searching in the absence of cues (29). E. affinis ovigerous females are also characterized by a superdiffusive swimming behavior, which belongs in the category of fractional Brownian motion, ζ(q) = qH, with H = 0.61 (Fig. 3B and Table S1).

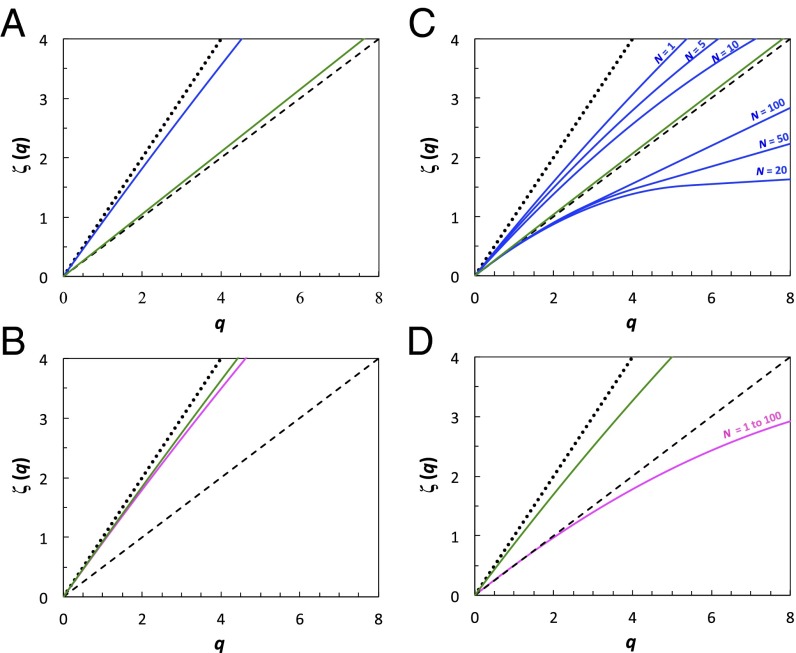
Fig. 2.

Effects of water conditioning on the search strategy of T. longicornis. Males (blue) and females (pink) diffusive properties are shown in the absence of any chemical cues in control seawater (A and B) and under conditions of increasing cue concentration from females (C) and males (D) obtained using control water that, respectively, held n = 1, 5, 10, 20, 50, and 100 adult males and females per liter during 24 h. The diffusive properties of virgin males (A and C) and virgin females (B and D) are shown in green. The linear functions expected for ballistic motion [ζ(q) = q; dotted line] and Brownian motion [ζ(q) = q/2; dashed line] are shown for comparison.

Virgin males and females also exhibit sex-specific behaviors. Both T. longicornis and E. affinis virgin males exhibit diffusive swimming behavior, with functions ζ(q) remaining indistinguishable (P > 0.05) from the normal diffusion case, ζ(q) = q/2 (Figs. 2A and 3A). In contrast, virgin females of both species exhibit a multifractal random walk that significantly diverges from the ballistic behavior ζ(q) = q for moments q > 3.75 (Figs. 2B and 3B), suggesting that optimal search strategy is only an innate behavioral property in females of T. longicornis and E. affinis.

The swimming behavior of T. longicornis males ranged from a superdiffusive regime clearly distinct from the ballistic case for water conditioned with 1, 5, and 10 females to a subdiffusive regime observed for water conditioned with 20, 50, and 100 females (Fig. 2C and Table S1). In both cases, the nonlinearity of the functions ζ(q) indicates a multifractal random walk that significantly diverges from the ballistic [ζ(q) = q] and the Brownian [ζ(q) = q/2] search patterns for moments larger than 1 and 2.5, respectively. This result indicates a switch from an extensive to an intensive search strategy with increasing cue concentration. This observation is consistent with the crossover between Lévy-like and Brownian search strategies exhibited by large marine predators in food-rich and food-depleted habitats (25, 33, 34, 44). When seawater was conditioned with more than 10 females, the functions ζ(q) become linear after a critical moment of order q_c that is decreasing as q_c = 5.2, q_c = 4.1, and q_c = 3.0 for seawater, respectively, conditioned with 20, 50, and 100 females (Fig. 2C). The critical moments of order q_c are related to a first-order multifractal phase transition as their values were independent of the sample size (SI Text and Fig. S4) and hence are associated with the occurrence of extremely rare large displacements (42). This result suggests a hyperstimulation of the sensory system of male T. longicornis that leads to the occurrence of more erratic long displacements, similar to the violent escape reactions of copepods in response to a range of stressors (6). For T. longicornis females, the departure from normal diffusion is only significant (P < 0.05) for moments larger than 2 (Fig. 2D), with no differences in the function 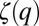measured for water conditioned with 1, 5, 10, 20, 50, and 100 males (Fig. 2D). This result suggests an acute, but density-independent, response of T. longicornis females to male pheromones and a density dependence of males to female pheromones.

E. affinis males and nonovigerous females both exhibit multifractal subdiffusive properties for pheromone-conditioned water. The departure from normal diffusion increases with the concentration of female- and male-conditioned water (Fig. 3 C and D and Fig. S3). Male and nonovigerous female anomalous diffusion increases with the number of individuals used to condition treatment water (Fig. 3 C and D and Fig. S3), indicating a density dependence in E. affinis pheromone receptivity. Specifically, male anomalous diffusion is stronger for water conditioned with nonovigerous females (Fig. 3B) than for water conditioned with ovigerous females (Fig. S3). This observation suggests either that nonovigerous and ovigerous females produce (i) the same pheromone, but in different quantities, leading to the observed differences in male response, or (ii) different pheromones, with males being less receptive to the smell of ovigerous female.

T. longicornis and E. affinis virgin males do not exhibit any behavioral changes related to the exposure to female-conditioned water, with functions ζ(q) remaining indistinguishable from the normal diffusion case, ζ(q) = q/2 (Figs. 2C and 3C and Fig. S3), suggesting a lack of innate behavioral response to female pheromones. In contrast, virgin females of both species respond to male-conditioned water through a slight decrease in their multifractal superdiffusive properties, which significantly diverge from the nearly ballistic behavior exhibited under control water conditions (Figs. 2 B vs. D and 3 B vs. D) for moments q ≥ 2.0 for T. longicornis (Fig. 2D) and q ≥ 2.8 for E. affinis (Fig. 3D). This result indicates an innate response of females to male pheromones and provides previously unidentified evidence for sex-specific innate adaptive behavioral properties in copepods.

We further suggest that the striking different searching responses of virgin and nonvirgin females to the pheromones of their own species reflect ontogenic behavioral changes; that is, virgin individuals learn about the underlying nature of background pheromone field as they gain mating experience. Note that the functions ζ(q) obtained from T. longicornis and E. affinis males and females exposed, respectively, to male-conditioned and female-conditioned water do not significantly differ (P > 0.05) from those obtained under control water conditions. Both T. longicornis and E. affinis males and females are exclusively susceptible to the pheromones released by the opposite sex. We also found that T. longicornis and E. affinis males and females do not change their swimming behavior when exposed to heterospecific pheromone-conditioned water (SI Text). This result is consistent with the lack of heterospecific trail following observed in our behavioral experiments (SI Text) and suggests a reproductive isolation of T. longicornis and E. affinis.

At the evolutionary scale, the emergence of multifractal random walks in the searching behavior of T. longicornis and E. affinis in response to conspecific pheromone cues suggests that it must confer an advantage in terms of fitness resulting from greater reproductive success. We approximated reproductive success by the relative increase in male-female encounter rates between random walkers and multifractal random walkers in both the absence and presence of cues. The encounter rate E between two organisms randomly moving freely in a 3D environment is given by E ∝ (u² + 3v²)/v, where u and v are, respectively, the mean swimming speed of the fastest and slowest organisms (45) (here males and females). The statistics of a stochastic process Q exhibiting multifractal anomalous diffusion are given by

where Q₀ = 〈Q_τ〉 is the mean of the process Q_τ (i.e., the average swimming speeds u₀ and v₀ of males and females under different water treatments), λ is the nondimensional scale-ratio over which Eq. 1 is verified (i.e., λ = 1,000; Fig. S2), and K(q) is a multifractal correction (40) to the ballistic, Brownian, or fractional Brownian case, i.e., ζ(q) = q – K(q), ζ(q) = q/2 – K(q), and ζ(q) = qH – K(q), respectively. The male-female encounter rate for anomalously diffusive searchers (either superdiffusive or subdiffusive) hence becomes 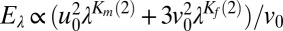, where K_m(2) and K_f(2) are the multifractal corrections, respectively, related to the anomalous diffusive properties of male and female searching behaviors and are estimated empirically from the exponents ζ_m(2) and ζ_f(2). The scale-ratio λ in Eq. 2 acts as an enhancing factor related to the multiscaling (multifractal) nature of the search patterns considered; a monoscaling (monofractal) search pattern would fundamentally return a value of K(q) = 0; hence, E = E_λ. Note that because of the additive effect of the correction factors λ^K_m(2) and λ^K_f(2) on the encounter rate E_λ, the relative effects of male and female searching behavior can also be investigated separately. For each experimental condition, the encounter rates E and E_λ were estimated for each of the N replicates (N = 10) using, respectively, the swimming speeds u₀ and v₀, and the values of K_m(2) and K_f(2) averaged over the N₁ and N₂ trajectories obtained for males and females. The relative increase in encounter rates due to anomalous diffusion is hence expressed as 100 × 〈E_λ〉/〈E〉, where 〈E_λ〉 and 〈E〉 are the averages of the N encounter rates E_λ(i) and E(i) estimated for each experimental condition.

In the absence of cues, the innate multifractal random walks observed in males and virgin females increased the encounter rate by 32.5% in T. longicornis (Fig. S5A) and 43.5% in E. affinis (Fig. S5B). Similarly, encounter rates between T. longicornis males and females and E. affinis males and nonovigerous females increase by 58.2% and 34.4%, respectively (Fig. S5). This fact stresses the highly adaptive value of multifractal random walks in the optimization of mate encounter rate. In the presence of cues, the emerging multifractal random walks increase encounter rates between males and virgin females in the range of 39.8–112.5% in T. longicornis (Fig. S5A) and 45.3–72.4% in E. affinis (Fig. S5B). Encounter rates between T. longicornis males and females and E. affinis males and nonovigerous females increase with the intensity of cues, respectively, from 65.5% to 138.2% (Fig. S5A) and from 45.6% to 110.8% (Fig. S5B). These results support the hypothesis that multifractal random walks may represent an emerging optimal search strategy in response to the concentration of olfactory stimuli.

Discussion

Complex Intermittent Search Patterns in a Featureless Environment.

Behavioral intermittency is an essential characteristic of the movement patterns exhibited by a wide range of organisms (46, 47). However, there is still a limited understanding of the causes of movement (2). In particular, it is unclear how much of an organism motion is internally governed without contributing external influences (48–51). Our results are consistent with the interesting possibility that, in the absence of chemical cues (in a featureless and uniform environment), copepods exhibit innate intermittent search patterns, which evolve with both the sex and the degree of experience of the tested individuals. Except virgin males, all of the individuals tested consistently exhibit a superdiffusive search pattern with both fractal and multifractal properties (Table S1). This fact is consistent with a neural control of intermittent locomotion as shown by the fractal/multifractal nature of the electrical activity of some neural networks (52) and the loss of the innate stochastic (fractal) properties in Drosophila melanogaster behavior (53) through synapse blockage (54). Superdiffusive movement patterns are a mathematically optimal search strategy for randomly and sparsely distributed resources. Our observations of copepod behavior in a featureless environment suggest that all of the required to produce such an optimal search strategy is a default motor neural network (named by analogy with the more complex motor cortex of insects) (55), which spontaneously generates behavior that is already close to optimal. The observed switch from Brownian motion (normal diffusion) in virgin males to superdiffusive in sexually experienced ones in the absence of chemical cues (Table S1) also suggests that this motor neural network needs to be activated in virgin males through reproductive experience, whereas it is intrinsically activated in virgin females. This hypothesis is consistent with the observed slight changes in search patterns of virgin female in water conditioned by conspecific males (Figs. 2 B and D and 3 B and D), whereas virgin males search patterns are not influenced by the presence of chemical cues (Figs. 2 A and C and 3 A and C and Fig. S3).

Emergent Intermittent Search Patterns in a Chemically Conditioned Environment.

The nearly ballistic search patterns exhibited by T. longicornis and E. affinis males and females in the absence of chemical cues consistently evolve toward multifractal random walks in reaction to bulk-phase water pheromone concentration (Table S1). These emergent behaviors are species and sex specific and arise from the reproductive experience of the females tested. In most cases, they depend on the strength of the olfactory cues, ranging from extensive to intensive search patterns in conditions of low and high cue concentration. The observed multifractal random walks can either be superdiffusive or subdiffusive depending on the species and the intensity of the cues (Table S1), suggesting they may be a general adaptive optimal search pattern. Besides, the multifractal scaling of Eq. 1 typically manifests itself from scales ranging from 0.08 to 90 s (Fig. S2) whether the resulting multifractal random walks are superdiffusive or subdiffusive. Multifractal random walks are then advantageous in the sense that they fundamentally offer the possibility of exploring a 3D environment combining different size of walk clusters and long travels at different scales. When the chemical cues are strong, it may be advantageous for copepods to remain in a limited area to minimize energy expenditure and hence to develop an area-restricted search strategy, which can be achieved through subdiffusion. In contrast to Brownian walks, which give rise to mostly homogeneous sampling effort and therefore to a relatively high probability of revisiting the same location in 3D searches (i.e., 0.35) (56), the intermittent relocations inherent to a subdiffusive multifractal random walk will further minimize the probability to revisit the same point. Subdiffusive multifractal random walks can then be thought as an alternative to Brownian searches considered optimal in environments rich in resources (23, 28, 29, 57).

The observed multifractal random walks are also consistent with the ecology of T. longicornis and E. affinis and the properties of the environments where they florish. The switch observed in T. longicornis males behavior from superdiffusive to subdiffusive multifractal random walks under conditions of low and high chemical cue concentrations (Fig. 2C) is consistent with theoretical models (23, 28, 29) and empirical evidence (24, 25, 34, 35) that superdiffusive searches are better than Brownian when resources are scarce and that a Brownian search strategy is optimal under high resource levels. In contrast, the acute, but density-independent, subdiffusive multifractal response of T. longicornis females to male pheromones (Fig. 2D) may be thought as a strategy to increase their chemical conspicuousness in their highly turbulent costal environment. Specifically, an area-restricted motion pattern of a female copepod (subdiffusive here) leads to a localized accumulation of pheromones, leading to the creation of a pheromone cloud (3, 13). Pheromone clouds are far more resilient to turbulence than pheromone trails (13) and hence attract males and enhance the efficiency of mate finding in a dilute environment. This hypothesis is consistent with the switch between superdiffusive to subdiffusive multifractal random walks observed in T. longicornis males under conditions of low and high chemical cue concentrations (Fig. 2C). Specifically, a superdiffusive search pattern will increase the probability of encountering a pheromone cloud under conditions of low background pheromone concentrations; it is also consistent with the emergence of superdiffusive properties in the search patterns of predators using chemotaxis to locate randomly distributed prey (58). In contrast, subdiffusion becomes optimal to locate a female once in the immediate vicinity of the cloud where the background pheromone concentration is higher. The area-restricted search behavior consistently exhibited by both E. affinis males and females in the presence of conspecific chemical cues (Fig. 3 C and D and Fig. S3) can also be thought as an evolutionary adaptation to the concentrations of individuals in estuarine waters, i.e., up to 250 individuals/L (59).

Conclusion

We suggest that these findings generalize to invertebrates previous evidence that large marine predators adaptively adjust their patterns of movement to different environmental resource densities, ranging from Lévy behavior in resource-depleted environments to Brownian movements in rich waters (34, 35). The observed multifractal search patterns significantly increase the probability of encountering a mate and hence may represent an optimal strategy to life in turbulent environments where chemical cues are diffuse. More specifically, the subdiffusive multifractal random walks observed in the presence of chemical cues are consistent with the multifractal distributions of ocean turbulence (60) and passive tracers such as phytoplankton (17, 42, 60) and copepods (61); they may be an evolutionary adaptive behavior to the stochastic patterns of the olfactory landscape (24).

The multifractal random walks observed in copepod search patterns substantially diverge, however, from the Lévy and Brownian models found in a diverse range of taxa (24, 25, 34, 35, 44, 62), especially when an external stimulus is present (Table S1). This result suggests that the Lévy flight foraging hypothesis may not be as general as previously thought (22, 24, 25, 63) and that optimal search strategies might instead be more complex and depend on taxa and the activity organisms are engaged in, that is, foraging for food or for sexual partners. This fact also supports the idea that Lévy search patterns might exist, but among many other properties (64), and that further work is needed to better understand the nature of behavioral intermittency that is likely to result from the interweaving of different behavioral modes (46, 48). More generally, our results confirm the theoretical expectation of a switching behavior as an optimal solution in different resource scenarios and suggest that the complex intermittent search patterns observed in copepods are shaped by both internal and external drivers. These results go well beyond the assessment of the model that best fits behavioral data (18–20, 36, 65–68), and the debate of the actual existence of Lévy search patterns in nature (18, 29, 67–70). The largest challenge yet is instead to understand the processes generating the observed patterns of movement (71–73) that is when and why searchers adopt a given strategy, which has critical implications to the wider problem of optimizing search strategies (62, 74, 75).