A multiphase model for three-dimensional tumor growth

Abstract

Several mathematical formulations have analyzed the time-dependent behaviour of a tumor mass. However, most of these propose simplifications that compromise the physical soundness of the model. Here, multiphase porous media mechanics is extended to model tumor evolution, using governing equations obtained via the Thermodynamically Constrained Averaging Theory (TCAT). A tumor mass is treated as a multiphase medium composed of an extracellular matrix (ECM); tumor cells (TC), which may become necrotic depending on the nutrient concentration and tumor phase pressure; healthy cells (HC); and an interstitial fluid (IF) for the transport of nutrients. The equations are solved by a Finite Element method to predict the growth rate of the tumor mass as a function of the initial tumor-to-healthy cell density ratio, nutrient concentration, mechanical strain, cell adhesion and geometry. Results are shown for three cases of practical biological interest such as multicellular tumor spheroids (MTS) and tumor cords. First, the model is validated by experimental data for time-dependent growth of an MTS in a culture medium. The tumor growth pattern follows a biphasic behaviour: initially, the rapidly growing tumor cells tend to saturate the volume available without any significant increase in overall tumor size; then, a classical Gompertzian pattern is observed for the MTS radius variation with time. A core with necrotic cells appears for tumor sizes larger than 150 μm, surrounded by a shell of viable tumor cells whose thickness stays almost constant with time. A formula to estimate the size of the necrotic core is proposed. In the second case, the MTS is confined within a healthy tissue. The growth rate is reduced, as compared to the first case – mostly due to the relative adhesion of the tumor and healthy cells to the ECM, and the less favourable transport of nutrients. In particular, for tumor cells adhering less avidly to the ECM, the healthy tissue is progressively displaced as the malignant mass grows, whereas tumor cell infiltration is predicted for the opposite condition. Interestingly, the infiltration potential of the tumor mass is mostly driven by the relative cell adhesion to the ECM. In the third case, a tumor cord model is analyzed where the malignant cells grow around microvessels in a 3D geometry. It is shown that tumor cells tend to migrate among adjacent vessels seeking new oxygen and nutrient. This model can predict and optimize the efficacy of anticancer therapeutic strategies. It can be further developed to answer questions on tumor biophysics, related to the effects of ECM stiffness and cell adhesion on tumor cell proliferation.

1. Introduction

With the aging world population, a surge in cancer incidence is anticipated in coming years, with major societal and economic impact. With such a scenario, the development of novel therapeutic strategies is critical for improving the prognosis, outcome of intervention, quality of life, and minimizing economical impact. In this context, computational models for tumor growth and its response to different therapeutic regimens play a pivotal role. Over the past two decades, multiple models have been developed to tackle this problem. As discussed in the comprehensive works of Roose et al. (2007), Lowengrub et al. (2010), and Deisboeck et al. (2011), three major classes of models have been proposed: discrete, continuum, and hybrid models. Discrete models follow the fate of a single cell, or a small cohort of cells, over time. As such, they cannot capture tissue mechanics aspects, nor are the modelled subdomains representative of the whole tumor. However, they explain cell-to-cell cross signalling and cell response to therapeutic molecules (Perfahl et al. 2011). On the other hand, continuum models describe cancerous tissues as domains composed of multiple homogeneous fluid and solid phases interacting one with the other. Differential equations describe the spatiotemporal evolution of the system, but no direct information is provided at the single cell level (Roose et al. 2007). Finally, hybrid models incorporate different aspects of discrete and continuum models, depending on the problem of interest. For instance they represent cells individually and extracellular water as a continuum (Anderson, 2005, Chaplain, 2000, Bearer et al. 2009).

At very early stages, solid tumors are composed of a few abnormal cells growing within an otherwise healthy tissue. The vasculature is generally absent, and the tumor cells take all their nutrients by diffusion from the surrounding tissue. This is defined as the avascular phase for a solid tumor. As the mass of tumor cells increases, the extracellular matrix undergoes extensive rearrangements with increased deposition of collagen fibers, making the resulting tissue thicker and more difficult to trespass (Jain, 1999,[; Jain and Stylianopoulos, 2010).Also, since the tumor cells divide much faster than normal cells, the growing tumor mass exerts mechanical stresses on the surrounding healthy tissue, leading to the localized constriction and, at times, collapse of blood and lymphatic vessels. At this point, the tumor cells are already in millions and the malignant tissue has reached a characteristic size of hundreds of microns. A necrotic zone appears deep inside, far from the pre-existing vasculature, and the interstitial fluid pressure (IFP) builds up against the vascular hydrostatic pressure mainly due to the compression of the healthy tissue, obstruction of the lymphatic vessels and hyper-permeability of the new blood vessels. Using proper biochemical stimuli, the tumor cells recruit new blood vessels (angiogenesis) to support a continuous transport of nutrients and oxygen. This is defined the vascular phase of a solid tumor. Over time, these new blood vessels become also a preferential route for the malignant mass to shed into circulation millions of abnormal cells that, transported by the blood flow, would reach distant sites and lead eventually to the develop secondary tumors. This is the metastatic phase, typically occurring for a few solid tumors. This briefly describes multiple phases and stages that characterize the evolution of tumors which cannot be accurately captured in a single, comprehensive computational model. Here, the focus will be on tumor initiation, and on a novel continuum model for the evolution of avascular tumors.

Most continuum models for avascular tumors describe the malignant mass as a homogeneous, viscous fluid and employ reaction-diffusion-advection equations for predicting the distribution and transport of nutrients and cells (Roose et al. 2007). Cell diffusion, convection and chemotactic motion are included, and cell proliferation is governed by mass and momentum balance equations. The first model was by Casciari et al. (1992). More advanced models also included intracellular mechanical interactions (pressure, shear, adhesion) and interaction of cells with the interstitial fluid pervading the extracellular matrix. In these cases, momentum balance equations and constitutive relations are also required for describing the stress-strain response of each individual phase. One of the earlier models (Byrne and Chaplain, 1996) treated the tumor cells as a viscous liquid and introduced, quite artificially, a hydrostatic pressure within the tumor domain representing the IFP. More sophisticated models since treated solid and fluid phases independently. For instance, Roose et al. (2003) modelled the tissue matrix as a linear poroelastic solid, whilst the interstitial fluid was prescribed to obey Darcy's law. Cell growth was incorporated in the stress-strain relationship, still imposing small displacements. See also Sarntinoranont et al. (2003).

Byrne et al. (2003) has proposed a new class of models derived in the multi-phase framework of mixture theory. Mixture theory consists in a macroscopic description (level of observation) of the system where conservation laws are introduced in analogy with the balance laws of single bodies. Additional terms are introduced to account for the interaction among phases. The disadvantage of this approach is that no connection is made with the microscopic reality. Interfacial properties are absent from both conservation laws and constitutive equations - a serious deficiency when applied to porous media (Gray and Miller, 2005). Within this approach the cellular phase (for both tumor and healthy tissues) is modelled as a viscous fluid and the interstitial fluid as inviscid. Although, the mixture theory formalism is potent and flexible, major challenges lie in the treatment of the interfaces arising the different phases. Traditionally, two classes have been proposed: the sharp interface method, considering the interface as a sharp discontinuity; and the diffuse interface method, considering the interface as a diffuse zone. The sharp interface approach – difficult to implement for interfaces separating pure media (interstitial fluid) and mixtures (tumor cells and healthy tissue) – has been followed by Preziosi and Tosin (2009), and Preziosi and Vitale (2011). However, necrotic cells are not distinguished from live tumor cells: tumors are modelled as if necrotic cells are no longer part of the tumor. They are hinted at in the source/sink term but the related balance equations are missing. Their inclusion would require accounting for an additional interface between living and dead cells, which is not sharp in nature. On the other hand, the diffuse interface approach introduces an artificial mixture at the interface, and the challenge here is to derive physically, mathematically, and numerically consistent thermodynamic laws for these interfaces. Wise et al. (2008), Cristini et al. (2009); Oden et al. (2010) and Hawkis Daarud et al. (2012) have all followed this approach. However, they include only one interface, separating the tumor cells from the healthy tissue. Strictly, this is insufficient in the mixture theory formalism where each interface should be accounted for throughout the whole computational domain. The models lack some rigour because the designation of phases as distinct from chemical constituents comprising a phase is unclear. Consequently some of the balance equations contain terms that cannot be justified on a theoretical basis. These simplified approaches lead to fourth-order-in-space parabolic partial differential equations, of Cahn-Hilliard type. This entails some difficulties for three-dimensional solutions with finite element methods because higher order basis functions are needed than in the realm of second order spatial operators (Gomez et al. 2008). Further, considering more than two or three phases becomes cumbersome, especially if a solid phase is included.

There is a need for tumor growth models for the dynamics of multiple phases and interfaces in a physically and numerically sound way. Recently the thermodynamically constrained averaging theory (TCAT) framework has been established (Gray and Miller (2005); Gray et al. (2012)) for continuum, porous media models that are thermodynamically consistent across scales. Here, the TCAT formalism will be used for predicting the growth of tumors under different physiologically relevant conditions. We show that second-order differential equations can accommodate more phases than most of the existing models. The interface behaviour is modelled through surface tension (Dunlop et al. 2011, Ambrosi et al. 2012) and adhesion (Baumgartner et al., 2000).

This paper is organized as follows: Sec.2 briefly introduces the TCAT framework. Sec.3 describes the general mathematical formulation together with the constitutive equations. Sec. 4 briefly explains the computational model, and its numerical solution. Three examples of biological relevance are presented in Sec.5, and Conclusions follow in Sec.6.

2. An overview of the thermodynamically constrained averaging theory (TCAT)

The TCAT framework provides a rigorous yet flexible method for developing multiphase, continuum models at any scale of interest. An important feature of the procedure is that it explicitly defines larger scale variables in terms of smaller scale variables. When modelling transport in multiphase systems, the length scale of the model impacts the form and parameterization of the governing equations. At the microscale - smallest scale at which the continuum hypothesis holds - a single (continuum) point contains a large number of molecules such that properties such as density, temperature, and pressure of a phase can all be defined. At the microscale, classical “point” conservation equations and thermodynamic expressions are written. However, the domains of many problems of interest are too large, and the phase distributions are too complex to be modelled at the microscale only. The level of detail required to account for geometric structure and the variability of variables at the microscale allows simulation of only very small domains. To overcome this challenge, many porous media models are formulated at a larger scale, called the macroscale, -adequate for describing system behaviour while filtering out the high frequency spatial variability. The standard continuum mechanics approach to formulating these models is a direct approach wherein the conservation equations are written at the larger scale and a rational thermodynamic approach is employed to obtain closure relations. Although this approach can be mathematically consistent, the use of rational thermodynamics fails to retain a connection between larger scale variables and their microscale precursors (Maugin 1999, Jou et al. 2001). Thus mathematical elegance is achieved typically at the price of inconsistent variable definitions and an inability to relate quantities at one scale to those at another scale. By averaging conservation and thermodynamic equations, TCAT avoids both of these pitfalls and leads to equations that are both thermodynamically and physically consistent.

The macroscale depends on the concept of the representative elementary volume (REV), an averaging volume that can be centred at each point in the system and which is large enough to include all phases present such that averages are independent of the REV size. The volume must also be sufficiently small so that quantities such as gradients are meaningful. TCAT consistently transforms microscale conservation and thermodynamic equations to the macroscale and converts averages of microscale derivatives into derivatives of macroscale average quantities. The description of a multiphase system must include dynamic conservation and thermodynamic equations for all phases, interfaces (where two phases meet), common curves (where three interfaces meet), and common points (where four common curves meet). Averaging theorems transform equations describing processes in these entities from the microscale to the macroscale (Gray et al., 1993). Thus a physically complete system description is obtained that differs from one obtained by only considering dynamic equations for phases with jump conditions at interfaces.

To close the conservation equations - which contain additional terms due to averaging - new model parameters and constitutive relations must be specified. While most methods use simplifications and the inclusion of approximate supplementary relations, TCAT employs averaged thermodynamic relations to guide closure of the system of equations. The microscale formalism chosen for averaging is the classical irreversible thermodynamics. This is adequate for the present model, but more complex formalisms can be employed (Gray and Miller, 2005). The results are required to be consistent with the averaged entropy inequality that is also consistent with its microscale formulation.

The benefits of using a TCAT approach are as follows. First, the model derivation proceeds systematically from known microscale relations to mathematically and physically consistent larger scale relations. This is accomplished by use of averaging theorems. Second, the thermodynamic analysis is consistent between scales, in the definitions of variables at different scales, and in satisfying the entropy inequality. The interscale consistency and explicit definition of variables are not achieved using a rational thermodynamic approach. Third, relations may be obtained for the evolution of the spaces occupied by phases and of the interfacial area density. These relations are based on the averaging theorems. Although TCAT has heretofore been employed primarily in hydrology, it can impact tumor modelling in that the underlying physics and mathematics needed to describe tumors are related. Additionally, if hybrid tumor models are to be developed in the future, it is essential that the relation between the smaller scale variables and continuum variables be known. TCAT ensures that these relations are known.

3. The multiphase model

The proposed computational model comprises the following phases: i) the tumor cells (TC), which partition into living cells (LTC) and necrotic cells (NTC); ii) the healthy cells (HC); iii) the extracellular matrix (ECM); and iv) the interstitial fluid (IF).

The ECM and IF pervade the whole computational domain, whereas the TC and HC are limited only to the subdomains with the tumor mass and the healthy tissue, respectively. The ECM is modelled as a solid, while all other phases are fluids. The tumor cells become necrotic upon exposure to low nutrient concentrations or excessive mechanical pressure. The interstitial fluid, transporting nutrients, is a mixture of water and biomolecules, as nutrients, oxygen and waste products. In the following mass and momentum conservation equations, α denotes an arbitrary phase, t the tumor cells (TC), h the healthy cells (HC), s the extra cellular matrix (ECM), and l the interstitial fluid (IF).

3.1. The governing equations

The governing equations are derived by averaging from the microscale to the macroscale and then using closure techniques to parameterize the resultant equations. The derivation is mathematically intensive such that providing it here in detail would distract from the main thrust of this paper. The techniques have been employed for transport and for multiphase systems elsewhere (Gray and Miller 2009, Jackson et al. 2009) and the procedure is the same for the current system, although the number of phases is different. An important feature of the approach is that the interphase contacts are explicitly accounted for.

The ECM is treated as a porous solid and porosity is denoted by ε, so that the volume fraction occupied by the ECM is ε^s=1- ε. The rest of the volume is occupied by the tumor cells (ε^t); the healthy cells (ε^h); and the interstitial fluid (ε^l). Indeed, the sum of the volume fractions for all phases has to be unit

$${\epsilon }^s+{\epsilon }^h+{\epsilon }^t+{\epsilon }^l=1$$ (1)

The saturation degree of the phases is: S^α=ε^α/ε. Indeed, based on the definition of porosity ε and volume fraction ε^α in eqn (1) it follows that

$$S^h+S^t+S^l=1$$ (2)

The mass balance equation for an arbitrary phase α based on application of the averaging theorems is written as

$$\frac{\partial \left({\epsilon }^{\alpha }{\rho }^{\alpha }\right)}{\partial t}+\nabla ·\left({\epsilon }^{\alpha }{\rho }^{\alpha }{\mathbf{v}}^{\overline{\alpha }}\right)-\sum _{\kappa \in {\Im }_{c\alpha }}\stackrel{\kappa \to \alpha }{M}=0$$ (3)

where ε^α is the volume fraction; ρ^α is the density, v^ᾱ is the local velocity vector, $\stackrel{\kappa \to \alpha }{M}$ are the mass exchange terms accounting for transport of mass at the interface between the phases κ and α, and $\mathrm{\sum }_{\kappa \in {\Im }_{c\alpha }}$ is the summation over all the phases exchanging mass at the interfaces with the phase α. However, if the interface is treated as massless, the transfer is to the adjacent phases, designated as κ. An arbitrary species i dispersed within the phase α has to satisfy mass conservation too, and therefore the following equation is derived by averaging

$$\frac{\partial \left({\epsilon }^{\alpha }{\rho }^{\alpha }{\omega }^{\overline{i\alpha }}\right)}{\partial t}+\nabla ·\left({\epsilon }^{\alpha }{\rho }^{\alpha }{\omega }^{\overline{i\alpha }}{\mathbf{v}}^{\overline{\alpha }}\right)+\nabla ·\left({\epsilon }^{\alpha }{\rho }^{\alpha }{\omega }^{\overline{i\alpha }}{\mathbf{u}}^{\overline{\overline{i\alpha }}}\right)-{\epsilon }^{\alpha }{r}^{i\alpha }+\sum _{\kappa }\stackrel{i\alpha \to i\kappa }{M}=0$$ (4)

Where ${\omega }^{\overline{i\alpha }}$ identifies the mass fraction of the species i dispersed with the phase α, ε^αr^iα is a reaction term that allows to take into account the reactions between the species i and the other chemical species dispersed in the phase α, and ${\mathbf{u}}^{\overline{\overline{i\alpha }}}$ is the diffusive velocity of the species i.

In particular, the mass conservation equation of the nutrient species i in the IF (phase l) reads

$$\frac{\partial \left({\epsilon }^l{\rho }^l{\omega }^{\overline{il}}\right)}{\partial t}+\nabla ·\left({\epsilon }^l{\rho }^l{\omega }^{\overline{il}}{\mathbf{v}}^{\overline{l}}\right)+\nabla ·\left({\epsilon }^l{\rho }^l{\omega }^{\overline{il}}{\mathbf{u}}^{\overline{\overline{il}}}\right)+\stackrel{il\to it}{M}=0$$ (5)

where it is assumed that no chemical reaction occurs within the phase and that the exchange of mass in the liquid is only with the tumor phase. Summing eqn (5) over all species gives

$$\frac{\partial \left({\epsilon }^l{\rho }^l\right)}{\partial t}+\nabla ·\left({\epsilon }^l{\rho }^l{\mathbf{v}}^{\overline{l}}\right)+\stackrel{l\to t}{M}=0$$ (6)

Where

$$\stackrel{l\to t}{M}=\sum _{i\in l}\stackrel{il\to it}{M}$$ (7)

Note that the mass exchange from the liquid to the tumor is actually to the living cell (LTC) portion of the tumor phase. The necrotic portion of the tumor is inert and does not exchange any nutrient with the IF. Also there is no need to make a distinction between the solvent part of the liquid phase and any of the dissolved species. All species are in the liquid phase. However, due to the relatively low concentrations of chemicals, the solvent phase is the dominant species and hence the global physical properties of the IF, such as density, intrinsic permeability and dynamic viscosity are essentially those of the solvent.

The tumor phase t comprises a necrotic portion with mass fraction ω^Nt̄ and a growing phase with living cells whose mass fraction is 1 − ω^Nt̄. Thus the conservation equation for each fraction would be similar to eqn (5). Assuming that there is no diffusion of either necrotic or living cells, and that there is no exchange of the necrotic cells with other phases the mass conservation equation for the necrotic portion reads as

$$\frac{\partial \left({\epsilon }^t{\rho }^t{\omega }^{N\overline{t}}\right)}{\partial t}+\nabla ·\left({\epsilon }^t{\rho }^t{\omega }^{N\overline{t}}{\mathbf{v}}^{\overline{t}}\right)-{\epsilon }^t{r}^{Nt}=0$$ (8)

where ε^tr^Nt is the rate of death of tumor cells, or in other words the rate of generation of necrotic cells.

Differently than a mass exchange term between phases ( $\stackrel{l\to t}{M}$ in eqn (6) for instance), the reaction term ε^tr^Nt is an intra-phase exchange term. The mass balance equation for the living tumor cells is given as

$$\frac{\partial \left[{\epsilon }^t{\rho }^t\right(1-{\omega }^{N\overline{t}}\left)\right]}{\partial t}+\nabla ·\left[{\epsilon }^t{\rho }^t\right(1-{\omega }^{N\overline{t}}\left){\mathbf{v}}^{\overline{t}}\right]+{\epsilon }^t{r}^{\mathit{\text{Nt}}}-\stackrel{l\to t}{M}=0$$ (9)

Where $\stackrel{l\to t}{M}$ includes the exchange of nutrients and solvent from the IF to the tumor. Summation of these two equations yields an overall mass conservation equation for the tumor phase as

$$\frac{\partial \left({\epsilon }^t{\rho }^t\right)}{\partial t}+\nabla \cdot ·\left({\epsilon }^t{\rho }^t{\mathbf{v}}^{\overline{t}}\right)-\stackrel{l\to t}{M}=0$$ (10)

We can expand eqn (8) by use of the product rule and substitute in eqn (10) to obtain an alternative form of the necrotic species equation as

$${\epsilon }^t{\rho }^t\frac{\partial {\omega }^{N\overline{t}}}{\partial t}+{\epsilon }^t{\rho }^t{\mathbf{v}}^{\overline{t}}·\nabla {\omega }^{N\overline{t}}+{\omega }^{N\overline{t}}\stackrel{l\to t}{M}-{\epsilon }^t{r}^{\mathit{\text{Nt}}}=0$$ (11)

For the ECM and HC, the mass conservation equation becomes respectively

$$\frac{\partial \left({\epsilon }^s{\rho }^s\right)}{\partial t}+\nabla ·\left({\epsilon }^s{\rho }^s{\mathbf{v}}^{\overline{s}}\right)=0$$ (12)

$$\frac{\partial \left({\epsilon }^h{\rho }^h\right)}{\partial t}+\nabla ·\left({\epsilon }^h{\rho }^h{\mathbf{v}}^{\overline{h}}\right)=0$$ (13)

For the ECM and the HC phases no mass exchange is expected with any other phase

The momentum equation for the arbitrary phase α, including multiple species i, is

$$\frac{\partial \left({\epsilon }^{\alpha }{\rho }^{\alpha }{\mathbf{v}}^{\overline{\alpha }}\right)}{\partial t}+\nabla ·\left({\epsilon }^{\alpha }{\rho }^{\alpha }{\mathbf{v}}^{\overline{\alpha }}{\mathbf{v}}^{\overline{\alpha }}\right)-\nabla ·\left({\epsilon }^{\alpha }{\mathbf{t}}^{\overline{\overline{\alpha }}}\right)-{\epsilon }^{\alpha }{\rho }^{\alpha }{\mathbf{g}}^{\overline{\alpha }}-\sum _{\kappa \in {\Im }_{c\alpha }}\left(\sum _{i\in {\Im }_s}\stackrel{i\kappa \to i\alpha }{M_v}{\mathbf{v}}^{\overline{\alpha }}+\stackrel{\kappa \to \alpha }{\mathbf{T}}\right)=0$$ (14)

Where g^ᾱ is the body force, $\stackrel{i\kappa \to i\alpha }{M_v}{\mathbf{v}}^{\overline{\alpha }}$ represents the momentum exchange from the κ to the α phase due to mass exchange of species i, ${\mathbf{t}}^{\overline{\overline{\alpha }}}$ is the stress tensor and $\stackrel{\kappa \to \alpha }{\mathbf{T}}$ is the interaction force between phase α and the adjacent interfaces. When the interface properties are negligible, this last term is simply the force interaction between adjacent phases. Given the characteristic times scales (hours and days) of the problem and the small difference in density between cells and aqueous solutions, inertial forces as well as the force due to mass exchange are neglected so that the momentum equation simplifies to

$$-\nabla ·\left({\epsilon }^{\alpha }{\mathbf{t}}^{\overline{\overline{\alpha }}}\right)-{\epsilon }^{\alpha }{\rho }^{\alpha }{\mathbf{g}}^{\overline{\alpha }}-\sum _{\kappa \in {\Im }_{c\alpha }}\stackrel{\kappa \to \alpha }{\mathbf{T}}=0$$ (15)

From TCAT, see Appendix A, it can be shown that the stress tensor for a fluid phase is of the form ${\mathbf{t}}^{\overline{\overline{\alpha }}}=-p^{\alpha }\mathbf{1}$, with p^α being the averaged fluid pressure and 1 the unit tensor, and that the momentum balance equation can be simplified to

$${\epsilon }^{\alpha }\nabla p^{\alpha }+{\mathbf{R}}^{\alpha }·({\mathbf{v}}^{\overline{\alpha }}-{\mathbf{v}}^{\overline{s}})=0$$ (16)

where R^α is the resistance tensor.

3.2. The constitutive equations

No special assumption has been made yet for the constitutive behaviour of the different phases, except for the fluid phases described by eqn (16). In this paragraph, constitutive relations are explicitly presented for describing i) the tumor cell growth and ii) the tumor cell death, as a function of the nutrients' mass fraction and local mechanical stresses, for eqn (6) and eqn (8), respectively; iii) the rate of nutrient consumption from the IF, in particular, to the living tumor cells, for eqn (5); iv) the diffusion of nutrients within the porous ECM, for eqn (5); v) the interaction force among the phases, for eqn (15); vi) the mechanical behaviour of the ECM; and vii) the differential pressure between the fluid phases.

The formulation presented in the above paragraph can be further simplified by assuming that the densities of the phases are constant and equal

$${\rho }^s={\rho }^h={\rho }^t={\rho }^l=\rho =\mathit{\text{const}}$$ (17)

3.2.1. Tumor cell growth

This is regulated by a variety of nutrient species and intracellular signalling. However, without losing generality, in the present model one single nutrient is considered: oxygen. The case of multiple species can be easily obtained as a straightforward extension of the current formulation. Tumor cell growth is related to the exchange of nutrients between the IF and the living portion of the tumor. Therefore the mass exchange term in eqn (6) represents tumor growth and, similarly to a part of the relevant equation in Preziosi and Vitale (2011), takes the form

$$\underset{\mathit{\text{growth}}}{\overset{l\to t}{M}}=\sum _{i\in l}\stackrel{\mathit{\text{il}}\to \mathit{\text{it}}}{M}=\left[{\gamma }_{\mathit{\text{growth}}}^t{\langle \frac{{\omega }^{\overline{\mathit{\text{nl}}}}-{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}}{{\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}-{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}}\rangle }_{+}H(p_{\mathit{\text{crit}}}^t-p^t)\right](1-{\omega }^{N\overline{t}})\epsilon S^t$$ (18)

where the coefficient ${\gamma }_{\mathit{\text{growth}}}^t$ accounts for the nutrient uptake and the consumption of water needed for cell growth from the IF; ${\omega }^{\overline{nl}}$ is the local mass fraction of the nutrient, a fundamental variable in the problem; ${\omega }_{\mathit{\text{crit}}}^{\overline{nl}}$ is a constant critical value below which cell growth is inhibited; and the constant ${\omega }_{\mathit{\text{env}}}^{\overline{nl}}$ is the environmental mass fraction of the nutrient. Also, p^t denotes the tumor cell pressure and its critical value $p_{\mathit{\text{crit}}}^t$ above which growth is inhibited. The Macaulay brackets 〈 〉₊ indicate the positive value of its argument. Note that, since the local nutrient mass fraction ${\omega }^{\overline{\mathit{\text{nl}}}}$ within the tumor domain can be equal or smaller than ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}$, it derives that the argument of the Macaulay brackets varies between $1({\omega }^{\overline{\mathit{\text{nl}}}}={\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}})$ and $0({\omega }^{\overline{\mathit{\text{nl}}}}<{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}})$. Consequently the growth rate for the viable tumor cells could at most be equal to ${\gamma }_{\mathit{\text{growth}}}^t$. Also in eqn (18), H is the Heaviside function which is zero for $p^t>p_{\mathit{\text{crit}}}^t$ and is unity for $p^t<p_{\mathit{\text{crit}}}^t$. Note that ${\omega }^{N\overline{t}}=\frac{{\epsilon }^{N\overline{t}}{\rho }^{N\overline{t}}}{{\epsilon }^t{\rho }^t}$ is the mass fraction of tumor cells that are necrotic and hence (1 – ω^{Nt ¯})εS^t is the volume fraction of viable tumor cells.

3.2.2. Tumor cell death

The rate of tumor cell death in eqn (8) can be described by the relation

$${\epsilon }^t{r}^{N^t}=\left[-{\gamma }_{\mathit{\text{necrosis}}}^t{\langle \frac{{\omega }^{\overline{\mathit{\text{nl}}}}-{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}}{{\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}-{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}}\rangle }_{-}+{\delta }_a^{t}H(p^t-p_{\mathit{\text{necr}}}^t)\right](1-{\omega }^{N\overline{t}})\epsilon S^t$$ (19)

Where ${\gamma }_{\mathit{\text{necrosis}}}^t$ is the rate of cell death. All the other terms are similar to those presented in eqn (18). However, the negative part of the argument of the Macaulay brackets 〈 〉₋ is considered. Also, $p_{\mathit{\text{necr}}}^t$ is the pressure above which the tumor stress has effect on the cell death rate, and δ_a is the additional necrosis induced by a pressure excess. Note that the mathematical form of eqn (19) is very similar to eqn (18) in that cell death is assumed to be solely regulated by insufficient concentration of nutrients (oxygen) and excessive mechanical pressure. No drugs or other pro-apoptotic molecules are used in the present model, but eqn (19) can be readily modified to include also this contribution. Mathematically, a therapeutic agent or drug would be treated just as a ‘nutrient’. Effects of cells membrane rupture and consequent transfer of liquid from the tumor cell phase to the interstitial fluid has been not yet included in the model. These aspects will certainly be included in future extensions of the current computational model. This will be also connected with the release of chemo-attractants and subsequent infiltration of macrophages. As such, these aspects can influence the local interstitial fluid pressure.

3.2.3. The rate of nutrient consumption

As tumor grows, nutrients are taken up from the IF so that the sink term in eqn (5) takes the following form

$$\stackrel{\mathit{\text{nl}}\to t}{M}=\stackrel{\mathit{\text{nl}}\to \mathit{\text{nt}}}{M}=\left[{\gamma }_{\mathit{\text{growth}}}^{\overline{\mathit{\text{nl}}}}{\langle \frac{{\omega }^{\overline{\mathit{\text{nl}}}}-{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}}{{\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}-{\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}}\rangle }_{+}H(p_{\mathit{\text{crit}}}^t-p^t)+{\gamma }_0^{\overline{\mathit{\text{nl}}}}sin\left(\frac{\pi }{2}\frac{{\omega }^{\overline{\mathit{\text{nl}}}}}{{\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}}\right)\right](1-{\omega }^{N\overline{t}})\epsilon S^t$$ (20)

Nutrient consumption from IF is due to two contribution namely i) the growth of the tumor cells, as given by the first term within the square brackets in eqn (20); ii) the normal metabolism of the healthy cells, as presented in the second term. Indeed, ${\gamma }_{\mathit{\text{growth}}}^{\overline{\mathit{\text{nl}}}}$ is related to the tumor growth, as discussed above; whereas the coefficient ${\gamma }_0^{\overline{\mathit{\text{nl}}}}$ relates to the normal cell metabolism. Being the nutrient mass fraction ${\omega }^{\overline{\mathit{\text{nl}}}}$ in the tumor extracellular spaces always equal to or smaller than ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}$, the argument of the sine function varies between π/2 and 0. The part of consumption of oxygen related to the cells metabolism depends on the oxygen availability and becomes zero when the mass fraction of oxygen is zero; this allows having always positive values of the local mass fraction of oxygen since negative values have not physical meaning.

3.2.4. The diffusion of nutrients through the ECM

To approximate the diffusive flux in eqn (5), Fick's law is used $({\rho }^l{\omega }^{\overline{\mathit{\text{nl}}}}{\mathbf{u}}^{\overline{\overline{\mathit{\text{il}}}}}=-D^{\overline{\mathit{\text{nl}}}}{\rho }^l\nabla {\omega }^{\overline{\mathit{\text{nl}}}})$. The effective diffusion coefficient of nutrients in the extracellular spaces is given as

$$D_{\mathit{\text{eff}}}^{\overline{\mathit{\text{nl}}}}=D_0^{\overline{\mathit{\text{nl}}}}{(\epsilon S^l)}^{\delta }$$ (21)

where $D_0^{\overline{\mathit{\text{nl}}}}$ is the diffusion coefficient in the unbound interstitial fluid and δ is a constant coefficient greater than one which takes into account the tortuosity of the porous network. Actually the effective diffusion coefficient of oxygen has not a linear dependence on the volume fraction of the IF, because it depends on the connectivity grade of the extra cellular spaces. δ is a parameter that has to be calibrated experimentally.

3.2.5. The interaction force among the phases

R^α of eqn (16) is the resistance tensor that accounts for the frictional interactions between phases. For example, porous medium flow of a single fluid encounters resistance to flow due to interaction of the fluid with the solid. If one has to model the flow at the microscale, a viscous stress tensor within the fluid phase would be employed. At the macroscale, the effects of the viscous interaction are accounted for as being related to the difference in velocities of the phases. The coefficient of proportionality is the resistance tensor. In multiphase flow, resistance tensors must be developed that account for the velocity differences between each pair of phases. Eqn (14) contains the interaction vector $\stackrel{\kappa \to \alpha }{\mathbf{T}}$ that arises between each pair of phases. In the full implementation of the TCAT analysis, the simplest result is that this vector is proportional to the velocity difference between the two indicated phases with the resistance tensor being the coefficient of proportionality. In the present version of the model, the interaction force $\stackrel{s\to \alpha }{\mathbf{T}}$ between the fluid phase α and the solid phase s (the ECM) is explicitly taken into account while the macroscopic effect of the interaction forces between the fluid phases $\stackrel{l\to t}{\mathbf{T}}$, $\stackrel{l\to h}{\mathbf{T}}$ and $\stackrel{t\to h}{\mathbf{T}}$ is taken care of through the relative permeability $k_{\mathit{\text{rel}}}^{\alpha s}$. The form of (R^α)⁻¹ is here assumed following the modelling of multiphase flow in porous media (Lewis and Schrefler, 1998), that is to say

$$\begin{array}{cc}{({\mathbf{R}}^{\alpha })}^{-1}=\frac{k_{\mathit{\text{rel}}}^{\alpha s}{\mathbf{k}}^{\alpha s}}{{\mu }^{\alpha }{({\epsilon }^{\alpha })}^2}& (\alpha =h,t,l)\end{array}$$ (22)

where k^αs and μ^α are the intrinsic permeability tensor and the dynamic viscosity, respectively. Since there is no information available about this relative permeability which is a nonlinear function of the saturation and varies between 0 and 1, the following form is assumed

$$\begin{array}{cc}{k}_{\mathit{\text{rel}}}^{\alpha }={(S^{\alpha })}^2& (\alpha =h,t,l)\end{array}$$ (23)

Eqn (23) respects the constraint $\sum _{\alpha =h,t,l}{k}_{\mathit{\text{rel}}}^{\alpha }<1$ and gives realistic results in agreement with the classical models present in the literature on porous media mechanics (Brooks and Corey (1964), Corey et al. (1956), Van Genuchten.(1980)). A more accurate determination of $k_{\mathit{\text{rel}}}^{\alpha s}$ should derive from specific experiments or by the application of Lattice-Boltzmann modelling or analysis of micro-models. By introducing (22) in (16), the relative velocity of the phase α is derived as

$$\begin{array}{cc}{\mathbf{v}}^{\overline{\alpha }}-{\mathbf{v}}^{\overline{s}}=-\frac{k_{\mathit{\text{rel}}}^{\alpha s}{\mathbf{k}}^{\alpha s}}{{\mu }^{\alpha }{\epsilon }^{\alpha }}\nabla p^{\alpha }& (\alpha =h,t,l)\end{array}$$ (24)

The intrinsic permeability tensor k^ls of the interstitial fluid phase is constant and isotropic.

Experimental evidence confirms that cells would stay in contact with the ECM if the mechanical pressure gradients exerted over the cell phase are smaller than a critical value (Baumgartner et al. 2000). For this reason, for the healthy and tumor cells the intrinsic permeability tensors (i.e. k^hs and k^ts) are isotropic but not constant, and are computed using the following equation

$$\begin{array}{cc}{\mathbf{k}}^{\alpha s}=max\left({\overline{\mathbf{k}}}^{\alpha s}{\langle 1-\frac{a_{\alpha }}{\left|\nabla p^{\alpha }\right|}\rangle }_{+},\frac{{\overline{\mathbf{k}}}^{\alpha s}}{100}\right)& (\alpha =h,t)\end{array}$$ (25)

This represents in mathematical terms the fact that if cells adhere firmly to the ECM, the phase permeability within the ECM is reduced. The minimum value of the permeability (set equal to K̄^αs/100) eliminates the indeterminacy in the case $\left|\nabla p^{\alpha }\right|<a_{\alpha }$, contained in the approach of Preziosi and Tosin (2009). This is an analogue in fluid dynamics to the stick-slip behaviour in contact mechanics (Zavarise et al, 1992).

3.2.6. The mechanical behaviour of the ECM

The closure relation for the stress tensor acting on the ECM (sole solid phase) is

$${\mathbf{t}}_{\mathit{\text{eff}}}^{\overline{\overline{s}}}={\mathbf{t}}_{\mathit{\text{tot}}}^{\overline{\overline{s}}}+\overline{\alpha }{p}^s\mathbf{1}$$ (26)

with ${\mathbf{t}}_{\mathit{\text{eff}}}^{\overline{\overline{s}}}$ the effective stress tensor in the sense of porous media mechanics and the solid pressure p^s given as (Gray and Schrefler, 2007)

$$p^s={\chi }^h{p}^h+{\chi }^t{p}^t+{\chi }^l{p}^l$$ (27)

where χ^α is the solid surface fraction in contact with the respective fluid phase, known as the Bishop parameter. This parameter is a function of the degree of saturation and is taken here equal to this last one (i.e. χ^α = S^α). The Biot coefficient ᾱ is equal to 1 because of the incompressibility of the ECM. Indeed, this does not mean that the ECM cannot deform. The constitutive behaviour of the solid phase is that of an elasto-visco-plastic solid in large deformation regime. (Zienkiewicz and Taylor, 2000).

3.2.7. The differential pressure between the three fluid phases

The differential pressure between the fluid phases is a different concept from the interaction forces dealt with in section 3.2.5. In brief, the interaction forces are in play when there is flow. The different velocities of the different phases set up resistance forces between the phases. These are the interaction forces discussed above. Differential pressure, on the other hand, can exist even at equilibrium. It is not related to flow processes but is a statement that the pressures in adjacent phases can be different. In multiple fluid flow in porous media, this difference in pressures can be attributed to the curvature of the interface between fluid phases and to the surface tension. In the tumor system, the interfaces between phases are also capable of sustaining a jump in pressure between phases. In fact cells have surface tension which influences their growth and adhesion behaviour (Dunlop et al. 2011, Bidan et al. 2012, Ambrosi et al. 2012). At the microscale, the pressure difference between the cell phases and the fluid phases is equal to the interfacial tension, σ_c, multiplied by the interfacial curvature. After transformation to the macroscale, a macroscale measure is needed as a surrogate for the interfacial curvature. In porous media analyses, a surrogate for the pressure difference between fluid phases is proposed heuristically as a function of the fluid saturations (e.g., Brooks and Corey 1966, van Genuchten 1990). The cell pressure becomes very large when the available pore space is occupied by the cells, i.e. when S^l tends to zero. This behaviour is depicted in figure 2. The following equation is proposed as a model for the pressure difference between the interstitial fluid phase pressure p^l and those of the cell phases p^t and p^h

Figure 2.

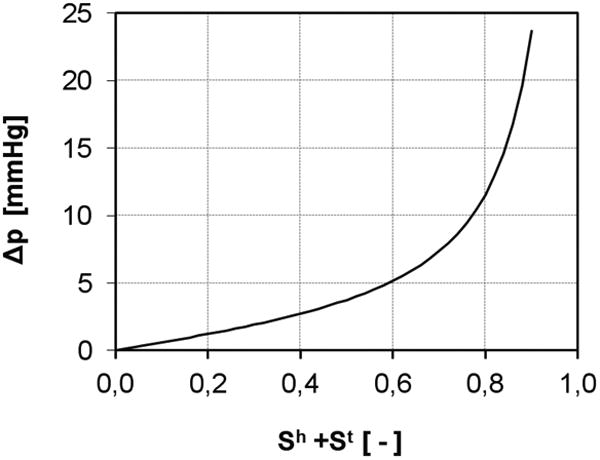
Pressure difference - saturation relationship.

$$\Delta p=p^t-p^l=p^h-p^l={\sigma }_{c}tan\left[\frac{\pi }{2}{(S^t+S^h)}^b\right]$$ (28)

where σ_c and b are constants. The use of eqn (28) to account at the macroscale for the curvature of the interface between the phases is an approximation that assumes the distribution of the cells within the pore space does not impact the pressure difference between the phases. This expression can be refined subsequently in light of experimental analysis.

3.3. Final form of the governing equations

The primary variables of the model are: the tumor saturation −S^t, the healthy cell saturation −S^h, the IF pressure − p^l, and the nutrient mass fraction $-{\omega }^{\overline{\mathit{\text{nl}}}}$, together with the displacement of the solid phase (ECM) u^s. The time derivative of the latter is the ECM velocity v^s. After substituting for the explicit form of the constitutive equations, the final form of the governing equations is obtained. The mass balance equations of the ECM, TC, HC and IF are, respectively:

$$\frac{\partial (1-\epsilon )}{\partial t}+\nabla ·\left[(1-\epsilon )\frac{\partial {\mathbf{u}}^s}{\partial t}\right]=0$$ (29)

$$\frac{\partial (\epsilon S^t)}{\partial t}+\nabla ·\left(\epsilon S^t\frac{\partial {\mathbf{u}}^s}{\partial t}\right)-\nabla ·\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{ts}}{{\mu }^t}\nabla p^t\right)=\frac{1}{\rho }\underset{\mathit{\text{growth}}}{\overset{l\to t}{M}}$$ (30)

$$\frac{\partial (\epsilon S^h)}{\partial t}+\nabla ·\left(\epsilon S^h\frac{\partial {\mathbf{u}}^s}{\partial t}\right)-\nabla ·\left(\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\nabla p^h\right)=0$$ (31)

$$\frac{\partial (\epsilon S^l)}{\partial t}+\nabla ·\left(\epsilon S^l\frac{\partial {\mathbf{u}}^s}{\partial t}\right)-\nabla ·\left(\frac{k_{\mathit{\text{rel}}}^l{\mathbf{k}}^{ls}}{{\mu }^l}\nabla p^l\right)=-\frac{1}{\rho }\underset{\mathit{\text{growth}}}{\overset{l\to t}{M}}$$ (32)

Summing equations (30-32), using the constraint equations on porosity and saturation, gives

$$\nabla ·\left(\frac{\partial {\mathbf{u}}^s}{\partial t}\right)-\nabla ·\left(\frac{k_{\mathit{\text{rel}}}^t{\overline{\mathbf{k}}}^{ts}}{{\mu }^t}\nabla p^t\right)-\nabla ·\left(\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\nabla p^h\right)-\nabla ·\left(\frac{k_{\mathit{\text{rel}}}^l{\mathbf{k}}^{ls}}{{\mu }^l}\nabla p^l\right)=0$$ (33)

The mass fraction of the necrotic cells is obtained from eqn (11) as

$$\frac{\partial {\omega }^{N\overline{t}}}{\partial t}=\frac{1}{\epsilon S^t\rho }\left[{\epsilon }^t{r}^{Nt}-\left({\omega }^{N\overline{t}}\underset{\mathit{\text{growth}}}{\overset{l\to t}{M}}\right)-(\epsilon S^t\rho v^{\overline{t}})·\nabla {\omega }^{N\overline{t}}\right]$$ (34)

The mass balance equation of the nutrient, using the Fick' Law to approximate the diffusive velocity $({\rho }^l{\omega }^{\overline{\mathit{\text{nl}}}}{\mathbf{u}}^{\overline{\overline{\mathit{\text{il}}}}}=-D^{\overline{\mathit{\text{nl}}}}{\rho }^l\nabla {\omega }^{\overline{\mathit{\text{nl}}}})$ and assuming (17) is:

$$\frac{\partial (\epsilon S^l{\omega }^{\overline{\mathit{\text{nl}}}})}{\partial t}+\nabla ·(\epsilon S^l{\omega }^{\overline{\mathit{\text{il}}}}{\mathbf{v}}^{\overline{l}})-\nabla ·(\epsilon S^l{D}_{\mathit{\text{eff}}}^{\overline{\mathit{\text{nl}}}}\nabla {\omega }^{\overline{\mathit{\text{nl}}}})=-\frac{\stackrel{\mathit{\text{nl}}\to t}{M}}{\rho }$$ (35)

Expanding eqn (35) by use of the product rule and substituting eqn (6) gives an alternative form of the advection-diffusion equation of the nutrient species:

$$\epsilon S^l\frac{\partial {\omega }^{\overline{\mathit{\text{nl}}}}}{\partial t}-\nabla ·(\epsilon S^l{D}_{\mathit{\text{eff}}}^{\overline{\mathit{\text{nl}}}}\nabla {\omega }^{\overline{\mathit{\text{nl}}}})=\frac{1}{\rho }\left({\omega }^{\overline{\mathit{\text{nl}}}}\stackrel{l\to t}{M}-\stackrel{\mathit{\text{nl}}\to t}{M}\right)-\epsilon S^l{\mathbf{v}}^{\overline{l}}·\nabla {\omega }^{\overline{\mathit{\text{nl}}}}$$ (36)

The linear momentum balance of the solid phase in a rate form (Schrefler, 2002) is

$$\nabla ·\left(\frac{\partial {\mathbf{t}}_{\mathit{\text{eff}}}^{\overline{\overline{s}}}}{\partial t}-\frac{\partial p^s}{\partial t}\mathbf{1}\right)=0$$ (37)

where the interaction between the solid and fluids, inclusive of the cell populations, has been accounted for through the effective stress principle, i.e., equations (26) and (27).

Finally for the solid phase the constitutive relationship between the effective stresses ${\mathbf{t}}_{\mathit{\text{eff}}}^{\overline{\overline{s}}}$ and the elastic strains ${\mathbf{e}}_{\mathit{\text{el}}}^s$, which is the difference between total strains e^s and visco-plastic strains ${\mathbf{e}}_{\mathit{\text{vp}}}^s$, reads as

$$\frac{\partial {\mathbf{t}}_{\mathit{\text{eff}}}^{\overline{\overline{s}}}}{\partial t}={\mathbf{D}}_s\frac{\partial {\mathbf{e}}_{\mathit{\text{el}}}^s}{\partial t}={\mathbf{D}}_s\left(\frac{\partial {\mathbf{e}}^s}{\partial t}-\frac{\partial {\mathbf{e}}_{\mathit{\text{vp}}}^s}{\partial t}\right)$$ (38)

where D_s is the tangent matrix containing the mechanical properties of the solid skeleton. An extensive description of the elasto-visco-plastic model and of the mechanical aspects will be presented in a successive paper.

4. Numerical solution and computational procedure

The weak form of equations (30), (31), (33), (36) and (37) is obtained by means of the standard Galerkin procedure and is then discretized in space by means of the finite element method (Lewis and Schrefler, 1998). Integration in the time domain is carried out with the generalized mid-point rule where an implicit procedure is used. Within each time step the equations are linearized by means of the Newton-Raphson method. For the FE discretization the primary variables are expressed in terms of their nodal values as

$$\begin{array}{lll}{\omega }^{\overline{\mathit{\text{nl}}}}(t)\cong {\mathbf{N}}_n{\overline{\mathbf{\omega }}}^{\overline{\mathit{\text{nl}}}}(t)\hfill & S^t(t)\cong {\mathbf{N}}_t{\overline{\mathbf{S}}}^t(t)\hfill & S^h(t)\cong {\mathbf{N}}_h{\overline{\mathbf{S}}}^h(t)\hfill \\ p^l(t)\cong {\mathbf{N}}_l{\overline{\mathbf{p}}}^l(t)\hfill & {\mathbf{u}}^s(t)\cong {\mathbf{N}}_u{\overline{\mathbf{u}}}^s(t)\hfill \end{array}$$ (39)

where ${\overline{\mathbf{\omega }}}_i^{\overline{\mathit{\text{nl}}}}(t)$, ${\overline{\mathbf{S}}}_i^t(t)$, ${\overline{\mathbf{S}}}_i^h(t)$, ${\overline{\mathbf{p}}}_i^l(t)$, ${\overline{\mathbf{u}}}_i^s(t)$ are vectors of nodal values of the primary variables at time instant t, and N_n, N_t, N_h, N_l, and N_u are vectors of shape functions related to these variables.

For the solution of the resulting governing equations, a staggered scheme is adopted with iterations within each time step to preserve the coupled nature of the system. The convergence properties of such staggered schemes have been investigated by Turska et al., (1994). In particular, for the iteration convergence within each time step a lower limit of Δt/h² has to be observed. Such a limit has also been found by Murthy et al, (1989) for Poisson equations and by Rank et al. (1983) invoking the discrete maximum principle. The existence of this limit means that we cannot diminish at will the time step below a certain threshold without also decreasing the element size.

Three computational units are used in the staggered scheme: the first is for the nutrient mass fraction, the second to compute S^t , S^h and p^l , and the third is used to obtain the displacement vector u^s. Within each coupling iteration, eqn (36) is solved for the mass fraction of the nutrient ${\omega }^{\overline{\mathit{\text{nl}}}}$. Then the group of eqs (30, 31, 33) is solved in a fully coupled way for S^t, S^h, p^l. In this second computational unit, at each iteration i the approximate solution $S_i^t$, $S_i^h$, $p_i^l$ is used to update the mass fraction of the necrotic tumor cells ${\omega }_i^{N\overline{t}}$, eqn (34), the mass exchange term, eqn (18), and the reaction term, eqn (19). Once convergence is achieved for the second computational unit, the pressure in the cells phases (given by eqn (28)) is used to compute the solid pressure, eq (27). The solid pressure is needed to solve the momentum balance equation (37). Once convergence is achieved within a time step the procedure can march forward.

Taking into account the chosen staggered scheme, the final system of equations can be expressed in a matrix form as follows, where some of the coupling terms have been placed in the source terms and are updated at each iteration to preserve the coupled nature of the problem.

$${\mathbf{C}}_{\mathit{\text{ij}}}(\mathbf{x})\frac{\partial \mathbf{x}}{\partial t}+{\mathbf{K}}_{\mathit{\text{ij}}}(\mathbf{x})\mathbf{x}={\mathbf{f}}_i(\mathbf{x})$$ (40)

with

$${\mathbf{C}}_{\mathit{\text{ij}}}=\left(\begin{array}{lllll}{\mathbf{C}}_{\mathit{\text{nn}}}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\mathbf{C}}_{\mathit{\text{tt}}}\hfill & {\mathbf{C}}_{\mathit{\text{th}}}\hfill & {\mathbf{C}}_{\mathit{\text{tl}}}\hfill & 0\hfill \\ 0\hfill & {\mathbf{C}}_{\mathit{\text{ht}}}\hfill & {\mathbf{C}}_{\mathit{\text{hh}}}\hfill & {\mathbf{C}}_{\mathit{\text{tl}}}\hfill & 0\hfill \\ 0\hfill & {\mathbf{C}}_{\mathit{\text{lt}}}\hfill & {\mathbf{C}}_{\mathit{\text{lh}}}\hfill & {\mathbf{C}}_{\mathit{\text{ll}}}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & {\mathbf{C}}_{\mathit{\text{uu}}}\hfill \end{array}\right){\mathbf{K}}_{\mathit{\text{ij}}}=\left(\begin{array}{lllll}{\mathbf{K}}_{\mathit{\text{nn}}}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\mathbf{K}}_{\mathit{\text{tt}}}\hfill & {\mathbf{K}}_{\mathit{\text{th}}}\hfill & {\mathbf{K}}_{\mathit{\text{tl}}}\hfill & 0\hfill \\ 0\hfill & {\mathbf{K}}_{\mathit{\text{ht}}}\hfill & {\mathbf{K}}_{\mathit{\text{hh}}}\hfill & {\mathbf{K}}_{\mathit{\text{hl}}}\hfill & 0\hfill \\ 0\hfill & {\mathbf{K}}_{\mathit{\text{lt}}}\hfill & {\mathbf{K}}_{\mathit{\text{lh}}}\hfill & {\mathbf{K}}_{\mathit{\text{ll}}}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right),{\mathbf{f}}_i=\left(\begin{array}{l}{\mathbf{f}}_n\\ {\mathbf{f}}_t\\ {\mathbf{f}}_h\\ {\mathbf{f}}_l\\ {\mathbf{f}}_u\end{array}\right)$$ (41)

where ${\mathbf{x}}^{\mathrm{T}}=\left\{{\overline{\mathbf{\omega }}}^{\overline{\mathit{\text{nl}}}},{\overline{\mathbf{S}}}^t,{\overline{\mathbf{S}}}^h,{\overline{\mathbf{p}}}^l,{\overline{\mathbf{u}}}^{\mathbf{s}}\right\}$ The non linear coefficient matrices C_ij (x), K_ij (x) and f_i (x) are given in the Appendix B.

The modular computational structure allows to take into account more than one chemical species, simply adding a computational unit (equivalent to the first one used for the nutrient) for each of the additional chemical species considered.

The procedure has been implemented in the code CAST3M (http://www-cast3m.cea.fr) of the French Atomic Energy Commission taking advantage of previous work done on modelling concrete at early age (Gawin et al., 2006). There is a striking analogy between the two physical problems (concrete hydration and tumor growth) as far as the balance equations are concerned. In both we have one solid phase and immiscible fluid phases together with reactions and mass exchanges.

5. Results

The computational framework above has been applied to solve three cases of practical interest: i) growth of a multicellular tumor spheroid (MTS) in vitro; ii) growth of a multicellular tumor spheroid (MTS) in vivo; and iii) growth of a tumor along micro-vessels (tumor cord model). For all cases, the growth of the tumor mass, including the necrotic mass and living tumor cells; and the consumption of nutrient (oxygen) are analyzed over time. A direct comparison with experimental data is presented for case i). The extracellular matrix (ECM) is assumed rigid for all three cases. This assumption will be relaxed in future studies. Results are presented in terms of volume fractions, ε^t, ε^h and ε^l, pressures, p^c and p^l, and mass fraction of oxygen ${\omega }^{\overline{\mathit{\text{nl}}}}$.

5.1. Growth of a multicellular tumor spheroid (MTS) in vitro

MTS can be efficiently used to study the in vitro growth of tumors in the avascular stage. The tumor size can be easily measured experimentally using microscopy techniques and can be predicted quite accurately by analytical and computational methods. Here, the time evolution of a MTS is considered, assuming that the cellular mass is floating in a quiescent, cell culture medium. The geometry and boundary conditions of the problem are described in figure 3. Modelled as a half sphere imposing cylindrical symmetry the MTS comprises three phases: i) the living and necrotic tumor cells (LTC and NTC); ii) the extracellular matrix (ECM); and iii) the interstitial fluid (IF). At time t = 0 h, these phases coexist in the red area shown in figure 3, having a radius of 50 μm. Within this region, the initial volume fraction of the tumor cells (TC) is set to 0.01; whereas the volume fraction of the ECM is set to 0.05 throughout the computational domain. Note that, assuming a characteristic cell diameter of 10 μm, the initial number of tumor cells in the red area would be ∼ 10.

Figure 3.

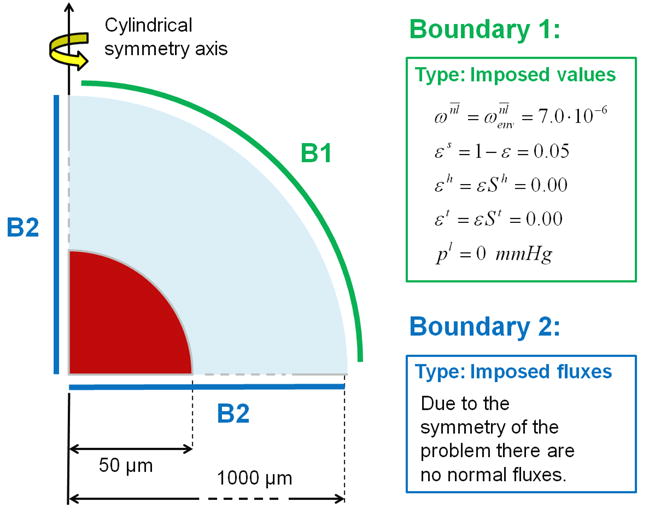
Geometry and boundary conditions for a multicellular tumor spheroid (red) in a medium (not to scale).

The blue shell in figure 3 - the cell culture medium surrounding the MTS - is the rest of the computational domain up to 1,000 μm. These initial conditions are summarized in table 1. At the outer boundary (B1), the primary variables S^t , ${\omega }^{\overline{\mathit{\text{nl}}}}$ and p^l are fixed with time (Dirichlet boundary conditions). At the symmetry boundaries B2, zero flux (Neumann boundary conditions) is imposed for all the phases. The atmospheric pressure is taken as the reference pressure. In this example, oxygen is the sole nutrient species, and its mass fraction is fixed to be ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}={7·10}^{-6}$ at B1 and throughout the computational domain at t = 0 h. The non-apoptotic cell death rate is calculated by eqn (19), where the critical value of the oxygen mass fraction is given by ${\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}={3·10}^{-6}$, and the cell pressure above which the cell death rate increases is $p_{\mathit{\text{necr}}}^t=930$ Pa. The necrotic regions are those where the mass fraction of necrotic cells ${\omega }^{N\overline{t}}=\frac{{\epsilon }^{N\overline{t}}{\rho }^{N\overline{t}}}{{\epsilon }^t{\rho }^t}$ exceeds 0.5. All other governing parameters are listed in table 2.

Table 1.

Initial conditions for a multicellular tumor spheroid in a medium.

	εs	εt	εh	pl	${\omega }^{\overline{\mathit{\text{nl}}}}$
Red zone	0.05	0.01	0.00	0.00	7·10-6
Blu zone	0.05	0.00	0.00	0.00	7·10-6

Table 2. Input parameters used to simulate the first case.

Parameter	Symbol	Value	Unit
Density of the phases	ρ	1000	kg/m3
Diffusion coefficient of oxygen in the interstitial fluid	$D_0^{\overline{\mathit{\text{nl}}}}$	3.2·10-9	m2/sec
Coefficient δ (eqn (21))	δ	2.00	—
Intrinsic permeability for interstitial fluid phase	kls	1.8·10-15	m2
Intrinsic permeability for tumor cell phase	kts	5·10-20	m2
Adhesion of tumor cells (to ECM)	at	1·106	N/m3
Growth coefficient of tumor cells (eqn (18))	${\gamma }_{\mathit{\text{growth}}}^t$	0.016	—
Critical mass fraction of oxygen (eqs (18,20))	${\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}$	3·10-6	—
Critical pressure for cell growth (eqs (18,20))	$p_{\mathit{\text{crit}}}^t$	1330	Pa
Necrosis coefficient (eqn (19))	${\gamma }_{\mathit{\text{necrosis}}}^t$	0.016	—
Cells pressure above which necrosis occurs (eqn (19))	$p_{\mathit{\text{necr}}}^t$	930	Pa
Pressure dependent additional necrosis (eqn (19))	${\delta }_a^t$	5·10-4	—
Consumption coefficient related to growth in eqn (20)	${\gamma }_{\mathit{\text{growth}}}^{\overline{\mathit{\text{nl}}}}$	4·10-4	—
Consumption coefficient related to metabolism in eqn (20)	${\gamma }_0^{\overline{\mathit{\text{nl}}}}$	6·10-4	—
Coefficient σc in eqn (28)	σc	532	Pa
Coefficient b in eqn (28)	b	1	—

The volume fractions of the tumor cells ε^t (TC – solid line) and of the living tumor cells (LTC – dashed line) with time is presented in figure 4a. The radius for which the volume fraction ε^t is zero gives the actual radius r^sph of the MTS. With time, the TC front moves outward and r^sph grows. The difference between the solid and dashed lines (TC – LTC) identifies the volume fraction of the necrotic tumor cells. The LTC lines present a peak that moves outward with time, implying a continuous growth of the necrotic area within the MTS. Figure 4a clearly shows that r^sph grows from 50 μm (t = 0h) to ∼ 400 μm at 360h.

Figure 4.

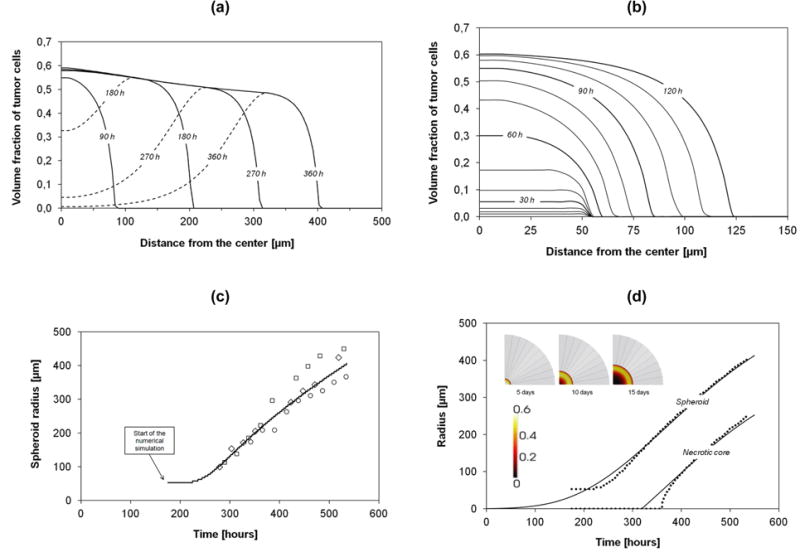
(a) Volume fraction of the tumor cells (total and living) during 360h. (b) Volume fraction of the tumor cells phase over 120h; lines drawn at every 10h of simulations. (c) Numerical results compared with different in vitro experiments. The symbols are data obtained in the following in vitro cultures: squares = FSA cells (methylcholantrene-transformed mouse fibroblasts, Yuhas et al., 1977); diamonds = MCF7 cells (human breast carcinoma, Chignola et al., 1995); circles = 9L cells (rat glioblastoma, Chignola et al., 2000). (d) Numerical results (points) for spheroid and necrotic core radii, and their interpolations (solid lines).

The early evolution of the tumor mass is shown with more details in figure 4b. Starting from a 50 μm radius with S^t = 0.01, the tumor does not grow significantly in size within the first 50h. The tumor cells are rapidly dividing, increasing the volume fraction but not the size of the tumor mass. Thence, the tumor enlarges with a monotonic growth of r^sph. The tumor radius (r^sph(t)) is presented in figure 4c (solid line) along with experimental data (open symbols). Notably, our prediction agrees well with three different MTS datasets (Yuhas et al. 1977; Chignola et al. 1995; Chignola et al. 2000). The growth rate of tumor is lower for the first 80h. The numerical results are interpolated in figure 4d using the Gompertzian growth function

$$r_{(t)}^{\mathit{\text{sph}}}=r_{\infty }exp(-aexp(-\beta t))$$ (42)

where r_∞ = 600 μm is the tumor radius r^sph at sufficiently large times (nominally t → ∞), a and β are two constants derived from numerical data (a = 7.5 and β = 0.00545 h^-1). The time t in eqn (42) is measured in hours. For the necrotic core, a similar functional relationship is here proposed as

$$r_{(t)}^{\mathit{\text{nc}}}={\langle r_{\infty }exp(-aexp(-\beta t))-{\delta }_{\mathit{\text{living}}}\rangle }_{+}$$ (43)

where δ_living is a constant, penalty term related to the thickness of the outer shell comprising mostly viable cells (LTC) which are still well nourished and oxygenated. The shell thickness depends on the cell line and nutrients availability (Mueller-Klieser et al., 1986), but it is well accepted that at distances larger than 100 – 200 μm, nutrient diffusion is impaired. From our simulation, the shell thickness is 150 μm. Figure 4d also shows the necrotic core and the viable shell at three different times: necrotic cells are in the darker zone.

Note that the measured (apparent) volume $V_{\mathit{\text{app}}}^{\mathit{\text{TC}}}$ of the MTS could be very different from the effective volume $V_{\mathit{\text{eff}}}^{\mathit{\text{TC}}}$. Figure 5a shows these along with the effective volume of the living tumor cells $V_{\mathit{\text{eff}}}^{\mathit{\text{TCL}}}$; these are defined as

Figure 5.

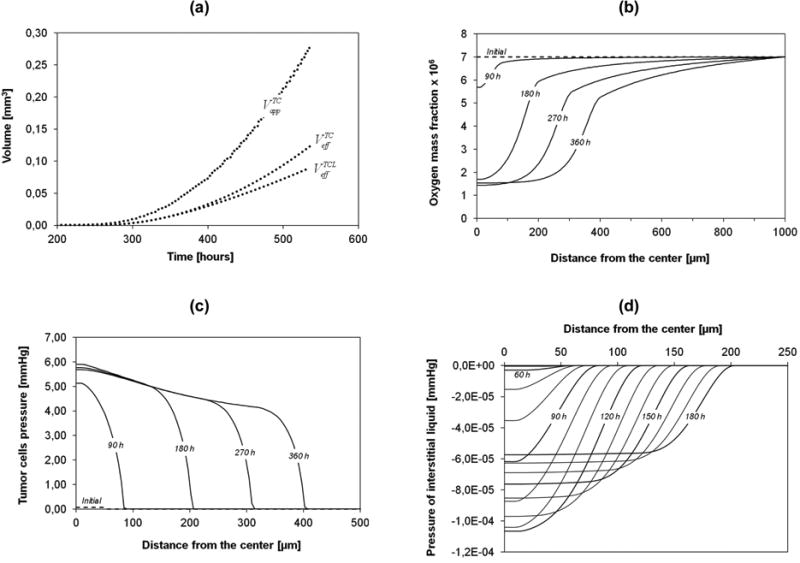
(a) Apparent volume of the tumor spheroid, effective volume of the tumor cells, and the effective volume of the living tumor cells, over time. (b) Mass fraction of oxygen over 360h. (c) Pressure in the tumor cells phase over 360h. (d) Numerical prediction of the interstitial fluid pressure over 180h; Lines drawn at every 10h of simulations.

$$V_{\mathit{\text{app}}}^{\mathit{\text{TC}}}=\underset{\mathrm{\Omega }}{\int }H({\epsilon }^t-{\epsilon }_0^t)d\mathrm{\Omega }{V}_{\mathit{\text{eff}}}^{\mathit{\text{TC}}}=\underset{\mathrm{\Omega }}{\int }{\epsilon }^{t}d\mathrm{\Omega }{V}_{\mathit{\text{eff}}}^{\mathit{\text{LTC}}}=\underset{\mathrm{\Omega }}{\int }(1-{\omega }^{N\overline{t}}){\epsilon }^{t}d\mathrm{\Omega }$$ (44)

Where ${\epsilon }_0^t=0.01$, H is the Heaviside function which is zero for ${\epsilon }^t\le {\epsilon }_0^t$ and unity for ${\epsilon }^t>{\epsilon }_0^t$, and Ω is the computational domain. The apparent volume contains also the IF while the effective volume comprises tumor cells alone. Figure 5a shows that for small times, $V_{\mathit{\text{eff}}}^{\mathit{\text{TC}}}$ and $V_{\mathit{\text{eff}}}^{\mathit{\text{LTC}}}$ are equal as necrosis is initially negligible.

The evolution of the oxygen mass fraction, the sole nutrient species considered here for cell proliferation and metabolism, is shown in figure 5b. As the spheroid increases in size, gradients of oxygen concentration develop from the periphery, where the oxygen mass fraction is fixed to ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}={7·10}^{-6}$, to the center of the spheroid. Once the nutrient concentration in the center goes below an imposed critical value $({\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}={3·10}^{-6})$, cell necrosis commences. Note that at the boundary between the tumor and the surrounding cell culture medium, a significant change in the gradient of the mass fraction of oxygen is observed as a kink in the curves (see figure 5b) - due to the lower effective diffusivity in the tumor. After a certain time, in the necrotic core the mass fraction of oxygen reaches a minimum value of about 1.5×10⁻⁶, lower than the threshold critical value $({\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}={3·10}^{-6})$. The oxygen concentration continues to fall below the threshold value until all cells are dead since in the necrotic region (here defined as the region where at least 50% of the cells are dead) the still living cells consume oxygen and slowly die. From figure 5b the necrotic core could be also identified as the portion of the MTS with a relatively homogeneous mass fraction of oxygen. The reasons: i) necrotic cells do not consume oxygen, hence no nutrient gradient in the core; ii) the local consumption of oxygen (regulated by eqn (20)) decreases substantially and tends to zero with the reduction of the oxygen availability.

The pressure of the tumor cells within the computational domain (computed using eqn (28)) is plotted in figure 5c. The maximum pressure of about 6.0 mmHg (∼ 800 Pa) in the core of the MTS is lower than the critical pressure for cell death $(p_{\mathit{\text{necr}}}^t=930\text{Pa})$. Thus oxygen deficiency is the sole cause of cell necrosis in the current example. Note that for relatively low saturations, the relationship between pressure and volume fraction is almost linear (see figure 2). Hence, the trends shown in the figures 4a and figure 5c are similar. However with increasing saturation level of the tumor cells, the relationship with the pressure becomes nonlinear and so the peak pressure in figure 5c is more pronounced than the peak volume fraction ε^t (ε^t = S^t/ε) in figure 4a. The interstitial fluid pressure (p^l) is plotted in figure 5d. Within the first 50h, the tumor cells grow locally, whilst the overall external radius of the tumor mass stays constant at its original value (50 μm). As the IF is consumed by the tumor cells, and the assumption (17) allows satisfying the volume balance locally the IF pressure gradient remains unaltered. Figure 5d shows that until 50h the IF pressure gradient is zero so that no additional interstitial fluid from the environment is needed (oxygen moves only by diffusion). After 50h, the spheroid increases its radius; hence with tumor growth the interstitial fluid must flow inward, per constraint eqn (2). Therefore the IF pressure in the MTS core decreases. The intrinsic permeability of the interstitial fluid phase is relatively high compared to that of the tumor cells phase (see table 2). For this reason, the variations in pressure (figure 5d) are minimal but significant to explain that IF flows into the viable tumor shell during growth. Indeed, the interstitial fluid pressure computed is slightly lower than in the surrounding tissue. This has to be ascribed to the lack of vasculature networks and lymphatic systems in the current model. The high interstitial fluid pressure measured in tumors is mostly associated to the higher permeability of the fenestrated tumor endothelium and lack, or reduction, in lymphatic flow. Therefore the plasma permeating the tumor from the vascular compartment cannot be drained out efficiently through the dysfunctional lymphatic systems leading the progressive liquid accumulation in the extracellular space and consequent pressure built up (Jain and Stylianopoulos, 2010). All this will be included in future extensions of the model incorporating also the vascular compartment and the lymphatic system. It should also be noted that, in the present computational model, the IFP depends among others strongly on the pressure difference-saturation relationship of section 3.2.7 and possibly also on the deformation of the ECM. This aspect is currently under investigation.

5.2. Multicellular tumor spheroid (MTS) in vivo

In this second example, the tumor is growing within the healthy tissue, which substitutes the cell culture medium in the previous case. Therefore, the initial configuration of the system comprises four phases: i) the living and necrotic tumor cells (LTC and NTC); ii) the host cells of the healthy tissue surrounding the tumor mass (HC); iii) the extracellular matrix (ECM); and iv) the interstitial fluid (IF). The ECM and IF are distributed throughout the computational domain. The growing MTS pushes on the healthy cells as its radius increases.

Also, it is anticipated that the diffusion of nutrients towards the tumor mass would be reduced by the presence of the healthy tissue. As the tumor, the thin healthy tissue corona is assumed here to be not vascularised.

The geometry and boundary conditions of the problem are described in figure 6. The MTS is modelled considering a half sphere and imposing cylindrical symmetry. The red region contain the tumor cells (TC) with an initial radius of 30 μm (t = 0 h) and an initial volume fraction set to 0.45. The orange region is the healthy tissue extending till the outer boundary B1 of the computational domain of 150 μm. The volume fraction of the host cells in the healthy zone is initially homogeneous and set to 0.45 (t = 0 h). At B1, the primary variables S^t, S^h, ${\omega }^{\overline{\mathit{\text{nl}}}}$ and p^l are prescribed and constant (Dirichlet boundary condition). At the boundaries B2, zero flux (Neumann boundary condition) is imposed for all phases and nutrients due to the radial symmetry. The atmospheric pressure is the reference pressure. As in the previous example, oxygen is the sole nutrient and its mass fraction is fixed at ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}=4.2·{10}^{-6}$ on B1 and throughout the computational domain at t = 0h. The chosen mass fraction of oxygen corresponds to the average of the dissolved oxygen in the plasma of a healthy individual. Although in this case the vasculature is not explicitly considered, the radius of the computational domain (here 150 μm) can be taken as an indicator of the vascularisation grade of the host tissue: higher radii correspond to smaller vascularisation and vice versa. Due to the lower reference environmental mass fraction of oxygen ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}$, the parameters ${\gamma }_{\mathit{\text{growth}}}^t$ and ${\gamma }_{\mathit{\text{necrosis}}}^t$, that govern growth and necrosis respectively, and one coefficient of the oxygen sink term function ( ${\gamma }_{\mathit{\text{growth}}}^{\overline{\mathit{\text{nl}}}}$, see eqn 20) are different from the first example (see table 4). The initial conditions are listed in table 3 while the parameters of the healthy phase are given in table 4. All the other parameters are the same as in table 1.

Figure 6.

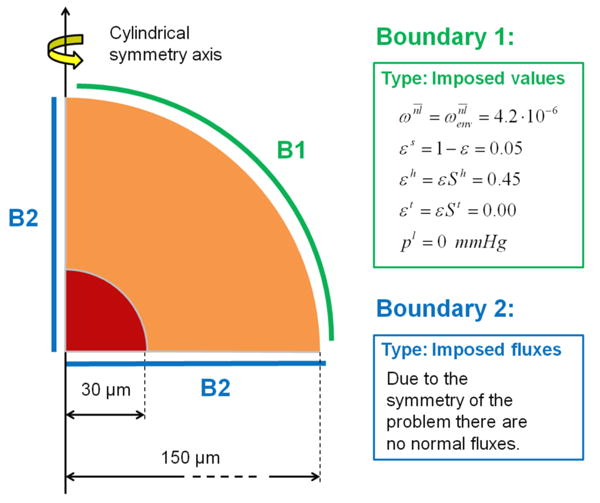
Geometry and boundary conditions for a multicellular tumor spheroid growing within a healthy tissue. (not to scale)

Table 4.

Additional input parameters for the second case.

Parameter	Symbol	Value		Unit
Intrinsic permeability for host cell phase	khs	5·10-20	m2
Adhesion of host cellsa (to ECM)	ah	1·106 / 1.5·106	N/m3
Growth coefficient of tumor cells (eqn (18))	${\gamma }_{\mathit{\text{growth}}}^t$	0.0096	—
Necrosis coefficient (eqn (19))	${\gamma }_{\mathit{\text{necrosis}}}^t$	0.0096	—
Consumption coefficient related to growth in eqn (20)	${\gamma }_{\mathit{\text{growth}}}^{\overline{\mathit{\text{nl}}}}$	2.4·10-4	—

^aIn the second case the effect of cells adhesion is analyzed; then more than one value is used

Table 3.

Initial conditions for a multicellular tumor spheroid growing within a healthy tissue.

	εs	εt	εh	pl	${\omega }^{\overline{\mathit{\text{nl}}}}$
Red zone	0.05	0.45	0.00	0.00	4.2·10-6
Blu zone	0.05	0.00	0.45	0.00	4.2·10-6

The adhesions of the cells to the ECM (a_t and a_h) has a more significant effect than in the first case, since there were no healthy cells surrounding the tumor mass. This example shows clearly that the relative cell adhesion plays a major role in affecting the overall tumor growth. The panels in figure 7a and figure 7b show the variation of the tumor cell volume fractions over time for two different adhesion conditions, namely a_h = a_t (left column, figure 7a) and a_h = 1.5 a_t (right column, figure 7b). The times for the 3 panels are 1h, 180h and 360h. As for the first example, the variation of the volume fraction for the tumor cells (TC) is presented as a solid line, the living portion of the tumor cells (LTC) by a dashed line; the difference between the two gives the fraction of necrotic cells (NTC). As expected, the overall tumor mass expands with time and a necrotic area appears in the core. Interestingly, the panels reveal a significant difference in the evolution of the volume fractions depending on the adhesion conditions. When a_h = a_t (figure 7a), the growing tumor mass displaces completely the healthy cells; whereas for a_h > a_t (figure 7b), the tumor spheroid during its growth pushes on the healthy cells and partially invades their domain. Interestingly, tumor invasion of the surrounding healthy tissue is controlled by the relative adhesion properties of the cell populations. Diffuse interface models and fourth order differential equations as used by Hawkins-Daarud et al. (2012) are not needed to capture the invasive behaviour.

Figure 7.

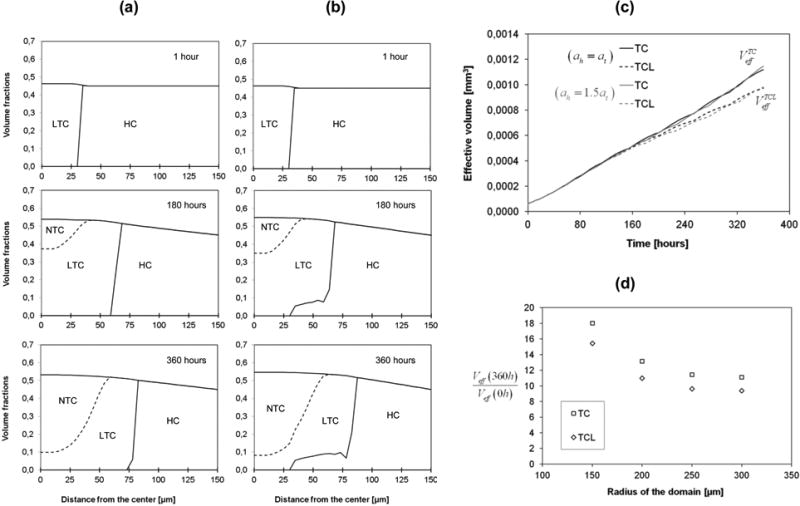
(a,b)Numerical prediction of the volume fractions of the living tumor cells (LTC), the necrotic tumor cells (NTC) and the host cells (HC), at different times (from up to down: 1h, 180h, and 360h). The left column (a) is for a_h = a_t, while the right column (b) is for a_h = 1.5·a_t.

(c) Evolution of the effective volume of the tumor cells, and the effective volume of the living tumor cells. The black lines refer to the case (a_h = a_t), while the grey lines refer to the case (a_h = 1.5a_t). (d) Scaled effective volume of tumor (normalized by initial value) after 360 hours for different radii of the computational domain.

Surprisingly, cell adhesion does not affect the overall volume size as clearly seen in figure 7c where the effective volumes of the tumor and the living tumor cells are plotted for the two adhesive conditions defined above. On the other hand, by comparing figures 7c and figure 5a, the growth patterns of an MTS in a medium and an MTS in tissue appear quite dissimilar. This is mostly due to the presence of the adhesive host cells phase that contrasts the tumor growth and reduces the nutrient supply. In addition to the difference in growth pattern, a one to two orders of magnitude difference in effective tumor volume can also be observed. Hence the experimental results obtained in vitro are not indicative of the in vivo cases since the growth environments are very different.

The radius of the computational domain can be taken as an indicator of the vascularisation grade of the host tissue, because at the boundary B1 the mass fraction is fixed to be ${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}=4.2·{10}^{-6}$ (mass fraction of dissolved oxygen in the plasma of a healthy individual). We have solved the case with a_h = 1.5a_t for r_ext= 200 μm, r_ext= 250 μm and r_ext= 300 μm, (values of the initial thickness of host cells respectively of 170 μm, 220 μm and 270 μm) to evaluate the influence of the vascularisation grade on the growth of tumor. The ratio between the effective tumor volume at 360h and at t = 0h has been plotted in figure 7d for the different considered spherical domains: after 360 hours the volume of the tumor is 18 times the initial volume for r_ext= 150 μm, and 13 times the initial volume for r_ext= 200 μm, hence if we increase r_ext the growth rate decreases.

5.3 Tumor growth along microvessels (tumor cord model)

In this last case, tumor cells grow in proximity of two otherwise healthy blood vessels that are the only source of oxygen. The presence of capillary vessels has an important impact on the tumor development and on its spatial configuration (Astanin and Preziosi (2009)); this is confirmed in our application case where the progressive migration of tumor cells among adjacent vessels is also shown.

The system comprises four phases: i) the living and necrotic tumor cells (TLC and NTC); ii) the healthy tissue surrounding the tumor mass; iii) the extracellular matrix (ECM); and iv) the interstitial fluid (IF). The ECM and IF are distributed throughout the computational domain. The geometry and the boundary conditions of the problem are described in figure 8b. We consider two straight blood vessels of 8 μm diameter. The tumor cells are initially located around one vessel only (see figure 8a). Two different separation distances between the vessels are considered: in the first simulation (S1) the distance is 80 μm; in the second (S2) the distance is 100 μm. Note that in these cases, a full three dimensional (3D) computational solution is required. The geometry has two planes of symmetry (i.e. the median horizontal plane and that passing through the two vessels, figure 8b); hence only a quarter of the complete geometry is discretized. The FE mesh here is more complex than that of the previous cases. The parameters used are those of the second case, as treated in the paragraph 4.2, with the exception of the volume fraction of the ECM, here set to 0.1. The mass fraction of the oxygen, $({\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}=4.2·{10}^{-6})$ is imposed as a boundary condition on the cylindrical surface of the two blood vessels. At the remaining bounding surfaces the flux of oxygen is zero. The fluxes of all the phases (l, h, t) are zero at the two symmetry planes and at the cylindrical surface of the two capillary vessels. For the remaining boundary the imposed conditions are shown in figure 8b. The initial conditions are summarized in figure 8a.

Figure 8.

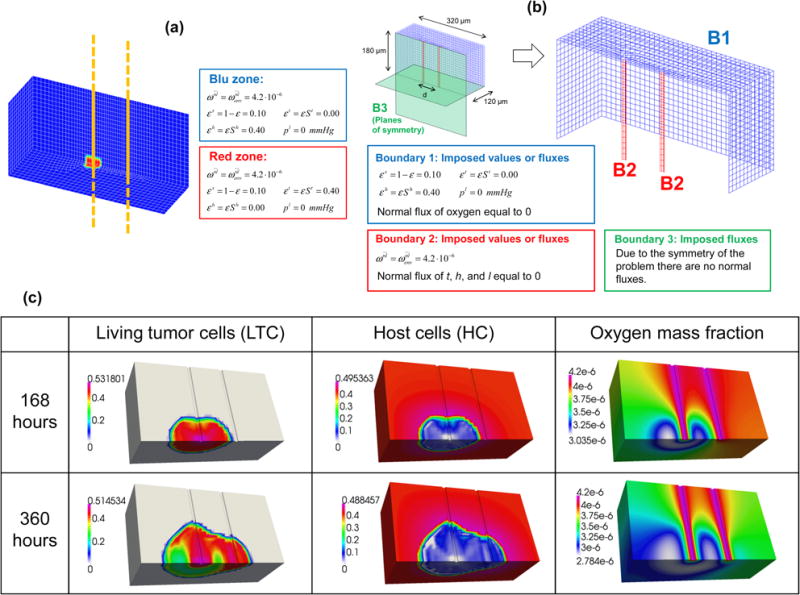
(a) Initial conditions of the third case. Yellow shows the axes of the two capillary vessels. (b) Geometry and boundary conditions. (c) Volume fractions of the living tumor cells (first column) of the healthy cells (second column) and mass fraction of oxygen (third column) for the case S1.

The volume fractions at 7 and 15 days of the healthy cell phase HC, and of the living tumor cells phase TCL are shown in figure 8c for case S1. The healthy cells are almost completely replaced by the tumor cells and after 15 days necrosis occurs in parts of the tumor which are more distant from the left blood vessel. Figure 8c shows also the oxygen mass fraction at 7 days and 15 days for the same simulation. The strong decrease in the oxygen mass fraction, caused by the presence of the tumor, can be readily observed by comparing the areas populated by the abnormal and healthy cells.

In the second numerical simulation (S2), the distance between the two vessels is higher than in case S1. The progressive expansion of the tumor mass from the left to the right vessel is therefore less. The results for the oxygen mass fraction are qualitatively similar to that of S1. Figure 9a shows the mass fraction of oxygen along a line passing through the two vessels, at different days. The effects of consumption of oxygen coming from the vessels are evident. Oxygen is here replenished only through the two blood vessels (two peaks). Figure 9b shows the tumor and the local mass fraction of oxygen (in the computational grid) at 15 days; clearly the higher values of the oxygen mass fraction are close to the two capillary vessels $({\omega }_{\mathit{\text{vessel}}}^{\overline{\mathit{\text{nl}}}}=4.2·{10}^{-6})$. In S2, the tumor has not yet completely reached the right vessel after 15 days. In figure 9c, the volume of the tumor after 20 days is represented for S2, and the necrotic area is clearly visible (only the finite elements in which the volume fraction of the tumor phase is higher than 0.01 are shown). In figure 9d, the time evolution of the tumor volume is plotted for the two cases, S1 and S2. The plotted volume is that of the finite elements with a volume fraction of the tumor cells higher than 0.01. Note that initially there is no difference between the two cases because the growth is mainly influenced by the left vessel. After 10 days, the growth rate increases for the S1 case due to the additional nutrient supply coming from the right vessel.

Figure 9.

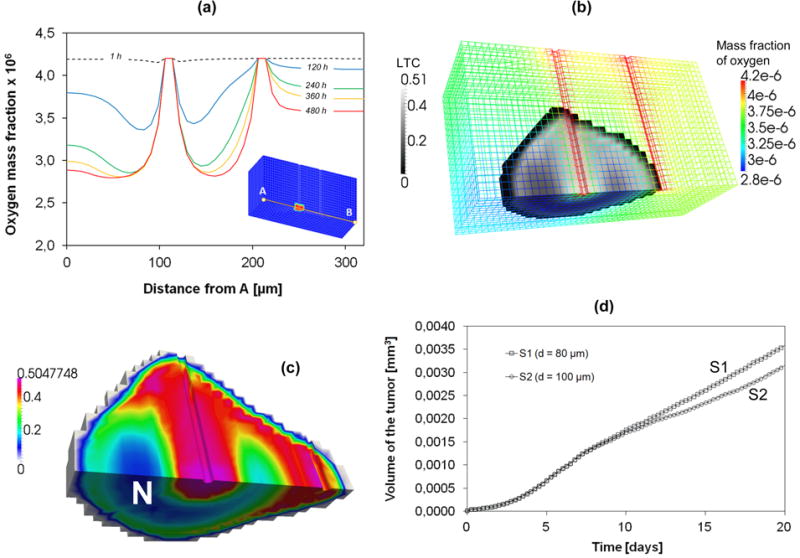
(a) Mass fraction of oxygen along the line joining points A and B for S2. (b) Volume fractions of the LTC and oxygen mass fraction for S2 at 15 days. (c) Volume fractions of the LTC for S2 at 20 days. “N” indicates the necrotic areas. (d) Volume of the tissue invaded by the tumor.

6. Conclusions

A tumor growth model has been developed based on multiphase porous media mechanics. The governing differential equations have been derived by means of the Thermodynamically Constrained Averaging Theory. These are mass balance equations for the different phases with the appropriate linear momentum balance equations. The equations have been discretized by means of the finite element method and a staggered procedure has been adopted for their solution. The lower limit of the ratio between time step size and square of the element size, necessary for a proper numerical behaviour of staggered schemes and Poisson type equations, has been determined by means of numerical tests.

The computational framework has been applied to three examples of practical interest, namely a multicellular tumor spheroid (MTS) immersed in a cell culture medium; a tumor spheroid surrounded by healthy tissue; and a tumor cord. Multiple phases have been considered in the model including i) the living and necrotic tumor cells (LTC and NTC); ii) the extracellular matrix (ECM); iii) the interstitial fluid (IF) and iv) the healthy cells (HC). For all cases, growth of the tumor mass, including the necrotic and living tumor cells areas; and the consumption of nutrient (oxygen) are analyzed over time within the whole computational domain.

For an MTS suspended in its culture medium, a direct comparison with three different experimental cases in the literature is presented. The agreement between the computational prediction of the tumor radius and the experimentally measured values is good. Also, the tumor growth follows the well know Gompertzian growth pattern demonstrating again the accuracy of the computational model. Interestingly, the early development of the malignant mass is characterized by a rapid division of the tumor cells accompanied by an equally rapid increase in tumor cell volume saturation, whilst the overall tumor size stays almost constant. This was observed up to 50-60h from the beginning. This early phase is then followed by fast exponential growth (Gompertzian growth pattern). The model allows the volume of each individual phase to be calculated at each time.

In the second example, the MTS is surrounded by a healthy tissue. The coexistence of two different cell populations (healthy and tumor) allows quantification of their relative adhesion to the ECM on tumor growth. In this respect two different conditions are analyzed showing that when the healthy cells adhere less to the ECM, the tumor advancing front displaces uniformly the healthy tissue; in the opposite case the tumor cells infiltrate the healthy tissue at discrete points. Interestingly, this result has been achieved without involving diffuse interface models and fourth order differential equations. The presence of the healthy tissue leads to an overall reduction in tumor growth mostly due to the lower nutrient transport and geometrical confinement.

In the third example, the of tumor cells along microvessels is predicted in a fully 3D geometry, with a clear delineation of necrotic and living tumor regions. The progressive migration of tumor cells among adjacent vessels in search of additional sources of nutrients and oxygen is revealed. Also shown is that a larger distance between adjacent vessels needs longer time tumor to grow, also demonstrating our model's capability to account for the vasculature.

The numerical accuracy and physical soundness of the computational model will increase the level of complexity that we can address in tumor biophysics - such as the contribution of the ECM stiffness, relative cell adhesion and IF pressure on the infiltration and development of malignant masses. Also, modelling the transport of therapeutic agents, in the form of individual drug molecules as well as nanoparticle, and angiogenic vascular growth will be introduced in future extensions. A direct comparison of the predicted tumor behaviour with experimental data derived from patients using clinically relevant imaging modalities should provide a validation of the presented approach. The modular structure of the framework allows straightforward inclusion of additional phases and nutrient types.

Faced with a continuously aging world population and the surge in cancer incidence, the approach presented here should engender novel therapeutic strategies and treatment optimization for improving the prognosis, outcome of intervention and quality of life.

Figure 1.

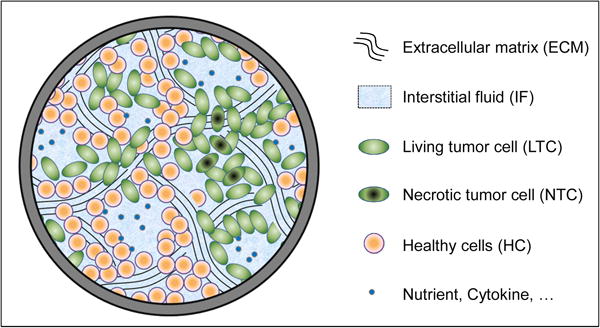
The multiphase system within a representative elementary volume (REV).

Appendix A. Linear momentum balance equation for a fluid phase

The general conservation of momentum eqn (14) will be denoted for the fluid phase using the letter f as a qualifier. In the paper the f will be specified as either l, h or t.

$$\frac{\partial ({\epsilon }^f{\rho }^f{\mathbf{v}}^{\overline{f}})}{\partial t}+\nabla ·\left({\epsilon }^f{\rho }^f{\mathbf{v}}^{\overline{f}}{\mathbf{v}}^{\overline{f}}\right)-\nabla ·\left({\epsilon }^f{\mathbf{t}}^{\overline{\overline{f}}}\right)-{\epsilon }^f{\rho }^f{\mathbf{g}}^{\overline{f}}-\sum _{\kappa \in {\Im }_{\mathit{\text{cf}}}}\left(\sum _{i\in {\Im }_s}\stackrel{i\kappa \to \mathit{\text{if}}}{M_v}{\mathbf{v}}^{\overline{f}}+\stackrel{\kappa \to f}{\mathbf{T}}\right)=0$$ (A.1)

where g^f̄ is the body force, $\stackrel{i\kappa \to \mathit{\text{if}}}{M_v}{\mathbf{v}}^{\overline{f}}$ represents the momentum exchange from the κ to the f phase due to mass exchange of species i, $\stackrel{\kappa \to f}{\mathbf{T}}$ is the interaction force between phase f and the adjacent interfaces, and ${\mathbf{t}}^{\overline{\overline{f}}}$ is the stress tensor. If the inertial terms are considered to be negligible, as is the case for slow flow in a porous medium, the first two terms in eqn (A.1) can be neglected. Additionally, the momentum exchange due to mass transfer, $\stackrel{i\kappa \to \mathit{\text{if}}}{M_v}{\mathbf{v}}^{\overline{f}}$ may also be considered small since this term is of the same order of magnitude as the inertial terms. Thus the momentum equation simplifies to

$$-\nabla ·\left({\epsilon }^f{\mathbf{t}}^{\overline{\overline{f}}}\right)-{\epsilon }^f{\rho }^f{\mathbf{g}}^{\overline{f}}-\sum _{\kappa \in {\Im }_{\mathit{\text{cf}}}}\stackrel{\kappa \to f}{\mathbf{T}}=0$$ (A.2)

The TCAT method of closure involves arranging terms in the entropy inequality into force-flux pairs. At equilibrium each member of the force-flux pair will be zero. This equilibrium constraint guides closure of the conservation system for near equilibrium situations. In the case here where the flows are slow, the near-equilibrium state assumption is appropriate. Based on the TCAT procedure, the elements of the entropy inequality relating to flow velocity that arise in the entropy inequality are

$$\frac{{\epsilon }^f}{{\theta }^{\overline{\overline{f}}}}\left({\mathbf{t}}^{\overline{\overline{f}}}+p^f\mathbf{1}\right):{\mathbf{d}}^{\overline{\overline{f}}}-\frac{1}{{\theta }^{\overline{\overline{f}}}}\left[{\epsilon }^f{\rho }^f{\mathbf{g}}^{\overline{f}}+{\epsilon }^f{\rho }^f\nabla \left({\varsigma }^{\overline{f}}+{\psi }^{\overline{f}}\right)-\nabla \left({\epsilon }^f{p}^f\right)+\sum _{\kappa \in {\Im }_{\mathit{\text{cf}}}}\stackrel{\kappa \to f}{\mathbf{T}}\right]·\left({\mathbf{v}}^{\overline{f}}-{\mathbf{v}}^{\overline{s}}\right)\ge 0$$ (A.3)

In this equation ${\theta }^{\overline{\overline{f}}}$ is the macroscale temperature of the f phase, ψ^f̄ is the gravitational potential, ς^f̄ is the chemical potential, p^f is the fluid pressure, v^s̄ is the velocity of the solid phase and ${\mathbf{d}}^{\overline{\overline{f}}}$ the rate of strain tensor of the phase $f({\mathbf{d}}^{\overline{\overline{f}}}=\frac{1}{2}\left[\nabla {\mathbf{v}}^{\overline{f}}+{\left(\nabla {\mathbf{v}}^{\overline{f}}\right)}^T\right])$. All of these quantities are macroscale averages.

Consider the variability in volume fraction of the f phase to be small. For this situation, ∇ψ^f̄ + g = 0. Additionally, consider an isothermal case such that the Gibbs-Duhem equation provides ρ^f∇ς^f̄ − ∇p^f = 0. Application of these two conditions to eqn (A.3) reduces it to

$$\frac{{\epsilon }^f}{{\theta }^{\overline{\overline{f}}}}\left({\mathbf{t}}^{\overline{\overline{f}}}+p^f\mathbf{1}\right):{\mathbf{d}}^{\overline{\overline{f}}}-\frac{1}{{\theta }^{\overline{\overline{f}}}}\left[-p^f\nabla {\epsilon }^f+\sum _{\kappa \in {\Im }_{\mathit{\text{cf}}}}\stackrel{\kappa \to f}{\mathbf{T}}\right]·\left({\mathbf{v}}^{\overline{f}}-{\mathbf{v}}^{\overline{s}}\right)\ge 0$$ (A.4)

This equation contains two independent force-flux products. The stipulation that both elements of each product pair must be zero at equilibrium and the requirement that the grouping of terms must be non-negative suggests the linear relations

$$\sum _{\kappa \in {\Im }_{\mathit{\text{cf}}}}\stackrel{\kappa \to f}{\mathbf{T}}-p^f\nabla {\epsilon }^f=-{\mathbf{R}}^f·\left({\mathbf{v}}^{\overline{f}}-{\mathbf{v}}^{\overline{s}}\right)$$ (A.5)

and

$${\mathbf{t}}^{\overline{\overline{f}}}+p^f\mathbf{1}={\mathbf{A}}^f:{\mathbf{d}}^{\overline{\overline{f}}}$$ (A.6)

In the first relation, R^f is a symmetric, positive, semi-definite tensor accounting for the resistance to flow. In the second relation, A^f is fourth order tensor that accounts for the dependence of the stress tensor on the rate of strain. At the macroscale for slow flow, this tensor is taken to be zero such that

$${\mathbf{t}}^{\overline{\overline{f}}}=-p^f\mathbf{1}$$ (A.7)

is the resulting form of the stress tensor. We note that this does not imply that the fluid is inviscid. The effects of viscosity are accounted for at the macroscale by the momentum exchange term $\stackrel{\kappa \to f}{\mathbf{T}}$.

Substitution of the closure relations eqns (A.5) and (A.7) into Eqn (A.2) provides the momentum equation in the form

$${\epsilon }^f\nabla p^f-{\epsilon }^f{\rho }^f{\mathbf{g}}^{\overline{f}}+{\mathbf{R}}^f·\left({\mathbf{v}}^{\overline{f}}-{\mathbf{v}}^{\overline{s}}\right)=0$$ (A.8)

Typically this relation is expressed as

$$-{\mathbf{k}}^f·\left(\nabla p^f-{\rho }^f{\mathbf{g}}^{\overline{f}}\right)={\epsilon }^f\left({\mathbf{v}}^{\overline{f}}-{\mathbf{v}}^{\overline{s}}\right)$$ (A.9)

Where K^f = (ε^f)² (R^f)⁻¹ is called the hydraulic conductivity.

The hydraulic conductivity depends on the properties of both the flowing fluid and the solid porous material. For an isotropic medium, K^f = K^f 1. The morphology and topology of the solid media are important in determining the hydraulic conductivity of the cellular solid phases. The conductivity is influenced by the cell size distribution, shape of the cells, tortuosity of passages, specific surface area, and porosity (the sum of the fluid volume fractions). It also depends on the density and viscosity of the fluid. Neglecting gravity in eqn (A.8) yields eqn (16).

Appendix B. Coefficients of the matrices appearing in equation (41)

In the following equations K^s is the Bulk modulus of the solid skeleton and $\frac{\partial {\mathbf{e}}_{\mathit{\text{sw}}}^s}{\partial t}=\frac{\mathbf{1}}{3K^s}\frac{\partial p^s}{\partial t}$.

$${\mathbf{C}}_{\mathit{\text{nn}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_n^T\left(\epsilon S^l{\mathbf{N}}_n\right)d\mathrm{\Omega }$$ (B.1)

$${\mathbf{C}}_{\mathit{\text{tt}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_t^T\left[\epsilon {\mathbf{N}}_t+\frac{S^t}{K^s}\left(S^t\frac{\partial p^t}{\partial S^t}+S^h\frac{\partial p^h}{\partial S^t}+p^t-p^l\right){\mathbf{N}}_t\right]d\mathrm{\Omega }$$ (B.2)

$${\mathbf{C}}_{\mathit{\text{th}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_t^T\left[\frac{S^t}{K^s}\left(S^t\frac{\partial p^t}{\partial S^h}+S^h\frac{\partial p^h}{\partial S^h}+p^h-p^l\right){\mathbf{N}}_h\right]d\mathrm{\Omega }$$ (B.3)

$${\mathbf{C}}_{\mathit{\text{tl}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_t^T\left[\frac{S^t}{K^s}\left(S^t\frac{\partial p^t}{\partial p^l}+S^h\frac{\partial p^h}{\partial p^l}+S^l\right){\mathbf{N}}_l\right]d\mathrm{\Omega }$$ (B.4)

$${\mathbf{C}}_{\mathit{\text{ht}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_h^T\left[\frac{S^h}{K^s}\left(S^t\frac{\partial p^t}{\partial S^t}+S^h\frac{\partial p^h}{\partial S^t}+p^t-p^l\right){\mathbf{N}}_t\right]d\mathrm{\Omega }$$ (B.5)

$${\mathbf{C}}_{\mathit{\text{hh}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_h^T\left[\epsilon {\mathbf{N}}_h+\frac{S^h}{K^s}\left(S^t\frac{\partial p^t}{\partial S^h}+S^h\frac{\partial p^h}{\partial S^h}+p^h-p^l\right){\mathbf{N}}_h\right]d\mathrm{\Omega }$$ (B.6)

$${\mathbf{C}}_{\mathit{\text{hl}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_h^T\left[\frac{S^h}{K^s}\left(S^t\frac{\partial p^t}{\partial p^l}+S^h\frac{\partial p^h}{\partial p^l}+S^l\right){\mathbf{N}}_l\right]d\mathrm{\Omega }$$ (B.7)

$${\mathbf{C}}_{\mathit{\text{lt}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_l^T\left[\frac{1}{K^s}\left(S^t\frac{\partial p^t}{\partial S^t}+S^h\frac{\partial p^h}{\partial S^t}+p^t-p^l\right){\mathbf{N}}_l\right]d\mathrm{\Omega }$$ (B.8)

$${\mathbf{C}}_{\mathit{\text{lh}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_l^T\left[\frac{1}{K^s}\left(S^t\frac{\partial p^t}{\partial S^h}+S^h\frac{\partial p^h}{\partial S^h}+p^h-p^l\right){\mathbf{N}}_h\right]d\mathrm{\Omega }$$ (B.9)

$${\mathbf{C}}_{\mathit{\text{ll}}}={\int }_{\mathrm{\Omega }}{\mathbf{N}}_l^T\left[\frac{1}{K^s}\left(S^t\frac{\partial p^t}{\partial p^l}+S^h\frac{\partial p^h}{\partial p^l}+S^l\right){\mathbf{N}}_l\right]d\mathrm{\Omega }$$ (B.10)

$${({\mathbf{C}}_{\mathit{\text{uu}}})}_{\mathit{\text{ij}}}=-{\int }_{\mathrm{\Omega }}{\mathbf{B}}^{\mathrm{T}}{\mathbf{D}}_s\mathbf{B}d\mathrm{\Omega }$$ (B.11)

$${\mathbf{K}}_{\mathit{\text{nn}}}={{\int }_{\mathrm{\Omega }}(\nabla {\mathbf{N}}_n)}^{\mathrm{T}}\left(\epsilon S^l{D}_{\mathit{\text{eff}}}^{\overline{\mathit{\text{nl}}}}\nabla {\mathbf{N}}_n\right)d\mathrm{\Omega }$$ (B.12)

$${\mathbf{K}}_{\mathit{\text{tt}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_t)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{\mathit{\text{ts}}}}{{\mu }^t}\frac{\partial p^t}{\partial S^t}\nabla {\mathbf{N}}_t\right)d\mathrm{\Omega }$$ (B.13)

$${\mathbf{K}}_{\mathit{\text{th}}}={\int }_{\mathrm{\Omega }}{(\nabla N_t)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{\mathit{\text{ts}}}}{{\mu }^t}\frac{\partial p^t}{\partial S^h}\nabla {\mathbf{N}}_h\right)d\mathrm{\Omega }$$ (B.14)

$${\mathbf{K}}_{\mathit{\text{tl}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_t)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{\mathit{\text{ts}}}}{{\mu }^t}\frac{\partial p^t}{\partial p^l}\nabla {\mathbf{N}}_l\right)d\mathrm{\Omega }$$ (B.15)

$${\mathbf{K}}_{\mathit{\text{ht}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_h)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\frac{\partial p^h}{\partial S^t}\nabla {\mathbf{N}}_t\right)d\mathrm{\Omega }$$ (B.16)

$${\mathbf{K}}_{\mathit{\text{hh}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_h)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\frac{\partial p^h}{\partial S^h}\nabla {\mathbf{N}}_h\right)d\mathrm{\Omega }$$ (B.17)

$${\mathbf{K}}_{\mathit{\text{hl}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_h)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\frac{\partial p^h}{\partial p^l}\nabla {\mathbf{N}}_l\right)d\mathrm{\Omega }$$ (B.18)

$${\mathbf{K}}_{\mathit{\text{lt}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_l)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{\mathit{\text{ts}}}}{{\mu }^t}\frac{\partial p^t}{\partial S^t}\nabla {\mathbf{N}}_t+\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\frac{\partial p^h}{\partial S^t}\nabla {\mathbf{N}}_t\right)d\mathrm{\Omega }$$ (B.19)

$${\mathbf{K}}_{\mathit{\text{lh}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_l)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{\mathit{\text{ts}}}}{{\mu }^t}\frac{\partial p^t}{\partial S^h}\nabla {\mathbf{N}}_h+\frac{k_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\frac{\partial p^h}{\partial S^h}\nabla {\mathbf{N}}_h\right)d\mathrm{\Omega }$$ (B.20)

$${\mathbf{K}}_{\mathit{\text{ll}}}={\int }_{\mathrm{\Omega }}{(\nabla {\mathbf{N}}_l)}^{\mathrm{T}}\left(\frac{k_{\mathit{\text{rel}}}^t{\mathbf{k}}^{\mathit{\text{ts}}}}{{\mu }^t}\frac{\partial p^t}{\partial p^l}\nabla {\mathbf{N}}_l+\frac{{\mathbf{k}}_{\mathit{\text{rel}}}^h{\mathbf{k}}^{\mathit{\text{hs}}}}{{\mu }^h}\frac{\partial p^h}{\partial p^l}\nabla {\mathbf{N}}_l+\frac{k_{\mathit{\text{rel}}}^l{\mathbf{k}}^{\mathit{\text{ls}}}}{{\mu }^l}\nabla {\mathbf{N}}_l\right)d\mathrm{\Omega }$$ (B.21)

$${\mathbf{f}}_n={\int }_{\mathrm{\Omega }}{\mathbf{N}}_n^T\left(\frac{1}{\rho }\left({\omega }^{\overline{\mathit{\text{nl}}}}\stackrel{l\to t}{M}-\stackrel{\mathit{\text{nl}}\to t}{M}\right)-\epsilon S^l{\mathbf{v}}^{\overline{l}}·\nabla {\omega }^{\overline{\mathit{\text{nl}}}}\right)d\mathrm{\Omega }$$ (B.22)

$${\mathbf{f}}_t={\int }_{\mathrm{\Omega }}{\mathbf{N}}_t^T\left[\frac{1}{\rho }\underset{\mathit{\text{growth}}}{\overset{l\to t}{M}}-S^t\text{tr}\left(\frac{\partial {\mathbf{e}}^s}{\partial t}-\frac{\partial {\mathbf{e}}_{\mathit{\text{sw}}}^s}{\partial t}\right)-\nabla (S^t)·\left(\epsilon \frac{\partial {\mathbf{u}}^s}{\partial t}\right)\right]d\mathrm{\Omega }$$ (B.23)

$${\mathbf{f}}_h={\int }_{\mathrm{\Omega }}{\mathbf{N}}_h^T\left[-S^h\text{tr}\left(\frac{\partial {\mathbf{e}}^s}{\partial t}-\frac{\partial {\mathbf{e}}_{\mathit{\text{sw}}}^s}{\partial t}\right)-\nabla (S^h)·\left(\epsilon \frac{\partial {\mathbf{u}}^s}{\partial t}\right)\right]d\mathrm{\Omega }$$ (B.24)

$${\mathbf{f}}_l={\int }_{\mathrm{\Omega }}{\mathbf{N}}_l^T\left[-\text{tr}\left(\frac{\partial {\mathbf{e}}^s}{\partial t}-\frac{\partial {\mathbf{e}}_{\mathit{\text{sw}}}^s}{\partial t}\right)\right]d\mathrm{\Omega }$$ (B.25)

$${\mathbf{f}}_u={\int }_{\mathrm{\Omega }}{\mathbf{B}}^T\left({\mathbf{D}}_s\frac{\partial {\mathbf{e}}_{\mathit{\text{vp}}}^s}{\partial t}\right)d\mathrm{\Omega }+{\int }_{\Omega }{\mathbf{B}}^T\left({\mathbf{D}}_s\frac{\partial {\mathbf{e}}_{\mathit{\text{sw}}}^s}{\partial t}\right)d\mathrm{\Omega }$$ (B.26)

Appendix C. Nomenclature

Abbreviation
eqn.	equation
eqs	equations
REV	Representative Elementary Volume
TCAT	Thermodynamically Constrained Averaging Theory

Roman letters
A α	fourth order tensor that accounts for the stress-rate of strain relationship
a	coefficient for the interpolation of the growth curve
aα	adhesion of the phase α
b	exponent in the pressure-saturations relationship
C ij	non linear coefficient of the discretized capacity matrix
${\mathbf{d}}^{\overline{\overline{\alpha }}}$	rate of strain tensor
$D_{\mathit{\text{eff}}}^{\overline{\mathit{\text{il}}}}$	diffusion coefficient for the species i dissolved in the phase l
$D_{\mathit{\text{eff}}}^{\overline{\mathit{\text{il}}}}$	effective diffusion coefficient for the species i dissolved in the phase l
D s	tangent matrix of the solid skeleton
e s	total strain tensor
${\mathbf{e}}_{\mathit{\text{el}}}^s$	elastic strain tensor
${\mathbf{e}}_{\mathit{\text{vp}}}^s$	visco-plastic strain tensor
${\mathbf{e}}_{\mathit{\text{sw}}}^s$	swelling strain tensor
f v	discretized source term associated to the primary variable v
H	Heaviside step function
K ij	non linear coefficient of the discretized conduction matrix
k αs	absolute permeability tensor of the phase α
$k_{\mathit{\text{rel}}}^{\alpha }$	relative permeability of the phase α
N v	vector of shape functions related to the primary variable v
pα	pressure in the phase α
$p_{\mathit{\text{crit}}}^t$	tumor pressure above which growth is inhibited
$p_{\mathit{\text{necr}}}^t$	tumor pressure above which stress causes an increase of the death rate
r ∞	coefficient for the interpolation of the growth curve: tumor radius at sufficiently large time
rsph	radius of the spheroid
rnc	radius of the necrotic core
R α	resistance tensor
Sα	saturation degree of the phase α
${\mathbf{t}}_{\mathit{\text{eff}}}^{\overline{\overline{s}}}$	effective stress tensor of the solid phase s
${\mathbf{t}}_{\mathit{\text{tot}}}^{\overline{\overline{s}}}$	total stress tensor of the solid phase s
u s	displacement vector of the solid phase s
x	solution vector

Greek letters
ᾱ	Biot's coefficient
β	coefficient for the interpolation of the growth curve
${\gamma }_{\mathit{\text{growth}}}^t$	growth coefficient
${\gamma }_{\mathit{\text{necrosis}}}^t$	necrosis coefficient
${\gamma }_{\mathit{\text{growth}}}^{\overline{\mathit{\text{nl}}}}$	nutrient consumption coefficient related to growth
${\gamma }_0^{\overline{\mathit{\text{nl}}}}$	nutrient consumption coefficient not related to growth
${\theta }^{\overline{\overline{\alpha }}}$	macroscale temperature of the phase α
δ	exponent in the effective diffusion function for the oxygen
${\delta }_a^t$	additional necrosis induced by pressure excess
δliving	coefficient for the interpolation: thickness of the viable rim of tumor cells
ε	porosity
εα	volume fraction of the phase α
μα	dynamic viscosity of the phase α
ρα	density of the phase α
σc	coefficient in the pressure-saturations relationship
ςα¯	chemical potential
Ψα¯	gravitational potential
χα	solid surface fraction in contact with the phase α
${\omega }^{N\overline{t}}$	mass fraction of necrotic cells in the tumor cells phase
${\omega }^{\overline{\mathit{\text{nl}}}}$	nutrient mass fraction in liquid.
${\omega }_{\mathit{\text{crit}}}^{\overline{\mathit{\text{nl}}}}$	critical nutrient mass fraction in liquid for growth
${\omega }_{\mathit{\text{env}}}^{\overline{\mathit{\text{nl}}}}$	reference nutrient mass fraction in the environment

TCAT symbols
$\stackrel{\kappa \to \alpha }{M}$	inter-phase mass transfer
ε α r iα	reaction term i.e. intra-phase mass transfer
$\stackrel{\kappa \to \alpha }{\mathbf{T}}$	inter-phase momentum transfer

Subscripts and superscripts
crit	critical value for growth
n	nutrient
h	host cell phase
l	interstitial fluid
necr	critical value for the effect of pressure on the cell death rate
s	solid
t	tumor cell phase
α	phase indicator with α=t,h,l, or s