Integration of visual motion and locomotion in mouse visual cortex

Abstract

Successful navigation through the world requires accurate estimation of one’s own speed. To derive this estimate, animals integrate visual speed gauged from optic flow and run speed gauged from proprioceptive and locomotor systems. The primary visual cortex (V1) carries signals related to visual speed, and its responses are also affected by run speed. To study how V1 combines these signals during navigation, we recorded from mice that traversed a virtual environment. Nearly half of the V1 neurons were reliably driven by combinations of visual speed and run speed. These neurons performed a weighted sum of the two speeds. The weights were diverse across neurons, and typically positive. As a population, V1 neurons predicted a linear combination of visual and run speed better than visual or run speeds alone. These data indicate that V1 in the mouse participates in a multimodal processing system that integrates visual motion and locomotion during navigation.

Introduction

There is increasing evidence that the activity of the primary visual cortex (V1) is determined not only by the patterns of light falling on the retina¹, but also by multiple non-visual factors. These factors include sensory input from other modalities^2,3, the allocation of spatial attention⁴, and the likelihood of an impending reward⁵.

In mice, in particular, the firing of V1 neurons shows strong changes with locomotion^6-8, but the precise form and function of this modulation are unclear. One possibility is that locomotion simply changes the gain of V1 neurons, increasing their responses to visual stimuli when animals are running compared to stationary⁶. Another possibility is that V1 neurons respond to the mismatch between what is seen by the animal and what is expected based on locomotion⁷. Overall, the computational function of locomotor inputs to V1 is still a mystery. Might they be useful for navigation?

One of the primary roles of vision is to help animals navigate. Successful navigation requires an accurate estimate of one’s own speed^9-11. To obtain this estimate, animals and humans integrate a measure of speed gauged from optic flow with one gauged from the proprioceptive and locomotor systems^9-15. Neural correlates of locomotor speed have been found in high-level structures such as the hippocampus^16,17, but the neural substrates in which multiple input streams are integrated to produce speed estimates are as yet unknown.

Integration of multiple inputs has been observed in several neural circuits^15,18-20, and typically involves intermediate neuronal representations^21-24. In early processing, the input streams are integrated into a distributed population code, in which the two signals are weighted differently by different neurons^21,24. Such an intermediate representation allows the integrated signal to be read out by higher level structures. Furthermore, properties of this intermediate representation (such as the statistical distribution of weights used by different neurons) are not random but adapted to the specific integration that must be performed^21,25.

Here we studied how visual and locomotion signals are combined in mouse V1, using a virtual reality system in which visual input was either controlled by, or independent of locomotion. We found that most V1 neurons respond to locomotion even in the dark. The dependence of these responses on running speed was gradual, and in many cells it was non-monotonic. In the presence of visual inputs, most V1 neurons that were responsive encoded a weighted sum of visual motion and locomotor signals. The weights differed across neurons, and were typically positive. As a population, V1 encoded positively weighted averages of speed derived from visual and locomotor inputs. We suggest that such a representation facilitates self-motion computations, contributing to the estimation of an animal’s speed through the world.

Results

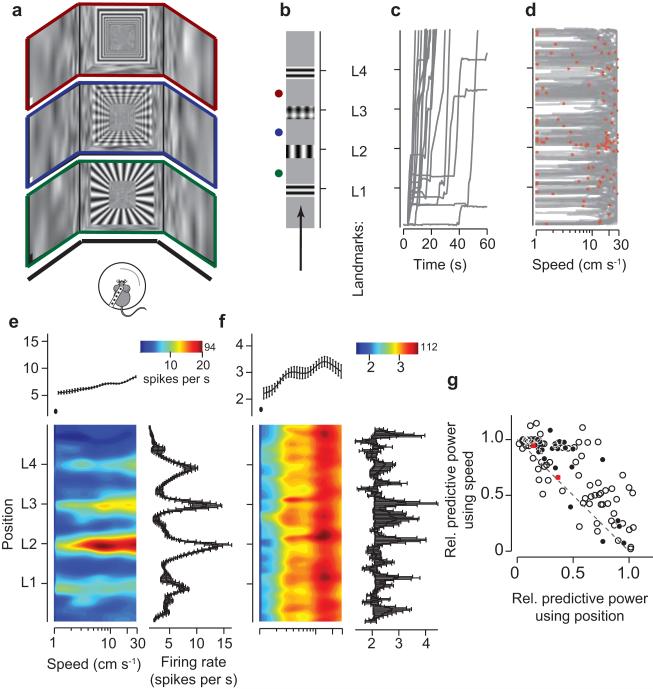
To study the effects of visual motion and locomotion, we recorded from mouse V1 neurons in a virtual environment based on an air-suspended spherical treadmill^26,27. The virtual environment was a corridor whose walls, ceiling and floor were adorned with a white-noise pattern (Fig. 1a). Four prominent landmarks – three gratings and a plaid – were placed at equal distances along the corridor (Fig. 1b). Head-fixed mice viewed this environment on three computer monitors arranged to cover 170° of visual angle (Fig. 1a), and traversed the corridor voluntarily by running on the treadmill at speeds of their own choosing (Fig. 1c, d & Supplementary Fig. 1).

Figure 1. Neuronal responses in V1 are strongly influenced by speed.

a. Examples of visual scenes seen by the animal during virtual navigation. b. The virtual environment was a corridor with four landmarks (three gratings and one plaid). Movement in the environment was restricted to the forward direction. Dots indicate the positions of the example scenes in a. c. The paths taken by an animal in 15 runs through the corridor. d. The same paths expressed in terms of speed at each position. Red dots: spikes generated by a V1 neuron. e-f. The firing rate of two neurons as a function of animal position and speed. Right: Dependence of firing rate on position alone. Top: Dependence of firing rate on speed alone; the leftmost point corresponds to all speeds ≤ 1 cm/s. Error bars are the standard deviation over different training sets. g. The relative power using position alone (Q_P/Q_PS) and speed alone (Q_S/Q_PS) to predict firing rate. The dotted line denotes Q_P + Q_S = Q_PS. Red dots indicate neurons in e and f. Solid dots indicate well isolated single units. Example neurons shown here and in all figures are all well-isolated units.

While the mice traversed this environment, we recorded from populations of V1 neurons with multisite electrodes and identified the spike trains of single neurons and multi-unit activity with a semi-automatic spike sorting algorithm²⁸ (Supplementary Fig. 2). We then used grating stimuli to measure the receptive fields of the neurons (receptive field size 24 ± 2 °, s.e., n = 81, receptive field centers 10°-70° azimuth, semi-saturation contrast 23 ± 3%, s.e., n = 38).

To measure the features that influenced neural activity in the virtual environment, we adopted a technique previously used for analysis of hippocampal place cells^29,30. For each neuron, we estimated the firing rate as a function of one or more predictor variables (e.g. speed alone, position alone, or both speed and position). Using a separate data segment (the “test set”), we defined a prediction quality measure Q as the fraction of the variance of the firing rate explained by the predictor variables. This measure of prediction quality does not require that stimuli be presented multiple times (Supplementary Fig. 3), a key advantage when analyzing activity obtained during self-generated behavior.

We first measured V1 responses in a closed-loop condition, where the virtual environment was yoked to running speed and thus faithfully reflected the movement of the animal in the forward direction. For each neuron, we computed our ability to predict the firing rate based on position alone (Q_P), on speed alone (Q_S), and on both position and speed (Q_PS: Supplementary Figs. 4 and 5). The responses of most V1 neurons (181/194) were predictable based on both the position and speed in the environment (Q_PS>0; Supplementary Fig. 5). Here we concentrate on 110 of these neurons whose firing rates were particularly predictable (Q_PS>0.1). Some of these neurons (51/110) showed clear modulation in firing rate as a function of position (Q_P>0.1). This tuning for position was expected due to the different visual features present along the corridor, and indeed neurons often responded most strongly as the animal passed the visual landmarks (Fig. 1e, Supplementary Fig. 5). The response of most neurons (81/110) also showed a clear dependence on speed (Q_S > 0.1). Typically, speed explained a larger fraction of the response than position (75/110 cells with Q_S> Q_P, Fig. 1g). Indeed, for many neurons the responses were as well predicted by speed alone as by speed and position together (Q_S/Q_PS ~ 1, Fig. 1g and Supplementary Fig. 5). Speed, therefore, exerts a powerful influence on the responses of most V1 neurons in the virtual environment.

But what kind of speed is exerting this influence? In virtual reality, the speed at which the virtual environment moves past the animal (virtual speed) is identical to the speed with which the animal runs on the air-suspended ball (run speed). Neurons in V1 can gauge virtual speed through visual inputs, but to gauge run speed they must rely on non-visual inputs. These could include sensory input from proprioception, and top-down inputs such as efference copy from the motor systems. Ordinarily, virtual and run speeds are identical, so their effects on V1 cannot be distinguished.

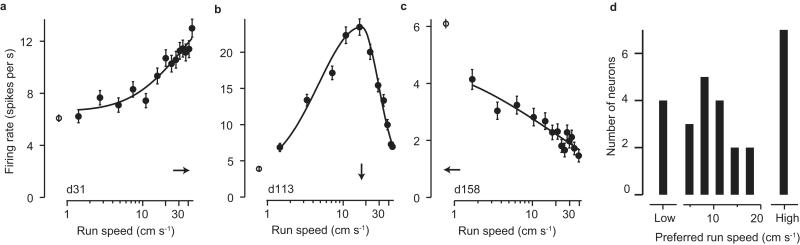
One way to isolate run speed from virtual speed is simply to eliminate the visual input. To do this, we turned off the monitors and occluded all other sources of light, and thus measured responses to run speed in the dark. Running influenced the activity of many V1 neurons even in this dark environment (39/55 well-isolated neurons were significantly modulated, p<0.001) modulating their activity by 50% to 200% (Supplementary Fig. 6). The dependence of firing rate on run speed was graded, rather than a simple binary switch between different rates in stationary and running periods (Fig. 2a-c). Indeed, among the neurons modulated by running, most (27/39) showed a significant (p<0.001) dependence on run speed even when we excluded stationary periods (run speed < 1 cm/s). About half of these neurons (16/27) showed a band-pass tuning characteristic, responding maximally to a particular run speed (Fig. 2b,d; Supplementary Fig. 7); in the rest, firing rate showed either a monotonic increase with run speed (Fig. 2a, 7/27 neurons), or a monotonic decrease with run speed (Fig. 2c, 4/27 neurons). Similar results were obtained when the monitors were turned on but displayed a uniform gray screen (not shown). Thus, the responses of V1 neurons depend smoothly and in diverse ways on the speed at which the animal runs, even in the absence of visual inputs.

Figure 2. Tuning of V1 neurons for run speed in the dark.

a-c. Dependence of firing rate on run speed for three V1 neurons measured in the dark. Error bars indicate 2 s.e. The sampling bins were spaced to have equal numbers of data points; curves are fits of a descriptive function (see Methods). Arrows indicate the speed at the maximal response, and open circles the firing rates when the animal was stationary. d. The preferred run speed (peak of the best fit curve) for the neurons that show a significant non-binary modulation of firing rate as a function of run speed (n = 27 well-isolated neurons). Neurons where the preferred speed was <2 cm/s are considered low-pass (Low; example in c); neurons where the preferred speed was >25 cm/s are considered high-pass (High; example in a), while the remainder are considered bandpass (example in b).

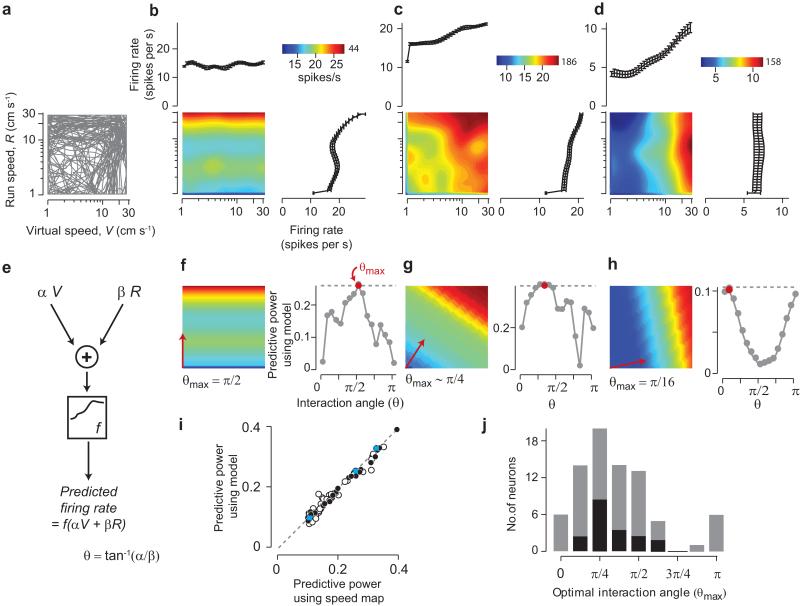
To understand how run speed affects V1 responses to visual stimuli, we reconfigured the virtual reality environment into an open-loop condition. In this condition we simply replayed movies of previous closed-loop runs, irrespective of the animal’s current run speed. Whereas in the closed-loop condition virtual speed and run speed were always equal, in the open-loop condition the animal went through the virtual environment at different combinations of virtual and run speeds (Fig. 3a). We could investigate the influence of both speeds because the mice did not attempt to adjust their running based on visual inputs: there was little correlation between run speed and virtual speed (r = 0.07 ± 0.05). Similarly, V1 neurons did not modify their responses in the two conditions: when the two speeds happened to match during open-loop, V1 responses were similar to those measured in closed-loop (Supplementary Fig. 8). We therefore used the open-loop responses to measure the effects and interactions of the two speeds.

Figure 3. V1 Neurons are tuned for a weighted sum of run speed and virtual speed.

a. Some paths in virtual speed and run speed taken by an animal in the open-loop condition. b-d. “Speed maps” showing firing rate of three example neurons as a function of virtual speed and run speed. Right: Dependence of firing rate on run speed alone. Top: Dependence of firing rate on virtual speed alone. e. In the weighted sum model, firing rate is a nonlinear function f of a weighted sum of virtual speed V and run speed R. The weights α and β are summarized by a single interaction angle θ = tan⁻¹(α/β). f-h. The model captures the main features of the full speed maps (left; compare to b-d). Right: the model’s predictive power as a function of θ. The optimal interaction angle θ_max is highlighted in red and indicated as a vector in the left panel. The dashed line represents the predictive power of the original speed map. i. Comparison of predictive power using the weighted sum model (Q_model) at the optimal interaction angle (θ_max), to that using the speed map (Q_RV). Dotted line indicates equal performance. Blue points mark the examples in f-h. Solid dots indicate well-isolated units. j. Distribution of optimal interaction angles θ_max across neurons. The black bars indicate the distribution for well-isolated units.

In the open-loop condition, V1 responses were modulated by both run speed and virtual speed. Some neurons were strongly influenced by virtual speed (Fig. 3c,d; 28/173 with Q_V > 0.1); this was expected because translation of the virtual corridor causes strong visual motion across the retina, and visual motion is a prime determinant of V1 responses. The responses of many neurons were also modulated by run speed (39/173 with Q_R > 0.1; Fig. 3b-d). This modulation was not due to eye movements (Supplementary Fig. 9). As in the absence of visual stimuli, responses varied smoothly with run speed. Indeed, firing rates were better predicted by a smooth function of speed, than by a binary function with one value each for the stationary and running conditions (Q_binary< Q_R: p < 10⁻⁸, sign-rank test).

There was no obvious relationship, however, between tuning for virtual speed and for run speed (Supplementary Figure 10); rather, the firing of most cells appeared to depend on the two speeds in combination, with different cells performing different combinations. To study these combinations, for each neuron we derived a “speed map”, an optimally smoothed estimate of the response at each combination of run and virtual speeds (Fig. 3b-d). Predictions of the firing rates based on these speed maps were superior to predictions based on either speed alone (Q_RV> max(Q_R,Q_V): p < 10⁻¹¹; sign-rank test). In total, 73/173 neurons were driven by some combination of virtual and run speeds (Q_RV > 0.1) and were selected for further analysis.

To summarize and quantify how a neuron’s firing rate depends on virtual speed and run speed, we adopted a simple model based on a weighted sum of the two speeds. This model requires a single parameter θ, the “interaction angle” determined by the two weights, and a nonlinear function f that operates on the weighted sum (Fig. 3e). We found that the modeled responses not only visually resembled the original speed maps (Fig. 3f-h), but also provided cross-validated predictions of the spike trains that were almost as accurate as those based on the original two-dimensional speed map (Fig. 3i, Q_map - Q_model = 0.006 ± 0.002). Therefore, each neuron’s responses depend on a linear combination of virtual speed and run speed.

To study the relative weighting that neurons give to virtual and run speed, we estimated for each neuron the optimal interaction angle θ_max that gave the best cross-validated prediction of its spike trains. This angle ranges from 0 to π, and describes the linear combination of speeds best encoded by each neuron. The most common value of θ_max, seen in about half of the neurons (34/73), was θ_max ≈ π/4, indicating that these neurons responded to an equal weighting of run and virtual speeds. Among the other neurons, some were selective for run speed only (27/73 neurons with θ_max ≈ π/2; Fig. 3j), and a few for virtual speed only (6/73 with θ_max ≈ 0). Even fewer neurons (5/73) were selective for the difference between virtual speed and run speed (θ_max ≈ 3π/4), which measures the mismatch between locomotion and visual motion⁷. Overall, the relative weighting of virtual speed and run speed varied between neurons, but showed a clear preference for equal weighting.

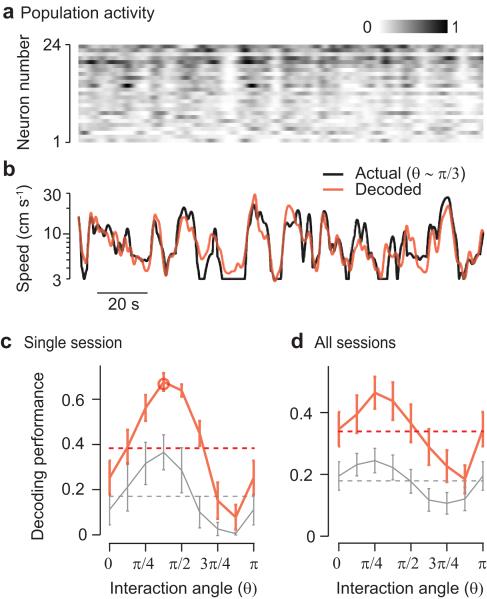
The fact that V1 neurons encode diverse combinations of run and virtual speed suggests that a downstream area could read out from the population of V1 neurons diverse combinations of visual and non-visual information. To investigate these population-level consequences of the single-neuron properties, we applied a decoding method to the spike data, aiming to infer the combination of run speed and virtual speed that had generated the data. We used the activity of simultaneously recorded V1 neurons (Fig. 4a) to estimate different linear combinations of run and virtual speeds, parameterized by the interaction angle. For example, to test whether the V1 population encodes a given combination of run and virtual speed (θ = π/3) we asked whether the decoder could predict this particular combination as a function of time (Fig. 4b), based on parameters obtained from a separate training set. The quality of the prediction depended on the linear combination of speeds being predicted (Fig. 4c, d). The combination that was decoded best had positive and approximately equal weighting of the two speeds (at θ ≈ π/4, circular mean = 52°). By contrast, virtual speed (θ ≈ 0 or π) and run speed (θ ≈ π/2) were decoded less precisely. The difference between the speeds (θ_max ≈ 3π/4) was predicted least precisely of all (circular-linear correlation p<10⁻³, Fig. 4c, d).

Figure 4. V1 population activity encodes positive combinations of virtual and run speed.

a. The activity of 24 V1 neurons during an epoch of open-loop navigation, represented as a grayscale map. The firing rate of each neuron was normalized for illustration purposes. b. Population activity was used to predict linear combinations of run speed and virtual speed using a linear decoder that was trained and evaluated on separate parts of the dataset. The black curve shows a weighted average of virtual speed and run speed (interaction angle θ ~ π/3), and the red curve its prediction from population activity, for the same epoch as in a. c. Performance of the population decoder as a function of interaction angle (θ), for a single experimental session. Error bars are s.e. across 5 runs of cross-validation. The dotted line indicates the mean performance across all interaction angles. The highlighted point indicates the example shown in b. The gray curve shown the performance when the decoding is restricted to periods when both virtual speed and run speed were > 3 cm/s. d. Decoding performance as a function of θ across recording sessions. Error bars are s.e. across sessions.

To assess the robustness of these results, we performed various additional tests. First, we established that these results did not overly rely on responses measured during stationary conditions. To do this, we restricted the decoding to epochs when both run speed and virtual speed were > 3 cm/s, and we found a similar dependence of decoding performance on interaction angle (gray curves of Fig. 4c,d: circular mean = 42°; circular-linear correlation p<0.01; the reduction in decoding performance in the restricted analysis suggests that the population encodes both smooth changes of speed and binary changes: stationary vs. moving). Second, we ensured that these results did not depend on the precise choice of decoding algorithm. Indeed, the same dependence of decoding performance on interaction angle was observed with two alternative decoders (Supplementary Fig. 11). Finally, we asked whether these results reflect the distribution of optimal interaction angles that we have measured. We used simulations of V1 populations with different distributions of interaction angles (Supplementary Fig. 12). We could replicate the profile of decoding performance present in the data only when the distribution of interaction angles in the simulated population resembled that of the real population (Supplementary Fig. 12c-j).

The population of V1 neurons therefore encodes positively-weighted linear combinations of run speed and virtual speed more accurately than virtual speed or run speed alone.

Discussion

Measuring activity in visual cortex in a virtual reality environment revealed a number of interactions between visual motion and locomotion. First, we replicated the observation that running affects V1 responses^6,7, even in the absence of visual stimuli, and we extended it by showing that these responses vary smoothly and often non-monotonically with run speed. Further, we found that V1 neurons typically respond to combinations of run speed (gauged from locomotor and proprioceptive systems) and visual speed (gauged from optic flow). This combination of run speed and visual speed is simply a weighted sum, with weights varying across neurons. Most neurons gave positive weights to visual and run speeds. Accordingly, the population of V1 neurons was most informative as to positively weighted linear combinations of run and visual speeds.

The fact that V1 integrates locomotor and visual signals in this manner suggests that it may be an early stage of a pathway for estimating an animal’s speed through the world, which can then help functions such as navigation. However, two alternative hypotheses have also been suggested for the presence of run speed signals in V1.

A first alternative hypothesis is that locomotion simply changes the gain of V1 sensory responses, without affecting the selectivity of visual neurons. In support of this hypothesis are observations that locomotion scales, but does not modify, the visual preferences of V1 neurons⁶. Our data are not fully consistent with this interpretation for multiple reasons. First, we and others⁷, find responses to run speed even in the absence of visual stimuli, suggesting that locomotor signals provide a drive to V1 neurons, and not just a modulation of visual responses. Also, there is evidence that even the visual preferences of V1 neurons (particularly preferred stimulus size) can be altered by locomotion⁸. Further, we found that responses to running were different across neurons, inconsistent with modulation of an entire visual representation by a single locomotor-dependent gain function. Previous data appeared to suggest that the effect of locomotion was binary⁶, as would be expected if running caused a discrete change in cortical state³¹. However, we found that a binary model did not predict the firing rate responses as well as a continuous dependence on firing rate. Our data therefore indicate that locomotor effect on the responses of V1 neurons go well beyond a uniform difference in gain between running and stationary animals.

A second alternative hypothesis holds that V1 signals the mismatch between actual visual stimuli and those that should have been encountered given the locomotion. This explanation fits the theoretical framework of predictive coding³², and is supported by a recent report using two-photon imaging of superficial V1 neurons⁷. By exploring all combinations of run speed and visual speed, however, we found that only a small minority of V1 neurons (5/73) were selective for mismatch. Perhaps this discrepancy results from different selection biases in the two recording methods: while our silicon probe recordings primarily recorded neurons from the deeper layers of cortex, two-photon imaging reports only neurons from layer 2/3; the possibility that prediction errors are specifically encoded in superficial layers has in fact been suggested by computational models³³. However, a more likely reason may be differences in stimulus design. We avoided sudden perturbations of the visual stimulus, while the previous study⁷ specifically focused on such sudden perturbations. Such perturbations may trigger a change in alertness and often evoked behavioral response (slowing down) in their study. Behavior can evoke calcium responses in sensory cortex^34,35, making it hard to disambiguate the influence of sensory mismatch from its behavioral consequences. Thus, the lack of sudden perturbations of the visual stimulus in our experiments might explain the differences in the observations.

What circuit mechanisms might underlie the effects we describe? The effects of locomotion on visual cortical processing may involve neuromodulators such as norepinephrine³⁶. Our data are not inconsistent with this possibility, although the smooth (and sometimes bandpass) modulation of firing with running speed would require the neuromodulatory signal to encode speed in an analog manner. Furthermore the diverse effects of running we observed across neurons would suggest a diverse prevalence of receptors or circuit connections underlie the tuning for run speed. These receptors or circuits are most likely the same that support the effects of locomotion on spatial integration: locomotion can affect size-tuning, preferentially enhancing responses to larger stimuli⁸. This finding is compatible with our current results, but not sufficient to predict them; for example, the tuning for run speed that we observed here in the dark certainly could not be predicted by changes in spatial integration.

In our experiments we recorded from animals that navigated a familiar environment, in which the distance between the animal and the virtual wall (equivalently, the gain of the virtual reality system) was held constant. The mice had experienced at least three training sessions in closed-loop mode before recording, which would be sufficient for the hippocampus to form a clear representation of the virtual environment¹⁵, and are presumably sufficient for the animal to learn the stable mapping between movements and visual flow. In a natural environment, however, an animal’s distance to environmental landmarks can rapidly change. Such changes can lead to rapid alteration in visuo-motor gain, accompanied by changes in neural activity at multiple levels, as demonstrated for instance in zebrafish³⁷. Furthermore, both animal behavior and neural representations can adjust to the relative noise levels of different input streams, in a manner reminiscent of Bayes-optimal inference^19,38. In the case of mouse navigation, such changes should cause a reweighting of run and visual speeds in the estimation of an animal’s own running velocity. Such a reweighting could occur through alteration of the V1 representation, by changing the distribution of weights of visual and running speed to center around a new optimal value. Alternatively, however, such changes could occur outside of V1. The latter possibility is supported by the fact that the representation we observed in V1 allows readouts of a wider range of run-visual mixtures than a simulated population in which all neurons encoded a single interaction angle (Supplementary Fig. 12). Further experiments will be required to distinguish these possibilities. We also note that, while head-fixed animals are certainly capable of navigation in virtual reality^15,27,39-41, animals that are not head fixed gain an important cue for speed estimation from the vestibular system. To understand how this vestibular signal affects integration of visual and locomotor information requires further recordings from V1 neurons in freely moving animals^42,43.

Our results suggest that the function of mouse visual cortex may be more than just vision. Indeed, a growing body of evidence suggests that neocortical areas are not specific to a single function, and that neurons of even primary sensory cortices can respond to a wide range of multimodal stimuli and non-sensory features^2,3,5,44,45. Our results provide a striking example of such integration, and suggest an ethological benefit it may provide to the animal. Estimation of speed through the world is a critical function for navigation and is achieved by integrating inputs from the visual system with locomotor variables. Our data indicate that, at least in the mouse, this integration occurs as early as primary visual cortex.

Online Methods

Experiments were conducted according to the UK Animals (Scientific Procedures) Act, 1986 under personal and project licenses issued by the Home Office following ethical review.

Surgery and training

Five wild-type mice (C57BL6, 20-26g) were chronically implanted with a custom-built head post and recording chamber (4 mm inner diameter) under isoflurane anesthesia. No statistical methods were used to predetermine group sizes; the sample sizes we chose are similar to those used in previous studies. We did not require blinding and randomization as only wild-type mice were used. In subsequent days, implanted mice were acclimatized to run in the virtual environment in 20-30 min sessions (4-12 sessions), until they freely ran 20 traversals of the environment in 6 minutes. One day prior to the first recording session, animals were anesthetized under isoflurane and a ~1 mm craniotomy was performed over area V1 (centered at 2.5 mm lateral from midline and 0.5 mm anterior from lambda). The chamber was then sealed using silicone elastomer (Kwik-Cast).

Recordings

To record from V1 we inserted 16-channel linear multi-site probes (with site of size 312 or 430 μm², spaced 50 μm apart, NeuroNexus Tech.) to a depth of 900 μm. Recordings were filtered (0.3 - 5 kHz), threshold crossings were auto clustered using KlustaKwik⁴⁶ followed by manual adjustment using Klusters⁴⁷. A total of 194 units were isolated, of which 123 were in deep layers (channel > 10), 11 in superficial layers (channel < 6, numbered surface to deep; we found layer 4 to be located around channels 6-10 based on a current source density analysis). 46 isolated units were judged to be well-isolated (Isolation distance⁴⁸ >20). All examples shown in the manuscript are well-isolated units. The analysis of data included all units (except dark condition), as restricting the analysis of the data to only well-isolated units did not affect the results. Indeed, there was no correlation between spike isolation quality and Q_R (ρ = 0.06) or Q_PS (ρ = 0.07). The firing rate of each unit was calculated by smoothing its spike train using a 150 ms Gaussian window. All the stimuli and spiking activity were then sampled at 60 Hz, the refresh rate of the monitors.

Virtual environment

Visual scenes of a virtual environment were presented on three monitors (19-inch LCD, HA191, Hanns.G, mean luminance 50 cd/m², 35 cm away from the eye) that covered a visual angle of 170° azimuth and 45° elevation). Mice explored this environment by walking over an air-suspended spherical treadmill⁴⁹ (Fig. 1a).

The environment was simulated in Matlab using the Psychophysics toolbox^{50, 51}. The virtual environment was a corridor (120 cm × 8 cm × 8 cm) whose walls, ceiling and floor were adorned all along the corridor with a filtered white noise patterns of full Michelson contrast (overall RMS contrast: 0.14), and four positions in the corridor had prominent patterns as landmarks: gratings (oriented vertical or horizontal of full Michelson contrast, overall RMS contrast: 0.35) in three positions and a plaid (overlapping half-contrast horizontal and vertical gratings, overall RMS contrast: 0.35) in the fourth (Fig. 1a, b). Movement in the virtual reality was constrained to one-dimensional translation along the length of the room (the other two degrees of freedom were ignored). All speeds < 1 cm/s were combined into a single bin unless otherwise specified. The gratings had a spatial wavelength of 1 cm on the wall, which is equivalent to a spatial frequency of 0.09 cycles/° at a visual angle of 45° azimuth and 0° elevation. The white noise pattern was low-pass Gaussian filtered with a cutoff frequency of 0.5 cycles/° at 45° azimuth. Due to the 3-dimensional nature of the stimulus, the spatial frequency (in cycles/s) and visual speed (in °/s) presented are a function of the visual angle. Therefore, the speed of the visual environment is defined in terms of the speed of movement through the virtual reality environment, the virtual reality speed (virtual speed in cm/s). In closed-loop, this is the speed matched to what the animal would see if it were running in a real environment of the same dimensions. For reference, at a visual angle of 60° azimuth and 0° elevation, a virtual speed of 1 cm/s corresponds to a visual speed of 9.6 °/s, 10 cm/s to 96 °/s and 30 cm/s to 288 °/s. The running speed of the animal is calculated based on the movement of the air-suspended ball in the forward/backward direction, as captured by the optical mice⁴⁹.

The closed-loop condition was run first (>20 runs through the corridor), followed by two sessions of the open-loop condition. On reaching the end of the corridor on each run, the animals were returned (virtually) to the start, after a 3 s period during which no visual stimuli were presented (gray screen). In the open-loop condition, movies generated in closed-loop were simply played back, regardless of the animal’s run speed. For three animals (6 sessions), the closed-loop condition was repeated after the open-loop sessions. Following the measurements in virtual reality for all animals, we mapped receptive fields using traditional bar and grating stimuli. Each animal was taken through 1-3 such recording sessions.

Response function

The response of each neuron (shown in Figs. 1 and 3) was calculated as a function of the variables of the virtual environment and their various combinations using a local smoothing method previously used to compute hippocampal place fields^52-54. For example, a neuron’s firing rate y(t), at time t, was modeled as a function χ_a(a(t)) over the variable a. To estimate the model χ_a, the variable a was first smoothed in time (150 ms Gaussian) and discretized in n bins to take values a₁, a₂,…, a_n (the number of bins n was taken as 150 for position, 30 for speeds; the precise bin numbers were not important as response functions were smoothed) We then calculated the spike count map S and occupancy map Φ. Each point of the spike count map was the total number of spikes when a(t) had a value of a_i: S_i = Σ_t:(a(t)=ai)y(t), where i is the index of bins of variable a. The occupancy map was the total time spent when the variable a had a value of a_i: Φ_i = Σ_t:(a(t)=ai) Δt where Δt was the size of each time bin (Δt = 16.67 ms). Both the spike count (S) and occupancy (Φ) maps were smoothed by convolving them with a common Gaussian window whose width σ (ranging between 1 bin to total no. of bins) was optimized to maximize the cross-validated prediction quality (explained below). The stationary/static bins were not included in the smoothing process. The firing rate model was then calculated as the ratio of the smoothed spike count and occupancy maps:

$${\chi }_a=\frac{S\ast {\eta }_{\mathrm{a}}(0,\sigma )}{\Phi \ast {\eta }_{\mathrm{a}}(0,\sigma )}$$

where η_a (0, σ) is a Gaussian of width σ, and the operator ‘*’ indicates a convolution. Based on the model, fit over training data, we predicted the firing rate over the test data as:

$$y^a\left(t\right)={\chi }_a\left(a\left(t\right)\right)$$

where y^a(t) is the prediction of firing rate based on variable a. A similar procedure was followed for the 2D “speed maps”, where two independent Gaussians were used to smooth across each variable.

Prediction quality

Response functions and models were fit based on 80% of the data and the performance of each of models was tested on the remaining 20% (cross-validation). We calculated the prediction quality Q_a of model χ_a, based on variable a, as the fraction of variance explained:

$$Q_a=1-\frac{\sum _t{\left(y\right(t)-y^a(t\left)\right)}^2}{\sum _t{\left(y\right(t)-\mu )}^2}$$

where y(t) is the smoothed firing rate (150 ms Gaussian window) of the neuron at time t, y^a(t) was the prediction by model χ_a for the same time bin and μ is the mean firing rate of the training data. A value of Q close to 0 suggests the model does not predict the firing rate of the neuron any better than using a constant and a higher Q suggests good performance. Values of Q close to 1 are unlikely as the intrinsic variability in the response of neurons, which is uncorrelated to the stimulus, is not captured by any of the models. Very low values of Q suggest that the response is unreliable. Therefore, we only concentrated on neurons whose responses were reliable for further analysis by setting a limit of Q > 0.1 (Fig. 1g: 110/194 neurons with Q_PS> 0.1 and Fig 2j: 73/194 neurons with Q_map> 0.1). To compare the metric explained variance of the mean response which is more commonly used, we calculated Q and explained variance on direction tuning of neurons. We found that neurons with a model for direction tuning of Q > 0.1 had an explained variance in the range of 0.75-0.97 (two examples are shown in Supplementary Fig. 3). To test the alternative hypothesis of a binary model of run speed, we only considered two bins, which were whether the animal ran (Speed > 1 cm/s) or not. We used the mean firing rate of the training data in these bins, to predict firing rate of the test data and calculate Q_binary.

Responses in darkness

We trained a separate set of animals (n = 3) with an additional 5-10 minute condition of complete darkness. The darkness was achieved by turning all the non-essential lights and equipment in the room off. Light from essential equipment outside the recording area (e.g. recording amplifiers) was covered with a red filter (787 Marius Red; LEE filters), rendering any stray light invisible to mice. As a result, the recording area was completely dark both for mice and for humans (luminance <10⁻² cd/m², i.e. below the limit of the light meter). We used 32-channel, 4 shank multisite probes (spaced 200 μm apart) to record one session on each animal; each shank had two sets of tetrodes spaced 150 μm apart (Each electrode had recording sites of 121 μm², Neuronexus). We recorded a total of 145 units of which 55 were well-isolated units (Mahalanobis distance > 20). We only considered the well-isolated units for analysis in the dark condition. Similar results were obtained when considering all units (not shown). The dark condition during the three recording sessions lasted 8, 9 and 13 mins. In this condition, speed was defined as the amplitude of the two-dimensional velocity vector.

Responses in the dark condition were calculated by discretizing the run speed such that each speed bin contained at least 7% of the dark condition (>30 s). In cases where the animal was stationary for long periods of time (>7%), the stationary speed (≤ 1 cm/s) bin had more data points. We calculated the mean and error of the firing rate in each of the speed bins (Fig. 2). The speed in any bin was the mean speed during the time spent at that speed bin. To assess statistical significance of modulation by run speed, for each neuron we recalculated the firing rate as a function of speed in each bin after shuffling the spike times. As a conservative estimate we considered a neuron’s response to be significantly modulated by run speed if the variance of its responses was greater than 99.9% of the variance of the its shuffled responses (p<0.001). To test if the neuron’s response was significantly non-binary, we followed the same procedure as above, but restricting the test to only periods when run speed was > 1 cm/s.

To characterize the run speed responses we fit the mean responses to speed s (s > 1 cm/s) by the following descriptive function^{55, 56}:

$$y\left(s\right)=y_{\mathit{max}}\mathit{exp}[-{(s-s_{\mathit{max}})}^2∕\sigma (s\left)\right]$$

where σ(s) was σ₋ if x < x_max and σ₊ if x > x_max, and y_max, x_max, σ₋ and σ₊ were the free parameters. We fit three curves by adding constraints on x_max: a) a monotonically increasing function was fit by constraining x_max to be greater than ≥ 30 cm/s, b) a monotonically increasing function was fit by constraining x_max to be ≤ 1 cm/s, and c) a bandpass curve by not constraining x_max. These three curves were fit on 80% of the data and we tested the fraction of explained variance of the firing rate on the remaining 20%. We considered a neuron bandpass only if the variance explained by the band-pass curve was greater than both a monotonically increasing or decreasing curve and when x_max was > 2 cm/s and < 25 cm/s.

Weighted sum model

The firing rate of a neuron i at time t, y_i(t) was modeled as:

$$y_i\left(t\right)=f\left[\alpha V\right(t)+\beta R(t\left)\right]$$

where α = sin(θ), β = cos(θ), V(t) is the virtual speed, R(t) the run speed of the animal at time t. The function f [ ] was estimated using a 1d version of the same binning and smoothing procedure described above for estimating response functions. For each cell, the model was fitted for a range of integration angles θ from 0 to π in steps of π/16. The optimal integration angle θ_max was chosen as the value of θ giving the highest cross-validated prediction quality.

Population decoding

The smoothed (0.9 s Gaussian window) firing rate vector of all simultaneously recorded neurons was used to predict a linear combination of virtual speed and run speed (sin(θ) V(t) + cos(θ) R(t)) for a range of interaction angles θ from 0 to π in steps of π/16. As our hypothesis is to test the decoding of speed relevant to navigation, we consider all speeds < 3 cm/s to be stationary (Red curves in Fig. 4b-d), or ignored all the times when either run speed or visual speed were < 3cm/s (Gray curves in Fig. 4c,d; we only considered sessions (9/11) where >100 seconds fulfilled this criterion). Reducing the limit to < 1 or 0.03 cm/s did not affect the trend in the decoding performance (shown in Supplementary Figs. 11 & 12). We used a linear decoder (ridge regression, with the ridge parameter optimized by cross-validation), to evaluate how well an observer could decode a combination of speeds given the firing rate of the population. The performance of the decoder was tested as the fraction of variance explained on an independent 20% of the data that was not used to train the decoder.