Interactions of Timing and Prediction Error Learning

Abstract

Timing and prediction error learning have historically been treated as independent processes, but growing evidence has indicated that they are not orthogonal. Timing emerges at the earliest time point when conditioned responses are observed, and temporal variables modulate prediction error learning in both simple conditioning and cue competition paradigms. In addition, prediction errors, through changes in reward magnitude or value alter timing of behavior. Thus, there appears to be a bi-directional interaction between timing and prediction error learning. Modern theories have attempted to integrate the two processes with mixed success. A neurocomputational approach to theory development is espoused, which draws on neurobiological evidence to guide and constrain computational model development. Heuristics for future model development are presented with the goal of sparking new approaches to theory development in the timing and prediction error fields.

Traditionally, the study of timing and associative learning has proceeded largely independently, but more recent research has suggested areas of connection between the two disciplines. Theories of timing and associative learning have also traditionally focused on one or the other process, but the last three decades have seen the emergence of hybrid theories, again reflecting overlap between the two processes (see, for example, Church and Kirkpatrick 2001; Kirkpatrick and Church 1998). The present paper discusses recent developments, both empirical and theoretical, in the fields of timing and associative learning that argue for the further development of theories that couple the two processes together, as well as further research to assess the nature of interactions between the two processes. Both behavioral and neurobiological evidence are brought to bear in an attempt to understand the functioning of timing and associative learning systems.

1. Historical foundations

1.1. Prediction error learning

Prediction error learning is driven by expectancies of the occurrence or non-occurrence of events, and has been proposed to serve as the basic process that underlies associative learning in classical and instrumental conditioning procedures. Prediction error learning has historically been viewed as the process of learning to anticipate events in relation to the occurrence of other events. As a simple example, an individual might experience a tone that lasts for 10 s and is followed by food delivery, a procedure known as delay conditioning. Prediction error learning in this case would lead to an expectation of food delivery during the tone stimulus. Prediction errors play an important role during the learning process as early in learning there is no expectancy of food, but this develops over the course of repeated experiences. Prediction errors could also play an important role if the circumstances were to change by, for example, changing the properties of the tone, by changing the amount or type of food delivery, or by ceasing food deliveries altogether. Prediction error learning also plays an important role in learning connections between multiple different events, such as connections between two or more conditioned stimuli (CSs) and relationships between responses and outcomes.

1.2. Conditioning and timing

The study of classical conditioning initially proceeded largely independently of the study of timing processes, even though the procedures used to study both processes are highly similar. For example, a common procedure used in classical conditioning research is the delay conditioning procedure, described previously, in which a CS (e.g., a tone or light) is turned on for a fixed duration and then is followed by a US (e.g., food). An intertrial interval (ITI) intervenes between successive signal presentations. Although responses have no consequence in this procedure, considerable responding can be observed if the CS duration is relatively short (depending on the relevant behavioral system), if the CS precedes the US, and if there is little or no gap between CS offset and US delivery. All of these phenomena indicate that conditioning is dependent on temporal aspects of the procedure. These facets of conditioning are well established and are foundational knowledge in basic learning textbooks. In addition, conditioned responses (CRs) are not distributed evenly across the CS duration, but instead increase in frequency and/or strength as the expectancy of the US increases. Measurement of CR timing in classical conditioning has been overlooked in the majority of research reports, even though CR timing is a robust phenomenon. The fact that CRs are timed in accordance with US expectancy indicates that conditioning is resulting in learning of whether and when the US will occur. And yet, both empirical research and theoretical developments have proceeded largely independently until more recently.

1.3. Reward processing and timing

Prediction error learning plays an important role in learning to anticipate reward occurrence and the specific features of rewarding stimuli. Changes in reward magnitude or other aspects of reward lead to prediction errors and this in turn can lead to timing changes (Section 2.2). Early research examining reward effects on timing suggested that timing of responding was relatively immune to the effects of reward variables, and that reward effects were restricted to the rate of responding rather than the timing of responding. For example, Roberts (1981) reported several experiments where different aspects of a peak procedure were manipulated. A peak procedure is a variation on a fixed interval (FI) schedule of reinforcement. FI and peak trials are both cued by the same signal (e.g., a tone or light). On FI trials, food is primed at a particular time after signal onset, for example, 30 s. The first response after the prime results in food delivery and signal termination. Peak trials are cued in the same fashion and usually last 3–4 times the FI duration. There are no food deliveries on peak trials and responses have no consequence, but are recorded. The average response rate on peak trials typically increases as a function of time since signal onset until around the expected time of food delivery and then decreases thereafter.

Roberts (1981) reported that differences in the FI duration resulted in differences in the time of occurrence of the peak time of responding, whereas differences in the probably of reinforcement resulted in differences in the peak rate of responding. As a result, Roberts developed a simple model in which the timing of reinforcement was proposed to affect clock processes which would result in effects on the timing of responding whereas other factors such as probability or amount of reinforcement or the motivational state of the individual would affect the rate of responding but should have no effect on the timing of responding. As a result of this and other early studies, little attention was paid to any possible intersection of reward processes and timing processes. However, more recent research, outlined in the next section, has indicated that reward processing and timing are not entirely independent.

2. Challenges: prediction error learning and timing are not independent

In the last three decades, there has been a growth of interest (both empirical and theoretical) in examining connections between prediction error learning and timing. This section will consider the major empirical developments that have stimulated the growth of hybrid theories, which are discussed in the following section.

2.1. Timing variables and prediction error learning

One important discovery linking prediction error learning and timing is that CRs appear to be timed appropriately at their earliest point of occurrence. This has been demonstrated in appetitive conditioning in rats (Kirkpatrick and Church 2000), aversive conditioning in goldfish (Drew et al. 2005), eyeblink conditioning in rabbits (Ohyama and Mauk 2001), autoshaping in birds (Balsam, Drew, and Yang 2002), and fear conditioning in rats (Davis, Schlesinger, and Sorenson 1989). The observation of CR timing at the start of associative learning indicates that learning to anticipate whether and when the US will occur (in relation to the CS) are most likely emerging in parallel and at a similar point in conditioning. This will be discussed further in relation to the neural substrates of timing and conditioning in Section 4.

Another important factor to consider is that interval durations directly affect the strength and/or probability of CR occurrence in simple conditioning procedures (Holland 2000; Kirkpatrick and Church 2000; Lattal 1999; Kirkpatrick 2002; Kirkpatrick and Church 2003). This relationship appears to take the form of a power function with a slope near −1.0 in a goal-tracking procedure in rats, as shown in Figure 1. In addition, this relationship is observed regardless of the events that cue the onset of the interval. To demonstrate this principle, the data in Figure 1 are taken from delay conditioning procedures with tone and light CSs and display the relationship between response rate and interval duration during the CS and ITI and for both noise and light CSs and ITIs of different durations (Jennings, Bonardi, and Kirkpatrick 2007; Kirkpatrick 2002). These data indicate that CS and ITI durations produce orderly effects on CR intensity (measured by head entry response rate), lending further support to the important role of temporal variables in conditioning. In addition, the similarity of response rates in the CS and ITI indicate that prior food delivery and CS onset both serve as timing cues for anticipating upcoming food deliveries, and may potentially rely on the same underlying mechanism (see also Kirkpatrick and Church 2000, 2003, 2004).

Figure 1.

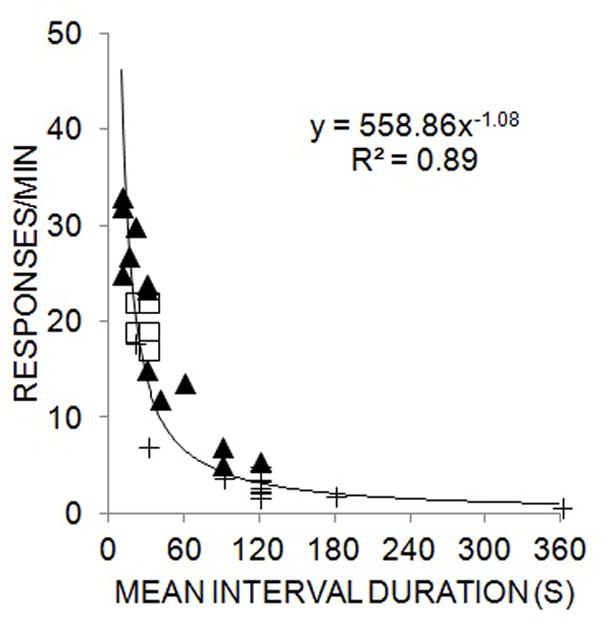
Mean response rate (in responses/min) of head entry responses as a function of mean interval duration. Filled triangles depict data from delay conditioning studies with a noise CS and open squares are data from light CSs. Plus signs are response rates during the inter-trial interval. A single power function is fit through the data, and the equation and goodness of fit (R²) are provided. The data are combined and adapted from Jennings, Bonardi and Kirkpatrick (2007) and Kirkpatrick (2002).

While the mean interval duration appears to primarily affect response rate, variability in interval durations affects the pattern of responding in simple conditioning procedures. For example, variable intervals lead to generally constant rates of responding, whereas fixed intervals lead to increasing rates of responding over the course of the CS-US interval (Kirkpatrick and Church 2000, 2003, 2004, 1998; Church, Lacourse, and Crystal 1998).

While it is clear that the duration and variability of intervals has an effect on the rate and distribution of responses, respectively, these effects could be occurring in parallel with prediction error learning with little or no contact between the two phenomena. Cue competition paradigms can provide a means to assess the interaction of temporal variables with conditioning, by pitting cues with different temporal information against one another. Here, it is clear that there may be an interaction of temporal variables and conditioning, but the nature of the interaction is not well understood and the literature has revealed an inconsistent picture. One simple cue competition procedure is overshadowing (Pavlov 1927), where two CSs of different properties are both associated with the US. Here, the more salient CS usually results in more robust conditioning. With regard to temporal properties, it appears that variability of the CS may affect overshadowing, with weaker overshadowing by variable than by fixed CSs (Jennings et al. 2011). In addition, overshadowing has been reported to be more robust with shorter CSs than with longer CSs (Kehoe 1983; but see Jennings et al. 2007; McMillan and Roberts 2010; Hancock 1982; Fairhurst, Gallistel, and Gibbon 2003), consistent with the idea that both shorter and less variable CSs may be more salient due to their higher information value in predicting the US (Balsam, Drew, and Gallistel 2010).

In addition, interval duration has been shown to affect cue competition in a blocking paradigm (Kamin 1968; Kamin 1969). Blocking involves pre-training with a CS1→US followed by later CS1+CS2→US pairings. One question of interest in terms of temporal variables has been the maintenance of CS1 durations between the pre-training and blocking phases. Shifts in CS1 duration can result in an attenuation of blocking in some cases (Barnet, Grahame, and Miller 1993; Schreurs and Westbrook 1982), but this effect has not consistently been observed (Kohler and Ayres 1979, 1982; Maleske and Frey 1979). A few investigations have also examined the importance of the relative duration of CS1 and CS2 in blocking, and here again the picture is mixed. Several studies have reported that a longer CS1 can block a shorter CS2 (Kehoe, Schreurs, and Amodei 1981; Gaioni 1982), but not vice versa (Jennings and Kirkpatrick 2006), but other studies have reported little or no asymmetry in blocking (Kehoe, Schreurs, and Graham 1987; Barnet, Grahame, and Miller 1993), or the opposite result with stronger blocking by a shorter CS1 (Fairhurst, Gallistel, and Gibbon 2003; McMillan and Roberts 2010). The issue of the variability in CS duration has not been as widely studied in blocking as interval duration effects, but one study reported temporal uncertainty (through variability in CS duration) did not undermine the ability of a CS1 to block a CS2 (Kohler and Ayres 1979). Further research is necessary to determine whether this result would hold across a range of different procedural variations.

In both overshadowing and blocking, the differences in the nature of effects of duration and variability may be due to various factors such as the modality of the two CSs, which has been shown to affect timing (e.g., Meck 1984), the paradigm employed (aversive or appetitive), the nature of the response, the species of animal tested, and whether the two stimuli are presented in an overlapping or serial compound. While disentangling these possibilities is an important goal, the most important aspect for the present purposes is that it does appear that temporal variables interact directly with prediction error learning. This indicates the need to consider that interaction in the development of future theories, as discussed below (Section 6).

3.2. Prediction error effects on timing

It is clear that temporal variables affect prediction error learning, and it also appears that prediction errors can lead to alterations in timing. Growing evidence indicates the importance of reward prediction and prediction error learning in the timing process (Doughty and Richards 2002; Galtress and Kirkpatrick 2009, 2010a, 2010b; Grace and Nevin 2000; Kacelnik and Brunner 2002; Ludvig, Balci, and Spetch 2011; Roberts 1981; Ludvig, Conover, and Shizgal 2007).

One factor that has been demonstrated to affect timing is the magnitude of the reward, as seen in Figure 2 (top panel), which is adapted from Galtress and Kirkpatrick (2009). In this study, rats were trained on a peak procedure where reinforcement was normally available for the first lever press 60 s after trial onset. On occasional peak trials, the trial signal remained on for 180 s and food was omitted. Rats were given initial training with 1 or 4 food pellet(s) as the usual reward and then the reward magnitude was increased to 4 pellets (in group 1-4-1) or decreased to 1 pellet (in group 4-1-4). The mean start time of responding during peak trials is shown in the figure for the initial (BASE 1) and final baseline (BASE 2) phases and the reward magnitude phase (MAG). When the magnitude was shifted from 1 to 4 pellets, there was a leftward shift in start times, indicating an effect of reward magnitude contrast on timing, and the reverse pattern was seen when shifting from 4 to 1 pellets. Upon return to the baseline reward condition, both groups showed a shift back to their original start times. Similar results have been reported in rats, pigeons and humans, with increasing reward magnitude shifting timing functions earlier and decreases in magnitude shifting timing functions later (Ludvig, Balci, and Spetch 2011; Ludvig, Conover, and Shizgal 2007; Balci et al. 2013; Grace and Nevin 2000). Additional research has indicated that changes in magnitude flatten response functions on a temporal discrimination task (Galtress and Kirkpatrick 2010a), suggesting that the effects of motivational changes on timing might operate through alterations in attention to time, or through changes in decision processes.

Figure 2.

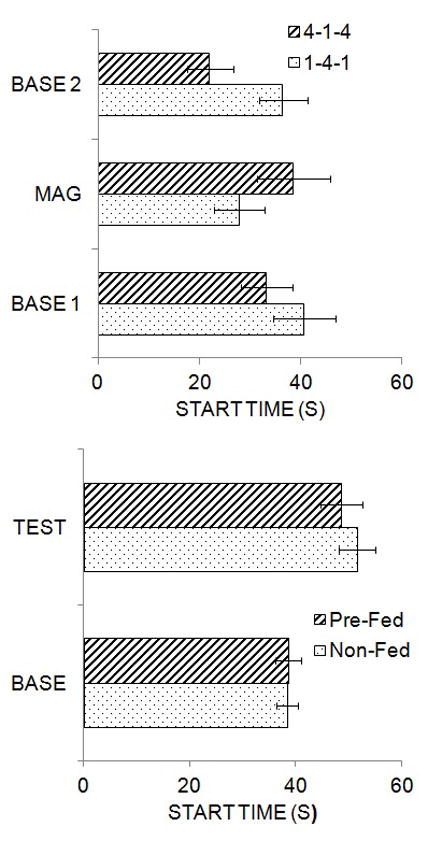
Top: Mean (± SEM) start times during original baseline (BASE 1), magnitude shift (MAG) and return to baseline (BASE 2) phases of training in Groups 4-1-4 and 1-4-1. The data are adapted from Galtress and Kirkpatrick (2009). Bottom: Mean (+ SEM) start times during baseline (BASE) and test (TEST) phases in groups that were pre-fed in original baseline and tested under deprivation (Pre-Fed) or were trained in the baseline phase under deprivation and tested under satiety (Non-Fed). The data are adapted from Galtress, Marshall, and Kirkpatrick (2012).

In addition to the effects of reward magnitude on timing, devaluation through satiety or through lithium chloride-induced taste aversion has also been shown to alter timing in both the peak and temporal discrimination procedures. Galtress and Kirkpatrick (2009) trained rats under normal food deprivation on a peak procedure and then tested them following satiety through pre-feeding or following pairing of the reward with lithium chloride. Both devaluation procedures produced a substantial reduction in response rate and shifted the peak to the right (see also Roberts 1981). This effect has also been reported to occur due to satiety within sessions under normal training procedures, where response rates decreased and peak times shifted to the right over the course of the session (Balci, Ludvig, and Brunner 2010). In addition, satiety has been reported to flatten the psychophysical function in temporal discrimination procedures, similar to the effect of changes in reward magnitude (Ward and Odum 2006). However, unlike changes in magnitude, which appear to produce directional selectivity in shifting peak functions, satiety effects do not appear to be directionally specific. Depicted in Figure 2 (bottom panel) are results from Galtress, Marshall and Kirkpatrick (2012). They trained rats on a peak procedure either under normal deprivation (Non-Fed), or under satiety where the rats were pre-fed prior to each experimental session (Pre-Fed). Training under different deprivation states produced differences in response rates, with the pre-fed rats displaying lower rates (similar to the effect of training with different magnitudes), but the start times in responding were highly similar, as seen in the figure. In a subsequent test phase, the deprivation state of the rats was switched. The rats that had been trained under deprivation and were tested under satiety showed a rightward shift in their peak, consistent with previous reports (Balci, Ludvig, and Brunner 2010; Galtress and Kirkpatrick 2009; Roberts 1981). Surprisingly, the rats that were trained under satiety and tested under deprivation also displayed a rightward shift in their peak, indicating that the general state change produced the shift and that this shift was not directionally selective. This suggests that somewhat different processes may be at work in satiety versus reward magnitude effects on timing, which will be discussed further in Section 5, in relation to the neural substrates of prediction error, valuation, and timing.

3. Theories of timing and prediction error learning

It is clear from the preceding section that modern theories need to integrate timing and prediction error learning in some fashion. There has been a general trend towards developing integrative models, but these models have tended to have a fairly limited scope, or have been focused on a single process. There are three main categories of integrative models: (1) time-based hybrid models that have incorporated prediction error learning; (2) prediction error models that have incorporated timing; and (3) information processing models.

3.1 Time-based hybrid models

The time-based hybrid models have developed along two lines -- those that incorporate some aspect of associative or prediction error properties and those that incorporate reward processing aspects. One example of a prediction-error type of model is the learning to time model (LeT; Machado 1997), which developed from behavioral theory of timing (BeT; Killeen and Fetterman 1988). In the LeT model, timing of durations is accomplished by a cascade of traces that are initiated at trial onset. Reinforcement strengthens the memory for the individual traces in accordance with their activity strength at the time of reinforcement and extinction weakens the memory for individual traces. This model does contain elements of prediction error models, particularly with regard to changes in associative strength, but it does not possess any mechanisms for cue competition or for dealing with the reward magnitude and satiety effects on timing discussed above.

Several additional hybrid models have taken a similar approach to LeT by assuming that reinforcement leads to the storage of a set of strengths based on the activation pattern of a set of perceptual functions at the time of reinforcement. The multiple oscillator model (MOM; Church and Broadbent 1990) proposes that the perception of time is accomplished by a set of oscillators with different periods. Memory strength is determined by an auto-association matrix, which encodes the strength of association of different oscillators; the memory coding in this fashion facilitates temporal generalization. The spectral timing theory (STT; Grossberg and Schmajuk 1989) proposes a perceptual representation which is a series of functions that increase nonlinearly at different rates (the gated spectral signal). The memory represents the strength of each perceptual function at the time of reinforcement according to a linear operator function. Neither of these models contains elements necessary for cue competition effects or for dealing with reward effects on timing.

Yet another sub-set of timing models have incorporated motivational processes with the goal of explaining some reward processing effects on timing. For example, the behavioral economic model (BEM; Jozefowiez, Staddon, and Cerutti 2009) proposes that reinforcer properties directly affect the decay rates for timing traces within the model. This model can partially account for the reward magnitude and value effects on timing, but the model fails to account for lack of directional specificity in the satiety effects on timing and also incorrectly predicts that reward magnitude changes should vertically shift the psychophysical function in temporal discrimination rather than flatten the function.

The multiple time scales model (MTS;Staddon and Higa 1996) was developed to deal with sudden changes in reward magnitude through short-term effects on timing traces. This model incorrectly predicts that smaller rewards should result in earlier responding than larger rewards, which is the opposite of the results that have been reported in the literature.

An additional set of time-adaptive drift diffusion models (TDDMs) have been recently developed to provide an approach for learning to time intervals (Rivest and Bengio 2011; Simen et al. 2011; Luzardo, Ludvig, and Rivest 2013). These models all assume that timing is accomplished by a ramping function, with a learning rule that incorporates prediction error relating to the time of occurrence of reinforcement. If the reinforcer arrives earlier than expected, then the accumulation rate is increased and if it arrives later than expected then the accumulation rate is slowed. This allows for potentially rapid learning and adaptation of behavior in the face of changing temporal information, depending on the learning rate parameter value. These models encode reward rate in a manner similar to BeT (Killeen and Fetterman 1988). Luzardo et al. (2013) developed an alternative linear threshold version of the TDDM to account for rapid changes in behavior under cyclic interval schedules using a rule in which the decision threshold was a linear function of the accumulation rate. This model performed similarly to MTS in accounting for cyclic schedule responding, but with the added benefit that it would be able to account for at least some aspects of reward processing effects on timing. However, none of the TDDMs currently incorporate cue competition effects, so they would not be well suited to deal with the effects of temporal variables on prediction error learning without further modification.

Another theory that is based on a ramping function for time perception is packet theory (PT; Kirkpatrick 2002; Kirkpatrick and Church 2003), which proposes that a single ramping function is generated during each interval and that these are averaged together (with a linear operator equation) to form an expected time function. The rate of responding is determined by the mean expected time and the pattern of responding is determined by the shape of the expected time function. While packet theory can explain a number of facets of CR rate and timing in simple conditioning, such as CR timing emerging in the same time course as CR rate, and the effects of interval duration and variability on CR rate and pattern, respectively, this model does not incorporate any cue competition effects due to a lack of a prediction error rule that sums strengths across multiple CSs. In addition, the model is ill-equipped to deal with the effects of prediction error learning on timing through reward magnitude/value changes. The modular theory (MOD; Guilhardi, Yi, and Church 2007) attempted to overcome some of these deficits by introducing separate memory stores for strength and pattern information. The strength memory follows a Rescorla-Wagner learning rule, and thus can predict a number of basic associative learning effects, and the pattern memory is the expected time function from the PT model. Although this model has a broader scope than the original PT model, it still fails to incorporate many the effects of temporal variables on prediction error learning and the effects of prediction errors on timing because the strength and pattern memory do not interact.

Overall, none of the time-based models fare very well in accounting for the effects of temporal variables on prediction error learning. Most of the models also fare poorly in understanding the effects of reward magnitude or value changes on timing, although MTS and BeM do account for some aspects of reward effects on timing. This indicates that a more comprehensive approach will be required in integrating timing and prediction error within a common framework.

3.2. Prediction error-based hybrid models

The class of temporal difference models (TD; Sutton and Barto 1981, 1990) have arisen out of a Rescorla-Wagner (1972) prediction error learning rule coupled with a temporal representation to provide a means of predicting CR timing. The temporal representation in TD models is a series of discrete units within the time course of a CS, so one difference between TD models and other theories of timing is the nature of the perception of time (discrete in TD models vs. continuous in most timing models). Because TD models incorporate timing into a prediction error model, they perform reasonably well in predicting at least some aspects of CR timing (Ludvig, Sutton, and Kehoe 2012) and can also predict at least some elements of the effects of temporal variables on conditioning (e.g., Jennings et al. 2011). Altering aspects of the stimulus representation can improve performance of CR timing by incorporating scalar variance into the temporal representation associated with the different CS components (Ludvig, Sutton, and Kehoe 2008). The TD models could incorporate reward processing aspects through prediction error changes, but these models perform better in explaining changes in response rate as a function of changes in reward parameters, rather than dealing with alterations in timing of responses.

In general, the asset of the TD models is that they can account for prediction error learning at least as well as standard associative models such as the Rescorla-Wagner model (Rescorla 1972), but they also open the door to explaining CR timing and allowing for CR timing acquisition to occur along with prediction error learning (Kirkpatrick and Church 2000; Balsam, Drew, and Yang 2002). These models are still evolving and need to expand their scope to fully incorporate the effects of temporal variables on prediction error learning and also the effects of prediction errors (produced through changes in reward variables) on timing.

3.3. Information processing models

Scalar expectancy theory (SET; Gibbon and Church 1984; Gibbon, Church, and Meck 1984) differs considerably from the hybrid models discussed above, most notably due to the lack of any prediction error or strength component in the memory store. The perception of time in SET is a ramping function that bears some similarity to the TDDMs and PT/MOD, but here the ramping function is proposed to emerge from a pacemaker that sends pulses to an accumulator. The memory is a collection of pulses from previously reinforced intervals. The model proposes that all pulse counts are stored as individual memories, rather than as an integrated strength representation. Because SET is an information processing model that is devoid of any prediction error component, this model does not account for acquisition of behavior (Church and Kirkpatrick 2001), but does predict many steady state features of timed behavior. The model does not encompass prediction error learning and thus on its own cannot account for any of the interaction effects discussed above.

In an attempt to incorporate some prediction error learning aspects with SET, rate expectancy theory (RET; Gallistel and Gibbon 2000; Gibbon and Balsam 1981) proposed an information processing model for prediction error learning. In the RET model, the acquisition of CRs is determined by a comparison of two rates of reinforcement: the rate during the intertrial interval and the rate during the CS-US interval (note that in the earlier Gibbon and Balsam formulation the inter-US interval, or cycle, was the basis for background reinforcer rate determination). As evidence accumulates, if the CS-US interval carries a stronger reward signal (a higher reinforcement rate) than the background rate, then CRs will begin to emerge. Following conditioning, SET has been proposed to determine CR timing; this model assumed that CR timing would occur after conditioning of CRs had begun to emerge, which is at odds with multiple observations noted above (Section 2.1). The RET model has successfully explained the effects of interval (and relative interval) durations on CR occurrence and intensity (such as depicted in Figure 1) and can explain a number of basic prediction error learning phenomena including most simple cue competition effects. The model also contains a basis for prediction errors surrounding changes in US magnitude, but those changes would only affect CR rate, and not CR timing. In addition, the model does not incorporate any of the effects of temporal variables on prediction error learning.

A newer variant on the RET model, based on Shannon’s information theory (Balsam, Drew, and Gallistel 2010; Balsam and Gallistel 2009), extends on the previous model by proposing that the information value of durations can affect CR occurrence. Information is encoded by an entropy formulation, and both the length and variability of an interval affect information value, with shorter, fixed intervals associated with higher information value than either longer or more variable intervals. This new variant on RET allows the model to incorporate many of the effects of temporal variables on prediction error learning, including differences in blocking and overshadowing based on relative length and variability (Section 2.1). This model has not yet been extended to deal with the prediction error effects on timing through reward magnitude and value manipulations, so this remains a weakness of the model.

While RET has developed as an information processing model to compliment to the original SET model, an additional variant, the striatal beat frequency model (SBF; Matell and Meck 2004), was developed as a biologically plausible variant of SET. The perception of time in the SBF model is accomplished by a set of pacemaker neurons of different frequencies that spike for brief periods (Miall 1989). The beat frequency of a pair of oscillators is the frequency of co-occurrence of spikes, which gives a metric of the rate of coincidence of firing of the oscillators. The set of oscillators are initiated at stimulus onset (the beginning of the temporal duration), but because they are all oscillating at different frequencies will quickly become desynchronized, similar to MOM. Oscillators that are spiking at the time of reinforcement result are strengthened via a Hebbian learning rule, similar to other time-based hybrid models such as STT. As a result, although SBF emerged out of the historical origins of information processing theories, it is fundamentally a time-based hybrid model more akin to STT, MOM, and LeT. Although this model does account for a number of timing phenomena, the current implementation of the model does not adequately time durations over 20 s (Matell and Meck 2004), which presents challenges for the breadth of application of the model to timing data. In addition, the model does not readily account for any of the prediction error interactions with timing, either the temporal duration effects on prediction error learning or the effects of reward properties on timing. Thus, the model will need to evolve to account for the results presented in Section 2 above.

4. Neurobiological evidence

Computational models that are derived from purported psychological processes have proven effective in understanding behavioral phenomena in the timing and prediction error fields, but such models have been criticized for failing the neural plausibility test (Bhattacharjee 2006). In addition, neurophysiological evidence has pointed towards a more distributed system for encoding temporal durations (see Coull, Cheng, and Meck 2011 for a review), suggesting the need for new physiologically-based approaches to modeling the timing system. Furthermore, psychological models do not readily accommodate the effects of other variables on the timing system such as the prediction error effects described above, or the effects of temporal variables on prediction error learning. In turning to the neural circuitry of the timing and prediction error learning systems, such interactions are expected to occur because prediction error and timing circuits are intricately interconnected. A consideration of the structure and function of these circuits may aid in guiding the development of new timing models that more readily incorporate the present results.

The following discussion of the reward system contains elements from studies involving rodents, non-human primates, and humans obtained with various techniques, and represents areas of convergence of the evidence from these varied sources where possible. The regions and pathways focus on the predominant structures and connections implicated in timing and prediction error learning. Although the timing and prediction error circuitry are discussed separately, they are diagrammed together in Figure 3. The brain regions and their connections that appear to be primarily involved in timing are represented by solid lines, whereas the regions and connections that appear to be more heavily involved in prediction error and reward valuation are represented by single dashed lines, and the regions and connections that may potentially be shared between the systems are represented by double-dashed lines.

Figure 3.

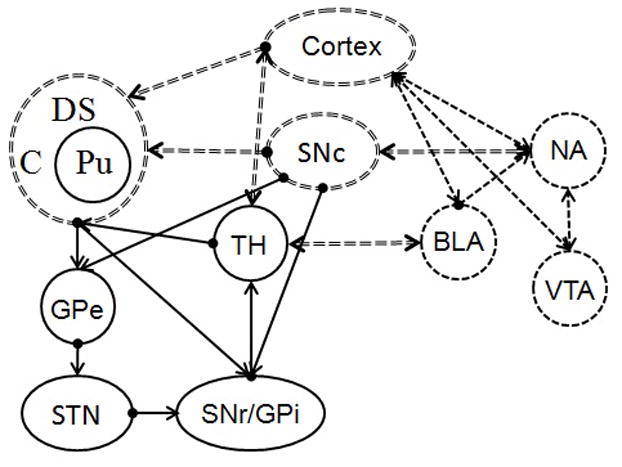
A diagram showing prediction error learning (dashed lines), timing (solid lines), and overlapping/shared (double-dashed lines) neural substrates. VTA = ventral tegmental area; NA = nucleus accumbens; BLA = basolateral amygdala; SNc = substantia nigra pars compacta; DS = dorsal striatum; C = Caudate; Pu = Putamen; TH = thalamus; GPe = external segment of globus pallidus; STN = subthalamic nucleus; SNr = substantia nigra pars reticula; GPi = internal segment of globus pallidus. Multiple cortical areas are represented as “Cortex” and include the pre-motor cortex, pre-frontal cortex, and orbitofrontal cortex.

4.1. Timing circuitry

The primary system for anticipatory timing in the seconds to minutes range that would most likely play a role in prediction error learning is the cortico-striatal-thalamic network (Coull et al. 2004; Coull, Nazarian, and Vidal 2008; Morillon, Kell, and Giraud 2009; Nenadic et al. 2003; Rao, Mayer, and Harrington 2001; Buhusi and Meck 2005; Matell and Meck 2004; Meck 1996). This system contains the nigrostriatal pathway that also features heavily in prediction error learning coupled with multiple cortical and thalamic (TH) connections to the dorsal striatum (DS).

The DS has been proposed to function as a “supramodal timer” (Coull, Cheng, and Meck 2011) that is involved in encoding temporal durations (Meck 2006; Matell, Meck, and Nicolelis 2003; Coull and Nobre 2008; Meck, Penney, and Pouthas 2008), and may also play a role in temporal integration and coincidence detection (Matell and Meck 2004; Matell, Meck, and Nicolelis 2003). There are two pathways from the DS to the thalamus (TH) via the BG. The direct pathway to the TH sends excitatory information to the cortex (particularly the pre-motor cortex, PMoC), and the indirect pathway to the TH results in the transmission of inhibitory signals to the PMoC. The SNc modulates the balance of excitation and inhibition across the two pathways, which is important for the expression of anticipatory timing behavior (see Coull, Cheng, and Meck 2011 for a review).

The timing system interfaces to the prediction error system through the shared substrates of the PMoC, SNc and DS, which are involved in prediction error coding as well as timing. This suggests a possible strong relationship between temporal and reward prediction, which is not surprising given that both tend to co-occur in many Pavlovian and instrumental conditioning procedures and emerge at around the same point in acquisition (Balsam et al. 2009; Kirkpatrick and Church 2000; Davis, Schlesinger, and Sorenson 1989; Ohyama and Mauk 2001; Drew et al. 2005), as discussed in Section 2.1.

4.2. Prediction error circuitry

The primary components of the prediction error system are situated in the mid-brain dopamine system (see Figure 3), composed of the mesolimbic and nigrostriatal pathways. The mesolimbic pathway is comprised of projections from the ventral tegmental area (VTA) to the nucleus accumbens (NA) and pre-frontal cortex (PFC). The nigrostriatal system initiates in the substantia nigra pars compacta (SNc) which sends projections to the DS. These two pathways are interfaced through a bilateral connection between the NA and the SNc. Prediction error learning and reward valuation substrates are strongly interrelated and so are considered together.

The mesolimbic projections from VTA to the NA and PFC contribute to reward processing and valuation. The VTA has been implicated in the valuation of rewards (Tobler, Fiorillo, and Schultz 2005; Schultz 1998; Roesch, Calu, and Schoenbaum 2007; Schultz, Dayan, and Montague 1997) and in the processing of prediction errors (Bayer and Glimcher 2005; Schultz 1998; Waelti, Dickinson, and Schultz 2001; Schultz, Dayan, and Montague 1997). The NA contributes to the assignment of the incentive motivational value of rewards (Galtress and Kirkpatrick 2010b; Peters and Büchel 2011; Olausson et al. 2006; Robbins and Everitt 1996; Zhang, Balmadrid, and Kelley 2003). As a result, it has been proposed as a possible target site for the computation of overall reward value (Gregorios-Pippas, Tobler, and Schultz 2009; Kable and Glimcher 2007).

Prediction error coding has been linked to the nigrostriatal pathway, particularly the dopaminergic neurons in the SNc (Schultz 1998; Waelti, Dickinson, and Schultz 2001; Bayer and Glimcher 2005; Schultz, Dayan, and Montague 1997). The SNc has also been implicated in anticipatory timing of rewards (Matell and Meck 2004; Meck 2006), indicating clear ties between timing and prediction error learning.

An additional component of the reward processing system is the orbitofrontal cortex (OFC). The OFC connects to the NA and the basolateral amygdala (BLA), both of which contribute to the reward prediction and valuation system. The OFC also sends outputs to pre-motor cortex (PMoC), which is a part of the timing system. In addition to the NA, the OFC has also been linked with establishing the incentive motivational value of different rewards (Peters and Büchel 2010, 2011; Kable and Glimcher 2009; Kringlebach and Rolls 2004) and updating the value of reward in response to devaluation (Winstanley 2004). The OFC also contributes to the working memory representations for reward information (Frank and Claus 2006). The lateral OFC has been noted to play a role in the prediction of future rewards (Daw et al. 2006), the reward value of predictive stimuli (Gottfried, O’Doherty, and Dolan 2003), and the determination of negative reward value (Frank and Claus 2006), all of which are linked with different aspects of prediction error learning. The medial OFC (also known as the ventromedial PFC) has been implicated in a variety of reward-processing activities including the representation of reward incentive value (Peters and Büchel 2010, 2011), the encoding of the magnitude of obtained monetary reward and prediction of future rewards (Daw et al. 2006), the determination of positive reinforcement values (Frank and Claus 2006), the processing of immediate rewards (McClure et al. 2004), and the determination of cost and/or benefit information (Cohen, McClure, and Yu 2007; Basten et al. 2010). The right-central OFC appears to be involved more heavily in evaluating delayed and/or probabilistic rewards (Peters and Büchel 2009b), the subjective value and/or variance of rewards (O’Neill and Schultz 2010), and the size of reward (da Costa Araujo et al. 2010), indicative of a general valuation mechanism residing in this region (Peters and Büchel 2009a). Given the widespread involvement in reward valuation, and its key connections to the timing system, the OFC is a candidate structure for integration of information across multiple components of the reward system and may be a key substrate in the interactions between timing, motivation, and prediction error computations.

The BLA is also an important contributor to this system, through its connection with the OFC. An intact BLA-OFC connection is necessary for the formation of reward expectancy and the usage of expectancies to guide goal-directed behavior (Holland and Gallagher 2004). The BLA has been demonstrated to play a role in representing the sensory properties of both rewarding (Blundell, Hall, and Killcross 2001) and aversive stimuli (see Baxter and Murray 2002). It also appears to be crucial for the acquisition of value representations (Frank and Claus 2006) that are then held within the medial OFC (Peters and Büchel 2011; Schoenbaum et al. 2003). The BLA also may contribute to the encoding of cost (or loss) signals (Basten et al. 2010) and may be important for maintaining a representation of reward in its absence (Winstanley 2004). The BLA also sends projections to the NA and PFC. The BLA input into the NA mediates incentive processes for goal-directed behaviors (Shiflett and Balleine 2010).

Overall, the reward prediction and valuation system is involved in complex aspects of prediction error learning in classical and instrumental conditioning. This system is also concerned with determining the sensory features of important events (BLA) and sending that sensory information to the NA for use in determining the overall value of the reward as well as to cortical areas that are involved in integrating information relating to prediction and valuation (OFC). The determination of reward value is then made available to the timing system through the SNc, DS, and cortical regions (OFC/PMoC). Timing is strongly interwoven with prediction error/reward learning, but there are also unique neural substrates involved in timing and prediction error learning.

5. Interpretations derived from neural circuitry

The more recent gains in understanding the neurobiology of timing and prediction error learning has opened the door for the development of neurocomputational models that may be more biologically plausible than was previously possible. By examining the structure and function of the neural circuitry, it is possible to gain deeper insights into the interactions between prediction error learning and timing, and use those insights to guide future theoretical developments.

5.1. Prediction error learning and timing

Section 2.1 described several core facets linking timing and prediction error learning: (1) CRs are timed appropriately from the beginning of conditioning; (2) CS-US interval duration is directly related to CR strength; and (3) relative CS duration and/or variability affects cue competition in blocking and overshadowing.

In terms of CR timing, the shared SNc role in prediction error learning and timing provides a route for simultaneous learning of both whether and when the US is expected relative to CS onset. The fact that the same substrates are implicated in both processes provides a natural explanation for why timing and conditioning emerge together, because they are controlled by the same pathway. However, that does imply that they may be one and the same process. Further research should examine the role of this pathway and any sub-structures in CR occurrence versus CR timing early in acquisition to determine whether these two aspects of CRs are locked together due to shared neural processing.

The effects of CS-US interval on CR strength could also emerge from the SNc-DS pathway since this pathway most likely encodes CS-US interval duration. However, the TH may play an additional role neurons within this structure show ramping activation patterns that are tuned to the CS-US interval duration (Komura et al. 2001). Because the TH has direct input to the DS, these ramping neurons could supply CS-US duration information that could modulate CR timing and CR strength through the DS output to the BG. Note that the BG system has bi-directional connections to the TH, providing a feedback loop for modulating CR timing in relation to CS-US interval duration (and also presumably variability in the CS-US interval). Further research should explore the role of this feedback loop in modulating CR strength and timing, and particularly in relation to the role of the SNc-DS pathway in affecting CR timing and strength.

Phasic dopamine firing in the midbrain dopamine reward system, including the VTA, NA, and PFC has been implicated in encoding prediction error signals that are critical for a variety of cue competition effects (see Hazy, Frank, and O’Reilly 2010 for a review). Since these areas are also clearly associated with a variety of timing phenomena, this system is a good candidate for involvement in the effects of temporal variables on blocking and overshadowing. However, our understanding of the involvement of this system in cue competition is fairly limited, even with respect to simple aspects of cue competition, so a considerable expansion of research in this area is needed to determine the role of these (and other) structures in the temporal modulation of cue competition phenomena.

5.2. Prediction error effects on timing

Based on the discussion in Section 2.2, there are a few fundamental effects of reward prediction errors on timing. With reward magnitude changes, there are directionally specific effects with increases in magnitude shifting the peak to the left and decreases shifting the peak to the right (Ludvig, Balci, and Spetch 2011; Ludvig, Conover, and Shizgal 2007; Balci et al. 2013; Grace and Nevin 2000; Galtress and Kirkpatrick 2009, 2010b). Satiety (or lithium chloride-induced taste aversion) shifted the peak to the right, but devaluation procedures do not appear to be directionally selective as release from satiety also shifted the peak to the right (Galtress and Kirkpatrick 2009; Galtress, Marshall, and Kirkpatrick 2012; Balci, Ludvig, and Brunner 2010). Temporal discrimination procedures have been less well studied, but it appears that both reward magnitude and devaluation procedures flatten the psychophysical function, suggesting that these effects may be operating on attention, or perhaps decision processes (Ward and Odum 2006; Galtress and Kirkpatrick 2010a).

The candidate areas for involvement in the prediction error effects on timing through changes in reward magnitude would be the NA which has been demonstrated to code the overall value of reward (Cardinal et al. 2001; Galtress and Kirkpatrick 2010b; Bezzina et al. 2007; Bezzina et al. 2008; Pothuizen et al. 2005; Winstanley et al. 2005; Peters and Büchel 2010, 2011). The NA is clearly involved in some manner in the reward magnitude shift effects on timing, as lesions of this area resulted in deficits in the reward magnitude-timing interactions (Galtress and Kirkpatrick 2010b). In addition, striatal dopamine 2 (D2) receptors and dopamine transporter (DAT) levels have been shown to play a key role in the motivational effects on timing, lending further evidence to the importance of the mid-brain dopamine system in contributing to the effects of reward prediction errors/motivational effects on timing (Balci et al. 2010; Balci et al. 2013; Ward et al. 2009). In addition, the SNc projections to DS would be expected to contribute to generating the prediction error signal (Schultz, Dayan, and Montague 1997) which would presumably be an important contributor to the reward magnitude/value effects on timing as these effects are driven by a change in reward magnitude rather than the absolute magnitude of reward (Galtress and Kirkpatrick 2009). Through its bidirectional connections with the DS, the SNc provides a route for the prediction error signal to influence timing. In addition, the SNc modulates the excitatory/inhibitory balance between the direct and indirect pathways from DS to TH, which sends excitation/inhibition signals to the motor cortex to induce response output. Changes in reward magnitude could shift the peak through the SNc altering the balance of excitation and inhibition on a moment-to-moment basis.

When the reward value is increased (through release from satiety) or decreased (through induction of satiety, or LiCl induced taste aversion), the peak has been reported to shift to the right in both cases (Galtress, Marshall, and Kirkpatrick 2012). Here, the most likely pathway leads through the OFC, which has been linked with processing changes in the incentive motivational value of rewards under devaluation conditions (Gottfried, O’Doherty, and Dolan 2003). The OFC would then transmit the altered reward value to the NA, which would then send this information to the SNc, which could then regulate the timing of responding through modulation of excitation/inhibition of the BG output pathways to TH.

The results from the temporal discrimination procedures, both with reward magnitude and satiety devaluation have implicated either attention or decision mechanisms (Galtress and Kirkpatrick 2010a; Ward and Odum 2006). One interesting connection is the effects of DAT knockdown (KD) on timing behavior. Mice with a DAT-KD manipulation have higher basal dopamine levels and also displayed deviations in their timing behavior with earlier start times than their wild type counterparts (Balci et al. 2010). Injections of the D2 antagonist raclopride normalized timing in the DAT KD mice, indicating that the deviations in their timing were most likely to due increased D2 receptor activity. Further testing with an attention-based task indicated that the DAT KD mice performed normally, suggesting that the increased DA levels may have altered the decision threshold for responding rather than attention to time. Further research is needed to verify this possibility and to more directly link these results with the prediction error manipulations.

6. Evaluating neural plausibility of current hybrid models

As new models are under development, one factor that is proving increasingly important is neural, or biological, plausibility. Currently, there is sufficient information on the neural processes involved in timing and prediction error learning to begin to incorporate those processes into modeling efforts. As more information becomes available, the models can evolve further. Neurobiological evidence has begun to impact on model development, leading to the evolution of new model frameworks, but this enterprise is still in its infancy.

In terms of biological plausibility, the TDDMs (Luzardo, Ludvig, and Rivest 2013; Rivest and Bengio 2011; Simen et al. 2011) are good candidates as they rely on noisy ramping functions that become tuned to the experienced temporal durations. Noisy ramping functions have been recorded in multiple brain areas within the timing system including the TH and several cortical regions (Komura et al. 2001; Leon and Shadlen 2003; Reutimann et al. 2004; Lebedev, O’Doherty, and Nicolelis 2008). The STT model (Grossberg and Schmajuk 1989) also was developed based on neuronal firing patterns and represents a reasonable early attempt at biological plausibility, but considerable new evidence has accumulated since this model was created and thus further development is required to incorporate more recent behavioral and neurobiological evidence. The SBF model (Matell and Meck 2004) has also been developed with neural plausibility as a driving factor. This model is based on observations of coincidence detectors within the striatum, and the dynamics of the model attempt to mimic the firing dynamics of neurons within this system (Miall 1989). However, as with the other models, the SBF model is in need of further development to account for a broad range of timing and prediction error learning phenomena. Although models such as TDDMs, STT and SBF show promise in integrating psychological and neurobiological evidence within the modeling framework, of all of the models under consideration, the TD models (Sutton and Barto 1981, 1990; Ludvig, Sutton, and Kehoe 2008, 2012) have fared the best in the test of biological plausibility. While the TD models are not without their weaknesses (see Section 3.2), there is considerable evidence in favor of prediction error coding within the midbrain dopamine system (Schultz, Dayan, and Montague 1997; Montague, Dayan, and Sejnowski 1996; Schultz 2006; Ludvig, Bellamare, and Pearson 2011; Hazy, Frank, and O’Reilly 2010; Maia 2009; Niv 2009), and so TD models represent a positive step forward in modeling behavior through the neural plausibility route.

7. Conclusions and looking ahead

The timing field is one of the richest in the array of different extant models, all of which have interesting computational properties. There are many different ideas relating to the nature of the perceptual functions that underlie timing, from pacemaker-type processes (SET and SBF) to oscillatory processes (MOM), individual ramping functions (TDDMs), sets of ramping functions (STT, LeT), and decaying functions (TD models). There are also different ideas for memory storage including storage of individual items (SEM), auto-association matrices (MOM) or average strength-based representations (LeT, STT, TDs, TDDMs, and RET).

Models are living organisms that evolve as new evidence becomes available. As a result, timing models have evolved over successive generations. The BeT model inspired the development of LeT, which coupled some of the timing aspects of BeT with some aspects of prediction error models, specifically excitation and extinction processes. SET eventually led to the development of RET, which was designed to provide a prediction error component to couple with the timing component of SET. And then later, RET evolved further to incorporate aspects of Shannon’s information processing theory. SET also sparked the creation of SBF, which incorporated neural plausibility and also included some prediction error components in the memory, which transformed into a memory strength instead of a collection of pulses. The PT model eventually led to the MOD theory, which expanded on PT by proposing separate memory structures for pattern learning (timing) and strength learning (prediction error). And, finally the TD models evolved out of the linear operator models such as the Rescorla-Wagner model, but these models incorporated timing aspects into a prediction error framework.

The speed and extent to which models are evolving is not a weakness of the timing field, but instead is a reflection of the richness of the phenomena to be explained. And, as more information on the behavioral and neurobiological aspects of timing and prediction error learning becomes available, this will spark further model development. The purpose of this special issue was to ask the question of whether timing and associative learning are separate processes and whether the brain mechanisms and computations differ. One area of importance in answering these questions is the effects of temporal variables on prediction error learning and the effects of prediction errors on timing. There still is much to learn about the nature of these interactions, and multiple methods incorporating quantitative behavioral analysis, neuroscientific investigations, and neurocomputational modeling are required to answer the most challenging questions. The development of biologically plausible models that bridge timing and prediction error learning should be one important focal area for the future of the field.

Highlights.

• Timing and prediction error learning have historically been treated as independent processes, but growing evidence has indicated that they are not orthogonal

• Modern theories have attempted to integrate the two processes with mixed success.

• A neurocomputational approach to theory development is espoused, which draws on neurobiological evidence to guide and constrain computational model development.

• Heuristics for future model development are presented with the goal of sparking new approaches to theory development in the timing and prediction error fields.