Abstract
Separated concerted proton-electron transfer (sCPET) reactions of two series of phenols with pendent substituted pyridyl moieties are described. The pyridine is either attached directly to the phenol (HOAr-pyX) or connected through a methylene linker (HOArCH2pyX) (X = 4-NO2, 5-CF3, 4-CH3, 4-NMe2). Electron-donating and -withdrawing substituents also have a substantial effect on the chemical environment of the transferring proton, as indicated by IR and 1H NMR spectra, X-ray structures and computational studies. One-electron oxidation of the phenols occurs concomitantly with proton transfer from the phenolic oxygen to the pyridyl nitrogen. The oxidation potentials vary linearly with the pKa of the free pyridine (pyX), with slopes slightly below the Nerstian value of 59 mV/pKa. For the HOArCH2pyX series, the rate constants ksCPET for oxidation by NAr3•+ or [Fe(diimine)3]3+ vary primarily with the thermodynamic driving force (ΔG°sCPET), whether ΔG° is changed by varying the potential of the oxidant or the substituent on the pyridine, indicating a constant intrinsic barrier λ. In contrast, the substituents in the HOAr-pyX series affect λ as well as ΔG°sCPET, and compounds with electron-withdrawing substituents have significantly lower reactivity. The relationship between the structural and spectroscopic properties of the phenols and their CPET reactivity is discussed.
Keywords: Proton-coupled electron transfer, phenol, oxidation, structure-activity relations, tunneling distance, tyrosine-Z
INTRODUCTION
Proton-coupled electron transfer (PCET) reactions are of considerable current interest, due to their importance in fundamental biological processes, energy transduction, and other chemical transformations.1–6 Of particular importance is developing an understanding of the parameters that affect PCET reactivity. This report is focused on one class of PCET reactions, in which a proton and an electron are transferred to different sites in a single kinetic step, termed separated concerted proton-electron transfer (sCPET)7,8 or alternatively multiple site electron-proton transfer (MS-EPT).2 Such reactions play important roles in a variety of chemical and biological processes, from energy conversion to the generation of reactive oxygen species.1 One important example is the oxidation of tyrosine to a neutral tyrosyl radical,9,10 for instance in the oxidation of water to O2 by Photosystem II.11–15 This catalytic cycle involves oxidation of tyrosine-Z by long-range electron transfer to an oxidized chlorophyll P680 molecule concomitantly with transfer of the phenolic proton to a near-by hydrogen-bonded histidyl imidazole.16,17
The understanding of separated CPET reactions is being developed through both experimental and theoretical studies. One of the goals of work reported here is to build stronger connections between experiment and theory, which is challenging because of the complexity of the theoretical formulations.5,18–23 Many of these formulations view sCPET as an outgrowth of the non-adiabatic form of the Marcus theory of electron transfer.24,25 Marcus theory relates the rate constant to a pre-exponential electronic coupling term Vel and exponentially to a free energy barrier ΔG* that is related to the thermodynamic reaction driving force (ΔG°) and an intrinsic barrier or reorganization energy λ (eq. 2). Extending this formalism to sCPET requires taking into account the proton tunneling probability, which can be done with a Franck-Condon (FC) term describing the overlap between proton vibrational wavefunctions in the reactants and products. The rate expression in equations 1 and 2 is a simplistic version of this formalism, and provides a framework with which to interpret experimental results.
| (1) |
| (2) |
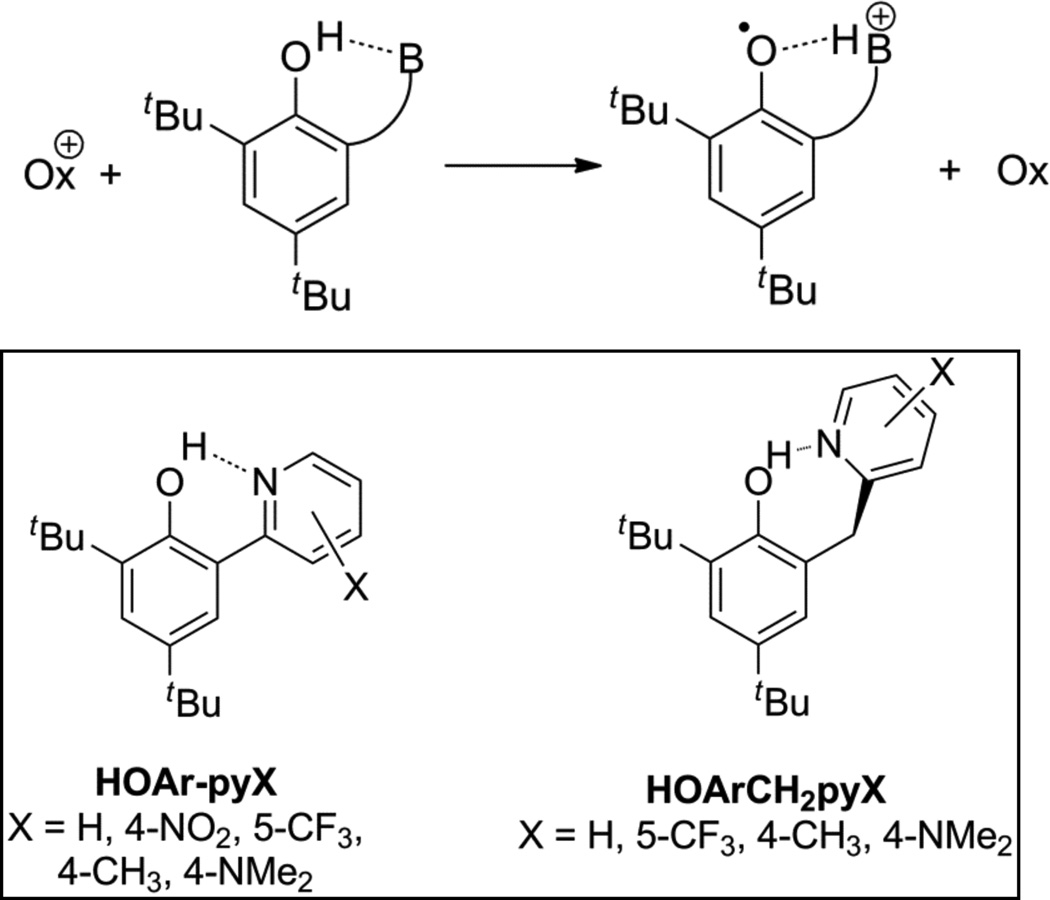
Phenol oxidations have been a focus of experimental studies of sCPET, apparently starting with Linschitz et al.’s study of photoexcited C60 oxidizing a hydrogen-bonded adduct between phenol and pyridine.26,27 More recent studies by the groups of Hammarström, Meyer, Thorp, Nocera, Savéant and others have used photochemical and electrochemical approaches to study sCPET.28–39 These studies have primarily been performed in aqueous solution with external proton acceptors, typically a buffer ion or hydroxide. However, these studies are complicated by termolecular kinetics and a lack of definition of the proton transfer coordinate. Our approach has used stopped flow kinetic studies of phenols with well-defined intramolecular hydrogen bonds in aprotic media, using model systems consisting of a di-tert-butyl phenol with a base attached ortho to the phenolic oxygen.7,40–42 When an electron is removed by an outer-sphere oxidant, the phenolic proton is transferred intramolecularly to the basic site to give a distonic radical cation (Scheme 1). The use of a pendent basic site in aprotic media is advantageous for studying the effect of various parameters on sCPET reactivity because the free energy change, ΔG°sCPET, is readily determined using cyclic voltammetry or chemical equilibration experiments. Also, the chemical environment of the transferring proton within the relatively strong O-H⋯N hydrogen bond can be probed experimentally and computationally.
Scheme 1.
sCPET reactivity of phenols with pendent bases, and the phenols with pendent pyridines used in this study, HOAr-pyX and HOArCH2pyX.
In previous studies of phenol-pyridines, our laboratory has found that changing the pendent base can substantially affect the sCPET reactivity, and that rate constants (ksCPET) across the whole series do not simply correlate with driving force.7,40 Specifically, phenols with pendent pyridyl and imidazolyl basic sites in conjugation with the phenol undergo sCPET with substantially higher rate constants than phenols with unconjugated pyridyl and primary amine basic sites, even at the same ΔG°sCPET. This effect was initially attributed to a lowering of λ in the conjugated systems due to stronger hydrogen bonding between the phenol and the basic site,40 and recent results indicate that differences in the exponential prefactor vibrational and electronic overlap terms also contribute.43
Herein, the properties of the phenol-pyridine molecules that affect their sCPET reactivity are examined in more detail. As shown in the bottom of Scheme 1, two series of di-tert-butyl phenols with pendent substituted pyridine bases have been synthesized and studied. The HOAr-pyX compounds (X = 4-NMe2, 4-CH3, 5-CF3, 4-NO2) have a substituted pyridine attached directly to the phenol, while the HOArCH2pyX series (X = 5-CF3, 4-CH3, 4-NMe2) have the pyridine attached to the phenol through a methylene linker. A preliminary account has described the chemistry of the unsubstituted compounds (X = H).40 In this study, the substituents allow systematic variation of the sCPET driving force, the strength of the OH⋯N hydrogen bond, the proton transfer distance (dON), the X–H vibrational frequencies, and other parameters relevant to sCPET kinetics. There is a strong contrast between the behaviors of the conjugated (HOAr-pyX) vs. the non-conjugated (HOArCH2pyX) compounds, in terms of how their reactivity depends on ΔG°sCPET and how their intrinsic reactivity (at ΔG°sCPET = 0) is modulated by the substituents.
RESULTS AND DISCUSSION
Synthesis and Characterization
The non-conjugated pyridyl-methyl-phenols HOArCH2pyX were synthesized by a modification of the previously reported method for the parent HOArCH2py.40 Ortho-lithiated substituted pyridines were prepared in situ from n-butyllithium and the corresponding substituted 2-halopyridine and were added to benzyl-ether protected 3,5-di-tert-butylsalicylaldehyde. The resulting alcohol was acylated, and catalytic hydrogenation removed both the acetate and the benzyl protecting group. The substituted pyridyl phenols HOAr-pyX were prepared via Suzuki couplings of 2,4-di-tert-butyl-methoxyphenyl-6-boronic acid with the appropriate halo-pyridine, followed by deprotection of the phenol. All the HOArCH2pyX and HOAr-pyX compounds were characterized by 1H and 13C NMR spectroscopy and mass spectrometry.
The substituents have a substantial effect on the 1H NMR chemical shift of the phenolic proton (δOH) in ‘dry’ CD3CN. In the pyridylmethyl series HOArCH2pyX, this proton appears as a singlet with δOH from 10.19 ppm for the nitro derivative (X = NO2) to 12.06 ppm for X = NMe2. This singlet is far downfield from δOH for phenols without pendent basic sites, such as tri-tert-butyl phenol (δOH = 5.3 in this solvent). The phenolic resonances for HOAr-pyX are even further downfield, ranging from δ14.01 to 15.45 ppm (Table 1).
Table 1.
Structural and spectroscopic properties of HOArCH2pyX and HOAr-pyX.
| X | pKaa | δOHb | dON (X-ray)c | dON(DFT)c | νOHDFTd | |
|---|---|---|---|---|---|---|
| -CH2pyX | 4-NMe2 | 18.5 | 12.06 | - | 2.726 | 3053 |
| 4-CH3 | 14.1 | 11.31 | 2.724(3) | 2.753 | 3137 | |
| He | 12.9 | 11.15e | 2.6914(13)e | 2.761 | 3160 | |
| 5-CF3 | 9.5 | 10.19 | [2.778(5), 2.766(5)]f | 2.782 | 3224 | |
| -pyX | 4-NMe2 | 18.5 | 15.45 | 2.500(4) | 2.551 | 2838 |
| 4-CH3 | 14.1 | 14.95 | 2.531(3) | 2.560 | 2897 | |
| Hg | 12.9 | 14.83 | [2.561(3), 2.567(3), 2.573(3)]f | 2.565 | 2918 | |
| 5-CF3 | 9.5 | 14.26 | [2.565(4), 2.547(4), 2.570(4)]f | 2.569 | 2958 | |
| 4-NO2 | 8.7 | 14.01 | 2.548(3) | 2.578 | 2999 | |
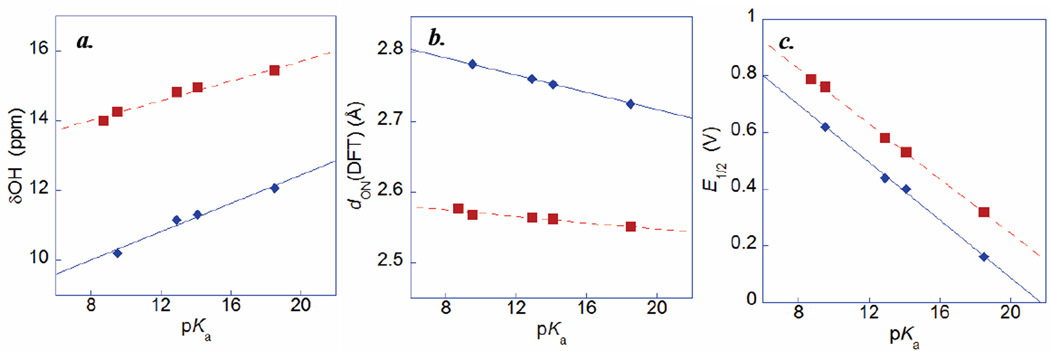
These large differences in chemical shift reflect differences in the OH⋯py hydrogen bonding. In general, stronger hydrogen bonding leads to more downfield δOH resonances,44 and the hydrogen bond strength increases as the pKa of the donor and [protonated] acceptor are more closely matched.45 Determining the effective base strength of the pyridine in these strongly H-bonded compounds is problematic, so we use the pKa of the free pyridine as a measure of the substituent effect. The substituted pyridines pyX vary in basicity by nearly ten orders of magnitude, as the protonated pyridinium ions in acetonitrile solution have estimated pKas ranging from 8.7 for 4-nitropyridinium to 18.5 for 4-dimethylaminopyridinium.46–52 The more electron-donating substituents raise the pKa of the pyridinium, bringing it closer to the pKa of the phenol (pKa of phenol = 27 in MeCN),54 and thereby leading to stronger hydrogen bonding and more downfield resonances. Given the large range of basicity, there should be notable differences in the hydrogen bonding environment of the phenolic proton, so the variation in δOH is not surprising. Within each series of compounds, δOH varies roughly linearly with the pKa of the pyridinium (Figure 1a), and for the same substituent the chemical shift for HOAr-pyX is almost 4 ppm downfield of HOArCH2pyX.
Figure 1.
Variation of thermochemical and structural parameters in HOArCH2pyX (blue  ) and HOAr-pyX (red
) and HOAr-pyX (red  ) versus the estimated pKa of the pyridinium (see Ref. 46).
) versus the estimated pKa of the pyridinium (see Ref. 46).
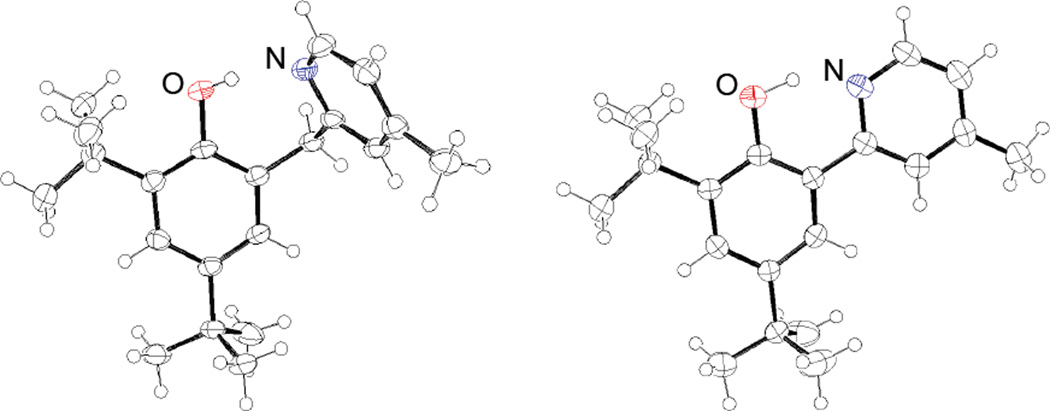
Another key parameter of the OH⋯N hydrogen bond is the donor-acceptor distance between the phenol oxygen and the pyridyl nitrogen, dON. X-ray crystal structures were obtained for all of the HOAr-pyX compounds and for all HOArCH2pyX derivatives except for X = NMe2 (Table 1). ORTEP drawings for two representative structures are given in Figure 2. The dON are ca. 0.2 Å longer for the HOArCH2pyX vs. the HOAr-pyX compounds, because of the larger ring size for the HOArCH2pyX derivatives. In most cases, smaller dON are found for compounds with more electron donating substituents, but the range of distances is small. A number of the structures have multiple independent molecules in the unit cell, which differ in their dON values by more than 0.01 Å, indicating that crystal packing plays a significant role in the observed dON.
Figure 2.
ORTEPs of HOArCH2pyCH3 (left) and HOAr-pyCH3 (right).
Computed structures may give a better indication of the dON in solution, avoiding the influence of crystal packing forces. Density functional theory gas-phase B3LYP/6–31G(d,p) optimized geometries (Tables 1 and S18) correlate more strongly with the pKa of the pyridyl group (Figure 1b). Calculated values of dON for HOArCH2pyX vary by 0.056 Å, and for HOAr-pyX they vary by 0.026 Å. While dON is a useful parameter for assessing trends in hydrogen-bonding, this is only a proxy for the underlying factors that determining CPET reactivity, i.e. the Franck-Condon overlap factors. These overlaps depend on parameters such as the proton tunneling distance, the shape of the proton wavefunctions, and the linearity of hydrogen bond (∠OHN) as well as the geometry of the hydrogen bond (the location of the proton). For the phenols compounds discussed here, the seven-membered ring in HOAr-CH2pyX allows for a more linear hydrogen bond. For instance, ∠OHN = 161° in HOAr-CH2pyH compared to ∠OHN = 149° in the six-membered ring in HOAr-pyH.40 Within each series, there is only a small variation in ∠OHN (< 2°), with the more electron rich pyridines having more linear as well as shorter H-bonds. In the radical cations, the opposite trends in dON and ∠OHN are observed: more electron-withrawing substituents lead to shorter, more linear O⋯H-N hydrogen bonds. This is because the low pKa of the phenoxyl radical (ca. 0) means that stronger hydrogen bonding is expected with electron-withdrawing substituents due to better pKa matching. The radical cations show a larger effect of substituents, for example dON varies by 0.08 Å and ∠OHN values span 4.8° for •OArCH2(H+)pyX. Because of these opposing trends, the difference in the equilibrium proton position in the neutrals vs. the radical cations decreases with more electron-withdrawing substituents, by 0.043 Å and 0.12 Å in HOAr-pyX and HOArCH2pyX. This is the opposite trend compared to dON in the neutral state. However, this calculation takes into account the movement of the heavy atoms (e.g. changes in dON) from reactants to products so it is not an accurate proton tunneling distance. A related study by Johannissen et al.32b took into account ∠OHN of the radical cation but not the changes in dON, and found an increase in the tunneling distance with electron-withdrawing substituents, but the magnitude is less than the changes in dON (by a factor of 3 in each series). These results highlight the complexity of predicting geometric effects on CPET reactivity.
Calculated gas phase OH stretching frequencies (νOHDFT), another measure of hydrogen bond strength, also correlate with the pKa of the base. These values are calculated from the second derivative of the potential energy surface at the minimum, and therefore do not capture the anharmonicity and mode mixing that strongly affect the experimental spectra.55 The calculated νOHDFT are ca. 250 cm−1 higher for the HOArCH2pyX compounds, and the values are higher with more electron withdrawing substituents (from 3053 cm−1 for X = NMe2 to 3224 cm−1 for X = CF3 for HOArCH2pyX; Table 1).
Taken together, the dON, νOHDFT, and δOH values indicate that there is weaker hydrogen bonding for the HOArCH2pyX compounds, and weaker hydrogen bonding with more electron-withdrawing X groups. The changes in these parameters across each series are somewhat smaller than the differences between the two series: i.e., HOAr-pyNO2 has a shorter dON, lower νOH, and higher δOH than does HOArCH2pyNMe2. Figures 1a and 1b also show that the effect of the substituent is more pronounced for the HOArCH2pyX compounds than for HOAr-pyX. This could be due to the HOArCH2pyX compounds having greater flexibility of their seven-membered rings, more linear O-H⋯N angles, or because the conjugation in HOAr-pyX allows for compensatory effects of the substituent on the pKa of the phenol, as discussed below.
Thermodynamics of HOArCH2pyX and HOAr-pyX Oxidation
The potentials for oxidation of HOArCH2pyX and HOAr-pyX were determined by cyclic voltammetry. Cyclic voltammograms (CVs) of HOArCH2pyX and HOAr-pyX in acetonitrile containing 0.1 M [n-Bu4N][PF6] are chemically reversible, with roughly equal anodic and cathodic currents. The separations between the anodic and cathodic peaks (ΔEp) are somewhat larger than the theoretical value of 0.059 V, as has been observed in related systems.6,7,40–42 These quasi-reversible CVs indicate that electrochemical oxidation is coupled to proton transfer to the pyridyl moiety. Reversible cyclic voltammograms have been observed for a variety of phenols with pendent bases in aprotic media,7,40–42,56 while the CVs of phenols without pendent bases in aprotic media are irreversible,57 in part due to proton transfer to the bulk solution upon oxidation. Proton transfer from the phenol is energetically favorable because the phenol radical cation is very acidic, with a pKa in acetonitrile of ~0.57 CVs of compounds with weaker hydrogen bonds, e.g. HOAr-pyNO2, HOAr-pyCF3, and HOArCH2pyCF3, show decreased cathodic currents, indicating instability of the oxidized product on the timescale of the experiment. CVs of these compounds at increased scan rates show greater electrochemical reversibility (see Supporting Information Figures S2 – S3). This instability may be due to partial deprotonation of the weakly basic pendent pyridines on the timescale of the CV experiment.
The measured redox potentials (E1/2) for HOArCH2pyX vary with substituent, ranging from 0.16 to 0.62 V vs. Cp2Fe+/0 for X = NMe2 and CF3, respectively (Table 2). The redox potentials vary linearly with the estimated pKa of the pyridyl moiety (Figure 1c), indicating that the thermodynamics of oxidation depend on the energy to transfer the proton to the basic site. The slope of this relationship is −0.051(2) V/pKa, just slightly lower than the predicted value of −0.059 V/pKa. This result underscores a key advantage of this system in the study of sCPET, as the thermodynamics of the proton transfer are varied in a systematic and well-defined way. The redox potentials of HOAr-pyX also vary linearly with the pKa of the pyridyl moiety (Table 2 and Figure 1c). The slope of this relationship, −0.048(1) V/pKa, is slightly further from the predicted value than for HOArCH2pyX. This somewhat greater deviation from the predicted value is likely due to the increased electronic communication between the phenol and the substituent on the pyridine in the conjugated compounds, which allows compensatory effects on the acidity of the phenol. For instance, an electron-donating substituent lowers the proton-coupled E1/2 primarily by increasing the pKa of the pyridine, but this effect is partially offset by an increase in the pKa of the more distant phenol.
Table 2.
Thermochemical properties of HOArCH2 pyX and HOAr-pyX.
Kinetics of sCPET Oxidations of HOArCH2pyX and HOAr-pyX
The kinetics of the reactions of HOArCH2pyX and HOAr-pyX with one-electron chemical oxidants in acetonitrile at 295(2) K were measured by stopped-flow UV/Vis spectroscopy. The one-electron oxidants used were the hexafluorophosphate salts of a variety of para-substituted triarylamminium cations, [N(C6H4X)3]+·, and substituted tris(bipyridyl) and tris(phenanthroline) iron(III) complexes, [Fe(R2bpy)3]3+ and [Fe(Mexphen)3]3+. Reaction kinetics were fit globally, but marked primarily by the disappearance of the blue amminium oxidant in reactions using [N(C6H4X)3]+· or by the appearance of the reduced FeII species in reactions performed with [Fe(R2bpy)3]3+ and [Fe(Mexphen)3]3+. Typical reactions were performed with ca. 0.01 mM oxidant and the phenol concentration varied from ca. 3 – 30 equivalents. Bimolecular rate constants were obtained by fitting to opposing second order kinetics using SpecFit™ global analysis software.58 The results are summarized in Table 3.
Table 3.
Kinetic data for oxidations of HOArCH2pyX and HOAr-pyX.
| Phenol | Oxidant | Erxn(V) | k (M−1 s−1) | k° (M−1 s−1)a |
|---|---|---|---|---|
| -CH2pyNMe2 | [N(C6H4OMe)3]+• | 0.00 | 5.4 ± 0.5 × 105 | 5.4 × 105 |
| -CH2pyCH3 | [N(C6H4OMe)(C6H4Br)2]+• | 0.08 | 8.0 ± 0.9 × 105 | 1.7 × 105 |
| [N(C6H4Me)3]+• | −0.02 | 1.4 ± 0.2 × 105 | 2.2 × 105 | |
| [N(C6H4OMe)2(C6H4Br)]+• | −0.08 | 4.4 ± 0.5 × 104 | 2.2 × 105 | |
| [Fe(4,7-Me2phen)3]3+ | 0.13 | 5.0 ± 0.5 × 105 | 4.0 × 104 | |
| -CH2py | [N(C6H4OMe)(C6H4Br)2]+• b | 0.04 | 5.3 ± 0.5 × 105 | 2.4 × 105 |
| [N(C6H4Me)3]+• b | −0.06 | 1.2 ± 0.1 × 105 | 3.9 × 105 | |
| [N(C6H4OMe)3]+• b | −0.28 | 8 ± 2 × 102 | 1.9 × 105 | |
| [Fe(4,7-Me2phen)3]3+b | 0.09 | 2.5 ± 0.3 × 105 | 4.3 × 104 | |
| CH2pyCF3 | [N(C6H4Br)3]+• | 0.05 | 7.5 ± 1.5 × 105 | 2.8 × 105 |
| [N(C6H4OMe)(C6H4Br)2]+· | −0.14 | 7.6 ± 0.8 × 103 | 1.2 × 105 | |
| [Fe(4,7-Me2phen)3]3+ | −0.09 | 3.4 ± 0.3 × 103 | 2.0 × 104 | |
| -pyCH3 | [Fe(5,5′-Me2bpy)3]3+ | 0.05 | 2.2 ± 0.2 × 106 | 8.3 × 105 |
| -py | [Fe(bpy)3]3+ c | 0.12 | 5.2 ± 0.8 × 106 | 5.0 × 105 |
| [Fe(5,5′-Me2bpy)3]3+ c | 0.00 | 5.8 ± 0.9 × 105 | 5.8 × 105 | |
| [Fe(4,4′-Me2bpy)3]3+ | −0.07 | 4.5 ± 0.9 × 105 | 1.8 × 106 | |
| [Fe(4,7-Me2phen)3]3+ c | −0.05 | 1.9 ± 0.4 × 106 | 5.0 × 106 | |
| [Fe(3,4,7,8-Me4phen)3]3+c | −0.12 | 3.3 ± 0.6 × 105 | 3.4 × 106 | |
| [Fe(4,4′-tBu2bpy)3]3+ | −0.06 | 4.6 ± 0.5 × 104 | 1.5 × 105 | |
| -pyCF3 | [Fe(bpy)3]3+ | −0.06 | 3.7 ± 0.4 × 104 | 1.2 × 105 |
| [Fe(phen)3]3+ | −0.07 | 1.6 ± 0.2 × 105 | 6.3 × 105 | |
| -pyNO2 | [Fe(bpy)3]3+ | −0.09 | 2.1 ± 0.2 × 104 | 1.2 × 105 |
| [Fe(phen)3]3+ | −0.10 | 7.5 ± 1.5 × 104 | 5.3 × 105 |
A. Substituent and driving force effects on CPET kinetics of HOArCH2pyX
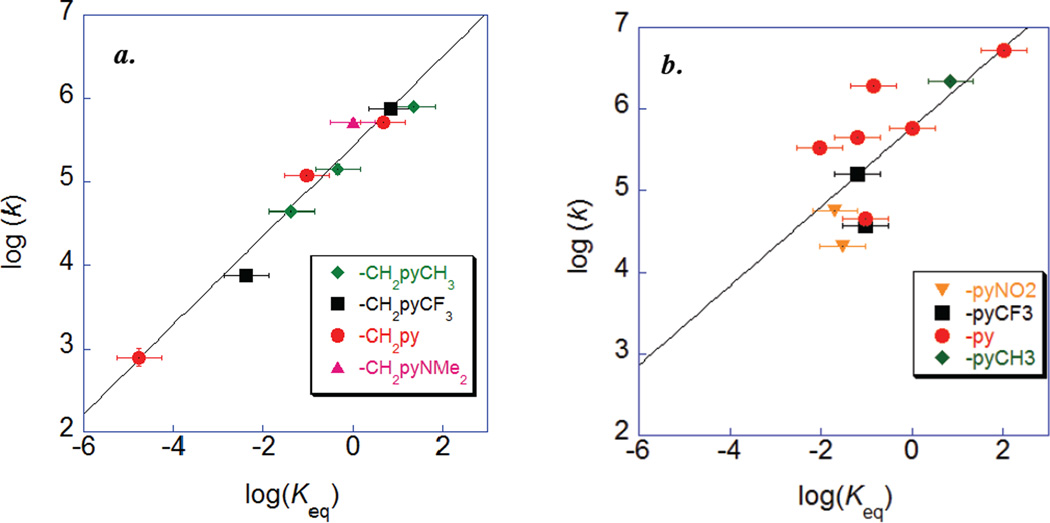
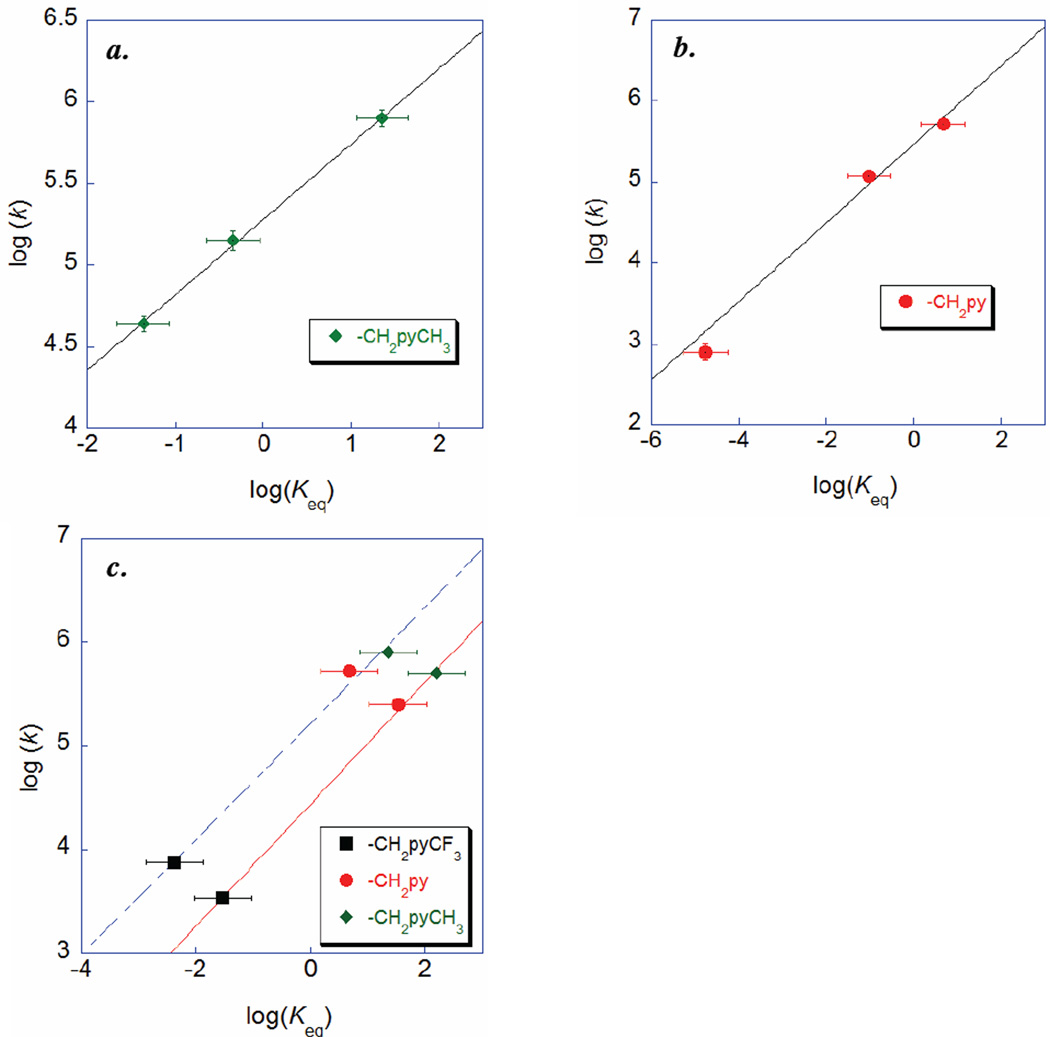
Bimolecular rate constants have been determined for nine CPET reactions of the substituted HOArCH2pyX compounds with various [N(C6H4X)3]+• oxidants. These rate constants span three orders of magnitude, while the ΔG° (from CV data) varies such that Keq spans 106, depending both on the choice of oxidant and internal base. A Brønsted plot, log(k) vs. log(Keq) (Figure 4a), of this data gives a strong linear correlation (R2 = 0.92) with a slope of α = 0.54(5). This value of α, which is equivalent to ∂ΔG*/∂ΔG°, is within error of the value of 0.5 predicted for CPET reactions in the limit where ΔG° << 2λ (eq. 2). Thus the rate constants for CPET reactions of HOArCH2pyX depend primarily of the driving force of the reaction, despite the changes in proton transfer coordinate discussed above. A similar result was obtained in our related studies of phenol-imidazoles (α = 0.55)42 and for a phenol-amine with oxidants of varying potential (α = 0.53).7 Fecenko, Thorp, and Meyer have reported a slope of ~0.6 for oxidation of tyrosine in aqueous buffers.31 Such a dependence of the rate on driving force has previously been shown to indicate a concerted proton-coupled mechanism rather than stepwise electron transfer/proton transfer or proton transfer/electron transfer.7,31,59
Figure 4.
Brønsted plots for (a.) reactions of HOArCH2pyX with [N(C6H4X)3]+·, and (b.) reactions of HOAr-pyX with [Fe(R2bpy)3]3+ and [Fe(Mexphen)3]3+.
While the correlation of rate constants with driving force in Figure 4a is quite strong, there are some modest deviations. These deviations could indicate whether the rate constants are affected differently when ΔG°sCPET is varied through the pKa of the base vs. E1/2 of the outersphere oxidant. In the reactions of HOArCH2pyCH3 and HOArCH2py, the ET component of ΔG° has been varied by changing the triarylamminium oxidant, [N(C6H4X)3]+·, as shown in the Brønsted plots of Figures 5a and 5b. These plots are linear (R2 = 0.99 for both) with α = 0.46(5) and 0.49(6), respectively. Alternatively, ΔG° can also be varied by the substituent on the pyridine. This affects primarily the ΔG°sCPET through well-defined changes in the pKa of the pyridine base (as indicated by the slope of the experimental E1/2 vs. estimated pKa). Figure 5c shows Brønsted plots for the oxidations of HOArCH2pyX (X = CF3, H, and Me) by [N(C6H4OMe)(C6H4Br)2]+· (points on dashed line) or by [Fe(Me2phen)3]3+ (points on solid line). Both of these plots are linear, with α = 0.57(6) (R2 = 0.99) for the amminium reactions and α = 0.59(6) (R2 = 0.99) for the iron reactions. At the same driving force, the amminium reactions have rate constants roughly ten times larger than the iron reactions, due to the smaller ET intrinsic barrier for the [N(C6H4X)3]+· reagents.7 The good agreement between the amminium and iron values of α suggests that in these reactions α is independent of the structure of the oxidant used.
Figure 5.
Brønsted plots for reactions of (a.) HOArCH2pyCH3 with [N(C6H4X)3]+·, (b.) HOArCH2pyH with [N(C6H4X)3]+·, and (c.) HOArCH2pyX with [N(C6H4OMe)(C6H4Br)2]+· (points on dashed blue line) and [Fe(Me2phen)3]3+ (points on solid red line).
The Brønsted slopes are larger when ΔG° is varied by changing the pyridine substituent [α = 0.57(6), 0.59(6)] than varying the oxidant [α = 0.46(5), 0.49(6)]. This conclusion is tentative because the plots each involve only three points, and the uncertainties are significant (due primarily to the large estimated uncertainties in the redox potentials and Keq values). However, the confidence level is raised by the agreement between the two series where the oxidant is varied (α = 0.48), and between the two series where the substituent is varied (α = 0.58). This result is in contrast to the previous study by Meyer et al., in which α ~ 0.6 was observed both when changing the oxidant potential and when changing the pKa of the buffer.31 There could be various reasons why the rate constants are more sensitive to variation in ΔG°sCPET from changes in the pKa of the base vs. changes in the E1/2 of the oxidant. In a purely classical picture, this could reflect an asymmetry in the reaction coordinate, with the transition structure involving more proton transfer.60 In the context of PCET theory (eq 1), changing the pyridine substituent could affect ksCPET via changes in the intrinsic barriers λ or quantum mechanical prefactor terms Vel and FC. This is discussed in more detail below. The net result is that more electron withdrawing substituents result in smaller rate constants than would be predicted if the substituent affected only ΔG°sCPET.
B. Substituent and driving force effects on CPET kinetics of HOAr-pyX
The reactions of the conjugated HOAr-pyX compounds are significantly faster than those of HOArCH2pyX at the same driving force, as was observed for the parent X = H compounds.40 This results in the reactions of HOAr-pyX with triarylamminiums being too fast to measure with our approach, because they are complete within the mixing time of the stopped-flow instrument even at the lowest practical concentrations. Still, the kinetics for ten reactions with [Fe(N-N)3]3+ oxidants have been measured (Table 3), with values of Erxn which vary by 0.24 V (or 104 in Keq) and rate constants that vary by a factor of 250. The majority of these are slightly uphill reactions (ΔG°CPET > 0), and have been measured with approach-to-equilibrium kinetics.
The Brønsted plot of log(k) vs. log(Keq) for oxidations of HOAr-pyX shows substantial scatter, as shown in Figure 4b above. The linear fit is very poor, with R2 = 0.53. For example, the reactions of HOAr-py + [Fe(4,7-Me2phen)3]3+ and HOAr-pyCF3 + [Fe(bpy)3]3+ have very similar driving forces (Erxn = −0.05 and −0.06 V) but their rate constants differ by a factor of 50. Thus for the HOAr-pyX series, other parameters besides the thermodynamic driving force play an important role in determining the sCPET rate. This contrasts with the non-conjugated HOArCH2pyX system, as well as the previous reports of sCPET phenol oxidations mentioned above.28–33,39,40,42
Examining the rate constants in Table 3, including the intrinsic rate constants k° described in the next section, it is apparent that the oxidation reactions with [Fe(Mexphen)3]3+ are significantly faster than the reactions with [Fe(R2bpy)3]3+. For instance, the oxidations of HOAr-pyCF3 and HOAr-pyNO2 are 4.3 and 3.6 times faster with [Fe(phen)3]3+ than with [Fe(bpy)3]3+ even though they are 10 mV less favorable. A small part of this is the ca. three-times larger electron transfer self-exchange reaction rate constants for [Fe(Mexphen)3]3+ vs. [Fe(R2bpy)3]3+.61 However, this should only account for a factor of about 1.7 (using the Marcus cross relation), which is almost exactly counterbalanced by the difference in driving force (accounting for a factor of 0.7 with α = ½). This effect was noted previously for of HOAr-py,7 but it is not observed in the reactions of HOArCH2pyX. In the context of Marcus models for CPET such as equation 1 above, the observation of a pyridyl-phenol reacting faster with [Fe(Mexphen)3]3+ than with [Fe(R2bpy)3]3+ at essentially the same driving force must be an effect of the electronic coupling Vel (also called HAB in ET theory). The other parameters that affect CPET rates are the Franck-Condon factors (FC) and the intrinsic barrier λ. The FC term is a property of the pyridyl-phenol, independent of the oxidant at the same ΔG°CPET, and the ET intrinsic barriers of the two oxidants are very similar based on the self-exchange rate constants given above.
The electronic coupling Vel is probably larger for the phenanthroline compounds than the bipyridine ones because the larger conjugated π system of phenanthroline provides a better conduit for electron transfer. The reason that this effect is seen for HOAr-pyX and not for HOArCH2pyX is most likely related to the conjugation of the phenol and substituted pyridine rings in HOAr-pyX. The optimal electron transfer pathway from the phenol to the oxidant could be via the pyridine since the phenol has two sterically protecting tertiary butyl groups. The significant interaction between the pyridyl and phenol groups in the HOAr-pyX compounds is indicated by the dependence of the CPET redox potential on the basicity of the pyridine, −0.048(1) V/pKa, which is lower than the 0.059 V/pKa predicted for non-interacting fragments (see above). In addition, the hydrogen bonds are significantly stronger for the HOAr-pyX compounds, as indicated by the O⋯N distances being ca. 0.2 Å shorter, the stretching frequencies being ~ 200 cm−1 lower, and the δOH being 3–4 ppm lower.
Understanding the substituent effect on sCPET kinetics
A. Intrinsic rate constants k°
To understand the effects of pyridine substitution on ksCPET, it is helpful to separate the thermodynamic contribution from other factors. The reactions described here all have |ΔG°| << 2λ,7 and in this limit the barrier ΔG* becomes linear with ΔG° and equation 1 reduces to equation 3. Separating out the thermochemical driving force from the intrinsic kinetic terms yields an “intrinsic rate constant” k° (eqs 4, 5). In essence, k° is the rate constant extrapolated to ΔG°= 0.62 This analysis is analogous to the derivation of the standard electrochemical rate constant by extrapolation to zero driving force using the Tafel slope, which is equivalent to the Brønsted α and is typically taken as ½, as in equations 3 and 4.
| (3) |
| (4) |
| (5) |
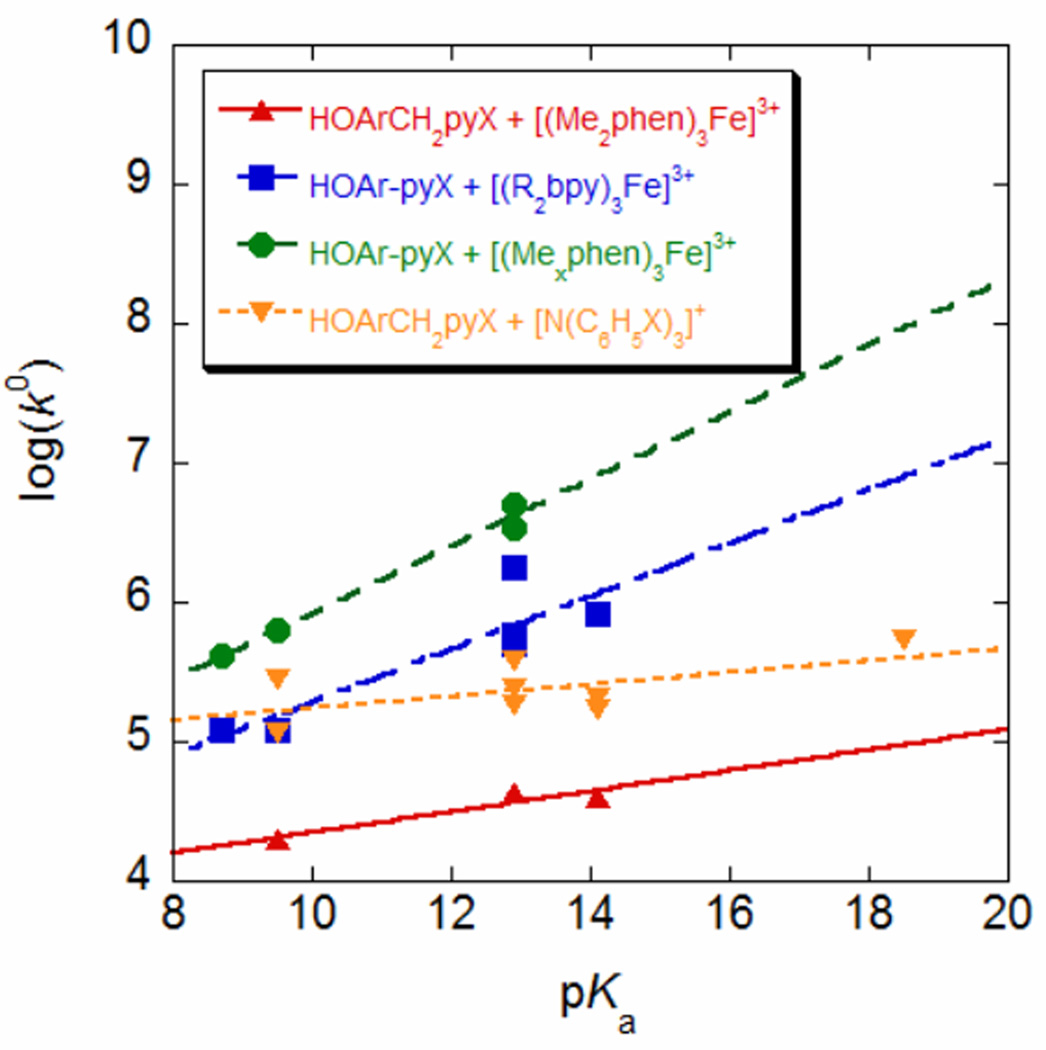
Plotting k0 vs. the pKa of the pyridyl moiety (Figure 6) illustrates clearly the difference between the HOArCH2pyX and HOAr-pyX reactions. For the oxidations of HOArCH2pyX by amminium ions, changing the pyridine substituent has almost no effect on k°. The slope of a linear fit is within error of zero [0.04 (4), R2 = 0.34], with some scatter. This indicates that the FC, Vel, and λ change only slightly with the pyridine substituent, so that all of the rate constants are fairly well predicted by a single value of k° and the ΔG°sCPET. This is consistent with the tightness of the Brønsted plot in Figure 4 above. For the three reactions of HOArCH2pyX with [Fe(4,7-Me2phen)3]3+, there appears to be a small increase in k0 with the pKa of the base [slope = 0.07(5), R2 = 0.88], in agreement with the deviation from α = ½ in the Brønsted plots in Figure 5c.
Figure 6.
Intrinsic kinetic rate constants k° (Table 3) plotted vs. the pKa of the pyridine (Table 1), for reactions of HOArCH2pyX and HOAr-pyX with different oxidants. The estimated error on log(k°) is ± 0.3.
In contrast, there is a strong dependence of k° on pyridine pKa for the reactions of HOAr-pyX with iron oxidants. First, it is immediately apparent that the reactions of [Fe(Mexphen)3]3+ have four-to-ten times greater k° values than reactions with [Fe(R2bpy)3]3+, as discussed above. Once the two iron oxidants are plotted separately, as in Figure 6, it is evident that k° depends strongly on the electron donating character of the substituent. The apparent scatter in the Brønsted plot (Figure 4b) is due to this variation. The values of k° vary by a factor of approximately seven over the ca. five orders of magnitude in pyridine pKa. Plots of log(k°) versus the pKa of the pendent base for oxidations of HOAr-pyX can be fit by a linear trend, with slopes of 0.19(10) (R2 = 0.79) and 0.24(4) (R2 = 0.98) for the bpy and phen reactions, respectively. Substituent effects on k° account for as much as 50% of the variation in rate constants for the reactions of HOAr-pyX with [Fe(4,7-Me2phen)3]3+, while changes in k° account for at most 5% of the variation in reactions of HOArCH2pyX with the same oxidant.
B. Analysis of the origin of the substituent effects
Experimental values for the intrinsic barriers λ, the electronic couplings Vel, and Franck-Condon proton transfer terms FC are not readily accessible.63 However, insight may be gained by looking for correlations of k° and computed values of λ with the available parameters dON, νOH, and δOH (Table 1).
First, it is remarkable that there is so little substituent effect on sCPET kinetics for the HOAr-CH2pyX compounds, apart from the effect of substituents on ΔG°. k° shows little change over this series despite changes in the base strength by nearly five orders of magnitude and the resulting changes in the hydrogen bond, e.g. the 170 cm−1 shift in calculated νOH.
In contrast, sCPET reactions of the conjugated HOAr-pyX compounds show a much larger variation of k° values with substituents – by roughly an order of magnitude – despite the fact that the variation in the key parameters is smaller for this series. The ranges, for HOArCH2pyX vs. HOAr-pyX, are 0.056 vs. 0.026 Å for dON, 171 vs. 161 cm−1 for νOH, and 1.87 vs. 1.44 for δOH. Thus the simple correlations of sCPET rates with structure and spectroscopy do not hold across all of the compounds discussed here. The k° values for the HOAr-pyX compounds are significantly smaller for those with more electron-withdrawing substituents, which have longer calculated dON, stiffer O–H modes, and weaker hydrogen bonds as indicated by the lower chemical shift for the hydroxyl protons δOH. This is consistent with the expected trends for both the Franck-Condon (FC) and λ parameters. The FC term describes the overlap of initial and final proton vibrational wavefunctions, the proton tunneling component of the CPET process. FC is known to be smaller for longer proton-donor acceptor tunneling distances,5,18,19 so it would be expected to be smaller for molecules with longer ground state O⋯N distances dON. This is only an approximate argument, however, because the proton actually tunnels at configurations of the molecules that have smaller dON than the ground state.5,19,21,32b,64 Still, molecules with longer ground state dON should have higher reorganization energies to reach good tunneling configurations, so they should still have smaller k°. The HOArCH2pyX compounds may not show this substituent effect in part because they have a hydrogen bond in a seven-membered ring, which is more flexible and allows a more linear OH⋯N structure. Calculations show that the energy to distort dON is smaller for HOArCH2pyX than for HOAr-pyX.55
Hammarström and co-workers recently reported a correlation between ln(k0) and crystallographic dON values for photo-initiated sCPET oxidations of four related phenol-base compounds.30 Their k0 values span 102.4 for compounds in which the crystallographic dON vary by ca. 0.2 Å, yielding a slope of ca. −27 Å−1, consistent with a theoretical prediction.21 This is a first approximation to the relationship between k0 and dON, because the reactive configurations have smaller dON than the ground state structures (as noted above), and because the crystallographic values are influenced by crystal packing (the structure which has the longest dON has an unusual bifurcated hydrogen bond in the crystal lattice and another of the compounds has four independent molecules in two structures, with dON which span 0.08 Å42). This is why we prefer to use computed dON values.42 Recasting the data in Figure 6 as ln(k0) vs. dON(DFT), the weak dependence of k0 on substituent for the HOArCH2pyX compounds is described by a distance dependence similar to that reported by Hammarström. However, for the reactions of the HOAr-pyX compounds that have the much larger intrinsic substituent effects, plots of ln(k0) vs. dON(DFT) have slopes roughly five times larger, ca. −150 Å−1 (see SI p. 27).
We have previously shown that DFT calculations of the inner-sphere reorganization energies λi qualitatively explained the two-order of magnitude faster sCPET reactions of HOAr-py versus HOArCH2py.40 Both inner-sphere and solvent reorganizations are involved in the intrinsic barrier λ, which is the energy to move the reactants into the geometry of the products. The solvent contributions are expected to be similar for all the reactions analyzed here because of the similar size of the phenol-pyridines. The calculations of λi(sCPET) followed Nelson’s four-point method for ET reorganization energies,65,66 with the proton transfer included in the reorganization energy, as we40 and others67 have done previously. The energies of the neutral molecule and radical cation (denoted E0 and E+, respectively) are calculated at the optimized neutral and cation geometries (denoted ng and cg, respectively), and λi(sCPET) is taken as the sum of the neutral and cation relaxation energies (denoted Erelax0 and Erelax+, respectively).65 This calculation provides an approximation of λi for the self-exchange reaction of the phenol-pyridine with its radical cation. While quantitative accuracy is not achieved from this simple model, which ignores the quantum mechanical character of the proton and the dynamic effects of promoting vibrations, its success for the parent compounds (X = H)40 encouraged us to apply it to the substituted derivatives. DFT (B3LYP/6–311+G(d,p)) was used to calculate the four needed energies for each of HOArCH2pyX, X = 4-CH3, 5-CF3, 4-NMe2, and HOAr-pyX, X = 4-NO2, 4-NMe2 using a polarizable continuum solvent model (PCM) for acetonitrile (Table 4). The λi(sCPET) values for HOAr-pyX are calculated to be ca. 10 kcal mol−1 lower than those for HOArCH2pyX (20–23 vs. 31–32 kcal mol−1), corresponding to a difference in k° of a factor of ca. 10 for reactions with oxidants of similar λi (k° is proportional to λ/4kBT, eq. 5). This difference in k° is roughly an order of magnitude less than the difference in k° observed experimentally, indicating that other factors make significant contributions to the differences k°. The calculated values of λi(sCPET) predict a slight decrease in λi (and thus faster rates) for the compounds with electron withdrawing substituents, the opposite of the experimentally observed trends Figure 6. However, the variation in these λi values is very small due to compensating effects on Erelax+ andErelax0. The insignificant variation of λi are consistent with the constant k° for the HOArCH2pyX series and suggests that this is not the origin of the substituent effects in HOAr-pyX.
Table 4.
Calculation of λi(sCPET) by four-point method.a
| X | Eng0 | Eng+ | Ecg0 | Ecg+ | Erelax0 | Erelax+ | λi | |
|---|---|---|---|---|---|---|---|---|
| HOArCH2pyX | 4-NMe2 | 0 | 134 | 9 | 111 | 9 | 23 | 32 |
| 4-CH3 | 0 | 135 | 13 | 117 | 13 | 18 | 31 | |
| 5-CF3 | 0 | 137 | 17 | 123 | 17 | 14 | 31 | |
| HOAr-pyXc | 4-NMe2 | 0 | 133 | 6 | 116 | 6 | 17 | 23 |
| 4-CH3 | 0 | 135 | 8 | 121 | 8 | 14 | 22 | |
| 4-NO2 | 0 | 139 | 10 | 129 | 10 | 10 | 20 | |
Energies in kcal mol−1 relative to Eng0, from calculations at the B3LYP/6–311+G(d,p)//B3LYP/6–31G(d,p) level of theory.
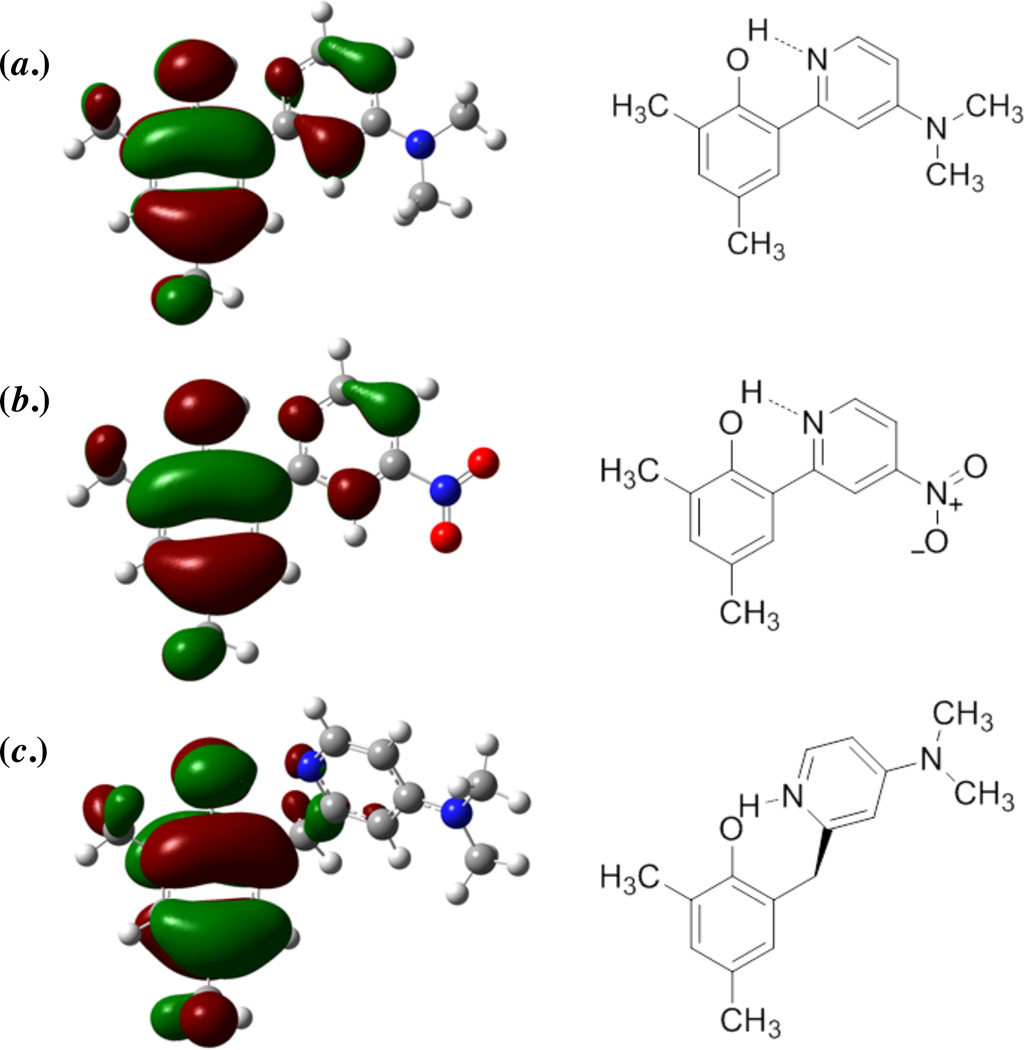
The DFT calculations show one other substantial difference between the HOAr-pyX and HOArCH2pyX series of compounds. The HOMOs of HOAr-pyX and HOArCH2pyX, and SOMOs of the corresponding radical cations, have most of their density in the π system of the phenol, but for HOAr-pyX significant electron density is delocalized onto the pyridine via the conjugated π system. More electron donating substituents may slightly increase the density of the HOMO and SOMO on the pyridine ring. For instance, the HOMO of HOAr-pyNMe2 has 8.8% pyridine contribution by Mulliken population analysis, compared to 7.3% for HOAr-pyNO2 (Figure 7).68 If the pathway for electron transfer is via the pyridine, this suggests that more electron donating substituents would be expected to lead to increased electronic coupling (larger Vel), and thereby increase k° as is observed experimentally. In contrast, the DFT calculated HOMO and SOMO orbitals for HOArCH2pyX (X = 4-CH3, 5-CF3, 4-NMe2) have relatively little density on the pyridine ring. Changing the substituent on the pyridine ring in HOArCH2pyX has almost no effect on the HOMO or SOMO, which are localized on the phenol ring. For example, even with X = 4-NMe2, only 1.5% of the electron density of the HOMO is on the pyridine (Figure 7). This would be expected to lead to small differences in Vel with substituent and therefore small differences in k°, consistent with experiment. While accurate calculations of Vel would require a more thorough theoretical analysis, the substituent effects on the phenol molecular orbitals seem likely to be a part of the origin of the differences between the conjugated and non-conjugated systems. However, the differences in orbital character with substituents are subtle, and it seems unlikely that these differences entirely account for observed substituent effect. There may also be a substituent effect on the proton transfer coordinate that has not been captured by these calculations.
Figure 7.
Kohn-Sham molecular orbital diagrams for the HOMOs of (a.) HOAr-pyNMe2, (b.) HOAr-pyNO2, and (c.) HOArCH2pyNMe2.
CONCLUSIONS
Studies of phenols with pendent substituted pyridines and −CH2pyridines, including the kinetics of their oxidations, reveal new features of separated concerted proton-electron transfer (sCPET). The substituent groups vary the pKa’s of the pyridinyl groups by almost 10 pKa units, causing substantial differences in the phenol-pyridine hydrogen bond strength, the proton transfer distance, and the proton-coupled oxidation potential. With the methylene linker between the phenol and the pyridine, there is little electronic communication between the two sites and they act almost as separate molecules, as evidenced by the −51(2) mV per unit change in the estimated pKa of the substituted pyridine. The rate constants for oxidation of HOArCH2pyX vary primarily with the changes in ΔG°, as has been found in related studies of phenol-imidazoles42 and aqueous phenol oxidations.31 There are, however, small differences in the effects of varying ΔG° via changes in the oxidant vs. the base, as indicated by different slopes in Brønsted plots of log(ksCPET) vs. log(KsCPET). Much larger substituent effects are observed for the HOAr-pyX series of compounds, in which the pyridine and phenol are in conjugation. The importance of this conjugation is evident in the smaller dependence of oxidation potential on pyridyl pKa (−48(1) mV/pKa), the stronger hydrogen bonds, and the nature of the frontier molecular orbitals. Extracting an intrinsic rate constant k° by extrapolating to ΔG° = 0 shows that substituents can have a substantial effect on the intrinsic reactivity, with electron donating groups leading to faster reactions. Surprisingly, while the HOAr-pyX compounds show greater sensitivity of their intrinsic sCPET rate constants to substituents, the HOArCH2pyX series shows a greater effect of substituents on ground state properties such as the proton-donor acceptor distance and the phenol proton chemical shift. The substituent effects in the two systems have been analyzed in the context of sCPET rate theory. Variations in electronic couplings Vel with substituent appear to be significant for reactions of the HOAr-pyX compounds.
EXPERIMENTAL
General Considerations
Unless otherwise noted, reagents were purchased from Aldrich, solvents from Fischer, and deuterated solvents from Cambridge. Acetonitrile was purchased from Burdick and Jackson (low-water brand) and stored in an argon-pressurized stainless steel drum plumbed directly into a glovebox. n-BuLi (1.6M in hexanes) was purchased from Acros. CD3CN was dried by stirring over CaH2 overnight, then distilled onto P2O5, followed by another distillation from CaH2, and was stored in a glove box. The iron-bipyridyl and phenanthroline complexes were synthesized according to literature procedures69 and were used as PF6− salts. 3,5-Di-tert-butyl-2-(benzyloxymethyl)benzaldehyde70 and 2-bromo-5-trifluoromethylpyridine71 were synthesized according to literature procedures. Triarylamminium hexafluorophosphate salts were prepared from the corresponding amines as described previously.7 1H NMR and 13C NMR spectra were recorded on Bruker AV300 or AV500 spectrometers at ambient temperatures; chemical shifts are reported relative to TMS in ppm by referencing to the residual solvent signals. Column chromatography used silica gel as the stationary phase. Mass spectrometry was performed on a Bruker Esquire Ion Trap Mass Spectrometer using electrospray ionization and on a Hewlett Packard 5971A Gas Chromatograph/Mass Spectrometer using electron impact ionization, and are reported as m/z with relative abundance in parentheses when multiple peaks were observed.
Syntheses
The syntheses of HOArCH2pyX and HOAr-pyX derivatives were carried out in a similar manner to the syntheses of the parent X = H compounds.40 Experimental details as well as spectroscopic and crystallographic refinement data for these compounds are given in the Supporting Information. ORTEPs of the crystal structures are presented in Figures 2 and S1 (in the SI).
Electrochemistry
Cyclic voltammetry (CV) was performed under N2 using an E2 Epsilon apparatus (BASi) equipped with Pt disc or glassy carbon working electrode (3.0 mm dia), platinum wire auxiliary electrode, and Ag/Ag(NO)3 (0.01 M) reference electrode. CV was carried out in acetonitrile with 0.1 M [n-Bu4N][PF6] as supporting electrolyte with ca. 5 mM substrate. [n-Bu4N][PF6] was recrystallized three times from EtOH and dried in vacuo for two days at 110 °C prior to use. Ferrocene was added as an internal standard and all potentials are reported vs. the Cp2Fe+/0 couple. For each compound, CVs were collected at a range of scan rates, from ca. 25 to 500 mV/s. Representative voltammograms can be found in Supporting Information.
Kinetics
All kinetics experiments were performed at room temperature in low-water acetonitrile using an OLIS USA stopped-flow instrument with an OLIS rapid scanning monochromator and UV-vis detector. Kinetic data were analyzed using SpecFit™ global analysis software,58 and were fit to opposing second order kinetics. Kinetic experiments using the iron oxidants were run in acetonitrile with 0.1 M [Bu4N][PF6] because the potentials of these compounds vary with ionic strength.72–74
DFT Calculations
All calculations were performed with Gaussian03.75 In all cases, tert-butyl groups were replaced with methyl groups to save computational time. All optimized geometries were confirmed to be local minima by vibrational analysis (NImag = 0). Four-point analysis of λ was performed following reference 65. Optimizations of the neutral and cation geometries of HOArCH2pyX and HOAr-pyX were performed at the B3LYP/6–31G(d,p) level of theory. Single point energies calculated for determination of λ on these geometries were performed at the B3LYP/6–311+G(d,p) level of theory with acetonitrile solvent modeled by a polarizable continuum model (PCM). In all cases, geometries corresponding to the non-proton-transferred radical cations ([HOAr-B]•+) or the zwitterions (−OAr-BH+) are not local minima. Energies are not corrected for zero-point vibrational energy. Cartesian coordinates of the optimized geometries of all species are given in the Supporting Information.
Supplementary Material
ACKNOWLEDGMENT
We gratefully acknowledge support from the U.S. National Institutes of Health (R01 GM50422). We thank Prof. Hirotaka Nagao for assistance with cyclic voltammetry and Dr. Adam Tenderholt for helpful discussions.
Footnotes
ASSOCIATED CONTENT:
Supporting Information. Syntheses and characterizations of HOArCH2pyX and HOAr-pyX derivatives. Spectroscopic, X-ray crystallographic, electrochemical, and kinetic data, including ORTEPs and cyclic voltammograms. CIF files. Computational results, and the complete citation for reference 75. This material is available free of charge via the Internet at http://pubs.acs.org
REFERENCES
- 1.Hammes-Schiffer S. Chem. Rev. 2010;110:6937–6938. doi: 10.1021/cr100367q. [DOI] [PubMed] [Google Scholar]
- 2.Huynh MHV, Meyer TJ. Chem. Rev. 2007;107:5004–5064. doi: 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mayer JM. Annu. Rev. Phys. Chem. 2004;55:363–390. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- 4.Hodgkiss JM, Rosenthal J, Nocera DG. In: Hydrogen Transfer Reactions. Hynes JT, Klinman JP, Limbach H-H, Schowen RL, editors. Weinheim: Wiley-VCH; 2007. pp. 503–562. [Google Scholar]
- 5.Cukier RI, Nocera DG. Annu. Rev. Phys. Chem. 1998;49:337–369. doi: 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]
- 6.Costentin C. Chem. Rev. 2008;108:2145–2179. doi: 10.1021/cr068065t. [DOI] [PubMed] [Google Scholar]
- 7.Rhile IJ, Markle TF, Nagao H, DiPasquale AG, Lam OP, Lockwood MA, Rotter K, Mayer JM. J. Am. Chem. Soc. 2006;128:6075–6088. doi: 10.1021/ja054167+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.The term ‘separated CPET’ emphasizes that these reactions are distinct from hydrogen atom transfer reactions (HAT) because of the separation of the e− and H+. Mayer JM. Acc. Chem. Res. 2011;44:36–46. doi: 10.1021/ar100093z.
- 9.Stubbe J, van der Donk W. Chem. Rev. 1998;98:705–762. doi: 10.1021/cr9400875. [DOI] [PubMed] [Google Scholar]
- 10.Pesavento RP, van der Donk WA. Adv. Prot. Chem. 2001;58:317–385. doi: 10.1016/s0065-3233(01)58008-0. [DOI] [PubMed] [Google Scholar]
- 11.Kuhne H, Brudvig GW. J. Phys. Chem. B. 2002;106:8189–8196. [Google Scholar]
- 12.Umena Y, Kawakami K, Shen J-R, Kamiya N. Nature. 2011;473:55–60. doi: 10.1038/nature09913. [DOI] [PubMed] [Google Scholar]
- 13.McEvoy JP, Brudvig GW. Chem. Rev. 2006;106:4455–4483. doi: 10.1021/cr0204294. [DOI] [PubMed] [Google Scholar]
- 14.Tommos C, Babcock GT. Acc. Chem. Res. 1998;31:18–25. [Google Scholar]
- 15.Renger G. Biochim. Biophys. Acta. 2012 [Google Scholar]
- 16.Hays A-MA, Vassiliev IR, Golbeck JH, Debus RJ. Biochemistry. 1998;37:11352–11365. doi: 10.1021/bi980510u. [DOI] [PubMed] [Google Scholar]
- 17.Meyer TJ, Huynh MHV, Thorp HH. Angew. Chem. Int. Ed. 2007;46:5284–5304. doi: 10.1002/anie.200600917. [DOI] [PubMed] [Google Scholar]
- 18.Cukier RI. J. Phys. Chem. B. 2002;106:1746–1757. [Google Scholar]
- 19.Hammes-Schiffer S, Stuchebrukhov AA. Chem. Rev. 2010;110:6939–6960. doi: 10.1021/cr1001436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hammes-Schiffer S. Acc. Chem. Res. 2001;34:273–281. doi: 10.1021/ar9901117. [DOI] [PubMed] [Google Scholar]
- 21.Kuznetsov AM, Ulstrup J. Can. J. Chem. 1999;77:1085–1096. [Google Scholar]
- 22.Tishchenko O, Truhlar DG, Ceulemans A, Nguyen MT. J. Am. Chem. Soc. 2008;130:7000–7010. doi: 10.1021/ja7102907. [DOI] [PubMed] [Google Scholar]
- 23.Stuchebrukhov AA. Electron transfer reactions coupled to proton translocation in proteins. Computational studies or redox driven proton pumps, cytochrome c oxidase, and biological energy transduction. In: Leitner D, Straub J, editors. Energy, Heat and Signal Flows in Proteins. Chapter 4. Taylor and Francis: CRC Press; 2009. pp. 71–106. [Google Scholar]
- 24.Marcus RA, Sutin N. Biochim. Biophys. Acta. 1985;811:265–322. [Google Scholar]
- 25.Barbara PF, Meyer TJ, Ratner MA. J. Phys. Chem. 1996;100:13148–13168. [Google Scholar]
- 26.Bíczók L, Gupta N, Linschitz H. J. Am. Chem. Soc. 1997;119:12601–12609. [Google Scholar]
- 27.Bíczók L, Linschitz H. J. Phys. Chem. 1995;99:1843–1845. [Google Scholar]
- 28.Irebo T, Reece SY, Sjödin M, Nocera DG, Hammarström L. J. Am. Chem. Soc. 2007;129:15462–15464. doi: 10.1021/ja073012u. [DOI] [PubMed] [Google Scholar]
- 29.Costentin C, Robert M, Savéant J-M. Acc. Chem. Res. 2010;43:1019–1029. doi: 10.1021/ar9002812. [DOI] [PubMed] [Google Scholar]
- 30.Zhang M-T, Irebo T, Johansson O, Hammarström L. J. Am. Chem. Soc. 2011;133:13224–13227. doi: 10.1021/ja203483j. [DOI] [PubMed] [Google Scholar]
- 31.Fecenko CJ, Thorp HH, Meyer TJ. J. Am. Chem. Soc. 2007;129:15098–15099. doi: 10.1021/ja072558d. [DOI] [PubMed] [Google Scholar]
- 32.(a) Irebo T, Johansson O, Hammarström L. J. Am. Chem. Soc. 2008;130:9194–9195. doi: 10.1021/ja802076v. [DOI] [PubMed] [Google Scholar]; (b) Johannissen LO, Irebo T, Sjödin M, Johansson O, Hammarström L. J. Phys. Chem. B. 2009;113:16214–16225. doi: 10.1021/jp9048633. [DOI] [PubMed] [Google Scholar]
- 33.Bonin J, Costentin C, Louault C, Robert M, Routier M, Savéant J-M. Proc. Nat. Acad. Sci., U.S.A. 2010:3367–3372. doi: 10.1073/pnas.0914693107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Costentin C, Robert M, Savéant J-M. J. Am. Chem. Soc. 2007;129:5870–5879. doi: 10.1021/ja067950q. [DOI] [PubMed] [Google Scholar]
- 35.Ishikita H, Soudackov AV, Hammes-Schiffer S. J. Am. Chem. Soc. 2007;129:11146–11152. doi: 10.1021/ja072708k. [DOI] [PubMed] [Google Scholar]
- 36.Song N, Stanbury DM. Inorg. Chem. 2008;47:11458–11460. doi: 10.1021/ic8015595. [DOI] [PubMed] [Google Scholar]
- 37.Sjödin M, Irebo T, Utlas TE, Lind J, Merényi G, Åkermark B, Hammarström L. J. Am. Chem. Soc. 2006;128:13076–13083. doi: 10.1021/ja063264f. [DOI] [PubMed] [Google Scholar]
- 38.Sjödin M, Styring S, Wolpher H, Xu Y, Sun L, Hammarström L. J. Am. Chem. Soc. 2005;127:3855–3863. doi: 10.1021/ja044395o. [DOI] [PubMed] [Google Scholar]
- 39.Reece SY, Nocera DG. J. Am. Chem. Soc. 2005;127:9448–9458. doi: 10.1021/ja0510360. [DOI] [PubMed] [Google Scholar]
- 40.Markle TF, Mayer JM. Angew. Chem. Int. Ed. 2008;47:738–740. doi: 10.1002/anie.200702486. [DOI] [PubMed] [Google Scholar]
- 41.Markle TF, Rhile IJ, Mayer JM. J. Am. Chem. Soc. 2011;133:17341–17352. doi: 10.1021/ja2056853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Markle TF, Rhile IJ, Mayer JM, DiPasquale AG. Proc. Nat. Acad. Sci. USA. 2008;105:8185–8190. doi: 10.1073/pnas.0708967105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schrauben JN, Cattaneo M, Day TC, Tenderholdt AL, Mayer JM. J. Am. Chem. Soc. doi: 10.1021/ja305668h. submitted to. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jeffrey GA. An Introduction to Hydrogen Bonding. New York: Oxford Univ Press; 1997. pp. 12–228. [Google Scholar]
- 45.Shan S-O, Loh S, Herschlag D. Science. 1996;272:97–101. doi: 10.1126/science.272.5258.97. [DOI] [PubMed] [Google Scholar]
- 46.Not all of the pKas of the pyridines in this study are known in acetonitrile. For consistency, we have estimated the acetonitrile pKas using the values of the aqueous pKas from ref. 47–52 and corrected them according to the correlational relationship pKa(MeCN) = 1.25 × pKa(H2O) + 6.34 derived in Ref. 47. The values estimated by this method are in good agreement with the experimental acetonitrile pKa values available in Ref. 47, 48, and 54.
- 47.Augustin-Nowacka D, Chmurzyñski L. Anal. Chim. Acta. 1999;381:215–220. [Google Scholar]
- 48.Kaljurand K, Kütt A, Sooväli L, Rodima T, Mäemets V, Leito I, Koppel IA. J. Org. Chem. 2005;70:1019–1028. doi: 10.1021/jo048252w. [DOI] [PubMed] [Google Scholar]
- 49.Perrin DD, Dempsey B, Serjeant EP. pKa Prediction for Organic Acids and Bases. New York: Chapman and Hall; 1981. pp. 108–139. [Google Scholar]
- 50.Chrystiuk E, Williams A. J. Am. Chem. Soc. 1987;109:3040–3046. [Google Scholar]
- 51.Perrin DD. Dissociation Constants of Organic Bases in Aqueous Solution. London: Butterworths; 1965. [Google Scholar]
- 52.The pKa of 3-trifluomethylpyridinium is estimated as 2.5 from the Hammet parameter, following Clark J, Perrin DD. Quart. Rev. (London) 1964;18:295–320.
- 53.ν(OH)DFT, corr = [ν(OH)DFT − 159.5] × 0.9904 from Korth H-G, de Heer MI, Mulder PJ. J. Phys. Chem. A. 2002;106:8779–8789.
- 54.Izutsu K. Acid-Base Dissociation Constants in Dipolar Aprotic Solvents. Boston, MA: Blackwell Scientific Publications; 1990. pp. 17–35. IUPAC Chemical Data Series No. 35. [Google Scholar]
- 55.Markle TF, Tenderholt AL, Mayer JM. J. Phys. Chem. B. 2012;116:571–584. doi: 10.1021/jp2091736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Costentin C, Robert M, Savéant J-M. J. Am. Chem. Soc. 2007;129:9953–9963. doi: 10.1021/ja071150d. [DOI] [PubMed] [Google Scholar]
- 57.Bordwell FG, Cheng JP. J. Am. Chem. Soc. 1991;113:1736–1743. [Google Scholar]
- 58.Binstead RA, Zuberbühler AD, Jung B. Specfit ™, version 3.0.36 (32-bit Windows) Chapel Hill, NC: Spectrum Software Associates; 2004. [Google Scholar]
- 59.Graige MS, Paddock ML, Bruce JM, Feher G, Okamura MY. J. Am. Chem. Soc. 1996;118:9005–9016. [Google Scholar]
- 60.Lee I-SH, Chow K-H, Kreevoy MM. J. Am. Chem. Soc. 2002;124:7755–7761. doi: 10.1021/ja011855u. and references therein. [DOI] [PubMed] [Google Scholar]
- 61.Wherland S. Coord. Chem. Rev. 1993;123:169–199. [Google Scholar]
- 62.A similar treatment is done in references 30, 31.
- 63.For one approach to such an analysis, see reference 32b.
- 64.Klinman JP. Biochim Biophys Acta. 2006;1757:981–987. doi: 10.1016/j.bbabio.2005.12.004. [DOI] [PubMed] [Google Scholar]
- 65.Nelsen SF, Blackstock SC, Kim Y. J. Am. Chem. Soc. 1987;109:677–682. [Google Scholar]
- 66.Nelsen SF, Weaver MN, Pladziewicz JR, Ausman LK, Jentzsch TL, O’Konek JJ. J. Phys. Chem. A. 2006;110:11665–11676. doi: 10.1021/jp064406v. [DOI] [PubMed] [Google Scholar]
- 67.Wander MCF, Kubicki JD, Clark AE, Schoonen MAA. J. Phys. Chem. A. 2009;113:1020–4630. doi: 10.1021/jp806842f. [DOI] [PubMed] [Google Scholar]
- 68.(a) Mulliken population analysis performed using QMForge software, Ref 68b. Tenderholt Adam L. QMForge, Version 2.1. Stanford, CA, USA.: Stanford University;
- 69.DeSimone RE, Drago RS. J. Am. Chem. Soc. 1970;92:2343–2352. [Google Scholar]
- 70.Ryu H-K, Kim W-Y, Nahm KS, Hahn YB, Lee YS, Lee C. Synthetic Metals. 2002;128:21–25. [Google Scholar]
- 71.Cottet F, Marull M, Lefebvre O, Schlosser M. Eur. J. Org. Chem. 2003:1559–1568. [Google Scholar]
- 72.Noel M, Vase KI. Cyclic Voltammetry and the Frontiers of Electrochemistry. London: 1990. pp. 141–143. Aspect. [Google Scholar]
- 73.Braga TG, Wahl AC. J. Phys. Chem. 1985;89:5822–5828. [Google Scholar]
- 74.Chan MS, Wahl AC. J. Phys. Chem. 1978;82:2542–2549. [Google Scholar]
- 75. Frisch MJ, et al. Gaussian 03, Revision D.02. Wallingford CT: Gaussian, Inc.; 2004. (See Supporting Information for full reference)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.