The Biology of Boundary Conditions: Cellular reconstitution in one, two, and three dimensions

Abstract

Reconstituting cellular behavior outside the complex environment of the cell allows the study of biological processes in simplified and controlled settings. Making the leap from cells to test tubes, however, carries the inevitable risk of removing too much context and therefore sacrificing the important biochemical, mechanical, or geometrical constraints that guide the system's behavior. In response to this challenge, reconstitution experiments have recently begun to focus not only on including the right molecules but also on faithfully recapitulating the constraints that are present within a cell. By setting the appropriate biological boundary conditions, these experiments are uncovering how dimensional constraints within the cellular environment guide biological processes.

Introduction

In cooking, the recipe for a dish begins with a list of ingredients, but it doesn't end there. The majority of the information a recipe contains – and the main source of difficulty in reproducing it faithfully – lies in its description of how those ingredients are to be organized and combined. Similarly, the recipe for a cell might naturally begin with a list of molecular components, but these components would serve only as a starting point; cell behavior is sensitively dependent on how these molecules are organized and constrained. While the grand goal of understanding the molecular basis of cell behavior depends in part on having a molecular ‘parts list’ detailing the identities, concentrations, and post-translational modifications of the molecules involved, mixing those molecules together at random is unlikely to ignite the spark of life. Rather, additional information is needed to describe how the molecules are connected to each other and to the larger cellular context – the external constraints known in physics and engineering as ‘boundary conditions’. Boundary conditions describe where the edges of a system are located, and how the system behaves at these edges, constraining the behavior of the entire system. Cellular processes are no different than any other physical system in their dependence on boundary conditions, culinary creations included; just as a spherical cookie bakes differently than a disk-shaped one and a cooking pan made of conductive metal cooks an omelet differently from one made of insulating glass, so too do shape and environmental context influence cellular organization and behavior. Although the reductionist approach to biology has been successful in identifying and characterizing the molecular parts involved in numerous processes, efforts to put those parts back together into a spatially organized and dynamic biological process – known as cellular reconstitution – have begun to reveal the significance of boundary conditions. In this review, we show how recent reconstitution efforts are leading to more complete recipes for biological processes that reveal how boundaries guide and constrain biology in one, two, and three spatial dimensions.

Boundaries are intimately related to dimensionality – the number of degrees of freedom a component within a system has to move around. For example, a molecule that diffuses or tracks along the length of a linear polymer can be thought of as a system with one spatial dimension, while molecules embedded in a membrane move within a two-dimensional system. By constraining the motion and orientation of molecules, dimensionality can have profound consequences for a wide range of cellular processes. Three properties of molecules – diffusive transport, self-avoidance, and molecular affinity – illustrate this point. First, a molecule with diffusion coefficient D will tend to move further in a three dimensional space than in a one dimensional space if the steps in each direction are independent. However, in the context of DNA binding, transitions between diffusion along the molecule and diffusion in three dimensions can provide a more efficient means of arriving at a targeted binding site than either alone [1]. A second example is self-avoidance, a constraint that prevents any part of a complex shape from overlapping with itself. This property leads a polymer chain in three dimensions to be more compact than one constrained to meander in two dimensions, and it has implications for organization of the genome as well as the spatial distribution of neural branches [2,3]. Third, dimensionality can alter molecular affinity by constraining the orientation in which molecules encounter each other, thereby making binding events more or less likely. This concept has recently been explored in the context of cadherin interactions at cell-cell contacts [4], as well as in the release of the EGF receptor from inhibition arising from its interactions with the membrane [5].

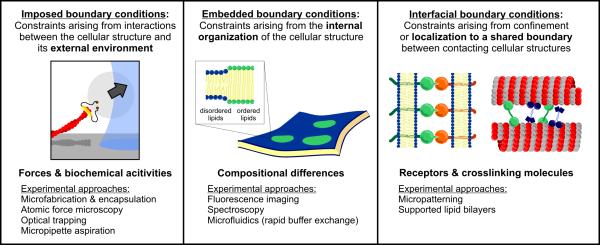
Successfully reconstituting many phenomena requires careful attention to different types of boundary conditions. By dividing them into three different types (Figure 1) we draw attention to their differences and place ourselves in a better position to achieve more realistic and informative cellular reconstitutions. The first type of boundary condition we consider are the imposed constraints that cellular structures encounter - parts of the cell that are distinct from or external to the structure being studied, but whose presence can nonetheless influence how the system behaves (Figure 1, left). In vitro, externally imposed constraints can often be mimicked by proxy, using microfabrication, micropatterning, or other techniques to define and control the reconstitution environment or perturb the reconstituted structure. A second category of biological boundary conditions are embedded constraints - the regions inside a cellular structure where its molecular components (proteins, lipids, or other biological molecules) confer distinct physical or biochemical properties (Figure 1, middle). In contrast to imposed constraints, embedded constraints in reconstitution experiments often arise spontaneously through the self-organization of the structure (e.g. lipid domains in a membrane or regions of different nucleotide state along a polymer); as a result, they may not need to be specifically engineered into the experiment. However, because these internal constraints are challenging to detect and monitor, determining their significance often requires new tools and techniques for characterizing them. The third category of constraints we will discuss are interfacial constraints (Figure 1, right), relevant for cellular systems in which specific molecules organize by forming links across multiple structures. These regions of adhesion (e.g. between polymers or membranes) differ from imposed constraints in that rather than acting on the system from the outside, the boundaries comprise the system itself. Reconstituting interfacial constraints on cellular structures therefore cannot be achieved by engineering the surrounding environment alone, but instead requires bringing together multiple reconstituted structures in such a way that they can serve as a host for the interfacial molecules being studied. While imposed, embedded, and interfacial constraints are not the only way to categorize biological boundary conditions, they have proven effective in guiding a wide variety of increasingly cell-like reconstitutions in the past few years. In the following sections, we take an unconstrained tour through this work on reconstituting one-, two-, and three-dimensional cellular structures with the appropriate constraints to illustrate how boundary conditions provide a foundation for the organization of cellular behavior.

Figure 1.

Types of biological boundary conditions and approaches to control or monitor them experimentally. Imposed, embedded, and interfacial boundary conditions each present unique constraints that, when incorporated into reconstitution experiments, can enable more accurate reproductions of the cellular environment.

Reconstitution in One Dimension

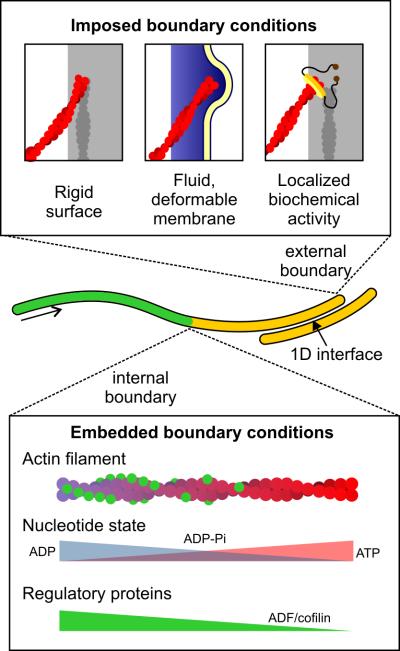
The canonical one-dimensional cellular structure is the linear polymer, variously assembled from sugar, nucleotide, or protein subunits. Polymers assembled from protein subunits – for example actin, tubulin, and intermediate filament proteins – comprise the eukaryotic cytoskeleton and are vital for establishing cell shape, supporting intracellular transport, and generating the forces involved in cell motility and division. Because the one-dimensional nature of cytoskeletal polymers constrains them to grow and shrink along a single axis, boundary conditions arising from imposed, embedded, and interfacial constraints can have multiple effects (Figure 2). For example, it is well known that external boundaries present impassable barriers, blocking or accelerating depolymerization of the polymer, or forcing it to bend, branch, or push back on an external boundary. This effect has been studied extensively in the case of actin and microtubules [6-8] and is now known to be relevant in bacterial filaments as well [9,10]. Yet boundary conditions in cells involve more than just geometrical constraints, as recent studies show.

Figure 2.

Boundary conditions on one-dimensional cytoskeletal polymers. Top: imposed boundary conditions can impart compressional forces, hold the filament's end stationary or allow it to glide, and can stabilize or destabilize growth through specific biochemical activities. Bottom: Internal constraints arise from different nucleotide states of the polymer's subunits and can influence the binding and activity of regulatory proteins.

1-D Imposed

Externally imposed constraints on a one dimensional polymer can be thought of as forces or chemical activities that are applied to the polymer's ends from the outside environment: for example, an encounter with a rigid boundary or fluid membrane, or capture by a processive enzyme. These types of boundaries have recently been shown to influence organization and behavior of one-dimensional cytoskeletal polymers. Using a microfabrication-based approach to encapsulate cellular structures and purified proteins in micron-scale chambers, Laan et al. recently demonstrated how microtubule interactions with cortical dynein influence centrosome positioning – an example of a one-dimensional system (the dynein-bound microtubule) influencing two-dimensional behavior (the encapsulated centrosome) [11**]. In the presence of dynein immobilized on the chamber walls, the authors found that microtubule plus ends captured by the surface-bound dynein had more frequent catastrophe events, leading to the generation of pulling forces on the centrosome as bound dynein remained attached to the shrinking microtubule. In the case of actin filaments, work by Jégou et al. and Courtemanche et al. has shown that tension on actin filaments can be sensed and maintained by the formins Bni1p and mDia1 [12*,13*]. Attaching these actin nucleators to a solid surface or supported bilayer in the presence of a shear flow allowed the authors to investigate how formin-mediated actin polymerization depended on force, increasing approximately two-fold in the presence of profilin. Analogously, Akiyoshi et al. demonstrated that the ability of kinetochores to track the plus ends of shrinking microtubules led to the generation of pulling forces of up to 11 pN, by harnessing the energy released upon depolymerization [14]. These examples serve to illustrate that, in addition to presenting geometrical constraints, boundaries can impart localized forces and specific biochemical activities that, when present, reveal new behaviors – in these cases, stable centrosome positioning, tension-dependent actin polymerization, and the establishment of the tensile forces necessary for chromosome segregation.

1-D Embedded

In contrast to external boundary conditions that influence the polymer by acting on its ends, internal constraints arise from the polymer itself and can be embedded within its structure. These constraints delimit the polymer into regions with different physical and biochemical properties. For both actin and microtubules, subunits that undergo nucleotide hydrolysis following incorporation into the filament can give rise to internal islands or barriers, regions in which subunits transition from one nucleotide state to another. These internal barriers have recently been the subject of several reconstitution studies [15-17] revealing their influence on polymer dynamics, and suggesting potential additional roles in localizing filament-binding proteins to regions with specific nucleotide state. For example, in the case of actin, the filament-severing protein cofilin has been shown to preferentially bind ADP subunits. This, combined with the observation that high densities of cofilin on a filament can be inhibitory, biases filament severing to occur at the internal boundaries where nucleotide state transitions from ADP to ADPPi actin, establishing these boundaries as rulers that guide filament length [18]. Improved understanding of the other ways in which these barriers couple to the activities of regulatory proteins will provide a new perspective on how internal constraints can regulate the behavior of one-dimensional systems.

1-D Interfacial

In addition to the ends of the polymer, the space between overlapping polymers can be influenced by boundary conditions that give rise to unique behaviors. This one-dimensional space between polymers offers a hospitable environment for specific molecules to bind and acts as a track to couple the energy of polymerization or processivity to uniaxial force and movement. The midzone of the mitotic spindle serves as an example of an essentially one-dimensional environment formed by overlapping antiparallel microtubules that guides the behavior of a complex cellular structure. Using a reconstitution approach, Bieling et al. created a minimal model of the spindle midzone, consisting of the microtubule bundling protein PRC1 and the kinesin-4 Xklp1 [19*]. They found that PRC1 binds specifically to overlapping antiparallel microtubules, leading to subsequent binding by Xklp1. Constrained to its one-dimensional microtubule track, Xklp1 migrates towards the plus end, where it becomes concentrated and decreases microtubule dynamics, causing the size of the overlapping region to stabilize. In this way, the size of the spindle midzone arises as a fundamental property of these two proteins under one-dimensional confinement.

Reconstitution in Two Dimensions

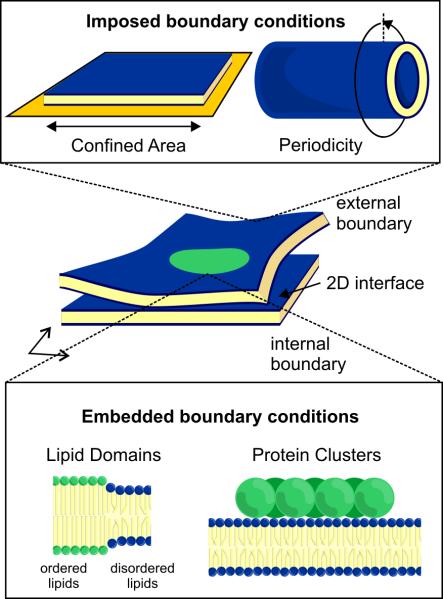
Reconstitution of cellular processes on membranes – two-dimensional surfaces comprised of a lipid bilayer – has become very popular in recent years due to the availability of synthetic lipids and techniques to create membranes with cylindrical, planar, and spherical geometries covering a >1000-fold range of curvatures. Besides being the biological idealization of a two-dimensional surface, lipid membranes are fluid and deformable; this allows them to assume the wide variety of geometries observed in cells and has led researchers to investigate the significance of these different geometries, as well as how they are established and maintained within the cell. Analogous to the one-dimensional systems defined by cytoskeletal polymers, membranes have provided examples of how imposed, embedded, and interfacial constraints can establish and govern the organization of two-dimensional biological systems (Figure 3).

Figure 3.

Imposed and embedded boundary conditions in two-dimensional membrane systems. Top: supported membranes can be confined to defined sizes and shapes by patterning the underlying substrate, while free-standing membranes with defined curvatures offer confinement through the periodicity of their surfaces. Bottom: membranes support internal clusters of lipids and/or proteins, which can have different biochemical and mechanical properties than the membrane as a whole.

2-D Imposed

Boundary conditions on a two-dimensional membrane system can be imposed in a variety of ways. First, by using planar supported bilayers - lipid membranes fluidly coupled to a flat surface – it is possible to constrain the size and shape of the membrane by patterning physical barriers on the surface, where the membrane will not adhere. This approach was used by Schweizer et al. to study the ability of reconstituted Min waves to “sense” the long axis of the membrane patches, as determined by the direction along which the waves propagate [20*]. A second way to impose boundary conditions on a two-dimensional membrane is through curvature. A lipid tube or vesicle that closes in on itself is subjected to constraints known as periodic boundary conditions – the system must effectively repeat itself with each 360 degree trip around the membrane. Domanov et al. have recently explored this type of imposed boundary condition by measuring the mobility of integral membrane proteins reconstituted into cylindrical membrane tubes of controlled radii [21]. In this study, the authors found that the measured mobility agreed with Stokes's paradox, a phenomenon in which the diffusion coefficient scales as the logarithm of the confining area – paradoxically diverging as the radius of the membrane tube becomes arbitrarily large. Given the diversity of highly-curved membranes found throughout the cell, this type of 2D confinement-through-curvature could play an important in role in modulating the functions of both lipids and proteins.

2-D Embedded

Even in the absence of external constraints imposed on a membrane's geometry, internal boundaries embedded within otherwise uniform membrane systems can be established through the organization of integral or peripheral membrane proteins, as well as through the lipids that make up the membrane itself. Recent reconstitution studies have helped to reveal how embedded constraints imposed by membrane shape and composition can influence protein dynamics, as well as the complementary question of how protein dynamics influence membrane organization[22-24]. A milestone in this direction was achieved by Wollert et al. with the reconstitution of ESCRT-mediated membrane scission [25,26**]. This dynamic, self-organizing process is initiated by the clustering of ubiquitinated cargo, delimiting the patch of membrane that subsequently buds and is severed through the action of ESCRT-I, II, and –III. While it appears that lipids play only a secondary role in creating the membrane deformation for ESCRT-mediated scission, Ewers et al. recently described a setting in which membrane invaginations are facilitated by lipids, with proteins playing a more auxiliary role [27]. In this work, the authors demonstrate that capsid proteins of Simian Virus 40 (SV40) create membrane invaginations through their interactions with the glycolipid GM1. Binding of the pentameric capsid subunit induces clustering of GM1 that produces invaginations only if the acyl chain of the glycolipid is long, suggesting that protein binding is inducing spontaneous curvature indirectly through a modification of the membrane line tension. Another example of proteins and membranes combining to create embedded membrane boundaries involves dynamin, a protein that forms a helical polymer around membrane tubes to drive their fission. Two recent studies by Morlot et al. and Shnyrova et al. demonstrate the importance of coordinated action by both lipids and proteins in this process; bending and fission is catalyzed both by reorganization of membrane lipids at the edge of the dynamin coil, as well as the conformational flexibility of dynamin itself [28,29]. Together with the reconstitutions of ESCRT-mediated budding and SV40 entry, this work illustrates the importance of considering the mechanics of both membranes and proteins in understanding the processes that shape the cell and its organelles.

2-D Interfacial

When apposing membranes are brought into close proximity, another form of two-dimensional system is created, populated by adhesion molecules that stabilize and reorganize the membrane-membrane interface. While these cell-cell adhesions play a central role in intercellular signaling, they are difficult to study due to their biochemical complexity and irregular geometries. An alternative approach that overcomes these challenges is to use a synthetic membrane (typically a supported lipid bilayer, or SLB) to interface with a cell, essentially creating an artificial signaling partner that is compatible with high-resolution imaging of the membrane-membrane interface down to the single-molecule level. Although applied extensively to study the immunological synapse, both cell-SLB as well as vesicle-SLB interfaces have recently been employed to look at the two-dimensional protein organization and dynamics associated with tissue maintenance [30], cell-to-cell transmission of viruses [31], and myelin biogenesis [32]. The ability to impose constraints on the organization of molecules within these two-dimensional environments has identified the requirements for signal activation in response to receptor clustering, as well as the effect of two-dimensional constraints on the cytoskeletal organization of the cell as a whole. Expanding reconstituted membrane-membrane interfaces into the third dimension – to understand how organization at the interface couples into the cytoplasm of the engaged cells – will be a crucial next step in dissecting the role of interfacial constraints on these cellular-scale processes.

Reconstitution in Three Dimensions

Although the inside of a cell is inherently a confined, three-dimensional space, the consequences of this confinement remain largely unknown. Using new techniques to encapsulate proteins and cytoplasmic extracts in enclosed spaces, cellular reconstitution is beginning to shed light on the role of three-dimensional confinement (Figure 4).

Figure 4.

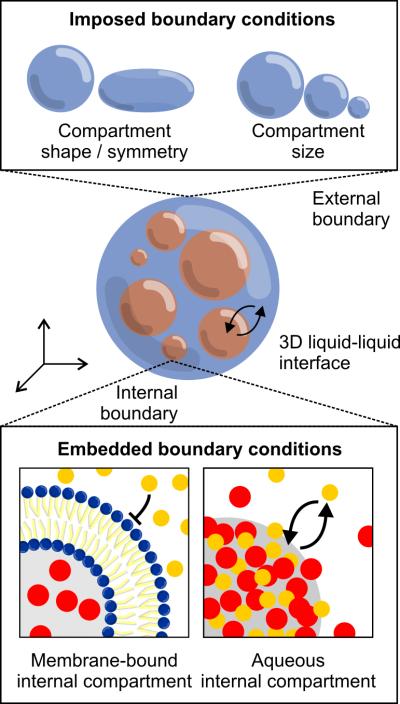
Reconstitutions in three dimensions. Top: encapsulation of proteins in defined shapes and sizes constrains symmetry and volume, and also allows differeing biochemical activities at the boundary. Bottom: compartmentalization of internal components (both with and without a surrounding membrane) creates embedded boundaries that freely exchange molecules with the surrounding environment (bottom right).

3-D Imposed

External constraints in 3D are imposed to study how confinement of biochemical reactions within a defined shape and volume influences spatial organization and function. One approach to 3D confinement that has been successfully employed to encapsulate both purified proteins and cytoplasmic extracts is to surround them by an external oil phase. The immiscibility of oil with aqueous protein solutions leads to the formation of spherical droplets whose boundaries can be rendered biochemically inert or active depending on the choice of stabilizing surfactant. Recent work from Pinot et al. showed that by encapsulating Xenopus egg extracts in droplets, the assembly and contraction of actin networks could be observed [33]. These contractions lead to F-actin-driven flows directed radially inward, providing an example of how the symmetry of a confining compartment can serve as a form of internal boundary condition, influencing the organization and evolution of a system in three dimensions. Similarly, work by Sanchez et al. studying synthetic assemblies of bundled microtubules and kinesin demonstrated that encapsulating these active gels led to spontaneous motility when the droplets were moderately compressed between glass coverslips, but not when the droplets were uncompressed [34]. These examples highlight how encapsulation, confinement, and the imposition of specific shapes and symmetries can lead to new phenomena. Given that compartment size and volume have been shown to influence organelle size in vivo [35,36], a promising direction in reconstitution will be to determine if these imposed constraints matter in vitro as well.

3-D Embedded

While encapsulation imposes confinement on a three-dimensional system, these systems can also contain internal boundaries in the form of compartments that differ compositionally from the surrounding environment. While membrane-bound organelles are the most familiar form of these compartments, recent work by Li et al. has focused on a different type of biochemical compartmentalization, showing that multivalent protein-protein interactions are sufficient to drive the partitioning of specific molecules into dynamic three-dimensional volumes with enhanced activity [37**]. In the case of nephrin, Nck, and N-WASP, enrichment of these components into micron-scale liquid domains accelerated Arp2/3-mediated actin assembly by 2- to 3-fold. In the context of RNA granules, Han et al. and Kato et al., reported the formation of hydrogels from concentrated solutions of proteins bearing low-complexity sequences [38,39]. These hydrogels are similar to pathologenic amyloid fibers, but with the important distinction that they are dynamic and reversible. Although the low-complexity sequences that drove gel formation do not themselves bind RNA, they are often found on RNA binding proteins, suggesting that gel formation could serve as a mechanism for enriching specific RNA-binding proteins (and their bound mRNAs) from the surrounding cytoplasm. Both this work and the work from Li et al. point to an important feature of organization in three-dimensions that allow a cell to partition it's components without necessarily isolating them with a surrounding membrane. Although these fluid compartments are discussed here as being an embedded boundary within a three-dimensional space, because they allow for the free exchange of molecules into and out of the compartment, they can also be thought of as three-dimensional interfaces, defining distinct yet overlapping volumes with the surrounding environment. Given the generality of this mechanism of segregation – multivalent protein-protein or protein-nucleic acid interactions – and the wide variety of non-membrane-bound, three-dimensional compartments that have been observed in cells, including P granules and nucleoli [40,41], understanding how three-dimensional partitioning of macromolecules in the cytoplasm is achieved and regulated is likely to be an active area in the field of reconstitution in the years ahead.

Future Outlook

Just as dimensionality and boundary conditions are necessary to solve differential equations (not to mention cook meals), so too do they provide essential information for understanding biological phenomena. Although the field of cellular reconstitution has begun to embrace the importance of biological boundary conditions, there remains much work to be done before we are able to fully recapitulate the intricacy of cellular boundaries and their coupling across one, two, and three spatial dimensions. Fortunately, recent advances in technology and computation are helping to move reconstitution beyond a simple list of ingredients and towards a more complete recipe of the cell.

One such advance is the development of encapsulation techniques to produce three-dimensional compartments in vitro that increasingly reflect the geometrical and biochemical constraints of real cells. Encapsulation of proteins or cytoplasmic extracts in oil-in-water emulsions, as described above, or in polymer-based membranes [33,42] is a robust approach to constraining the volume of a system, while microfabricated compartments offer the complimentary ability to produce complex geometries [9,43]. Despite the strengths of these techniques, lipid vesicles remain in many ways the ideal compartment for many reconstitution experiments due to their mechanical, geometrical, and biochemical similarity to the actual boundaries of the cell. Although membrane-based encapsulation is becoming increasingly prevalent [44-46], the next step in the technological evolution of reconstitution will be the development of more robust and higher throughput techniques for performing these types of experiments. Along these lines, an additional challenge is the reconstitution of integral membrane proteins [47,48], an active area of research that would enable physiological connections between the inside and outside of three-dimensional compartments, and the creation of tissue-like networks[49].

In addition to encapsulation techniques, the ability to simulate increasingly complex systems has also advanced significantly. One of the primary advantages of reconstitution is that it enables researchers to study biology in a fully-defined setting; simulations take this advantage to its logical conclusion, offering complete measurement and control of every element of a system in a way that experiments cannot. Recent work modeling mitotic spindle scaling, membrane budding, and the importance of conformational fluctuations in protein activity illustrate the tremendous potential of this approach [50-52]. Nonetheless, simulations must be grounded and constrained by experiments, and it is important that these two complimentary approaches continue to evolve in parallel, each informing the other as their respective techniques advance.

Although cellular processes exhibit richness and complexity beyond typical boundary value problems like a vibrating drum or plucked string, the recent work surveyed here illustrates that boundaries in biology are no less central to understanding the dynamics and spatial organization of a cell than the molecules themselves. Vive la Réconstitution!