Abstract
Substitutional hydrogen at oxygen site (HO) is well-known to be a robust source of n-type conductivity in ZnO, but a puzzling aspect is that the doping limit by hydrogen is only about 1018 cm−3, even if solubility limit is much higher. Another puzzling aspect of ZnO is persistent photoconductivity, which prevents the wide applications of the ZnO-based thin film transistor. Up to now, there is no satisfactory theory about two puzzles. We report the bistability of HO in ZnO through first-principles electronic structure calculations. We find that as Fermi level is close to conduction bands, the HO can undergo a large lattice relaxation, through which a deep level can be induced, capturing electrons and the deep state can be transformed into shallow donor state by a photon absorption. We suggest that the bistability can give explanations to two puzzling aspects.
Since ZnO-based oxide semiconductors are promising materials for transparent oxide electronics and blue LED, the oxides have been extensively investigated1,2. Hydrogen is an ubiquitous element, and in semiconductors, hydrogen-related problems have always been important subjects, since hydrogen shows complicated properties and plays a role as either carrier-generating or trapping center. Generally, oxide materials are easily contaminated by hydrogen impurities due to the strong bonding of the H atoms to an O atom, and hydrogen contamination is believed to be an important source of the natural n-type conductivity of ZnO3,4. Hydrogen impurities are suggested to have two kinds of donor-like states in ZnO: (i) interstitial hydrogen (Hi) at a bond-center (HBC+) or at an antibonding (HAB+) site4,5,6,7 and (ii) substitutional H at an O site (HO)8. The interstitial H can be easily removed through thermal annealing due to its high mobility5, and thus, HO is suggested to be robust source for n-type conductivity8. However, there is a long-term unresolved puzzle. The maximum available free carrier concentration (ne,max) in H-rich ZnO is limited to only about ~1018 cm−3 9,10,11, even if the H concentration in ZnO can be as high as ~1020 cm−3 12 and the O-deficiency is simultaneously serious13. Since a heavier n-type doping can be achieved (~1020 cm−3) in Al-doped ZnO14, the formation of acceptor-like native defects such as Zn-vacancy is not considered to be the main reason for compensation15,16.
There is another puzzling aspect in ZnO, which is persistent photo-conductivity (PPC) in ZnO17. Since the PPC is a source of the light-induced instability of ZnO-based active device in flat panel display18, many researches are now invested to prevent it. Generally, the PPC is suggested to be explained by the presence of bi-stable centers such as DX center in AlGaAs:Si19. Lany and Zunger have suggested an interesting mechanism by considering that VO level in ZnO is sensitively lowered by electron occupancy due to the strong electron-lattice coupling20. Normally, the VO is a deep donor, but the fully-ionized VO2+ state can be a metastable shallow donor state, since the defect level of VO2+ is located above the conduction band minimum (CBM), and thus an electron at CBM may not be easily excited into the defect level. However, the metastability of VO2+ + 2e has not yet been proven explicitly. Later, the more direct calculations showed that bi-stability of VO does not exist for all (0), (+), and (2+)-charge states, although the breathing type of atomic relaxation depending on charge state is quite large, which is not enough to explain the room-T PPC21. Therefore, up to now, there is no satisfactory theory to explain the puzzles in ZnO.
In this paper, we report the bistability of shallow donor HO in ZnO, which has never been discussed yet. We find that the bistability of O-vacancy can be realized, when it is coupled by a hydrogen. We show that as Fermi level is close to the conduction band, the HO can undergo a large lattice relaxation (LLR), capturing electrons at a deep level which is created by the LLR. It is shown that the bistability can give clear explanations to the microscopic mechanisms of long-term puzzling phenomena in ZnO: the persistent photo-conductivity in ZnO and the low doping limit of H-rich ZnO.
Results
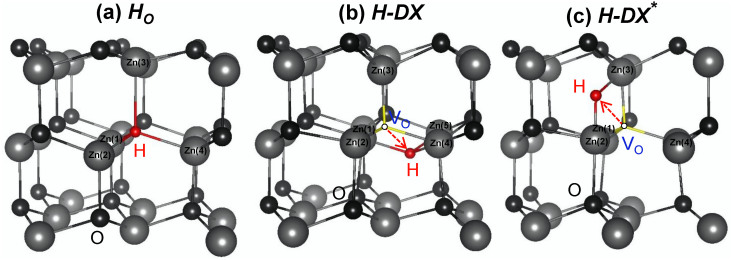
In ZnO, a H atom is suggested to be strongly captured by an O-vacancy, which is a substitutional impurity at O-site (HO), as shown in Fig. 1(a). The HO state is known to be a robust state, and normally positively charged, as suggested by Janotti et al.8, since the highest occupied state from the hydrogen state is located above the CBM. However, here we find that HO can be negatively charged and capture electrons through a large lattice relaxation (LLR). We find that in the negative charge state, the H atom can be significantly displaced into an interstitial hollow (H)-site22,23. The LLR structure is described by Fig. 1(b).
Figure 1. Atomic structures of the various structures of hydrogen at an O-site in ZnO: (a) HO, (b) H-DX, and (c) H-DX*.
The (red)-dashed arrow lines in (b) and (c) indicate the direction of H-displacement for the formations of H-DX− structures. (c) H-DX* is a meta-stable structure. The open circles describe VO0 site in the H-DX− which is a complex defect of Hi− and VO0.
Through the LLR, the H is separated from O-vacancy site, and thus the LLR structure can be considered as a pair of Hi− and VO0, that is a Frenkel defect. In this respect, it is similar to the well-known DX center in AlGaAs19. Thus, we call the LLR structure as “H-DX”. The present H-DX is slightly different from DX center. In the former, two H-O bonds are broken by LLR [see Fig. 1(b)], while in the latter, only one bond is broken. In the H-DX, as shown in Fig. 1(b), the H couples with three Zn atoms which are located altogether at a same layer of ab-plane. Electronic structure calculations indicate that a deep level within gap is created by the LLR and it captures two electrons, as shown in Fig. 2(a). The more detail will be discussed below. We examined another metastable LLR structure, which is described as H-DX* in Fig. 1(c), where the displaced H is located between two ab-layers. This state is less stable by 0.26 eV than H-DX, and the H-DX* is less probable to be formed, compared to the H-DX. We also examined another LLR: only one Zn atom is separated from the H, similarly to conventional DX center, but we find that these states are unstable, the deep level is not formed by the LLR.
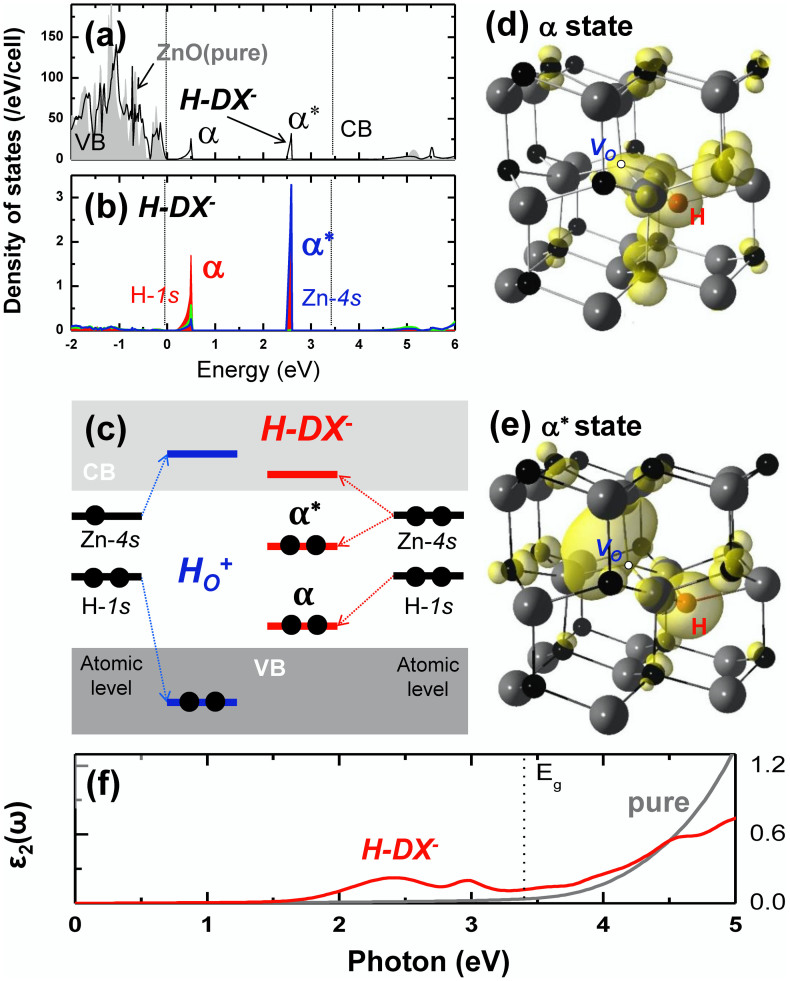
Figure 2. Electronic structures and optical properties of H-DX−.
Calculated (a) total and (b) partial densities of states for H-DX− in ZnO are shown. The total density of states for perfect (pure) ZnO is also shown (gray filled area) in (a). (c) A schematic diagram for the electronic structures of HO+ and H-DX−. The charge densities of (d) α and (e) α* states are shown with the isosurface value of 3.50 × 10−5 Å−3. (f) The imaginary dielectric function [ε2(ω)] calculated for H-DX− is shown. The dielectric function is calculated by using the Kubo formula based on the electric-dipole-approximation25 and averaged over the x-, y-, and z-polarization vectors. Here, we used a 72 atom supercell.
As shown by Figs. 2(a) and 2(b), electronic structure calculations indicate that two deep levels are created by H-DX−. The lower α level is located at 0.49 eV above the VBM, and the upper α* level is located at 1.06 eV below the CBM. As shown by Fig. 2(d), the α level is found to come mainly from the H atom and the nearby H-coupled Zn atoms ((Zn(1), Zn(4), Zn(5) in Fig. 1(b)), and, as shown by Fig. 2(e), the upper α* level comes mainly from the O-vacancy site, i.e., from the Zn(2) and Zn(3) atoms separated from H. The two defect levels are fully occupied. The electronic energy reduction by the capture of two electrons at α* level contributes to the stabilization of the H-DX.
In the isolated point defect VO, four nearby Zn atoms are relaxed inward by the electron capture of VO. In the VO0, the Zn atoms are relaxed inward by about 0.24 Å from ideal positions (ideal Zn-O bond lengths: dZn-O = 1.97 and 1.99 Å)21. Similarly, in the H-DX−, Zn(2) and Zn(3) atoms are inward relaxed by 0.28 Å and 0.32 Å, respectively. Three Zn host cations coupled to the H move towards the H by about 0.12 Å (0.10 Å for Zn(5)), from ideal locations. For the H-DX− LLR structure, the H atom is largely displaced by 1.92 Å from the original location of HO.
In the neutral state, the H-DX structure becomes unstable, since the electronic energy reduction by one electron trap is not enough to stabilize it. Similarly, in the positive charge state, the H-DX structure is unstable. The H-DX− structure is stable only in the negative charge state, having two electrons at α* level, and it is more stable than the HO in the negative charge state, which is actually HO+ + 2e (at CBM), since the donor level of HO is located much higher than CBM.
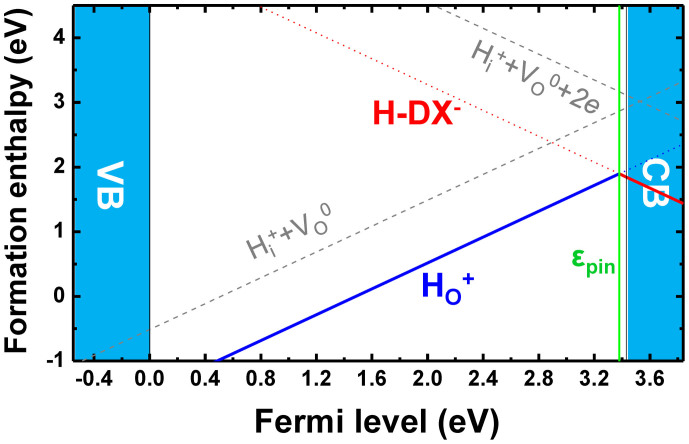
Now, we examine the stability of H-DX state relative to the normal HO+, depending on Fermi level (εF), by calculating the formation enthalpies. Since two structures have different charge states, the relative stability should depend on Fermi level. The calculated results of εF-dependent formation enthalpies of these states are shown in Fig. 3. Here, we assumed O-poor and H-rich conditions (simulating the O-deficient and H-rich case). Since HO is shallow-donor-like, only the positive charge state is stable when Fermi level is inside the band gap. The calculational results indicate that as Fermi level is located above 0.05 eV below the CBM, electron-capturing H-DX− becomes more stable than HO+. We did not consider the interstitial H (Hi) state, assuming that substitutional HO is much more dominant than interstitial hydrogenic Hi state, since the Hi is suggested to be easily removed through thermal annealing due to its high mobility. These results indicate that when Fermi level is close to the 0.05 eV below CBM, the concentration of the H-DX states becomes comparable to that of HO. These indicate that the pinning position of the Fermi level is located at about 0.05 eV below CBM.
Figure 3. Calculated formation enthalpies of HO+ (blue lines) and H-DX− (red lines) in ZnO as a function of Fermi level, assuming H-rich and O-poor condition.
We also show those of the separated Hi+ and VO defects (HO+ → Hi++VO0 and HO+ → Hi+ + VO0 + 2e by (gray)-dashed lines). The vertical solid lines indicate the VBM and the CBM, and the vertical (green) solid-line indicates the pinning position of Fermi-level (εpin). The calculational details are written in supplementary information.
The results indicate that HO state can be self-compensated through LLR transition. An electron can be generated by a shallow donor such as HO, and the electron is captured by other HO:
 |
 |
The overall process is found to be exothermic by 0.10 eV, when Fermi level is located at CBM.
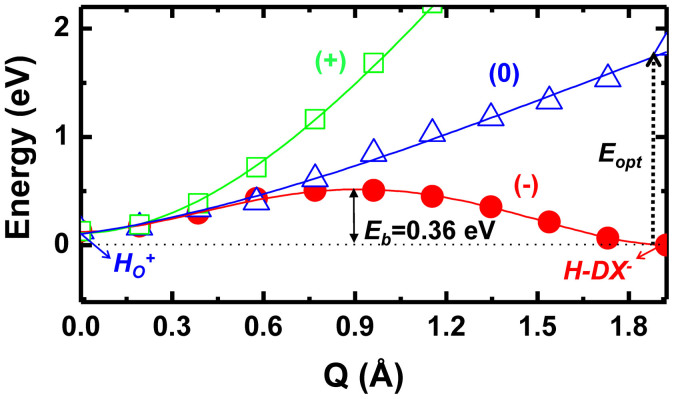
We estimated total energy profile for the structural transformation between HO and H-DX. The H-DX structure in the neutral or (+)-charge state is unstable. When the high concentration of electron carriers is present at conduction band, two electrons can be captured by the HO through the deformation toward H-DX structure, and the H-DX− state can be more stable than the HO+ + 2e (at CB). We calculated the variation of the total energy according to the structural deformation, as shown in Fig. 4, and we find that there is the energy barrier for the structural recovery: HO+ + 2e → H-DX−. It is estimated to be 0.36 eV.
Figure 4. Total energy profiles of the structural transitions between HO and H-DX configurations as a function of H displacement (Q) in the (1−), (0), and (1+) charge states.
The energy barrier (Eb) for the structural transition from the HO+ + 2e to the H-DX− is indicated, and the optical excitation energy (Eopt) for the transition from H-DX− to H-DX0 is also shown.
We calculated the imaginary dielectric function [ε2(ω)]24 of the H-DX−, as shown in Fig. 2(f), which describes the optical absorption spectrum. The peak in the phonon energy spectrum was estimated to be about 2.3 eV. The minimum optical excitation energy (Eopt) from α* level to CBM in the H-DX− was estimated to be about 1.06 eV.
We examined the binding energies of HO+ and H-DX− with respect to well-separated Hi and VO. The binding energies of HO+ and H-DX− were estimated by comparing two states, i.e., by using [E(Hi+) + E(VO0)] − [E(HO+) + E(pure)] and using [E(Hi+) + E(VO0) + 2e (at CBM)] − [E(H-DX−) + E(pure)], respectively. As shown by (gray)-dashed lines in Fig. 3, the binding energy of HO+ is estimated to be 0.97 eV, which is largely exothermic, which is comparable to the previous large values of 0.80 eV (in LDA) and 3.8 eV (in LDA + U) in other calculations. The binding energy of H-DX− is also estimated to be largely exothermic by 1.27 eV. Thus, this indicates that substitutional H-DX− is a thermally-stable complex defect.
Discussion
The electronic structure of H-DX, as schematically described by Fig. 2(c), can be understood with respect to interaction between Hi and VO. As Takenaka and Singh suggested, H itself in HO+ is anion-like, capturing two electrons25, indicating that HO+ is rather a complex defect composed of the Hi− and VO2+. The anionic behavior is not a surprising one, since H electronegativity (ζ) is between those of Zn and O [ζ(H) = 2.2, ζ(Zn) = 1.65, and ζ(O) = 3.44]. The VO2+ in complex defect HO cannot trap the electron25, since the Zn-s-levels around the H atom are pushed upward above the CBM by the strong interaction between the upper Zn-s-level and the lower H-s-level8. Therefore, the electronic property of the H atom is anionic either at HO25 or at H-DX state22,23 and the level of H-s orbital is located lower than that of Zn-s-orbital.
In the HO, a H atom interacts strongly with four Zn atoms, while a Zn atom with one H atom, and thus, the H-level is largely pushed down to below the valence band maximum (VBM) and all of Zn-s-levels are located above the CBM, as described in Fig. 2(c). On the other hand, in the H-DX, the H atom at H-site interacts with just three Zn atoms, so the hydrogenic level is less pushed-down and becomes located above VBM (α level in Fig. 2b). Through the LLR from HO to H-DX, the interaction between the H and the VO becomes weaker and the VO level becomes deeper below the CBM [see Fig. 2(a)]. Two Zn atoms (Zn(2) and Zn(3) in Fig. 1(b)) are separated from H by the LLR, and the generated Zn dangling bonds can induce a deep level (α* level), which becomes deeper through the interaction between two Zn-dangling bonds, described by red lines in Fig. 2(c). We, thus, suggest that the electronic energy reduction by the capture of electrons at the deep α* level stabilizes the displaced H-DX structure.
The fact that the H-DX structure is more stable than HO structure in the negative charge state indicates that as εF becomes close to the CBM, the HO can undergo a shallow-to-deep transition through a LLR. Figure 3 indicates that H-DX structure can be stable only for the εF close to CBM (εF > 0.05 eV below CBM). From the estimated pinning position of Fermi-level, we can estimate maximum electron concentration (ne,max) in H-rich ZnO, assuming the high concentration of HO, to be about 1018 cm−3 at room temperature, which is surprisingly in a good agreement with the experimental data9,10,11. Therefore, we suggest that the present bistability can give an explanation to the doping limit puzzle for H-rich ZnO. As the εF is close to the CBM, HO can undergo the large lattice relaxation into H-DX−, and the electrons generated by HO are trapped in the deep H-DX α* level, i.e., the HO's are self-compensated.
We find that the bistability of HO can give explanation to the persistent photo-induced conductivity (PPC) reported for ZnO. ZnO is well-known to be easily H-contaminated due to strong bonding between H and O atoms. In the H-rich and O-deficient ZnO, the concentrations of HO+ and H-DX− states can be comparable due to the above-discussed self-compensation. The PPC effect can be explained by next process: (i) Since the H-DX structure is stable only in the negative charge state, the H-DX− can be transformed into the HO structure, when an electron at H-DX state is excited by light illumination, and (ii) next it becomes spontaneously transformed into the HO+. The process is described as H-DX− ⇒ H-DX0 + e → HO+ + 2e (‘⇒’ indicates photo-excitation). Overall the deep H-DX− state can be transformed into the shallow donor-like HO+ structure under light. By these processes, the concentration of free electrons can be increased, that describes the photo-induced conductivity. (iii) A larger energy barrier between HO and H-DX should prevent the structural recovery transformation from HO to H-DX at room-temperature. Thus, the photo-excited HO+ state is metastable but persistent, even in the presence of the high concentration of electron carriers at CBM. These results can give a good explanation to the metastable and persistent formation of shallow donor HO+ (PPC). The metastable HO+ state can be transformed into the stable H-DX− state at a temperature high enough to overcome the energy barrier of 0.36 eV. It can describe the thermal recovery process of the photo-excited HO+ state. The estimated energy barrier for the transition from HO to H-DX is in a good agreement with the experimental value of 0.3 eV17 for the energy barrier for thermal recovery of PPC state.
Seghier and Gislason measured the photon energy spectrum for PPC17. The calculated optical absorption spectrum for H-DX state is found to be in a good agreement with the measured optical data17. The peak in the calculated optical absorption spectrum of H-DX around 2.3 eV agrees with measured peak in the photon excitation spectrum for PPC effect at 2.15 eV. The minimum optical excitation energy (Eopt) of H-DX− at about 1.06 eV, which comes from the electron excitation from α* level to CBM, also agrees with the measurement indicating 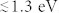 . Therefore, we suggest that the bistability of HO should be an important source of persistent photoconductivity in ZnO. These propose that in order to prevent the light-induced instability of the ZnO-based devices, either hydrogen contamination or O-deficiency should be reduced. We would note that the scenario of the PPC by metastable VO20 suggested by Lany and Zunger works in the VO coupled by an H atom, which is HO.
. Therefore, we suggest that the bistability of HO should be an important source of persistent photoconductivity in ZnO. These propose that in order to prevent the light-induced instability of the ZnO-based devices, either hydrogen contamination or O-deficiency should be reduced. We would note that the scenario of the PPC by metastable VO20 suggested by Lany and Zunger works in the VO coupled by an H atom, which is HO.
In conclusion, we identify a bistability of shallow donor HO center in ZnO. We find that when Fermi level is close to CBM, the HO can undergo a large lattice relaxation and create a deep level, trapping electrons. It gives an explanation to the low doping limit in H-rich n-type ZnO. We find that H-DX− is unstable against shallow-donor state HO by light-induced electron ionization, and there is a large energy barrier between HO+ and H-DX− states. Thus, we suggest that the bistability of HO gives also a microscopic explanation for persistent photo-conductivity in ZnO. The bistability of the H donor will provide a new way to consider the physics of hydrogen in oxide materials.
Methods
We performed DFT calculations as implemented in the Vienna ab initio simulation package (VASP) code26. The projector augmented wave (PAW) pseudopotentials27,28, the plane wave basis set with a kinetic energy cutoff of 400 eV, and the hybrid functional of Heyd-Scuseria-Ernzerhof (HSE)29 with a mixing parameter of 0.375 and a screening parameter of 0.2 Å−1 were used. The calculated lattice constants (a = 3.24 Å and c = 5.23 Å), the band gap (Eg = 3.42 eV), and the heat of formation (ΔHf = −3.13 eV) of ZnO were in good agreements with the other HSE calculations30,31 and the experiments32. With a hexagonal 96-atom supercell, a 2 × 2 × 2 k-point mesh including Γ was mainly used. All the atomic positions were fully optimized until the Hellmann-Feynman forces were less than 0.01 eV/Å.
Author Contributions
H.N. suggested the original main idea of this work and performed all calculations. C.P. and H.N. wrote the main manuscript text and Y.K. provided some ideas and wrote some manuscript parts. All authors reviewed the manuscript.
Supplementary Material
Supplimentary Information
Acknowledgments
C.H.P. acknowledges the support from the BRL program through the National Research Foundation (NRF) of Korea funded by the Ministry of Education, Science, and Technology (MEST) (No. 2012-0000345) and Y.S.K. acknowledges the support from Nano R&D program through NRF (No. 2012-0006199).
References
- Janotti A. & Van de Walle C. G. Fundamentals of zinc oxide as a semiconductor. Rep. Prog. Phys. 72, 126501 (2009). [Google Scholar]
- Özgür Ü. et al. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 98, 41301 (2005). [Google Scholar]
- Van de Walle C. G. & Neugebauer J. Universal alignment of hydrogen levels in semiconductors, insulators and solutions. Nature 423, 626–628 (2003). [DOI] [PubMed] [Google Scholar]
- Van de Walle C. G. Hydrogen as a Cause of Doping in Zinc Oxide. Phys. Rev. Lett. 85, 1012–1015 (2000). [DOI] [PubMed] [Google Scholar]
- Wardle M. G., Goss J. P. & Briddon P. R. First-principles study of the diffusion of hydrogen in ZnO. Phys. Rev. Lett. 96, 205504 (2006). [DOI] [PubMed] [Google Scholar]
- Shi G. A. et al. Hydrogen local modes and shallow donors in ZnO. Phys. Rev. B 72, 195211 (2005). [Google Scholar]
- Jokela S. J. & McCluskey M. D. Structure and stability of O-H donors in ZnO from high-pressure and infrared spectroscopy. Phys. Rev. B 72, 113201 (2005). [Google Scholar]
- Janotti A. & Van de Walle C. G. Hydrogen multicentre bonds. Nature Mater. 6, 44–47 (2007). [DOI] [PubMed] [Google Scholar]
- Strzhemechny Y. M. et al. Remote hydrogen plasma doping of single crystal ZnO. Appl. Phys. Lett. 84, 2545 (2004). [Google Scholar]
- Li Y. J. et al. Electronic properties of H and D doped ZnO epitaxial films. Appl. Phys. Lett. 92, 152105 (2008). [Google Scholar]
- Ohashi N. et al. Lowered stimulated emission threshold of zinc oxide by hydrogen doping with pulsed argon–hydrogen plasma. J. Cryst. Growth. 306, 316–320 (2007). [Google Scholar]
- Brauer G. et al. Identification of Zn-vacancy-hydrogen complexes in ZnO single crystals: A challenge to positron annihilation spectroscopy. Phys. Rev. B 79, 115212 (2009). [Google Scholar]
- Halliburton L. E. et al. Production of native donors in ZnO by annealing at high temperature in Zn vapor. Appl. Phys. Lett. 87, 172108 (2005). [Google Scholar]
- Minami T., Nanto H. & Takata S. Highly Conductive and Transparent Aluminum Doped Zinc Oxide Thin Films Prepared by RF Magnetron Sputtering. Jpn. J. Appl. Phys. 23, L280 (1984). [Google Scholar]
- Noh J.-Y., Kim H., Kim Y.-S. & Park C. H. Electron doping limit in Al-doped ZnO by donor-acceptor interactions. J. Appl. Phys. 113, 153703 (2013). [Google Scholar]
- T-Thienprasert J. et al. Compensation in Al-Doped ZnO by Al-Related Acceptor Complexes: Synchrotron X-Ray Absorption Spectroscopy and Theory. Phys. Rev. Lett. 110, 055502 (2013). [DOI] [PubMed] [Google Scholar]
- Seghier D. & Gislason H. P. Characterization of donor states in ZnO. Physica B 401–402, 404–407 (2007). [Google Scholar]
- Hoffman R. L., Norris B. J. & Wager J. F. ZnO-based transparent thin-film transistors. Appl. Phys. Lett. 82, 733–735 (2003). [Google Scholar]
- Chadi D. J. & Chang K. J. Theory of the Atomic and Electronic Structure of DX Centers in GaAs and AlxGa1−xAs Alloys. Phys. Rev. Lett. 61, 873–876 (1988). [DOI] [PubMed] [Google Scholar]
- Lany S. & Zunger A. Anion vacancies as a source of persistent photoconductivity in II–VI and chalcopyrite semiconductors. Phys. Rev. B 72, 035215 (2005). [Google Scholar]
- Janotti A. & Van de Walle C. G. Oxygen vacancies in ZnO. Appl. Phys. Lett. 87, 122102 (2005). [Google Scholar]
- Du M.-H. & Biswas K. Anionic and Hidden Hydrogen in ZnO. Phys. Rev. Lett. 106, 115502 (2011). [DOI] [PubMed] [Google Scholar]
- Park C. H. & Chadi D. J. Hydrogen-Mediated Spin-Spin Interaction in ZnCoO. Phys. Rev. Lett. 94, 127204 (2005). [DOI] [PubMed] [Google Scholar]
- Adolph B., Furthmüller J. & Bechstedt F. Optical properties of semiconductors using projector-augmented waves. Phys. Rev. B 63, 125108 (2001). [Google Scholar]
- Takenaka H. & Singh D. J. Bonding of H in O vacancies of ZnO: Density functional calculations. Phys. Rev. B 75, 241102(R) (2007). [Google Scholar]
- Kresse G. & Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996). [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Joubert J. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
- Heyd J., Scuseria G. E. & Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003). [Google Scholar]
- Oba F., Togo A., Tanaka I., Paier J. & Kresse G. Defect energetics in ZnO: A hybrid Hartree-Fock density functional study. Phys. Rev. B 77, 245202 (2008). [Google Scholar]
- Lyons J. L., Janotti A. & Van de Walle C. G. Why nitrogen cannot lead to p-type conductivity in ZnO. Appl. Phys. Lett. 95, 252105 (2009). [Google Scholar]
- Madelung O. Semiconductors-Basic Data (Springer, Berlin, 1996). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplimentary Information