Preferential Loading of the ACL Compared With the MCL During Landing

Abstract

Background

Strong biomechanical and epidemiological evidence associates knee valgus collapse with isolated, noncontact anterior cruciate ligament (ACL) injuries. However, a concomitant injury to the medial collateral ligament (MCL) would be expected under valgus collapse, based on the MCL’s anatomic orientation and biomechanical role in knee stability.

Purpose/Hypothesis

The purpose of this study was to investigate the relative ACL to MCL strain patterns during physiological simulations of a wide range of high-risk dynamic landing scenarios. We hypothesized that both knee abduction and internal tibial rotation moments would generate a disproportionate increase in the ACL strain relative to the MCL strain. However, the physiological range of knee abduction and internal tibial rotation moments that produce ACL injuries are not of sufficient magnitude to compromise the MCL’s integrity consistently.

Study Design

Controlled laboratory study.

Methods

A novel in sim approach was used to test our hypothesis. Seventeen cadaveric lower extremities (mean age, 45 ± 7 years; 9 female and 8 male) were tested to simulate a broad range of landings after a jump under anterior tibial shear force, knee abduction, and internal tibial rotation at 25° of knee flexion. The ACL and MCL strains were quantified using differential variable reluctance transducers. An extensively validated, detailed finite element model of the lower extremity was used to help better interpret experimental findings.

Results

Anterior cruciate ligament failure occurred in 15 of 17 specimens (88%). Increased anterior tibial shear force and knee abduction and internal tibial rotation moments resulted in significantly higher ACL:MCL strain ratios (P < .05). Under all modes of single-planar and multiplanar loading, the ACL:MCL strain ratio remained greater than 1.7, while the relative ACL strain was significantly higher than the relative MCL strain (P < .01). Relative change in the ACL strain was demonstrated to be significantly greater under combined multiplanar loading compared with anterior tibial shear force (P = .016), knee abduction (P = .018), and internal tibial rotation (P < .0005) moments alone.

Conclusion

While both the ACL and the MCL resist knee valgus during landing, physiological magnitudes of the applied loads leading to high ACL strain levels and injuries were not sufficient to compromise the MCL’s integrity.

Clinical Relevance

A better understanding of injury mechanisms may provide insight that improves current risk screening and injury prevention strategies. Current findings support multiplanar knee valgus collapse as a primary factor contributing to a non-contact ACL injury.

An anterior cruciate ligament (ACL) injury is common in adolescent and young adult athletes, with a prevalence estimated to be 1 in 3000 in the United States population.³³ Many ACL injuries occur through a noncontact mechanism (without a direct blow to the knee joint⁸) during landing^3,36 and lateral cutting maneuvers.^1,31,38 Although intrinsic and extrinsic risk factors for a noncontact ACL injury have been studied extensively, the factors surrounding the inciting event and the underlying injury mechanisms during landing remain elusive.

The tibiofemoral frontal-plane loading mechanism has become a recent topic of debate as a primary factor contributing to noncontact ACL injuries. A recent systematic review⁴¹ reported that more than 80% of the identified ACL injury mechanism studies (1966-2008) support frontal-plane mechanisms as a contributor to a multiplanar injury mechanism of the ACL during landing after a jump. “Valgus” refers to the outward angulation of the distal segment of a bone or joint. Knee valgus collapse may occur under pure abduction motions of the distal tibia relative to the femur and/or transverse-plane knee rotation motions.³⁹ A prospective study by Hewett et al¹¹ demonstrated that patients who subsequently suffered an ACL injury had greater knee valgus angles at initial contact and peak abduction compared with uninjured control athletes. Koga et al¹⁹ showed significant knee valgus rotation within 40 milliseconds of initial contact in 10 cases of non-contact ACL injuries during handball and basketball utilizing model-based image-matching techniques. These findings are in agreement with those of Olsen et al³⁶ and Krosshaug et al,²⁰ who reported dynamic knee valgus collapse as the most common mechanism for an ACL injury in handball and basketball, respectively. Markolf et al^22,23 showed a significant increase in ACL tension (force) in cadaveric specimens subjected to knee abduction moments under 0° to 30° of knee flexion. Similar findings have been reported in cadaveric studies conducted by Miyasaka et al³⁴ and Wascher et al.⁵²

McLean et al²⁷ utilized motion analysis and mathematical modeling to simulate injurious conditions. They demonstrated that abduction loads reach values high enough to rupture the ACL during cutting maneuvers. Further, they showed that perturbations to the lower extremity during side-step cutting maneuvers could lead to external abduction loads capable of rupturing the ACL.²⁸

Despite strong biomechanical and epidemiological evidence supporting knee valgus as a mechanism in most cases of ACL injuries during landing tasks, controversy and debate surround this assertion.^6,11,39,51 The medial collateral ligament (MCL) has been reported to be the primary restraint against knee valgus motions and abduction loads.⁹ If a noncontact ACL injury occurs as a result of valgus collapse of the knee joint, a high incidence of combined ACL and MCL injuries would be expected. However, concomitant ACL and MCL injuries make up only a small percentage (4%-17%) of total ACL injuries, which is contrary to what is expected by clinicians and researchers.^15,33,43,44 The predominance of isolated ACL injuries under noncontact mechanisms is challenging for clinicians and researchers to explain based on the existing literature. Hence, this study aimed to investigate the relative ACL and MCL strain patterns during the physiological simulation of a wide range of high-risk dynamic landing conditions. We hypothesized that both knee abduction and internal tibial rotation moments would generate disproportionate increases in the ACL strain relative to the MCL strain.

MATERIALS AND METHODS

Biomechanical Testing (Ex Vivo)

Seventeen unembalmed, fresh-frozen cadaveric lower limbs (mean age, 45 ± 7 years; 9 female and 8 male), free from any signs of soft or hard tissue injuries, were acquired. Specimens were sectioned at the midfemoral diaphysis and potted for rigid attachment to the testing frame. The quadriceps (rectus femoris) and medial and lateral hamstring (semitendinosus, biceps femoris, and semi-membranosus) tendons were isolated and clamped to allow for the application of simulated transknee muscle loads. The foot and ankle joint were maintained intact to provide a realistic load transfer interface.

Landing in cadaveric specimens was simulated using a novel, custom-designed drop stand.²¹ Specimens were oriented to simulate a lower extremity posture during ground strike while landing from a jump (Figure 1). All specimens were tested while inverted with the knee at 25° of flexion, as this flexion angle has previously been reported during video analysis of ACL injury events.¹⁹ Each specimen was rigidly fixed at the proximal femur to a fixture with an embedded 6-axis load cell (RA Denton Corp, Rochester Hills, Michigan), and the tibia was oriented vertically with the foot above the knee joint. This configuration allowed for a broad range of loading conditions to be applied during simulated landing. Cable-pulley systems and static weights were used to apply constant forces to the quadriceps and hamstring tendons to simulate transknee muscle forces. An external fixation frame with an integrated pulley system was rigidly attached to the tibia to apply external loads, such that different landing postures could be simulated. The distal extremity (lower leg and foot) was not constrained until after loading and repositioning of the lower limb. Further, an athletic shoe was placed on the foot to simulate realistic load transfer during initial contact. Landing was simulated by the release of a specific weight from a specific height, utilizing a hemispherical impactor with an integrated weight stack (different magnitudes of weight and height defined impact severity). The drop weight exerted an impulsive axial compressive force to simulate ground reaction force during landing from a jump. A detailed summary of the test setup is described by Levine et al.²¹

Figure 1.

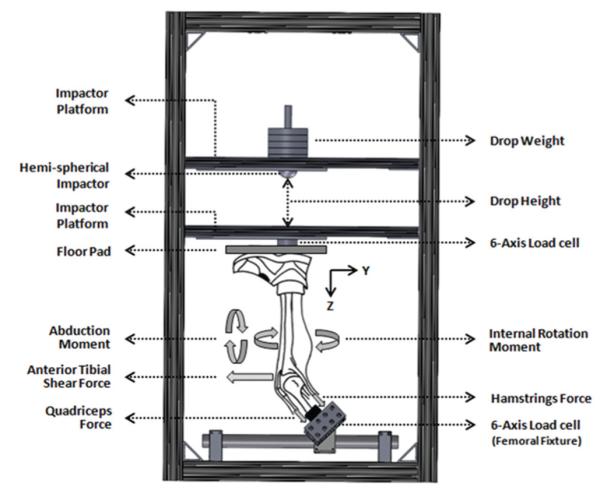
Custom-designed drop-stand testing apparatus.

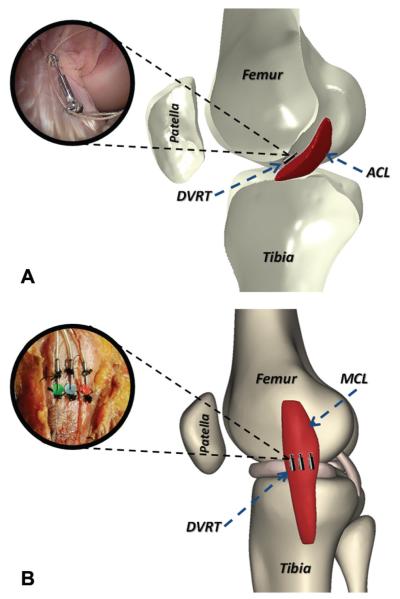
The ACL strain was calculated based on measurements from a differential variable reluctance transducer (DVRT) (MicroStrain Inc, Williston, Vermont), which was arthroscopically placed on the ACL’s anteromedial bundle after a notchplasty procedure (Figure 2).⁶ The superficial MCL was exposed, and 3 DVRTs for displacement were securely sutured to the anterior, middle, and posterior aspects of the ligament across the joint line as shown in Figure 2. To calculate absolute strain values, the ACL and regional MCL reference lengths were calculated based on established methods as the distinct inflection point in force/moment versus DVRT displacement data.^14,21 These data were collected by placing each specimen through 4 cycles of anterior-posterior shear force and abduction/adduction moment before testing. The selected inflection point was chosen as the proper reference between ligament-taut and -slack conditions. Therefore, reference length is not dependent on the initial gauge length of the DVRT at the time of insertion.

Figure 2.

Insertion of the differential variable reluctance transducer (DVRT) on the (A) anterior cruciate ligament’s anteromedial bundle and (B) superficial medial collateral ligament across the joint line.

Generated impulsive impact forces were captured using another 6-axis load cell (RA Denton Corp) embedded within the floor pad. Analog data (load cells and DVRTs) were collected at 4 kHz using a 16-bit analog-to-digital board. The peak ACL and regional MCL strains were defined as the maximum strain levels subsequent to the peak axial impact load during the course of simulated landings. The average peak MCL strain was calculated as the mean peak local strain (from the readings of 3 DVRTs) recorded across the superficial MCL. The ACL:MCL strain ratio along with the relative strain (defined as an incremental increase in strain due to applied external off-axis loads compared with the baseline) for both the ACL and the MCL under each loading condition were calculated.

Loading Protocol

Bipedal and unipedal landings after a jump were simulated by the release of half (350 N) and full (700 N) body weight, respectively, both from heights of 30 and 60 cm.⁷ To simulate high-risk injurious conditions, multiple combinations of knee abduction and internal tibial rotation moments with or without anterior tibial shear force were used to establish 2 loading groups (Table 1). Both loading protocols began and ended with similar loading conditions to facilitate comparisons between the specimens while evaluating a broad range of injurious conditions. Shin et al⁴⁷ have reported knee abduction moments of up to 51 N·m and internal tibial rotation moments of up to 30 N·m during non-injurious landings. However, higher magnitudes of the above-mentioned loads were applied to simulate high-risk injurious conditions. Specimens were randomly assigned to each loading group and sequentially tested from loading 1 through 20 or until failure was observed. Observations of the mechanical response during testing were monitored as indicators of ACL failure. Ultimately, manual evaluation of joint laxity and arthroscopic inspection were employed to confirm catastrophic tissue failure.

TABLE 1.

Loading Protocol^a

Knee Abduction Loading Group					Internal Tibial Rotation Loading Group
Drop Weight, *BW	Drop Height, cm	Anterior Shear Force, N	Abduction, N·m	Internal Rotation, N·m	Drop Weight, *BW	Drop Height, cm	Anterior Shear Force, N	Abduction, N·m	Internal Rotation, N·m
0.5	30	0	0	0	0.5	30	0	0	0
0.5	30	134	0	0	0.5	30	134	0	0
0.5	30	268	0	0	0.5	30	268	0	0
0.5	30	0	25	0	0.5	30	0	0	10
0.5	30	134	25	0	0.5	30	0	0	20
0.5	30	0	50	0	0.5	30	268	0	20
0.5	30	134	50	0	0.5	30	0	0	40
0.5	30	268	50	0	0.5	30	268	0	40
0.5	30	0	75	0	0.5	30	0	0	60
0.5	30	268	75	0	0.5	30	268	0	60
0.5	30	0	75	20	0.5	30	0	0	80
0.5	30	0	75	60	0.5	30	268	0	80
0.5	30	268	75	60	0.5	30	268	75	60
0.5	30	268	100	60	0.5	30	268	100	60
0.5	30	268	125	60	0.5	30	268	125	60
0.5	30	268	150	60	0.5	30	268	150	60
0.5	60	268	150	60	0.5	60	268	150	60
1	60	268	150	60	1	60	268	150	60
1	60	268	150	80	1	60	268	150	80
1	60	268	150	100	1	60	268	150	100

^aBW, body weight.

Statistical Analysis

Analysis of variance (ANOVA) with post hoc Bonferroni correction for multiple comparisons and an independent 2-sample t test were used to investigate the change in the ACL:MCL strain ratio under each loading condition. A paired-sample t test was used to compare the relative change in the ACL and average MCL strain levels. Finally, a general linear model was used to determine the sensitivity of the ACL:MCL strain ratio to each of the applied loading parameters under simulated dynamic landings. Differences were considered statistically significant at P < .05.

Computer Modeling (FE Analysis)

An anatomic finite element (FE) model of the lower extremity was previously developed from anatomic data of a healthy, skeletally mature young female athlete (age, 25 years; height, 170 cm; weight, 64.4 kg) with no history of knee injuries.¹⁷ The model consists of 3-dimensional representations of the lower extremity’s bony structure (pelvis, femur, patella, fibula, tibia, and foot) in addition to soft tissue structures of the knee joint such as major ligaments, transknee muscles, articular cartilage, and menisci. The model was extensively validated against cadaveric measurements of tibiofemoral kinematics, ACL and MCL strains, and tibiofemoral cartilage pressure over a wide range of quasistatic and dynamic loading conditions.¹⁷ Details of the model are described by Kiapour et al.¹⁷ To better interpret experimental findings, parametric FE analyses were conducted over continuous ranges of knee abduction (0-150 N·m) and internal tibial rotation (0-100 N·m) moments in the presence of 268 N of anterior tibial shear force and simulated muscle forces (quadriceps, 1200 N; hamstring, 800 N).

RESULTS

Simulated landings resulted in an average axial impact load of 3775 ± 290 N, 4607 ± 594 N, and 4875 ± 153 N over a period of 70 milliseconds for half the body weight from 30 cm, half the body weight from 60 cm, and full body weight from 60 cm, respectively. The average peak ACL and MCL strains occurred at 49.7 ± 12.1 milliseconds and 53.3 ± 34.9 milliseconds after peak axial impact, respectively (P = .82). Anterior cruciate ligament failure occurred in 15 of 17 specimens (88%). Of 15 specimens with ACL failure, 3 (20%) failed under anterior tibial shear force, 1 (7%) sustained ACL failure under an internal tibial rotation moment, and 4 (27%) sustained ACL failure under a knee abduction moment. Seven of the 15 specimens (47%) sustained an ACL injury under combined multiplanar knee abduction and internal tibial rotation moments and anterior tibial shear force. Details of the peak ACL strain at failure and associated loading mechanisms were previously presented by Levine et al.²¹

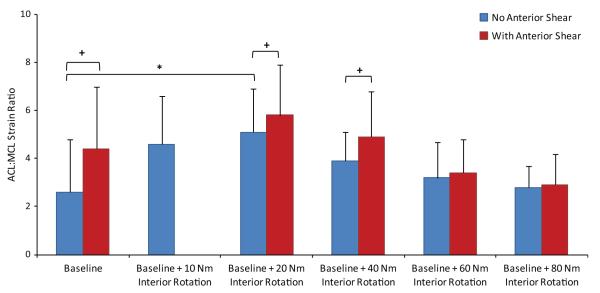
Under simulated neutral landings (no off-axis loading), the addition of anterior tibial shear force (268 N) significantly (P = .041) increased the ACL:MCL strain ratio by 69% compared with baseline (Figure 3). The addition of knee abduction moments up to 50 N·m significantly (P = .011) increased the ACL:MCL strain ratio by 170% compared with baseline (neutral landing). While the strain ratio remained greater than 1.7 under an applied knee abduction moment of 75 N·m, the resultant strain ratio was not significantly different from the baseline condition (Figure 4). The addition of anterior tibial shear force resulted in increased magnitudes of the ACL:MCL strain ratio compared with abduction moments alone (Figure 4). These changes were statistically significant for up to 75 N·m of knee abduction (P < .03 for all comparisons). Simulated landings under internal tibial rotation moments (20 N·m) significantly (P = .014) increased the ACL:MCL strain ratio by 94% compared with baseline. However, increased magnitudes of applied internal rotation moments beyond 20 N·m resulted in no significant difference compared with baseline, while the resultant strain ratio remained greater than 2 (Figure 5). The addition of anterior tibial shear force increased the ACL:MCL strain ratio compared with internal rotation moments alone (Figure 5). The changes in the ACL:MCL strain ratio were significant for up to 60 N·m of internal tibial rotation moments (P < .05 for all comparisons). Combined multiplanar loading conditions including anterior tibial shear force and knee abduction and internal tibial rotation moments resulted in no significant difference in the strain ratios compared with baseline (Figure 6). Increased impact severity (simulated bipedal and unipedal landings from a 60-cm height) resulted in an increasing trend in the ACL:MCL strain ratio (P > .7) (Figure 7). The general linear model demonstrated that anterior tibial shear force (P = .021) and knee abduction (P = .004) and internal tibial rotation (P = .031) moments are significant determinants of the ACL:MCL strain ratios during simulated landings.

Figure 3.

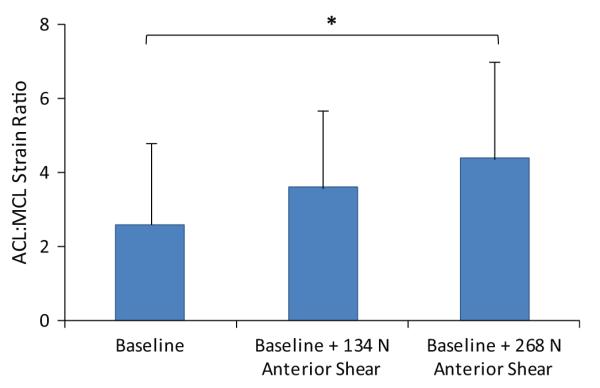
Increase in the ACL:MCL strain ratio under applied anterior tibial shear forces during simulated neutral landings. *P = .041.

Figure 4.

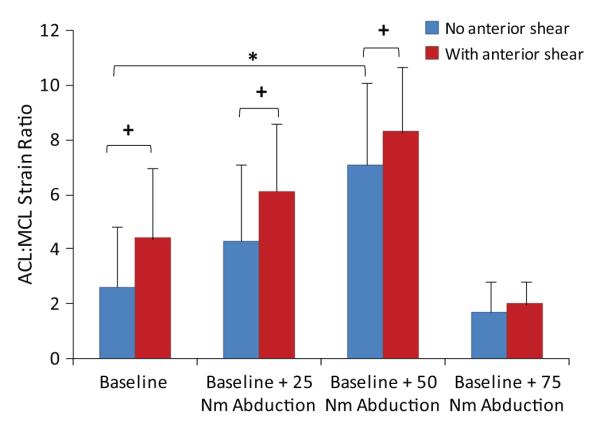
Change in the ACL:MCL strain ratio under applied knee abduction moments with and without additional anterior tibial shear force (134 N for 25 N·m of knee abduction moments and 268 N·m for the rest of the loading conditions) during simulated landings. *P = .011 and ⁺P < .03 for all comparisons.

Figure 5.

Change in the ACL:MCL strain ratio under applied internal tibial rotation moments with and without additional anterior tibial shear force (268 N) during simulated landings. *P = .014 and ⁺P < .05 for all comparisons.

Figure 6.

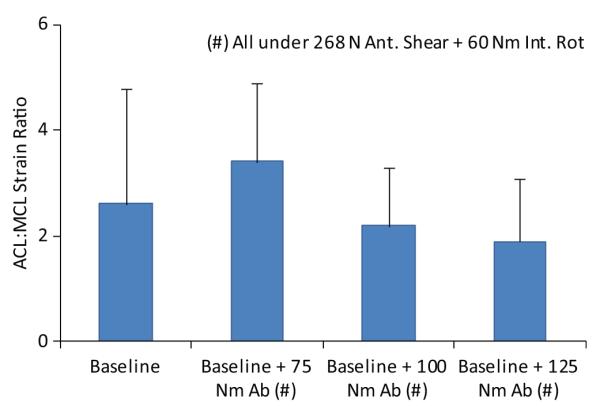
Change in the ACL:MCL strain ratio under combined multiplanar loading conditions during simulated landings. Ab, abduction; Ant., anterior; Int. Rot, internal rotation.

Figure 7.

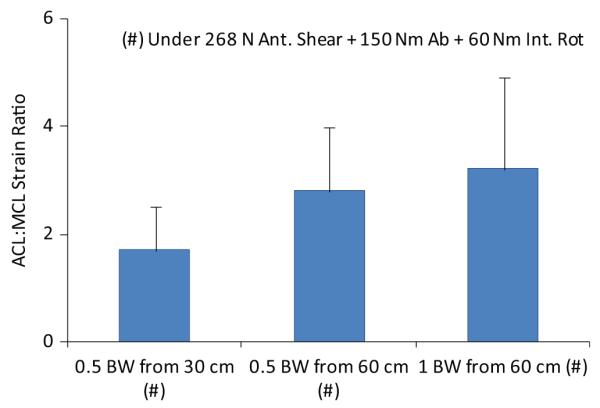
Change in the ACL:MCL strain ratio under increased impact severity during simulated landings. Ant., anterior; BW, body weight; Int. Rot, internal rotation.

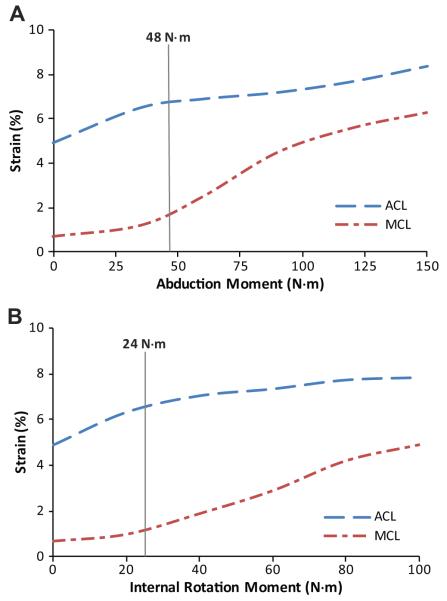
Data further demonstrated that the ACL:MCL strain ratio remains greater than 1.7 under all modes of loading. Figure 9 shows how the relative peak ACL strain is significantly higher than the relative peak average MCL strain under anterior tibial shear force (P < .0005), knee abduction (P = .006), internal tibial rotation (P < .0005), and combined multiplanar (P = .001) loading conditions. Also, combined multiplanar loading resulted in significantly increased normalized ACL strains compared with anterior tibial shear force (P = .016) and knee abduction (P = .018) and internal tibial rotation (P < .0005) moments alone (Figure 8). The FE analyses demonstrated consistently higher levels of the ACL strain compared with the MCL strain over continuous ranges of applied knee abduction (0-150 N·m) and internal tibial rotation (0-100 N·m) moments (Figure 9). However, the rate of increase in the MCL strain surpasses that of the ACL after 48 N·m of knee abduction and 24 N·m of internal tibial rotation moments.

Figure 9.

The finite element–predicted change in anterior cruciate ligament and medial collateral ligament strains under applied 268 N of anterior tibial shear force combined with (A) continuous ranges of knee abduction moment and (B) internal tibial rotation moment all under simulated muscle loads.

Figure 8.

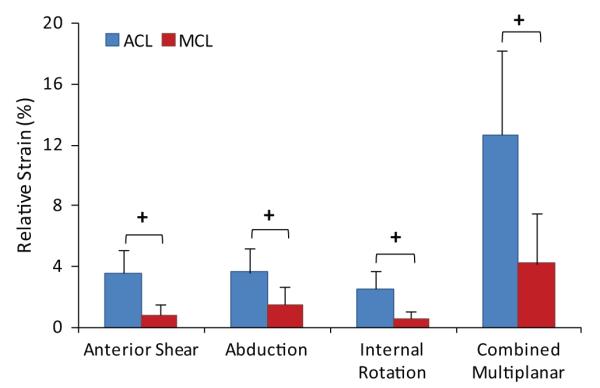
Relative anterior cruciate ligament and medial collateral ligament strains (compared to baseline) under different modes of loading (⁺P < .003).

DISCUSSION

Characterization of the complex mechanisms associated with an ACL injury can help prevent and better treat this injury.¹⁰ In spite of extensive evidence supporting knee valgus collapse as a mechanism of a noncontact ACL injury during landing,^†† clinicians and biomechanists are unable to demonstrate how valgus collapse can lead to an ACL rupture without a concomitant MCL injury. This study was designed to investigate strain patterns across the ACL and MCL during high-risk injurious dynamic landing. Several high-risk injurious loading conditions were simulated using single-planar and multiplanar loads that potentially produce a noncontact ACL injury. Moreover, FE parametric analyses were conducted to further investigate the preferential loading of the ACL relative to the MCL as indicated by FE-predicted ACL and MCL strains. The results indicate that externally applied anterior tibial shear force and knee abduction and internal tibial rotation moments are significant determinants of resultant ACL:MCL strain ratio levels.

Effects of Anterior Tibial Shear Force on ACL:MCL Strain Ratio

Externally applied anterior tibial shear force with (Figures 4 and 5) or without (Figure 3) the addition of knee abduction or internal tibial rotation moments resulted in elevated ACL:MCL strain ratios at 25° of knee flexion. All of these conditions consistently resulted in a significantly greater relative ACL strain than the relative MCL strain (Figure 8). This is in agreement with previous studies reporting that the ACL is the primary soft tissue knee constraint against anterior tibial translation at low knee flexion angles.^4,24,25 The externally applied anterior tibial shear force was used to simulate the effects of different factors such as excessive quadriceps contraction,^5,54 deceleration,⁴⁶ or other factors that may lead to increased shear forces and should not be mistaken for the shear force that was generated across the knee as a result of ground-reaction force.³⁰

Effects of Knee Abduction Moment on ACL:MCL Strain Ratio

The current findings indicate that knee abduction moments act to disproportionately increase the ACL strain relative to the MCL strain at 25° of knee flexion. While the relative ACL strain was consistently observed to be significantly greater than the relative MCL strain under applied knee abduction moments (Figure 8), abduction moments greater than 50 N·m resulted in an ACL:MCL strain ratio similar to the baseline condition (~2). This observation is surprising, as the MCL has been reported to be the primary restraint against knee abduction loads.⁹ Matsumoto et al²⁶ demonstrated that the MCL acts to resist knee valgus rotation by limiting joint distraction across the medial compartment. The transition from 50 to 75 N·m of knee abduction may represent the initiation of joint opening during landings simulated in the current study. This finding is supported by the FE results, indicating that the rate of increase in the MCL strain surpasses that of the ACL after 48 N·m of knee abduction, while the ACL undergoes higher levels of strain compared with the MCL over a continuous range of knee abduction moments (0-150 N·m) (Figure 9). This sudden increase in the MCL strain compared with under 48 N·m resulted in a decreased ACL:MCL strain ratio to the baseline level. Oh et al³⁵ have reported the initiation of medial knee joint opening when knee abduction moments exceed 100 N·m using a computer modeling approach. This variation between our findings and those of Oh et al³⁵ may be caused by differences between applied loading conditions during simulated landing.

Effects of Internal Tibial Rotation Moment on ACL:MCL Strain Ratio

This study demonstrates that applied internal tibial rotation moments result in increased ACL:MCL strain ratios compared to baseline at 25° of knee flexion. While the relative ACL strain was consistently observed to be significantly greater than the MCL strain under applied internal tibial rotation moments (Figure 8), increased levels of internal tibial rotation moments (>20 N·m) resulted in an ACL:MCL strain ratio similar to the baseline condition (~2). This threshold effect is in agreement with the current FE results, indicating that the rate of increase in the MCL strain surpasses that of the ACL after 24 N·m of internal tibial rotation, while the ACL undergoes higher levels of strain compared with the MCL over a continuous range of internal tibial rotation moments (0-100 N·m) (Figure 9). This relative change in ACL and MCL strain patterns may be caused by coupled valgus rotation generated by internal tibial rotation moments as reported previously.³⁷ This phenomenon may be attributed to the interaction between the meniscus and the contour of the tibial plateau with the femoral condyles. This concept is supported by an in vivo study by McLean et al,²⁹ who reported a significant correlation between peak knee valgus and the tibial plateau slope ratio (medial:lateral) during dynamic single-leg landing.

Effects of Combined Multiplanar Loading on ACL:MCL Strain Ratio

Simulated landings under combined multiplanar loading conditions resulted in ACL:MCL strain ratios similar to the baseline level (~2), while magnitudes of the relative ACL strain were consistently greater than those of the MCL strain (Figure 8). In this study, combined multiplanar loading resulted in the highest levels of relative ACL strain (Figure 8), generating 7 of 15 (47%) ACL injuries. These findings reinforce the assertion that combined multiplanar loading is the most likely mechanism of a noncontact ACL injury. Previous studies also considered combined multiplanar loading to be the worst-case scenario of an ACL injury.^21,35,47 Increased impact severity (greater mass and height) under multiplanar loading conditions led to greater ACL:MCL strain ratios (Figure 7). This finding is in agreement with previous prospective in vivo studies that demonstrated an increased risk of an ACL injury under higher ground-reaction forces associated with unipedal and bipedal landings from greater heights.^11,12

Isolated ACL Injury Under Valgus Collapse Mechanism

Considering strain as an established quantifiable measure of injury risk, data demonstrated that the ACL is at a significantly greater risk of injury than is the MCL under all modes of single-planar and multiplanar loading with the knee at 25° of flexion. Previous studies have shown that MCL disruption occurs at higher load levels than the ACL.^16,50 Combined, these factors explain the predominance of isolated ACL injuries reported over concomitant ACL and MCL injuries (4%-17% of total ACL injuries).^15,33,43,44 Biomechanical data from video analyses and in vivo studies demonstrated an increase in the risk of ACL injuries under knee valgus collapse.^3,13,19,20 Knee valgus collapse may occur under pure abduction motions of the distal tibia relative to the femur and/or transverse-plane knee rotation motions.³⁹ Valgus rotation of the tibia increases the lateral compression of the femur and tibia.^18,21,40 This compression, combined with axial impact loading across the joint during vertical landing, can generate bone bruises of the femur and tibia across the knee lateral compartment.^40,42 This finding is in agreement with bone bruise patterns associated with more than 80% of the ACL injuries located on the lateral femoral condyle and tibial plateau.^32,48,49 These reported bone bruise patterns support the aforementioned multiplanar loading conditions including knee abduction, internal tibial rotation, and/or anterior tibial translation.^21,40 Simulated landings in this study resulted in damage to both the articular cartilage and subchondral bone similar to clinically observed bone bruise patterns across the tibial plateau during actual cases of noncontact ACL injuries.²¹

This work represents the first cadaveric study to compare ACL and MCL strains under a diverse range of simulated landing conditions utilizing a novel in sim approach including cadaveric experiments and computational modeling. In summary, the findings support our hypothesis that both knee abduction and internal tibial rotation moments generate a disproportionate increase in the ACL strain relative to the MCL strain. However, the physiological ranges of knee abduction and internal tibial rotation moments that produced ACL injuries were not of sufficient magnitude to overcome joint stability and compromise the MCL’s integrity consistently. This is supported by significantly greater relative strain levels across the ACL compared with the MCL in addition to ACL:MCL strain ratios greater than 1.7 observed under all modes of loading. Cumulatively, the results of this study provide evidence to help explain the high incidence of reported isolated ACL tears in the absence of a concomitant MCL injury. In addition, the current findings agree with clinical and video analysis studies that demonstrate the high incidence of knee valgus collapse at the time of a noncontact ACL injury.

Study Limitations

As with any study, inherent limitations exist. First, potential differences in the tissue properties associated with cadaveric specimens compared with the in vivo tissue properties of young athletes might affect the accuracy of the absolute reported values. We have tried to minimize this factor by testing relatively young specimens. Second, while care was taken to identify any obvious damage to the specimens between loading conditions, inherent cumulative microdamage associated with injury biomechanics may have resulted in the increased severity of tissue damage and elevated strain levels, especially at failure. This presents challenges in conducting robust parametric studies for high-rate mechanical characterization on any single specimen. Third, the effect of change in knee flexion angles was not evaluated, as all the specimens were tested at 25° of knee flexion; however, this flexion angle has been reported during real cases of ACL injuries.¹⁹ Fourth, the ACL strain was represented by local strain measurements across the anteromedial bundle, as the attachment of a second DVRT to the posterolateral bundle of the ACL would have been associated with potential measurement artifacts due to a compromised joint capsule.² Fifth, simulated muscle loads did not include all the muscle groups surrounding the knee joint, which may have affected the tibiofemoral joint reaction during simulated landings. Finally, as with all computer and mathematical models, certain standardized assumptions and simplifications are necessary. However, the developed FE model was extensively validated with regard to the primary independent variables of interest in this study. Care was taken to understand these limitations during the interpretation of our findings. None of these limitations would affect the reported qualitative findings.

CONCLUSION

Data from this study demonstrate the relative contribution of both the ACL and MCL to resist knee valgus during landing. However, physiological magnitudes of the applied loads leading to high ACL strain levels and injuries were not high enough to compromise the MCL’s integrity consistently.