The Control Outcome Calibration Approach for Causal Inference With Unobserved Confounding

Abstract

Unobserved confounding can seldom be ruled out with certainty in nonexperimental studies. Negative controls are sometimes used in epidemiologic practice to detect the presence of unobserved confounding. An outcome is said to be a valid negative control variable to the extent that it is influenced by unobserved confounders of the exposure effects on the outcome in view, although not directly influenced by the exposure. Thus, a negative control outcome found to be empirically associated with the exposure after adjustment for observed confounders indicates that unobserved confounding may be present. In this paper, we go beyond the use of control outcomes to detect possible unobserved confounding and propose to use control outcomes in a simple but formal counterfactual-based approach to correct causal effect estimates for bias due to unobserved confounding. The proposed control outcome calibration approach is developed in the context of a continuous or binary outcome, and the control outcome and the exposure can be discrete or continuous. A sensitivity analysis technique is also developed, which can be used to assess the degree to which a violation of the main identifying assumption of the control outcome calibration approach might impact inference about the effect of the exposure on the outcome in view.

Unobserved confounding is a well-known threat to valid causal inference, which can seldom be ruled out with certainty in an observational study. An approach that is sometimes used in epidemiologic practice to evaluate whether empirical results are subject to confounding bias entails evaluating whether the treatment or exposure in view is associated with a so-called negative control outcome upon adjustment for observed confounders (1–4). An outcome is said to be a valid negative control variable to the extent that it is influenced by unobserved confounders of the exposure effects on the outcome in view, although not directly influenced by the exposure (3). Thus, a negative control outcome found to be empirically associated with the exposure indicates that unobserved confounding may be present for the primary outcome provided that, upon adjustment for observed covariates, there is no unobserved confounder of the negative control outcome that does not also confound the primary outcome (3).

Suppose that in an application, a negative control outcome is found to be associated with the treatment in view, thus correctly indicating the presence of unobserved confounding. Then, it may seem natural to consider the observed association between the exposure and the control outcome as an estimate of bias due to unmeasured confounding, and one may be tempted to simply correct the confounded estimate of the exposure-outcome association by subtracting the estimated bias. Although this ad hoc bias correction approach may sometimes be appropriate, it often is not. A difficulty with the approach is that it relies on the key assumption that the bias observed for the negative control outcome is somehow equivalent to the bias one would have observed between the exposure and the primary outcome under the null hypothesis of no causal effect of the exposure. A natural prerequisite for this “bias equivalence” assumption is that the outcomes are measured on comparable scales, which would be the case if, for example, the control outcome was a preexposure measure of the outcome process. However, outside of this special case, the assumption may not be appropriate if the outcomes are clearly measured on different scales, such as, for example, if the negative control outcome were dichotomous and the primary outcome were continuous. The assumption would then likely be violated because an additive association of the exposure with the control outcome would a priori be restricted by the binary nature of the outcome, whereas the additive association of the outcome in view with the exposure would not.

In this paper, we propose to use control outcomes in a simple but formal counterfactual or potential outcome–based approach to correct causal effect estimates for bias due to unobserved confounding, while avoiding the above assumption of bias equivalence. The proposed control outcome calibration approach (COCA) is motivated by noting that the ultimate set of unobserved confounders in an analysis relating the exposure to the primary outcome entails the set of counterfactuals for the outcome of interest under all possible treatment values. This is because conditioning on the set of counterfactuals for the primary outcome renders the latter constant and, thus, independent of the treatment assignment, a sufficient requirement for identification of a causal effect of treatment on the outcome. Furthermore, when, as we have assumed, there is no unobserved confounder of the treatment effect on the control outcome that does not confound the treatment effect on the primary outcome, it is natural to expect that the set of the observed covariates together with the counterfactuals for the primary outcome under all possible treatment values also suffices to identify the effects of treatment on the control outcome. This is the fundamental assumption made when using the COCA. In the context of a negative control outcome, the COCA produces an effect estimate of the association between treatment and the primary outcome under an assumed causal model. This effect estimate is obtained upon calibrating the parameters of the causal model so that the set of all counterfactuals for the primary outcome recovered from the observed data under the calibrated model suffices, together with the observed covariates, to fully adjust for confounding in a regression analysis for the negative control outcome and correctly recovers the null association between the exposure and the control outcome. The COCA is separately developed for a continuous outcome and a binary outcome, and the control outcome and the exposure in view can be either binary, a count, or continuous. Finally, a sensitivity analysis technique is developed in the Appendix to assess the extent to which a violation of the main identifying assumption of the COCA might affect inference about the effect of the exposure on the outcome in view.

THE COCA FOR ADDITIVE CAUSAL EFFECTS

We introduce the notation and definitions we will be using throughout. Let A denote the exposure or treatment received by an individual, let Y denote a posttreatment outcome, and let C denote the value of a set of observed preexposure confounding variables of the effects of A on Y. Let U denote a set of unmeasured preexposure confounders of the effects of A. Let Z denote a negative control outcome variable. Then, the relationships between these variables may be depicted as in the causal diagram in Figure 1.

Figure 1.

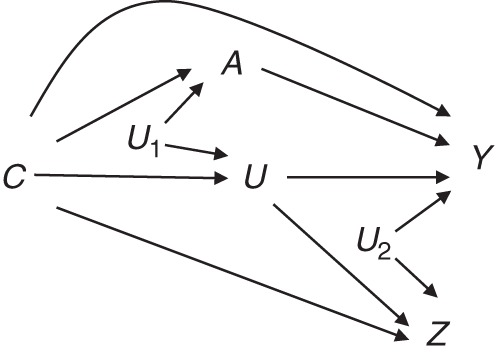
Causal diagram depicting unmeasured confounding of the A − Y association and the negative control outcome Z, where A represents exposure; Y represents outcome; U, U₁, and U₂ represent unobserved confounders; and C represents observed confounders.

Figure 1 gives a graphical representation of the assumption that adjustment for both C and U would suffice to account for confounding of the causal effects of A on Y and on Z, respectively. The variables U₁ and U₂ on the graph represent the possible presence of unobserved factors that correlate U with A and Y with Z, respectively. Formally, this graph is a causal directed acyclic graph representing the observed variables together with both observed and unobserved common causes. As shown in Figure 1, Z is an ideal negative control outcome because it is not directly influenced by exposure, but it is influenced by the unmeasured confounders of the exposure-outcome association (3).

We also consider counterfactuals or potential outcomes under possible interventions on the treatment. Let Y_a denote a subject's outcome if treatment A were set, possibly contrary to fact, to a. Also, let Z_a denote a subject's counterfactual value for Z if A were set to a. By assumption, Z_a = Z, a = 0,1, for a negative control outcome and, by the consistency assumption usually made in the causal inference literature, Y_a = Y if A = a. The assumption encoded in Figure 1, that {U, C} suffices to account for confounding of the causal associations between A and Y and between A and Z, respectively, is equally expressed using counterfactuals

(1)

(2)

Note that U is an unobserved confounder for the effects of A on Y in the sense that, although equation 1 is satisfied, it is also the case that

so that C alone does not suffice to adjust for confounding, whereas {U, C} does.

Focusing on negative control outcomes, one may formalize its definition as follows.

Definition 1. Z is said to be a negative control outcome if

Definition 1 formalizes the idea that the exposure–negative control outcome association cannot be confounded by a variable that does not also confound the exposure-outcome association. Although this assumption may suffice to detect the presence of unobserved confounding, it does not suffice to identify the causal effect of A on Y. To make progress, we make an additional identifying assumption, depicted in the graph in Figure 2, which is similar but more elaborate than the graph in Figure 1, and which encodes the following assumption.

Figure 2.

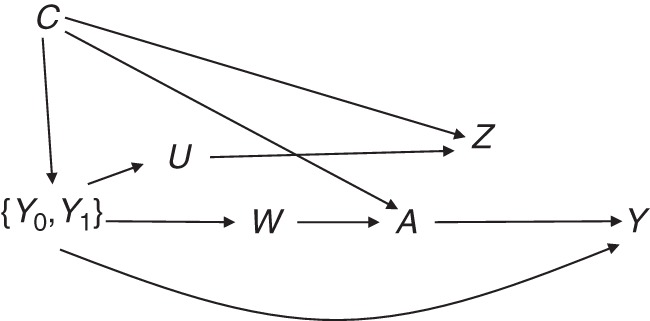
Causal diagram depicting unobserved confounding by U and W and the negative control outcome Z, where A represents exposure; Y represents outcome; U and W represent unobserved predictors of Z and A, respectively; C represents observed confounders; and {Y₀, Y₁} are counterfactual outcomes for different exposure values.

Assumption 1: Let 𝒴_A = {Y_a : a ∈ 𝒜} denote the set of all counterfactuals for the primary outcome under all possible values of treatment in the set 𝒜. Then, the treatment assignment is independent of Z_a conditional on {C, 𝒴_𝒜}, or

Assumption 1 states that, even though C may not suffice to account for unobserved confounding to make correct inferences about the relation between A and Z, that is,

enriching the adjustment set of covariates with the set 𝒴_𝒜 suffices to adjust for confounding. Note that in Figure 2, U represents unobserved predictors of the outcomes, whereas W represents unobserved factors that may have influenced treatment selection. Our causal model encodes an assumption that these 2 factors are independent conditional on (Y₀, Y₁, C) and not otherwise. Thus, if observed, (W, C) and (U, C) would also suffice to account for confounding of the A − Y and A − Z associations, respectively. An intuitive explanation of assumption 1 is obtained upon noting that, when A is binary, Y₀ and Y₁ can be viewed as baseline covariates that capture all relevant information about an individual's health status prior to treatment assignment; thus, such variables are ideal proxy measures of unobserved factors that may influence treatment selection (i.e., W) and unobserved risk factors of the outcomes (i.e., U).

To further ground ideas, it is helpful to consider the familiar context of a point exposure study with A binary and where we assume that the observed data (Y, Z, A, C) follow the model

(3)

(4)

(5)

This model is consistent with the graph depicted in Figure 2. The variables (U, W) are not observed, and under the consistency assumption Y = Y_A, so that Y_a is observed only for persons with A = a, and Y_1−A remains unobserved. The model allows the relation between (U, C) and Z encoded by the function g₁ to remain unrestricted and encodes the fact that A does not directly influence Z. Likewise, the model allows the relation between (W, C) and A encoded by the function g₂ to remain unrestricted. The parameter

encodes a constant additive individual causal effect of A on Y. This is a strong assumption because it implies so-called rank-preservation of individuals' counterfactuals under treatment versus control conditions. The assumption can be relaxed somewhat by incorporating interactions of A with components of C, and the assumption can be dropped entirely for binary outcomes, as we later demonstrate. The model is consistent with the graph in Figure 2, because 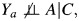and therefore, the effect of A on Y is confounded due to dependence between Y_a, U, and W, even if one conditions on C. Note that although the model specifies an additive causal effect, the relation between Y₀ and (A, Z, C) is otherwise unrestricted.

To describe the COCA, let Y(ψ) = Y − ψA, and note that Y₀ = Y(ψ₀) and Y₁ = Y(ψ₀) + ψ₀. Further note that under the model, conditioning on Y₀ is equivalent to conditioning on the set 𝒴_A = {Y₀, Y₁}, because the 2 counterfactuals in the set are deterministically related. This, in turn, implies that under assumption 1,

if and only if ψ = ψ₀. This is the key insight by which the COCA identifies ψ₀. A regression-based approach to implement the COCA then entails searching for the parameter ψ such that

(6)

For example, a simple implementation of the approach uses linear models, whereby for each value of ψ, one obtains an estimate of the regression model by using ordinary least squares (OLS).

(7)

with estimated coefficients 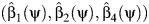. Then, a 95% confidence interval for ψ₀ consists of all values of ψ for which a valid test of the null hypothesis 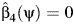fails to reject at the 0.05 type 1 error level. The latter hypothesis test may be performed by verifying whether the interval 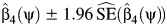contains 0, with 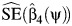the OLS estimate of the standard error (SE) of 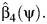An alternative, potentially simpler, approach is obtained by evaluating the regression model 7 at ψ₀ under model 5,

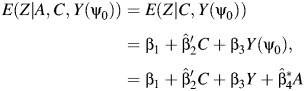(8)

where 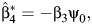assuming that β₃ ≠ 0. The parameter ψ₀ is then identified by regressing Z on (C, Y, A) via OLS, which produces the estimate 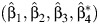and

A corresponding variance estimate can be obtained by a straightforward application of the delta method, giving

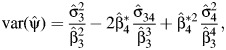where

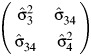is the OLS estimate of the variance covariance matrix of .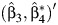

The first COCA strategy described in the previous paragraph is quite general in the sense that the regression model E(Z|A, C,Y(ψ)) can be estimated using any appropriate regression approach, including any generalized linear model with appropriate link function, say, the logit link or the log link for binary or count Z, respectively. Furthermore, for a given choice of model, a statistical test of the null hypothesis displayed in equation 6 can be performed using a standard likelihood ratio test, a score test, or a Wald test statistic, regardless of the underlying functional form of the regression. In principle, a more flexible model could be used to estimate the left-hand side of equation 6, including nonlinear terms and interactions to improve the fit of the model. Note also that our choice of a constant additive causal model (model 5) is made mainly for convenience, and that the underlying causal model can be easily modified to incorporate possible effect heterogeneity with observed covariates. For instance, model 5 can be replaced with Y = Y₀ + (A, A × C′)ψ₀, thus incorporating effect modification of the causal effect of A on Y with respect to C.

Note also that the simplified second COCA strategy described above is tailored to the linear functional form of both models 5 and 6. Although the models make some simplifying assumptions, the approach reveals a simple strategy to test and correct for unmeasured confounding using the COCA under the foregoing formalization. Under the sharp null of no causal effect of A on Y, that is, ψ₀ = 0, a straightforward test of no unmeasured confounding then entails assessing whether Z and A are additively associated conditional on Y and C. This strategy is reasonable, because under the sharp null, Y = Y₀ is a proxy of unmeasured common causes of Y and A and therefore, adjustment for Y in the regression of Z on A essentially amounts to adjustment for unobserved confounding to the extent that Z is a valid negative control outcome for the effects of A on Y. The COCA formalizes this basic idea so that it may be used equally both under and away from the sharp null hypothesis, that is, even when ψ₀ ≠ 0, by leveraging the causal model to recover the proxy measure of unobserved confounding Y₀ to use for adjustment in the negative control outcome regression model. This essentially describes the COCA, which accomplishes the above task by calibrating the causal model by varying the value of ψ until confounding control based on Y(ψ) in the control outcome regression is satisfactory.

DATA EXAMPLE: CHROMOSOME DAMAGE FROM CONTAMINATED FISH

We use the proposed approach in a reanalysis for the purpose of illustration of a simplified version of a study conducted by Skerfving et al. (5) on the relation between consumption of contaminated fish and chromosome damage. The authors studied 23 subjects who had eaten large quantities of fish contaminated with methylmercury (A = 1). These subjects lived in different areas in Sweden and included fishermen, fishermen's wives, workmen, farmers, and clerks. Each of the 23 exposed subjects reported eating at least 3 meals a week of contaminated fish for more than 3 years. The comparison group included 16 subjects who were exposed to substantially lower amounts of contaminated fish and who reported consuming less fish of all kinds (A = 0). These subjects were from the Stockholm metropolitan area and included clerks, craftsmen, porters, workmen, and a glass washer. The 2 outcomes of primary interest consist of the amount of mercury found in the person's blood, recorded in ng/g and log transformed for the analysis (Y), and the percent of cells exhibiting a particular chromosome abnormality called C_u cells (Y*). Although the original study considered a variety of chromosome abnormalities, we proceed as in the report by Rosenbaum (2), who focused on these particular outcomes to illustrate the use of negative control outcomes to detect the presence of unobserved confounding. The negative control outcome in this example consists of a count of other health conditions experienced by each of the 39 subjects enrolled in the study (Z). This composite outcome includes other diseases such as hypertension and asthma, drugs taken regularly, diagnostic radiography over the previous 3 years, and viral diseases such as influenza. Although these outcomes were observed during the period when exposed individuals consumed contaminated fish, one does not expect that eating fish contaminated with methylmercury causes influenza or asthma or prompts radiography of the hip or lumbar spine. We make the additional assumption 1 (with C the empty set), and thus assume that Z may be used to detect and correct for unobserved confounding for the association between A and Y using the COCA. Referring back to Figure 1, our assumption is thus that there is no unobserved common cause of A, and any chronic condition used to define Z that does not also confound the relation between fish consumption and mercury in the blood Y, and thus Z, may be used to account for unobserved confounding for the association between A and Y using the COCA. Similar assumptions are made about Y*. For each outcome, we assume the constant additive effect model 5, that is, Y = Y₀ + ψ₀A and 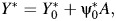so that ψ₀ encodes the causal effect of A on Y and likewise for 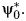For the COCA, we assume events contributing to the count Z are mutually independent and take Z to be Poisson distributed with conditional mean

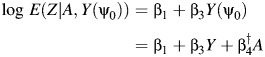where, as before, 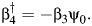Thus, we compute the COCA estimator 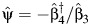, where 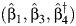is obtained by maximum likelihood. For comparison, we also compute the standard OLS estimator 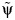of the linear (crude) association between A and Y*. Similar models were used for Y*.

The OLS crude estimate of ψ₀ was 2.77 for Y (95% confidence interval: 2.26, 3.27), and was comparable to the COCA estimate of 2.32 (95% confidence interval: 1.36, 3.28), thus indicating little empirical evidence of unobserved confounding. In contrast, the OLS crude estimate of ψ₀ was 1.70 for Y* (95% confidence interval: 0.426, 2.97) and was considerably smaller than the COCA estimate of 4.14 (95% confidence interval: 0.08, 8.19). The large difference between the COCA estimate and the OLS estimate is suggestive of unobserved confounding; however, the COCA estimate of the causal effect was also considerably more variable than the OLS estimate. To formally assess whether the OLS and COCA estimates are within sampling variability of each other, that is, that there was no bias due to unobserved confounding, we implemented a Hausman test (6), which entails computing a confidence interval for the limiting value of using the simple formula

and verifying whether 0 falls in the above interval as would be consistent with the null hypothesis of no confounding, where 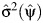and 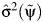are consistent estimates of the asymptotic variance of 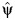and 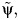respectively (6). Note that, although under the null hypothesis of no unobserved confounding, 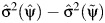converges to a positive number with increasing sample size, it can be negative in the observed finite sample or if the null hypothesis is false, in which case its square root is not a real number. In such cases, it is recommended to instead use the nonparametric bootstrap approach to estimate the variance of 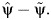The above 95% confidence intervals were (−0.36, 1.268) for Y, indicating no statistically significant evidence of bias due to unobserved confounding for the crude association between consumption of contaminated fish and level of mercury in the blood; and (−1.40, 6.28) for Y*, indicating no statistically significant evidence of bias due to unobserved confounding for the crude association between consumption of large quantities of fish contaminated with methylmercury and percent chromosome abnormality. In closing, we should note that the foregoing analysis and its conclusions may dismiss unobserved confounding by certain, but not all, hidden variables. Assumption 1 may not be entirely credible if, say, an ingredient other than methylmercury in contaminated fish caused the chromosomal abnormalities, or if lack of eating meat by fish consumers were the culprit. This is because the unobserved confounder may no longer be shared between the outcome and the negative control outcome, so that the negative control outcome would have no power to detect unobserved confounding, let alone correct for it. The analysis should be interpreted with caution, particularly because no additional covariates C were available for adjustment, which would have helped to make the identifying assumption more credible.

THE COCA FOR A DICHOTOMOUS OUTCOME

The foregoing presentation focused primarily on settings in which the outcome in view is continuous. Dichotomous outcomes are also quite common in epidemiologic practice; thus, in this section, we extend the COCA to the context of a binary Y, and we present similar methodology to estimate the effect of treatment on the treated (ETT),

To proceed, one may note that the observed crude difference E(Y = 1|A = 1) − E(Y|A = 0) is biased for the ETT, with

Therefore, to nonparametrically identify the ETT, one must identify Pr(Y₀ = 1|A = 1). Suppose that Z satisfies assumption 1, with 𝒜 = {0}, that is,

Under the assumption, the conditional mean E(Z|A) may be written as

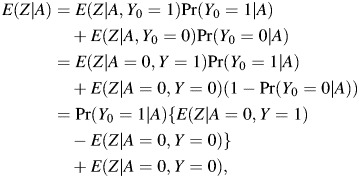which gives

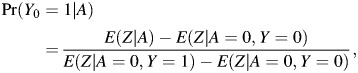(9)

provided that

Thus,

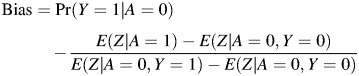and

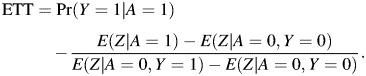The result states that Pr(Y₀ = 1|A = 1) is nonparametrically identified by the ratio of differences displayed in equation 9, and because Pr(Y₁ = 1|A = 1) = Pr(Y = 1|A = 1) by the consistency assumption, this in turn implies that the ETT is nonparametrically identified. Note that Z can be either discrete or continuous, and that the approach easily incorporates observed confounders C. In fact, by following similar steps as above, one can show that

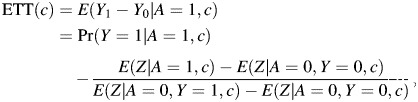(10)

and the marginal ETT is given by

Estimation could then proceed by fitting using standard maximum likelihood, parametric models for Pr(Y = 1|A, C) and E(Z|A, C) and plugging the latter into equation 10. A straightforward application of the delta method could be used to obtain standard errors for the resulting estimator, or alternatively, the nonparametric bootstrap could also be used.

Note that when C is not empty, one may also write

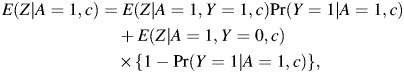(11)

which may be used to evaluate equation 10. This would simplify estimation by allowing the analyst to fit separate regression models for E(Z|A, Y, C) and Pr(Y|A, C), say, standard logistic regression models if Z and Y are both binary, which are ensured not to conflict with a model for E(Z|A = 1, C) obtained using equation 11. Inference for the causal risk ratio parameter

or for the causal odds ratio parameter

can likewise be obtained by simply using the above expression for Pr(Y₀ = 1|A = 1, C) as a baseline risk in a standard (multiplicative or logistic) regression model. To fix ideas, suppose that γ(a, c) = ψ₀a on a given scale (either risk ratio or odds ratio scale), so that we assume that the effect of treatment is constant in the treated across levels of c. Then, one can estimate ψ₀ by fitting the regression model

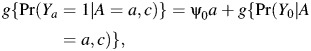(12)

where g is either the logit link function or the log link function, and Pr(Y₀ = 1|A = a, c) is estimated by evaluating equation 9. The “no interaction” assumption is easily relaxed by replacing the causal model with a model incorporating interactions between A and C.

Case-control studies are quite common in epidemiologic practice, and the COCA extends to this context but requires some modification to appropriately account for the study design, which is provided in the Appendix.

DISCUSSION

Some degree of unobserved confounding is almost certainly present in most observational studies. For this reason, it was recently argued that researchers should routinely supplement the primary analysis of such observational studies with some form of negative control outcome (or negative control exposure) analysis to demonstrate that exposure effects known not to be present in the population are in fact not observed in the study sample (1, 3). The extent to which such an analysis may reveal unobserved confounding bias relies on the non–empirically verifiable assumption that the negative control outcome is carefully chosen so that it is solely influenced by observed and unobserved confounders of the exposure-outcome relation in view. Here, we propose to use a negative control outcome not only to detect, but also to correct for unmeasured confounding bias. Some analytical strategies are described for continuous and binary outcomes, under the assumption that the primary outcome that would be observed were exposure widthheld in the population suffices together with observed confounders to completely account for confounding of the exposure–negative control outcome association. We leverage this assumption to calibrate the causal effect, so that the assumption is empirically met. A sensitivity analysis technique is also described in the Appendix, which allows one to assess the degree to which a violation of the main identifying assumption, assumption 1, could alter the results.

Though a regression-based calibration approach is emphasized, in the context of a continuous outcome, in principle, upon obtaining the proxy measure of unobserved confounding, one could evaluate the adjusted association between the exposure and the control outcome using alternative approaches to the regression approach taken here without additional difficulty, for example, propensity score methods or doubly robust estimation (7–9).

Time-to-event outcomes are also common in epidemiologic practice, and the methods developed in this paper can, in principle, be extended to allow for a censored time-to-event outcome. For example, the standard rank preserving structural accelerated failure time model (10) relates the log event time to the treatment using an additive model of the form given by model 5 and, therefore, the methodology described herein immediately applies for this model. However, one would have to ensure that the negative control outcome and the primary outcome are not competing risks, and one would also need to appropriately account for censoring. Similar methodology for the Cox proportional hazards model (11) or for the Aalen additive hazards model (12) still needs to be developed.

A positive control outcome can be defined for an outcome with a well-established nonnull causal association with the exposure, which is confounded in the observed sample by a subset of unobserved confounders for the exposure effects on the primary outcome. Positive control outcomes can, in a manner similar to negative controls, be used to detect unobserved confounding by verifying whether the known association is replicated in the observed sample. The methods described in this paper could be extended for use with positive control outcomes.

Negative control exposures are also quite common in epidemiologic practice (3, 13, 14). These are observed exposures known not to causally influence the primary outcome. It may be possible to also develop an approach similar to that given in this paper to leverage negative control exposures to correct for unobserved confounding bias. This will be investigated elsewhere.

APPENDIX

Extension to case-control design

Case-control studies are quite common in epidemiologic practice, and COCA extends to this context but requires some modification to appropriately account for the study design. Thus, suppose cases (with Y = 1) and controls (with Y = 0) are obtained in a population with rare disease rate, and let S denote the indicator of selection into the case-control sample. The case-control design typically oversamples cases for more cost-effective and statistically efficient inference. We propose to estimate the causal effect of A via case-control COCA for a logistic regression model of the form given by equation 12 in the main text, upon redefining Pr(Y₀ = 1|A = a, c) as Pr(Y₀ = 1|A = a, c, S = 1), where

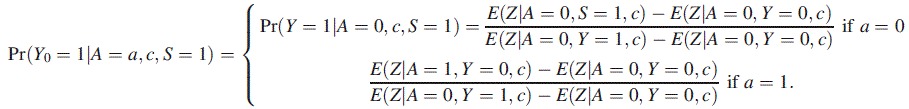The key insight justifying the approach is that E(Z|A = 1,Y = 0, c) approximates E(Z|A = 1, c) under the rare disease assumption, and therefore Pr(Y₀ = 1|A = 1, c, S = 1) approximates Pr(Y₀ = 1|A=a, c), which suffices for identification of ψ, and furthermore, this is the case even though Pr(Y = 1|A = 0, c, S = 1) fails to identify Pr(Y = 1|A = 0, c). If the disease is not rare in the target population but the sampling fraction for cases and control is known, a straightforward application of inverse-selection-probability-weighting COCA estimation may be used to recover the correct population inference.

Sensitivity analysis for an imperfect negative control

Heretofore, we have assumed a perfect negative control outcome is available, such that assumption 1 holds exactly in the observed data. We now propose to relax this assumption, in order to allow for the possibility that 𝒴_𝒜 may not fully account for unobserved confounding between A and Z. This could happen, say, if there was an unobserved common cause of A and Z that does not also confound the relation between A and Y. If this were the case, COCA as developed in previous sections would fail to unbiasedly estimate the causal effect of A on Y, even if all fitted models are correctly specified. To address this potential issue, a sensitivity analysis approach is proposed, which may be used to assess the extent to which inference about the causal effect of A on Y may be altered by a violation of assumption 1.

To describe the sensitivity analysis technique, suppose that Y, A, and Z are continuous, and to simplify the exposition, suppose that there are no covariates (i.e., C is the empty set). Furthermore, we shall suppose that the following linear models generated the observed data:

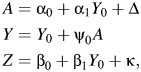where Δ and κ are mean 0 error terms, uncorrelated with Y₀. Then, if assumption 1 holds, we have that κ and Δ are independent, and therefore E(κΔ) = 0. To encode a violation of assumption 1, we set

where χ is an independent error term, and ρ is a sensitivity parameter that encodes the magnitude of unobserved confounding for the association between A and Z upon adjustment for Y₀. To implement the sensitivity analysis requires an estimate of Δ = {A − E(A|Y₀)}. For fixed ψ, let 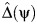denote the OLS residual from regressing A on Y(ψ) using a simple linear regression. Define 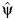(ρ) as the midpoint of the 95% confidence interval corresponding to values of ψ such that the null hypothesis of β₂(ρ, ψ) = 0 fails to reject at the 0.05 α level in the following regression model:

(1)

with (ρ, ψ) fixed and (β₀(ρ, ψ), β₁(ρ, ψ), β₂(ρ, ψ)) estimated by OLS of Z on A with an offset equal to 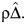A sensitivity analysis is then obtained by repeating the above steps for different values of ρ on an interval containing ρ = 0 (which recovers the analysis obtained under assumption 1). Although we have motivated the sensitivity analysis technique assuming continuous A, the approach equally applies for binary A, upon replacing linear regression with binary regression, such as, say, logistic regression, to fit E(A|Y(ψ)) and to construct Δ(ψ) = A − E(A|Y(ψ)). We also note that the parametric models used above were specified primarily to simplify the exposition, and it is possible to more formally motivate the parametrization for the linear regression (1) using nonparametric arguments along the lines of Robins et al. (7), allowing for a more general functional form for the models and also incorporating covariates.