Accounting for Outcome Misclassification in Estimates of the Effect of Occupational Asbestos Exposure on Lung Cancer Death

Abstract

In studies of the health effects of asbestos, lung cancer death is subject to misclassification. We used modified maximum likelihood to explore the effects of outcome misclassification on the rate ratio of lung cancer death per 100 fiber-years per milliliter of cumulative asbestos exposure in a cohort study of textile workers in Charleston, South Carolina, followed from 1940 to 2001. The standard covariate-adjusted estimate of the rate ratio was 1.94 (95% confidence interval: 1.55, 2.44), and modified maximum likelihood produced similar results when we assumed that the specificity of outcome classification was 0.98. With sensitivity assumed to be 0.80 and specificity assumed to be 0.95, estimated rate ratios were further from the null and less precise (rate ratio = 2.17; 95% confidence interval: 1.59, 2.98). In the present context, standard estimates for the effect of asbestos on lung cancer death were similar to estimates accounting for the limited misclassification. However, sensitivity analysis using modified maximum likelihood was needed to verify the robustness of standard estimates, and this approach will provide unbiased estimates in settings with more misclassification.

The relationship between asbestos and lung cancer death has been examined for more than half a century, and epidemiologic studies have provided strong evidence that asbestos is a lung carcinogen (1–3). Although asbestos is no longer mined in the United States, approximately 1,000 tons of asbestos are imported into the United States each year for use in construction materials, brake linings, and other products (4). Moreover, a substantial amount of asbestos remains in US infrastructure and eventually will be removed, either during remediation, renovations, or demolition. Significant production and use is also ongoing in other countries, including Brazil, India, China, and Russia. Therefore, asbestos continues to pose important occupational hazards in the United States and worldwide (5).

Most analyses of asbestos exposure in occupational settings have estimated the effect of asbestos on lung cancer death in place of lung cancer incidence for practical reasons. Because many countries have comprehensive databases containing standardized information about deaths, investigators can identify the observed deaths that are due to lung cancer. The number of lung cancer deaths approximates the number of incident lung cancer cases because the time between lung cancer diagnosis and death tends to be short, and few effective treatments exist.

Outcome ascertainment in studies of lung cancer death involves determining both the date and cause of death. In the current paper, we focus on the scenario in which the underlying cause of death is used to classify each decedent with respect to the outcome. In most cases, particularly in developed countries, the date of death is recorded typically with negligible error. However, misattribution of the underlying cause of death remains more likely. If such misattribution results in a death due to lung cancer being classified as a death due to another cause, or vice versa, the outcome is misclassified. Despite evidence of imperfect sensitivity and specificity for cause of death data abstracted from death certificates (6–13), most studies of occupational asbestos exposure assume no misclassification.

To present estimates of the effect of asbestos exposure on lung cancer death that account for outcome misclassification, we propose an approach that uses modified maximum likelihood to estimate rate ratios under chosen values of sensitivity and specificity, as in a sensitivity analysis. Until the discussion, we assume that the date of death is measured without error, but that the cause of death is subject to misclassification. We illustrate this approach using data from a cohort of textile workers in South Carolina assembled to assess the relationship between the chrysotile form of asbestos and lung cancer death.

METHODS

Study population

The study population comprised workers at a textile production plant in South Carolina that produced asbestos beginning in 1896 and chrysotile asbestos textile products beginning in 1909 (1). Initiation of follow-up for this retrospectively defined cohort was defined as the date at which workers had been employed at the plant for at least 1 month between January 1, 1940, and December 31, 1965. Employment records of the 3,072 men and women enrolled in the study were used to obtain information on date of birth, year of study entry (defined as the difference between the worker's start date and 1940), race (white or other race), sex, and employment status in each year. The study did not collect information on smoking history. Cohort members were censored at the date of becoming lost to follow-up, age 90 years, or December 31, 2001.

Exposure assessment

The plant produced asbestos-containing materials until 1977. Detailed work histories were available for each member of the cohort, and cumulative exposure to asbestos was estimated using a job-exposure matrix to link work history to asbestos exposure. The job-exposure matrix was informed by industrial hygiene sampling measurements taken between 1930 and 1975, as previously described (3). Asbestos exposure concentrations, expressed as fibers longer than 5 micrometers per milliliter of air (fibers/mL), were estimated for each day of each cohort member's work history. Yearly exposure values were calculated as the product of the proportion of the year worked and the average daily exposure concentration and reported as fiber-years per milliliter. Yearly exposure values were summed into a cumulative exposure estimate for each worker. To allow for an induction and latent period for the effect of asbestos on lung cancer death, we lagged cumulative exposure estimates by 10 years. Exposure that accrued prior to study entry or after the plant ceased to use asbestos-containing materials in 1977 was not included in the cumulative exposure estimate for each cohort member.

Death ascertainment

Cohort members were followed for lung cancer death between initiation of follow-up (defined above) and January 1, 2001. Between 1940 and 1978, vital status was determined by using data from the Social Security Administration (Baltimore, Maryland), Internal Revenue Service (Washington, DC), US Department of Veterans Affairs (Washington, DC), state drivers' license files, vital statistics offices, and postal mail correction services. Between 1979 and 2001, vital status was determined by using the National Death Index (Centers for Disease Control and Prevention, Atlanta, Georgia). Those who were confirmed as being alive in 1979 and not listed in the National Death Index were assumed to be alive at the end of the study. For those who died, cause of death was determined from information recorded on the death certificates and coded by a qualified nosologist according to the revision of the International Classification of Diseases (ICD) in effect at the date of each death. A death was considered to be due to lung cancer if the underlying cause was classified as lung cancer (defined as code 162 in ICD, Eighth Revision and ICD, Ninth Revision or codes C33–C34 in ICD, Tenth Revision) (1–3).

Statistical methods

The 121,010 person-years contributed by 3,072 cohort members were grouped into 3,059 populated strata, indexed as j = 1, 2, …, J. These strata are defined by sex, age (5-year intervals from 15 to 90), year at study entry (1-year intervals from 1940 to 1965), and cumulative asbestos exposure. Cumulative asbestos exposure was categorized into 1–fiber-year/mL intervals for values of 10 fiber-years/mL and under, 5–fiber-year/mL intervals for values from 10 to 50 fiber-years/mL, 10–fiber-year/mL intervals for values from 50 to 100 fiber-years/mL, and 25–fiber-year/mL intervals for values above 100 fiber-years/mL, and the category score was set to the mean value of cumulative asbestos exposure for each interval.

In stratum j, we have n_j person-years with d_j deaths. We observe w_j possibly misclassified lung cancer deaths, but the true unobserved number of lung cancers is y_j. The true numbers of person-years and deaths remain n_j and d_j, respectively, under the assumption that the dates of death are correct.

We would like to estimate the effect of occupational asbestos exposure on lung cancer death by estimating the rate ratio of lung cancer death per 100 fiber-years/mL of cumulative asbestos exposure. The parameter estimating the desired rate ratio is exp(β₁) in the Poisson model

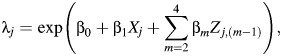(1)

where λ_j represents the rate of true lung cancer deaths in stratum j, X_j is the cumulative asbestos exposure, and Z is a J × 3 matrix with columns for sex, log(age), and calendar year of study entry.

However, because we observe w_j possibly misclassified lung cancer deaths in place of y_j true lung cancers, the model above cannot be fit directly. Instead, standard analyses typically fit the model

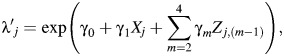(2)

where represents the rate of a possibly misclassified version of the outcome variable, w_j. We fit this second (standard) model to the data from the South Carolina textile plant cohort, where w_j is the number of deaths due to lung cancer recorded on death certificates in stratum j.

We account for outcome misclassification using values of sensitivity and specificity of lung cancer classification obtained from existing literature. Sensitivity is defined as the probability that a participant is correctly classified as a lung cancer case, given that the participant died of lung cancer. Specificity is the probability that an individual is correctly classified as a non–lung cancer death, given than the individual died of a cause other than lung cancer. Because validation studies report varying estimates of the accuracy of cause-of-death information obtained from death certificates, we perform a sensitivity analyses in which we set sensitivity and specificity to each of several plausible values.

Sensitivity analysis

We demonstrate how to modify the Poisson likelihood to account for outcome misclassification by setting the values of sensitivity and specificity, following Neuhaus (14), Carroll et al. (15), and Lyles et al. (16). We begin by specifying the Poisson likelihood for the situation with 2 causes of death and no misclassification,

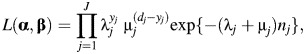(3)

where λ_j is described above, α = (α₀, α₁, …, α₄), β = (β₀, β₁, …, β₄), and μ_j is the estimated rate of other types of death for stratum j,

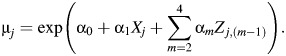(4)

In this work, we take a standard approach and compare cause-specific rates of lung cancer death among workers exposed to various levels of asbestos exposure (17). We model log(age) and year of study entry as continuous variables; the use of additional flexibility in the functional forms of these variables (i.e., addition of restricted cubic splines and polynomial terms) did not alter the point or interval estimates. The likelihood for the 2 causes of death will be maximized at the same parameter estimates for β as the likelihood for the lung cancer death–specific rate model shown in equation 1 (17).

Because the true number of lung cancer deaths is unavailable for strata where d_j > 0, we rewrite the likelihood using the count of potentially misclassified lung cancer deaths for each stratum, w_j and investigator-assigned misclassification probabilities (i.e., sensitivity (se) and specificity (sp)) to modify the likelihood as follows:

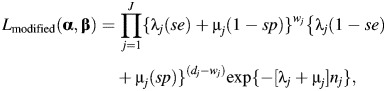(5)

where sensitivity and specificity are treated as constants in the modified likelihood function. Under the assumption that sensitivity and specificity are correct, the modified likelihood function given by equation 5 will provide consistent estimates for α and β that match the estimates that would be obtained by applying the likelihood function shown in equation 3 to the true data. However, estimates obtained using the modified likelihood function will have larger standard errors as sensitivity and specificity move away from 1.

To identify plausible values of the misclassification probabilities, we turn to existing literature on the accuracy of cause-of-death information reported on death certificates. The Mayo Lung Project, conducted between 1971 and 1983 among outpatients at the Mayo Clinic (Rochester, Minnesota), reported that death certificates identified lung cancer as the underlying cause of death in 89% (210/237) of autopsy-confirmed lung cancer cases (18), and specificity was 99%. A validation study conducted in the Third National Cancer Survey found that lung cancer was recorded as the underlying cause of death on the death certificate in 95% (9,568/10,059) of lung cancer cases diagnosed by hospital physicians (11). Sensitivity from other validation studies was similar to estimates from the Mayo Lung Project. For example, a study of 4,951 deaths occurring among 17,800 workers exposed to asbestos reported that death certificates identified lung cancer as the cause of death in 86% of the deaths designated as lung cancer deaths by autopsy and other medical evidence (13).

We allow sensitivity to range from 0.6, a hypothetical lower bound, to 0.9, as seen in the Mayo Lung Project. Because few validation studies provided the specificity of death certificates to identify lung cancer deaths, we investigate the following 3 plausible values for specificity: 0.98, 0.95, and 0.90. We estimate the rate ratio of lung cancer death per 100 fiber-years/mL of cumulative asbestos exposure for the following scenarios: 1) assuming no misclassification of cause of death, which corresponds to the standard analysis of these data; 2) setting specificity to 0.98 and sensitivity to 0.9, 0.8, or 0.6; 3) setting specificity to 0.95 and sensitivity to 0.9, 0.8, or 0.6; and 4) setting specificity to 0.90 and sensitivity to 0.9, 0.8, or 0.6. In all scenarios, we assume that outcome misclassification is nondifferential with respect to cumulative asbestos exposure. The sensitivity analysis is performed using the NLMIXED procedure in SAS, version 9.3, software (SAS Institute, Inc., Cary, North Carolina) as a tool to maximize the modified likelihood function directly using standard maximization techniques (i.e., the Newton-Raphson algorithm) instead of using an approach such as the expectation-maximization algorithm (15). SAS code to perform this analysis is available in Web Appendix 1, available at http://aje.oxfordjournals.org/.

We evaluate the performance of the modified maximum likelihood approach to account for outcome misclassification through Monte Carlo simulations. Bias, 95% confidence interval coverage, and mean squared error were compared between standard methods and the analysis using modified maximum likelihood to set values of sensitivity and specificity for 5 scenarios with varying degrees of outcome misclassification. The design of the simulation study is detailed in Web Appendix 2.

RESULTS

Example

The study enrolled 3,072 textile workers between 1940 and 1965. The cohort was predominantly male and white and began follow-up at a median age of 23 years (Table 1). The median occupational exposure to asbestos at study entry was 0.2 fiber-years/mL, and the median cumulative exposure to asbestos at the end of follow-up was 5.0 fiber-years/mL. There were 198 lung cancer deaths and 1,763 other deaths recorded between 1940 and 2001, and 265 participants were censored because of loss to follow-up (9%) (Table 1).

Table 1.

Characteristics of 3,072 Textile Workers in Charleston, South Carolina, 1940–2001

Characteristic	Median (IQR)	No.	%
Age at study entry, years	23 (19–29)
Calendar year at study entry	1943 (1941–1946)
Male		1,807	58.9
White		2,500	81.4
Cumulative asbestos exposure at end of follow-up, fiber-years/mL	4.99 (1.45–21.38)
Lung cancer deaths		198	6.5
Non–lung cancer deaths		1,763	57.4
Lost to follow-up		265	8.6

Abbreviation: IQR, interquartile range.

Table 2 provides the estimated rate ratios for lung cancer death per 100 fiber-years/mL of cumulative asbestos exposure under several assumptions about sensitivity and specificity. Assuming perfect sensitivity and specificity of cause-of-death information, as in standard analyses, the rate of lung cancer deaths increased by a factor of 1.94 per 100 fiber-years/mL (95% confidence interval (CI): 1.55, 2.44) after adjustment for sex, race, age, and calendar year of study entry.

Table 2.

Rate Ratio of Lung Cancer Deaths per 100 Fiber-years/mL of Cumulative Asbestos Exposure Under Several Outcome Misclassification Scenarios, Charleston, South Carolina, 1940–2001

Model	Specificity	Sensitivity	RR	95% CI	−2 Log Likelihood
Crude	1	1	3.52	2.86, 4.33	21,102
Adjusteda	1	1	1.94	1.55, 2.44	18,783
	0.98	0.90	2.03	1.57, 2.61	18,811
	0.98	0.80	2.02	1.57, 2.60	18,811
	0.98	0.60	2.00	1.56, 2.56	18,812
	0.95	0.90	2.19	1.60, 3.00	18,820
	0.95	0.80	2.17	1.59, 2.98	18,820
	0.95	0.60	2.12	1.56, 2.89	18,820
	0.90	0.90	2.97	1.34, 6.56	18,850
	0.90	0.80	3.03	1.32, 6.94	18,850
	0.90	0.60	3.07	1.54, 6.10	18,850

Abbreviations: CI, confidence interval; RR, rate ratio.

^a Adjusted for sex, race, age, and year of study entry.

The rate ratios under scenarios assuming varying degrees of outcome misclassification that was nondifferential by exposure status were further from the null than the rate ratio from the standard analysis. The change in the rate ratio was determined primarily by the specificity. With specificity set to 0.98, the rate ratios were relatively unchanged at 2.03 (95% CI: 1.57, 2.61), 2.02 (95% CI: 1.57, 2.60), and 2.00 (95% CI: 1.56, 2.56) when sensitivity was varied at 0.9, 0.8, and 0.6, respectively. The average standard error for the natural log of the rate ratio was 0.13 when specificity was set to 0.98, similar to the standard error when specificity was assumed to be perfect, which was 0.12.

When specificity was reduced to 0.95, the estimated rate ratios were 2.19 (95% CI: 1.60, 3.00), 2.17 (95% CI: 1.59, 2.98), and 2.12 (95% CI: 1.56, 2.89) for sensitivity set to 0.9, 0.8, and 0.6, respectively, and the average standard error was 0.16. When specificity was further reduced to 0.9, estimates of the rate ratio were even further from the null but much less precise.

Simulations

Table 3 compares the performance of the standard method and the modified maximum likelihood estimate to account for misclassification in the rate ratio for 10,000 simulated cohorts under several scenarios of outcome misclassification. As expected, the standard estimates of the rate ratio were biased toward the null when sensitivity and specificity were imperfect, and bias increased as the degree of outcome misclassification increased. In contrast, estimates accounting for sensitivity and specificity, which were assumed to be known values, using modified maximum likelihood showed little bias, even when sensitivity and specificity were quite low.

Table 3.

Results Accounting for Outcome Misclassification Using Modified Maximum Likelihood in Poisson Regression in 10,000 Simulated Cohorts^a

Scenario	Measure		Method	Rate Ratio	Biasb	95% CI Coveragec	Mean Squared Errord
	Specificity	Sensitivity
1	1	1	Truth	2.00	0	95	0.77
2	0.95	0.9	Standard ML	1.89	−5	91	1.15
			Modified ML	2.00	0	95	0.95
3	0.95	0.6	Standard ML	1.84	−8	89	1.96
			Modified ML	2.01	0	95	1.30
4	0.9	0.9	Standard ML	1.80	−10	79	1.93
			Modified ML	2.01	0	95	0.96
5	0.9	0.6	Standard ML	1.72	−15	72	3.55
			Modified ML	2.01	1	95	1.46

Abbreviations: CI, confidence interval; ML, maximum likelihood.

^a The models accounting for imperfect sensitivity and specificity did not converge in 6, 7, 9, and 5 simulated cohorts for scenarios 2, 3, 4, and 5, respectively.

^b Bias was defined as 100 times the difference between the true ln(rate ratio) and the estimated ln(rate ratio).

^c The 95% confidence interval coverage was the proportion of simulations in which the estimated 95% confidence interval contained the true value.

^d Mean squared error was the sum of the square of the bias and the square of the standard deviation of the bias.

The confidence limits from the modified maximum likelihood estimates showed appropriate coverage in all scenarios examined, and mean squared error was improved when compared with the standard estimates under all combinations of sensitivity and specificity. The difference in mean squared error between the standard and modified maximum likelihood estimates was small in scenario 2, where sensitivity was 0.9 and specificity was 0.95, because the inflated standard error of the modified maximum likelihood estimate offset the small bias in the standard estimate. However, as sensitivity and specificity decreased, the difference in mean squared error became more pronounced. In the scenario with the most extreme outcome misclassification (sensitivity of 0.6 and specificity of 0.9), the bias in the standard estimate overwhelmed the increase in standard error of the modified maximum likelihood estimate, resulting in a large improvement in mean squared error for the modified maximum likelihood estimate when compared with the standard estimate.

DISCUSSION

Misclassification of cause of death has been a concern in analysis of cancer trends and etiological research in cancer epidemiology for decades (6, 11–13, 19). By using a modified maximum likelihood approach, we accounted for misclassification of lung cancer death in a cohort of textile factory workers exposed to asbestos. The covariate-adjusted rate ratio of lung cancer death per 100 fiber-years/mL of asbestos exposure of 1.94, obtained by using standard methods, rose to over 3 when sensitivity and specificity were assumed to be poor, though it rose only to 2.17 under more plausible values of sensitivity and specificity.

Estimates of the rate ratio from a sensitivity analysis assuming imperfect sensitivity and specificity were always further from the null than the standard analysis assuming perfect outcome classification, though less precise. In simulations with imperfect sensitivity and specificity, using modified maximum likelihood to account for outcome misclassification removed bias in all scenarios examined and resulted in smaller mean squared error than did the standard analysis. The −2 log likelihood was larger for models that used the modified likelihood function to account for imperfect sensitivity and specificity than for the model assuming perfect outcome classification. However, the −2 log likelihood should not be used to guide model choice; in this setting, investigators should choose values for sensitivity and specificity that reflect substantive knowledge about the misclassification probabilities, not the goodness of fit of the model to the observed (mismeasured) data.

Sensitivity analysis showed that estimates of the rate ratio were relatively insensitive to changes in hypothetical values of sensitivity, but changed substantially when specificity was altered. The sensitivity of the rate ratio to changes in specificity is not surprising; when the event is rare, even small changes in the specificity result in considerable changes in the number of events assumed to have occurred.

Because the specificity of lung cancer death reported on death certificates is thought to be high, modified maximum likelihood estimates of the rate ratio per 100 fiber-years/mL of asbestos exposure assuming likely values of sensitivity and specificity were similar to the adjusted rate ratio from standard analysis. We would expect rate ratios using modified maximum likelihood to differ more dramatically from the standard estimates of the rate ratio for outcomes subject to more severe misclassification. For example, asbestos has been implicated in the elevated risk of death from cardiovascular disease seen in cohorts of miners, mill workers, and shipyard workers (20–25). Unlike that of lung cancer, the specificity of cardiovascular disease reported on death certificates is relatively low (9, 26). We expect that future studies of the relationship between asbestos and cardiovascular disease deaths that account for outcome misclassification using methods such as those detailed here would produce estimates of the rate ratio that differ substantially from standard estimates.

We used results from existing validation studies on the accuracy of cause-of-death information on death certificates to inform the misclassification parameters for the sensitivity analysis. Here, we discuss the misclassification probabilities in terms of sensitivity and specificity instead of the detection rates and confirmation rates often presented in such validation studies. Sensitivity and detection rate both refer to the probability that the underlying cause of death recorded on the death certificate is lung cancer, given that a participant died of lung cancer. The confirmation rate is the probability that a participant died of lung cancer, given that the death certificate listed lung cancer as the underlying cause of death, and is also known as the positive predictive value. We chose to frame our method to account for outcome misclassification in terms of sensitivity and specificity instead of detection and confirmation rates because the confirmation rate is sensitive to changes in the prevalence of the outcome.

This work extends existing approaches to account for outcome misclassification to the time-to-event setting. Magder and Hughes (27), Lyles et al. (16), and Edwards et al. (28) have illustrated maximum likelihood–based approaches to account for outcome misclassification in logistic regression. As in the present work, Lyles et al. (16) used simulations to illustrate that coefficients from logistic models using the modified maximum likelihood approach are unbiased and have appropriate 95% confidence interval coverage. Here, we show that the modified maximum likelihood approach produces unbiased estimates of the rate ratio and appropriate 95% confidence interval coverage in Poisson regression models. We further apply a modified likelihood function to account for misclassification between lung cancer deaths and other types of death in Poisson regression, similar to work by Sposto et al. (29) and Stamey et al. (30), who have used an expectation-maximum algorithm and Bayesian methods, respectively, in this setting. The current work complements the methods set forth in these papers by providing a straightforward modified maximum likelihood solution to account for the misclassification of outcomes.

The direct maximum likelihood approach presented here could be extended to incorporate validation data, as in Lyles et al. (16), or to account for uncertainty in the misclassification parameters by placing prior distributions on sensitivity and specificity, as in Stamey et al. (30) instead of setting sensitivity and specificity to investigator-assigned values. The Bayesian approach is appealing because it allows investigators to express uncertainty about the misclassification parameters. However, this approach can pose challenges because sensitivity and specificity are, at best, weakly identifiable in the observed data, and eliciting dependent prior distributions for the misclassification parameters can be difficult without extensive prior knowledge. In addition, the interpretation of posterior estimates using the Bayesian approach is nuanced, because it averages over a range of sensitivities and specificities represented by prior densities.

The sensitivity analysis presented above could also be extended to account for outcome misclassification that is differential with respect to exposure. For example, lung cancer might be suspected earlier in someone known to have had substantial exposure to asbestos. To account for differential outcome misclassification, sensitivity and specificity would be specified as a function of exposure. Differential outcome misclassification may be of interest in studies of self-reported outcomes or other situations in which the person recording the outcome of interest is aware of the participant's exposure status. In our analysis, outcome misclassification was assumed to be nondifferential with respect to exposure. Similarly, outcome classification may depend on covariates other than exposure status. For example, if investigators believe that the validity of cause-of-death information on death certificates improves over time or varies by place of death, sensitivity and specificity could be made a function of calendar time or other relevant covariates.

In our analysis, we have assumed that the date of death was correct and that only the cause of death was subject to error. Under this assumption, the event time is assumed to be measured correctly, though the event indicator is error-prone. However, if the date of death were recorded incorrectly, a death was never recorded, or a death was falsely recorded, the event times would also be subject to error. Under these conditions, the modified maximum likelihood approach presented here would be insufficient to account for the bias due to outcome mismeasurement. When the outcome is death, event times are usually correct in countries that require standardized reporting of all deaths. However, studies of other outcomes, such as disease incidence, are more likely to have mismeasured event times, especially if detection of the disease is difficult.

Here, we have presented a maximum likelihood approach to account for misclassification of lung cancer–specific death in a cohort of workers exposed to asbestos. Results from the sensitivity analysis suggest that, at plausible values of sensitivity and specificity, outcome misclassification of lung cancer death is unlikely to produce substantial bias in standard estimates of the rate ratio for the effect of asbestos exposure on lung cancer death. However, sensitivity analysis suggests that standard methods to estimate rate ratios for outcomes subject to greater probability of misclassification, particularly those subject to poor specificity, are likely to produce notably biased estimates. The maximum likelihood–based sensitivity analysis presented here provides an approach to account for outcome misclassification in estimation of the rate ratio under various beliefs about the misclassification parameters.