Are Gestational Age, Birth Weight, and Birth Length Indicators of Favorable Fetal Growth Conditions? A Structural Equation Analysis of Filipino Infants

Abstract

The fetal origin hypothesis emphasizes the life-long health impacts of prenatal conditions. Birth weight, birth length, and gestational age are indicators of the fetal environment. However, these variables often have missing data and are subject to random and systematic errors caused by delays in measurement, differences in measurement instruments, and human error. With data from the Cebu (Philippines) Longitudinal Health and Nutrition Survey, we use structural equation models (SEMs), to explore random and systematic errors in these birth outcome measures, to analyze how maternal characteristics relate to birth outcomes, and to take account of missing data. We assess whether birth weight, birth length, and gestational age are influenced by a single latent variable that we call Favorable Fetal Growth Conditions (FFGC) and if so, which variable is most closely related to FFGC. We find that a model with FFGC as a latent variable fits as well as a less parsimonious model that has birth weight, birth length, and gestational age as distinct individual variables. We also demonstrate that birth weight is more reliably measured than is gestational age. FFGC were significantly influenced by taller maternal stature, better nutritional stores indexed by maternal arm fat and muscle area during pregnancy, higher birth order, avoidance of smoking and maternal age 20-35 years. Effects of maternal characteristics on newborn weight, length and gestational age were largely indirect, operating through FFCG.

The fetal origins hypothesis [1] has generated tremendous interest across several disciplines [2–4]. Fetal growth reflects a composite of environmental and genetic conditions that can “program” the fetus in ways that might prove harmful (or helpful) throughout life. Favorable fetal growth conditions (FFGC) together are a latent variable, not subject to direct measurement. Instead birth outcomes such as birth weight, gestational age, and birth length are taken as indicators of FFGC [5]. For instance, an early systematic review identified 80 papers examining the association of birth weight with adult blood pressure [6, 7], with most finding an inverse association interpreted to indicate long term risk of small size at birth. Similarly, Whincup et al. [8] reviewed studies in 31 populations relating birth weight to adult diabetes risk. While the association was inverse in 23 (9 statistically significant), it was positive in 8 (2 statistically significant), suggesting heterogeneity in the long term consequences of differences in birth weight.

The strategy of using measured birth weight or other proxy variables for FFGC has several drawbacks. First, to the degree that birth weight is just a proxy for FFGC, birth weight might not be sufficiently correlated with FFGC to provide an accurate assessment. In addition, when it comes to studying birth weight, gestational age, and other birth outcomes, there are many practical problems encountered in collecting data. Inaccurate scales, poor measurement techniques, and differences in the timing of measurements in different delivery settings are sources of error in birth weight, gestational age, and birth length. Missing data are another issue. These problems are particularly acute in developing countries where many births occur outside of clinical settings and measurements may not be taken on the day of birth. Even under near ideal conditions we expect errors in our usual measures. This raises concern about using any of these variables as perfect measures of their intended concept (e.g., birth weight), but casts even more doubt about their appropriateness as measures of FFGC. The typical response to these issues is to mention them as limitations, but to either ignore them or to use ad hoc solutions that lead to inaccurate results. For instance, listwise or pairwise deletion might be turned to for missing data; multiple measures of the same trait are sometimes combined; and the measurement error often is left untreated. These can result in biased estimates and conclusions. Our paper will show that there is another way to handle these practical constraints.

Our study is both methodological and substantive. It does not provide new methodology, but instead illustrates the use of Structural Equation Models (SEMs) to incorporate random and systematic measurement error in our indicators of birth weight and gestational age. Also, it demonstrates a maximum likelihood method to take account of data that are missing at random (MAR) and illustrates a comparison of models, one in which a latent variable mediates most of the effects of one set of variables on another and a second without the latent variable.¹ Our illustration of the process of model selection can also be applied more broadly in similar situations with the hypothesized presence of a mediating variable. In other words, we use existing SEM methods to address important questions about fetal conditions, birth weight, gestational age, and birth length. It is substantive in that it estimates the degree of measurement error in birth weight and gestational age measures; it tests the plausibility of postulating a FFGC latent variable that is largely responsible for the associations between birth weight (BW), birth length (BL), and gestational age (GA); it estimates the impact of maternal characteristics on fetal outcomes; it reveals the degree to which delays in measurement and differences in weighing scales impact measures; and it provides evidence on the strength of association between FFGC and BW, BL, and GA net of measurement error.

Nearly all of the papers on SEMs published in Statistics in Medicine have been methodological in nature [e.g., 11–14] though occasionally a substantive paper using SEMs has appeared [e.g., 15]. Our illustration of SEMs uses data from metropolitan Cebu in the Philippines. A direct maximum likelihood (DML) estimator for our models with missing data permits us to make use of all available data without needing to impute data or analyze multiple imputed data sets [16]. A similar SEM approach could be applied to other studies of pregnancy and birth or more generally to other health issues where random and systematic measurement errors threaten the analysis of health data.

Data and Variables

Data come from the Cebu Longitudinal Health and Nutrition Survey (CLHNS) conducted in selected areas of Metropolitan Cebu, Philippines, described more fully elsewhere [17]. This community-based observational study included all pregnant women in 33 randomly selected municipalities who gave birth between May 1983 and April 1984.² Data were collected in months 6-7 of pregnancy, immediately after birth, then bimonthly for 24 months, with later follow-up surveys extending to 2009. We restrict our analysis to 3,080 singleton live births but exclude 21 cases.³ Of these excluded cases, 16 are omitted as a result of having Ballard assessments conducted more than 10 days after birth⁴ while the other 5 cases were excluded after being identified as multivariate outliers using a Mahalanobis distance measure.

Mother's Traits

Highly trained staff measured height, weight, mid-upper arm circumference, and triceps skinfold thickness of the mother. We represent maternal nutritional status during pregnancy with arm fat (AFA) and arm muscle area (AMA), calculated from mid-arm circumference and triceps skinfold thickness in cm².

Smoking data reflect the mother's report of number and type of cigarettes smoked per day. Given the relatively low frequency and amount of smoking, we categorized women as smokers or non-smokers (SMOKERS). Owing to the known non-linear association of maternal age with birth outcomes, we categorized women as <20 (YOUNGER), 20-35 (referent category), or >35 years of age (OLDER). Parity was categorized to represent first pregnancy (FIRSTPRG) or not.

Birth Measures

The CLHNS has two measures of gestational age. The first relies on Last Menstrual Period (LMP) date and delivery date (LMPGA). If the mother recalled the month but not the day of her LMP, the 15^th of the month was assigned. If LMP was unknown, infant birth weight was < 2500 g, the mother reported bleeding during her pregnancy, she had no menstrual period since a prior birth, and/or she had diabetes or other complications during her pregnancy, then trained nurses conducted a Ballard clinical assessment of the newborn [18]. Six developmentally staged neuromuscular and six physical infant characteristics were scored by nurses and converted to a gestational age (BALGA) based on the Ballard standard, which gives whole number values in 2-week intervals. We interpolated measures to exact weeks. Assessments were conducted within the first ten days after birth, however, the validity of Ballard assessments after 7 days is not established [19]. To reduce skewness and kurtosis, we used the natural logs of BALGA and LMPGA in the analysis. WHENBAL is the infant's age when the Ballard assessment was done and is coded as missing when not done. LMPGA is subject to recall error, and measurement error in BALGA relates to interobserver reliability, timing of assessment and the aforementioned lack of precision.

We also have two measures of newborn weight. The first (BW1) was measured in grams by the birth attendant. Infants born at home (62%) were weighed by birth attendants who were provided with and trained in the use of 10kg CMS dial faced hanging scales. The rest were weighed on hospital or clinic scales at their place of birth. Because different weighing scale types and quality might lead to weight measurement differences, we include a dummy variable to distinguish whether the project scale was used or not (NOTPROJ). We also include a variable, NOTONE, indicating whether or not BW1 was measured on the day of birth. Weight was subsequently measured by trained study staff (BW2) using project scales as soon as they were notified of a birth. In the analyses, BW1 and BW2 are scaled by dividing by 100. Since timing of BW2 measurement varied, and early postpartum weight changes are non-linear, we accounted for this with the natural log transformation of infant age (WHENBW2) and the inclusion of its quadratic (WHENBW2SQ).

Length, in cm, was measured by teams of trained study staff using custom length boards. Although we only had one measure of birth length in the data (HTCM), we treated it as a latent variable with the measured value as its only manifest indicator. To acknowledge the possibility of measurement error in this measurement we set its error variance to a fixed value resulting in a reliability of approximately 0.8.⁵ In our sensitivity analysis section we use higher and lower reliability figures to assess the sensitivity of our results to our implementation of these values. Length was measured at the same time as BW2, so WHENBW2 refers to the child's age, in days, and when birth length was measured. GIRL is a dummy variable that distinguished girl from boy babies.

Table 1 gives basic descriptive statistics for all measured variables that are part of the analysis.

Table 1. Characteristics of Cebu Longitudinal Health and Nutrition Survey Mothers and Infants.

Infant's Variables	Description	N	Mean or Proportion	S.D.
BW1	Newborn weight at place of delivery, g	2615	3028	472
BW2	Newborn weight measured by project staff, g	3031	2994	435
HTCM	Newborn length, cm	3032	49.25	2.11
NOTONE	Weight not measured day of birth, proportion	2627	0.02	0.14
NOTPROJ	Infant not weighed on project scale	2593	0.32	0.47
WHENBW2	Infant age at weighing by project staff, days	3031	4.49	4.38
BALGA	Gestational age from Ballard assessment, weeks	597	3.66	0.04
LMPGA	Gestational age from LMP date, weeks	2843	3.66	0.07
WHENBAL	Infant age at Ballard assessment, days	597	3.58	1.80
GIRL	Infant sex=female, proportion	3059	0.47
Mother's Variables	Description	N	Mean or Proportion	S.D.
MOHT	Height, cm	3059	150.56	5.00
AMA	Arm muscle area during pregnancy at baseline, cm2	3058	34.10	5.59
AFA	Arm fat area during pregnancy at baseline, cm2	3058	14.73	5.67
SMOKERS	Smoked during pregnancy, proportion	3059	0.13	0.34
FIRSTPRG	Primiparous, proportion	3059	0.22	0.42
YOUNGER	Age < 20 y	3059	0.13	0.34
OLDER	Age > 35 y	3059	0.10	0.30
Mother's Background Variables	Description	N	Mean or Proportion	S.D.
INGESTWK	Gestation week at baseline	3059	30.00	4.78
PNIRONVIT	Took prenatal vitamins or iron during pregnancy, proportion	3059	0.58	0.49
NPISHORT	Pregnancy interval < 38 weeks, proportion	3059	0.27	0.45
NUPUB	Number of prenatal visits to public clinic	3059	1.12	1.51
NUPRV	Number of prenatal visits to private clinic	3059	0.61	1.56
MOINSUR	Has health insurance, proportion	3059	0.10	0.30
DYHHTOT	Total household income deflated, baseline	3038	283.52	531.36
MOTGRD	Highest grade completed	3059	7.10	3.30

Models

One of our primary interests is whether BW, BL, and GA are distinct factors with distinct causes or if it is plausible to view them as having a common dependence on a latent FFGC variable. The latter suggests that there is a collection of genetic and environmental factors that coalesce into a variable that simultaneously influences what happens to BW, BL, and GA. A model without FFGC represents the view that there is no mediating, common latent variable for BW, BL, and GA and that each variable has a separate and distinct set of relationships to the mother's traits. We represent these ideas in two models that we will compare.

Model 1: Unmediated Effects

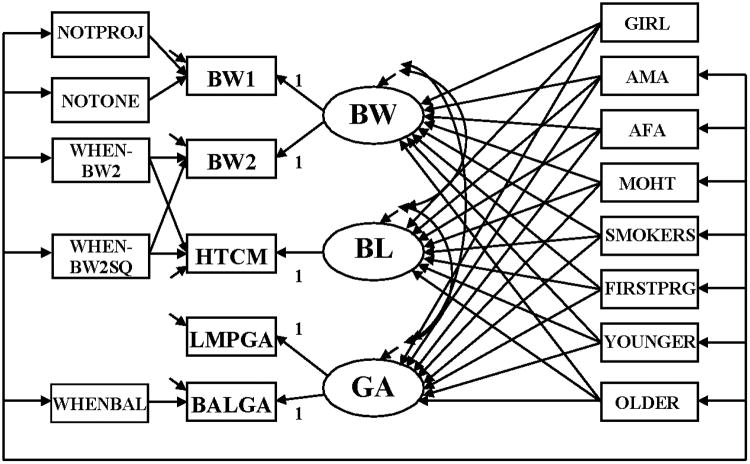
In our first model mother's traits have direct effects on GA, BW, and BL (Figure 1).

Figure 1.

SEM relating mother's traits among CLHNS newborns to characteristics of an infant's birth: BW, BL, and GA. BW=latent newborn weight; BL=latent newborn length, GA=latent gestational age; BW1=newborn weight measured by birth attendants; BW2=newborn weight measured by study staff; HTCM = newborn length; LMPGA=gestational age estimated from mother's report of date of her last menstrual period; BALGA=gestational age estimated from Ballard assessment of newborn; NOTPROJ=newborn not weighed on project scale; NOTONE= weight not measured day of birth; WHENBW2=infant age in days when measured by study staff; WHENBW2SQ=WHEN2BW squared; WHENBAL=age in days when Ballard assessment was done; NOTONE=newborn not weighed on day 1; GIRL=newborn is a girl; AMA=maternal arm muscle area during pregnancy; AFA=maternal arm fat area during pregnancy; MOHT=mother's height; SMOKERS=mother smoked during pregnancy; FIRSTPRG=newborn was firstborn; YOUNGER=mother was <20 years old when pregnant; older=mother was >35 years old when pregnant

The ovals in the diagram signify that GA, BW, and BL are latent variables. We treat them as latent variables since their measures (BALGA, LMPGA, BW1, BW2, and HTCM) contain measurement error and we need to distinguish the latent variable that is free from error from the measures that contain errors. Observed variables are shown in boxes. In addition to the measures of GA, BW, and BL, the other observed variables are exogenous (GIRL, AMA, AFA, MOHT, SMOKERS, FIRSTPRG, YOUNGER, OLDER, WHENBAL, WHENBW2SQ, WHENBW2, NOTONE, and NOTPROJ), which were defined in the Data and Variables section. All these exogenous variables are allowed to correlate as represented by the line that connects them with the short arrows pointing toward each variable. The only exception is GIRL for which there is no reason to expect the baby's sex to correlate with these other exogenous variables. All exogenous variables are uncorrelated with all the errors or disturbances.

Single-headed arrows represent the impact of the variable at the base of the arrow on the variable at the head of the arrow. Endogenous variables are ones that are influenced by at least one other variable in the model. In Figure 1 the latent endogenous variables are BW, BL, and GA. The observed endogenous variables are: BW1, BW2, HTCM, LMPGA, and BALGA. Each endogenous variable has an error which is represented by a short arrow that points toward it. The errors or disturbances contain all of the other influences on the measure or latent variables not included in the model.

GA influences its two measures LMPGA and BALGA. The “1” on the paths from GA to LMPGA and BALGA indicates that for a one week difference in the latent GA variable we expect one week difference in the LMPGA and BALGA measures. The intercepts of the equations for LMPGA and BALGA are set to zero. This represents a classical measurement error model. We tested and found support for the constraints of having both paths set to 1 and the intercepts to 0. WHENBAL has a direct effect on the BALGA to control for development that might have occurred when the Ballard measurement was not done immediately after birth.

BW affects BW1 and BW2 and we set each path to 1, though we do allow the intercept for BW2 to differ from zero. To control for a non-linear effect of the timing of measurement, the model permits WHENBW2 and WHENBW2SQ to influence BW2 and HTCM, which were measured at the same time. NOTPROJ is allowed to influence BW1 to account for possible systematic error in the type of scale, but is also a proxy for place of delivery, since project scales were not used in hospitals or clinics.

This model shows GIRL and each mother's trait with direct effects on BW, BL, and GA. In addition, we allow the disturbances or errors in these latter variables to correlate with each other, which signify that conditional on GIRL and the mother's traits there remains some association among these latent variables.

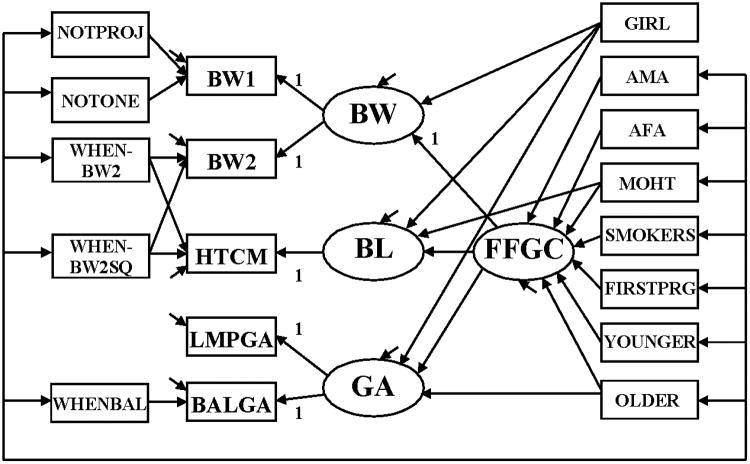
Model 2: FFGC as a Mediator

Our second model allows a FFGC latent variable to mediate most of the effects of the mother's traits on BW, BL, and GA (Figure 2).

Figure 2.

SEM relating mother's traits among CLHNS newborns to characteristics of an infant's birth: BW, BL, and GA with a mediating latent variable Favorable Fetal Growth Conditions (FFGC).

The measurement model for the determinants of the measures – BW1, BW2, HTCM, LMPGA, and BALGA – is the same in Figures 1 and 2. The primary difference lies in the relationship between the mother's traits and the latent BW, BL, and GA variables. In Model 2 we hypothesize a single latent variable, FFGC, that coalesces environmental and genetic factors that create favorable or unfavorable conditions for fetal growth and that this FFGC simultaneous affects BW, BL, and GA. According to this structure, if FFGC improves we expect that BW, BL, and GA each will improve; if FFGC declines we expect each to diminish. The two exceptions to this pattern are that GIRL does not have a direct effect on FFGC, though it is permitted to directly affect BW, BL, and GA and MOHT is allowed to directly affect BL given the likely close links between a mother's height and the length of the baby.

Model 2 is more parsimonious than Model 1 in that it suggests that a FFGC latent variable replaces the need for numerous direct effects between the mother's traits and the BW, BL, and GA of the baby. It suggests that factors that influence FFGC have implications for all three variables. In Model 1 we allowed a correlation among the errors of BW, BL, and GA even after controlling for their common dependence on the mother's traits. Model 2 suggests that these correlations are due to a common dependence on FFGC so that when the latter variable is controlled, there is no necessity for these correlated errors.

In both models, the error variables are assumed to be uncorrelated with all exogenous variables. In addition, we assume that all measurement errors for the indicators of BW, BL, and GA are uncorrelated with each other. All exogenous variables (except GIRL) are allowed to correlate with each other. An absence of a single-headed arrow between two endogenous variables or from an exogenous to endogenous variable represents the “strong” causal assumption of no direct effect between the variables [20]. The plausibility of these assumptions is assessed when we test the fit of the models to the data and compare their fit to each other. In addition, in a subsection on Sensitivity Analysis we consider a range of additional variables to determine possibly omitted variables and their impact on our results.

Results

We estimate models using a distributionally robust maximum likelihood estimator (MLR) that takes account of possible nonnormality in the distribution of the errors in the model. “The MLR standard errors are computed using a sandwich estimator. The MLR chi-square test statistic is asymptotically equivalent to the Yuan-Bentler T2* test statistic” [21].

The MLR estimator also permits us to test whether the model is consistent with the data in that it explains the association among the variables as well as a saturated model. A higher p-value for the likelihood ratio chi square test adjusted for nonnormality is evidence in favor of the hypothesized model. Given the large sample size and the resulting statistical power, a statistically significant chi square is common. Supplemental fit statistics used to assess overall model fit are the [1-RMSEA] [22, 23], IFI [24], and BIC [25, 26]. The closer that [1-RMSEA] and IFI are to 1 and the larger is the negative value of BIC, the better is the model fit.

As the descriptive statistics in Table 1 indicate, there is substantial missing data for a few of the variables in our analysis. Listwise or pairwise deletion of cases could bias our estimator unless data are Missing Completely at Random (MCAR) [27]. Missing at Random (MAR) is a less restrictive assumption than MCAR. We use a Direct Maximum Likelihood (DML) estimator for missing data that is asymptotic unbiased and consistent when data are MAR. Given the observed variables in our model and the relative completeness for key ones like BW2, we use this DML estimator assuming MAR. In addition, in our sensitivity analysis section we mention our experiments with adding auxiliary variables [28] for missing data and whether they make a difference.

We first look at the overall fit of the two models to determine which one best corresponds to the data. Table 2 provides the MLR chi square test statistic, degrees of freedom (df), p-value, IFI, (1-RMSEA), and BIC estimates for each model. The models in Figures 1 and 2 both have statistically significant chi-squares which is not too surprising given the large sample size (N=3059) and the large statistical power to detect even minor discrepancies. The supplemental fit measures indicate excellent fit to the data with the IFI and (1-RMSEA) close to their ideal fit of 1. The difference between the models is small for these two fit measures. However, a more substantial gap is visible for the BIC. According to the Jeffreys-Raftery [26] guidelines, a difference of 10 or more in the BICs of two models suggests strong evidence in favor of the model with the most negative BIC. Using these guidelines, the difference of more than 150 is exceptionally strong evidence favoring Model 2. Recall that Model 2 has the FFGC latent variable as a mediator variable between the mother's traits and BW, BL, and GA.

Table 2. Global Fit Measures for SEMs.

Model	Test Statistica	df	p-value	IFI	(1- RMSEA)	BIC
Model 1	118.569	40	<.001	0.994	0.975	-202.47
Model 2	169.006	65	<.001	0.993	0.977	-352.67

^a= Chi square test statistic from robust maximum likelihood estimator. See text.

Before choosing Model 2 over Model 1, it is important to also examine the components of fit to ensure that they do not indicate problems. Poor estimates might be present in the coefficients or other estimates even when the overall fit of a model is acceptable.

We present the parameter estimates for the Model 2 in two tables. Table 3 gives the coefficient estimates, 95% confidence intervals, and the R-square for the direct effects of the mother's traits on the FFGC latent variable. The signs of all coefficients are as predicted: the nutritional variables (AMA, AFA, and MOHT) have statistically significant positive effects on the FFGC latent variable. SMOKERS, FIRSTPRG, and YOUNGER have statistically significant negative effects on FFGC while OLDER is negative but not statistically significant. A joint test of whether YOUNGER and OLDER have zero effects is not supported by our model. There is a statically significant chi-square test statistic of 10.362 with 2 degrees of freedom when a zero effects model is compared to our full model. All the mother's traits explain about 11% of the variation in the FFGC latent variable.

Table 3. MLR Estimates of Direct Effects of Mother's Characteristics on Favorable Fetal Growth Conditions (FFGC) From Figure 2.

Exogenous Variable	β̂a [95 % c.i.]b
	FFGC
Maternal Arm Muscle, cm2 (AMA)	.049 [.022, .076]
Maternal Arm Fat, cm2 (AFA)	.088 [.059, .117]
Mother's Height, cm (MOHT)	1.505 [1.223, 1.787]
Mother was a smoker (SMOKERS)	-.835 [-1.262, -.408]
First Pregnancy (FIRSTPRG)	-1.242 [-1.642, -.842]
Mother < 20 (YOUNGER)	-.766 [-1.232, -.300]
Mother > 35 (OLDER)	-.121 [-.629, .387]
R2	.110

^a= estimate of coefficient;

^b= 95 % confidence interval

Table 4 gives the direct effects of the FFGC on BW, BL, and GA, and the direct effects of BW, BL, GA, and the exogenous observed variables on BW1, BW2, HTCM, LMPGA, and BALGA. We start with an evaluation of the BW1, BW2, LMPGA, and BALGA measures. The BW1 and BW2 indicators have relatively high R² s with 70% and 94% variance explained by the latent BW variable and the systematic measurement error due to NOTONE and NOTPROJ for BW1 and WHENBW2 and WHENBW2SQ for BW2. The effect of not being measured on the first day (NOTONE) is nonsignificant, but using a scale different than the project scale (NOTPROJ) leads to roughly an expected 60 gram lighter weight than if the project scale were used holding constant the latent BW. Turning to the timing of the BW2 measurement, the estimates suggest a significant nonlinear relationship such that an initial decline in weight is followed by weight gain. The quadratic term is highly statistically significant. This pattern of newborn weight change is consistent with prior studies [29, 30] and including these terms as determinants of BW2 takes account of this systematic error due to delays in weighing the baby.

Table 4. MLR Estimates of Direct Effects and R² in Model 2 Excluding the Direct Effects to FFGC (N=3059).

Covariates	Endogenous Variable β̂a [95 % c.i.]b
	GA	BW	BW1 (g/100)	BW2 (g/100)	BL	HTCM (cm)	LMPGA	BALGA
FFGC	.004 [.0033, .0047]	1 [N/A]			.348 [.315, .381]
Birth Weight (BW)			1 [N/A]	1 [N/A]		[N/A]
	Gestational Age (GA)							1 [N/A]	1 [N/A]
	Not One (NOTONE)			-.741 [-1.523, .041]
Not Project Scale (NOTPROJ)			-.573 [-.810, -.336]
Number of Days b/f BW2 (WHENBW2)				-2.058 [-2.824, -1.292]		-.255 [-.655, .145]
Number of Days b/f BW2 (sq.) (WHENBW2S)				1.277 [1.024, 1.530]		.401 [.279, .523]
Gestational Age at Ballard								.0012 [.0003, .0022]
Girl (GIRL)	.005 [.001, .009]	-.450 [-.728, -.172]			-.381 [-.518, -.244]
Mother's Height (MOHT)					.298 [.184, .412]
R2	.710	1.000*	.697	.937	.684	.802	.090	.274

^a= estimate of coefficient;

^b= 95 % confidence interval;

^*R² results from small negative error variance estimateset to zero.

Turning to the measurement of GA, we find rather disappointing results for the reliability of the LMPGA and BALGA indicators. The R² for LMPGA is less than 10% and that for BALGA is less than 30%. This means that more than 90% of the variance in LMPGA and more than 70% of the variance in LMPGA is due to measurement error. Systematic error due to delays in doing the Ballard measure (WHENBAL) has a statistically significant effect on BALGA. If these low reliabilities are representative of what occurs in other studies, it is cause for serious concern especially when the measurement error is not considered in empirical analyses.

The last sets of effects are those of FFGC and GIRL on GA, BW, and BL. Roughly 70% of the variance in GA is explained by FFGC and GIRL. The same is true for BL with the addition of mother's height as a covariate. Though these are moderately high values, BW has essentially all its variance explained by these variables. This is impressive, but subject to misunderstanding. First note that it is the latent BW that has this near perfect association with the postulated latent FFGC variable. This is different than saying that BW1, BW2, or some other measure of BW has this strong of a relationship to FFGC. As discussed above, BW1 and BW2 have random and systematic error that make them less than perfect representations of BW. But the estimates imply that to the degree we have measures of BW that are free of error, these measures are extremely highly correlated with the latent FFGC variable. The coefficient estimates for GIRL indicate a slightly longer GA for girls than boys and lower BW and BL for girls.

In Model 2, the mother's traits have indirect effects [31] on GA, BW, and BL that are mediated through FFGC (Table 5). All indirect effects are in the predicted direction and are statistically significant with the exception of those from OLDER.

Table 5. Indirect Effects of Mother's Characteristics on GA, BW, and BL Mediated by FFGC.

Exogenous Variable	β̂a [95 % c.i.]b
	GA	BW	BL
Maternal Arm Muscle, cm2 (AMA)	.0002 [.0001, .0003]	.049 [.022, .076]	.017 [.007, .027]
Maternal Arm Fat, cm2 (AFA)	.0004 [.0002, .0005]	.088 [.059, .117]	.031 [.019, .043]
Mother's Height, cm (MOHT)	.007 [.005, .009]	1.505 [1.223, 1.787]	.52 [.414, .634]4
Mother was a smoker (SMOKERS)	-.004 [-.006, -.002]	-.835 [-1.262, -.408]	-.291 [-.444, -.138]
First Pregnancy (FIRSTPRG)	-.006 [-.008, -.004]	-1.242 [-1.642, -.842]	-.433 [-.568, -.298]
Mother < 20 (YOUNGER)	-.003 [-.005, -.001]	-.766 [-1.232, -.300]	-.267 [-.436, -.098]
Mother > 35 (OLDER)	-.001 [-.003, .001]	-.121 [-.629, .387]	-.042 [-.218, .134]

^a= estimate of coefficient;

^b= 95 % confidence interval

Table A1 in the appendix gives the estimates from Model 1. Because this model excludes FFGC, the effects of the mother's traits on GA, BW, and BL are quite similar to the sum of direct and indirect effects of the mother's traits from Model 2.

Sensitivity Analysis

We explored several alternative model specifications and potential sensitivities of the model estimates. A reviewer raised a question about the sensitivity of the results to choosing BW to scale FFGC in Model 2 and whether this somehow made FFGC essentially the same as BW. Scaling sets the metric of the latent variable, but does not make the latent variable it scales identical to its scaling variable. In fact, if we use BL as the scaling indicator for FFGC, the R-squares for GA, BW, and BL stay the same as do the R-squares for indicators of these latter variables. So regardless of our scaling decision, we find that BW is highly correlated with FFGC even though it is a different variable.

Another potential issue is the timing of the measurement of the arm fat and muscle measurement. Though these measurements occurred at approximately the same weeks, there was some variation. We reran our model controlling for the timing of measurement and found essentially no differences.

The birth length variable had a single measure that we assumed to have reliability of 0.8 as it was not possible to estimate the proportion of error in that measure with only one manifest indicator. To check the sensitivity of our results to this reliability constraint, we re-estimated the model assuming that the reliability ranged between 0.7 - 0.9. The estimated effects were essentially unchanged. Across all of these sensitivity analyses all of the parameters remained unchanged except for those for the residual variances and reliabilities of the latent variable and the birth length measure that were manipulated in the analyses. A decrease in reliability for the latent variable increased the reliability of the manifest variable and vise-versa. The overall result was that the model was robust across the sensitivity analyses.

We also tried a model that replaced the latent FFGC variable with direct effects among GA, BW, and BL; another included both FFGC and direct effects of GA, BW, and BL. We tested alternate transformations of the observed variables to capture nonlinearity. These led to similar estimates, but had inferior model fits, or resulted in unrealistic coefficient values or predictions. We also compared the parameter estimates that were common across models 1 and 2 to see if these changed much between specifications. The only parameter estimate that changed in a noteworthy manner was that of BL regressed on MOHT. The estimated parameter drops from 0.819 (11.6) to 0.298 (5.2) when only the direct effects are compared. However, when the total effects, the direct and indirect effects, are considered the estimated parameter is 0.822 (11.7). Comparing only the direct effects of BL on MOHT belies the similarity found in the total effects. MOHT in Model 2 model is the only instance where any of the mother's characteristics are not completely mediated by the FFGC latent variable.

We also added a series of additional exogenous variables to the model as a check on potentially omitted variables and to examine the sensitivity of our reported estimates. These new variables were gestation week at baseline, did mother take prenatal vitamins or iron during pregnancy, was the pregnancy interval less than 38 weeks, the number of prenatal visits to a public clinic, the number of prenatal visits to a private clinic, has health insurance, total household income deflated at baseline, and mother's highest grade completed. We checked the statistical significance of these new variables using a Bonferroni correction in both Model 1 and Model 2. In addition, we noted whether the coefficient estimates from the original models and interpreted above had substantially changed when controlling for these additional variables. We found that household income had a statistically significant effect on birth length and the gestation week at baseline had a statistically significant effect on gestational age in Model 1. However, none of the new variables emerged as significant in Model 2. In addition, our estimates and substantive conclusions from the original model remained essentially unchanged. Furthermore, another unpublished study [32] examined the MAR assumptions that we used for our missing data procedures and found that our results are essentially unchanged when auxiliary variables are entered in the model.

Discussion

Birth weight, birth length, and gestational age are key indicators of newborn health. In practice, the collection of such data is subject to delays in measurement, the use of different instruments, or other factors contributing to systematic and random measurement error. Treating these birth measures as if they were free of error creates biases in the analyses that utilize them. In this paper we use the CLHNS birth data to illustrate that the random and systematic sources of error can be modeled and the reliability of measures estimated using SEMs. Furthermore, we explore the hypothesis that a FFGC latent variable explains the associations among BW, BL, and GA.

Substantively, we found statistically significant influences of both the timing of measurement and type of scale on the measure of birth weight, though the birth weight measures are far more accurate than the gestational age measures. Having just a single measure of birth length, we were not able to estimate its reliability though we found that our estimates were robust to assuming a range of different reliability values for the length variable. Comparing a model where mother's traits directly affected BW, BL, and GA to one where these effects were largely mediated by FFGC, we discovered that the FFGC mediating model had a superior fit. The only unmediated effect of maternal height in Model 2 may reflect a genetic effect of maternal height on newborn size. Furthermore, we estimated that the latent birth weight variable is extremely highly correlated with the FFGC latent variable. Thus, despite extensive critiques of BW as a proxy for fetal growth [33], our results suggest that if we could largely eliminate the error in a birth weight measure, then it would be highly correlated with the latent FFGC variable. Given the heightened interest in the impact of fetal conditions on adult health [34], this has useful practical implications.

But this is based on the assumption that the latent variable is FFGC rather than another latent variable. For instance, a reviewer suggested that given the near perfect association of FFGC and BW, it is possible that FFGC is in reality the same as BW. If true, then we would need to explain the mechanisms by which BW mediates the effects of mother's traits on GA and BL. In other words, if the latent variable that we hypothesized to be FFGC is BW or something different, then we need to describe what that variable is and how it plausibly can play the role of a mediating variable. On the other hand, to defend our specification that the latent variable is FFGC requires replication and additional tests of its plausibility as a latent variable.

Methodologically, our study illustrates how SEMs are usefully applied to take account of systematic and random measurement error and to test for the presence of latent mediating variables that can explain the association among component variables. SEMs are also advantageous in the handling of missing data using maximum likelihood procedures without imputation. Similar modeling strategies could be followed in the modeling of other health and medicine problems so that a number of measurement problems that plague these areas could be incorporated into and controlled for in the model. Of course, like all statistical models, we can never prove or test all of the assumptions of SEMs. However, we often can find evidence of discrepancies when the model is not a good match to the data. In other words, we can reject SEMs even if we can never definitively accept them as valid.

APPENDIX A.

Table A1. MLR Estimates of Direct Effects of Mother's Characteristics on GA, BW, and BL (Figure 1).

Exogenous Variable	β̂a [95 % c.i.]b
	GA	BW	BL
Maternal Arm Muscle, cm2 (AMA)	.001 [.0001, .0014]	.050 [.023, .077]	.011 [-.003, .025]
Maternal Arm Fat, cm2 (AFA)	.0002 [.0001, .0004]	.087 [.058, .116]	.035 [.021, .049]
Mother's Height, cm (MOHT)	.001 [-.003, .005]	1.508 [1.226, 1.79]	.819 [.680, .958]
Mother was a smoker (SMOKERS)	-.009 [-.015, -.003]	-.830 [-1.257, -.403]	-.303 [-.521, -.085]
First Pregnancy (FIRSTPRG)	-.010 [-.016, -.004]	-1.26 [-1.648, -.872]	-.184 [-.380, .012]
Mother < 20 (YOUNGER)	-.005 [-.013, .003]	-.753 [-1.214, -.292]	-.422 [-.663, -.181]
Mother > 35 (OLDER)	-.005 [-.013, .003]	-.115 [-.623, .393]	-.079 [-.328, .170]
Girl (GIRL)	.005 [.001, .009]	-.449 [-.727, -.171]	-.379 [-.516, -.242]
R2	.117	.118	.113

^a= estimate of coefficient;

^b= 95 % confidence interval