The Stochastic Evolutionary Game for a Population of Biological Networks Under Natural Selection

Abstract

In this study, a population of evolutionary biological networks is described by a stochastic dynamic system with intrinsic random parameter fluctuations due to genetic variations and external disturbances caused by environmental changes in the evolutionary process. Since information on environmental changes is unavailable and their occurrence is unpredictable, they can be considered as a game player with the potential to destroy phenotypic stability. The biological network needs to develop an evolutionary strategy to improve phenotypic stability as much as possible, so it can be considered as another game player in the evolutionary process, ie, a stochastic Nash game of minimizing the maximum network evolution level caused by the worst environmental disturbances. Based on the nonlinear stochastic evolutionary game strategy, we find that some genetic variations can be used in natural selection to construct negative feedback loops, efficiently improving network robustness. This provides larger genetic robustness as a buffer against neutral genetic variations, as well as larger environmental robustness to resist environmental disturbances and maintain a network phenotypic traits in the evolutionary process. In this situation, the robust phenotypic traits of stochastic biological networks can be more frequently selected by natural selection in evolution. However, if the harbored neutral genetic variations are accumulated to a sufficiently large degree, and environmental disturbances are strong enough that the network robustness can no longer confer enough genetic robustness and environmental robustness, then the phenotype robustness might break down. In this case, a network phenotypic trait may be pushed from one equilibrium point to another, changing the phenotypic trait and starting a new phase of network evolution through the hidden neutral genetic variations harbored in network robustness by adaptive evolution. Further, the proposed evolutionary game is extended to an n-tuple evolutionary game of stochastic biological networks with m players (competitive populations) and k environmental dynamics.

Introduction

Biological network evolution is the physical, genetic, or behavioral change in populations of biological networks over time. Natural selection is a process that causes biological networks to adapt to their environments. Network robustness is important in ensuring the stability of phenotypic traits of biological networks that are constantly exposed to genetic variations and non-genetic environmental disturbances. A better understanding of network robustness is paramount for understanding biological network evolution. Network robustness can be discussed sensibly only if two cardinal questions have been resolved: what is the phenotypic trait of interest in network evolution, and what is the network perturbation of interest?^1–4 There are three principal kinds of network perturbations to which a biological network needs to be robust: stochastic intrinsic molecular noise, environmental change and genetic variation.^5–7 Stochastic intrinsic molecular noise refers to the stochastic fluctuations that occur in any biological network, for example, in the concentration of a biological molecule. Environmental change is the variation in the external environment, for example, a change in temperature, salinity, or nutrient availability. Genetic variation is genetic change, either through de novo mutation or through recombination in the evolutionary process.¹ The ability to buffer genetic variation is called genetic robustness, the noise filtering ability to attenuate the effect of intrinsic molecular noise is called noise robustness, and the ability to resist environmental change is called environmental robustness. The ability to maintain a desired phenotypic trait is called phenotypic robustness. In order to maintain the desired phenotypic trait, a biological network needs an evolutionary strategy with high network robustness to confer genetic robustness (buffering genetic variation), noise robustness (filtering stochastic intrinsic molecular noise), and environmental robustness environmental change in the evolutionary process.

Network evolvability is defined as the ability to deviate from a phenotypic trait to adapt to an environmental change. The network evolvability of a biological network appears to be the reverse of network robustness. If phenotypic traits are robust against genetic variations and external disturbances, a network population may be expected to have difficulty adapting to an environmental change, as several studies have suggested.^2,3,10 However, other studies contend that robust networks are more adaptable.^4–7 The relationship between network robustness and network evolvability is complex, because robust network populations harbor a large diversity of neutral genotypes that may be important in adaptation. The study of the evolvability and robustness of biological networks is still in its infancy. In fact, network robustness allows changes in the structure and components of biological networks, due to genetic variations, while still allowing the desired phenotypic trait to be maintained. Network evolvability allows some environmental changes to influence a biological network, so that a new phenotypic trait of the biological network may evolve by natural selection, to adapt to the new environment.^8–11

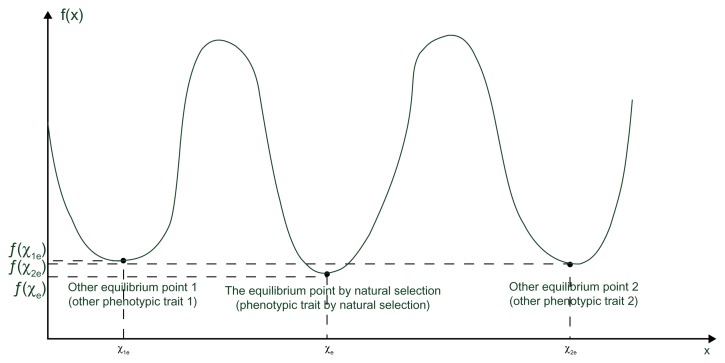
In the evolutionary process, a population of evolving biological networks can be represented by a nonlinear stochastic system with heritable random genetic variations and non-heritable random environmental disturbances. A phenotypic trait of a biological network can be represented by an equilibrium point of the nonlinear stochastic system in the fitness landscape (see Fig. 1). There are many variations of phenotypes (population) around this equilibrium point, due to intrinsic random genetic variations and random environmental disturbances.^8–11 When a phenotypic trait is perturbed so much that it can transit from the domain of its equilibrium point into the domains of other equilibrium points, a new phenotypic trait is generated and presented. A heritable genetic variation that does not directly help a biological network to evolve a new phenotypic trait is neutral. In evolution, a robust biological network can harbor a large number of neutral genetic variations, before a phenotypic trait is pushed from one equilibrium point to another one. The capacity to harbor these neutral genetic variations is a measure of the genetic robustness of the biological network in evolution. If the amount of stochastic neutral genetic variations is larger than the genetic robustness of a biological network, so that a phenotypic trait can transit from one equilibrium point to another, a new phenotype is presented to start another period of network evolution. Although it has been shown that many features of biological networks can arise by non-adaptive processes,¹² this study will offer a different possible understanding of biological network adaptive processes by natural selection in evolution.

Figure 1.

The equilibrium points of a nonlinear biological network in a phenotypic landscape. The nonlinear stochastic biological network has many local equilibrium points (phenotypic traits). The phenotypic landscape of three stable equilibrium points with a vertical scale illustrating the relative network robustness of the equilibrium points (phenotypic traits) of the nonlinear stochastic biological network in evolution, ie, the equilibrium point at x_e with deeper and wider basin, is more robust. Here, x_e is the equilibrium point (phenotypic trait) of interest by natural selection.

In this study, the network evolvability in response to stochastic environmental changes and genetic variations of a nonlinear stochastic network can be formulated for the first time as a stochastic game problem, because the environmental changes in the evolutionary process are unpredictable. In this situation, the minimization of the worst-case phenotypic deviation for all possible environmental changes is therefore considered as the phenotypic robustness strategy used by a biological network to resist the effect of environmental changes and to maintain its phenotype in the evolutionary process. Therefore, both the network evolvability and the phenotypic robustness of a nonlinear stochastic biological network in the evolutionary process can be discussed from the nonlinear stochastic game perspective. In other words, the stochastic biological network wants to minimize network evolvability (or maximize network robustness) while the stochastic environmental disturbances try to maximize the network evolvability (or minimize the network robustness). The interplay between genetic robustness, environmental robustness, and network robustness in the phenotypic robustness of an evolutionary biological network^13–15 can also be investigated from the point of view of a stochastic Nash game. In this paper, using the evolutionary game strategy, we find that some genetic variations in the evolutionary process are selected to construct new negative feedback loops to efficiently improve network robustness, thereby maximizing the fitness (or minimizing the evolution level) of the biological network in evolution. We also find that with the evolutionary game strategy, a biological network has enough network robustness and that the stochastic evolutionary biological network becomes more robust near the equilibrium point. This is the so-called ‘phenotypic robustness criterion’ of biological networks in the evolutionary process. However, when random neutral genetic variations harbored by network robustness are accumulated to the extent of violating the phenotypic robustness criterion new material is provided for more evolutionary paths to other phenotypes of the gene network by random drift. In the face of a large environmental change, the phenotypic trait of the biological network cannot be maintained and a phenotype transition may eventually occur by a shift to another equilibrium point. In other words, while the evolutionary game strategy can improve the network robustness for the phenotype at the beginning, the accumulated neutral genetic variations harbored by improved network robustness will finally violate the network phenotypic robustness criterion to break down the network phenotype and make a new phenotypic adaptation in network evolution.

Based on nonlinear stochastic game theory, the study of network robustness and network evolvability needs to solve a very difficult Hamilton-Jacobi-Isaac inequality (HJII).¹⁶ At present, no good way exists to efficiently solve the HJII analytically or numerically. In this study, a global linearization method is employed to interpolate several local linear stochastic systems, at different operation points, to approximate the nonlinear stochastic biological network in evolution. In this situation, linear stochastic game techniques can be employed to solve the nonlinear stochastic evolutionary game problem of the biological network, in which the HJII is replaced by a set of linear matrix inequalities (LMIs). Based on the global linearization technique and linear system theory, the network evolvability and robustness are related to the locations of the eigenvalues of the local linearized stochastic evolutionary biological networks. If the eigenvalues are located in the far left-hand side of the s-complex domain, then the nonlinear stochastic biological network is more robust with the phenotypic trait (or the equilibrium point) and less adaptive to other equilibrium points (or other phenotypic traits) in the evolutionary process. On the other hand, if these eigenvalues are near the image axis of the s-complex domain, then they are more easily perturbed to the right-hand side of the s-complex domain. In this situation, the phenotypic trait of the nonlinear stochastic evolutionary biological network is less robustly stable but more adaptable to environmental change in the evolutionary process. In order to maintain the phenotype robustness of the evolutionary biological network, the evolutionary game strategy can select some genetic variations to generate adequate negative feedback loops, so that the eigenvalues of the local linearized biological network can be shifted to the far left-hand side of the s-complex domain. Obviously, the evolutionary game strategy can efficiently enhance network robustness by developing adequate negative feedback loops to buffer neutral genetic variations and to resist environmental disturbance in the evolutionary process.

In this study, we investigate quantitative measures of network evolvability and network robustness from a stochastic game theory point of view. The phenotype robustness criterion for a nonlinear stochastic evolutionary biological network can be measured by solving an evolutionary game strategy based on the LMIs of local linearized stochastic biological networks. That is, if the genetic robustness plus the noise robustness and environmental robustness is less than the network robustness in each local linearized stochastic network, then the phenotypic trait of the nonlinear stochastic biological network is robustly stable in the evolutionary process. If not, the biological network might evolve to another phenotypic trait with the release of accumulated cryptic neutral genetic variations and the aid of strong environmental changes. In this study, we first reveal the evolutionary strategy for adaptive fitness of a biological network in evolution from a stochastic game perspective, and then we investigate the tradeoffs between genetic robustness and environmental robustness and the antagonistic properties between network robustness and network evolvability from a system theory perspective. If there exist m competitive populations and k environmental changes in the network evolutionary process, then the proposed evolutionary game strategy can be easily modified to the n-tuple evolutionary game problem of biological network with m players (competitive populations) and k environmental dynamics. Finally, an in silico example is given to illustrate the stochastic evolutionary game of stochastic biological networks and to determine their network evolvability and fitness in evolution.

The Stochastic Evolutionary Game of the Linear Biological Network Under Natural Selection

For simplicity of analysis, we first consider a linear biological network as follows

$$\frac{dx}{dt}=Ax(t),$$ (1)

where the state vector $x(t)={\left[\begin{array}{cccc}{x}_1(t)& x_2(t)& \cdots & x_n(t)\end{array}\right]}^T$ denotes the concentrations of n genes in a genetic regulatory network, or protein concentrations of n proteins in a protein-protein interaction network, or the population densities of an ecological network with n different species, and x_i(t) represents the number, density, or biomass of individuals of species i. Although we have assumed that there are n different genes, proteins or species, these numbers need not be fixed. In fact, one feature of Darwinian dynamics is that the evolutionary process may determine the number n of genes, proteins, or species as a product of the evolutionary network. In the evolutionary network, the interaction matrix A ∈ ℝ ^n×n among species is denoted as

$$A=\left[\begin{array}{cccc}{a}_{11}& \dots & \dots & a_{1n}\\ ⋮& a_{22}& \hspace{0.17em}& ⋮\\ ⋮& \hspace{0.17em}& \ddots & ⋮\\ a_{n1}& \dots & \dots & a_{nn}\end{array}\right],$$ (2)

where a_ij denotes the interaction from species j to species i, ie, A denotes the dynamic interactions between species in a biological network from the present generation to the next generation.

Remark 1

(i) The linear biological network in (1) can be considered as a linearized system of a nonlinear biological network $\frac{dx}{dt}=f(x(t))$ at an equilibrium point (phenotypic trait) x_e of interest by natural selection in Figure 1, ie, $A={\frac{\partial f(x)}{\partial x}|}_{x=x}$. Without loss of generality, the origin of the nonlinear biological network is always shifted to the equilibrium point (phenotypic trait) x_e, ie, x_e = 0. This detail will be discussed later. (ii) The interaction matrix A between species may suffer from environmental disturbances due to climate and salinity change, and from random genetic variations due to heritable DNA mutation, genetic transition, and recombination in the evolutionary process.

In the evolutionary process, the biological network (1) suffers from both extrinsic disturbances due to environmental changes as well as intrinsic phenotypic variations due to heritable random genetic variations. In order to maintain the favorable phenotypic trait at x_e = 0 by natural selection (ie, phenotypic trait robustness in evolution), the biological network needs to select some heritable genetic variations (the evolutionary strategy of the biological network) to improve network robustness so that intrinsic variations and environmental disturbances can be resisted. In this situation, the evolutionary biological network can be represented as follows

$$\frac{dx(t)}{dt}=\left(A+\sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)\right)\hspace{0.17em}x(t)+B\upsilon (t),$$ (3)

where the weighted Poisson point (counting) process¹⁷

$$s(t)=\sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)=\sum _{k=1}^{N(t)}{A}_k,t\ge 0,$$ (4)

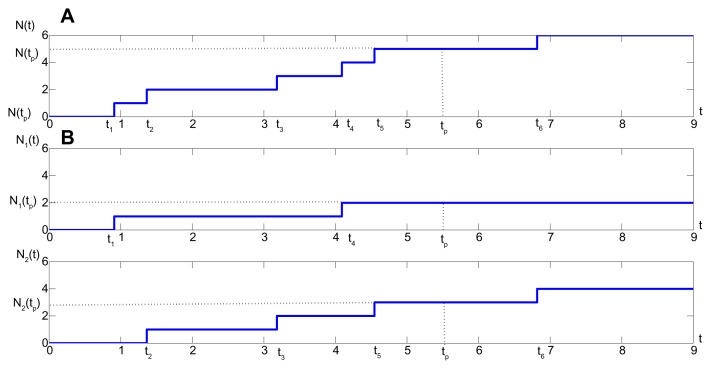
denotes heritable network interaction variations due to some genetic variations occurring at t₁, t₂,…, t_p; N(t) denotes a Poisson point (counting) process of genetic variation to be selected by natural selection at t_k, where k = 0, 1,…, p. Amongst these $s_1(t)\triangleq {\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)$ are selected by natural selection to change the interaction matrix A, in order to improve network robustness to resist an environmental disturbance v(t) due to the surrounding change and interference from other competitive populations. In addition, $s_2(t)\triangleq {\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$ are due to neutral genetic variations, which have no effect on A to directly change a phenotypic trait, ie, s(t) = s₁(t) + s₂(t) in the evolutionary process (Fig. 2). The Poisson counting process N(t) is denoted by

Figure 2.

(A) The Poisson counting process of genetic variations occurring at t_k in the evolutionary process, where t_p denotes the present time. (b) The Poisson counting process N(t) of genetic variations divided into two parts, (top) genetic variations N₁(t) selected by natural selection, and (bottom) neutral genetic variations N₂(t) in the evolutionary process.

$$N(t)=\sum _{k=1}^{N(t)}p(t-t_k)=\sum _{k=1}^{N(t)}1$$ (5)

with mean λt and variance λt.¹⁷ The matrix A ∈ ℝ ^n×n denotes the random phenotypic variation of the biological network due to the heritable genetic point variation p(t − t_k); occurring at t = t_k; ν(t) ∈ ℝ^n×m denotes the effect of environmental disturbances; and B ∈ ℝ^n×m denotes the coupling matrix between the environmental disturbance and the biological network,

$$\begin{array}{l}{A}_k=\left[\begin{array}{cccc}{a}_{k11}& \dots & \dots & a_{k1n}\\ ⋮& a_{22}& \hspace{0.17em}& ⋮\\ ⋮& \hspace{0.17em}& \ddots & ⋮\\ a_{kn1}& \dots & \dots & a_{knn}\end{array}\right],B=\left[\begin{array}{cccc}{b}_{11}& \dots & \dots & b_{1m}\\ ⋮& b_{22}& \hspace{0.17em}& ⋮\\ ⋮& \hspace{0.17em}& \ddots & ⋮\\ b_{m1}& \dots & \dots & b_{mn}\end{array}\right]\\ \upsilon (t)=\left[\begin{array}{c}{\upsilon }_1(t)\\ {\upsilon }_2(t)\\ ⋮\\ {\upsilon }_m(t)\end{array}\right],\end{array}$$ (6)

where a_kij = 0 if the kth genetic variation has no phenotypic effect on the interaction a_ij between species i and species j in the biological network; b_ij = 0 if the v_j(t) has no effect on the species i.

Remark 2

(i) The weighted Poisson point process $s(t)={\sum }_{k=1}^{N(t)}{A}_{k}p(t-t_k)={\sum }_{k=1}^{N(t)}{A}_k,t\ge 0$, denotes the heritable network interaction variations accumulated by the biological network, some of which are to be selected by natural selection to resist environmental disturbances in evolution. Since the weighted Poisson point process ${\sum }_{k=1}^{N(t)}{A}_{k}p(t-t_k)$ is a random process due to random genetic variations, the stochastic evolutionary network in (3) can represent a population of biological networks over all possible Poisson random genetic variations in the evolutionary process. In other words, one possible Poisson genetic variation represents one possible biological network in the network population. (ii) The accumulated phenotypic variations s(t) may lead to permanent changes in the phenotypic trait. (iii) v(t) denotes external disturbances due to environmental changes or stresses, such as temperature or salinity or interferences from other competitive populations. Environmental disturbance can perturb x(t) away from its phenotypic trait at the equilibrium point x_e = 0. Since the environmental disturbance v(t) cannot affect the interaction matrix A of the biological network directly, its effect on the biological network is non-heritable. In order to resist the effect of the environmental disturbance, some phenotypic variations $s_1(t)={\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)$ are to be selected for the biological network to change the network interaction matrix A by natural selection, to improve the network robustness (ie, the so-called evolutionary strategy of a biological network for phenotypic trait robustness in the evolutionary process). The remaining genetic variations $s_2(t)={\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$, which have no direct phenotypic effect on the network interaction matrix A, are called neutral genetic variations, ie, s(t) = s₁(t) + s₂(t) and N(t) = N₁(t) + N₂(t), where the Poisson processes N₁(t) and N₂(t) have means λ₁t and λ₂t, respectively, and λ = λ₁ + λ₂ (see Fig. 2(b)).

Therefore, the stochastic gene network under environmental disturbances and natural selection in (3) can be represented as the following Poisson point process

$$\begin{array}{l}\frac{dx(t)}{dt}=Ax(t)+\sum _{k=1}^{N(t)}{A}_{k}p(t-t_k)x(t)+B\upsilon (t)\\ =Ax(t)+s_1(t)x(t)+s_2(t)x(t)+B\upsilon (t)\\ =Ax(t)+u(t)+s_2(t)x(t)+B\upsilon (t),\end{array}$$ (7)

where $u(t)=s_1(t)x(t)={\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)x(t)$ denotes the evolutionary strategy of the biological network to select adequate phenotypic variations by natural selection to modify the network interaction matrix A, thus improving network robustness to tolerate the neutral genetic variations and resist the environmental disturbance, maintaining the phenotypic trait in the evolutionary process. The main evolutionary problem of the stochastic biological network in (7) for natural selection is how to determine the evolutionary strategy $u(t)=s_1(t)x(t)={\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)x(t)$, ie, how to select some adequate genetic variations to enhance system matrix A to improve the network robustness. This enables the biological network to tolerate the accumulated neutral genetic variations $s_2(t)={\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$ and efficiently resist the environmental disturbance v(t) to achieve phenotypic trait robustness in the evolutionary process. Since environmental disturbances are stochastic and unpredictable, the phenotypic robustness strategy u(t) of the biological network to resist the environmental disturbances is based on the worst-case effect of all possible environmental disturbances. Let us denote the set of all possible bounded environmental disturbances as L₂[0,t_p], ie, v(t) ∈ L₂[0,t_p] if ${\int }_0^{t_p}\upsilon {(t)}^T\hspace{0.17em}\upsilon (t)dt<\infty$, where t_p denotes the present time, ie, L₂ [0, t_p] denotes the set of all possible bounded environmental disturbances to the present time. (Unbounded environmental disturbances are not considered here because they will lead to the extinction of all biological networks.)

Remark 3

(i) The stochastic system in (7) can be considered a Darwinian dynamic to describe a linear dynamic biological network underlying natural selection. Darwinian dynamics are systems of equations that satisfy Darwin’s conditions of variability, heritability, and the strategy to survive.¹⁸ (ii) If the stochastic biological network in (7) is robustly stable at x_e = 0 (if x_e ≠ 0, then the origin of the linear dynamic network in (7) must be shifted to x_e for simplicity of analysis, ie, the phenotypic trait survives at x_e = 0), then the evolutionary strategy u(t) = s₁(t)x(t) is a robust evolutionary strategy by natural selection. The Poisson genetic variations ${\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)x(t)$ are not selected by natural selection, and are called neutral genetic variations without direct phenotypic effect on the system matrix A of the genetic network. These variations are further accumulated and harbored in the deeper basin around the phenotypic trait x_e of the robust biological network (see Fig. 1).

Let us denote the phenotypic deviation around x_e as x̃ (t) = x (t) − x_e. Then the evolution level of the stochastic biological network due to the effect of all possible bounded environmental disturbances in the evolutionary process is defined as

$$e=\underset{v(t)\in L_2[0,t_p]}{\text{max}}\frac{E{\int }_0^{t_p}\left(\tilde{x}{(t)}^T\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)\right)dt}{E\tilde{x}{(0)}^T\hspace{0.17em}\tilde{x}(0)+E{\int }_0^{t_p}v{(t)}^T\hspace{0.17em}v(t)dt},$$ (8)

where E(·) denotes the expectation of (·), Q is a positive definite weighting matrix, and t_p denotes the present time. The biological meaning of (8) is that the worst-case (maximum) effect of all possible bounded but unpredictable environmental disturbances on both phenotypic deviation around x_e and the evolutionary strategy u(t) is considered as the evolution level of the biological network on the basis of the average energy. Since the initial phenotypic deviation x̃(0) also has an effect on x̃(t) and u(t), its effect on the evolution level is considered in the denominator of (8). If x(0) = x_e or x̃(0) = 0, ie, the initial phenotypic trait x(0) is at the equilibrium point x_e, then the term Ex̃(0)^T x̃ (0) in the denominator should be neglected.

The fitness (phenotypic robustness) of the biological network around the phenotypic trait at the equilibrium point x_e is inversely correlated to the evolution level of the biological network and is defined as

$$f=\frac{1}{e}.$$ (9)

A biological network with a low evolution level will have a high fitness to the phenotypic trait, and vice versa. Therefore, the fitness maximization of a biological network to the phenotypic trait x_e is equivalent to the minimization of the evolution level, as follows,

$$\text{max\hspace{0.17em}}f=\frac{1}{\text{min\hspace{0.17em}}e}.$$ (10)

Combining (8) and (10), the evolutionary strategy u(t) for the maximization of the fitness of the biological network is formulated for the first time as the following stochastic minimax evolution (evolutionary game) problem

$$e_o\triangleq \underset{u(t)}{\text{mine}}=\underset{u(t)v(t)\in L_1[0,t_p]}{\text{min\hspace{0.28em}}\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{max}}\frac{e{\int }_0^{t_p}\left(\tilde{x}{(t)}^T\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)\right)dt}{E\tilde{x}{(0)}^T\hspace{0.17em}\tilde{x}(0)+E{\int }_0^{t_p}v{(t)}^T\hspace{0.17em}v(t)dt}.$$ (11)

The minimum evolution level e_o in (11) is called the network evolvability of the biological network in the evolutionary process. The physical meaning of network evolvability is the minimum worst-case effect of environmental disturbances on the biological network with a minimax evolutionary strategy u(t). The minimax evolutionary strategy is performed for the biological network by natural selection to resist unpredictable environmental disturbances from the point of view of the game in the evolutionary process. The minimax performance in (11) has been used for robust control design under intrinsic perturbations and external disturbances.^19,20 Therefore, the maximum phenotypic robustness (or fitness maximization) problem of the evolutionary biological network in (7) can be formulated as a stochastic evolutionary game problem in (11), ie, how to select $u(t)={\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)x(t)=s_1(t)x(t)$ to achieve the fitness maximization in (10) for the biological network in (7) with the phenotype at x_e. The evolutionary strategy of a biological network to maintain its phenotypic trait against intrinsic parameter fluctuations and environmental disturbances is to develop a feasible evolutionary strategy u(t) = s₁(t)x(t) to enhance the biological network with the maximum fitness at x_e, or equivalently, to select some genetic variations s₁(t) to modify the interaction matrix A of the biological network to minimize the worst-case (maximum) effect of environmental disturbance v(t) on both the variation of the phenotypic trait x̃(t) and the evolutionary strategy u(t) in (11) on the basis of mean energy.

Why is u(t) also considered in the numerator of (11) or (8)? The reason is that the biological network aims to achieve the maximum fitness f_o (or minimum evolution level e_o) with a minimum effort (or cost). This effort or cost can be described as change a change ${\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)$ on system matrix A of the biological network. There are two players, u(t) and v(t), in the evolutionary game problem in (11). The player v(t) will try to maximize the effect of environmental disturbances on the deviation of the phenotype from its equilibrium point x_e, and the other player u(t) will try to select some genetic variations to improve network robustness in order to maintain the phenotype around x_e by minimizing the worst-case phenotypic deviation due to all possible environmental disturbances. In general, it is very difficult to solve the stochastic evolutionary game problem in (11) for the stochastic gene network in (7). Therefore, the following indirect method is employed to solve the stochastic evolutionary game problem¹⁶

$$e_0=\underset{u(t)v(t)\in L_2[0,t_p]}{\text{min\hspace{0.28em}}\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{max}}\frac{E{\int }_0^{t_p}{\left(\tilde{x}(t)\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)\right)}^{T}dt}{E\tilde{x}{(0)}^T\tilde{x}(0)+E{\int }_0^{t_p}v{(t)}^T\hspace{0.17em}v(t)dt}\le e,$$ (12)

where the positive value e denotes the upper bound of the evolvability e_o. The upper bound e of e_o will be given beforehand and then decreased to as small a value as possible to approach e_o and attain the real minimax problem, which is the so-called suboptimal approach to the stochastic evolutionary game problem in (11). The suboptimal stochastic evolutionary game in (12) is equivalent to the following constrained stochastic Nash game^16,21,22

$$\underset{u(t)v(t)\in L_2[0,t_p]}{\text{min\hspace{0.28em}}\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{max}}E{\int }_0^{t_p}\left(\tilde{x}{(t)}^T\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)-ev{(t)}^T\hspace{0.17em}v(t)\right)dt\le eE\tilde{x}{(0)}^T\hspace{0.17em}\tilde{x}(0).$$ (13)

Let us denote

$$J\triangleq E{\int }_0^{t_p}\left(\tilde{x}{(t)}^T\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)-ev{(t)}^T\hspace{0.17em}v(t)\right)dt.$$ (14)

We then need two steps to solve the constrained stochastic game problem in (13). The first step is to solve the following stochastic Nash game problem

$$\begin{array}{l}{J}_o\triangleq \underset{u(t)v(t)\in L_2[0,t_p]}{\text{min\hspace{0.28em}}\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{max}}\hspace{0.17em}J=\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{v(t)}{\text{max}}\\ E{\int }_0^{t_p}\left(\tilde{x}{(t)}^T\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)-ev{(t)}^T\hspace{0.17em}v(t)\right)dt,\end{array}$$ (15)

and the second step is to solve the following constraint problem

$$J_o\le eE\tilde{x}{(0)}^T\hspace{0.17em}\tilde{x}(0).$$ (16)

By solving (15) and (16) for the constrained stochastic Nash game in (13), we get the following result.

Proposition 1

The stochastic evolutionary game problem of the evolutionary gene network in (13) can be solved by the following evolutionary strategy u^*(t) and the worst-case environmental disturbance v^*(t)

$$u^{*}(t)=s^{*}(t)x=\sum _{k=1}^{N_1(t)}{A}_{k}p(t-t_k)x=-Px,v^{*}(t)=\frac{1}{e}{B}^{T}Px,$$ (17)

where the positive definite matrix P is the solution of the following Riccati-like inequality

$$A^{T}P+PA-PP+\frac{1}{e}PB{B}^{T}P+Q+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_k^{T}P{A}_k\le 0\hspace{0.17em}and$$ (18)

$$0<P\le eI$$ (19)

where N_2p ≜ N₂ (t_p) represents the total number of neutral genetic variations to the present time t_p.

Proof

See Supplementary Data Appendix 1.1.

The term ${\lambda }_2{\sum }_{k=1}^{N_{2p}}{A}_k^{T}P{A}_k$ is the effect of random genetic variations that are not selected by evolutionary strategy, ie, the effect of neutral genetic mutations on the gene network in the evolutionary process. The solution of the evolutionary game in (17) is that based on the worst-case environmental disturbance v^*(t) on the biological network (due to the uncertainty and unpredictability of environmental disturbances, the evolutionary strategy u^*(t) needs to consider the effect of the worst-case disturbance v^*(t) from the game’s perspective), thus the minimax strategy is to select adequate genetic variations as new network interactions amounting to $s^{*}(t)={\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)={\sum }_{k=1}^{N_1(t)}{A}_k=-P$ to enhance the system matrix A, which can minimize the evolution level or maximize the fitness of the biological network with the phenotype at x_e. Since e is the upper bound of the evolvability e_o in the stochastic evolutionary game in (12), the minimum value of e in (12) will approach the evolvability $e_o=\frac{1}{f_o}$, where f_o is the maximum fitness of the biological network by the minimax evolutionary strategy. Therefore, we need to solve the following constrained optimization problem for e_o or f_o in the stochastic biological network in evolution

$$\frac{1}{f_o}=e_o\triangleq \underset{P>0}{\text{min}}\hspace{0.17em}e$$ (20)

subject to (18) and (19).

Remark 4

(i) The solution of e_o in (20) can be solved by decreasing e until no positive solution P > 0 exists in (18) and within 0 < P ≤ eI in (19). (ii) After solving e_o and f_o from (20), then the Riccati-like inequality in (18) becomes

$$A^{T}P+PA-PP+\frac{1}{e_o}PB{B}^{T}P+Q+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_k^{T}P{A}_k\le 0.$$ (21)

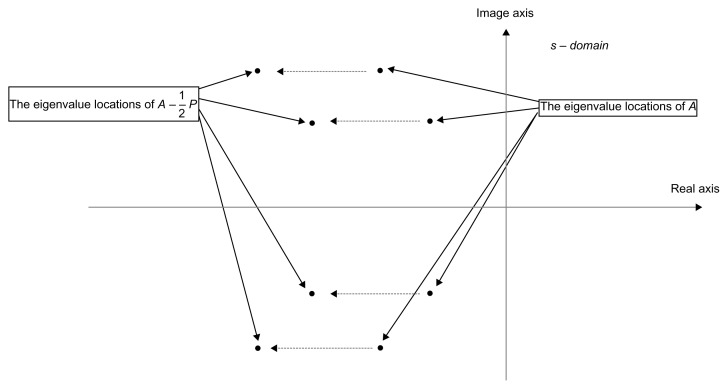
The inequality can be considered to be the phenotypic trait robustness criterion for the stochastic biological network (7) under the minimax (game) evolutionary strategy in the evolutionary process. For the nominal linear biological network in (1), if A^TP + PA ≤ 0 for some P > 0, then the biological network is stable based on Lyapunov stability, ie, all the eigenvalues of A have to be in the left-hand side of the complex s-domain (see Fig. 3). Therefore, −(A^TP + PA) is a measure of network robustness. The term ${\lambda }_2{\sum }_{k=1}^{N_{2p}}{A}_k^{T}P{A}_k$ is the effect of ${\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$ on the phenotypic trait robustness of the biological network. The term $\frac{1}{e_o}PB{B}^{T}P+Q$ is the effect of an environmental disturbance on the phenotypic trait robustness and a measure of the environmental robustness of the biological network. If the evolvability e_o is small, then the environmental robustness of the biological network should be large enough to resist the phenotypic effect of environmental changes and vice versa. The term −PP due to the evolutionary strategy u^*(t) = −Px (ie, $s^{*}(t)={\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)=-P$) could improve the phenotypic trait robustness in (21) by enhancing network robustness through negative feedback loops −Px as follows

Figure 3.

The eigenvalues of system matrix A in the evolution network are shifted further to the left-hand side of the s-domain by the evolutionary strategy u^* = −Px, ie, the eigenvalues of $A-\frac{1}{2}P$ are farther left than those of A.

$${\left(A-\frac{1}{2}P\right)}^{T}P+P\left(A-\frac{1}{2}P\right)+Q+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_k^{T}P{A}_k+f_{o}PB{B}^{T}P\le 0.$$ (22)

The eigenvalues of $\left(A-\frac{1}{2}P\right)$ are farther to the left of the complex s-domain than those of A, such that the network robustness of the biological network is improved (see Fig. 3). Although the selected phenotypic variations up to the amount −Px caused by the minimax evolutionary strategy can improve the network robustness, the accumulated random neutral genetic variations ${\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$ harbored in the robust genetic network during the evolutionary process can also lead to a negative effect on the phenotypic trait robustness of the biological network (ie, the term ${\lambda }_2{\sum }_{k=1}^{N_{2p}}{A}_k^{T}P{A}_k$will make the network robustness inequality in (22) more difficult to satisfy). In this situation, the phenotypic trait robustness criterion in (22) for the stochastic biological network in (3) under the minimax (game) evolutionary strategy in (11) can be reformulated as follows

$$\begin{array}{l}\underset{genetic\hspace{0.17em}robustness}{\underbrace{{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_k^{T}P{A}_k}}+\underset{environmental\hspace{0.17em}robustness}{\underbrace{Q+\frac{1}{e_o}PB{B}^T\hspace{0.17em}P}}\\ \le \underset{enbanced\hspace{0.17em}network\hspace{0.17em}robustness\hspace{0.17em}through\hspace{0.17em}the\hspace{0.17em}\mathit{minimax}\hspace{0.17em}evolutinary\hspace{0.17em}game\hspace{0.17em}strategy}{\underbrace{-\left[{(A-\frac{1}{2}P)}^{T}P+P(A-\frac{1}{2}P)\right]}}.\end{array}$$ (23)

The physical meaning of (23) is that if the enhanced network robustness of the biological network through the stochastic minimax (game) evolutionary strategy in (11) can confer both genetic robustness to tolerate random Poisson phenotypic variations due to the accumulated neutral genetic variations and environmental robustness to resist environmental disturbance, then the phenotypic trait of the biological network is maintained in the evolutionary process. Otherwise, the phenotypic trait may not be maintained under environmental disturbance and random genetic variations. In de Visser et al.²³ the evolutionary causes of genetic robustness were discussed, using different evolutionary criteria. The correlation with environmental robustness is considered to be the most probable cause of genetic robustness in evolution. From (23), based on the congruence scenario, it can be seen that the genetic robustness of a biological network is a by-product of the environmental robustness of the biological network. This is because environmental changes are more frequent than genetic variations in evolution, ie, when a biological network has developed network robustness to resist environmental disturbances, it would simultaneously provide genetic robustness to tolerate genetic variations.

(iii) By the stochastic minimax (game) evolutionary strategy in (11), the total accumulated network inter-action variations ${\sum }_{k=1}^{N_1(t)}{A}_{k}p(t-t_k)={\sum }_{k=1}^{N_1(t)}{A}_k$ are chosen by natural selection to the amount of −P to construct negative feedback loops −Px(t) in (17). The stochastic evolutionary biological network is thus of the following form

$$\frac{dx(t)}{dt}=(A-P)x(t)+\sum _{k=1}^{N_2(t)}{A}_{k}p(t-t_k)x(t)+B\upsilon (t).$$ (24)

Since the eigenvalues of A–P are in the farther left-hand side of the complex s-domain, the biological network has been made more robust by the minimax evolutionary strategy to resist all possible environmental disturbances in (24). (iv) An evolutionary biological network in (24) with greater network robustness in (23) will provide a greater buffer to harbor numerous neutral genetic variations simultaneously in the evolutionary process^1,2,4 (these neutral genetic variations ${\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$ have no obvious phenotypic effect on the system matrix A of the biological network). However, a large amount of neutral genetic variations may provide raw material for new evolutionary possibilities. Therefore, a robust biological network may finally lead to network evolution in the long run when the accumulated neutral genetic variations ${\sum }_{k=1}^{N_2(t)}{A}_{k}p(t-t_k)$ are large enough, ie, the term ${\lambda }_2{\sum }_{k=1}^{N_{2}p}{A}_k^{T}P{A}_k$ in (22) or (23) is large enough that the phenotypic trait robustness criterion is violated. (v) In order to provide a buffer against the accumulated neutral genetic variations and all possible environmental disturbances, a biological network needs to develop negative feedback loops to improve its network robustness. This is the minimax evolutionary strategy u*(t) = −Px, providing negative feedback loops to enhance network robustness in (22) or (23). Furthermore, hubs and redundant mechanisms are frequently found in biological networks to provide efficient responses to external stimuli and to attenuate the effect of genetic variations, respectively. They are therefore also favored by natural selection to improve the phenotypic trait robustness of the biological network in the evolutionary process. The evolutionary game strategy through negative feedback interactions u*(t) = −Px in a genetic network might result in these hubs and redundant mechanisms, in order to improve phenotypic trait robustness in the evolutionary process.

The Stochastic Game of Nonlinear Biological Network Evolution

In real biological networks, the system dynamics in (1) are always nonlinear and should be modified as follows

$$\frac{dx(t)}{dt}=f(x),$$ (25)

where f(x) denotes the nonlinear interactive vector among n different species in the biological network. For a nonlinear stochastic biological network with stochastic heritable random parameter fluctuations and non-heritable environmental disturbances in the evolutionary process, the stochastic biological network in (7) is modified as in the following Poisson point process

$$\begin{array}{l}\frac{dx(t)}{dt}=f(x)+\sum _{k=1}^{N(t)}{f}_k(x)p(t-t_k)+B\upsilon (t)\\ =f(x)+\sum _{k=1}^{N_1(t)}{f}_k(x)p(t-t_k)+\sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k)+B\upsilon (t)\\ =f(x)+u(t)+\sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k)+B\upsilon (t)\end{array}$$ (26)

with

$$\sum _{k=1}^{N(t)}{f}_k(x)p(t-t_k)=\sum _{k=1}^{N_1(t)}{f}_k(x)p(t-t_k)+\sum _{k=1}^{N_2(t)}{f}_k(x)p(t-t_k),$$

where f_k(x), for k = 1, 2,…, N(t), denotes the nonlinear stochastic heritable phenotypic variations due to Poisson random genetic variations in the evolutionary process. Sources of these random genetic variations include DNA mutation, deletion, recombination, duplication, inversion, and translocation of chromosomes in the evolutionary process. The nonlinear stochastic system in (26) represents a nonlinear biological net-work under the evolutionary strategy $u(t)={\sum }_{k=1}^{N_1(t)}{f}_k(x)p(t-t_k)$ by natural selection, the neutral genetic variations ${\sum }_{k=1}^{N_2(t)}{f}_k(x)p(t-t_k)$, and the environmental disturbances v(t) in the evolutionary process.

For the nonlinear stochastic biological network in (26), there exist many equilibrium points (phenotypic traits) (see Fig. 1). Suppose that the phenotypic trait near a stable equilibrium point x_e is of interest in natural selection. For convenience of analysis, the origin of the nonlinear stochastic biological network in (26) is shifted to the equilibrium point (phenotypic trait) x_e. In this case, if the shifted nonlinear stochastic network is robustly stable at the origin, then the equilibrium point (phenotypic trait) of interest in natural selection is also robustly stable. Therefore, the analysis of the minimax evolutionary strategy of the nonlinear stochastic biological network in evolution is simplified. Let us denote the phenotypic deviation around the phenotype at x_e as x̃(t) = x(t) − x_e, so then the following shifted nonlinear stochastic biological network is obtained

$$\begin{array}{l}\frac{d\tilde{x}(t)}{dt}=f(\tilde{x})+B\upsilon (t)+\sum _{k=1}^{N(t)}{f}_k(\tilde{x})p(t-t_k)\\ =f(\tilde{x})+B\upsilon (t)+u(t)+\sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k).\end{array}$$ (27)

For convenience of notation, we denote f(x̃+x_e) and f(x̃+x_e) as f(x̃) and f_k(x̃), respectively. In this situation, the origin x̃(t) = 0 of the nonlinear stochastic biological network in (27) is at the equilibrium point x_e of the original nonlinear stochastic network in (26), and $u(t)=s_1(\tilde{x})={\sum }_{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)$ denotes the evolutionary strategy of the biological network to select some phenotypic variations by natural selection to improve the network robustness, and thus tolerate the effect of neutral genetic variations ${\sum }_{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k)$, as well as to resist the environmental disturbances v(t). To maintain the robustness of the phenotypic trait at x_e, which is favored by natural selection, the robust evolution of the nonlinear stochastic biological network is to develop an evolutionary strategy u(t) to select some genetic variations to solve the stochastic minimax evolutionary game problem in (11) or (12). By considering the nonlinear stochastic minimax evolution problem (11) of the nonlinear stochastic biological network in (27), we get the following result.

Proposition 2

For the nonlinear stochastic biological network in (27), the nonlinear stochastic evolutionary game problem in (13) is solved by the following minimax evolutionary strategy u^*(t) and the worst-case environmental disturbance v^*(t)

$$\begin{array}{l}{u}^{*}(t)=s^{*}(\tilde{x})=\sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)=-\frac{1}{2}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right),\\ {\upsilon }^{*}(t)=\frac{1}{2e}{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right),\end{array}$$ (28)

where the positive function V(x̃) > 0 is the positive solution of the following (HJII)

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}f(\tilde{x})+{\tilde{x}}^{T}Q\tilde{x}-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\\ \frac{1}{4}{\left(\frac{\partial V(\overline{x})}{\partial \overline{x}}\right)}^T\hspace{0.17em}B{B}^T\left(\frac{\partial V(\overline{x})}{\partial \overline{x}}\right)+\\ \frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})\le 0\end{array}$$ (29)

$$\text{with\hspace{0.28em}}V(\tilde{x}(0))\le e\tilde{x}{(0)}^T\tilde{x}(0).$$ (30)

Proof

See Supplementary Data Appendix 1.2.

The last term in (29) is the effect of random neutral genetic variations, which are not selected by natural selection but are harbored by network robustness in the evolutionary process.^10,11 The biological meaning of the evolutionary strategy in (28) is that the worst-case environmental disturbance v^*(t) represents the worst-case effect of all possible uncertain environmental disturbances on both the phenotypic deviation and the evolutionary strategy of the biological network in the stochastic game (12). In addition, the minimax evolutionary game strategy u^*(t) in (28) denotes that, if the number of phenotypic variations selected by natural selection is equal to the number of negative feedback loops $-\frac{1}{2}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)$, then the worst-case effect of all possible environmental disturbances on the phenotypic trait will be minimized; ie, the phenotypic trait of the biological network will achieve the maximum fitness or the minimum evolution of x_e in (12) or (20). Since e is the upper bound of the evolvability e_o of the stochastic evolutionary network in (12), e_o could be approached for the nonlinear stochastic evolutionary network in (26) by minimizing its upper bound e as follows

$$\begin{array}{l}\frac{1}{f_o}=e_o=\underset{V(\tilde{x})>0}{\text{min}}\hspace{0.17em}e\\ \text{subject\hspace{0.17em}to\hspace{0.17em}}(29)\text{and}(30).\end{array}$$ (31)

Remark 5

(i) In general, the solution of the network evolvability e_o in (31) could be obtained by decreasing e until the HJII in (29) has no positive solution V(χ̄) > 0. (ii) After solving f_o and e_o in (31), then the HJII in (29) can be modified as

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}f(\tilde{x})+{\tilde{x}}^{T}Q\tilde{x}-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\frac{1}{4e_o}{\left(\frac{\partial V(\overline{x})}{\partial \overline{x}}\right)}^T\hspace{0.17em}B{B}^T\left(\frac{\partial V(\overline{x})}{\partial \overline{x}}\right)+\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})\le 0$$ (32)

with V (x̃(0)) ≤ e_o x̃ (0)^T x̃ (0). This HJII can be considered as the phenotypic trait robustness criterion of the nonlinear stochastic biological network in (27) with the minimax evolutionary game strategy u^*(t) in the evolutionary process. The term $\frac{1}{4e_o}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)$ is due to the effect of environmental disturbances on the biological network, and is considered as a measure of environmental robustness. The term $\frac{1}{2}{\lambda }_2{\sum }_{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})$ is the random effect of the accumulated random neutral genetic variations on the biological network in the evolutionary process. The term $-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)$ is due to the mini-max evolutionary game strategy u^*(t), ie, the robust effect of phenotypic variations ${\sum }_{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)$, which are selected by natural selection to construct the negative feedback loops $-\frac{1}{2}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)$ to minimize the worst-case effect of all possible environmental disturbances. When the biological network is free of genetic fluctuations, environmental disturbances, and the evolutionary game strategy as in (25), ie, in the nominal nonlinear network case in (25), the Lyapunov stability criterion at the equilibrium x_e is ${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}f(\tilde{x})\le 0$, and ${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}f(\tilde{x})$ can be considered as the measure of phenotypic stability of x_e for the nominal biological network in (25). With the minimax evolutionary game strategy u^*(t) to improve the network robust stability of the biological network in (26) and to maintain the phenotype at x_e in order to resist the effects of genetic variations and environmental disturbances, the phenotypic trait robustness criterion of the evolutionary biological network in (32) can be rewritten as follows

$$\begin{array}{l}\underset{genetic\hspace{0.17em}robustness}{\underbrace{\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})}}+\\ \underset{environmental\hspace{0.17em}robustness}{\underbrace{{\tilde{x}}^{T}Q\tilde{x}+\frac{1}{4e_o}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}}\\ \le \underset{network\hspace{0.17em}robustness\hspace{0.17em}through\hspace{0.17em}the\hspace{0.17em}minimax\hspace{0.17em}evolutionary\hspace{0.17em}game\hspace{0.17em}strategy}{\underbrace{-{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x})-\frac{1}{4}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)}}\end{array}$$ (33)

From the right-hand side of (33), it is apparent that the minimax evolutionary game strategy can improve the network robustness in the evolutionary process by making ${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\times \left(f(\tilde{x})-\frac{1}{4}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)$ more negative, letting the basin of the phenotypic trait at x_e become much deeper and wider in Figure 1. The physical meaning of the phenotypic trait robustness criterion in (33) is that if the enhanced network robustness by the mini-max evolutionary game strategy can confer enough genetic robustness to buffer random neutral genetic variations and enough environmental robustness to resist environmental disturbances, then the phenotypic trait of the nonlinear stochastic biological network in (27) is maintained in the evolutionary process. By substituting the minimax evolutionary game strategy u^*(t) into the nonlinear stochastic biological network in (27), we get

$$\frac{d\tilde{x}(t)}{dt}=\left(f(\tilde{x})-\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+B\upsilon (t)+\sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k).$$ (34)

Since the term $f(\tilde{x})-\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}$ will make the nonlinear stochastic biological network more robustly stable than f(x̃) due to the negative feedback $-\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}$ the biological network with the minimax evolutionary strategy will be more robust to tolerate the random neutral genetic variations and to resist the environmental disturbances v(t) in (34) in the evolutionary process. (iii) If the network robustness on the right-hand side of (33) is improved by the minimax evolutionary game strategy so that the genetic robustness is increased, then the nonlinear biological network can harbor a large amount of neutral genetic variations. If the stochastic neutral genetic variations are accumulated in a sufficiently large amount in (27) or (34) in the evolutionary process, so that the phenotypic trait robustness criterion in (33) may finally be violated, then they may provide raw material for a new evolutionary possibility, causing a transition from one phenotypic trait to another through genetic drift;^6,7 for example, from the basin x_e to another basin x_1e in Figure 1. At first sight, one might expect an evolutionary strategy to significantly improve network robustness to slow or even stop the evolution of a phenotypic trait in a biological network, but, because the more robust phenotypic trait can harbor a large number of neutral genetic variations, the robust phenotypic trait of the stochastic biological network might show increased rather than decreased evolutionary potential, in the long term of the biological network’s evolution. The reasons why increasing network robustness may eventually lead to increasing network evolution include the accumulation of hidden neutral genetic variations that may be useful for later evolution. This is why network robustness is intrinsic to evolution and can eventually improve evolution.^5,6 This study extends these evolution results from the genetic level to the nonlinear stochastic gene network level, using the systematic methods in (32) and (33) from the point of the view of a stochastic evolutionary game. (iv) The tradeoff between network robustness and the evolvability of the nonlinear stochastic biological network in evolution can be seen from the phenotypic trait robustness criterion in (33); ie, genetic robustness plus environmental robustness is less than or equal to network robustness. In this phenotypic trait robustness criterion, if the biological network has less evolvability (a small e_o or a large fitness f_o) in evolution, then its environmental robustness becomes larger. In this situation, the network robustness has to be enough large to confer a large environmental robustness to resist environmental disturbances in order to maintain the phenotypic trait robustness, ie, less evolvability implies a larger network robustness, and vice versa. (v) In general, the cost of the minimax evolutionary strategy in selecting phenotypic variations as negative feedback loops $u^{*}(t)=-\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}$ in order to improve network robustness and resist environmental disturbances is much higher.²⁴ In the case of the stress-avoidance strategy (u(t) = 0), the basin of the equilibrium point x_e in Figure 1 becomes shallow, ie, the term ${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(f(\tilde{x})-\frac{1}{4}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)$ on the right-hand side of (33) is reduced to ${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}f(\tilde{x})$ and is less negative. In this case, network robustness becomes smaller and environmental robustness must also be smaller in evolution, so that the evolvability e_o will become larger and the biological network will be more adaptive in responding to environmental stresses and rapid environmental changes.²⁴

The Stochastic Evolutionary Game of the Nonlinear Stochastic Biological Network Based on the Global Linearization Method

In general, it is still very difficult to solve the HJII-constrained optimization problem in (31) for the stochastic minimax evolutionary strategy in a nonlinear stochastic biological network in evolution or the HJII problem in (33) for the phenotypic trait robustness criterion of a nonlinear stochastic biological network under natural selection in evolution. At present, there is no good method to solve the nonlinear partial differential HJII problem either analytically or numerically.^19,25,27 In this case, in order to simplify the stochastic evolutionary game problem, the global linearization technique^28,29 is employed to interpolate a nonlinear stochastic biological network with a set of local stochastic linearized biological networks.

Using the global linearization method, we suppose that all the global linearizations of the nonlinear stochastic biological network in (27) are bounded by a polytope, consisting of M vertices as^28,29

$$\left[\begin{array}{c}\frac{\partial f(\tilde{x})}{\partial \tilde{x}}\\ \frac{\partial f_1(\tilde{x})}{\partial \tilde{x}}\\ ⋮\\ \frac{\partial f_{N(t)}(\tilde{x})}{\partial \tilde{x}}\end{array}\right]\in C_0\left[\left[\begin{array}{c}{A}_1\\ A_{11}\\ ⋮\\ A_{N(t)1}\end{array}\right]\cdots \left[\begin{array}{c}{A}_i\\ A_{1i}\\ ⋮\\ A_{N(t)i}\end{array}\right]\cdots \left[\begin{array}{c}{A}_M\\ A_{1M}\\ ⋮\\ A_{N(t)M}\end{array}\right]\right],\forall \tilde{x}(t),$$ (35)

where C₀ denotes the convex hull of the polytope with M vertices. That is, if the local linearized systems at all x̃ are inside the convex hull C₀, then the evolutionary trajectory χ̄ of the nonlinear stochastic evolutionary network in (27) will belong to the convex combination of the stable trajectories of the following M local linearized networks, defined at M vertices of the polytope^28,29

$$\frac{d\tilde{x}(t)}{dt}=A_i\tilde{x}+B\upsilon (t)+u(t)+\sum _{k=1}^{N_2(t)}{A}_{ki}p(t-t_k)\tilde{x},\hspace{0.17em}i=1,\dots ,M.$$ (36)

Based on the global linearization theory,²⁹ if (35) holds, then every evolutionary trajectory of the nonlinear stochastic biological network in (27) can be represented by a convex combination of the M local linearized biological networks in (36). This combination can be represented by

$$\frac{d\tilde{x}(t)}{dt}=\sum _{i=1}^M{\alpha }_i(\tilde{x})\left(A_i\tilde{x}+B\upsilon (t)+u(t)+\sum _{k=1}^{N_2(t)}{A}_{ki}p(t-t_k)\tilde{x}\right),$$ (37)

where the interpolation function α_i(x̃) satisfies 0 ≤ α_i(x̃) ≤ 1 and ${\sum }_{i=1}^M{\alpha }_i(\tilde{x})=1$, ie, the evolu-tionary trajectory of the nonlinear stochastic biological network in (27) can be represented by the evolutionary trajectory of the interpolated biological network in (37). In (37), the evolutionary strategy $u(t)={\sum }_{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)$ can be constructed as ${\sum }_{i=1}^M{\sum }_{k=1}^{N_1(t)}{\alpha }_i(\tilde{x})A_{ki}p(t-t_k)\tilde{x}$ by the global linearization technique. For the minimax evolutionary strategy problem (11) of the interpolated evolutionary biological network in (37), we get the following result.

Proposition 3

For the interpolated evolutionary biological network in (37), the stochastic evolutionary game problem in (13) is solved by the following minimax evolutionary strategy u^*(t) and the worst-case environmental disturbance v^*(t)

$$u^{*}(t)=\sum _{i=1}^M\sum _{k=1}^{N_1(t)}{\alpha }_i(\tilde{x})A_{ki}p(t-t_k)\tilde{x}=-P\tilde{x},\hspace{0.17em}{\upsilon }^{*}(t)=\frac{1}{e}{B}^{T}P\tilde{x},$$ (38)

where the positive definite matrix P is the solution of the following Riccati-like inequalities

$$A_i^{T}P+P{A}_i+Q-PP+\underset{i=1,\dots ,M}{\frac{1}{e}PB{B}^{T}P}+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_{ki}^{T}P{A}_{ki}\le 0,$$ (39)

$$0<P\le eI$$ (40)

Proof

See Supplementary Data Appendix 1.3.

Remark 6

(i) In comparison with Proposition 1 of the stochastic linear biological network, the Riccati-like inequality in (18) is based only on the local linearized network at x̃ (t) = 0, while the Riccati-like inequalities in (39) are based on M local linearized networks in (36) at the M vertices of the polytope in (35). Therefore, the result of the minimax evolutionary game strategy in Proposition 3 is more suitable for nonlinear stochastic biological networks in evolution. (ii) The Riccati-like inequalities in (39) can be considered as the local linearized HJII in (29) at M vertices of the polytope in (35). In general, it is very difficult to solve the HJII. However, it is very easy to solve the Riccati-like inequalities in (39) by transforming (39) into equivalent linear matrix inequalities (LMIs)

$$\left[\begin{array}{ccccc}X{A}_i^T+A_{i}X-I+\frac{1}{e}B{B}^T& X& X{A}_{1i}^T& \cdots & X{A}_{N_{2p}i}^T\\ X& -Q^{-1}& 0& \cdots & 0\\ A_{1i}X& 0& -\frac{1}{{\lambda }_2}X& \ddots & ⋮\\ ⋮& ⋮& \ddots & \ddots & 0\\ A_{N_{2p}i}X& 0& \cdots & 0& -\frac{1}{{\lambda }_2}X\end{array}\right]\le 0$$ (41)

and X ≜ P⁻¹ > 0, for i = 1,…,M,

using the Schur complement transformation method.²⁹ These can be easily solved by the LMI toolbox in Matlab.

Since e in (39) is the upper bound of the evolvability of the evolutionary game in (12), the minimum value of e will approach the evolvability $e_o=\frac{1}{f_o}$. Therefore, we need to solve the following constrained optimization problem for e_o or f_o in the nonlinear stochastic biological network in evolution

$$\frac{1}{f_o}=e_o=\underset{P>0}{\text{min\hspace{0.17em}}e}$$ (42)

subject to (40) and (41).

Remark 7

(i) The e_o can be solved by decreasing e until (41) has no positive solution P within 0 < P ≤ eI with the help of the LMI toolbox in Matlab. (ii) After solving e_o and f_o from (42), the Riccati-like inequalities in (39) and (40) then need to be modified as

$$\begin{array}{c}{A}_i^{T}P+P{A}_i+Q-PP+\frac{1}{e_o}PB{B}^{T}P+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_{ki}^{T}P{A}_{ki}\le 0,\\ i=1,\dots ,M\end{array}$$ (43)

$$0<P\le e_{o}I.$$ (44)

After solving P in (43), then u* (t) = −Px̃ and $v^{*}(t)=\frac{1}{e_o}{B}^{T}P\tilde{x}$ in (38) form the minimax evolutionary strategy in (11) for the nonlinear stochastic biological network in evolution. (iii) With the minimax evolutionary strategy, the Riccati-like inequalities in (43) and (44) can be considered as the phenotypic trait robustness criteria of the biological network in evolution. If (43) and (44) are satisfied, then the phenotypic trait of the nonlinear stochastic biological network in (27) or (37) is maintained in the basin around the equilibrium point x_e under environmental disturbances and neutral genetic variations in the evolutionary process. If (43) and (44) have no positive solution P with 0 < P ≤ e_oI, then the phenotypic trait at x_e might not exist again or might transit to another phenotypic trait at another equilibrium point under environmental disturbances and genetic variations in evolution. (iii) The minimax evolutionary strategy u^*(t) in (38) can enhance network robustness by shifting the eigenvalues of the local linear networks farther to the far left-hand side of the s-complex domain as follows

$${(A_i-\frac{1}{2}P)}^{T}P+P(A_i-\frac{1}{2}P)+Q+\frac{1}{e_o}PB{B}^{T}P+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_{ki}^{T}P{A}_{ki}\le 0,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }i=1,\dots ,M.$$ (45)

That is, every interaction matrix so that A_i of the local linearized biological networks is shifted by $-\frac{1}{2}P$ so that eigenvalues of $\left(A_i-\frac{1}{2}P\right)$ are on the farther left-hand side of the s-complex domain, and thus the evolutionary network is more robust to simultaneously tolerate local genetic variations and resist environmental disturbances. In general, the minimax evolutionary game strategy is to select the total network variations ${\sum }_{i=1}^M{\sum }_{k=1}^{N_1(t)}{\alpha }_i(\overline{x})\hspace{0.17em}{A}_{ki}p(t-t_k)=-P$, which consist of negative feedback loops for some positive matrix P. This is in order to select adequate genetic variations to form negative feedback circuits in the biological network, so as to improve network robustness by resisting environmental disturbances and attenuating the effects of neutral genetic variation in the evolutionary process. (iv) The phenotypic trait robustness criterion in (45) can be reformulated as follows

$$\begin{array}{l}\underset{local\hspace{0.17em}genetic\hspace{0.17em}robustness}{\underbrace{{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_{ki}^{T}P{A}_{ki}}}+\underset{local\hspace{0.17em}environmental\hspace{0.17em}robustness}{\underbrace{Q+\frac{1}{e_o}PB{B}^{T}P}}\\ \le \underset{local\hspace{0.17em}network\hspace{0.17em}robustness\hspace{0.17em}through\hspace{0.17em}the\hspace{0.17em}minimax\hspace{0.17em}evolutionary\hspace{0.17em}game\hspace{0.17em}strategy}{\underbrace{-\left[{(A_i-\frac{1}{2}P)}^{T}P+P(A_i-\frac{1}{2}P)\right]}},i=1,\dots ,M.\end{array}$$ (46)

The biological meaning in (46) is that if the enhanced local network robustness of each local linearized biological network by the minimax evolutionary game strategy can confer both local neutral genetic robustness to buffer local genetic variations and local environmental robustness to resist the local environmental disturbance in evolution, then the phenotypic trait of the nonlinear stochastic biological network with the minimax evolutionary game strategy can be maintained in the basin of the equilibrium point at x_e in the evolutionary process. (v) Since the minimax evolutionary game strategy can improve the local network robustness of local linearized networks on the right-hand side of (46), the nonlinear stochastic biological network will harbor more neutral genetic variations and will have greater environmental robustness to decrease the evolvability e_o (or increase the fitness f_o) to attenuate the effect of environmental stimulus. However, when the harbored neutral genetic variations are accumulated to the extent that the first term on the left-hand side of (46) becomes very large and the phenotypic robustness criterion in (46) cannot be guaranteed in the evolutionary process the phenotype of the biological network might be shifted, with the help of an environmental disturbance, from one equilibrium point to another equilibrium point in Figure 1 and start another period of network evolution at the other equilibrium point (phenotype) favored by natural selection.

Remark 8

If we consider that network evolution can only be plausibly studied at a population level, the evolutionary game should naturally invoke an n-tuple game with m-players under k environmental dynamics. In this n-tuple evolutionary game problem, the linear stochastic biological network in (7) should be modified as

$$\begin{array}{l}\frac{dx(t)}{dt}=Ax(t)+u(t)+s_2(t)x(t)+\\ \sum _{i=1}^m{B}_i{u}_i(t)+\sum _{j=1}^k{D}_j{v}_j(t),\end{array}$$ (47)

where u_i(t) denotes the ith decision variable from other players (ie, other competitive populations) and v_j(t) denotes the jth environmental dynamics. Further, the evolutionary game problem in (11) should be modified as the following n-tuple evolutionary game

$$\underset{u(t)}{\text{min}}\underset{\begin{array}{l}{u}_i(t),i=1,\dots ,m\\ v_j(t),j=1,\dots ,k\end{array}}{\text{max}}\frac{E{\int }_0^{t_p}\left(\tilde{x}{(t)}^{T}Q\tilde{x}(t)+u{(t)}^{T}u(t)\right)dt}{E\tilde{x}{(0)}^T\hspace{0.17em}\tilde{x}(0)+E{\sum }_{i=1}^m{\int }_0^{t_p}{u}_i{(t)}^T\hspace{0.17em}{u}_i(t)dt+E{\sum }_{j=1}^k{\int }_0^{t_p}{v}_j{(t)}^T\hspace{0.17em}{v}_j(t)dt},$$ (48)

The decision variables u_i(t) from other players and v_j(t) from environmental dynamics are decided to maximize their effect on the phenotypic deviation x̃ (t) and evolutionary strategy u(t) of the evolutionary network while the evolutionary strategy u(t) is decided by the evolutionary network to minimize the worst-case phenotypic deviation and the effort (or cost) of evolutionary strategy. For simplicity of solving this n-tuple evolutionary game in the evolutionary network problem, the stochastic network dynamics in (47) can be represented by

$$\frac{dx(t)}{dt}=Ax(t)+u(t)+s_2(t)x(t)+BV(t),$$ (49)

where

$$\begin{array}{l}B\triangleq \left[\begin{array}{cccccccc}{B}_1& B_2& \cdots & B_m& D_1& D_2& \cdots & D_k\end{array}\right],\\ V(t)\triangleq \left[\begin{array}{cccccccc}{u}_1(t)& u_2(t)& \cdots & u_m(t)& v_1(t)& v_2(t)& \cdots & v_k(t)\end{array}\right].\end{array}$$

In this situation, the n-tuple game in (48) is reduced to the 2-tuple game in (11), ie, the decision variable v(t) of the 2-tuple game in (11) can represent V (t) of m-players and k environmental dynamics in (47) and the n-tuple evolutionary game problem in (48) can be replaced by the 2-tuple evolutionary game in (11). Similarly, the result of the nonlinear stochastic evolutionary game problems in (26) and (11) can be easily extended to an n-tuple game problem of nonlinear stochastic network with m-players (populations) and k environmental dynamics. Therefore, the proposed theoretical approach to evolutionary game strategy naturally invokes an n-tuple game with m competitive populations and k environmental disturbances if B and V (t) in (7) can be replaced by B = [B₁ B₂… B_m D₁ D₂… D_k] and V (t) = [u₁(t) u₂(t)… u_m(t) v₁(t) v₂(t)… v_k(t)] of the evolutionary network in (49), respectively.

Simulation Example

Consider the generic inhibition and activation model in evolution in Figure 4, which is a known metabolic pathway and has been widely used for imitating characteristics of a real metabolic pathway.^30,31 In this metabolic pathway, the metabolite X₃ converted from the metabolite X₂ inhibits an early step in its own production pathway, which is the synthesis of X₁. The metabolite X₂ is converted from the metabolite X₁, which is a divergence branching point. The degradation processes of X₁ into X₂ or X₄ are independent of each other. Then, the metabolite X₄ modulates downstream to activate the transformation of X₃. Let’s denote x₁(t), x₂(t), x₃(t), and x₄(t) as the concentrations of metabolites X₁, X₂, X₃, and X₄, respectively. Based on the metabolic pathway^30,31 in evolution in Figure 4, we have the following metabolic reaction network

Figure 4.

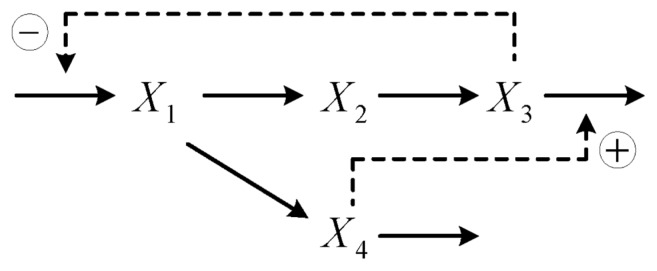
A real branched metabolic pathway of the generic inhibition and activation model where X₁,…, X₄ are metabolites.

$$\begin{array}{l}\left[\begin{array}{c}\frac{d{x}_1\hspace{0.17em}(t)}{dt}\\ \frac{d{x}_2\hspace{0.17em}(t)}{dt}\\ \frac{d{x}_3\hspace{0.17em}(t)}{dt}\\ \frac{d{x}_4\hspace{0.17em}(t)}{dt}\end{array}\right]=\left[\begin{array}{c}{f}_1\hspace{0.17em}(x)\\ f_2\hspace{0.17em}(x)\\ f_3\hspace{0.17em}(x)\\ f_4\hspace{0.17em}(x)\end{array}\right]+\sum _{k=1}^{N_1(t)}\left[\begin{array}{cccc}{\lambda }_{11k}& {\lambda }_{12k}& \cdots & {\lambda }_{14k}\\ {\lambda }_{21k}& {\lambda }_{22k}& \cdots & {\lambda }_{24k}\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{41k}& {\lambda }_{42k}& \cdots & {\lambda }_{44k}\end{array}\right]\\ \left[\begin{array}{c}{x}_1\hspace{0.17em}(t)\\ x_2\hspace{0.17em}(t)\\ x_3\hspace{0.17em}(t)\\ x_4\hspace{0.17em}(t)\end{array}\right]p(t-t_k)+\sum _{k=1}^{N_2(t)}\left[\begin{array}{c}{\lambda }_{1k}\times {\alpha }_1{x}_3^{g_{13}}(t)\\ {\lambda }_{2k}\times {\alpha }_2{x}_3^{g_{21}}(t)\\ {\lambda }_{3k}\times {\alpha }_3{x}_2^{g_{32}}(t)\\ {\lambda }_{4k}\times {\alpha }_4{x}_1^{g_{41}}(t)\end{array}\right]p(t-t_k)+\left[\begin{array}{c}{v}_1\hspace{0.17em}(t)\\ v_2\hspace{0.17em}(t)\\ v_3\hspace{0.17em}(t)\\ v_4\hspace{0.17em}(t)\end{array}\right]\end{array}$$ (50)

with

$$f(x)\triangleq \left[\begin{array}{c}{f}_1\hspace{0.17em}(x)\\ f_2\hspace{0.17em}(x)\\ f_3\hspace{0.17em}(x)\\ f_4\hspace{0.17em}(x)\end{array}\right]\triangleq \left[\begin{array}{c}{\alpha }_1{x}_3^{g_{13}}(t)-{\beta }_1{x}_1^{b_{11}}(t)\\ {\alpha }_2{x}_1^{g_{21}}(t)-{\beta }_2{x}_2^{b_{22}}(t)\\ {\alpha }_3{x}_2^{g_{32}}(t)-{\beta }_3{x}_3^{b_{33}}(t)x_4^{b_{34}}(t)\\ {\alpha }_4{x}_1^{g_{41}}(t)-{\beta }_4{x}_4^{b_{44}}(t)\end{array}\right].$$

where α₁,…, α₄ and β₁,…, β₄ are the rate constants of net influxes and effluxes with kinetic orders g_ij and h_ij, i, j ∈ S and S = ≜ {1,2,3,4}. The parameters λ_1k,…, λ_4k are represented as weights of the random phenotypic variations of the biological network, which have no direct phenotypic effect on the network. The parameters of this metabolic reaction network are chosen as follows:

$$\begin{array}{l}{\alpha }_1=12;{\alpha }_2=8;{\alpha }_3=3;{\alpha }_4=2;{\beta }_1=10;{\beta }_2=3;{\beta }_3=5;\\ {\beta }_4=6;g_{13}=-0.8;g_{21}=0.5;g_{32}=0.75;g_{41}=0.5;\\ h_{11}=0.5;h_{22}=0.75;h_{33}=0.5;h_{34}=0.2;h_{44}=0.8;\\ E{V}_{ik}=V=0.1;E{V}_{ik}^2=0.04;E{\lambda }_{ik}=0.1;E{\lambda }_{ik}^2=\mathrm{0.04.}\end{array}$$

The mean of the Poisson process p(t) is imposed on λ = 0.01. The equilibrium point x_e of the nominal metabolic reaction network is [ x_e1, x_e2, x_e3, x_e4]^T ≃ [0.400, 2.006, 2.228, 0.143]^T simulated from the initial condition x(0) ≜ [1.4, 2.25, 1.25, 0.45]^T. For simplicity of analysis, the state of the network is shifted via the form x̃ (t) = x (t) −x_e. Thus, the new equilibrium point of the phenotype concerned is at x̃_e = 0_4×1 throughout this simulation example.

Based on the above evolutionary game strategy, the following phenotypic variations in the network in (50)

$$\sum _{k=1}^{N_1(t)}\left[\begin{array}{cccc}{\lambda }_{11k}& {\lambda }_{12k}& \cdots & {\lambda }_{14k}\\ {\lambda }_{21k}& {\lambda }_{22k}& \cdots & {\lambda }_{24k}\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{41k}& {\lambda }_{42k}& \cdots & {\lambda }_{44k}\end{array}\right]\hspace{0.17em}\left[\begin{array}{c}{\tilde{x}}_1(t)\\ {\tilde{x}}_2(t)\\ {\tilde{x}}_3(t)\\ {\tilde{x}}_4(t)\end{array}\right]\hspace{0.17em}p(t-t_k)$$ (51)

are selected by natural selection to construct negative feedback circuits to modify the metabolic reaction network, in order to resist environmental disturbance and tolerate the following effect due to neutral genetic variations

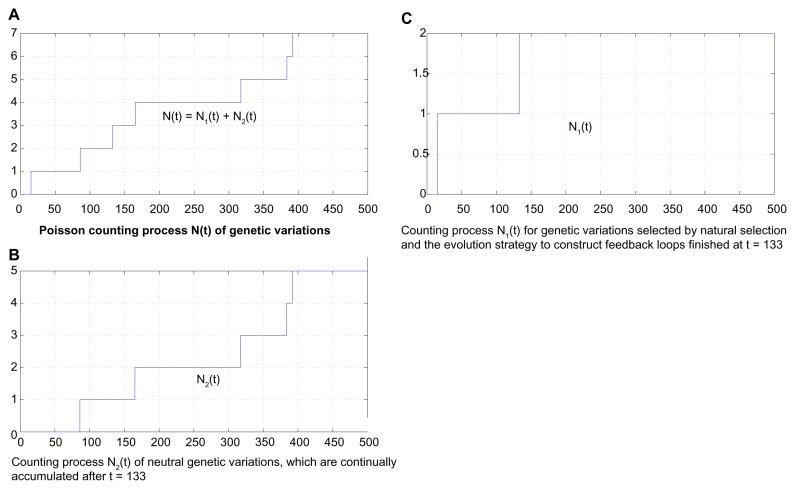
$$\sum _{k=1}^{N_2(t)}\left[\begin{array}{c}{\lambda }_{1k}\times {\alpha }_1{x}_3^{g_{13}}(t)\\ {\lambda }_{2k}\times {\alpha }_2{x}_3^{g_{21}}(t)\\ {\lambda }_{3k}\times {\alpha }_3{x}_2^{g_{32}}(t)\\ {\lambda }_{4k}\times {\alpha }_4{x}_1^{g_{41}}(t)\end{array}\right]p(t-t_k),$$ (52)

where the Poisson counting process N(t) = N₁(t) + N₂(t) for genetic variations in the evolutionary process is described in Figure 6. The evolutionary game strategy in Proposition 3 is to select genetic variations to construct the following negative feedback loops to improve the network robustness

Figure 6.

Poisson counting processes of genetic variations in the evolutionary process, for (A) N(t) = N₁(t) + N₂(t). (B) N₁(t), denoting the counting process of genetic variations selected for constructing negative feedback loops u* =−Px̃ by natural selection. (C) N₂(t), denoting the neutral genetic variations harbored by the robust network, without direct effect on the network phenotype.

$$\begin{array}{l}{u}^{*}(t)=\sum _{k=1}^{N_1(t)}\left[\begin{array}{cccc}{\lambda }_{11k}& {\lambda }_{12k}& \cdots & {\lambda }_{14k}\\ {\lambda }_{21k}& {\lambda }_{22k}& \cdots & {\lambda }_{24k}\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{41k}& {\lambda }_{42k}& \cdots & {\lambda }_{44k}\end{array}\right]\hspace{0.17em}\left[\begin{array}{c}{\tilde{x}}_1\hspace{0.17em}(t)\\ {\tilde{x}}_2\hspace{0.17em}(t)\\ {\tilde{x}}_3\hspace{0.17em}(t)\\ {\tilde{x}}_4\hspace{0.17em}(t)\end{array}\right]p(t-t_k)\\ =-P\tilde{x}(t),\end{array}$$ (53)

where P is solved from the constrained optimization problem in (42). Based on the minimax game, the global linearization technique and the LMI toolbox in Matlab, the following result is obtained

$$P\simeq {10}^{-4}\times \left[\begin{array}{cccc}1.352& 0.039& -0.290& 0.116\\ *& 0.003& -0.003& -0.008\\ *& *& 0.074& -0.050\\ *& *& *& 0.064\end{array}\right].$$ (54)

We also find the evolvability e_o ≃ 0.7843 and the maximum fitness f_e ≃ 1.2750. The simulation result of the metabolic reaction network with the evolutionary game strategy is shown in Figure 5. It can be seen that the phenotypic trait of the metabolic reaction network is maintained at the equilibrium point x̃_e = 0_4×1 or x_e ≃ [0.400, 2.006, 2.228, 0.143]^T for a period of time from t = 0 to t = 383 in Figure 5, and the evolvability of the metabolic reaction network by the evolutionary game strategy in this period is estimated with v_i(t), i = 1,…, 4, standard white noises, by a Monte Carlo simulation with 10000 runs, as follows

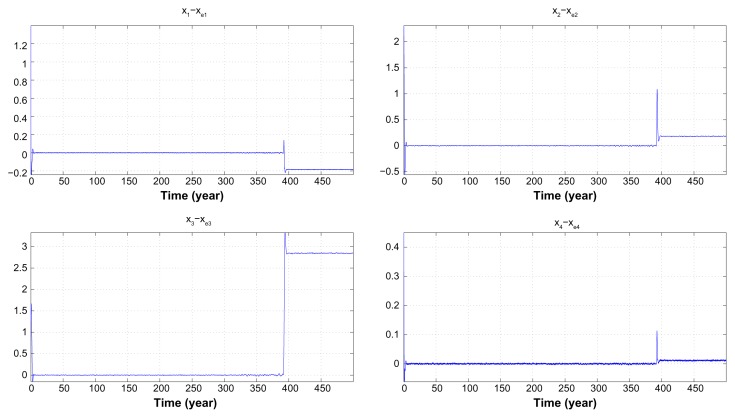
Figure 5.

The trajectories of the metabolic reaction network with states x̃₁,..., x̃₄ where x̃_i (t) = x_i (t) − x_ei, for i = 1,…, 4, suffering from environmental disturbances v₁(t),…, v₄(t) and the Poisson genetic variations with the Poisson counting processes N(t) = N₁(t) + N₂(t) are shown in Figure 6. It can be seen that the evolutionary game strategy can maintain phenotype stability around x_e for a period of time from t = 0 to t = 383. However, when neutral genetic variations are continually accumulated by the robust network, it is seen that the phenotype robustness criterion in (46) is violated, and the phenotype of the metabolic reaction network becomes perturbed by neutral genetic variations after t = 383, finally shifting to another equilibrium point to start another evolutionary period.

$$\frac{E{\int }_0^{383}\left(\tilde{x}{(t)}^T\hspace{0.17em}Q\tilde{x}(t)+u{(t)}^T\hspace{0.17em}u(t)\right)dt}{E\tilde{x}{(0)}^T\hspace{0.17em}\tilde{x}(0)+E{\int }_0^{383}v{(t)}^T\hspace{0.17em}v(t)dt}\simeq 0.7066\le e_o=\mathrm{0.7843.}$$ (55)

From the calculation of the evolvability of the metabolic reaction network in (55), it can be seen that the estimated evolvability e_o by the proposed method is conservative. The main reasons are the conservativeness of the global linearization and the LMIs used to approximate the nonlinear stochastic reaction network and the HJIIs, respectively. Furthermore, the convex optimization method employed by the LMI toolbox in Matlab to solve the LMI constraints for evolvability in (42) can also lead to conservative results.

From the simulation results in Figure 5, it can be seen that by the evolutionary game strategy, as the neutral genetic variations are continually accumulated, after the negative feedback loops in (53) have been constructed by the evolutionary game strategy (see Fig. 6), the environmental disturbance can be buffered and neutral genetic variations can be tolerated by the metabolic reaction network only for a certain period of evolution time (from t = 0 to t = 383). However, when the neutral genetic mutations accumulate to the extent that the phenotypic trait robustness criterion of the evolutionary biological network in (33) or (46) is violated at approximately t = 383, the network stability will be destroyed and the phenotype transits to another equilibrium to begin another period of network evolution.

Discussion

In this study, a population of evolutionary biological networks with genetic variations selected by natural selection to resist intrinsic genetic variations and buffer environmental disturbances, maintaining its phenotypic trait, is modeled as a robust nonlinear stochastic stabilization system. Since environmental disturbances are uncertain and unpredictable, in order to maintain the robust stability of the phenotypic trait of interest by natural selection, the minimax evolutionary game strategy for phenotypic trait robustness in (11) is developed to select adequate phenotypic variations by natural selection for improving network robustness. This minimizes the worst-case effect of uncertain environmental disturbances on the phenotypic deviation from its phenotypic trait in the evolutionary process. The minimax design scheme has been widely used for robust control in robot systems,^21,16 robust synthetic biology design,^32,22 and robust reference control of economic systems¹⁶ when some system parameters are perturbative and external disturbances are uncertain and unpredictable, so that their worst-case effect on system performance has to be as small a value as possible.^{32,23,18,33,21,16,22,45,46} With the minimax evolutionary game strategy, the phenotypic trait robustness criterion of the biological network in evolution is found to be: genetic robustness plus environmental robustness is less than or equal to enhanced network robustness. That is, if the enhanced network robustness by the evolutionary game strategy can confer both genetic robustness to buffer random neutral genetic variations and environmental robustness to resist environmental disturbances in the evolutionary process, then the network phenotypic trait is robustly stable in the basin around the equilibrium point at x_e of interest by natural selection. The minimax evolutionary game strategy can improve network robustness to enhance phenotypic trait robustness by modifying the network interaction matrix A by $\left(A-\frac{1}{2}P\right)$ in (23) (or f(x̃) by $f(\tilde{x})-\frac{1}{4}\left(\frac{\partial V(\tilde{x})}{\partial x}\right)$ in (33)) through negative feedback loops, which could decrease the evolvability e_o of the biological network in the evolutionary process. This result extends the idea of Waddington³⁴ from the gene level to the biological network level. Based on the phenotypic trait robustness criterion in (23), (33), or (46), the correlation between genetic robustness, environmental robustness, and network robustness by recent genomic experiments in yeast³⁵ (genes with similar robustness to genetic, environmental, and phenotypic perturbations in evolution) can be rationally explained from the network robustness perspective. That is, if the network robustness of a biological network is enhanced by the minimax evolutionary game strategy (ie, the basin of x_e in Figure 1 becomes larger and deeper), then more neutral genetic variations and environmental disturbances can be overcome singly or simultaneously, and the phenotypic trait can be maintained by the minimax evolutionary game strategy through natural selection during the evolutionary process. The fitness f_o of the biological network, which is inversely proportional to the evolvability e_o, is increased by the minimax evolutionary game strategy via natural selection in Proposition 2, so that the phenotypic trait is more robust in (33) due to the larger and deeper basin caused by the adaptive negative feedback loops $u^{*}(t)={\sum }_{k=1}^{N_1(t)}{f}_k\hspace{0.17em}(\tilde{x})\hspace{0.17em}p(t-t_k)=-\frac{1}{2}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)$ in the evolutionary process. However, when large amounts of neutral genetic variations are accumulated continuously to enhance network robustness through the minimax evolutionary game strategy, they may provide more raw material for new evolutionary possibilities through random genetic drift.³⁴ Therefore, the minimax evolutionary game strategy may improve the network robustness to maintain the phenotypic trait in a period of evolutionary process, and may eventually improve the evolution of the biological network in the long term. This phenomenon has been illustrated by the in silico example of the evolutionary genetic regulatory network in Figure 5.

From the phenotypic trait robustness criteria in (23) and (33), it is observed that there are two ways to improve phenotypic trait robustness in evolution. One way is to improve the network robustness (ie, to make the right-hand side of (23) or (33) as large a value as possible so that the phenotypic trait robustness criterion always holds), and the other way is to reduce the effect of neutral genetic variations and environmental disturbances on the biological network (ie, to make the left-hand side of (23) or (33) as small a value as possible). The minimax evolutionary game strategy is to select heritable phenotypic variations such that u^*(t) = −Px in (17) for linear biological networks or $u^{*}(t)=-\frac{1}{2}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)$ in (28) for nonlinear biological networks, in order to develop negative feedback loops as the first way to improve the network robustness on the right-hand side of (23) or (33) to resist environmental disturbances. This is why there are many negative feedback loops in biological networks – to improve the network robustness. Furthermore, there are numerous redundant, modular, and scale-free structures in biological networks, which are helpful in attenuating the effect of intrinsic neutral genetic variations and environmental disturbances on the left-hand side of (23) or (33), which is the second way to maintain the phenotypic trait in the evolutionary process. Therefore, based on the phenotypic trait robustness criterion of the evolutionary biological network, we can gain a deeper evolutionary insight into the development of negative feedback, redundant, modular, and scale-free structures for biological networks by adaptive or non-adaptive processes¹² in evolution. In different levels of biological networks, two favored strategies can improve phenotypic trait robustness in evolution. One is to improve the network robustness to tolerate more intrinsic neutral genetic variations and to resist environmental disturbances. Negative feedback is the systematic mechanism to improve network robustness, and it is favored by natural selection at different levels of the biological network in evolution, which matches the minimax evolutionary game strategy in this study. Another strategy is to reduce the effect of intrinsic neutral genetic variations and environmental disturbances on different biological networks. Redundancies and repairs are the mechanisms of this strategy, and are also favored by natural selection. This is why there are many different redundancies from duplicated genes in gene regulatory networks, redundant pathways in biological chemical networks, and species redundancies in ecological networks.²³

Recently, synthetic biology has focused on the rational construction of biological systems based on engineering principles to fulfill a particular purpose and to allow a better understanding of biological design, using synthetic circuits.^36–44 High-throughput techniques are necessary to determine what is evolved and how engineered genetic networks in vivo mimic the evolutionary processes of genetic networks. An approach involving network evolution has been used to rationally design a synthetic network with a desired behavior in the host cell.⁴¹ Unfortunately, synthetic biologists are faced with the uncertainties of modeling variation, evolutionary genetic variation, and environmental disturbances in vivo (ie, the phenotypic trait robustness problem of the synthetic biological network).^38–40 Given this situation, a robust synthetic network design is currently an important topic in the field of synthetic biology.^41–45 As the intrinsic genetic perturbations and environmental disturbances are unpredictable for synthetic biologists, the proposed minimax evolutionary game strategy should be an efficient robust design method for a synthetic gene network with evolutionary genetic variations, intrinsic uncertainties, and environmental disturbances.^41–45

The contributions of this study include the following: (i) The Poisson point process in (7) is used to model genetic variations in stochastic gene network; (ii) the evolution level (8) is defined for the stochastic biological network in the evolutionary process, ie, the worst-case effect of all possible environmental disturbances on the phenotypic deviation around x_e and the effect (cost) of evolutionary strategy u(t). Then, the fitness of the biological network around the phenotypic trait is inversely correlated to the evolution level of the biological network in (9). Therefore, the problem of evolvability or fitness can be considered as the minimax evolutionary game problem in (11). Based on the evolutionary game strategy, we also find some accumulated genetic variations can provide negative feedback via natural selection to maximize the robust stability of networks; (iii) then the global linearization method is proposed to solve the nonlinear stochastic game problem for the evolutionary game strategy of nonlinear stochastic biological network in the evolutionary process; (iv) based on the evolutionary game strategy in (17) or (28), we could obtain the phenotypic trait robustness criterion in (23) or (33) for stochastic biological networks in evolution. Finally, the phenotypic trait robustness criterion is further analyzed for the evolutionary network to get insight into evolutionary game strategy from the systematic point of view.

In the conventional evolution network,¹⁸ the evolvability and fitness of biological networks are not well defined. Therefore, the evolutionary game problem is not easily formulated for evolutionary biological networks. Actually, they only solve some evolutionary optimization problems without considering random genetic variations and environmental disturbances. Further, these methods could not provide an efficient method to solve Hamilton-Jacobi equations (HJE) for evolutionary problems. Hence, it is not easy to get insight into the evolutionary mechanisms of nonlinear biological networks from the systematic point of view.

Conclusion

In this study, biological networks with random genetic variations and uncertain environmental disturbances in the evolutionary process are described as nonlinear stochastic systems. In order to maintain the phenotypic trait favored by natural selection, a biological network needs to select some heritable phenotypic variations to improve network robustness, so as to tolerate neutral genetic variations and to buffer environmental disturbances in the evolutionary process. Since the environmental disturbances are uncertain and unpredictable, the evolutionary strategy of a biological network needs to minimize the worst-case effect of all possible bounded environmental disturbances (ie, to perform the minimax evolutionary game strategy) in the evolutionary process. We have found that the minimax evolutionary game strategy of a biological network is equivalent to accumulating some phenotypic variations due to random genetic variations to approach a robust negative feedback scheme, in order to efficiently improve the network robustness, resist the uncertain environmental disturbances, and tolerate neutral genetic variations. However, those harbored random neutral genetic variations also have an effect on network robustness when they accumulate to a large enough amount, serving to provide raw material for new adaptation and evolutionary innovation. If network robustness can be improved by the minimax evolutionary game strategy, conferring both environmental robustness against the environmental disturbance as well as genetic robustness to tolerate the neutral genetic variations, then the phenotypic trait of the biological network can be maintained in the evolutionary process. Otherwise, the phenotypic trait at an equilibrium point might be destroyed and shifted to another phenotypic trait at a neighboring equilibrium point to commence another period of network evolution.

In general, to gain insight into the minimax evolutionary game strategy of a nonlinear evolutionary biological network, it is necessary to solve a difficult optimization problem constrained by a Hamilton-Jacobi-Isaac inequality (HJII). A global linearization technique is employed to simplify the minimax evolutionary game problem, ie, the HJII-constrained optimization problem for the minimax evolutionary game strategy can be simplified to an equivalent optimization problem constrained by linear matrix inequalities (LMIs). Based on the global linearization technique, the tradeoff between evolvability, genetic robustness, and network robustness based on the minimax game strategy in evolution can be easily discussed from the local stability robustness and local filtering ability of a set of local evolutionary biological networks on the basis of linear system theory. Finally, the proposed evolutionary game strategy is also extended to an n-tuple evolutionary game problem of a population of biological networks with m players (competitive populations) and k environmental dynamics in the evolutionary process.

Supplementary Data: Appendix

The proof of proposition 1 is in the supplementary data 1.1.

The proof of proposition 2 is in the supplementary data 1.2.

The proof of proposition 3 is in the supplementary data 1.3.

1.1. Proof of Proposition 1:

From

$$J\underset{\_}{\underset{\_}{\mathrm{\Delta }}}\hspace{0.17em}E{\int }_0^{t_p}(\tilde{x}{(t)}^{T}Q\tilde{x}(t)+u{(t)}^{T}u(t)-e\upsilon {(t)}^T\upsilon (t))dt.$$

and by the fact ^{x̃(t) = x(t)} i.e. x_e = 0 in the linear biological case, we get

$$\begin{array}{l}J=E{\int }_0^{t_p}(x{(t)}^{T}Qx(t)+u{(t)}^{T}u(t)-e\upsilon {(t)}^T\upsilon (t))dt\\ =Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)+E{\int }_0^{t_p}(x{(t)}^{T}Qx(t))+u{(t)}^{T}u(t)-e\upsilon {(t)}^T\upsilon (t)+\frac{d(x(t)Px(t))}{dt})dt\end{array}$$ (A1)

where $V(x(t),t)\underset{\_}{\underset{\_}{\mathrm{\Delta }}}\hspace{0.17em}{x}^T(t)Px(t)$, P = P^T ≥ 0 By using the Itô formula¹,²,³,⁴,⁵,⁶,⁷,⁸, we can get

$$\begin{array}{l}J=Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)\\ +E\{{\int }_0^{t_p}{x}^{T}Qx+u^{T}u-e{\upsilon }^T\upsilon +{\left(\frac{\partial V}{\partial x}\right)}^T\\ \times (Ax+B\upsilon +u)+{\lambda }_2\left[\sum _{k=1}^{N_{2p}}{x}^T{A}_k^T\right]P\left[\sum _{l=1}^{N_{2p}}{A}_{l}x\right]\}dt\\ =Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)\\ +E{\int }_0^{t_p}\{x^T[Q+A^{T}P+PA]x+u^{T}Px+x^{T}Pu\\ +u^{T}u-e{\upsilon }^T\upsilon +x^{T}PB\upsilon +{\upsilon }^T{B}^{T}Px+{\lambda }_2\sum _{k=1}^{N_{2p}}{x}^T{A}_k^{T}P{A}_{k}x\}dt\\ =Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)\\ +E{\int }_0^{t_p}\{x^T[Q+A^{T}P+PA-PP+\frac{1}{e}PB{B}^{T}P\\ +\sum _{k=1}^{N_{2p}}{\lambda }_2{A}_k^{T}P{A}_k]x+{(Px+u)}^T(Px+u)\\ -{(\frac{1}{\sqrt{e}}{B}^{T}Px-\sqrt{e\upsilon })}^T(\frac{1}{e}{B}^{T}Px-\sqrt{e\upsilon })\}dt.\end{array}$$ (A2)

$$\begin{array}{l}\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{\upsilon (t)}{\text{max}}\hspace{0.17em}J=Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)\\ +\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{u(t)}{\text{max}}\hspace{0.17em}E{\int }_0^{t_p}\{x^T[Q+A^{T}P+PA]\\ -PP+\frac{1}{e}PB{B}^{T}P+\sum _{k=1}^{N_{2p}}{\lambda }_2{A}_k^{T_2}P{A}_k]x+{(Px+u)}^T(Px+u)\\ -{(\frac{1}{\sqrt{e}}{B}^{T}Px-\sqrt{e\upsilon })}^T(\frac{1}{e}{B}^{T}Px-\sqrt{e\upsilon })\}dt.\end{array}$$ (A3)

Then we get the solution of minimax game as

$$u^{*}(t)=-Px$$ (A4)

$${\upsilon }^{*}(t)=\frac{1}{e}{B}^{T}Px$$ (A5)

$$\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{\upsilon (t)}{\text{max}}\hspace{0.17em}J=Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)+E{\int }_0^{t_p}\{x^T[Q+A^{T}P+PA-PP+\frac{1}{e}PB{B}^{T}P+\sum _{k=1}^{N_{2p}}{\lambda }_2{A}_k^{T}P{A}_k)x\}dt.$$ (A6)

By the inequality

$$A^{T}P+PA-PP+\frac{1}{e}PB{B}^{T}P+\sum _{k=1}^{N_{2p}}{A}_k^{T}P{A}_x\le 0,$$

we get

$$J_o=\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{\upsilon (t)}{\text{max}}\hspace{0.17em}J\le Ex{(0)}^{T}Px(0)-Ex{(t_p)}^{T}Px(t_p)\le Ex{(0)}^{T}Px(0).$$

By the inequality

$$J_o\le eE\tilde{x}{(0)}^T\tilde{x}(0),$$

we get

$$P\le eI$$ (A7)

which is the inequality

$$0<P\le eI.$$

Q.E.D.

1.2. Proof of Proposition 2:

From

$$J\underset{\_}{\underset{\_}{\mathrm{\Delta }}}E{\int }_0^{t_p}(\tilde{x}{(t)}^{T}Q\tilde{x}(t)+u{(t)}^{T}u(t)-e\upsilon {(t)}^T\upsilon (t))dt.$$

for some positive function

$$V(\tilde{x})$$

$$J=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\left({\tilde{x}}^{T}Q\tilde{x}+u^{T}u-e{\upsilon }^T\upsilon \right)\hspace{0.17em}dt+EdV(\tilde{x}).$$ (A8)

By the Itô formula¹,²,³,⁴,⁵,⁶,⁷,⁸ for nonlinear stochastic network

$$\begin{array}{l}\frac{d\tilde{x}(t)}{dt}=f(\tilde{x})+B\upsilon (t)+\sum _{k=1}^{N(t)}{f}_k(\tilde{x})p(t-t_k)\\ =f(\tilde{x})+B\upsilon (t)+u(t)+\sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k),\end{array}$$

and by the fact that $u(t)={\sum }_{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)$ we can get

$$EdV(\tilde{x})=\left[{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T(f(\tilde{x})+u+B\upsilon )+\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2f}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})\right]\hspace{0.17em}dt$$ (A9)

Substituting (A9) into (A8), we get

$$\begin{array}{l}J=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\{{\tilde{x}}^{T}Q\tilde{x}+u^{T}u-e{\upsilon }^T\upsilon +{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}f(\tilde{x})\\ +{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}u+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B\upsilon +\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})\}dt.\end{array}$$ (A10)

By the fact that

$$u^{T}u+{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}u={\left(u+\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(u+\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\frac{\partial V(\tilde{x})}{\partial \tilde{x}}$$ (A11)

$$-e{\upsilon }^T\upsilon +{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B\upsilon =-{\left(\sqrt{e\upsilon }-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)}^T\times \left(\sqrt{e\upsilon }-\frac{1}{2\sqrt{e}}{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)+\frac{1}{4e}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right).$$ (A12)

Substituting (A11) and (A12) into (A10), we get

$$\begin{array}{l}J=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+E{\int }_0^{t_p}\{{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x})+{\tilde{x}}^{T}Q\tilde{x}\\ +\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})+\frac{1}{4e}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\\ -{\left(\sqrt{e\upsilon }-\frac{1}{2\sqrt{e}}{B}^T\hspace{0.17em}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)}^T\hspace{0.17em}\left(\sqrt{e\upsilon }-\frac{1}{2\sqrt{e}}{B}^T\hspace{0.17em}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)\\ -\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\frac{\partial V(\tilde{x})}{\partial \tilde{x}}+{\left(u+\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}\left(u+\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\}dt.\end{array}$$ (A13)

Then

$$\begin{array}{l}\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{\upsilon (t)}{\text{max}}\hspace{0.17em}J=EV(\tilde{x}(0))-EV(\tilde{x}(t_p))+\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{\upsilon (t)}{\text{max}}\hspace{0.17em}E{\int }_0^{t_p}\{{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x})+{\tilde{x}}^T{Q}^{\tilde{x}}\\ +\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_k(\tilde{x})+\frac{1}{4e}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\hspace{0.17em}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\\ -{\left(\sqrt{e\upsilon }-\frac{1}{2\sqrt{e}}{B}^T\hspace{0.17em}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)}^T\left(\sqrt{e\upsilon }-\frac{1}{2\sqrt{e}}{B}^T\hspace{0.17em}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\right)\\ -\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\frac{\partial V(\tilde{x})}{\partial \tilde{x}}+{\left(u+\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(u+\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\}dt.\end{array}$$ (A14)

Then we get the minimax solution

$$\begin{array}{l}{u}^{*}(t)=s^{*}(\tilde{x})=\sum _{k=1}^{N_1(t)}{f}_k(\tilde{x})p(t-t_k)=-\frac{1}{2}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right),{\upsilon }^{*}(t)\\ =\frac{1}{2e}{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right).\end{array}$$

Further, by the HJII

$${\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}f(\tilde{x})+{\tilde{x}}^{T}Q\tilde{x}-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\hspace{0.17em}\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)=\frac{1}{4e}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+\frac{1}{2}{\lambda }_2\sum _{k=1}^{N_{2p}}{f}_k^T(\tilde{x})\frac{{\partial }^{2}V(\tilde{x})}{\partial {\tilde{x}}^2}{f}_x(\tilde{x})\le 0,$$

we get

$$J_o=\underset{u(t)}{\text{min}}\hspace{0.17em}\underset{\upsilon (t)}{\text{max}}J\le EV(\tilde{x}(0))-EV(\tilde{x}(t_p))\le EV(\tilde{x}(0)).$$ (A15)

By the inequality constraint

$$J_o\le eE\tilde{x}{(0)}^T\tilde{x}(0),$$

we get

$$EV(\tilde{x}(0))\le eE\tilde{x}{(0)}^T\tilde{x}(0)$$ (A16)

which in the inequality

$$V(\tilde{x}(0))\le e\tilde{x}{(0)}^T\tilde{x}(0).$$

Q.E.D.

1.3. Proof of Proposition 3:

Since we replace the nonlinear stochastic biological network

$$\begin{array}{l}\frac{d\tilde{x}(t)}{dt}=f(\tilde{x})+B\upsilon (t)+\sum _{k=1}^{N(t)}{f}_k(\tilde{x})p(t-t_k)\\ =f(\tilde{x})+B\upsilon (t)+u(t)+\sum _{k=1}^{N_2(t)}{f}_k(\tilde{x})p(t-t_k)\end{array}$$

by the interpolated biological network

$$\frac{d\tilde{x}(t)}{dt}=\sum _{i=1}^M{\alpha }_i(\tilde{x})\hspace{0.17em}\left(A_i\tilde{x}+B\upsilon (t)+u(t)+\sum _{k=1}^{N_2(t)}{A}_{ki}p(t-t_k)\tilde{x}\right).$$

can be replaced by

$$\begin{array}{l}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\sum _{i=1}^M{\alpha }_i(\tilde{x})A_i\tilde{x}\right)+{\tilde{x}}^{T}Q\tilde{x}-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\\ +\frac{1}{4e}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)+{\lambda }_2\sum _{i=1}^M\sum _{i=1}^M\sum _{k=1}^{N_{2p}}{\alpha }_i(\tilde{x}){\alpha }_j(\tilde{x}){\tilde{x}}^T{A}_{ki}^{T}P{A}_{kj}\tilde{x}\\ \le {\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\sum _{i=1}^M{\alpha }_i(\tilde{x})A_i\tilde{x}\right)+{\tilde{x}}^{T}Q\tilde{x}-\frac{1}{4}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)\\ +\frac{1}{4e}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^{T}B{B}^T\hspace{0.17em}{\left(\frac{\partial V(\tilde{x})}{\partial \tilde{x}}\right)}^T+{\lambda }_2\sum _{i=1}^M\sum _{k=1}^{N_{2p}}{\alpha }_i(\tilde{x}){\tilde{x}}^T{A}_{ki}^{T}P{A}_{ki}\tilde{x}\le 0\end{array}$$ (A17)

with V (x̃(0)) ≤ ex̃(0)^T x̃(0). If we choose V (x̃ ) = x̃^T Px̃ by the fact ${\sum }_{i=1}^M{\alpha }_i(\tilde{x})=1$ and $\frac{\partial V(\tilde{x})}{\partial \tilde{x}}=2P\tilde{x}$ in (A17), then we get

$$\begin{array}{l}\sum _{i=1}^M{\alpha }_i{\tilde{x}}^T\hspace{0.17em}\left[A_i^{T}P+P{A}_i+Q-PP+\frac{1}{e}PB{B}^{T}P+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_{k_i}^{T}P{A}_{ki}\right]\\ \tilde{x}\le 0.\end{array}$$ (A18)

The above inequality holds if the Riccati-like inequalities

$$A_i^{T}P+P{A}_i+Q-PP+\underset{i=1,\dots ,M}{\frac{1}{e}PB{B}^{T}P}+{\lambda }_2\sum _{k=1}^{N_{2p}}{A}_{ki}^{T}P{A}_{ki}\le 0,$$

hold. Further,

$$u^{*}=-\frac{1}{2}\frac{\partial V(\tilde{x})}{\partial \tilde{x}}=-P\tilde{x},{\upsilon }^{*}(t)=\frac{1}{e}{B}^{T}p\tilde{x}$$ (A19)

which are the solution of minimax evolutionary game problem

$$u^{*}(t)=\sum _{i=1}^M\sum _{k=1}^{N_1(t)}{\alpha }_i(\tilde{x})A_{ki}p(t-t_k)\tilde{x}=-P\tilde{x},{\upsilon }^{*}(t)=\frac{1}{e}{B}^{T}P\tilde{x}.$$

Q.E.D.