Strong selection genome-wide enhances fitness tradeoffs across environments and episodes of selection

Abstract

Fitness tradeoffs across episodes of selection and environments influence life history evolution and adaptive population divergence. Documenting these tradeoffs remains challenging as selection can vary in magnitude and direction through time and space. Here, we evaluate fitness tradeoffs at the levels of the whole organism and the quantitative trait locus (QTL) in a multiyear field study of Boechera stricta (Brassicaceae), a genetically tractable mustard native to the Rocky Mountains. Reciprocal local adaptation was pronounced for viability, but not for reproductive components of fitness. Instead, local genomes had a fecundity advantage only in the high latitude garden. By estimating realized selection coefficients from individual level data on viability and reproductive success and permuting the data to infer significance, we examined the genetic basis of fitness tradeoffs. This analytical approach (Conditional Neutrality-Antagonistic Pleiotropy, CNAP) identified genetic tradeoffs at a flowering phenology QTL (costs of adaptation) and revealed genetic tradeoffs across fitness components (costs of reproduction). These patterns would not have emerged from traditional ANOVA-based QTL mapping. Our analytical framework can be applied to other systems to investigate fitness tradeoffs. This task is becoming increasingly important as climate change may alter fitness landscapes, potentially disrupting fitness tradeoffs that took many generations to evolve.

Introduction

Fitness tradeoffs have profound evolutionary implications in natural populations (Miller et al. 2008; Hereford 2009). For example, fitness tradeoffs across episodes of selection can structure life history evolution (Reznick 1992; Stearns 1992; Miller et al. 2008; Cox and Calsbeek 2010). In nature, individuals often have limited resources to allocate to survival, growth and reproduction. For perennial species, investing in fecundity can reduce future viability and reproductive success, suggesting that reproduction can be costly (Primack and Stacy 1998; Obeso 2002). Allocation to reproduction can deplete reserves necessary to maintain fitness in subsequent years, and/or increase susceptibility to natural enemies (Reznick 1992; Stearns 1992; Miller et al. 2008; Cox and Calsbeek 2010). Theory predicts that genetic costs of reproduction can constrain life history evolution and accelerate senescence (Reznick 1992; Stearns 1992; Roff 1999, 2002). Nevertheless, identifying genetic costs of reproduction has been difficult, and we lack a thorough understanding of the prevalence of such costs (Primack and Stacy 1998; Obeso 2002).

Similarly, reciprocal local adaptation in heterogeneous landscapes represents a classic fitness tradeoff: specialization to one environment reduces fitness in alternative habitats, reflecting a cost of adaptation (Kawecki and Ebert 2004; Leimu and Fischer 2008; Lowry et al. 2008; Hereford 2009; Poisot et al. 2011). In plants, fitness tradeoffs across environments are common, but not ubiquitous (Leimu and Fischer 2008; Hereford 2009; Anderson and Geber 2010; Paul et al. 2011; Bennington et al. 2012). Extensive interhabitat gene flow and limited genetic diversity in small populations can constrain local adaptation (Kawecki and Ebert 2004; Kawecki 2008; Leimu and Fischer 2008; Hereford 2009; Anderson and Geber 2010). Local maladaptation can also arise from complex coevolutionary interactions between plants and natural enemies (Garrido et al. 2012).

The extent of local adaptation might depend on the specific episode of selection (e.g., survival or fecundity) (Sambatti and Rice 2006; Gonzalo-Turpin and Hazard 2009) and focusing on only one fitness component could obscure patterns of natural selection integrated across the lifespan (Mojica and Kelly 2010). Reciprocal local adaptation is sometimes only evident after analysis of multiple episodes of selection (Gonzalo-Turpin and Hazard 2009). For example, middle and high elevation genotypes of the alpine grass Festuca eskia have the greatest survivorship in their home elevations, whereas low elevation genotypes have a fecundity advantage in their native sites (Gonzalo-Turpin and Hazard 2009). It is clearly crucial to examine multiple life history stages to achieve a complete understanding of local adaptation, especially in perennial species.

We still understand very little about the genetic basis of local adaptation (Fournier-Level et al. 2011). At the single locus level, fitness tradeoffs across environments could be caused by antagonistic pleiotropy, wherein selection favors local alleles in contrasting environments (Kawecki and Ebert 2004; Hall et al. 2010; Lowry and Willis 2010; Colautti et al. 2012; Lowry 2012; Anderson et al. 2013; Leinonen et al. 2013). Alternatively, some loci could influence fitness in one environment, but not others (Fournier-Level et al. 2011). Local adaptation can emerge if native alleles at those loci have a fitness advantage in their home environment, but no cost in alternative environments - a pattern known as conditional neutrality (Verhoeven et al. 2004). Through evolutionary time, however, gene flow could spread the conditionally advantageous alleles at these loci across populations, eroding local adaptation at the organismal level (Hall et al. 2010). In contrast, antagonistic pleiotropy can maintain genetic variation as a result of divergent selection across environments (Kawecki and Ebert 2004; Hall et al. 2010; Lowry and Willis 2010; Colautti et al. 2012; Lee and Mitchell-Olds 2012; Lowry 2012; Anderson et al. 2013; Leinonen et al. 2013). Elucidating the genetic basis of fitness tradeoffs could reveal the mechanisms that maintain genetic variation in space and time.

Local adaptation and fitness tradeoffs can take multiple years to manifest in perennial species (Primack and Stacy 1998; Bennington et al. 2012) and temporal variation in conditions can alter the magnitude and directionality of selection (Siepielski et al. 2009). Thus, multiyear field experiments may be necessary to provide robust tests of fitness tradeoffs. Our objective here was to examine local adaptation to contrasting environments, both at the level of the whole genome and the quantitative trait locus (QTL), while simultaneously evaluating fitness tradeoffs across multiple episodes of selection in a multi-year field experiment. We focused our study on Boechera stricta (Brassicaceae), a genetically tractable ecological model species native to the North American Rocky Mountains (Rushworth et al. 2011). In a previous study, we documented antagonistic pleiotropy at a life history QTL using data on only one fitness component: the probability of flowering (Anderson et al. 2013). In the current study, we examine multiple fitness components, from juvenile survivorship to flowering success and fruit production measured in reciprocal common garden experiments in the field. By integrating genotypic data with this sequence of fitness metrics, we evaluate genetic tradeoffs across life history stages to test for a cost of reproduction and across environments to test for a cost of adaptation.

Materials and Methods

Study species and field experiment

Boechera stricta (Brassicaceae) is a short-lived perennial forb native to the Rocky Mountains. In our gardens, experimental individuals survive for 2-3 summers, although the lifespan of naturally recruiting B. stricta plants could be several years longer. Boechera stricta primarily self-pollinates in nature, which facilitated the creation of advanced generation hybrid families for quantitative trait locus (QTL) mapping (Song et al. 2006; Song et al. 2009; Anderson et al. 2011). As part of a long-term effort to investigate the evolutionary genetics of ecologically relevant traits, we generated F₆ recombinant inbred lines (RILs) by crossing a Montana father and a Colorado mother and propagating the lines through self-pollination and single-seed descent (Schranz et al. 2007; Prasad et al. 2012). Although RILs enable QTL mapping, progeny of two individuals contain only a limited amount of genetic variation, even in this inbred species. Our design does not allow us to address the role of the cytoplasmic genome in local adaptation (for an excellent examination of cytoplasmic effects on local adaptation see Leinonen et al. 2013).

Boechera stricta inhabits a broad range of elevations and latitudes (Lee and Mitchell-Olds 2011). In this study, we examine fitness tradeoffs at two distinct latitudes (Montana vs. Colorado), where climatic conditions differ appreciably. The Montana environment has longer winters, cooler growing season temperatures, more precipitation, and different plant communities than the Colorado environment (Schranz et al. 2007; Prasad et al. 2012). Differences in abiotic and biotic conditions at these sites could impose divergent selection, potentially resulting in fitness tradeoffs. Indeed, our previous analyses documented polygenic local adaptation to latitude for the probability of flowering (Anderson et al. 2013).

We transplanted 172 F₆ RILs and parental lines into the parental environments in Montana (45.7° N, 2460 m in elevation) and Colorado (38.7° N, 2530 m in elevation) (for a map for the region, see Fig. 1 of Schranz et al. 2005. The Colorado site is Map ID 0 in Figure 1c and the Montana site is Map ID 28 in Figure 1b). The parental lines are the Montana and Colorado genotypes that were initially crossed to generate the RILs. We established common gardens in meadows at similar elevations and habitats as the parental populations. The Montana garden in Ravalli County near Lost Trail Pass was located 300 m from the site where the Montana genotype was collected, and the Colorado garden in Gunnison County near Crested Butte was 8.0 km from the collection site of the Colorado genotype (Prasad et al. 2012). Natural Boechera populations are present in both garden sites. In the common gardens, the advanced generation hybrid lines were exposed to natural conditions that shaped the evolution of the parents (e.g., Brunelle et al. 2005; Anderson et al. 2011; Anderson et al. 2013).

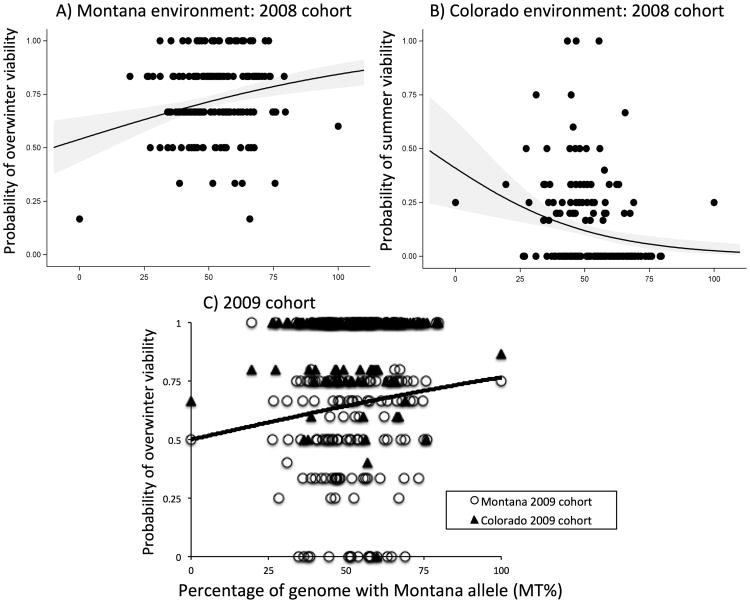
Figure 1.

Genotype by environment interactions for viability components of fitness in 172 F₆ Recombinant Inbred Lines and two parental lines planted into the parental environments in the 2008 cohort. Results in both environments reflect local adaptation for the 2008 cohort. (A) In Montana, overwinter viability improves as a function of the percentage of the genome with Montana alleles (MT%). (B) In Colorado, summer viability declined with increasing MT%. (C) For the 2009 cohort, overwinter viability increased with MT% in both environments, suggesting local maladaptation in Colorado. In panel C, open circles represent families in the Montana environment and filled triangles represent families in the Colorado environment. Logistic regressions were conducted with family level data.

In September 2008, we outplanted 2160 RIL and parental line individuals into our two common gardens (N= 6 individuals/RIL/garden and 30 individuals/parental line/garden; N =170 RILs and two parental lines). In September 2009, we planted an additional 1522 RIL and parental line individuals [N =751 plants in Colorado, and 771 in Montana; N = 1-5 individuals/RIL/garden (average = 4.2) and 15 individuals/parental line/garden, except in Montana, where only 2 individuals from the Colorado line were planted; N =174 RILs and two parental families]. In both years, we transplanted directly into the matrix of natural vegetation with 10 cm spacing between our experimental plants. Experimental individuals were juvenile rosettes approximately 3 months old at the time when they were planted. Initial plant size was measured for the 2009 cohort, but not the 2008 cohort.

From September 2009 to June 2010, N =205 individuals in the Montana 2009 cohort died as a direct result of gopher tunneling over the winter. Those plants are excluded from analyses, resulting in an overall sample size of N =3,477 individuals from 172 RIL and 2 parental lines for both sites and cohorts combined.

We genotyped the RILs at 164 polymorphic molecular markers, with an average spacing of 5.5 cM (62 microsatellite loci and 102 Single Nucleotide Polymorphisms, Anderson et al. 2011). Here, we leverage those genotypic data to map quantitative trait loci (QTL) for fitness and to evaluate genetic tradeoffs across environments and episodes of selection. Previous QTL mapping studies in this system focused on the age and stage at first flowering and leaf damage from herbivory, but only analyzed one fitness component (the probability of flowering) (Schranz et al. 2009; Anderson et al. 2011; Prasad et al. 2012; Anderson et al. 2013). Here, we extend those mapping efforts to include multiple fitness components from juvenile survivorship to lifetime fitness.

Fitness components

During each growing season, we quantified: (1) overwinter viability, i.e., survivorship from the fall to the beginning of the next growing season; (2) flowering success; and (3) fecundity (number of fruits). We monitored fitness and life history traits over the course of three growing seasons (2009-2011); therefore, we have data for three growing seasons for the 2008 cohort and two growing seasons for the 2009 cohort.

Fitness can be quantified sequentially from overwinter survivorship to flowering to fecundity, where individuals that fail to survive or flower are not included in the analysis of subsequent fitness components. That sequence allows us to test whether the extent of local adaptation changes through life history. In addition, we analyzed lifetime fitness separately, assigning fitness=0 to all plants that failed to survive, flower, or fruit. Thus, lifetime fecundity is a composite fitness component integrating across multiple episodes of selection from juvenile success to fecundity. Since we planted three month old rosettes, we could not examine critical early life history fitness components, including the seed to seedling transition or the seedling to rosette transition.

The Colorado 2008 cohort experienced severe herbivory during the 2009 growing season. Not a single individual in that experimental garden flowered successfully and only one individual survived until 2010. Therefore, we were only able to analyze overwinter survivorship (2008-2009) and survivorship over the course of the 2009 growing season jointly for both sites for the 2008 cohort. The 2009 cohort fared substantially better, permitting tests of local adaptation across episodes of selection.

Analyses

We evaluated local adaptation at the level of the whole genome and at individual loci using traditional approaches (univariate QTL mapping), multivariate least squares interval QTL mapping of multiple fitness components simultaneously (e.g., see Anderson et al. 2011), and an analytical framework that directly tests conditional neutrality vs. antagonistic pleiotropy and can evaluate genetic tradeoffs across fitness components (Conditional Neutrality – Antagonistic Pleiotropy, or ‘CNAP’, see Anderson et al. 2013). Below, we describe these analyses.

Whole-genome fitness tradeoffs

To assess the extent of local adaptation at the organismal level, we calculated the percentage of the genome that originated from the Montana parent (MT% alleles) for each of the F₆ recombinant inbred lines and both parental families. We first conducted analyses using family mean fitness (survivorship, flowering and fecundity). For these analyses, we estimated family mean fecundity (LSMEANs) for each site and cohort separately in mixed models (Proc Mixed, SAS ver. 9.3) that included family as a fixed effect, block as a random effect, and covariates for the density of neighboring vegetation and initial size of experimental B. stricta at planting (available for 2009 cohort only). We then tested whether fitness varied as a function of transplant environment (E), MT% alleles (Genotype) and the interaction of environment by MT% alleles (G × E), in models with a random effect for family (e.g., see Verhoeven et al. 2004). We analyzed the two cohorts (2008 and 2009) separately and together. If G × E interactions were significant, we examined whether fitness increased with MT% in the Montana garden, and decreased with MT% in the Colorado garden, as would be expected under the hypothesis of reciprocal polygenic local adaptation.

We modeled binary fitness components (viability and probability of flowering) using logistic regression in Proc Glimmix (SAS, ver. 9.3) and fecundity with mixed model ANOVA (Proc Mixed). Fecundity was log transformed in some cases to achieve normality and homoscedasticity of the residuals (see Results). Finally, we conducted a separate set of analyses that excluded the parental families (Table S1).

We also analyzed the individual level data (not family mean fitness), incorporating random effects for family, family nested within site and block nested within site. In SAS, we analyzed all fitness components separately using logistic regression and zero-inflated Poisson models. These individual-level results were qualitatively similar to the results of family level analyses (See Table S2 for details of the analyses and results). We did a complementary analysis in the R package ‘aster’ (ver. 0.8-20), which jointly analyzes multiple fitness components and can accommodate random effects (Geyer et al. submitted). Results from aster models differed slightly owing to the structure of the input data, but still support overall patterns (Table S3).

Quantitative trait locus (QTL) mapping

We conducted quantitative trait locus (QTL) mapping using family-level fitness LSMEANs (Anderson et al. 2011). We assessed univariate QTL using composite interval mapping (model 6) in Windows QTL Cartographer ver. 2.5 (Wang et al. 2012). For each trait, we determined genome-wide significance thresholds at α=0.05 by 1000 permutations (Churchill and Doerge 1994). We generated initial models for composite interval mapping using forward and backward stepwise regressions (p=0.05) with a 2 cM walk speed, a 10 cM window size, and five markers as cofactors. We calculated 1.0 and 2.0 LOD confidence limits for each QTL (van Ooijen 1992) and graphed the results using MapChart ver. 2.2 (Voorrips 2002). We mapped QTL separately for each fitness component, site, and cohort. Additionally, we used WinQTL Cartographer to test QTL × environment interactions for fitness components with comparable data from each site (2008 cohort: overwinter viability and survivorship in the first growing season; 2009 cohort: overwinter viability, probability of flowering, and fecundity).

Multivariate Least-Squares Interval Mapping (MLSIM)

We performed multivariate least squares interval mapping (MLSIM) across the genome to identify QTL underlying multiple fitness components in both field environments (Anderson et al. 2011). We conducted separate analyses for each cohort, and then combined cohorts in a final analysis using all fitness components. Complementary analyses excluded plants that died or failed to flower from fecundity LSMEANs estimate, which generated missing data for many families (Supplementary Table S4).

Conditional Neutrality-Antagonistic Pleiotropy (CNAP) analysis

Traditional QTL mapping can identify QTL genotype by environment interactions (Wang et al. 2012), but cannot directly distinguish between conditional neutrality and antagonistic pleiotropy nor address fitness tradeoffs across episodes of selection without additional analyses. In contrast, our Conditional Neutrality-Antagonistic Pleiotropy (CNAP) program explicitly examines these tradeoffs at loci distributed across the genome (Anderson et al. 2013). CNAP estimates realized selection coefficients in each environment and cohort based on changes in allele frequency caused by viability selection, or predicted changes in allele frequency due to fecundity selection. All calculations were based on individual-level data, which reduce estimation errors associated with family-level averages.

We transformed absolute fitness to relative fitness, w_ij, with mean = w̄ = 1.0. Generally, the selection coefficient, s, gives the reduction in relative fitness from the most fit genotype to the least fit genotype. Here, w₁₁ and w₂₂ refer to the Montana and Colorado homozygotes, respectively. We calculate w₂₂ = w₁₁(1 − s), so positive selection coefficients indicate higher fitness for Montana homozygotes and negative coefficients indicate higher fitness for Colorado homozygotes. Although heterozygous markers were uncommon in the recombinant inbred lines, we assume additive fitness in the heterozygote, hence w₁₂ = ½(w₁₁ + w₂₂). Letting f_ij = frequency of the ij-th genotype, mean fitness, w̄ = f₁₁w₁₁ + f₁₂w₁₂ + f₂₂w₂₂, hence s = [1 – (w̄/w₁₁)]/[½*f₁₂ + f₂₂].

We updated our CNAP program (Anderson et al. 2013) to enable estimation and significance testing of selection coefficients and their correlations in multiple episodes of selection (available at http://biology.duke.edu/mitchell-olds/Software.html). We applied permutation tests of significance by shuffling the relationship between multi-locus genotype and fitness component, leaving the relationship unchanged among molecular markers or among fitness components. Genotype-phenotype relationships were shuffled 1000 times, and each observed statistic was compared to this null distribution to infer significance levels. This permutation approach is equivalent to Doerge & Churchill (1996), and it retains the relationship among linked genetic markers.

Many fitness components severely violate normality assumptions. For example, as many individuals fail to reproduce in nature, zero values can be overrepresented for lifetime fitness; however, even zero-inflated distributions can show poor fit to such complex data (Chandler et al. 2008). Family mean fitness often requires transformation prior to analysis. Thus, QTL for fitness components can be difficult to detect using traditional ANOVA-based approaches, which assume that residuals are normally distributed (Kao et al. 1999; Yang et al. 2009). In contrast, the non-parametric permutation tests in CNAP can accommodate multiple fitness components with a variety of distribution patterns.

Genome-wide thresholds for selection coefficients

This procedure provides conservative significance thresholds. For each of 1000 permutations we identified the maximum and minimum selection coefficients across all loci for each unique combination of fitness component, cohort and site. From these null distributions of permuted extremes, we used the 2.5% tails of maximum (minimum) values for a two-tailed test of significance, which gives a 5% chance that even one marker will exceed this confidence interval by chance alone

Per-locus thresholds for selection coefficients

This procedure is less conservative. Under the null hypothesis that fitness is unrelated to genotype, the most extreme coefficients will exceed these thresholds in 5% of experiments. Therefore, when more than 5% of selection coefficients exceed these thresholds this suggests that multiple genomic regions influence traits or fitness. These thresholds are calculated from the permutations above. For each permutation, the upper and lower 2.5% thresholds are determined from among all marker loci. These 2.5% and 97.5% thresholds are saved, and their average is determined across all permutations. Thus, this procedure computes the expected two-tailed thresholds containing 95% of coefficients when the null hypothesis is true. In some episodes of selection (see Results) many more than 5% of selection coefficients exceed these thresholds, because multiple genomic regions influence fitness, and the genome-wide thresholds are conservative.

Correlated selection coefficients among episodes of selection

For two episodes of selection, the correlation among selection coefficients can be computed across the genome. We refer to this marker-by-marker correlation as the allelic correlation, to distinguish it from the genetic correlation used in trait-based quantitative genetics. Because nearby markers are not independent, and because a matrix of correlations contains many non-independent results, levels of statistical significance must be computed by permutation, based on shuffling between genotype and phenotype across all individuals (as above). The observed correlation matrix is compared to 1000 reshuffled correlation matrices under the null hypothesis. From each permuted matrix, the program identifies the correlation with the maximum absolute value, and saves this extreme to the null distribution. Finally, the 5% tail of this null distribution is used for a one-tailed genome-wide, matrix-wide test. When the null hypothesis is true, this gives a 5% chance that even one correlation will have an absolute value exceeding this significance threshold.

Assumptions of the CNAP model

As a first approximation, CNAP uses an additive model at target loci, assuming that heterozygote phenotypes are intermediate between the two homozygotes. This assumption has little consequence with recombinant inbred lines, since heterozygotes are rare. CNAP makes no assumptions regarding genotype frequencies or Hardy-Weinberg equilibrium. CNAP uses single marker analyses across the genome, with the assumption that phenotypes are determined by effects at a given marker, plus uncorrelated genetic and environmental influences. Obviously, tightly linked chromosome regions are correlated with each molecular marker, so selection coefficients summarize effects of local chromosome segments. However, unlinked QTLs (>25 cM in recombinant inbred lines) are independent of local effects at a target chromosome segment. Because the effects of unlinked genomic regions are assumed to be independent, this model also makes the implicit assumption that epistatic interactions with other chromosome regions do not occur. Finally, genotypes were randomized in each experiment to avoid correlations with environmental factors. Provided that these assumptions are plausible, CNAP can be applied at the level of individual plants within genotypes, or to analyses of genotype means.

Permutation tests of statistical significance assume that data (random errors) are identically and independently distributed (iid), but do not require normal or other parametric distributions. Because traits are influenced by many loci, we expect individuals of the same genotype to show similar phenotypes due to a target locus, as well as other loci across the genome. Permutations will accommodate the iid assumption when there are many genotypes in the experiment, so that (nearly) all permutations pair an individual with a different genotype, and the error variance therefore combines both individual and family deviations. Consequently, these analyses implicitly assume that the number of genotypes is large compared to the number of individuals per genotype.

Principal Components Analysis

To visualize patterns of genome-wide selection in these field experiments for multiple fitness components, we used principal components analysis. The data set for this analysis is the selection coefficients for each molecular marker during each episode of selection (the transpose of rows 14 - 177 in Supplementary Table S5a, shown in Supplementary Table S5b). We used JMP to compute the first two principal components based on the correlation matrix.

Results

In the Montana site, survivorship, flowering and fruiting success were high in both cohorts (see Table S6 for more details). In the Colorado environment, overwinter survivorship of the 2008 cohort was high (60.6% of N =1080), but all experimental plants failed to flower in 2009 owing to extensive herbivory. The 2009 Colorado cohort had high survivorship, flowering and fruiting success, enabling tests of fitness tradeoffs (Table S6).

Whole-genome fitness tradeoffs

Whole genome results were sometimes consistent with the hypothesis of polygenic local adaptation, but patterns changed during different episodes of selection (Tables 1-3, Figure 1).

Table 1.

Tradeoffs across environments for viability components of fitness for F₆ recombinant inbred lines and parental families reciprocally transplanted into the two parental environments. These analyses quantified the effect of environment, genotype (MT%) and interactions on fitness. MT% represents the proportion of the genome at N=164 molecular markers carrying the allele present in the Montana parent. Under the hypothesis of local adaptation, we expect a significant MT% × Environment interaction, reflecting an increase in fitness with MT% in the Montana environment and a decrease in Colorado. Since herbivory severely affected fitness in the Colorado 2008 cohort, we were unable to analyze reproductive components of fitness for that cohort. For that reason, we evaluated two viability components of fitness for the 2008 cohort: overwinter survivorship and survivorship during the first growing season. NA= Not applicable. These analyses were conducted at the family level, using line means for fitness components.

	2008 cohort: Overwinter viability		2008 cohort: Summer viability		2009 cohort: Overwinter viability		Both cohorts combined: Overwinter viability
Source	F1,170	p-value	F1,165	p-value	F1,165	p-value	F1,505	p-value
Environment	0.61	0.44	10.9	0.0012	11.89	0.0007	20.87	<0.0001
MT%	1.21	0.272	0.8	0.37	4.04	0.046	2.96	0.0857
MT% × Environment	6.73	0.0103	8.02	0.0052	0.07	0.8	5.83	0.016
Cohort	NA	NA	NA	NA	NA	NA	3.57	0.059
Environment × cohort	NA	NA	NA	NA	NA	NA	14.59	0.0002
MT% × cohort	NA	NA	NA	NA	NA	NA	1.4	0.24
MT% × Environment	NA	NA	NA	NA	NA	NA
×cohort							0.02	0.9
Random effects	χ2	p-value	χ2	p-value	χ2	p-value	χ2	p-value
Family	66.77	<0.0001	1.91	0.0837	0.95	0.16	71	<0.0001

Table 3.

Fitness tradeoffs across environment for lifetime fecundity of all plants. Plants that failed to set fruit were assigned fitness = 0 and then family means (LSMEANS) were calculated in SAS. Raw fitness data were used in the analysis of the Montana 2008 cohort, but fitness required log transformation for the 2009 cohort and both cohorts combined.

	Montana 2008 cohort: Lifetime fitness		2009 cohort: Lifetime fitness		Both cohorts combined: Lifetime fitness
Source	F1,170	p-value	F1,165	p-value	F1,335	p-value
Environment	NA	NA	7.4	0.0072	12.51	0.0005
MT%	11.68	0.0008	2.63	0.11	3.31	0.07
MT% × Environment	NA	NA	1.27	0.26	2.04	0.15
Cohort	NA	NA	NA	NA	2.67	0.1
MT% × cohort	NA	NA	NA	NA	0.04	0.84
Random effects	χ2	p-value	χ2	p-value	χ2	p-value
Family	NA		0	1	8	0.0046

Viability

For the 2008 cohort, we found a significant interaction of MT% (the percentage of the genome with MT alleles) by environment for overwinter viability, reflecting adaptation to Montana (1.3% increase in fitness for every 1% increase in MT%; odds ratio: 1.013; 95% Confidence Limits = 1.002, 1.024), but not Colorado (odds ratio: 0.998; 95% CL: 0.99, 1.01; a confidence interval spanning 1 indicates a lack of relationship in logistic regression; Table 1). For growing season survivorship, the MT% by environment interaction (Table 1) resulted from a 3.2% decline in fitness for every 1% increase in MT% in Colorado (OR: 0.968; 95% CL =0.95,0.99), but no relationship in Montana (OR: 1.016: 95% CL: 0.99, 1.05). Taken together, these results suggest polygenic local adaptation for viability selection.

For the 2009 cohort, we found no evidence for local adaptation in overwinter viability (Table 1). Nevertheless, there was a significant main effect of MT% (Table 1), such that a 1 unit increase in MT% augmented survivorship by 1.1% in both locations (OR: 1.011; 95% CL: 1.0002,1.024; Figure 1c).

Flowering success and fecundity

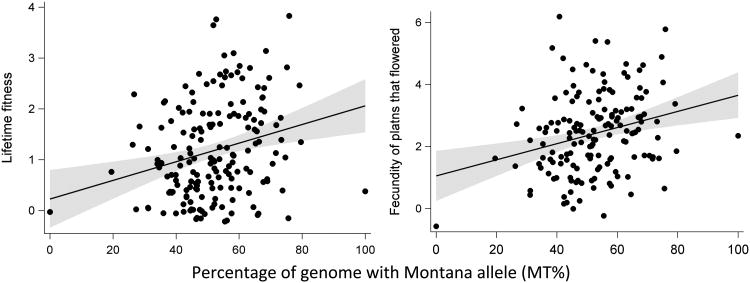
Data on reproductive success in the Montana 2008 cohort were compatible with local adaptation. The probability of flowering increased with MT% in individual level analysis (OR: 1.018, 95% CL: 1.001, 1.036; Supplementary Table S2), but not family level analysis (Table 2). Lifetime fitness improved with MT% in individual level analyses (Table S2) and family level analyses (β = 0.018 ± 0.005 fruits per 1 unit increase in MT%; Table 3, Figure 3).

Table 2.

Tradeoffs in the probability of flowering across environments. In these logistic regression analyses of family means, the probability of flowering improves with MT% in the Montana environment.

	2008 Montana cohort: Probability of flowering		2009 cohort: Probability of flowering		Both cohorts combined: Probability of flowering
Source	F1,179	p-value	F1,152	p-value	F1,321	p-value
Environment	NA	NA	10.61	0.0014	12.4	0.0005
MT%	2.59	0.11	4.04	0.046	0.26	0.61
MT% × Environment	NA	NA	13.06	0.0004	14.96	0.0001
Cohort	NA	NA	NA	NA	20.2	<0.0001
MT% × cohort	NA	NA	NA	NA	4.68	0.03
Random effects	χ2	p-value	χ2	p-value	χ2	p-value
Family	NA		12.5	0.0002	54.4	<0.0001

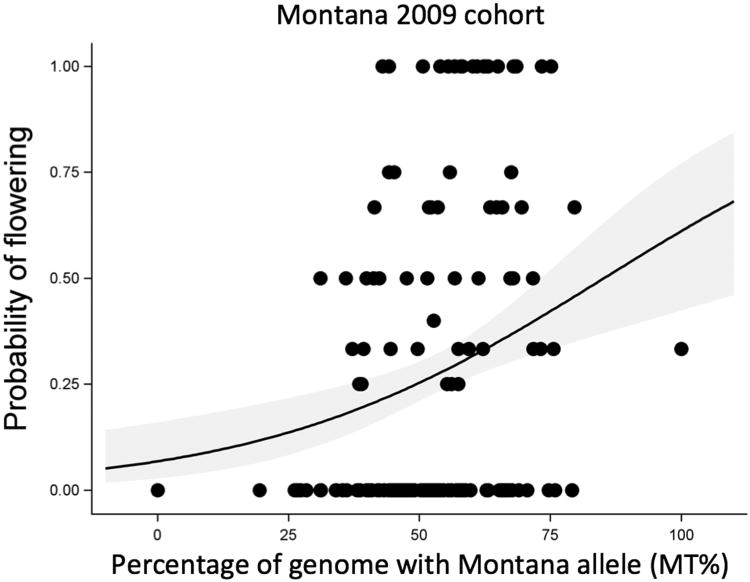
Figure 3. Success of local genomes via the probability of flowering in Montana.

Flowering success increases with MT% in Montana. Data points represent family means for the Montana 2009 cohort. We found no evidence that flowering success declines with MT% in Colorado.

For the 2009 cohort, local genomes enhanced flowering success in Montana (OR: 1.033; 95% CL: 1.014,1.052; Figure 2), but there was no effect of MT% on the probability of flowering in Colorado (OR: 0.99; 95% CL: 0.98, 1.01; Table 2). We found no evidence for local adaptation in fecundity or lifetime fitness (Table 3).

Figure 2.

Fecundity components of fitness increase as a function of the percentage of the genome with Montana alleles (MT%) for the 2008 Montana cohort. We found no relationship between the number of fruits and MT% in the 2009 cohort for either environment.

Both cohorts

These same general patterns hold when both cohorts are analyzed together. Overwinter viability in the combined dataset improved as a function of MT% in Montana (OR: 1.015, 95% CI: 1.005, 1.026), but there was no effect in Colorado (OR: 1.001, 95% CI: 0.99, 1.012; Table 1). Flowering success improved with MT% in Montana (OR: 1.03; 95% CI: 1.01, 1.04, Table 2) and appeared to decline with MT% in Colorado (odds ratio: 0.98, 95%CI: 0.96,1.0009). However, as the 95% confidence interval in Colorado spans 1, the decline in flowering success there does not reach statistical significance. Among plants that flowered successfully (Table S1), fecundity increased with MT% in both sites (log transformed fecundity; β = 0.0028 ± 0.008 log(fruits) per 1 unit increase in MT%, F_1,152 = 11.6, p=0.0008), suggesting local adaptation to the Montana environment and maladaptation to the Colorado environment. We found no evidence for genetic tradeoffs for lifetime fitness (Table 3).

Family level analyses that excluded the parental lines (Table S1) produced qualitatively similar results. Those analyses uncovered additional benefits of MT% for fecundity (both cohorts analyzed together) and lifetime fitness (for the 2008 and 2009 cohorts and both cohorts together).

Results of individual level analyses were similar to family level analyses (see Tables S2 for results and the description of the results). The joint analyses of fitness components in aster (Table S3) suggested reciprocal polygenic local adaptation for viability in the 2008 cohort (MT% × E: p=0.0057). An increase of 1% in MT% improved survivorship by 1.2% in Montana and depressed survivorship by 3.2% in Colorado. For the 2008 Montana cohort, a 1 unit increase in MT% corresponded with a 1.4% rise in flowering success (p=0.035). Finally, aster identified a significant interaction between MT% and environment for the probability of flowering for the 2009 cohort (p=0.0015). In this case, MT% enhanced the probability of flowering in Montana (odds ratio: 1.03) and depressed flowering success in Colorado (OR: 0.969).

QTL mapping

Univariate and multivariate analyses detected QTL for multiple fitness components and identified genomic regions that are known to influence life history traits in B. stricta (Figure 4, Table S7 for univariate and Table S8 for multivariate results). Previous studies highlighted the effect of the nFT QTL on flowering phenology and the probability of flowering (Anderson et al. 2011; Anderson et al. 2013). Furthermore, the BCMA QTL and underlying causal loci influence resistance to insect herbivory in natural settings (Schranz et al. 2009; Prasad et al. 2012). Our current endeavor identified both the nFT and the BCMA QTL, suggesting that these loci also affect fitness. This study also detected QTL in an inversion on chromosome 1, and additional regions of linkage groups 3, 4 and 6 (Figure 4). We did not identify any QTL with significant genotype by environment interactions in WinQTL Cartographer.

Figure 4. Quantitative trait loci (QTL) for fitness components.

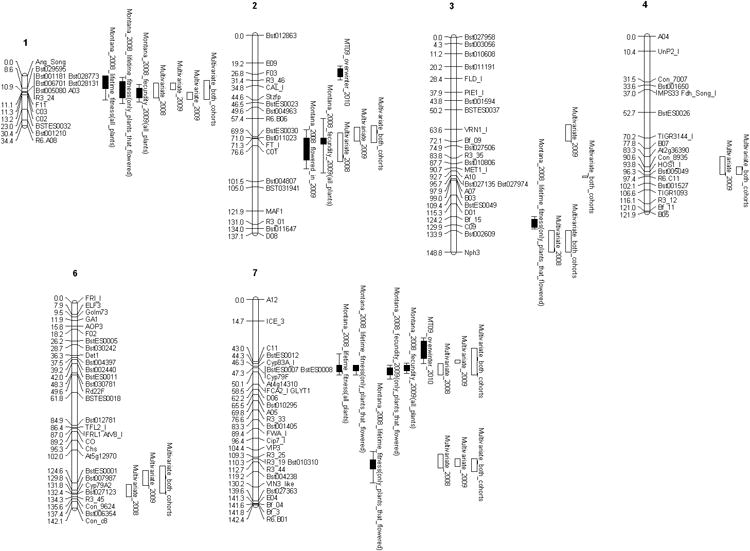
Positions of quantitative trait loci detected by univariate analysis (black boxes) and multivariate analysis (open boxes). The 1 and 2 LOD confidence intervals are indicated by the box and bars, respectively for univariate QTL. The open bars indicate confidence intervals in multivariate mapping. We found no QTL on linkage group 5 (not pictured here).

CNAP

Many episodes of natural selection significantly altered allele frequencies (Figure 5; Table S5), and selection coefficients with absolute values > 0.5 were common. Occasionally selection coefficients had absolute values >1.0 when there were large fitness differences between the most and least fit homozygotes. Selection was consistently stronger in Montana than in Colorado, where the high mortality levels and limited reproduction in the 2008 cohort often did not distinguish among genotypes, and selection coefficients did not exceed the conservative genome-wide threshold. Nevertheless, aggregate patterns of selection across many loci show detectable genetic influences, resulting in highly significant allelic correlations among episodes of selection within and between the Montana and Colorado environments (Table 4).

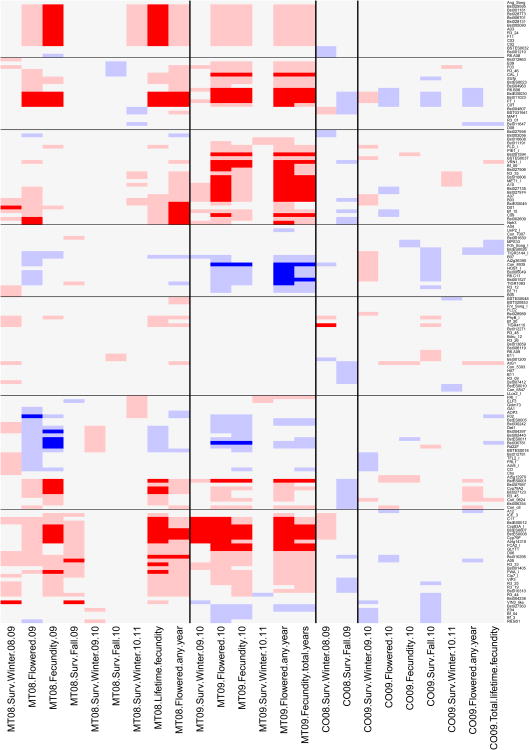
Figure 5. Heatmap of significant QTL for fitness components.

Rows show results for each molecular marker, and columns indicate individual episodes of selection. Sites and cohorts are separated by black vertical lines, and chromosomes are delimited by horizontal black lines. Marker names and fitness components are indicated along the right and bottom margins, respectively. For the fitness components, sites and cohorts are represented by state codes and two number years (e.g., MT08 is Montana 2008 cohort). Surv.Winter is overwinter survivorship, flowered is the probability of flowering, fecundity is the number of fruits, Surv.Fall indicates growing season survivorship. Non-significant selection coefficients are in light gray. Dark red (dark blue) indicates selection favoring the Montana (Colorado) allele, with significance based on the genome-wide threshold. Light red (light blue) indicates selection favoring the Montana (Colorado) allele, with significance based on the per-locus threshold. See text for details.

Table 4.

Allelic correlations among selection coefficients in different episodes of selection. Negative correlations indicate genetic tradeoffs, while positive correlations reflect synergistic gene action. Experiments were conducted in Montana (MT) and Colorado (CO) in 2008 and 2009. Significance levels were computed by permutation using data on molecular markers in individual plants, controlling for linkage among markers and multiple testing among selection episodes (see text for details). Correlations with experiment-wise significance levels are indicated in bold.

	MT08 survival winter 08-09	MT08 fruits 09	MT08 survival winter 09-10	MT08 survival fall 10	MT08 survival winter 10-11	MT09 survival winter 09-10	MT09 fruits 10	MT09 survival winter 10-11	CO08 survival winter 08-09	CO08 survival fall 09	CO09 survival winter 09-10	CO09 fruits 10
MT08 fruits 09	−0.065
MT08 survival winter 09-10	0.199	−0.63***
MT08 survival fall 10	−0.18	0.029	−0.22
MT08 survival winter 10-11	0.064	−0.009	−0.015	0.31**
MT09 survival winter 09-10	0.17	0.45***	−0.25	0.031	0.25
MT09 fruits 10	−0.064	0.76***	−0.59***	−0.099	−0.035	0.43**
MT09 survival winter 10-11	−0.39***	−0.207	0.14	−0.179	0.021	−0.054	−0.051
CO08 survival winter 08-09	0.31**	0.38***	0.02	−0.31**	−0.25	0.27*	0.26	−0.26
CO08 survival fall 09	−0.064	−0.59***	0.34***	0.21	0.34***	−0.20	−0.61***	0.051	−0.35***
CO09 survival winter 09-10	−0.36***	0.26*	−0.53***	0.11	0.094	0.028	0.24	0.17	−0.14	−0.14
CO09 fruits 10	−0.12	0.44***	−0.42***	0.01	−0.16	0.022	0.46***	−0.21	0.18	−0.55***	0.2
CO09 survival winter 10-11	0.29*	0.18	0.000	−0.051	0.22	0.40***	0.12	−0.016	0.14	0.12	−0.24	−0.23

^*p<0.05.

^**p<0.01,

^***p<0.0001

Fecundity showed strong selection coefficients in Montana in both cohorts across three years. Consistent with univariate and multivariate QTL mapping, fecundity selection at the inversion near marker A03 on linkage group 1 (Schranz et al. 2007) favored the local allele in Montana, but had no fitness effect in Colorado (Figures 4 and 5). The Montana allele at BCMA-Cyp79F on linkage group 7 was strongly favored in Montana (s up to 0.77 for reproductive fitness), reflecting univariate and multivariate QTL results (Figure 4), and supporting recent studies on the importance of this polymorphism (Schranz et al. 2009; Prasad et al. 2012). Other regions on linkage groups 2, 3, 4 and 6 showed significant selection coefficients for some fitness components, mirroring univariate and multivariate QTL mapping results. Usually the Montana allele was favored in Montana, but sometimes the Colorado allele had higher fitness.

Genetic basis of local adaptation

Except for the nFT region on linkage group 2, we find little evidence for fitness tradeoffs at particular QTLs. Our current results at nFT are congruent with previous findings (Anderson et al. 2013), here supported by a more extensive dataset.

Fitness tradeoffs across episodes of selection

Because ecologically-important traits are usually controlled by many loci that are difficult to detect individually, we examined the allelic correlation of selection coefficients among episodes of selection. Genome-wide matrix-wide significance tests are expected to show a single spurious correlation in 5% of experiments due to chance alone. However, our results showed many highly significant allelic correlations in different episodes of selection (Table 4), reflecting polygenic correlated selection. For one, we found positive correlations among similar episodes of selection (e.g., r = 0.76 between fecundity in the first summer for the 2008 and 2009 Montana cohorts).

We also found evidence for fitness tradeoffs (polygenic costs of reproduction). For example, for the 2008 Montana cohort, genomic regions causing high fecundity in summer 2009 reduced survival the following winter (r = −0.63). Similar fecundity-survival genetic tradeoffs were apparent between cohorts in Montana (r = −0.59 for the 2010 fecundity of the 2009 Montana cohort vs. overwinter survivorship of the 2008 Montana cohort) and Colorado (r = −0.55 for 2010 fecundity of the 2009 Colorado cohort vs. 2009 growing season survival of the 2008 Colorado cohort). However, other correlations failed to show significant patterns, perhaps reflecting environmental differences between years, or reduced sample sizes as cohorts aged.

Fitness tradeoffs across environments

Between environments, we found no consistent trend towards tradeoffs among selection episodes. Although both positively and negatively correlated selection episodes were common, the most extreme correlations were negative, compatible with tradeoffs between components of fitness in different environments. Therefore, much (but not all) of these data are compatible with polygenic local adaptation, similar to our whole genome results (Tables 1-3).

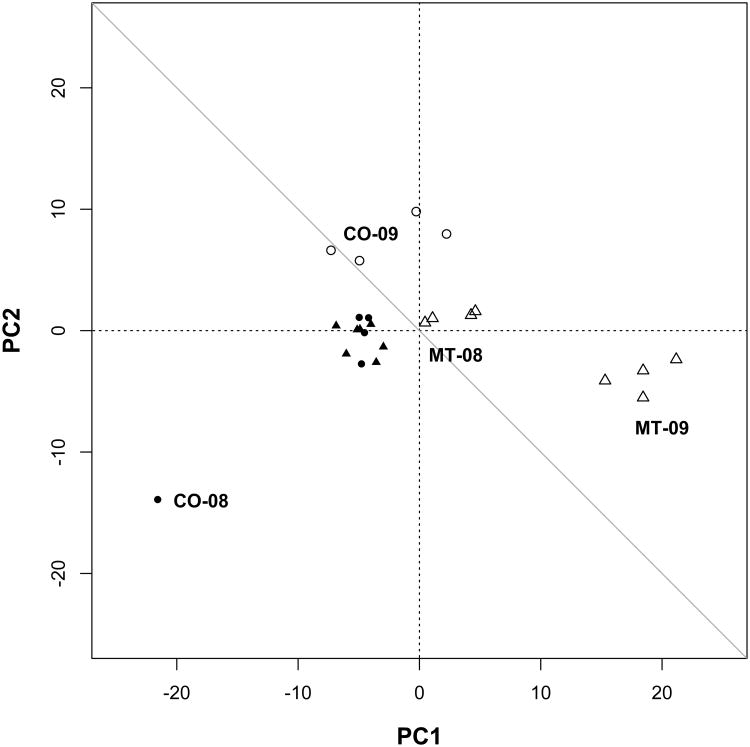
Principal Components Analysis

The first two principal components explained 58.5% and 13.8% of total variation, respectively. These two axes (Figure 7) revealed clear differentiation between fecundity (above the diagonal) and viability (below the diagonal). Genome-wide patterns of selection for summer survival in Colorado 2008 diverged from other episodes of viability selection. The reproductive episodes of selection showed differentiation among sites and cohorts.

Figure 7. Patterns of genome-wide selection coefficients for multiple episodes of selection.

Episodes of viability selection are indicated by filled symbols and reproductive selection components are open symbols for Montana (triangles) and Colorado (circles). Except for the unusual selection pressures on summer survival in Colorado 2008 (extreme lower left), other episodes of viability selection show similar patterns in both sites (closed cluster near center). Selection coefficients for reproductive components of fitness (at or above the diagonal) are labeled for each site and cohort. PC1 and PC2 account for 58.5% and 13.8% of total variation, respectively.

Discussion

Our analyses document heterogeneous patterns of local adaptation, with fitness tradeoffs across environments and episodes of selection. Local genotypes had a viability advantage in each of the environments, but fecundity selection favored local genomes in the Montana environment only. Univariate, multivariate and Conditional Neutrality - Antagonistic Pleiotropy (CNAP) mapping detected many quantitative trait loci (QTL) underlying various fitness components. Yet these analyses only demonstrated selective tradeoffs across environments for nFT, a flowering phenology QTL (Anderson et al. 2011; Anderson et al. 2013). Our CNAP approach identified a cost to reproduction, in which fruiting during one growing season showed a negative allelic correlation with subsequent overwinter viability in the 2008 Montana cohort. This allelic correlation quantifies the marker-by-marker correlation of selection coefficients across the genome.

Local adaptation and fitness tradeoffs across environments

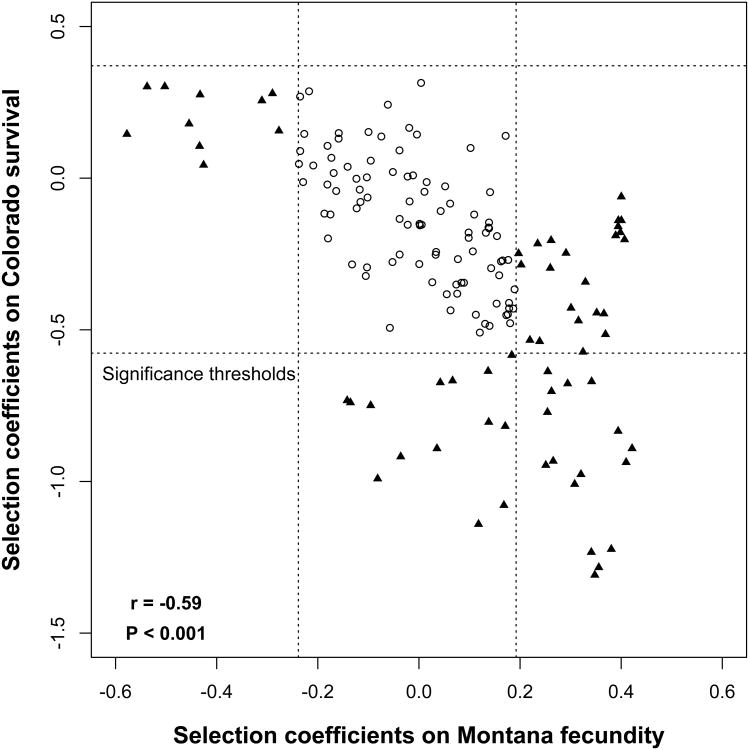
While plant populations are often adapted to very localized abiotic and biotic conditions, several meta-analyses indicate that reciprocal home-site advantage is not a general rule (Leimu and Fischer 2008; Hereford 2009). As with other recent studies (Sambatti and Rice 2006; Gonzalo-Turpin and Hazard 2009), the extent of local adaptation in our study of Boechera stricta depended on the episode of selection. At the level of the whole genome, reciprocal polygenic local adaptation was evident for binary fitness components, such that local alleles enhanced viability and the probability of flowering in both Montana and Colorado. Likewise, during their first summer, plants in the 2008 cohort showed a genome-wide negative allelic correlation between selection coefficients for fecundity in Montana and survival in Colorado (Figure 6), suggesting that local adaptation may only become apparent when multiple fitness components are considered. Concordant with local adaptation, genetic tradeoffs occur between environments during some episodes of selection.

Figure 6. Genome-wide correlation between selection coefficients in Montana and Colorado.

These two episodes of selection in the 2008 cohort compare first summer fruit production in Montana (“MT fecundity”) and first summer survival in Colorado (“CO survival”). Plotted are pairwise correlations of selection coefficients at all markers, including non-significant loci. Black triangles indicate significant markers in one or more environments. White circles show loci below the significance thresholds, which are indicated by dotted lines. Significance thresholds are determined by CNAP permutation (see Methods for details).

Nevertheless, in whole genome analyses, fecundity only improved with genome-wide local allele representation in the Montana environment. Similarly fecundity showed positive allelic correlations between environments, indicating that selection favored Montana alleles in both environments (Table 4). Our results contrast with a meta-analysis documenting higher levels of local adaptation in fecundity relative to viability (Hereford 2009). Nevertheless, in Montana, realized selection coefficients were consistently smaller for survival than for reproduction, consistent with observations in the literature that viability selection on traits is often weaker than fecundity selection (Kingsolver et al. 2001; Hereford et al. 2004; Hereford 2009).

Local genotypes actually had lower fecundity in the Colorado environment than did foreign genotypes. Reciprocal transplant studies often indicate some level of maladaptation (Hereford 2009). Additionally, foreign alleles at some QTL had enhanced fitness in each of the sites. Since we examined multiple components of fitness, which sometimes are negatively correlated, it is not surprising that a local allele may be maladaptive during some episodes of selection. Interannual temporal variation in selection could also alter the fitness landscape, favoring foreign alleles under some conditions. As climatic conditions continue to change, patterns of local maladaptation may become more pronounced, especially for populations with limited capacity to track their preferred climate through migration and distributional shifts (Davis and Shaw 2001; Wang et al. 2006; Wang et al. 2010; Bennington et al. 2012). It is possible that climate change could shift the fitness landscape such that the southern (Colorado) allele might acquire a fitness advantage in the northern (Montana) site.

Genetic basis of local adaptation

Using univariate, multivariate and CNAP mapping approaches, we detected QTL underlying various fitness components in nearly all linkage groups across the genome, including a flowering phenology QTL (nFT) on linkage group 2 (Anderson et al. 2011; Anderson et al. 2013), and BCMA, a locus on linkage group 7 that influences the production of glucosinolates, defensive compounds that protect plants from insect herbivores (Schranz et al. 2009; Prasad et al. 2012). Our current mapping efforts reveal that the nFT QTL and the BCMA polymorphism have profound evolutionary consequences through their significant relationships with numerous fitness components at multiple life history stages. Additional genomic regions warrant further exploration because of their strong effect on fitness, especially an inversion on chromosome 1 (Schranz et al. 2007).

Using the CNAP approach in a previous study, we documented that the local allele at the nFT QTL enhanced the probability of flowering in the Montana and Colorado environments (Anderson et al. 2013). Our current analyses extend that result to viability and fecundity, demonstrating fitness tradeoffs across environments (Figure 5). Antagonistic pleiotropy at the nFT QTL would not have been detected using traditional univariate QTL mapping approaches, as QTL Cartographer found no significant QTL × environment interactions for any fitness component. This dataset does not support antagonistic pleiotropy at other loci, perhaps because of the limited number of significant fitness QTL in the Colorado environment, or perhaps because conditional neutrality underlies the genetic basis of local adaptation in this population. Indeed, it is likely that both antagonistic pleiotropy and conditional neutrality, operating in different genomic regions, could contribute to local adaptation at the organismal level.

Selection varies across sites, years, and chromosome regions. Additionally, allelic correlations among episodes of selection range from positive to negative to non-significant (Table 4). Nevertheless, our multivariate analysis of selection coefficients (Figure 7) revealed a clear separation between viability and fecundity selection. This approach enables comparisons among spatially and temporally varying environments using a common metric based on genome-wide fitness effects. Future analyses with other species and environments may shed light on genetic influences on trait variation in complex environments.

Fitness tradeoffs across episodes of selection

CNAP uncovered evidence for genetic tradeoffs across episodes of selection, in some cases reflecting polygenic costs of reproduction. For example, in the Montana 2008 cohort, fruiting during the summer of 2009 was negatively genetically correlated (r=-0.63) with overwinter viability from 2009-2010. Thus, alleles that facilitate reproduction in one season reduce subsequent survivorship. This quantitative genetic framework can be applied to numerous fitness components to address questions such as: Does investment in reproduction come at a cost of future fecundity, especially during stressful years? Or does delaying reproduction until stress has abated enhance lifetime fitness? Might offspring receive a fitness advantage via maternal effects or epigenetic modifications if the mother successfully reproduces during a stressful season? Evaluating life history tradeoffs will become more important as climate change continues to increase temporal variability in abiotic conditions and exacerbate environmental stress.

Conclusions

Our analyses highlight the importance of multiyear field studies. The most compelling evidence for local adaptation came from the joint analysis of multiple fitness components in both sites and cohorts, for which we had the greatest statistical power. Our CNAP framework proved a novel tool for evaluating fitness tradeoffs across environments and episodes of selection, uncovering patterns that would not have been detectable with traditional ANOVA-based QTL approaches.