L-shell x-ray fluorescence computed tomography (XFCT) imaging of Cisplatin

Abstract

X-ray fluorescence computed tomography (XFCT) imaging has been focused on the detection of K-shell X-rays. The potential utility of L-shell x-ray XFCT is, however, not well studied. Here we report the first Monte Carlo (MC) simulation of preclinical L-shell XFCT imaging of Cisplatin. We built MC models for both L- and K-shell XFCT with different excitation energies (15 and 30 keV for L-shell and 80 keV for K-shell XFCT). Two small-animal sized imaging phantoms of 2-cm and 4-cm diameter containing a series of objects of 0.6 to 2.7 mm in diameter at 0.7 to 16 mm depths with 10 to 250 μg/mL concentrations of Pt are used in the study. Transmitted and scattered x-rays were collected with photon-integrating transmission detector and photon-counting detector arc, respectively. Collected data were rearranged into XFCT and transmission CT sinograms for image reconstruction. XFCT images were reconstructed with filtered back-projection (FBP) and with iterative maximum-likelihood expectation maximization (ML-EM) without and with attenuation correction. While K-shell XFCT was capable of providing accurate measurement of Cisplatin concentration, its sensitivity was 4.4 and 3.0 times lower than that of L-shell XFCT with 15 keV excitation beam for the 2-cm and 4-cm diameter phantom, respectively. With inclusion of excitation and fluorescence beam attenuation correction, we found that L-shell XFCT was capable of providing fairly accurate information of Cisplatin concentration distribution. With a dose of 29 and 58 mGy, clinically relevant Cisplatin Pt concentrations of 10 μg/mg could be imaged with L-shell XFCT inside a 2-cm and 4-cm diameter object, respectively.

1. Introduction

Cisplatin is a platinum-based chemotherapy drug causing crosslinking of DNA triggering apoptosis that is widely used for treatments of sarcomas, carcinomas, and lymphomas (Boulikas and Vougiouka, 2003; Le Chevalier et al., 2004; McGuire et al., 1996). Imaging of the three-dimensional (3D) distribution of the drug within the tumor would be useful information for understanding the relationship between Cisplatin tumor uptake and treatment outcomes. The low clinically relevant Cisplatin tumor uptake with approximately 10 μg/g of Pt is difficult to visualize with x-ray CT due to its low imaging sensitivity. For highly sensitive imaging, Cisplatin can be tagged with radioactive Pt and imaged with an external detector, similar to single-photon emission tomography (SPECT). Maximum Cisplatin Pt tumor concentrations of 4.9 μg/g were measured in fourteen cancer patients using ¹⁷¹Pt-tagged Cisplatin and a gamma camera (Areberg et al., 1999). In another study, tumor uptake of Cisplatin in two glioblastoma patients was imaged using ¹³N-labelled Cisplatin in a PET scanner (Ginos et al., 1987). Jonson et al. avoided the labor-intensive radiolabelling of Cisplatin by directly detecting Cisplatin with x-ray fluorescence (XRF) (Jonson et al., 1991). Pt tumor concentrations of 14–40 μg/g were measured in testicular, head and neck, and brain cancer patients undergoing Cisplatin treatments. In a recent study, gold nanoparticle concentrations of 20 μg/mL have been detected in a 12 mm-diameter phantom using an L-shell XRF bench-top system (Manohar et al., 2013).

X-ray fluorescence computed tomography (XFCT) has been recently studied as a method for 3D imaging of low concentrations of probes containing high atomic number (Z) elements (Bazalova et al., 2012; Cheong et al., 2010; Jones and Cho, 2011; Kuang et al., 2013b; Kuang et al., 2013a; Cong et al., 2013). XFCT showed promising results in detecting low concentrations of iodine, gadolinium, gold nanoparticles, and Cisplatin (Kuang et al., 2013b). Until recently, XFCT images have been reconstructed based on K-shell fluorescence x-rays. K-shell x-rays are emitted from the probe after excitation by x-rays with energies above the K-edge of the high-Z element. Simulation and experimental results suggested, that Cisplatin concentrations of 100 μg/g could be imaged with currently designed K-shell XFCT systems. Inspired by the achievable high sensitivity of L-shell XRF in the detection of trace amounts of gold nanoparticles (Ricketts et al., 2012), we investigate the feasibility of L-shell XFCT imaging of small animals using Monte Carlo simulations. Note that in a very recent study, Fu et al. used synchrotron radiation and novel imaging geometries to image osmium in zebra fish with L-shell XFCT (Fu et al., 2013).

Physically, there are two important reasons why L-shell x-ray production is more effective than that of K-shell. Even though atomic radiative yield for Pt L shell is three times lower than for K shell (Krause, 1979), Figure 1a demonstrates that the cross-section for L-shell photoelectric effect is 21 times higher compared to K-shell photoelectric effect (Berger et al., 2005). Combination of the two phenomena could theoretically result in increase of XFCT imaging sensitivity by a factor of 7. Additionally, the relative contribution of Compton scatter in water contaminating fluorescence signal is lower for L-shell x-rays compared to K-shell x-rays. However, the significant attenuation of low-energy L-shell x-rays (Table 1) in tissue shown in Figure 1b results in lower signal at the detector, which in turn decreases XFCT sensitivity when larger objects with imaging probes located deep in tissue are imaged. Another drawback of L-shell XFCT imaging is the fast fall-off of low-energy L-shell x-rays and the fact, that lower-energy L-shell x-rays deposit more dose compared to higher-energy K-shell x-rays. As a result, this work explores L-shell and K-shell XFCT solely for imaging of small animals of 2–4 cm in size.

Figure 1.

The photoelectric effect contribution to the mass attenuation coefficient of Pt and the Compton effect contribution to the mass attenuation coefficient of water as a function of energy (a). Relative x-ray fluence decrease as a function of depth in water for the studied excitation beam energies and L_α1 and K_α1 fluorescence x-rays (b).

Table 1.

K-shell and L-shell x-ray transition energies and intensities for Pt from (Thompson and Vaughan, 2001).

	Kα1	Kα2	Kβ1	Kβ2
Energy (keV)	66.83	65.11	75.75	77.85
Intensity w (%)	100	5	23	8
	Lα1	Lα2	Lβ1	Lβ2	Lγ1
Energy (keV)	9.44	9.36	11.07	11.25	12.94
Intensity w (%)	100	11	67	23	13

2. Materials and methods

2.1. Imaging geometry and phantoms

The simulation geometry of XFCT and transmission CT imaging of two water phantoms with Cisplatin contrast solutions is shown in Figure 2. Imaging was performed with monoenergetic photon pencil beams with energies of 15, 30, and 80 keV. The pencil beam was scanned along 55 transverse positions across the extent of the phantom and rotated by 360° in 1° steps. A 5-cm in diameter energy resolving detector arc covering 270° (not covering the transmitted beam) with 500 eV energy bins and an ideal detector energy response was simulated for XFCT imaging. The detector arc width along the axis of the cylindrical phantoms was 2 cm. Note that this was idealized geometry with detectors placed behind the x-ray source. In practice, the x-ray beam would be transmitted through a small gap in the detector arc. Transmission CT imaging was performed with a photon-integrating detector opposite of the source.

Figure 2.

Monte Carlo simulation geometry of XFCT and CT imaging (a) of a phantom with Cisplatin contrast objects using 1^st generation CT geometry. Examples of transmission CT (b) and XFCT (c) sinograms generated with a 15 keV excitation beam are shown.

Two cylindrical 3-cm high water phantoms of 2 and 4 cm in diameter with Cisplatin solutions were imaged. The 2-cm diameter phantom (Figure 3 top) contained 0.6 to 2.2-mm diameter objects aligned in a spiral pattern with solutions of Cisplatin containing Pt concentrations of 10, 90, 170, and 250 μg/g at 0.7 to 7.6 mm depths. The 4-cm diameter phantom (Figure 3 botom) contained 2.7-mm diameter Cisplatin vials with Pt concentrations of 100, 150, 200, and 250 μg/g at depths of 2.0 to 16.3 mm.

Figure 3.

Imaging phantom and imaging doses to the 2-cm diameter (top) and 4-cm diameter (bottom) phantom with Cisplatin contrast objects imaged with 15 keV (a), 30 keV (b), and 80 keV (c). The mean dose to the phantom is 20 mGy for all imaging protocols.

2.2. Monte Carlo simulations

The EGSnrc (Kawrakow and Rogers, 2006b)/BEAMnrc (Rogers et al., 2006) and DOSXYZnrc (Walters et al., 2007) Monte Carlo (MC) codes were used to simulate transmission CT and XFCT imaging. Relevant low energy electron and photon physics, such as electron impact ionization, bound Compton scattering, Rayleigh scattering, atomic relaxations, and photoelectron angular sampling were included in the simulations that were run on a 64×3 GHz Quad-Core Intel Xeon computer.

2.2.1 XFCT and transmission CT geometry simulations

XFCT and transmission geometry was simulated in the 2011 version of the DOSXYZnrc code that was modified for simulations of CT geometry. The parallel rectangular beam from multiple directions was chosen as the source to simulate parallel-beam XFCT geometry, more details about the simulation can be found in our previous publication (Bazalova et al., 2012). In brief, apart from the default .3ddose dose distribution file, .sinogram files containing the number of photons in each energy bin for each x-ray beam position and angle were also generated as a result of all MC simulation for both the photon-counting detector arc and the transmission detector.

2.2.2 Phantom simulations

The cylindrical phantoms were represented with a voxelized geometry using 80-μm and 160 μm voxels for the 2-cm diameter and 4-cm diameter phantom, respectively. Cisplatin solutions with 10 to 250 μg/g of Pt were modeled as solutions of water and H₆Cl₂N₂Pt, which is the chemical composition of the drug. The solution materials were generated using the PEGS4 code (Kawrakow and Rogers, 2006a). The mass densities of the materials were set to 1.000 g/cm³ due to the very low concentrations of Cisplatin. The air between the phantom and the detector arc was modeled.

XFCT and CT images were simulated for 15, 30, and 80 keV with equal imaging dose of 20 mGy. The imaging dose to the phantom was quantified as the mean dose to the phantom. Figure 3 shows the dose distributions in the phantoms imaged with 15, 30, and 80 keV x-rays. Table 2 summarizes the dose fall-off in the phantoms as well as the number of simulated histories for the 20 mGy imaging dose for the three excitation beam energies.

Table 2.

Imaging dose to the center D_center of the phantom as a function of maximum phantom dose D_max and the number of simulated particles for 20 mGy mean dose to the phantom for the three excitation beam energies.

	2-cm diameter phantom			4-cm diameter phantom
	15 keV	30 keV	80 keV	15 keV	30 keV	80 keV
Dcenter/Dmax	33%	84%	92%	7%	70%	86%
Number of particles	1.72×1010	3.35×1010	6.60×1010	6.54×1010	8.26×1010	1.44×1011

2.3. Image reconstruction

X-ray spectrum was collected at each pencil beam position and sinograms were derived from the spectral data. Parallel beam sinograms were processed to reconstruct XFCT and transmission CT images in MATLAB (The Mathworks, Natick, MA).

2.3.1 XFCT image reconstruction

XFCT sinograms were generated using K-shell (for the 80 keV scan) and L-shell (for 15, 30, and 80 keV scans) fluorescence x-rays listed in Table 1. Sinograms for XFCT image reconstruction were generated by calculation of the sum of the net K and L counts for all fluorescence energies. The net number of counts for each fluorescence energy was simply calculated as the total number of counts minus the background number of counts approximated by linear interpolation of the number of counts of the two neighboring energy bins separated by 500 eV.

First, XFCT images were reconstructed using FBP. Then an iterative reconstruction technique, maximum likelihood expectation maximization (ML-EM) with 50 iterations was applied in two ways: without attenuation correction (Nuyts et al., 1998) and with attenuation correction. In the general form, ML-EM images are reconstructed iteratively using the following equation:

$$p_j^{\mathit{new}}=\frac{p_j}{{\displaystyle \sum _i}{c}_{ij}}\sum _i{c}_{ij}\frac{m_i}{{\displaystyle \sum _{\xi }}{c}_{i\xi }{p}_{\xi }},$$ (1)

where p_j is the relative Pt concentration of voxel j, c_ij is the is the contribution of voxel j to the projection line i normalized to the case in which the projection line intersects the centre of the voxel, so 0 ≤ c_ij ≤ 1, ∀i,j, and m_i is the sinogram. In XFCT m_i is the measured value at i, where i indicates both the angle of the projection line θ and its position d within the detector array.

Due to the low energy of L-shell x-rays, excitation and fluorescent beam attenuation correction is crucial for accurate quantification of Cisplatin concentrations. The photoelectric effect contribution to the mass attenuation coefficient (Berger et al., 2005) Cisplatin for 1–100 keV x-rays is plotted in Figure 1a. Figure 1b represents relative attenuation in water for monoenergetic 15, 30, and 80 keV x-ray beams and L_α1 and K_α1 Pt x-rays. The x-ray fluence at 1 mm depth drops to 54%, 84%, and 96% for L_α1 fluorescence, 15 keV, and 30 keV x-rays, respectively. Therefore, in L-shell XFCT imaging, excitation and fluorescence beam attenuation correction should be applied for imaging of objects of >1 mm in size.

Excitation beam attenuation correction was calculated by multiplying the system matrix c_ij by the following attenuation correction:

$$a_{ij}^e=exp(-{\mu }_e{e}_{ij}),$$ (2)

where μ_e is the linear attenuation coefficient of the media at the excitation beam energy and e_ij is the beam traversal distance to voxel j (Figure 4). In addition, simple fluorescence attenuation correction was applied by dividing the system matrix c_ij by the fluorescence attenuation correction a^f_j calculated using the following:

$$a_j^f=\sum _f{w}_{f}exp(-{\mu }_f\langle f_j\rangle ),$$ (3)

where μ_f is the linear attenuation coefficient of f-th fluorescence x-ray spectral line with normalized intensity w_f (Table 1) and 〈f_j〉 is the mean path from voxel j to the edge of the scanned object based on the uniform angular distribution of fluorescence x-rays (Figure 4). The calculation of 〈f_j〉 assumed isotropic three-dimensional emission of fluorescence x-rays and their detection by the 2-cm wide 270° detector arc. Parameters μ_e, e_ij, and f_j can be accurately derived from reconstructed transmission CT images. In the presented phantom study, attenuation coefficients of fluorescence x-rays μ_f were approximated by μ_f of water. The reconstructed XFCT images represented by relative Pt concentration p_j calculated with Equation (1) were normalized to absolute Pt concentration using a priori knowledge of the highest Pt concentration in the 250 μg/mL Pt vials. The normalization factor was calculated as the mean signal of all 250 μg/mL Pt vials for each phantom.

Figure 4.

Definition of phantom paths for excitation e_ij and fluorescence f_j beam attenuation correction.

2.3.2 Transmission CT image reconstruction

Transmission CT images were reconstructed using only transmission data. Sinograms were generated by integrating the number of counts of each transmission sinogram point over the entire energy spectrum. The number of counts was converted into projections p using p=−ln(I/I₀), where I is the number of counts and I₀ is the maximum number of counts found in the sinogram, corresponding to an air-scan. Transmission CT images expressed by linear attenuation coefficients were reconstructed using filtered back-projection (FBP) and converted into CT numbers using CT number = 1000× (μ/μ_w−1), where μ is the linear attenuation coefficient of a voxel and μ_w is the linear attenuation coefficient of water.

2.4. Image quality evaluation

Excitation beam energies were varied to be 15, 30, and 80 keV. The difference between L-shell and K-shell imaging was studied using 15 and 80 keV images. The effects of low-energy excitation beam attenuation for L-shell imaging were evaluated by means of XFCT images generated with 15 and 30 keV excitation beams. The reconstructed signal m_vial was evaluated as the mean value of each contrast object. Contrast-to-noise ratio (CNR) of XFCT and transmission CT images was calculated as the ratio of the difference between the mean values of the signal of each contrast object m_vial and water m_w and background noise σ_w :

$$\mathit{CNR}=\frac{m_{\mathit{vial}}-m_w}{{\sigma }_w},$$ (4)

where m_w and σ_w were calculated as the mean and the standard deviation of an 8×8-voxel water region in the center of the phantom.

Cisplatin imaging sensitivity limits were estimated using CNR of 4, as defined by the Rose criterion (Rose, 1973). Note that since CNR depends on object shape, size, and location, sensitivity limits calculated in this work were only estimates of object detectability.

3. Results

3.1. Reconstructed images

MC-simulated transmission CT and XFCT images reconstructed with FBP, ML-EM without and with attenuation correction for a 20 mGy imaging dose for the 2-cm and 4-cm diameter phantom are presented in Figures 5 and 6, respectively. The contrast of transmission CT images increased with decreasing imaging beam energy. XFCT images reconstructed with 50 iterations of ML-EM without attenuation correction were less noisy and less sharp than FBP reconstructed images. Higher contrast of objects towards the periphery of the phantom was more evident for the 15 keV XFCT images, followed by the 30 keV XFCT images. The contrast of the 80 keV images was nearly uniform in all objects across the phantoms. After attenuation correction was applied, object contrast was nearly uniform in the 15 as well as 30 keV XFCT images. The object contrast in the noisy 80 keV XFCT images was not affected by attenuation correction.

Figure 5.

Transmission CT images (first column), and XFCT images of the 2-cm diameter phantom reconstructed with FBP (second column), ML-EM with 50 iterations without attenuation correction (third column) and with attenuation correction (fourth column) for 15 keV (first row), 30 keV (second row), and 80 keV (third row) excitation beams.

Figure 6.

Transmission CT images (first column), and XFCT images of the 2-cm diameter phantom reconstructed with FBP (second column), ML-EM with 50 iterations without attenuation correction (third column) and with attenuation correction (fourth column) for 15 keV (first row), 30 keV (second row), and 80 keV (third row) excitation beams.

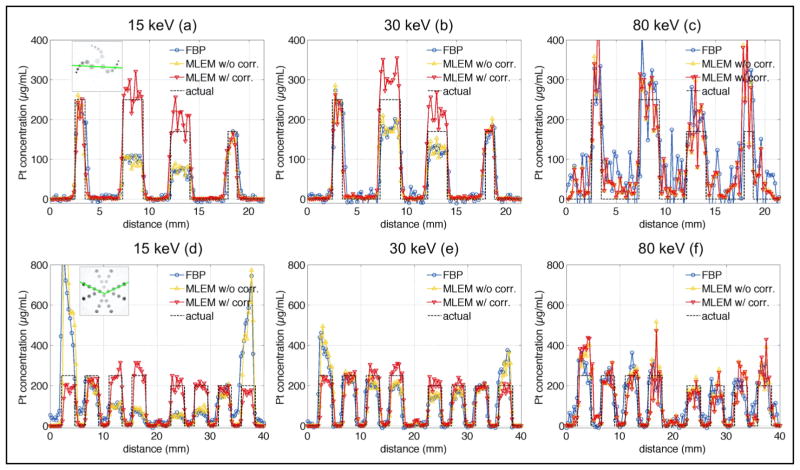
Phantom profiles in units of Pt concentration reconstructed with FBP, and ML-EM without and with attenuation correction for the 15, 30, and 80 keV excitation beams are shown in Figure 7. In the 2-cm diameter phantom, central object Pt concentrations were underestimated by 63% and 34% in uncorrected FBP and ML-EM 15 keV and 30 keV images, respectively. After attenuation corrections were applied, XFCT Pt concentrations were within 12% of true values. Attenuation correction did not affect the noisy K-shell 80 keV XFCT images, in which Pt concentration was reconstructed accurately within 5%.

Figure 7.

Profiles through the 2-cm diameter (a–c) and 4-cm diameter (d–f) phantoms shown in the thumbnails in (a) and (d) for 15 keV (a,d), 30 keV (b,e), and 80 keV (c,f) XFCT images reconstructed with FBP and ML-EM without and with attenuation correction. Actual profiles are shown with black dashed line.

Attenuation correction played even more important role in the 4-cm diameter phantom, where peripheral object Pt concentrations were overestimated by up to 300% and central object concentrations were underestimated by 70% in the uncorrected FBP and ML-EM 15 keV images. The 80 keV images appear to have a higher concentration on the periphery of the phantom due to the higher probability of fluorescence x-ray detection from the periphery of the phantom. This is thanks to the very close proximity of the peripheral voxels to the detector arc and the larger solid angle the voxels are viewed by the detector arc compared to the central voxels.

3.2. Contrast-to-noise ratio

CNR of FBP-reconstructed transmission XFCT images as a function of Pt concentration and object depth are presented in Figure 8. In 15 and 30 keV L-shell XFCT images, CNR significantly decreased with increasing object depth due to significant excitation and fluorescence x-ray attenuation in the center of the phantom. The CNR in the 4-cm phantom decreases more with object depth than CNR in the 2-cm phantom due to the larger object depths. In 80 keV K-shell XFCT images, CNR was most uniform and least dependent on object depth.

Figure 8.

CNR of XFCT images generated with 15 keV (a,d), 30 keV (b,e), and 80 keV (c,f) excitation beam reconstructed with FBP as a function of object depth and Pt concentration for the 2-cm phantom (a–c) and the 4-cm phantom (d–f).

CNR of XFCT images reconstructed with ML-EM without attenuation correction are not presented. Similar to FBP-reconstructed 15 keV and 30 keV XFCT images, the CNR of objects located deep in the phantom significantly decreased compared to objects located at the periphery. Due to the decrease of noise in ML-EM images, CNR increased by a factor of approximately 6 compared to FBP-reconstructed images.

CNR of XFCT images reconstructed with ML-EM with attenuation correction is presented in Figure 9. CNR of vials with the same concentration became more uniform with attenuation corrections for all excitation beam energies. Highest CNR was observed in 15 keV XFCT images of the 2-cm phantom, for which the objects with 10 μg/mL of Pt were just below the detection limit. CNR of the 4-cm diameter phantom was lower than CNR for the 2-cm diameter phantom.

Figure 9.

CNR of XFCT images generated with 15 keV (a,d), 30 keV (b,e), and 80 keV (c,f) excitation beam reconstructed with ML-EM with attenuation correction as a function of object depth and Pt concentration for the 2-cm phantom (a–c) and the 4-cm phantom (d–f).

CNR in transmission CT images is not shown, but it decreased with increasing energy. The objects with 250 μg/mL solutions of Pt placed in the smaller 2-cm phantom were the only detectable objects with CNR>4 in transmission CT images.

3.3. XFCT sensitivity limits

The mean CNR calculated from XFCT images reconstructed with ML-EM with attenuation correction is plotted in Figure 10. For the studied imaging dose of 20 mGy, the lowest detectable Pt concentrations in the smaller 2-cm diameter phantom (calculated for CNR=4) were 12, 25, and 53 μg/mL for the 15, 30, and 80 keV excitation beam, respectively. For the larger 4-cm diameter phantom, the lowest detectable Pt concentrations were 19, 32, and 57 μg/mL for the 15, 30, and 80 keV excitation beam, respectively. The data is summarized in Table 3. The imaging sensitivity for 15 keV L-shell XFCT imaging compared to 80 keV K-shell XFCT imaging was increased by a factor of 4.4 and 3.0 for the 2-cm and 4-cm diameter phantom, respectively.

Figure 10.

Mean CNR of all objects in XFCT images generated with 15 keV, 30 keV, and 80 keV excitation beam reconstructed with ML-EM with attenuation correction as a function of Pt concentration for a dose of 20 mGy for the 2-cm diameter (a) and 4-cm diameter (b) phantom.

Table 3.

Estimates (CNR = 4) of lowest detectable Pt concentration in μg/mL for the two phantoms as a function of excitation beam energy.

	2-cm phantom			4-cm phantom
	15 keV	30 keV	80 keV	15 keV	30 keV	80 keV
Detectable concentration (μg/mL)	12	25	53	19	32	57

4. Discussions

We have presented an L-shell XFCT imaging strategy and compared the results with K-shell approach. By accounting for the attenuation of both excitation and fluorescence x-ray beams, a sensitivity of 12 μg/mL, which was 4.4 times higher than that of K-shell XFCT, was readily achievable with L-shell XFCT and imaging dose of 20 mGy in a small mouse-sized phantom of 2-cm diameter. Increasing the phantom size to 4-cm in diameter decreased the L-shell XFCT imaging sensitivity to 19 μg/mL, which was 3.0 times higher sensitivity compared to K-shell XFCT. Without attenuation correction, the accuracy in quantitation of Cisplatin concentration with 15 keV L-shell XFCT was poor with errors of up to 63% and 300% for the 2-cm and 4-cm diameter phantom, respectively. Cisplatin concentration error decreased to 12% when attenuation correction was incorporated in L-shell XFCT iterative image reconstruction algorithm.

XFCT imaging sensitivity linearly increases with square root of imaging dose. Based on Figure 10, clinically-relevant 10 μg/mL concentrations of Cisplatin can be detected with L-shell XFCT using imaging dose of 29 mGy and 58 mGy in the 2-cm and 4-cm diameter phantom, respectively. However, imaging dose of approximately 0.6 Gy is needed to detect the same concentration with K-shell XFCT in both phantoms.

K-shell cone-beam XFCT imaging of gold nanoparticles using a polyenergetic x-ray beam has been simulated with the Monte Carlo method (Jones and Cho, 2011). The study demonstrated that gold concentrations of 1 mg/mL could be imaged in a 5-cm diameter phantom. Detectable Pt concentrations presented in this work of approximately 0.055 mg/mL were lower compared to the study by Jones and Cho due to the assumed idealized imaging geometry with a 270° detector arc and the use of monoenergetic x-ray beam with energy just above the K-edge of Pt to maximize fluorescence x-ray production.

XFCT imaging with monoenergetic excitation beams was modeled in this work. Synchrotrons are common source of monoenergetic x-ray beams and they have been used for XFCT imaging in the past (Rust and Weigelt, 1998; Takeda et al., 2009; Yu et al., 2001). In reality, one can generate quasi-monoenergetic x-ray beams by extensive filtering of x-ray tube beams. If Compton scattered x-rays have energy distinct from fluorescence x-rays of interest, XFCT imaging sensitivity might be decreased. Detector energy response of 500 eV was assumed in this paper. Such energy resolution can be achieved with HPGe detectors (Perez et al., 1999). When Takeda et al. used a synchrotron source with 37 keV x-rays to image iodine solutions, they were able to visualize 5 μg/mL iodine concentration in a 1-cm diameter phantom with K-shell XFCT and a dose of 0.36 Gy (Takeda et al., 2009). The lower detectable iodine concentration compared to our K-shell results can be explained by the high imaging dose, the use of monoenergetic synchrotron x-ray source and a large-area high-purity germanium detector (HPGe) with 230 eV energy resolution at the iodine K_α line.

In our implementation of XFCT, the detector was simulated as a single crystal with no position information of the detected x-rays that were integrated over the entire detector arc. An array of small crystals with individual readout channels is a more practical setup for experimental XFCT imaging. Spatial information of detected x-rays can be incorporated in image reconstruction for correction of scattered Compton x-rays, which might result in higher imaging sensitivity.

It should be pointed out, however, that this study simulated an idealized XFCT system. The presented XFCT system used monoenergetic beams, which greatly reduced the uncertainty in attenuation due to scatter and beam hardening. The preciseness of Monte Carlo simulations in combination with pencil beam scanning eliminated any geometric uncertainty in phantom/detector/source alignment. More realistic simulations or experimental validation will reveal the practically achievable detection limits of L-shell XFCT.

5. Conclusions

A preclinical imaging system for XFCT imaging of Cisplatin with L-shell x-rays was modeled with Monte Carlo and attenuation correction for imaging with low-energy x-rays was incorporated into an iterative image reconstruction technique. L-shell XFCT imaging sensitivity compared to K-shell XFCT imaging sensitivity was increased by a factor of 4.4 for a 2-cm diameter phantom. The increase of L-shell XFCT sensitivity compared to K-shell XFCT sensitivity dropped to a factor of 3.0 for a larger 4-cm diameter phantom. With adequate incorporation of attenuation correction, clinically relevant Cisplatin concentrations of 10–40 μg/mg could be imaged in mice using L-shell XFCT and iterative image reconstruction techniques. We should point out that K-shell XFCT likely outperforms L-shell XFCT for larger animals due to the significant x-ray attenuation. Further XFCT L-shell imaging sensitivity increase can be achieved by modeling of advanced imaging geometries and employing more sophisticated image reconstruction techniques with Compton scatter correction algorithms.