Abstract
High-frequency pure tones (>6 kHz), which alone do not produce salient melodic pitch information, provide melodic pitch information when they form part of a harmonic complex tone with a lower fundamental frequency (F0). We explored this phenomenon in normal-hearing listeners by measuring F0 difference limens (F0DLs) for harmonic complex tones and pure-tone frequency difference limens (FDLs) for each of the tones within the harmonic complexes. Two spectral regions were tested. The low- and high-frequency band-pass regions comprised harmonics 6–11 of a 280- or 1,400-Hz F0, respectively; thus, for the high-frequency region, audible frequencies present were all above 7 kHz. Frequency discrimination of inharmonic log-spaced tone complexes was also tested in control conditions. All tones were presented in a background of noise to limit the detection of distortion products. As found in previous studies, F0DLs in the low region were typically no better than the FDL for each of the constituent pure tones. In contrast, F0DLs for the high-region complex were considerably better than the FDLs found for most of the constituent (high-frequency) pure tones. The data were compared with models of optimal spectral integration of information, to assess the relative influence of peripheral and more central noise in limiting performance. The results demonstrate a dissociation in the way pitch information is integrated at low and high frequencies and provide new challenges and constraints in the search for the underlying neural mechanisms of pitch.
1 Introduction
Pitch – the perceptual correlate of acoustic waveform periodicity – plays an important role in music, speech, and animal vocalizations. Periodicity is represented in the time waveform and can be extracted via the autocorrelation of either the waveform or a representation of the stimulus after peripheral processing (e.g., cochlear filtering and hair-cell transduction), with a peak in the autocorrelation function occurring at (and at multiples of) the waveform period (e.g., Licklider 1954; Meddis and O’Mard 1997). Alternatively, periodicity can be represented via the power spectrum before or after auditory transformations, with spectral peaks occurring at harmonics of the fundamental frequency (F0) (Cohen et al. 1995; Schroeder 1968; Wightman 1973).
Whether pitch perception depends on peripheral timing (e.g., autocorrelation) or rate-place (e.g., spectral) information (or both) remains a central question in auditory research. The fact that the autocorrelation is the Fourier transform of the power spectrum limits the extent to which this question can be answered via psychoacoustics or simple stimulus manipulations. Instead, it is necessary to rely on putative limitations of the auditory system in order to infer how information is extracted. For instance, physiological data on cochlear tuning, along with psychophysical estimates of frequency selectivity, have suggested that harmonics beyond about the sixth to tenth are not spectrally resolved and so do not provide spectral information. Thus, the fact that pitch can be heard with harmonics all above the tenth has been used as evidence for a pitch code that does not depend on a spectral representation in the auditory periphery (e.g., Houtsma and Smurzynski 1990; Kaernbach and Bering 2001).
Similarly, based on physiological data from other species (Palmer and Russell 1986; Rose et al. 1967), it has often been assumed that phase locking to pure tones in the human auditory nerve is degraded above 1–2 kHz and is not available beyond about 4 kHz, thereby potentially ruling out temporal coding of pure tones above about 4 kHz (Sek and Moore 1995). Consistent with a temporal code for pitch, humans’ ability to discriminate the frequency of pure tones degrades rapidly between 4 and 8 kHz, as would be expected if temporal information were necessary for accurate discrimination (Moore 1973). In addition, studies have found that melody perception becomes dif fi cult or impossible when all the tones are above 4–5 kHz, even when the melodies are highly familiar (e.g., Attneave and Olson 1971; Licklider 1954), but see Burns and Feth (1983). Thus, the upper limit of melodic pitch, and perhaps even the upper limit of the musical instruments, may be due to the physiological phase-locking limits of the auditory nerve.
Here we review some data suggesting that pure tones well above 6 kHz, which alone produce very poor melodic pitch perception, can, when combined within a harmonic complex, produce a pitch that is salient enough to carry a melody. We explore this phenomenon further, estimating the accuracy of the representation of the individual tones, along with the complex tones, by measuring frequency (or F0) difference limens. We fi nd an interesting dissociation between the relationship between pure-tone and complex-tone pitch discrimination at low (<4 kHz) and high (>6 kHz) frequencies. Finally, some possible explanations of these findings are offered.
2 Melody Perception with All Components Above 6 kHz
2.1 Methods
Details of the methods can be found in Oxenham et al. (2011). Briefly, listeners were presented with two four-note melodies and were asked to judge whether the two melodies were the same or different. The notes from each melody were selected randomly from the diatonic (major) scale within a single octave. On half the trials, the second melody was the same as the first; on the other half of the trials, the second or third note of the second melody was changed up or down by one scale step. The tones were presented at a level of 55 dB SPL per component (65 dB SPL per component for pure tones below 3 kHz) and were embedded in a background threshold-equalizing noise (TEN) with a level of 45 dB SPL per equivalent rectangular auditory-filter bandwidth (ERBN) (Moore et al. 2000), with an additional TEN, presented at 55 dB SPL per ERBN, and low-pass filtered at 6 kHz. Each note was 300 ms, including 10-ms onset and offset ramps, and was separated from the next by 200 ms.
Three conditions were tested in the main experiment. In the first (pure-tone low), the first melody was constructed from pure tones on a diatonic scale between 500 and 1,000 Hz, and the second melody was constructed from pure tones between 2,000 and 4,000 Hz, i.e., two octaves higher than the first melody. In the second condition (pure-tone high), the first melody was constructed from pure tones between 1,500 and 3,000 Hz, and the second melody was constructed from pure tones between 6,000 and 12,000 Hz. In the third condition (complex-tone high), the first melody was constructed from pure tones between 1,000 and 2,000 Hz, and the second melody was constructed from harmonic complex tones with F0s between 1,000 and 2,000 Hz, band-pass filtered with corner frequencies of 7,500 and 16 kHz and 30-dB/octave slopes, so that all components below 6 kHz fell below their masked threshold in the background noise.
Six young listeners with audiologically normal hearing passed the screening to ensure that their 16-kHz pure-tone thresholds in quiet were no higher than 50 dB SPL. Listeners were presented with the melodies in blocks of 60 trials, each with 20 trials per condition (10 same and 10 different). After practice consisting of 2 blocks, a total of 10 blocks were run per condition, yielding 200 trials per subject and condition. No feedback was provided.
2.2 Results
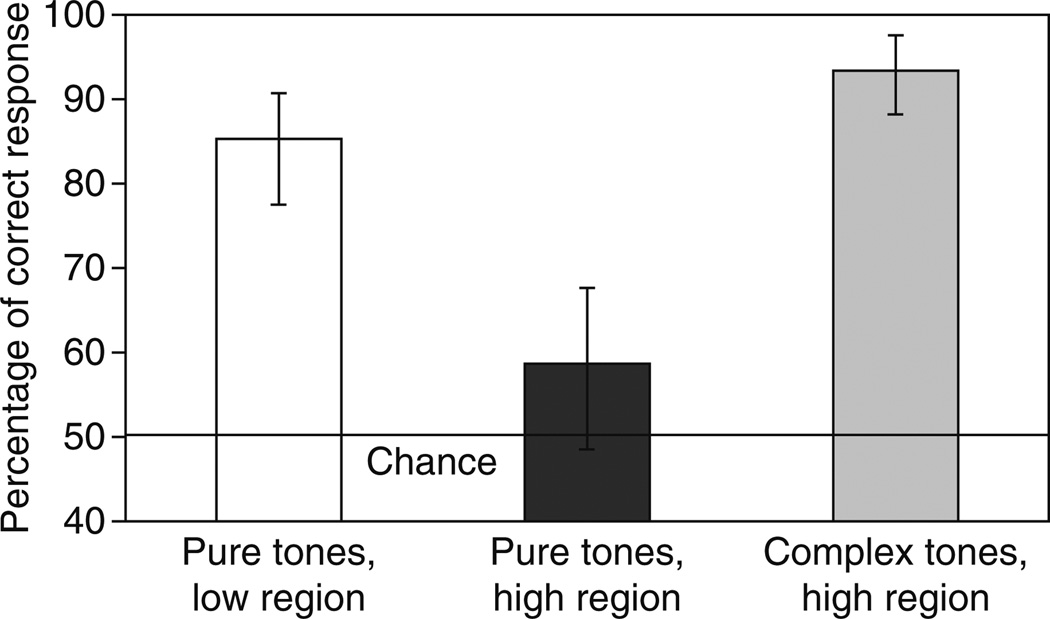
The results are shown in Fig. 16.1. As expected, performance in the pure-tone low condition was good, with an average score of about 85 % correct (based on the unbiased maximum percent correct for the obtained value of d′), and performance in the pure-tone high condition was poor, with an average score of about 59% correct. Performance in the complex-tone high condition was good (94%) and was not significantly different from that for the pure-tone low condition, despite the fact that none of the audible components in the complex tone was below 6 kHz.
Fig. 16.1.
Percentage of correct responses in the melody-discrimination task. Error bars show 95% confidence intervals
2.3 Discussion
The results suggest that tones above 6 kHz can elicit a salient pitch, sufficient for melody recognition, when they combine to form a harmonic complex tone with a lower F0 (in this case between 1 and 2 kHz). A less interesting interpretation would be that the components are at least partly unresolved and that listeners are sensitivity to the waveform (or temporal envelope) repetition rate of between 1 and 2 kHz, rather than to the individual frequencies. This explanation was unlikely because the tones were presented in random phase, which weakens envelope cues, and because the repetition rates were so high (1–2 kHz) that sensitivity to envelope pitch was expected to be very poor (Carlyon and Deeks 2002). Indeed, two control conditions (run with new groups of six subjects), involving shifted harmonics and dichotic presentation, produced results consistent with predictions based on the processing of individual components, rather than the temporal envelope: when the harmonics were shifted to produce inharmonic complexes but with an unchanged temporal envelope rate, performance dropped to near-chance levels of about 55%. On the other hand, when the harmonics were presented to opposite ears, performance remained high and not significantly different from that for the original (dichotic) condition. Overall, the results are not consistent with the previously defined “existence region” of pitch (Ritsma 1962). The results also highlight an interesting dissociation, whereby high-frequency tones, which alone do not induce a salient pitch, combine within a complex tone to elicit a salient pitch.
3 Comparing Frequency and F0 Difference Limens
There are different possible explanations for why a dissociation in pitch salience is observed between high-frequency pure tones and complex tones. One possible explanation is that the upper limit for perceiving melodic pitch is determined at a level higher than the auditory nerve, perhaps due to lack of exposure to high (>4 kHz) F0s in normal acoustic environments. Thus, when individual high-frequency tones are presented, they elicit a pitch beyond the “existence region” of melodic pitch. However, when the high-frequency tones are presented in combination with other harmonically related tones, they elicit a pitch corresponding to the F0, which falls within the “existence region.”
Another explanation is that the limits of melodic pitch perception are determined peripherally and that multiple components elicit a more salient pitch simply due to a combination of multiple independent information sources. Based on the results from lower frequencies, this explanation seems less likely: little or no improvement in pitch discrimination is found when comparing the results from individual pure tones with the results from a complex tone comprised of those same pure tones (Faulkner 1985; Goldstein 1973). However, similar measurements have not been made at high frequencies, so it is unclear whether a similar pattern of results would be observed.
3.1 Methods
Seven young normal-hearing listeners participated in this experiment, screened as before for detection thresholds in quiet at 16 kHz no higher than 50 dB SPL. Difference limens for complex-tone F0 (F0DLs) and difference limens for pure-tone frequency (FDLs) were measured. Two nominal F0s were tested: 280 Hz and 1,400 Hz. FDLs were measured for two sets of eight nominal frequencies, corresponding to harmonics 5–12. The complex tones were generated by band-pass-filtering broadband harmonic complexes, such that only harmonics 5–11 of the complex tones at the nominal F0s were within the filter passband. All tones were presented at a level of 55 dB SPL per component within the filter passband. The filter slopes were 30 dB/octave. As in the previous experiment, random component starting phases were used on each presentation. The tones were 300-ms long each, including 10-ms onset and offset ramps, and both pure and complex tones were presented in the same combination of broadband noise and low-pass TEN that was used in the previous experiment. The background noise started 200 ms before the onset of the first tone and ended 200 ms after the offset of the last tone, for the current trial. The interstimulus interval was 500 ms.
The F0DLs and FDLs were measured using both a 2I-2AFC task and a 3I-3AFC task. The first requires a labeling (up vs. down), whereas the second requires only identification of the interval that was different. For both tasks, thresholds were measured using an adaptive, two-down one-up procedure (Levitt 1971). The stimuli were generated digitally and played out via a soundcard (Lynx Studio L22) with 24-bit resolution and a sampling frequency of 48 kHz. They were presented monaurally to the listener via Sennheiser HD 580 headphones.
3.2 Data Analysis
The individual FDLs within each of the two spectral regions were used to compute predicted F0DLs for the respective spectral region using the following equation:
| (16.1) |
where θ̂ is the predicted F0DL and θn denotes the FDL measured using a nominal test frequency corresponding to the nth harmonic of the considered nominal F0. The equation stems from the general equation for predicting sensitivity based on multiple, statistically independent observations, assuming an optimal (maximum-likelihood ratio) observer (Goldstein 1973; Green and Swets 1966). The measured and predicted thresholds were log-transformed before statistical analyses using repeated measure analyses of variance (ANOVAs).
3.3 Results
Figure 16.2 shows the mean F0DLs and FDLs for the two F0s and two tasks (2- or 3-AFC). Considering first the complex-tone F0DLs, a two-way RMANOVA was performed on the log-transformed data, with the task (2I-2AFC, 3I-3AFC) and F0 (280 Hz, 1,400 Hz) as within-subject factors. No significant main effect of task was observed [F(1, 6) = 0.08, p = 0.786]. The effect of nominal F0 just failed to reach significance [F(1, 6) = 5.57, p = 0.056]. No significant interaction between the two factors was observed either [F(1, 6) = 0.015, p = 0.906].
Fig. 16.2.
Mean F0DLs (left) and FDLs (right). The numbers at the top are the pure-tone frequencies (kHz) for the high-frequency (upward-pointing triangles) and low-frequency (downward-pointing triangles) regions. Error bars show 95% confidence intervals
Considering next the FDLs, a three-way RMANOVA on the log-transformed FDLs yielded a significant difference between the low- and high-frequency regions [F(1,6) = 99.31, p < 0.0005], reflecting the fact that FDLs were generally larger in the high-frequency than low-frequency region. A significant main effect of harmonic number was observed [F(7, 42) = 6.29, p < 0.0005], as was a significant interaction between the frequency region and harmonic number [F(7, 42) = 7.08, p < 0.0005], consistent with the observation that FDLs varied more with harmonic number in the high- than in the low-frequency region. Finally, a significant main effect of task [F(1, 6) = 8.28, p = 0.028] was observed: on average, FDLs measured with the 3I-2AFC task were slightly, but significantly, smaller than the FDLs measured with the 2I-2AFC task. The seemingly better FDLs at the highest frequencies may be due to loudness or audibility cues, as the higher-frequency tones become less audible due to the band-pass filter, and to the steeply rising absolute-threshold curve, at and above 16 kHz.
The small filled symbols represent the predicted F0DLs based on optimal integration of the information from the individual components. In the low-frequency region, the predicted F0DL was lower (better) than the measured F0DL. In contrast, in the high-frequency region, the predicted F0DL was on par with the measured F0DL.
3.4 Discussion
The finding of poorer-than-predicted F0DLs in the low-frequency region is in line with earlier studies (Gockel et al. 2005; Goldstein 1973; Moore et al. 1984 b) and suggests either that the human auditory system is unable to optimally combine information across frequency when estimating F0 or that mutual interference between simultaneous harmonics degrades the peripheral information on which the optimal processor operates (e.g., Moore et al. 1984 a). However, the fact that a different pattern of results was observed in the high-frequency region complicates the interpretation, as it is not immediately clear why mutual interference should occur at low but not at high frequencies or why information integration should be optimal at high, but not at low, frequencies. Again, multiple interpretations are possible.
One is that FDLs and F0DLs are not limited by peripheral-coding limitations at low frequencies, but by a more central “noise” source at the level of pitch representations. That may explain the limited benefit of combining several low-frequency harmonics. However, at very high frequencies, a more peripheral “noise” may begin to dominate performance, perhaps due to poorer phase locking, and “swamp” the influence of more central noise sources. Once the peripheral noise (which may be uncorrelated across channels) becomes dominant, then more optimal integration of information may occur.
In summary, the comparison of FDLs and F0DLs has revealed an interesting difference between the pattern of results at low and high frequencies. Further exploration of this difference may help in the search for the basic coding principles of pitch perception.
Acknowledgments
Data from Experiment 1 were published in Oxenham et al. (2011). We thank Adam Loper for help with data collection. The work was supported by NIH grant R01 DC 05216.
References
- Attneave F, Olson RK. Pitch as a medium: a new approach to psychophysical scaling. Am J Psychol. 1971;84:147–166. [PubMed] [Google Scholar]
- Burns EM, Feth LL. Pitch of sinusoids and complex tones above 10 kHz. In: Klinke R, Hartmann R, editors. Hearing - physiological bases and psychophysics. Berlin: Springer; 1983. pp. 327–333. [Google Scholar]
- Carlyon RP, Deeks JM. Limitations on rate discrimination. J Acoust Soc Am. 2002;112:1009–1025. doi: 10.1121/1.1496766. [DOI] [PubMed] [Google Scholar]
- Cohen MA, Grossberg S, Wyse LL. A spectral network model of pitch perception. J Acoust Soc Am. 1995;98:862–879. doi: 10.1121/1.413512. [DOI] [PubMed] [Google Scholar]
- Faulkner A. Pitch discrimination of harmonic complex signals: residue pitch or multiple component discriminations. J Acoust Soc Am. 1985;78:1993–2004. doi: 10.1121/1.392656. [DOI] [PubMed] [Google Scholar]
- Gockel H, Carlyon RP, Plack CJ. Dominance region for pitch: effects of duration and dichotic presentation. J Acoust Soc Am. 2005;117:1326–1336. doi: 10.1121/1.1853111. [DOI] [PubMed] [Google Scholar]
- Goldstein JL. An optimum processor theory for the central formation of the pitch of complex tones. J Acoust Soc Am. 1973;54:1496–1516. doi: 10.1121/1.1914448. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. New York: Krieger; 1966. [Google Scholar]
- Houtsma AJM, Smurzynski J. Pitch identification and discrimination for complex tones with many harmonics. J Acoust Soc Am. 1990;87:304–310. [Google Scholar]
- Kaernbach C, Bering C. Exploring the temporal mechanism involved in the pitch of unresolved harmonics. J Acoust Soc Am. 2001;110:1039–1048. doi: 10.1121/1.1381535. [DOI] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49:467–477. [PubMed] [Google Scholar]
- Licklider JCR. “Periodicity” pitch and “place” pitch. J Acoust Soc Am. 1954;26:945. [Google Scholar]
- Meddis R, O’Mard L. A unitary model of pitch perception. J Acoust Soc Am. 1997;102:1811–1820. doi: 10.1121/1.420088. [DOI] [PubMed] [Google Scholar]
- Moore BCJ. Frequency difference limens for short-duration tones. J Acoust Soc Am. 1973;54:610–619. doi: 10.1121/1.1913640. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Glasberg BR, Shailer MJ. Frequency and intensity difference limens for harmonics within complex tones. J Acoust Soc Am. 1984;75:550–561. doi: 10.1121/1.390527. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Huss M, Vickers DA, Glasberg BR, Alcantara JI. A test for the diagnosis of dead regions in the cochlea. Br J Audiol. 2000;34:205–224. doi: 10.3109/03005364000000131. [DOI] [PubMed] [Google Scholar]
- Oxenham AJ, Micheyl C, Keebler MV, Loper A, Santurette S. Pitch perception beyond the traditional existence region of pitch. Proc Natl Acad Sci U S A. 2011;108:7629–7634. doi: 10.1073/pnas.1015291108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer AR, Russell IJ. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hear Res. 1986;24:1–15. doi: 10.1016/0378-5955(86)90002-x. [DOI] [PubMed] [Google Scholar]
- Ritsma RJ. Existence region of the tonal residue. I. J Acoust Soc Am. 1962;34:1224–1229. [Google Scholar]
- Rose JE, Brugge JF, Anderson DJ, Hind JE. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel monkey. J Neurophysiol. 1967;30:769–793. doi: 10.1152/jn.1967.30.4.769. [DOI] [PubMed] [Google Scholar]
- Schroeder MR. Period histogram and product spectrum: new methods for fundamental-frequency measurement. J Acoust Soc Am. 1968;43:829–834. doi: 10.1121/1.1910902. [DOI] [PubMed] [Google Scholar]
- Sek A, Moore BCJ. Frequency discrimination as a function of frequency, measured in several ways. J Acoust Soc Am. 1995;97:2479–2486. doi: 10.1121/1.411968. [DOI] [PubMed] [Google Scholar]
- Wightman FL. The pattern-transformation model of pitch. J Acoust Soc Am. 1973;54:407–416. doi: 10.1121/1.1913592. [DOI] [PubMed] [Google Scholar]