BETASEQ: a powerful novel method to control type-I error inflation in partially sequenced data for rare variant association testing

Abstract

Summary: Despite its great capability to detect rare variant associations, next-generation sequencing is still prohibitively expensive when applied to large samples. In case-control studies, it is thus appealing to sequence only a subset of cases to discover variants and genotype the identified variants in controls and the remaining cases under the reasonable assumption that causal variants are usually enriched among cases. However, this approach leads to inflated type-I error if analyzed naively for rare variant association. Several methods have been proposed in recent literature to control type-I error at the cost of either excluding some sequenced cases or correcting the genotypes of discovered rare variants. All of these approaches thus suffer from certain extent of information loss and thus are underpowered. We propose a novel method (BETASEQ), which corrects inflation of type-I error by supplementing pseudo-variants while keeps the original sequence and genotype data intact. Extensive simulations and real data analysis demonstrate that, in most practical situations, BETASEQ leads to higher testing powers than existing approaches with guaranteed (controlled or conservative) type-I error.

Availability and implementation: BETASEQ and associated R files, including documentation, examples, are available at http://www.unc.edu/∼yunmli/betaseq

Contact: songyan@unc.edu or yunli@med.unc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recent advances in next-generation sequencing technologies have made it possible to detect rare variant associations in genetic studies of complex diseases. While rare variants tend to exert stronger effects on complex traits than common variants (Cohen et al., 2004; Fearnhead et al., 2004; Gorlov et al., 2008; Pritchard, 2001), accurate detection of rare variant association typically requires sequencing at least hundreds or thousands of individuals at high coverage, which remains cost prohibitive for most investigators. In the literature, a two-stage design is often adopted in rare variant association studies (Prokopenko et al., 2009; Raychaudhuri et al., 2011; Sanna et al., 2011) to reduce costs. In the two-stage design, a subset of individuals are sequenced in stage 1 to discover variants, and the identified variants are then genotyped on the remaining individuals in stage 2. With a fixed budget, this two-stage design enjoys the advantage of increased sample size at potentially influential variants and thus may achieve a higher testing power than a one-stage approach in which all individuals used for association analysis are sequenced.

Under the reasonable assumption that causal variants are enriched in cases, it is appealing to sequence only cases to improve power of association testing in the two-stage design. However, as has been shown (Li and Leal, 2009), sequencing only cases leads to inflated type-I error if stage 1 (sequence) and stage 2 (genotype) data are simply combined, because this partial sequencing strategy causes the distribution of detected (and thus tested) variants to be different between cases and controls. Several methods have been proposed to correct this inflated type-I error. Among them, using genotyped samples only (GSO) (Liu and Leal, 2012) and removing one variant carrier from the sequenced sample per variant nucleotide site (ROPS) (Longmate et al., 2010) manage to control type-I error by dropping all or a subset of cases sequenced in stage 1. GSO and ROPS do not make full use of the genetic information in a sample and thus inevitably incur loss in efficiency. A more powerful method, SEQCHIP (Liu and Leal, 2012), was proposed recently to correct the inflation created by such two-stage partial sequencing design. Instead of discarding some sequenced cases, SEQCHIP corrects genotypes of sequenced individuals in terms of the genotypes of genotyped individuals, such that the corrected genotypes of sequenced individuals follow an almost identical distribution as those among genotyped individuals. SEQCHIP does not drop any individuals in the analysis and thus is potentially more efficient than GSO and ROPS. However, SEQCHIP suffers from abandoning some identified rare variants during the correction process and is thus still underpowered. Moreover, the minor allele frequency (MAF) in SEQCHIP can be slightly underestimated, which may further impair the performance of SEQCHIP.

Clearly and intrinsically, the inflated type-I error is due to only a portion of cases being sequenced. Motivated by the intuition that more variants would be discovered if the un-sequenced individuals were also sequenced, we propose BETASEQ, a beta distribution-based method, to correct inflation of type-I error when sequencing only a subset of cases. Unlike existing methods, BETASEQ keeps all original sequence and genotype data intact and corrects inflation of type-I error by supplementing pseudo-variants to the original data. The pseudo-variants are meant to mimic the extra variants that would be discovered under the counterfactual situation where individuals genotyped in stage 2 were also sequenced. Since no sequencing information is dropped, BETASEQ has the potential to be more powerful than existing methods. The number of pseudo-variants added by BETASEQ and their MAFs are estimated on the basis of the algorithm proposed by Ionita-Laza et al. (2009). BETASEQ can work with any existing rare variant association methods (Ionita-Laza et al., 2011; Lee et al., 2012; Li et al., 2010; Liu and Leal, 2010; Madsen and Browning, 2009; Morris and Zeggini, 2010; Price et al., 2010; Zawistowski et al., 2010; Wu et al., 2011) that use genotypes or imputed genotypes as input data. Moreover, unlike SEQCHIP, BETASEQ can be applied in situations where not only cases but also a small number of controls are sequenced. Extensive simulations were carried out to evaluate the performance of BETASEQ and SEQCHIP with three typical rare variant association methods: the cumulative minor-allele test (CMAT) (Zawistowski et al., 2010), extensions of the aggregated number of rare variants (ANRV) test (Morris and Zeggini, 2010) and the variable threshold (VT) test (Price et al., 2010). In addition, we also applied both BETASEQ and SEQCHIP to a real sequencing dataset (Nelson et al., 2012) from the population-based CoLaus study (Firmann et al., 2008) with the three rare variant association tests. Results from simulations and real data application demonstrate the advantages of the proposed method over existing ones and establish that BETASEQ is effective for combining sequence and genotype data from the two stages for rare variant association testing.

2 METHODS

Suppose there is a dataset of 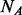cases and 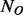controls. Without loss of generality, we assume 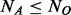. In this article, we will focus on the situation where rare variants in a genomic region increase susceptibility to disease and assume all variants are biallelic. 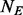cases and 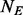controls ( 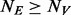and 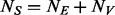) are randomly selected and sequenced to discover variants in stage 1 then in stage 2 the remaining 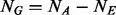cases and 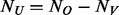controls are genotyped at the variant sites identified in the 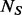sequenced individuals. Our BETASEQ algorithm is composed of three key steps. First, following Ionita-Laza et al. (2009), we assume the spectrum of MAFs of the variants follows a scaled beta distribution and estimate its parameters from the 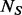sequenced individuals. Second, we estimate the number and MAFs of pseudo-variants which would be discovered if the un-sequenced 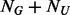individuals were also sequenced and add these pseudo-variants. Lastly, we compare the distributions of rare variants among cases and that among controls and supplement additional rare variants into controls by criteria specified in section 2.3. A theoretical justification of BETASEQ can be found in Appendix A of supplementary materials.

2.1 Step I: estimate the parameters of scaled beta distribution

The spectrum of MAFs is assumed to follow a scaled beta distribution. As shown in the literature (Ionita-Laza et al., 2009; Wright, 1951), the scaled beta distribution is a good approximation for the spectrum of MAFs at biallelic markers under a neutral selection and mutation-drift equilibrium. It is mathematically convenient and has been frequently used (Coram and Tang, 2007; Ionita-Laza et al., 2009; Ionita-Laza and Laird, 2010; Wright, 1951). We hereby follow Ionita-Laza et al. (2009) to estimate the parameters of the scaled beta distribution from variants discovered among sequenced individuals. Assume the total number of biallelic variants in the given genomic region is an unknown scalar 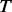. Let 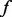be the unobserved MAF at a variant site, and let 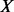be the number of minor alleles at that site observed among the sequenced 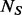individuals (that is, among 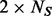alleles, minor allele count is X). By Hardy–Weinberg equilibrium, 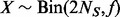. 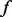is assumed to follow a scaled beta distribution and its density takes the following form:

(1.1)

where 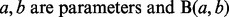is beta function. Let 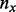be the number of variants with exactly 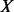minor alleles observed. and 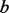can be estimated by maximizing the following likelihood function based on variants detected in the 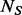sequenced individuals:

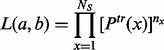(1.2)

where

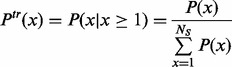(1.3)

and

(1.4)

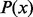is the probability that exactly 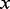minor alleles are observed at a variant site and 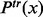follows a zero-truncated beta-binomial distribution for 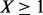. The existing optimization package in R or SAS can be used to maximize the likelihood function and the integrals in the likelihood function can be calculated by Gaussian quadrature in terms of the scaled beta distribution in equation (1.1).

In the original Ionita-Laza et al. (2009), the proportion of individuals carrying at least one minor allele at a variant site is assumed to follow a beta distribution. Since supplementing pseudo-variants entails the MAF distribution, our algorithm further assumes MAF 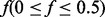to follow a scaled beta distribution.

2.2 Step II: add pseudo-variants by the scaled beta distribution

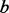With and estimated, Ionita-Laza et al. (2009) provided a method to predict the number of potential variants that would be detected if the un-sequenced individuals were also sequenced for any given minimum frequency. However, to generate these pseudo-variants, we need not only the number but also the MAFs of these pseudo-variants. While MAFs of ‘all’ single nucleotide polymorphisms (SNPs) in the genetic region follow the scaled beta distribution, MAFs of pseudo-variants to be added (variants missed by partial sequencing) do not necessarily follow the same distribution.

Based on the algorithm of Ionita-Laza et al. (2009), we propose to estimate the MAFs of the pseudo-variants and generate them from the scaled beta distribution in the following way. First, split 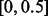(domain of variant MAFs) into equally spaced intervals each with length 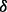, denote the intervals by 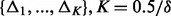. Next, estimate the number of potentially discovered variants 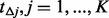for each small interval 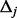(details to follow). Afterward, for each small interval 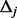, generate 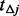minor allele frequencies 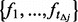from a uniform distribution bounded by the interval 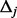. Finally, within each small interval 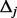, generate the minor alleles of 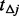variants among the un-sequenced individuals in terms of 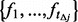based on binomial distributions with size 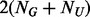and success probability 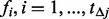. Note that if 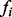is so small such that no minor alleles are generated then that variant is simply dropped.

The choice of interval length 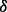. The choice of 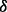cannot be arbitrary and should depend on the size of the un-sequenced individuals (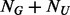). As illustrated in Appendix B of supplementary materials, given the value o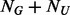f , if 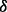is too small then inadequate rare variants will be generated, which will consequently cause the algorithm to fail to control type-I error even after we supplement extra rare variants in step III; if 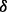is too large then we might produce too many rare variants such that type-I error will become over-corrected and testing power will be suppressed. Conceivably, a good 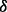should allow the first MAF interval 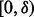to maximally generate variants with only one minor allele observed in the 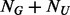individuals. Here we propose to obtain an optimal 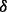by maximizing the expectation of the probability of observing one minor allele over the first MAF interval 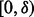in the 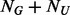individuals. That is,

(1.5)

Estimation of the number of pseudo-variants. Following Ionita-Laza et al. (2009), let 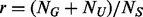denote the ratio between the number of un-sequenced individuals and the sequenced. 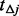(the number of potential variants to be discovered in the MAF interval 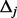if the 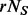individuals were sequenced) can be estimated by

(1.6)

where 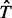is an estimator of 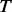(the total number of biallelic variants in the given genomic region) and 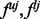are the upper and lower bounds of the interval Δ_j. The details of derivation for 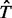and equation (1.6) can be found in Appendix C and D of supplementary materials.

2.3 Step III: supplement additional pseudo-variants

2.3.1 Why should we supplement additional pseudo-variants?

Overall, step II works well and is capable of predicting the number of pseudo-variants closely to the truth, especially when r is small (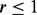) and MAFs are not very low (MAF 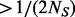). However, step II cannot completely predict the number of potential variants with extremely low MAFs especially when 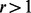(similar observation was reported in Ionita-Laza et al., 2009) for the following reasons: (i) beta distribution is only an approximation of the spectrum of MAFs and cannot completely predict the number of extremely low frequency variants; (ii) the number of sequenced individuals is usually smaller than that of un-sequenced ones and it is unstable to extrapolate beyond the limit of the actually sequenced data. Consequently, 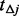will be underestimated when increases or 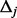falls at the very low end of the MAF spectrum. Because of the underestimation of 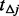, under null hypothesis, the spectrum of rare variants can still differ considerably between cases and controls even after step II.

For the reasons above, it is impossible to make precise prediction regarding MAF distribution among controls from sequenced individuals without making additional assumptions. Intuitively, a simple way to eliminate the difference in the low end of the MAF spectrum between cases and controls is to add some additional variants into un-sequenced controls. Based on this intuition, in step III, an algorithm is developed to add additional pseudo-variants into un-sequenced controls as a further remedy for step II. Calculations in step III are based on combination of real variants discovered among the sequenced individuals and pseudo-variants added by step II.

2.3.2 Type of additional pseudo-variants.

In step III, we only add pseudo-variants into un-sequenced controls and the focus is on rare variants that are found exclusively in cases or exclusively in controls. These variants usually have the lowest MAFs and thus suffer most from the underestimation of 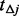and contribute most to the MAF spectrum difference between cases and controls. Under the null hypothesis, if all cases and controls were sequenced, rare variants present only among controls can be assumed to distribute similarly as their counterparts among cases for a balanced design where the numbers of cases and controls are the same or similar. Based on this assumption, the algorithm supplements additional variants into the un-sequenced 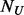controls by comparing rare variants exclusively found in cases with those in controls. The details of the algorithm are described in 2.3.2, 2.3.3 and 2.3.4.

2.3.3 The procedure of adding additional pseudo-variants.

In our algorithm, step III always adds minor alleles of additional variants to un-sequenced controls, which are compared with a group of cases of the same size 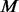. If 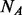(the number of cases) equals to 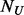(the number of un-sequenced controls), then 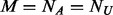and add extra variants to the un-sequenced 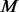controls by comparing with the MAF spectrum of the 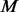cases. If 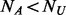, let 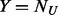and the algorithm iterates between the next two stages: (i) let 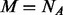choose the first 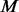un-sequenced controls out of the 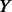un-sequenced controls and add extra variants to the chosen 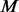controls based on the MAF spectrum of the 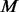cases; (ii) afterward, let 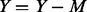, for the remaining 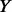un-sequenced controls if 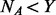, then go back to stage (i), otherwise proceed to stage (iii): let 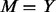and add additional variants to the remaining 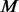un-sequenced controls by comparing with the 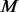cases, which are randomly selected out of the 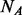cases. Under the rare scenario where 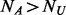, let 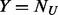and simply follow stage (iii) above. The MAFs and number of additional pseudo-variants to be added for each pair of 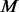cases and 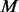un-sequenced controls are specified in the following sections 2.3.4, 2.3.5 and 2.3.6.

2.3.4 The MAFs of additional pseudo-variants.

For the purpose of comparison, in step III, MAFs are estimated separately for 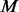cases and 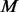un-sequenced controls. For a group of size 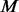, the estimable MAFs of variants are discrete and can only take values from set 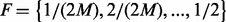. Given the value of 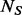(number of sequenced individuals), 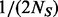is the minimum MAF that can be estimated from the observed data. Define 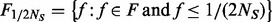, the number of variants exclusively found in controls with MAF 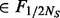is thus likely to be underestimated in step II. Based on the analysis above, our algorithm adds additional variants for any MA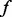F if 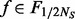. Under the rare scenario where 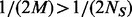, additional variants with 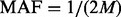will be supplemented in the same manner detailed below in sections 2.3.5 and 2.3.6.

2.3.5 The numbers of additional pseudo-variants.

For each 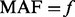satisfying conditions described above that needs additional variant supplementation, let 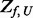denote the number of variants with 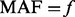and found exclusively among 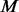un-sequenced controls and let 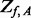be the counterpart among 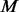compared cases. 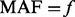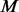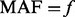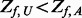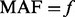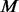The additional variants with are supplemented into the controls by the following two criteria: (i) additional variants of will be added only if after step II; (ii) additional variants with in controls are added such that .

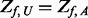2.3.6 The way to add additional pseudo-variants.

To make newly added variants found exclusively among 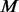un-sequenced controls, we randomly assign the calculated number of minor alleles (determined by MAF f and M) of the newly added variants to the 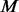controls and set genotypes of these variants to major allele homozygote for all other individuals.

After step III, the number of variants with every estimable MAF satisfying the conditions in 2.3.3 is equal to or greater than that in 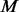cases, which could result in overcorrection of type-I error especially when r is big. We note that under the alternative hypothesis, some bona fide MAF spectra differences between cases and controls would be removed by step III and power is reduced to a certain extent due to the loss of bona fide frequency differences. Specifically, testing power will decrease as r increases. This is not surprising since low testing power is expected when only a small portion of individuals are sequenced. We provide an example in Appendix E of supplementary materials to show the number and MAFs of pseudo-variants added by BETASEQ in each step.

3 SIMULATIONS

3.1 Simulation design

Extensive simulations under a range of settings were carried out to evaluate the performance of the proposed and existing methods. Genotypes were generated using COSI (Schaffner et al., 2005), which mimics the linkage disequilibrium pattern, local recombination rate and the population history for Europeans using a coalescent model. In all settings, genotypes were determined by simulating 10 000 chromosomes for a 1 MB region. We randomly generated 100 sets of the 1 MB region and each set contains ∼20 K SNPs on average. The middle 2 K SNPs were chosen from the ∼20 K variants for each of the 100 sets. The number of actually observed variants for any given dataset depends on the sample size and is expected to be <2K. We considered four scenarios of sample size: 500 cases/500 controls, 400 cases/600 controls, 1000 cases/1000 controls and 750 cases/1250 controls. For each scenario, 10 datasets were simulated from each of the 100 sets and a total number of 1000 replicates were created. Let q be the percentage of sequenced cases, following the simulation design in Liu and Leal (2012), in each of the 1000 replicates, we sequenced q = 5, 10, 30, 50, 70 and 90% of cases to discover variants, and the detected variants were genotyped in the remaining individuals. Considering some controls may also be sequenced in practice, we also conducted simulations in which 90% of cases and 10% of controls were sequenced for all the sample size scenarios.

The case/control status under alternative hypothesis was generated in the same way as in Wu et al. (2011). For each dataset, 5% of variants that have MAF <3% were selected to be causal. The case/control status y for each individual was determined using the following logistic model:

(1.7)

where 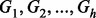are genotypes of 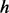causal variants and betas are the effect sizes of the causal rare variants. 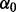is the disease prevalence and was set to be 1%. The magnitude of each 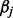was chosen in a way to make rarer variants have greater effects. Here 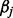was set to 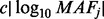and .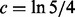

Type-I errors and powers of three rare variant association tests, VT, ANRV and CMAT, were calculated under BETASEQ and SEQCHIP. We used the VT, ANVR and weighted sum statistics (WSS) functions implemented in the SEQCHIP R package (Liu and Leal, 2012) to carry out these three rare variant tests (CMAT is regarded as an extension of weighted sum statistics method in the SEQCHIP R package and thus named WSS). GSO and ROPS have been demonstrated inferior to SEQCHIP (Liu and Leal, 2012) and thus were not evaluated in this article. For each of these tests, variants with observed MAF <3% were considered as rare. One-sided tests were performed, that is, the alternative hypothesis states that more causal alleles are in cases than in controls. The P-values for CMAT and VT were obtained empirically using 1000 permutations. Significant level 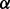was set to 0.05 throughout the simulation study. Only results for settings 400 cases/600 controls and 750 cases/1250 controls are presented in the main text. Those for 500 cases/500 controls and 1000 cases/1000 controls show similar patterns and are displayed in Appendix F of supplementary materials.

We also conducted simulations to compare BETASEQ and SEQCHIP when genetic effect does not depend on MAF. The results can be found in Appendix G of supplementary materials. Moreover, we also performed simulations under a more stringent significant threshold (0.001). Results can be found in Supplementary Appendix H. Furthermore, to demonstrate the performance of BETASEQ and SEQCHIP for quadratic test, we applied SKAT on the datasets corrected by BETASEQ and SEQCHIP and display the results in Supplementary Appendix I. In addition, we also evaluated the effect of the size of collapsing unit in Supplementary Appendix J. Finally, since each method is more powerful than the other in most settings where it is less conservative, we also compared the powers when Type-I error was controlled at exactly 0.05 for both methods. Supplementary Appendix K presents these true power results when we used empirical significance threshold to control Type-I error at exactly 0.05.

3.2 Type-I error

Table 1 shows the type-I errors of the VT, ANRV and CMAT tests when only cases are sequenced and the data are corrected by SEQCHIP and BETASEQ. Table 2 presents the type-I errors of the VT, ANRV and CMAT tests when all cases and controls are sequenced. As indicated in Table 1, the type-I errors of the three tests in all the settings are controlled under 0.05. Compared with Table 2, both BETASEQ and SEQCHIP in Table 1 are conservative. As q (percentage of sequenced cases) increases from 5 to 90%, the conservativeness of BETASEQ is substantially mitigated, whereas SEQCHIP tends to be increasingly more conservative. For example, when 5% cases are sequenced in a sample of 750 cases and 1250 controls, the type-I errors for VT, ANRV and CMAT under SEQCHIP are 0.044, 0.026 and 0.028, whereas when 90% cases are sequenced in the same scenario, the type-errors for VT, ANRV and CMAT reduce to 0, 0 and 0, respectively. This conservativeness makes the powers of the three tests under SEQCHIP decline as q increases and we will elaborate this issue in later paragraphs. More detailed explanation for difference between SEQCHIP and BETASEQ can be found in Supplementary Appendix L of supplementary materials. Supplementary Table S8 in Supplementary Appendix M presents the type-I errors of the three tests when 90% of cases and 10% of controls are sequenced and data are integrated by BETASEQ. As shown in Supplementary Table S8, type-I errors are well controlled in all the scenarios.

Table 1.

Type-I error evaluation for partially sequenced data

Sample size cases/controls		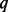Type-I errors
		VT		ANRV		CMAT
		SEQ	BETA	SEQ	BETA	SEQ	BETA
400/600	0.05	0.049	0.004	0.032	0.013	0.035	0.011
400/600	0.1	0.027	0.004	0.023	0.014	0.02	0.012
400/600	0.3	0.009	0.006	0.008	0.016	0.009	0.019
400/600	0.5	0.002	0.009	0.006	0.018	0.004	0.02
400/600	0.7	0.002	0.017	0.003	0.018	0.002	0.021
400/600	0.9	0	0.019	0.002	0.022	0.002	0.026
750/1250	0.05	0.044	0.006	0.026	0.023	0.028	0.018
750/1250	0.1	0.022	0.006	0.020	0.027	0.019	0.021
750/1250	0.3	0.005	0.007	0.005	0.029	0.004	0.023
750/1250	0.5	0.002	0.01	0.002	0.035	0	0.031
750/1250	0.7	0	0.034	0	0.044	0	0.045
750/1250	0.9	0	0.037	0	0.048	0	0.046

^aSEQ is SEQCHIP, BETA is BETASEQ. ^b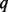 is the percentage of sequenced cases.

Table 2.

Type-I error evaluation for completely sequenced data

Sample size cases/controls	Type-I errors
	VT	ANRV	CMAT
400/600	0.042	0.045	0.053
750/1250	0.046	0.055	0.059

3.3 Power results

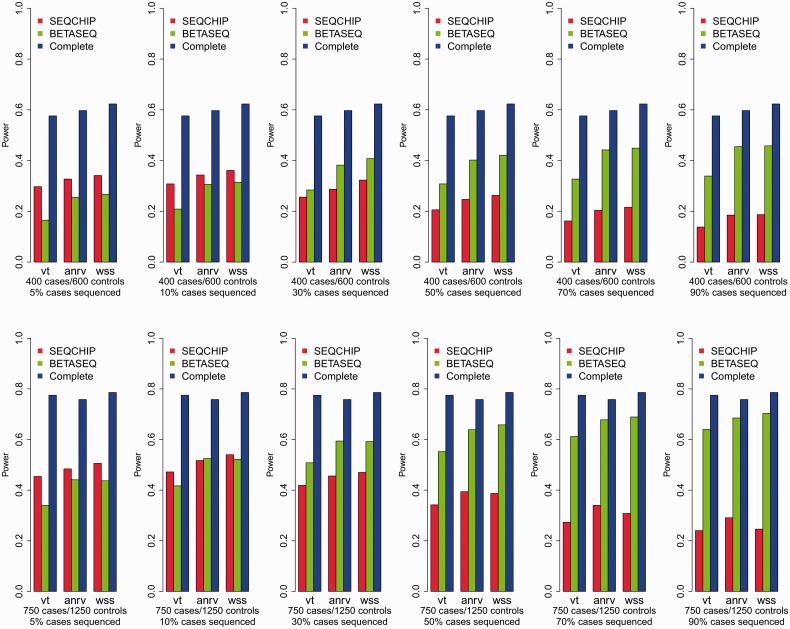
We evaluate the performance of the two data integration methods, namely SEQCHIP and BETASEQ, for VT, ANRV and CMAT in four different sample size settings. As shown in Figure 1, BETASEQ outperforms SEQCHIP in most of the scenarios. In many settings when 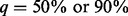, the powers under BETASEQ are close to those by sequencing all individuals in a sample (noted as Complete in Fig. 1). Under BETASEQ, the powers of VT, ANRV and CMAT keep growing as 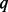(percentage of sequenced cases) increases from 5 to 90% in all the scenarios. For example, when sample size is 750 cases and 1250 controls, the powers of VT, ANRV and CMAT are 0.340, 0.441 and 0.437 when only 5% of cases are sequenced; the three powers rise to 0.552, 0.639 and 0.658 when 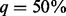and up to 0.64, 0.685 and 0.703, respectively, when 90% of cases are sequenced. In the same scenario, the full powers (Complete) of VT, ANRV and CMAT are 0.775, 0.758 and 0.786, respectively, when all cases and controls are sequenced. Thus in the setting of 750/1250 cases/controls, with only 18.75% of all individuals being sequenced (50% of cases being sequenced), we can obtain ∼80% of maximal possible powers when using BETASEQ to integrate sequence and genotype data. Similarly in the same setting under BETASEQ, ∼90% of possible full powers can be achieved by sequencing only 33.75% of all individuals (90% of cases being sequenced). In contrast, when SEQCHIP is used the powers of all three tests show a mixed pattern: they grow as 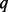increases from 5 to 10% and after that, they decrease as 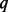rises up to 90% (Fig. 1). SEQCHIP outperforms BETASEQ in many scenarios when 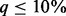, but its performance deteriorates and becomes increasingly inferior to BETASEQ as 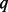increases. Taking the scenario of 750 cases and 1250 controls, for example, under SEQCHIP, if 5% of the cases are sequenced, the powers of VT, ANRV and CMAT are 0.454, 0.484 and 0.506; the three powers increase to 0.472, 0.517 and 0.540 when 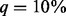; they fall to 0.342, 0.394 and 0.387 when 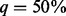and finally down to 0.24, 0.291 and 0.246, respectively, when 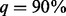. The reason for the decline in power is discussed in details in Supplementary Appendix L of supplementary materials and in appendix of Liu and Leal (2012). Briefly speaking, SEQCHIP relies on the accurate estimation of MAFs. However, SEQCHIP tends to slightly underestimate MAF (a rigorous proof using probability theory can be found in appendix of Liu and Leal, 2012). When 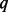is small and when not many rare variants are detected, this underestimation of MAFs does not result in severe consequences. When 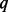increases and more cases are sequenced, the biases in MAF estimation accumulate, become increasingly serious and thus reduce the power of rare variant association tests, despite the fact that more causal rare variants are discovered at the same time. Moreover, as demonstrated in Figure 1, the highest powers under SEQCHIP are uniformly lower than those under BETASEQ. Supplementary Figure S7 of Appendix M presents the powers of the three tests when 90% of the cases and 10% of the controls are sequenced in four sample size scenarios and BETASEQ is applied to correct data. As can be seen, BETASEQ is robust, as the powers in Supplementary Figure S7 are almost the same as those when 90% of the cases and no controls are sequenced.

Fig. 1.

Comparisons of BETASEQ and SEQCHIP when sample sizes are 400 cases/600 controls and 750 cases/1250 controls. VT, ANRV and CMAT are used to test the rare variant association. The powers were calculated under a significance level of 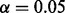with 1000 simulated datasets

4 REAL DATA ANALYSIS

We applied BETASEQ and SEQCHIP to a targeted sequencing dataset from the CoLaus study. Two thousand fifty-nine CoLaus subjects were sequenced at relatively high depth (medium depth ∼27) in the exons of 202 genes (Nelson et al., 2012). Our primary outcome of interest is anxiety. Among the 2059 subjects, 290 subjects did not have anxiety information and thus were dropped. Seven out of 202 genes on chromosome X were also excluded from analysis. The final data contained 604 cases/1165 controls and 195 genes. We adjusted for eight covariates in the analysis: gender, age, 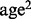, and the top five principal components constructed from CoLaus genomewide genotype data (Affymetrix 5.0) to control population stratification. Among the three rare variant association tests, ANRV itself can adjust continuous and discrete covariates while VT and CMAT cannot. For these two methods, we used BiasedUrn (Epstein et al., 2012), a permutation procedure to adjust covariates in rare variant association test, to adjust for the eight covariates (number of permutation was set to be 1000 in BiasedUrn). Variants with missingness >10% were removed. Same as in our simulations, variants with observed MAF <3% were considered as rare and one-sided tests were performed. A gene was considered to be significant if its P < 0.05 and is among the five smallest P-values by VT, ANRV and CMAT. We performed the three rare variant tests under Complete (all cases and controls are sequenced), BETASEQ and SEQCHIP. Hundred percent of the cases were sequenced and the discovered variants were genotyped on the controls under BETASEQ and SEQCHIP.

Table 3 shows the significant genes under Complete, BETASEQ and SEQCHIP. As shown in Table 3, two genes (A and B) were identified as significant by all the three tests when all the individuals were sequenced (Complete). Gene A was also identified by BETASEQ as significant. SEQCHIP failed to identify both A and B but identified another gene C as significant. For gene A, the P-values of the three tests are (0.014, 0.024, 0.076) under SEQCHIP; for gene B, the P-values are (0.36, 0.191, 0.157) under BETASEQ and (0.37, 0.236, 0.172) under SEQCHIP. For gene C, which was identified as significant under SEQCHIP, the P-values are (0.06, 0.048, 0.05) under BETASEQ and (0.059, 0.032, 0.038) under Complete. These significant genes could still be false positives because we defined significant genes according to a combination of nominal threshold of 0.05 and the rank among the tested genes instead of using stringent multiple testing correction methods. But our results suggest better concordance between BETASEQ and the oracle (that is, those under complete sequencing when all individuals are sequenced) results. Qqplots and the correlations of P-values with the oracle values are also displayed in Supplementary Appendix N.

Table 3.

Analysis of the CoLaus dataset

	Complete	BETASEQ	SEQCHIP
Significant genes	Gene A (0, 0.015, 0.015)	Gene A (0.005, 0.019, 0.017)	Gene C (0.015, 0.008, 0.015)
	Gene B (0.02, 0.007, 0.005)

Note: The three numbers under each gene are P-values of VT, ANRV and CMAT tests

5 DISCUSSION

In this article, to control type-I error of rare variant association testing, a novel method is proposed to correct partially sequenced data in case-control studies, in which only a subset of individuals (mainly cases) are sequenced to detect variants and the discovered variants are genotyped in the remaining individuals. Different from all the existing methods in literature, which drop either some sequenced cases or some detected variants to control type-I errors, our method BETASEQ conducts an in silico sequencing on the un-sequenced individuals by supplementing pseudo-variants into them, such that the spectrum of MAFs in controls becomes approximately the same as that in cases. Meanwhile, the original sequence and genotype data are kept intact. All the existing rare variant association methods that use genotypes or imputed genotypes as input data can be applied directly on the dataset corrected by BETASEQ. Besides the situations where only cases are sequenced, BETASEQ can be applied when not only cases but also a small number of controls are sequenced. BETASEQ can also be applied when study sample is stratified by some confounders and cases within each subgroup are partially selected out to sequence. In that situation, BETASEQ can be used within each subgroup stratified by confounders.

We demonstrated the performance of BETASEQ by three typical rare variant association tests: VT, ANVR and CMAT. Extensive simulations showed that when BETASEQ is used to correct partially sequenced data, the inflation of type-I errors of all the three variant association tests is well corrected. Type-I errors under BETASEQ can be conservative when 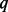(percentage of sequenced cases) is small. But the conservativeness alleviates substantially as 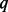increases. The powers of the three tests under BETASEQ increase with 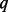and are higher than those under SEQCHIP in most scenarios. When SEQCHIP is used to integrate sequence and genotype data, type-I errors keep decreasing and eventually become conservative as 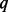increases; meanwhile powers increase first and then decrease. Under SEQCHIP, there exists an optimal fraction of cases to sequence to maximize testing power (Liu and Leal, 2012). Sequencing a larger number of samples may discover more causal variants but does not necessarily improve testing power. The optimal 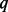depends on the underlying disease model and other factors of the settings and needs to be decided on a case by case basis (Liu and Leal, 2012), which renders explanation difficult and limits the practical utility of SEQCHIP.

In this article, we assume rare variants in a genomic region are deleterious. If rare variants are protective or exert effects in both directions, sequencing only cases may decrease testing power. If rare variants are assumed to be protective, we should sequence only controls in stage 1 because causal variants are enriched in controls. Under that situation, our algorithm can still be applied by supplementing pseudo-variants to cases. If we assume rare variants exert effects in both directions, it is more appropriate to sequence both cases and controls in stage 1 for causal variant detection. In that case, variant ascertainment bias and subsequently Type-I error control are likely no longer issues. Because BETASEQ (and all other correction methods reviewed including SEQCHIP) is proposed under the design where corrections are unidirectional, we have found, not surprisingly, that one-sided tests benefit more from our method than quadratic methods like SKAT (Supplementary Appendix I).

There is still room to improve the algorithm of supplementing pseudo-variants into un-sequenced individuals. Currently, our method is based on a parametric beta distribution to approximate the MAF spectrum of biallelic variants in a given genomic region. In some situations, real MAF spectrum can depart from the beta distribution assumption and then prediction of potential SNPs may become inaccurate. A nonparametric approach may be adopted to improve prediction accuracy. Moreover, in step III of our algorithm, we simply make the number of variants with MAFs satisfying the criteria in 2.3.4 in 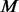controls equivalent to the counterpart in 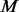cases, which can be conservative especially when percentage of sequenced cases is small. A more flexible supplementing scheme in step III might be developed to further improve testing power. However, the current algorithm strives for a balance at this point between simplicity/parsimony and efficiency, and already demonstrates satisfactory performance compared with existing approaches. Finally, BETASEQ correction is specific to the unit of analysis because the number of variants and their MAF distribution vary from one region to the next (thus specific to each analysis unit). For genome-wide usage, one can apply BETASEQ to different analysis units independently and in parallel.

In summary, results from the extensive simulations and real data analysis suggest that our proposed method is more efficient than existing methods. As rare variants are precious in rare variant association analysis, our method provides a more effective way to test rare variant association by not dropping any genetic information generated when only part of the individuals are sequenced in two-stage case-control studies.