A Statistical Framework to Guide Sequencing Choices in Pedigrees

Abstract

The use of large pedigrees is an effective design for identifying rare functional variants affecting heritable traits. Cost-effective studies using sequence data can be achieved via pedigree-based genotype imputation in which some subjects are sequenced and missing genotypes are inferred on the remaining subjects. Because of high cost, it is important to carefully prioritize subjects for sequencing. Here, we introduce a statistical framework that enables systematic comparison among subject-selection choices for sequencing. We introduce a metric “local coverage,” which allows the use of inferred inheritance vectors to measure genotype-imputation ability specifically in a region of interest, such as one with prior evidence of linkage. In the absence of linkage information, we can instead use a “genome-wide coverage” metric computed with the pedigree structure. These metrics enable the development of a method that identifies efficient selection choices for sequencing. As implemented in GIGI-Pick, this method also flexibly allows initial manual selection of subjects and optimizes selections within the constraint that only some subjects might be available for sequencing. In the present study, we used simulations to compare GIGI-Pick with PRIMUS, ExomePicks, and common ad hoc methods of selecting subjects. In genotype imputation of both common and rare alleles, GIGI-Pick substantially outperformed all other methods considered and had the added advantage of incorporating prior linkage information. We also used a real pedigree to demonstrate the utility of our approach in identifying causal mutations. Our work enables prioritization of subjects for sequencing to facilitate dissection of the genetic basis of heritable traits.

Introduction

A major goal in human genetics is the identification of genetic variants responsible for heritable diseases. Study designs based on pedigrees in which heritable diseases segregate have successfully led to the identification of over 4,500 relevant genes.¹ Although genome-wide association studies (GWASs) based primarily on unrelated subjects have also become a widely used design in the search for common risk alleles,² the hypothesis that many heritable diseases are influenced by rare risk alleles continues to support the use of pedigrees as one efficient design for identifying risk alleles.^3,4 As part of the process of risk-allele identification, the use of sequence data enables direct evaluation of variants, possibly within candidate regions already identified by linkage analysis.^5–16 However, sequencing large numbers of subjects is difficult for multiple reasons, including high cost and the need for relatively large amounts of high-quality DNA. A cost-effective way to obtain genotypes on subjects who are not sequenced is to infer missing genotypes via imputation^17–19 by combining existing sparse genotypes available on many subjects with sequence data collected on only some subjects in pedigrees. Pedigree-based imputation is particularly effective for rarer, segregating variants¹⁸ (and unpublished data).

Determining which subjects to sequence is an important design decision. Because it could be infeasible or impractical to sequence all available subjects in a pedigree, this constraint requires prioritization of a subset of subjects for sequencing. These subjects can be selected all at one time, or an initial small group of subjects can be selected for sequencing and any additional subjects can be selected depending on the results from the initial sample. When only a few subjects can be sequenced, the choice of subject selection in either case is particularly critical. All of these possibilities create challenges for the design of sequencing studies in pedigrees and suggest the need for a flexible and adaptive approach to subject selection.

It is worthwhile to consider two important issues. First, subject selection should benefit subsequent genotype imputation. Additional subjects with imputed genotypes can form an integral part of downstream analyses and have the potential to increase the statistical power to detect causal variants^19,20 (and unpublished data). Second, subject selection should benefit from the incorporation of prior knowledge of candidate regions when such information is available from, e.g., linkage analyses or GWASs.²¹ This information allows us to prioritize subjects to optimize genotype imputation in these regions.

Decisions related to subject selection should incorporate relevant information in a systematic and quantitative manner. A suitable metric is necessary for quantification of the relative values of different sequencing choices. In addition, an automated tool that systemically selects subjects would be useful. In the absence of such a tool, investigators need to use ad hoc methods to choose subjects for sequencing. Furthermore, selecting subjects manually for multiple pedigrees is tedious, so methods that facilitate automated and efficient prioritization of subjects would be helpful.

Existing tools that automate selection of subjects for sequencing are limited. PRIMUS is a program that selects subjects for sequencing.²² However, because PRIMUS aims to identify a set of maximally unrelated subjects, this approach might not be ideal for subject selection in pedigrees. ExomePicks is another program that selects subjects for sequencing (see Web Resources). Its approach is based on selecting units of related subjects from the oldest to youngest generations, which is logical because this encourages determination of haplotypes across loci. However, this algorithm does not leverage information about the descent of chromosomes in a local region of interest, nor does the program incorporate existing information about subjects who might have already been sequenced.

Here, we introduce a general subject-selection framework that facilitates the evaluation and comparison of subject-selection choices in sequencing studies. We also introduce “coverage” as one metric to naturally relate pedigree-based genotype imputation to subject selection. This metric enables the use of inferred inheritance vectors (IVs)²³ to optimize imputation of alleles in candidate regions when such information is available. Our approach can incorporate information about IVs to guide subject selection for sequencing. If a candidate region is not available, a variant of this metric can be used for optimizing selection genome-wide. This approach also provides options for manual selection of some subjects before deciding on the remaining subjects to sequence, and it optimizes choices (within realistic constraints) only among subjects who are available for sequencing. In our study, we used simulation to compare our approach with existing methods and used a real-pedigree example to demonstrate the utility of our approach. We implemented our approach in the program GIGI-Pick.

Subjects and Methods

Overview

We describe here the primary scenario that motivates our work. Linkage analysis might have already identified a candidate region that potentially contains a risk allele in a gene influencing the phenotype. For identifying the risk allele(s), sequence data are collected for directly evaluating variants in a candidate region. A limited budget is available for sequencing a maximum number of subjects. Therefore, the plan is to select a few subjects for sequencing and then impute missing genotypes for further evaluation to reduce the need for follow-up genotyping. For brevity, here we refer to the selection of subjects for sequencing as “subject selection.”

Our framework focuses on genotype imputation. In pedigrees, genotypes are imputed with information from either inferred inheritance or external population data, such as population allele frequencies.¹⁸ When information from inheritance is used, alleles are imputed with very high accuracy, even for rare alleles, and are referred to as “practically” determined¹⁸ (and unpublished data). Using imputed genotypes, we can then perform desired downstream analyses, ranging from exploratory analyses to formal statistical tests, such as family-based association tests of variants, including those for single variants^24–26 or regional associations.^20,27

Statistical Framework

Inheritance Vectors

Our framework for subject selection capitalizes on the concept of IVs. IVs²³ represent the descent of chromosomes in a pedigree at specified positions. Using IVs, we can also represent independent founder chromosomes with founder genome labels (FGLs)²⁸ (Figure S1, available online). Each subject has a pair of FGLs because he or she has two copies of chromosomes originally descended from founder chromosomes. Identity-by-descent (IBD) graphs partition FGLs into distinct components.^29,30 In an IBD graph, the nodes are the FGLs and the edges are the subjects who are sequenced and observed for the genotypes at the locus of interest. By connecting FGLs to observed subjects who have these FGLs, we can construct one or multiple disjoint IBD graphs (Figure S1). Because of meiotic recombination, IBD graphs can be different at different positions on the chromosome.

The program gl_auto³¹ from the MORGAN v.3 software package uses genotypes of relatively sparse markers, marker map positions, pedigree structure, and population allele frequencies to sample IVs that are consistent with the observed data. Here, we define these sparse markers as framework markers, which can be markers from linkage panels that consist of short tandem repeats (STRs) or sparse SNPs. Similar to many pedigree-based linkage-analysis methods,^29,32 gl_auto uses the Lander-Green framework²³ for small pedigrees. To handle large pedigrees, gl_auto uses a hybrid Markov-chain Monte-Carlo (MCMC) sampler^33,34 that is based on both the Elston-Stewart³⁵ and the Lander-Green algorithms.

Connection between Genotype Imputation and Subject Selection

In pedigrees, subject selection can affect genotype imputation. For illustration, we assume that the IV at a position of interest in the sequence data is known. If all observed alleles at that position can be unambiguously assigned to FGLs at some point in the pedigree, alleles from all unobserved subjects who share copies of these FGLs can be imputed (Figure 1A). We refer to the ability to unambiguously assign marker alleles to FGLs as the ability to phase the observed genotypes with respect to the FGLs, or for brevity, the ability to phase the observed genotypes. If the observed genotypes cannot be phased, alleles from subjects who share copies of these FGLs cannot be imputed (Figure 1B), except from subjects who share the same pair of FGLs with observed subjects (Figure 1C). Thus, the choice of subject selection affects the percentage of alleles called, defined as the percentage of alleles that are either observed or imputed with the IV in pedigree-based genotype imputation.

Figure 1.

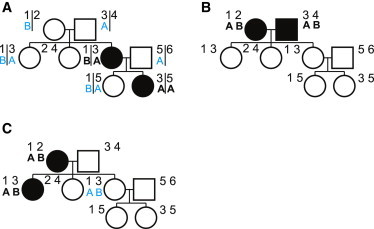
Sequencing Choices Affect the Percentage of Alleles Called

Founder chromosomes and copies of those same founder chromosomes in descendants are labeled with numbers, and alleles of genotypes are labeled with letters. Observed alleles are in bold black, and imputed alleles are in nonbold blue. Vertical lines represent alleles that can be phased unambiguously to FGLs. Subjects who were selected for sequencing are indicated by shading. Three subject-selection choices are presented: (A) parent and child are selected, and the child is homozygous for the marker, (B) founder spouses are selected, and both are heterozygous for the marker, and (C) parent and child are selected, and both are heterozygous for the marker.

Metric: Coverage

We introduce coverage as a metric to compare subject-selection choices. At this point, we continue to assume that the IV at a locus on the chromosome is known, but we will relax this assumption later. Conditional on a fixed IV for a particular choice of subject selection, coverage is the expected percentage of the copies of alleles called for a variant at a random locus. Because genotypes are not observed before sequencing, coverage is an expected value integrated over all potential genotype configurations in subjects intended for sequencing for the particular subject-selection choice. This expectation accounts for the probability of phasing genotypes, given that the probability of phasing affects the number of alleles that can be called. If no subjects are sequenced, the coverage is 0. If all subjects are sequenced or if all alleles from subjects who are not sequenced can be imputed, the coverage is 1.

Coverage is easily computed. The calculation first translates the known IV into I disjoint IBD graphs,^28,30 as denoted by ibdg_i, where i = 1, 2, …, I (Figure S1). N is defined as the number of subjects in the pedigree, so 2N is the total number of alleles in the pedigree at a locus and is the denominator for the computation of coverage. In each ibdg_i, there is a probability, p_i, that the observed genotypes can be phased and a remaining probability, q_i = 1 − p_i, that the observed genotypes cannot be phased. If the observed genotypes can be phased, a total of F_i alleles in the pedigree can be called. If the observed genotypes cannot be phased, a total of G_i alleles can be called, where 0 ≤ G_i ≤ F_i. Then, the calculation combines the number of alleles expected to be called from all ibdg_i partitions. Thus, coverage is expressed as

$$\text{coverage}=\sum \left(F_i{p}_i+G_i{q}_i\right)/2N\text{.}$$ (Equation 1)

The terms F_i and G_i in Equation 1 are easily calculated. Each term has two components: (1) F_i = w_i + x_i, where w_i is the number of copies of alleles that are directly genotyped and x_i is the number of copies of alleles that can additionally be imputed because we can infer alleles in unobserved subjects who share FGLs with some observed subjects from ibdg_i; and (2) G_i = w_i + y_i, where w_i is defined above and y_i is twice the number of unobserved subjects who have both alleles identical by descent with those of some observed subjects from ibdg_i (see Figure 1C).

It is also simple to calculate q_i in Equation 1. The probability q_i is equal to the probability that alleles from ibdg_i display a pattern of alternating allelic types for two alleles, because such genotype configurations are the only configurations for which the genotypes cannot be phased in ibdg_i. For instance, if an ibdg_i is a linear graph, i.e., 1-3-5, then q_i = P_AP_aP_A + P_aP_AP_a = P_AP_a (where P_a is the population minor allele frequency [MAF] and P_A = 1 − P_a) for diallelic variants, which include the majority of SNPs or sequence variants.

Estimating Coverage

Although coverage is a conceptual quantity defined for an arbitrary known IV, we need to estimate coverage for practical use without having the known IV. Here, we extend the concept of coverage. First, we define local coverage as the estimated coverage in a region of interest. The use of local coverage can optimize genotype imputation in a specific chromosomal region and is ideal for targeting subject selection in a region with positive evidence of linkage. We sample a set of n IVs at the beginning and end points of the region of interest as previously described.^18,36 To reduce the amount of computation and to select representative MCMC-based samples, we alternatively select IVs between the beginning and end points of the region of interest so that coverage is computed on a total of n instead of 2n IVs. (Although in our evaluation here we only sampled IVs at the beginning and end points of a region, our implementation allows selecting sampled IVs at multiple points, which could be desired for use in a large candidate region of interest.) After sampling IVs, we calculate coverage on each sampled IV. Finally, we take the average of the coverages to get the final estimate of the expected coverage. Second, we propose genome-wide coverage as a local-coverage variant estimated from the expected coverage at a random locus in the genome. This metric is useful if prior information about a candidate chromosomal region is not available or if multiple trait phenotypes are collected on the pedigree, so identifying rare variants related to many different genomic regions might be of interest. In this case, it might not be obvious which subjects or region to focus on. Genome-wide coverage is estimated by calculation of the average coverage across a large set of randomly sampled IVs compatible with the pedigree structure. To randomly sample an IV at a locus while conditioning on the pedigree structure, the method simulates each meiotic event corresponding to the transmission of a chromosome from a nonfounder’s parent to the nonfounder with an equal chance of maternal or paternal transmission. For example, to sample a random IV in the pedigree of Figure 1, the method simulates a total of ten meiotic events belonging to the three siblings in the second generation and the two siblings in the third generation, in which each meiotic event has a 50% chance of inheriting the maternal chromosome and a 50% chance of inheriting the paternal chromosome. Thus, a collection of these randomly simulated IVs (generated by conditioning on the pedigree structure) is used for estimating coverage at a random locus in the genome.

Joint-Prioritized Selection Algorithm

Using estimated coverage, we use a “joint-prioritized” algorithm for sequential selection of subjects. This method aims to select m subjects from n subjects available for sequencing (Figure 2). First, the algorithm selects the first subject by iterating through the entire list of subjects available for sequencing and computes the estimated coverage on each subject. The desired estimated coverage, which is either the local or the genome-wide coverage, is calculated with the method described above. Second, the method ranks the estimated coverages among the choices, retains the ranked top γ choices with the highest estimated coverages, and discards all other choices. These top choices are called templates for the next step. Third, the algorithm selects a second subject by using each template one by one in turn. For each template, the algorithm loops through the subjects not in the template, temporarily adds an unselected subject to the template, and calculates the estimated coverage on each temporary selection. Thus, with γ templates and n − 1 unselected subjects available for sequencing, a total of γ (n − 1) estimated coverage scores are calculated. Fourth, the algorithm retains γ unique combinations of selected subjects with the highest estimated coverage among these γ (n − 1) temporary coverages. These top γ selections now become the new templates for the next step. The fifth step repeats steps 1–4 but replaces n − 1 unselected subjects with n − x, where x is the number of subjects already selected at the beginning of each step, until m subjects are selected. After m subjects are selected, the top template becomes the final subject-selection choice.

Figure 2.

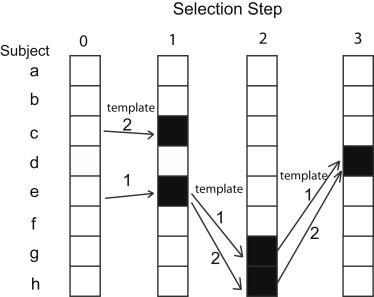
Joint-Prioritized Subject-Selection Method

In this example, the number of templates to keep (γ) is 2. In the first selection, the method computes coverage for each subject (a–h). Subject e has the highest coverage, and subject c has the second-highest coverage, so they are kept as templates. In the second selection, the method considers adding another subject to each template, e.g., (e, a), (e, b), (e, c), (e, d), (e, f), (e, g), (e, h), (c, a), (c, b), (c, d), (c, f), (c, g), and (c, h). Set (e, g) gives the highest coverage, and set (e, h) gives the second-highest coverage, so they are kept as templates for the third selection. This scheme repeats until the desired number of subjects is selected. After the third step, sets (e, g, d) and (e, h, d) give the highest and second-highest coverages, respectively. If a total of three subjects are desired, set (e, g, d) becomes the final selection.

The joint-prioritized subject-selection algorithm has a few features. First, this algorithm is a forward-selection extension that allows exploration of more selection choices. When γ = 1, this algorithm reduces to forward selection, and when γ > 1, the algorithm has a higher chance of finding a better choice after multiple selection steps. Second, unlike forward selection, the joint-prioritized selection algorithm does not make permanent selection after each step but instead continues to refine selection choices on the basis of current templates to maintain flexibility. Third, the algorithm considers multiple first choices so that different starting choices can be explored. Fourth, the algorithm keeps computation costs low by focusing only on templates with high potential for an improved selection outcome, under the assumption that only top templates are likely to be high quality. Fifth, this algorithm enables efficient computation, given that the number of calculations is only γ times more than forward selection, where γ is much smaller than n.

In computing the estimated coverage, P_a is assumed to be a fixed value and is treated as a tuning parameter. Because there are multiple variants in a chromosomal region, the use of coverage must assume one fixed value of P_a. To avoid confusion between the fixed value of P_a used for computing coverage and the population MAFs of different variants in a chromosome, we denote P_a as α when it is used as the fixed value tuning parameter for computing coverage. When α is high (e.g., α = 0.5), the probability of expecting heterozygous genotypes is also high, so the predicted probability of phasing alleles in the IBD graph would be lower than if α were low.

A high value of α is used for optimizing genotype imputation of rare alleles. A low value of α assumes that most founder alleles of a marker have copies of the common allele, so most genotypes are expected to be trivially phased because they would be homozygous for the common alleles. When genotypes are expected to be trivially phased with high probability, the method achieves maximizing coverage by selecting subjects who provide independent unobserved FGLs instead of selecting subjects who are more closely related to encourage phasing of existing observed genotypes. Thus, to instead encourage phasing of genotypes that contain rare alleles, the method needs to use a high value of α. Unless otherwise specified, the default value of α is 0.5.

Evaluation

Implementation in GIGI-Pick

We implemented our approach in the program GIGI-Pick. This program provides both batch and interactive modes that allow users to easily explore and compare selection choices. To compute genome-wide coverage, the program only requires a pedigree file, whereas to compute local coverage, the program further requires IVs at the positions of framework markers. These IVs can be obtained via the program gl_auto.³¹

Simulated Data

To evaluate and compare results from GIGI-Pick with those from alternative approaches, we simulated data on a 52-member five-generation pedigree also used in previous studies^18,37 (Figure S2). To resemble a realistic scenario in which subjects in the upper generations would typically be deceased, we defined only the 46 subjects from the lowest three generations as available for sequencing. Because of the size of this pedigree, it was computationally infeasible to evaluate all sequencing choices. For instance, there are over 53 million combinations of selecting seven subjects among 46 available subjects.

On a 100 cM chromosome, we simulated three types of markers. First, we simulated diallelic framework markers to infer IVs. These markers were simulated in a previous study at a density of one marker per 0.5 cM and had a MAF of 0.5.¹⁸ We retained genotypes of framework markers on 36 subjects (Figure S2) to resemble a common scenario that genotypes from an existing panel of genome-scan markers are available on most subjects. Second, we simulated dense SNPs to specifically evaluate the performance of imputing genotypes across the full range of possible allele frequencies. Within the 48–52 cM region of the chromosome, we used a total of 1,000 simulated SNPs at a density of one marker per 0.004 cM and MAF uniformly distributed between 0 and 0.5.¹⁸ Third, we simulated 5,000 rare variants in the same 4 cM region of the chromosome to evaluate the performance of imputing rare alleles, which might be more likely to represent the variants of interest in sequence data. For each rare variant, we selected a single random FGL to contain the rare allele. For all types of markers, we simulated alleles in founders and propagated founder alleles through the pedigree by using previously simulated descent patterns^18,37 to create the original marker data sets. This implies that multiple subjects who have copies of the randomly selected FGL with the rare variant contain copies of the rare allele. To ensure consistency in our interpretations, we repeated the simulation for a total of ten independent data sets with different patterns of chromosomal descent. The variability of the results among data sets was low, so these data sets were sufficient for our purpose (see Results).

Comparing Subject-Selection Choices in Simulated Data

We compared selected subjects obtained with GIGI-Pick to those obtained with five other methods of subject selection (Figures S3 and S4). The first category of methods selects subjects via automated programs GIGI-Pick, PRIMUS, and ExomePicks. Details on program use are given further below. We obtained results from GIGI-Pick by using either local (GIGI (local)) or genome-wide (GIGI (GW)) coverage. We obtained results from PRIMUS²² with an option to select a set of maximally unrelated subjects. This addresses the efficacy of maximizing the number of ascertained independent chromosomes for pedigree-based genotype imputation. We also obtained results from ExomePicks. The second category of methods chooses subjects manually via defined selection schemes. Inspired by designs in which distantly related affected subjects from the bottom generations are selected,^6,38 the “bottom-only” scheme selects affected subjects from the lowest generation of the pedigree. The “bottom and parents” scheme is a variant of the “bottom-only” scheme and replaces some bottom subjects with their parents (descended from the central branch of the pedigree) to facilitate phasing. The final category of selection method selects subjects randomly. We performed this random selection a total of 200 times to characterize the spectrum of imputation performance and to create a benchmark for comparison.

For each selection method, the experiment followed three steps. First, we used the method to select subjects for genotyping. Second, we retained genotypes on the chosen subjects. Third, we performed pedigree-based genotype imputation by using GIGI v.1.02, which is a program that can handle genotype imputation in large pedigrees.¹⁸

We performed three evaluations. First, we compared imputation performance (described below) among various selection methods and among random subject selections for five, seven, or ten selected subjects. Second, we computed the correlation between the estimated coverage and the actual imputation performance to evaluate the usefulness of estimated coverage for predicting imputation performance. Third, we varied the values of α (0.01, 0.1, 0.3, and 0.5) for GIGI-Pick (local) to evaluate how changing the values of the tuning parameter affects subject selection (Figure S5).

Given different choices for selecting subjects, we used different performance measures to evaluate genotype imputation for SNPs and rare variants. For SNPs, we computed accuracy, defined as the percentage of genotypes correctly called with the most likely genotype configuration, and averaged it over all SNPs. The reason for calling the most likely genotypes was to ensure that all alleles were called in every subject-selection choice in order to establish a common basis for comparison. For rare variants, computing the genotype accuracy on the basis of the most likely genotype configuration was less relevant because we were mainly interested in determining which subjects had the rare alleles and less interested in the large number of genotypes that were homozygous for the common alleles. Therefore, we computed sensitivity for calling rare alleles as the percentage of rare alleles called correctly after genotype imputation and averaged it over all variants. We computed sensitivity by using high-confidence calling, which calls both alleles of a genotype if the estimated probability of a genotype configuration is over 90% or calls one of the two alleles if the estimated probability of a specific allele is over 95%.¹⁸ For any alleles not called, the common allele was filled in. We also calculated specificity as the percentage of common alleles called correctly and averaged it over all variants. Because the specificity was always high (>99.7%) under all subject-selection choices, our comparison focused on sensitivity. We called genotypes strictly for the purpose of evaluation. Unless otherwise specified, all results were further averaged across the ten simulated data sets.

Program-Use Details

GIGI-Pick (local) uses a set of sampled IVs at the positions of interest. Using a set of framework markers as described in the text, we inferred IVs at the positions of framework markers via gl_auto.³¹ Then, using a previously described method¹⁸ implemented in GIGI-Pick, we sampled 1,000 IVs at the bounding positions 48 and 52 cM. GIGI-Pick (GW) uses a set of sampled IVs based on the pedigree structure. On the basis of the pedigree structure, we simulated 500 IVs with random descent patterns. GIGI-Pick was run for ten selection steps with γ = 8. Using the final ten subject selections, we retained the appropriate number of subjects as specified in the analysis plan (e.g., seven subjects selected) according to the order of these subjects selected in GIGI-Pick.

PRIMUS selected a set of maximally unrelated subjects, and this set corresponded to a set of founders in the pedigree. Because PRIMUS does not have an option to ignore certain subjects, it selected founders who were actually not available for sequencing from the top two generations. Given that we could not include subjects from the upper two generations, we instead manually selected relatives of these upper founders before other subjects were selected. To be consistent with the PRIMUS scheme for selecting the maximally unrelated subjects, we first selected the leftmost child from each of the two branches in the third generation. We then selected subjects from the top to the bottom generations among the maximum independent sets determined by PRIMUS.

In ExomePicks, we selected subjects by using the “per family” output as recommended. Groups of subjects who yielded the highest expected gain were selected.

Real Data

We evaluated the use of GIGI-Pick on a large real pedigree (Figure 3) in which a causal, dominant disease mutation was previously discovered.³⁹ This pedigree contains strong evidence of linkage in a region on chromosome 1,³⁹ thus providing a candidate region. It also contains 26 affected subjects scattered across three branches, but the disease has reduced penetrance. Thirty-nine subjects were typed for the causal variant, and copies of the causal mutation were observed in 14 subjects. Here, the causal variant represents a variant that would be detected from sequencing and is the variant that we would hope to rediscover through statistical testing using the imputed genotypes and the phenotype of interest. Among the 39 subjects typed for the causal variant, 32 subjects were also typed for SNP genotypes. These 32 subjects were assumed to be the subjects available for sequencing. All subjects or their representatives gave written informed consent, and the study was approved by the University of Washington Human Subject Review Board.

Figure 3.

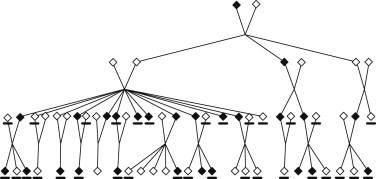
Real Pedigree Used for Subject Selection

Affected subjects are shaded, and subjects available for sequencing are underlined. Only subjects with some genotype data or descendants with genotype data were included. Some subjects were omitted from this figure for the protection of confidentiality.

Our use of this example resembles a realistic scenario. First, we manually selected two affected subjects available for sequencing from two different branches of the pedigree. It is practical to use information about disease status to first target subjects who potentially have copies of the causal mutation, and selecting two affected subjects is a common strategy in which some distantly related affected subjects in the pedigree are sequenced.^{6,11,16,38,40} Second, we selected three additional subjects for genotyping by using GIGI-Pick initially running with a total of 15 selection steps and γ = 8. This corresponds to sequencing a total of fewer than 10% of subjects in this pedigree. To incorporate linkage information, we estimated local coverage with inheritance vectors inferred by the program gl_auto³¹ by using 31 STRs supplemented with 70 SNPs near the region with evidence of linkage. Third, we used GIGI¹⁸ to impute genotypes at the causal variant and performed an association test correcting for relatedness²⁵ on the called imputed genotypes to evaluate whether the subjects selected for sequencing would provide evidence of association after genotype imputation. For this purpose, we used the pedigree-based kinship matrix and a corrected chi-square test²⁴ with a p value derived from the theoretical distribution of the test statistic. For imputation, we used a MAF of 0.2 for the variant because it was a more conservative specification of the MAF than a low MAF and minimized the chance of false-positive conclusions.⁴¹ We also evaluated a lower allele frequency such as might be used in the context of strong outside prior information. Fourth, because the result from this analysis might be sensitive to the original choice of which of the two initial subjects was manually selected, we repeated the analysis above on all of the 23 pairs of affected subjects from different branches.

Results

Simulations

There was a clear relationship between the number of subjects selected and the sensitivity in calling rare alleles, as well as a generally consistent ranking of the selection methods (Figure 4). Among all subject-selection methods, GIGI-Pick (local) yielded the highest sensitivity over the entire range of numbers of subjects selected. GIGI-Pick (GW) yielded lower sensitivity than did GIGI-Pick (local), suggesting that incorporating a candidate region identified by linkage analysis can further improve subject selection toward the goal of identifying causal variants. However, GIGI-Pick (GW) still substantially outperformed other methods. ExomePicks yielded the third-highest sensitivity at seven or fewer subjects selected, but the “bottom and parents” design yielded higher sensitivity than did ExomePicks at seven or more subjects selected. In this “bottom and parents” design, the first six subjects selected were identical to those in the “bottom-only” design, so the sensitivity values from the two methods were identical in this range. However, at seven to ten subjects selected, typing parents in the “bottom and parents” design led to higher sensitivity than did typing siblings in the “bottom-only” design. Finally, PRIMUS performed poorly in comparison to all other subject-selection methods, and its relative performance decreased with increasing numbers of selected subjects.

Figure 4.

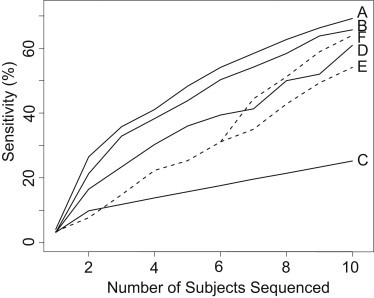
Sensitivity of Calling Rare Alleles as a Function of the Number of Subjects Selected

Programs (solid lines) are as follows: (A) GIGI (local), (B) GIGI (GW), (C) PRIMUS, and (D) ExomePicks. Ad hoc schemes (dashed lines) are as follows: (E) bottom only and (F) bottom and parents. Refer to Figures S3 and S4 for the actual subjects selected. The “bottom and parents” and “bottom-only” designs had the same sensitivity in the first six selected subjects because the subjects selected were the same until the seventh choice.

Differences in imputation performance among selection methods were substantial. Here, we focus the results on seven subjects selected (Figure 5 and Table 1). GIGI-Pick (local) yielded the highest sensitivity (58.4%) and was better than all random choices (100^th percentile relative to the distribution of random selections of subjects). GIGI-Pick (GW) was the second-best selection method (54.2% sensitivity; 99.5^th percentile) but had 4.2% lower sensitivity than did GIGI-Pick (local). GIGI-Pick (local) yielded a markedly 14.4% absolute difference in sensitivity over the “bottom and parents” design and had a 38.8% absolute difference in sensitivity in comparison to the least effective selection method, PRIMUS (19.6% sensitivity; <1^st percentile). For imputing more common SNPs, GIGI-Pick also yielded better accuracy than did other selection methods (Table 1), although the absolute differences in accuracy among methods were less dramatic than those for the rare variants. Nevertheless, the rank order of imputation performance was the same for rare variants and SNPs (Table 1). In addition, the qualitative findings above were similar for five or ten subjects selected (Tables S1 and S2), and summaries per data set also suggested similar interpretations (Table S3).

Figure 5.

Sensitivity Computed for Different Selection Methods against the Distribution from 200 Samples of Random Subject Selection for Seven Subjects Selected

The histogram describes the distribution of sensitivity values from samples of random subject selection. Subject-selection methods are compared against random subject selection, and the locations of the lines indicate the sensitivity of the methods. Programs are depicted by solid lines, and ad hoc schemes are represented by dashed lines.

Table 1.

Methods of Subject Selection for Seven Selected Subjects Affect the Performance of Genotype Imputation

Method of Subject Selectiona	Rare Variants			SNPs
	Sensitivity (%)	Percentile (%)b	Rank	Accuracy (%)	Percentile (%)	Rank
GIGI-Pick (local)	58.4	100	1	81.9	100	1
GIGI-Pick (GW)	54.2	99.5	2	80.4	99.5	2
PRIMUS	19.6	<1	6	75.1	0.5	6
ExomePicks	41.3	39.5	4	77.4	29.0	4
Bottom only	35.0	10.5	5	77.3	27.5	5
Bottom and parents	44.4	65.0	3	79.1	84.5	3

^aResults were averaged across all ten simulated data sets. Refer to Figures S3 and S4 for actual subjects selected.

^bRelative to 200 random selections of subjects for sequencing.

Results from other methods for subject selection also have interesting features. First, sensitivity varied substantially across random choices (∼25% to ∼58%) (Figure 5), which further illustrates that the choice of subject selection can strongly affect imputation of rare alleles. Second, PRIMUS had substantially lower sensitivity than did all other subject-selection methods and was considerably worse than random selection for subsequent pedigree-based imputation (19.6%; <1^st percentile) (Table 1). Third, by focusing on selecting subgroups of related subjects, ExomePicks (41.3%; 39.5^th percentile) yielded markedly higher sensitivity than did PRIMUS. Interestingly, ExomePicks was less effective in imputing SNPs (29^th percentile) than in imputing rare variants (39.5^th percentile) relative to random choices, but it still underperformed random selections (<50^th percentile) even for rare variants.

High estimated coverage is a strong indicator of high genotype-imputation performance. The correlation between the accuracy and local coverage was strong (e.g., 0.90 in data set 1), suggesting that coverage is useful for comparing selection choices (Figure 6). In particular, the observations in which the local-coverage values were high generally corresponded to high accuracy values. This result was consistent across data sets (data not shown). The correlation between sensitivity and local coverage was weaker (0.72 in data set 1) than the correlation between accuracy and local coverage, but high coverage values were still correlated with high sensitivity values (Figure 6). As would be expected, genome-wide coverage was less indicative of the per-run imputation performance in the particular region evaluated (correlations of 0.57 for accuracy and 0.46 for sensitivity in data set 1). However, genome-wide coverage was still highly predictive of the average imputation performance across data sets (correlations of 0.88 for accuracy and 0.74 for sensitivity across data sets; Figure 6). Thus, the selection of subjects who optimize the estimated coverage is expected to yield high imputation performance.

Figure 6.

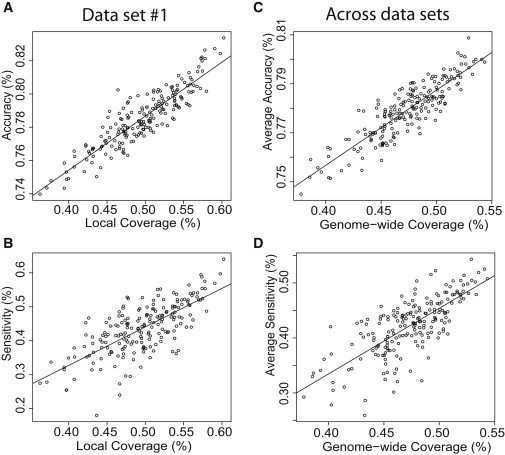
Correlation between Imputation Performance and Estimated Coverage for Seven Subjects Selected

Per-data-set accuracy (A) and sensitivity (B) versus local coverage computed for data set 1 and average accuracy (C) and sensitivity (D) versus genome-wide coverage computed across ten data sets.

The performance was relatively insensitive to the specific choice of α (Table S4). Among the considered values of α, GIGI-Pick (local) had the highest sensitivity (58.4%; 100^th percentile) and accuracy (81.9%; 100^th percentile) for α = 0.5. As α decreased, both sensitivity and accuracy decreased. The changes were small for α = 0.3, but sensitivity decreased sharply for α = 0.1, although the accuracy remained high relative to random selections. For α = 0.01, both sensitivity and accuracy were low. This was because GIGI-Pick selected more distantly related subjects or married-ins at a low value of α (Figure S5), as was predicted in the Subjects and Methods.

Real Data

The real-pedigree example demonstrates that GIGI-Pick can provide useful guidance regarding which subjects to select for genotyping (Table 2). When using genotypes from only a selected pair of affected subjects, GIGI was unable to impute the causal mutation in other subjects with high confidence, and after imputing genotypes, there was no evidence of association between the causal variant and the disease (χ² = 2.06; p = 0.152). Because the causal mutation is rare, the two selected subjects both had heterozygous genotypes, so their genotypes could not be phased. After adding the three subjects suggested by GIGI-Pick, GIGI was able to impute the presence of the causal mutation in 22 other subjects. Among the 12 confirmed subjects who had known copies of the causal mutation, GIGI was able to impute copies of the causal mutation in 11 subjects. For the single subject in which the causal mutation was not imputed with high confidence (the “missed” subject), the estimated probability that the genotype contained the causal mutation was still 63%. Moreover, GIGI-Pick imputed copies of the causal mutation in 13 subjects who were originally not typed and thus could not be confirmed. Among these subjects, ten were affected, so these subjects were highly likely to indeed have copies of the causal mutation. Using these imputed genotypes, we observed strong evidence that this causal mutation is associated with the disease (χ² = 16.85; p = 4.05 × 10⁻⁵). Even though this analysis started with only five observed subjects, the results match closely with what could be obtained from the use of all 39 originally observed subjects for imputing additional genotypes and then performing the same association test (χ² = 18.19; p = 2.00 × 10⁻⁵).

Table 2.

Analysis of a Real Pedigree

No. of Subjects Observed	No. of Subjects Imputed	No. of Causal Mutations Calleda	χ2(p value)b
2c	63	2	2.06 (0.152)
5c,d	60	25	16.85 (4.05 × 10−5)
39	26	26	18.19 (2.00 × 10−5)

^aEither observed or imputed with high-confidence threshold by GIGI with t₁ = 0.9 and t₂ = 0.95.

^bComputed at the causal variant.

^cAll choices of the initial chosen pair of affected subjects gave the same numerical values.

^dUsing the two preselected affected subjects, we used GIGI-Pick to suggest three more subjects for sequencing, giving a total of five subjects.

Analysis of other initial pairs of affected subjects gave similar results. In any pairs of affected subjects, GIGI also could not impute causal mutations in the relatives, most often because genotypes at the causal locus in both of these subjects were heterozygous. In each of these pairs, the addition of three subjects suggested by GIGI-Pick enabled imputation of copies of the causal mutation: the same 25 copies of the causal mutation were always called. In the pairs that contained the “missed” subject as one of the five sequenced subjects, GIGI called an extra copy of the causal mutation because the causal mutation from the “missed” subject was then directly genotyped. We note that in our primary analysis with a MAF of 0.2, GIGI could not impute the causal mutation into other subjects unless additional subjects were added, but with a low MAF of 0.01, GIGI imputed the causal mutation even with only two affected subjects in 17 out of 23 pairs of subjects. This is because of the strong prior information provided by the low frequency. However, in most cases, such allele frequency information would not be initially available, or for more complex traits, the causal allele(s) might not be so rare.

Discussion

The framework that we describe here effectively guides subject selection for sequencing in pedigrees. The results from our simulations show that relative to other methods considered, GIGI-Pick yields superior genotype imputation performance, especially for rare alleles. Comparisons between GIGI-Pick (local) and GIGI-Pick (GW) also show that leveraging inferred IVs further improves genotype imputation within a focused region with prior evidence of linkage. In addition, high local and genome-wide estimated coverages are indicative of high subsequent genotype-imputation performance, so the use of estimated coverage is a beneficial metric for determining final selection choices. Using a real pedigree with a known mutation, we also demonstrated that GIGI-Pick can flexibly accommodate preselected subjects who are affected by the disease to suggest additional subjects to sequence; thus, it can lead to accurate and extensive imputation of the causal mutation and demonstrates the value of such imputed data in association testing.

Our results also provide valuable insight into how various subject-selection programs perform with regard to subsequent genotype imputation. At one extreme, PRIMUS selected mostly founders. At the other extreme, ExomePicks selected groups of closely related subjects from the top to the bottom generations of the pedigree. GIGI-Pick fell between these extremes and balanced between selecting closely related subjects to increase the chance of phasing genotypes and selecting distantly related subjects to increase the number of copies of independent founder chromosomes. The results from our study illustrate that such an approach can substantially improve imputation performance. Along with the use of inferred IVs to target selection for a specific region, GIGI-Pick enables efficient selection of subjects for genotype imputation.

The coverage metric accounts for phasing genotypes relative to IVs and focuses on using information from IVs to impute genotypes. When genotypes are imputed with IVs, the accuracy is well controlled,¹⁸ so maximizing coverage essentially maximizes the average percentage of alleles that can be called. The estimation of local and genome-wide coverage extends the theoretical measure of coverage to two realistic situations: where linkage information is and is not already available. Even though coverage is not specifically designed for imputing rare alleles, our results from simulated and real pedigrees demonstrate that this metric works well in practice. Finally, we anticipate that the use of imputed results from subject-selection choices based on maximizing coverage will improve the power of association tests of rare variants segregating in individual pedigrees over the use of imputed results from less ideal selection choices because the validity of the association test ultimately depends on high sensitivity and specificity of calling such rare alleles.

Variant prioritization based on linkage evidence and subsequent causal-variant search using imputed genotypes are together an effective approach to screening sequence variation. Because linkage information is derived from the transmission of alleles in pedigrees, it offers strong prior information to narrow the search space of causal variants.^5,7,14 We have shown here that making use of this information in selecting sequencing subjects is both possible and also useful. In a focused region, the use of statistical tests with imputed genotypes can formally quantify scientific evidence, and the use of imputed genotypes can markedly improve the power of statistical testing while negligibly increasing cost^19,20 (and unpublished data). In addition, because the use of arbitrary bioinformatics filters is not always regarded as safe,^7,15 performing statistical tests on sequenced variants might be needed prior to more expensive direct genotyping of variants. This might be the case especially in studies that involve complex diseases with reduced penetrance and genetic heterogeneity and in which the use of bioinformatics filters is less effective.⁴² Recently, the use of a comprehensive evaluation of imputed genotypes along with statistical tests has been shown to be an effective strategy for nominating causal variants from sequence data in a study of a complex trait (triglyceride levels) in a large human pedigree⁴³ and in a study of an outbred rat cross to identify causal mutations in multiple phenotypes.⁴⁴ GIGI-Pick can facilitate such an approach by optimizing the selection of subjects. Of course, other options, including direct genotyping, can also be used for following up on the sequencing results. More generally, prioritizing variants for sequencing studies and subsequent analyses is important in both GWASs and pedigree-based studies. Other aspects pertinent to the design of the studies are worth considering but are beyond the scope of the current paper.²¹

In addition to the incorporation of existing genotypes, the incorporation of phenotype information could be beneficial if it is available. In our example with real analysis, we leveraged phenotype information by first selecting two affected subjects. Alternatively, potential extensions to our framework could allow phenotype information to be leveraged explicitly, both in cases when IVs are available and in cases when only the pedigree structure is available. With inferred IVs, further incorporation of phenotypes might provide additional information to inform which affected subjects with rare alleles should be sequenced, and this could be particularly useful when the inferred IVs are not perfectly informative regarding the transmission of chromosomes in pedigrees. This future direction would be interesting to pursue, given that in a large population with many related subjects, leveraging phenotype information with kinship coefficients even without leveraging inferred IVs to select subjects suggests the potential to improve power to detect association (M. Wang et. al, 2013, IGES, abstract). Future investigation would enable us to understand the power to incorporate phenotype information to our flexible framework.

We have introduced a quantitative framework to address the issue of subject selection for sequencing in pedigrees. The metric used here for evaluating selection choices relates to genotype imputation. However, other metrics are also possible and could be developed for the incorporation of intended analyses and other sources of information, including trait phenotypes. Future work will be needed for evaluating other such options. With this framework, we have implemented the computer program GIGI-Pick to facilitate efficient and informed decision of subject selection for sequencing; this will be immediately useful in view of the large number of sequencing projects now being carried out in existing pedigree samples.

Web Resources

The URLs for data presented herein are as follows:

• ExomePicks, http://genome.sph.umich.edu/wiki/ExomePicks

• GIGI, http://faculty.washington.edu/wijsman/software.shtml

• GIGI-Pick, http://faculty.washington.edu/wijsman/software.shtml

• MORGAN, http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml

• PRIMUS, http://sourceforge.net/projects/primus-beta/

• Relationship corrected chi-square testing, http://faculty.washington.edu/wijsman/software.shtml