Detecting Radiation-Induced Injury Using Rapid 3D Variogram Analysis of CT Images of Rat Lungs

Abstract

Rationale and Objectives

To investigate the ability of variogram analysis of octree-decomposed CT images and volume change maps to detect radiation-induced damage in rat lungs.

Materials and Methods

The lungs of female Sprague-Dawley rats were exposed to one of five absorbed doses (0, 6, 9, 12, or 15 Gy) of gamma radiation from a Co-60 source. At 6 months post-exposure, pulmonary function tests were performed and 4DCT images were acquired using a respiratory-gated microCT scanner. Volume change maps were then calculated from the 4DCT images. Octree decomposition was performed on CT images and volume change maps, and variogram analysis was applied to the decomposed images. Correlations of measured parameters with dose were evaluated.

Results

The effects of irradiation were not detectable from measured parameters, indicating only mild lung damage. Additionally, there were no significant correlations of pulmonary function results or CT densitometry with radiation dose. However, the variogram analysis did detect a significant correlation with dose in both the CT images (r=−0.57, p=0.003) and the volume change maps (r=−0.53, p=0.008).

Conclusion

This is the first study to utilize variogram analysis of lung images to assess pulmonary damage in a model of radiation injury. Results show that this approach is more sensitive to detecting radiation damage than conventional measures such as pulmonary function tests or CT densitometry.

Introduction

With the onset of certain diseases, lung tissue becomes more heterogeneous (i.e. tissue density may present increased spatial variability), as is frequently evident in CT images (1, 2). Recent work by Subramaniam et al. (3) used quadtree decomposition in 2D slices of lung CT images to analyze heterogeneity. Selected slices were iteratively subdivided into quadrants based on an intensity range threshold, and heterogeneity measured as the number of squares per area. However, this 2D approach neglects large portions of the lung and ignores 3D spatial relationships. We extended the quadtree concept to 3D by using octrees to iteratively and nonsubjectively divide an entire 3D image into homogeneous cubes. This approach focuses on the parenchyma by eliminating tissue boundaries and reducing the influence of the vasculature (4). Instead of simply calculating the cube density, we analyzed spatial relationships for indications of heterogeneity using variograms, a well-established geostatistics tool for measuring spatial variability that compares sample variances to the distance of separation without a priori assumptions about the spatial relationships (5, 6). Recent biological applications of the variogram include the characterization of brain white matter in magnetic resonance images (7).

In this paper we demonstrate the use of non-invasive imaging and a novel 3D image analysis approach using variograms of octree-decomposed images to detect subtle injury in radiation-exposed rat lungs. It has been shown that lung injury in radiation-exposed rat lungs includes acute inflammation in the weeks after exposure and chronic fibrosis in the months after exposure while providing a relatively uniform injury over the dosed area (8–10). We show that the results of variogram analysis on octree-decomposed CT images and 4DCT-based volume maps of irradiated lungs correlates with radiation dose better than physiological measurements, conventional pulmonary function tests, or CT density measurements.

Materials and Methods

All animal use followed a protocol approved by the Institutional Animal Care and Use Committee of our institution. Twenty-five female Sprague-Dawley rats weighing 216 ± 9 g were used.

Lung irradiations employed a ~6400 Ci Co-60 gamma source with a ~30 cm thick lead collimator. The collimator was trapezoidal to match the basic outline of the lungs, with dimensions based on a 3D image of a weight-matched control rat: 15 mm wide at the top, 30 mm wide at the bottom, and 26 mm high. The bottom was convexly tapered by 5 mm in the center to minimize exposure to the liver. The resulting beam was then calibrated in terms of absorbed dose to tissue (Gy/min) using a tissue-equivalent ionization chamber (Exradin model A12, Standard Imaging, Middleton, WI) connected to an electrometer (model 617, Keithley Instruments, Cleveland, OH) to collect the resulting current. Appropriate corrections were applied to convert from exposure in air to absorbed dose in tissue (11). The measured absorbed dose rate for the estimated location of the lung center (~1.5 cm from collimator face) was 3.74 Gy/min. It was determined that 1.5 cm of tissue results in approximately 5% reduction in absorbed dose rate, resulting in an estimated 3.55 Gy/min at lung center. One of five calculated doses of 0.0, 5.9, 8.8, 11.8, and 14.7 Gy (hereafter referred to as 0, 6, 9, 12, and 15 Gy) was delivered to the thorax; this dose range has been shown to cause significant injury in other rat strains (10, 12, 13). The dose rate to the body was measured to be ≤0.3% of that at the lung center. The dosed region was confirmed in a weight-matched rat using an x-ray source and Polaroid radiographic film.

Anesthetized rats were placed in a custom-made, contoured holder to facilitate reproducible positioning of the rat thorax directly in front of the collimator. Rats were randomly assigned a radiation dose, with 5 rats per group. Irradiations were blind to the staff performing other measurements in order to reduce bias.

Following irradiation, rats were returned to the animal facility where they were individually housed, provided food and water ad libitium, and observed daily for general well being. One rat from the 6 Gy group developed a ~3 cm growth on its back and was eliminated from the study. Otherwise, no mortality or outward signs of poor health were observed. Two additional rats were kept in the same room as health sentinels, and at the end of the study they were confirmed to be seronegative for common rat pathogens.

At 6 months post-irradiation, rats were subjected to pulmonary function tests (PFT) and microCT imaging. First, a whole body plethysmograph (WBP; Buxco Research Systems, Wilmington, NC) was used to measure breathing rate, tidal volume, and minute volume of unanesthetized, unrestrained rats for ~5 minutes. Rats were acclimated to the chamber for ~10 minutes per day for several days prior to the test.

Next, rats were imaged using 4DCT (multi-time-point 3D imaging). Details of animal preparation, ventilation, and 4DCT imaging closely follow those described in (14). Rats were anesthetized with 4% isoflurane in oxygen, orally intubated with a 14 gauge catheter tube, and connected to a computer-controlled mechanical ventilator (model 830/AP, CWE Inc., Ardmore, PA). Rats were maintained on isoflurane and ventilated with 30% O₂ (balance N₂) at 54 breaths per minute, with a 500 ms inhale duration and no breath hold. Periodic sighs were delivered every 100 breaths to maintain lung recruitment. The ventilator recorded tracheal pressure, inspiratory volume, and expiratory volume. Peak inspiratory volume (PIV) was ≈2.1 mL. No positive end expiratory pressure was used so that images could be acquired at full passive exhalation when the lung volume was at functional residual capacity (FRC). A microCT scanner (eXplore 120, GE Healthcare, Waukesha, WI) with ventilatory gating was used to acquire eleven images throughout the breathing cycle in 26 minutes with 100 ms temporal resolution (we note that only the images at the breathing cycle extremes – FRC and PIV – were analyzed for this study). Gating was tested by comparing the ventilator gate signal to a signal sent by the scanner upon firing x-rays; the delay between the ventilator trigger and x-ray firing was found to be ≤250 μs. CT imaging parameters were: 80 kVp, 32 mA, 16 ms exposure time, and 360 projections with 1° angular separation. The estimated radiation dose from all images was 940 mGy. Images were reconstructed to 200 μm isotropic resolution using supplied software. We empirically found that this resolution provided sufficient detail for later analysis.

Following imaging, PFT were performed. Rats were anesthetized with an ip injection of Ketamine/Xylazine and surgically intubated for measurement of inspiratory volumes, forced expiratory volumes, and quasistatic chord compliance using a Forced Maneuvers system (Buxco Research Systms, Wilmington, NC). PFT measurements took ~5 minutes. Immediately after the pulmonary function tests, animals were euthanized via CO₂ asphyxiation, and lungs were excised to obtain wet and dry weights.

Acquired images were processed with a 5 pixel diameter 3D median filter to remove noise while maintaining feature boundaries. These filtered images were then masked to assign intensity value 0 to non-lung regions; filtered images were multiplied with a binary image created using the 3D connected threshold tool in the 3D Plugins Toolkit of ImageJ (15, 16) to delineate lung from non-lung based on intensity. From these masked images, the mean and standard deviation σ of the distribution of Hounsfield units (HU) in the lung were determined. The coefficient of variation (CoV) was then calculated by taking the ratio of σ to the mean.

Octree subdivision reduces the original volume into eight octants of equal dimension (see Figure 1). Images were first zero-filled to 256×256×256 so that octree subdivision would result in isotropic cubes. Iteratively, each octant was further subdivided if it contained any mask voxels or if its σ exceeded a threshold value t, unless the octant reached a minimum size of 2×2×2. All octants containing the mask value of 0 were discarded from further analysis. Remaining octants larger than 2×2×2 represented relatively homogeneous sections of the lung, while the 2×2×2 cubes defined boundaries and regions with high spatial variability. In developing this approach, we empirically determined the optimal t to be approximately two-thirds the mean of the control group’s whole-lung σ; t was 38 HU in this study. Octree decomposition was executed in Python on a Mac Pro 3.1 in ~2 minutes.

Figure 1.

Octree decomposition. Each cube may be decomposed into eight smaller cubes, or octants. Decomposition of cubes is applied iteratively when specific conditions regarding contents of a cube are met.

After octree decomposition, variogram analysis was performed to determine spatial relationships between octants. A variogram is a distance vs. variance (or semi-variance) graph, whereby variance is the square of the difference in mean signal intensity between two given octants, and distance is between octant centroids. Variograms were constructed using only 8×8×8 octants – the largest that were generated from the decomposition. This selection assumes that any radiation-induced abnormalities would generally be manifest on a scale larger than an 8×8×8 cube, which had dimensions of 1.6 mm × 1.6 mm × 1.6 mm. Furthermore, this eliminated the smaller cubes that tended to define features of high spatial variability. Because of the complex geometry of the lung – generally independent lobes often separated large distances by non-lung tissue – we limited variogram analysis to a maximum distance d_max (7), which we defined as approximately one half the characteristic diameter of the left lobe. From the control group images, d_max was measured to be about 12 mm. Variogram calculation was executed in Python in ~7 seconds. The octree decomposition improved the speed of the 3D variogram calculation ~700-fold as compared to previous approaches (7).

To examine potential alterations to lung ventilation patterns, volume change maps (maps showing the volume change between FRC and PIV, also known as ventilation maps) were calculated from CT images as described in (17) using a method closely following (18). In brief, the PIV image was warped to the FRC image, then voxel-by-voxel volume change was calculated using the determinant of the Jacobian of the resulting warp vector field and the HU values of the original CT images. Figure 2 is an example of CT images at FRC and corresponding volume change maps. CoV measurement, octree decomposition, and variogram analysis were performed on the volume change maps as described above.

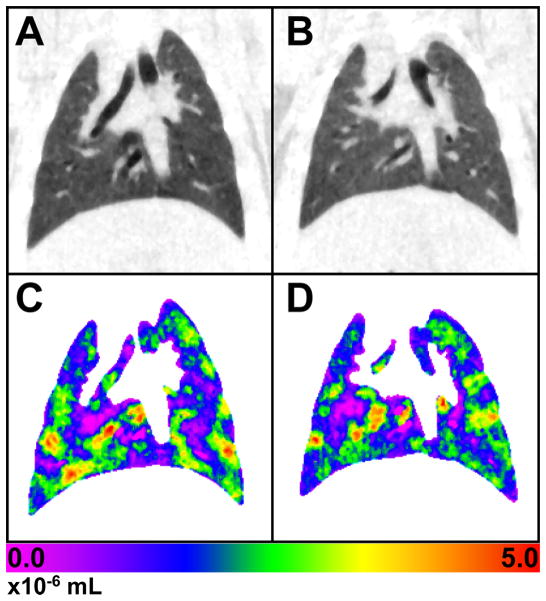
Figure 2.

Representative coronal slice at functional residual capacity (FRC) of: A) a control rat, and B) a rat exposed to 15 Gy. C and D are maps of the volume change between FRC and peak inspiratory volume (PIV) for the control and exposed rats, respectively. There are few, if any, observable differences between the images of the control and 15 Gy rats. The color scale is in units of 10⁻⁶ mL.

We attempted to fit standard variogram models to the resulting data. For the raw CT images, a power-law equation of the form:

$$y=C+{md}^{\alpha }$$ [1]

was least-squares fit to the data. C is a constant, m is the initial slope, d is the distance between octree cube centerss, and α is an exponent that represents how rapidly the octree cubes become increasingly spatially dissimilar. Higher values of α (for α>1) indicate that the variance is increasing at an increasing rate, implying that the lung becomes more heterogeneous on average with increasing distance from any given location. The ventilation maps, on the other hand, were fit to a model of exponential rise to an asymptotic value:

$$y=S[1-exp(-3d/R)],$$ [2]

where S is the asymptote (referred to the “sill” in geostatistics), d is the distance between octree cubes, and R (the “range”) is the distance at which the variance reaches ≈95% of S. The range characterizes the local “roughness,” with a larger R indicative of smoother variation. At distance R, the image becomes random, with little spatial change in variance. The sill indicates the degree of randomness or variety across the image. To compare measured parameters of the dosed groups against those of the control group, an analysis of variance was performed with a Dunnett post hoc test, using a null hypothesis of α=0.05. The significance of the correlation of dose level to different measured parameters (i.e. dose-response) was tested using a paired t-test, also with a null hypothesis of α=0.05.

Results

Table 1 summarizes by measurement type and dose group the PFT results and other physiological measurements. “Physical Measures” refers to body weight and lung weights; “Forced Maneuvers” are PFT results for anesthetized rats, “Spontaneous Breathing” are the WBP results, “Ventilation” are parameters from mechanical ventilation during imaging, and “Imaging” are results derived from the CT images at FRC and PIV. All measurements show the mean and σ from n=5 rats, except the previously noted 6 Gy group with n=4. In addition, the volume map of one rat in the 12 Gy group displayed a large anomalous ventilation defect in the right lung and was therefore eliminated from all volume map calculations. Significance levels, as compared to the control group, are indicated in the table. Of the measurements in Table 1, those that had a significant correlation with dose level were the dry lung weight (p=0.03, r=0.45) and the volume map CoV (p=0.013, r=−0.51). We note that significant functional deteriorations were seen only in the 6 Gy group. We hesitate to speculate why due to the lack of time-course data or other supporting evidence.

Table 1.

Measured parameters 6 months post-irradiation

		0 Gy	6 Gya	9 Gy	12 Gy	15 Gy
Physical Measures	BW	286 (9)	279 (11)	300 (10)	289 (13)	299 (14)
	Water Wt	1.44 (0.18)	1.41 (0.06)	1.44 (0.14)	1.36 (0.14)	1.45 (0.07)
	Dry Wt	0.302 (0.011)	0.315 (0.010)	0.306 (0.025)	0.321 (0.016)	0.327 (0.020)*
Forced Maneuvers	TLC	24.6 (4.3)	19.5 (2.2)*	24.1 (1.2)	23.0 (1.2)	23.4 (3.0)
	FRC	7.3 (1.3)	5.7 (0.5)	7.6 (1.4)	6.3 (0.5)	6.7 (1.2)
	RV	2.7 (1.5)	2.5 (0.2)	2.6 (1.2)	2.7 (0.7)	3.0 (0.5)
	TLC/BW	8.59 (1.31)	6.95 (0.54)	8.03 (0.46)	7.97 (0.67)	7.81 (0.90)
	Cchord	1.43 (0.27)	1.10 (0.07)*	1.29 (0.11)	1.26 (0.07)	1.25 (0.18)
	FEV20	2.5 (0.1)	2.5 (0.2)	2.4 (0.1)	2.6 (0.2)	2.4 (0.4)
	FEV50	7.7 (0.3)	7.6 (0.5)	7.4 (0.3)	7.9 (0.4)	7.2 (1.1)
	FEV100	15.5 (0.9)	14.4 (1.1)	14.8 (0.9)	14.7 (0.7)	13.7 (2.5)
	FEV200	21.4 (2.4)	17.7 (1.4)	20.8 (2.3)	19.3 (0.8)	19.1 (2.8)
	PEF	178 (6)	173 (12)	170 (8)	182 (9)	165 (23)
Spontaneous Breathing	BPM	122 (12)	136 (10)	133 (12)	119 (9)	129 (19)
	TV	2.5 (0.3)	2.3 (0.3)	2.5 (0.2)	2.1 (0.3)	2.3 (0.2)
	MV	306 (62)	318 (49)	329 (44)	256 (51)	295 (61)
Ventilation	PIP	5.1 (0.6)	5.6 (0.1)	4.9 (0.3)	5.2 (0.3)	5.1 (0.5)
	EEP	0.52 (0.11)	0.42 (0.09)	0.48 (0.09)	0.46 (0.08)	0.41 (0.07)
	PIV	2.13 (0.07)	2.05 (0.10)	2.15 (0.04)	2.14 (0.07)	2.12 (0.07)
	Cave	0.48 (0.08)	0.41 (0.02)	0.50 (0.03)	0.46 (0.02)	0.47 (0.05)
Imaging	HU (FRC)	−621 (30)	−554 (13)*	−602 (35)	−588 (27)	−578 (41)
	HU (PIP)	−684 (20)	−637 (9)*	−668 (27)	−660 (21)	−653 (25)
	CoV (FRC)	0.076 (0.003)	0.088 (0.005)*	0.079 (0.008)	0.079 (0.004)	0.083 (0.009)
	CoV (PIP)	0.069 (0.002)	0.075 (0.002)	0.069 (0.007)	0.070 (0.003)	0.072 (0.007)
	Vol CoV	0.60 (0.05)	0.48 (0.03)‡	0.52 (0.03)	0.52 (0.06)a	0.50 (0.05)†

Results are reported as mean values with standard deviations in parenthesis. BW=body weight (g); Water Wt=water weight (g); Dry wt=dry weight (g); TLC=total lung capacity (mL); FRC=functional residual capacity (mL); RV=residual volume (mL); Cchord=quasistatic chord compliance (mL/cmH₂O); FEV(t)=forced expiratory volume in t milliseconds; PEF=peak expiratory flow (mL/sec); BPM=breaths per minute; TV=tidal volume (mL); MV=minute volume (mL); PIP=peak inspiratory pressure (cmH₂O); EEP=end expiratory pressure (cmH₂O); PIV= peak inspiratory volume (mL); Cave=average compliance (mL/cmH₂O); HU=Hounsfield Units; CoV=coefficient of variation; Vol=volume map.

^*p<0.05;

^† p<0.01;

^‡ p<0.005;

^an=4

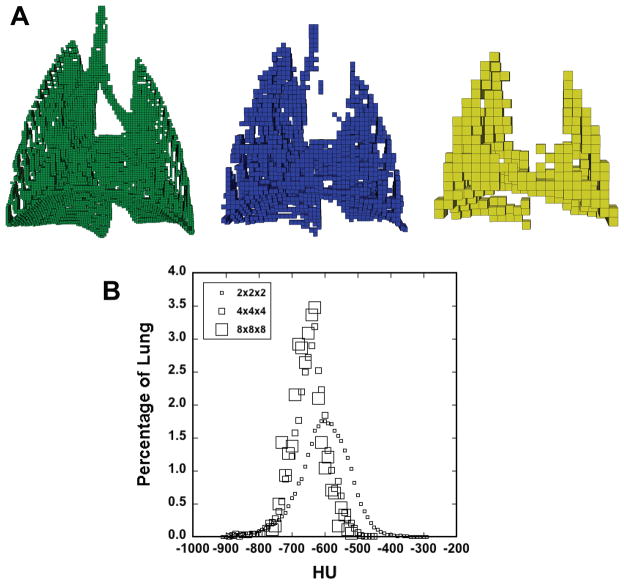
Figure 3A demonstrates octree decomposition, illustrating the 2×2×2, 4×4×4, and 8×8×8 octants and their spatial distribution in a typical control rat. Figure 3B is a histogram of the octree cubes of Figure 3A, indicating the fraction of lung occupied by the different block sizes for the range of HU values. The 4×4×4 and 8×8×8 cubes are approximately normally distributed about the mean lung HU value because they tend to occupy the parenchymal regions.

Figure 3.

A) Representative octree decomposition, with 2×2×2 (left), 4×4×4 (center), and 8×8×8 (right) octree cubes. 8×8×8 cubes are 1.6 mm in each dimension. The smaller cubes generally define edges, airways, and vascular features; thus, only the 8×8×8 cubes are retained for analysis. B) Histogram showing the percentage of lung occupied by each box size at each HU value. Bin width was 10 HU.

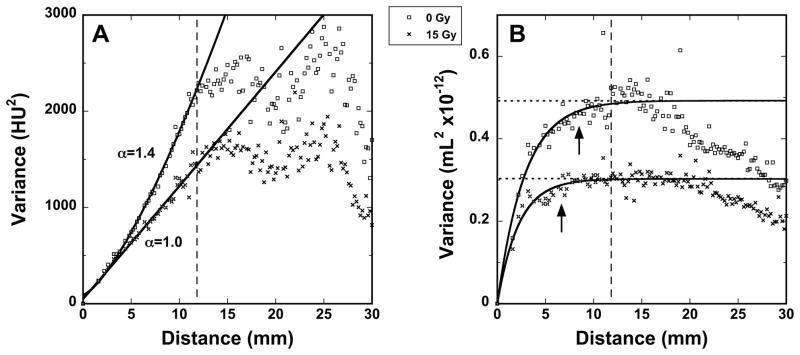
Figure 4A shows representative variograms, made from the FRC images of two typical rats, one 0 Gy and one 15 Gy (those shown in Figure 2). The more rapid rise of the control variogram is indicative of comparatively greater variance at a given distance, which is interpreted as greater heterogeneity. Figure 4B shows representative variograms from volume change maps (those shown in Figure 2).

Figure 4.

Representative variograms from 0 Gy and 15 Gy rats showing the average HU variance of 8×8×8 cubes vs. distance of separation. The distance d_max for which the variogram is expected to be valid is indicated by the dashed line. Curve fits were applied to the range d ≤ d_max. A) Variograms from CT images at functional residual capacity (FRC), with the corresponding exponent α (see Equation 1), with resulting α values of 1.38±0.05 and 1.01±0.09 for the 0 Gy and 15 Gy rats, respectively. B) Variograms from the volume maps. The dotted lines represent S and the arrows indicate the extent of R (see Equation 2). For the 0 Gy and 15 Gy rats, R (in mm) is 8.51±0.83 and 6.61±0.53 and S (in 10⁻¹² mL) is 0.49±0.01 and 0.30±0.01, respectively.

Figure 5 shows reconstructed variograms based on the mean parameters of each dose group for the CT images at FRC (Figure 5A) and the volume maps (Figure 5B). Distinct differences between the 0 Gy and the 15 Gy groups are visible, with the other groups distributed in between. We note that the presence of outliers influences the mean, resulting in some overlap between intermediate dose groups.

Figure 5.

A: Variogram group averages of: A: CT images at functional residual capacity (FRC) following the form of Equation 1, and B: 4DCT volume change maps following the form of Equation 2.

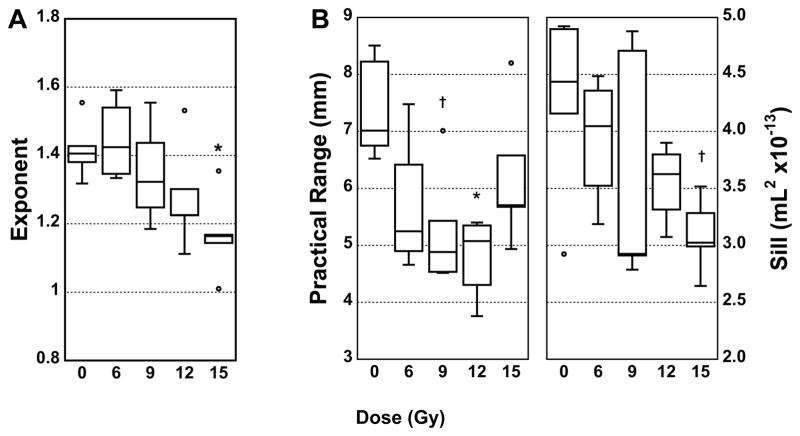
Figure 6 shows box plots of the variogram parameters. In Figure 6A, α at FRC becomes increasingly more distinct from the 0 Gy group with increasing dose to the point that the 15 Gy group is significantly different from control. Indeed, α correlates significantly with dose (p=0.003, r=−0.57). We note that the correlation of dose with α is not significant at PIV (p=0.09, r=−0.35). For the volume change maps, S correlated significantly with dose (p=0.008, r=−0.53). However R showed different behavior, apparently varying with dose in a quadratic manner (see Figure 6B).

Figure 6.

Box plots showing variogram parameters versus dose. A: The exponent α (see Equation 1) from the CT images at functional residual capacity (FRC). B: The range (R) and sill (S) from the volume change maps (see Equation 2). †p<0.05; *p<0.01.

Discussion

We have reported a rapid, objective method of lung CT image analysis that was better able to detect radiation-induced lung damage than conventional pulmonary function tests or image analysis techniques. In particular, variogram parameters from both the octree-decomposed CT images at FRC and the volume change maps correlated significantly with radiation dose. Results indicated that increased exposure to radiation was associated with reduced heterogeneity in this animal model, perhaps indicative of a widespread damage or repair response across the lung. We hesitate to speculate further about the nature of the reduced heterogeneity; however, this point may be elucidated by studies that incorporate blood and alveolar lavage fluid biomarkers as well as lung histological analysis.

Prior studies of radiation-induced lung damage in rats have focused on biomarker expression, DNA damage, non-invasive imaging, pulmonary function changes, and mechanical changes (10, 13, 19–24), often with a lack of consensus. An issue that complicates the body of research is the variety of animal models used, including rat strains, radiation doses, irradiated lung fractions, and elapsed time before data collection. Apparent discrepancies include whether there are significant changes to body weight, respiratory rate, collagen content, or CT density. For example, in this study HU did not correlate with dose, consistent with the findings of Wiegman et al. (19) but contrary to the results of Vujaskovic et al. (20). Both of these studies used male albino Wistar rats and employed hemithoracic or partial-lung irradiation. Pauluhn et al. (23) measured significant differences in several physiological parameters between control and irradiated rats (e.g. body weight, lung volumes, etc.) using a hemithoracic exposure of 20 Gy in Fisher rats. In our study, we observed no significant differences between dose and control groups in most of the measurements made, indicating that the radiation damage was below the threshold of detection using these methods and group sizes.

The dose-response correlation in the variogram analysis detected at FRC was not detectable at PIV, suggesting that spatial variations in the lung decrease as the lung expands and fills with air. We found a decrease in α of the control group between FRC and PIV, which supports this hypothesis, since the lower exponent indicates a slower increase in spatial variation of the mean HU values. Thus, inflation results in a loss of information that masks the effects of subtle disease and potentially confounds diagnosis. Indeed, Kauczor et al. (25) showed that the mean HU values in the human lung correlated better with several lung function parameters at expiration than at inspiration, also implying a loss of information in images acquired at inspiration.

The correlation with dose of volume change map parameters CoV and S implies that volume change maps may be useful diagnostic tools, in addition to their potential to characterize ventilation defects. However, such maps require multiple computational steps, and they demand the acquisition of 4DCT images at two different known inflation levels. The CT-based variograms, on the other hand, require only a single CT image, and α correlated as well or better with dose than S. These attributes make the CT approach more amenable to a clinical setting than the 4DCT approach.

A limitation of this study was the small numbers of animals in each group. Although a significant dose-response correlation was found from the variogram parameters, a clear separation of dose groups was not possible due to the range of response within each group; however, this could be also a consequence of closely-spaced dose levels. Future work may need to include larger sample sizes to establish sensitivity and specificity.

Our results suggest that variogram analysis of octree-decomposed CT images is a rapid, automated approach that may be highly sensitive to subtle lung damage or disease. Future investigation of this potentially powerful method is warranted for application to other species, such as humans, and other lung diseases in which subtle variations in tissue structure may be present, including emphysema.