Unlocking the secrets of multi-flagellated propulsion: drawing insights from Tritrichomonas foetus

Abstract

In this work, a high-speed imaging platform and a resistive force theory (RFT) based model were applied to investigate multi-flagellated propulsion, using Tritrichomonas foetus as an example. We discovered that T. foetus has distinct flagellar beating motions for linear swimming and turning, similar to the ‘run and tumble’ strategies observed in bacteria and Chlamydomonas. Quantitative analysis of the motion of each flagellum was achieved by determining the average flagella beat motion for both linear swimming and turning, and using the velocity of the flagella as inputs into the RFT model. The experimental approach was used to calculate the curvature along the length of the flagella throughout each stroke. It was found that the curvatures of the anterior flagella do not decrease monotonically along their lengths, confirming the ciliary waveform of these flagella. Further, the stiffness of the flagella was experimentally measured using nanoindentation, allowing for calculation of the flexural rigidity of T. foetus's flagella, 1.55×10⁻²¹ N m². Finally, using the RFT model, it was discovered that the propulsive force of T. foetus was similar to that of sperm and Chlamydomonas, indicating that multi-flagellated propulsion does not necessarily contribute to greater thrust generation, and may have evolved for greater manoeuvrability or sensing. The results from this study have demonstrated the highly coordinated nature of multi-flagellated propulsion and have provided significant insights into the biology of T. foetus.

1. Introduction

For microorganisms, which reside at low Reynolds number (from 10⁻⁵ to 10⁻⁴), reciprocal types of motion are incapable of generating net forward propulsion [1–3]. In order to overcome this limitation, microorganisms have evolved highly specialized propulsive structures, such as cilia and flagella, to generate non-reciprocal travelling waves. In the case of prokaryotic flagella, a rotary motor drives the flagella resulting in a helical waveform, which acts as a propeller to move the microorganism [4]. Eukaryotic flagella, however, are able to generate planar waveforms from the sliding of microtubules along the length of the flagella [4–6]. In addition to these differing flagella structures, prokaryotes and eukaryotes have adopted both single- and multi-flagellar configurations to generate propulsion. While much research has been conducted on multi-flagellated propulsion and manoeuvrability in prokaryotes, specifically the ‘run and tumble’ strategy of peritrichous bacteria [7–9], fewer studies have examined multi-flagellated propulsion in eukaryotes, with the exception of the biflagellated algae Chlamydomonas [10–12]. In fact, researchers have recently discovered that Chlamydomonas exhibits a similar ‘run and tumble’ behaviour, where cells switch from nearly straight swimming to abrupt large reorientations [13]. Previously, we developed a high-speed imaging platform that allowed for increased resolution of flagella, allowing for detailed qualitative analysis of propulsion in the octo-flagellated eukaryote Giardia lamblia [14,15]. In this work, we combined the previously developed high-speed imaging platform with a state-of-the-art nanoindenter and resistive force theory (RFT) to quantitatively analyse multi-flagellated propulsion using Tritrichomonas foetus as a test case.

Unlike the bilaterally symmetric multi-flagellar arrangement of Chlamydomonas and Giardia, the quadri-flagellated trophozoites of T. foetus have four flagella that originate at the anterior pole, with the single recurrent flagellum curving back along the cell body, attaching at several points to form the undulating membrane (figure 1a) [16–23]. The three anterior flagella (one free and two stalked at their base) extend freely from the anterior pole. Previous studies have revealed that the cytoskeleton (i.e. axostyle and costa) of T. foetus remains rigid throughout the entirety of its swimming motion [24], as opposed to other trichomonads [25] and Giardia [14], in which body flexion can be observed. Because the cell body of T. foetus is shown to be rigid during swimming, the propulsive forces necessary for swimming must be the result of flagellar beating [24], making this microorganism ideally suited for the study of multi-flagellated propulsion.

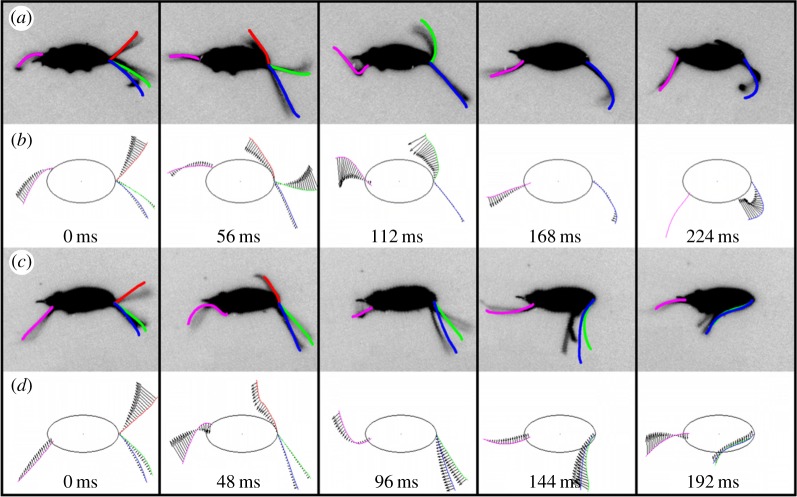
Figure 1.

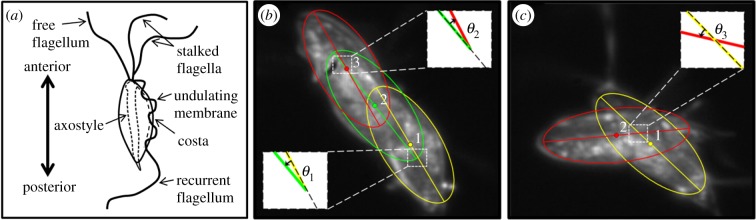
Morphological diagram of T. foetus and motion of the cell body during linear swimming and turning. (a) Morphology of T. foetus trophozoite, demonstrating the positioning of the four flagella, anterior and posterior poles, and internal cytoskeletal structures. (b) Motion of the cell body during linear swimming, showing its ability to correct for angular changes in consecutive beats resulting in an overall linear path. Ellipses have been superimposed over the body at the initial and final positions of each beat to identify the centre of mass of the cells, marked as points 1–3. The change in angle over the first beat (θ₁) with respect to the initial orientation (dotted line) was approximately 15°. After the second beat, the change in angle (θ₂) was approximately 15°, which resulted in a net angular change of 0° over two beats. (c) The change in angle of the cell body during turning (θ₃) was approximately 30°, and because the body does not spin around the longitudinal axis during this beat, no angular correction takes place in consecutive beats.

In order to comprehensively analyse multi-flagellated propulsion in T. foetus, quantitative analyses of the flagella motion, including kinematics and curvature changes, mechanical properties of the flagella and thrust generation were conducted. Quantitative data for the movement of the cell body and flagella were obtained using the increased resolving capabilities of the CytoViva microscopic platform, coupled with a high-speed particle image velocimetry camera. While previous attempts have been made to characterize the flagella beating of T. foetus, the low speed of capture, 30 frames per second (fps), and poor resolution used in these studies were not able to fully account for the complex dynamics of their rapid motion [24,26]. Using the improved spatio-temporal resolution of this platform, two distinct flagella beating patterns were discovered for either linear swimming or abrupt changes in orientation (termed turning). These distinct patterns demonstrate sophisticated coordination and control, and indicate specific roles for the anterior and recurrent flagella in propulsion. In addition, the ability of the cell to rapidly alter its flagella beating pattern for linear swimming and turning suggests a eukaryotic ‘run and tumble’ behaviour, similar to Chlamydomonas. Further, nanoindentation was used to determine mechanical properties of the flagella, whereas curvature changes along the length of the flagella were calculated for both linear and turning motions. Quantitative analysis of the curvature of the flagella confirmed that T. foetus exhibits two distinct flagellar beating patterns. Additional analyses using the RFT model revealed that the observed rotation of the cell along its longitudinal axis in linear swimming allows the cell to maintain a linear trajectory. Using this model, we were also able to calculate the thrust generated by each flagellum and compare the propulsive force of T. foetus with other microorganisms using both single- and multi-flagellated swimming strategies.

2. Results

2.1. Experimental analysis

Using the integrated experimental platform, the motion of T. foetus trophozoites was captured at 167 fps, 40 times greater than the reported beating frequency of the anterior flagella [24,26]. Analysis of the swimming motions from more than 100 cells revealed two distinct flagella beating patterns resulting in two different trajectories of the cell body, recognized as either linear swimming or turning. It was discovered that the cell moves in a linear trajectory (figure 1b) by using the rotation of the cell about its longitudinal axis (termed spinning) to offset the angular changes from consecutive beats. The turning motion was found to generate a large angular change from sequential beats, with no observable spinning. When the cell used the turning motion, it was able to make more radical and abrupt changes to its orientation and trajectory (figure 1c). To confirm that the two swimming motions were distinct, quantitative analyses of the flagella dynamics for both motions were further characterized.

As illustrated in previous studies, the anterior flagella beating motion of T. foetus can be separated into two time-dependent phases: the active and recovery strokes [24,26]. During the active stroke, the anterior flagella extend out in front of the cell body, resulting in a backwards motion of the cell, similar to Chlamydomonas [27]. The recovery stroke immediately follows the active stroke, as the anterior flagella are pulled back towards the cell body, propelling the cell forward. Because the active stroke was obscured by the cell body, only the motion during the recovery stroke was considered in this work. It was determined that the recovery stroke for linear swimming was 32% (p = 6.6 × 10⁻¹¹) longer in duration and that the cell travelled 27% (p = 0.018) farther during linear swimming when compared with turning (table 1). The angular change of the cell body during the turning stroke was also found to be 2.4 times larger (p = 0.005) despite the shorter duration of its beat (table 1). Additionally, linear swimming cells were found to spin approximately 180° during a single beat (see electronic supplementary material, movie S1), while in turning, there was no detectable spinning (see electronic supplementary material, movie S2), as can be seen by the position of the axostyle in figure 2a,c. Owing to the spinning observed in linear swimming, no difference in the beating pattern of the recurrent flagellum was observed. Considering that the cytoskeleton (i.e. axostyle and costa) of T. foetus remains rigid during the entire swimming motion [24], it was determined that the forces generating the two distinct motions of the cell body in linear swimming and turning were the result of altered flagella beating patterns.

Table 1.

Data obtained from experimental analysis of T. foetus during linear swimming and turning.

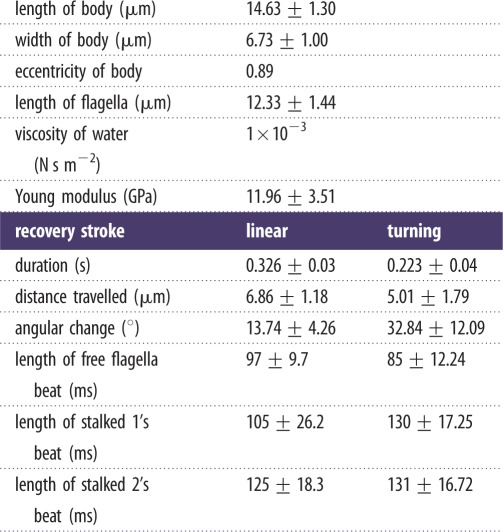Figure 2.

Comparison of flagella motion during linear swimming and turning in the body-fixed frame. (a) The average flagella traces for linear swimming were overlaid onto inverted images of a single cell to demonstrate the fit of the average traces. (b) The polynomial fits of the flagella during linear swimming, with the fluid force vectors indicated. (c) The average flagella beat motion during turning overlaid onto inverted images of a typical turning cell. (d) The polynomial fits of the flagella during turning, with the fluid force vectors indicated. As clearly illustrated in the figure, the two stalked flagella beat simultaneously during turning, with vectors oriented in the same direction with similar magnitudes. For linear swimming, the stalked flagella beat over separate time intervals. In all images, red indicates the free flagellum, green represents stalked 1, blue represents stalked 2 and pink represents the recurrent.

In order to correlate the motion of the cell body with that of the flagella, traces of the recovery stroke for all four flagella were generated for both linear swimming and turning (figure 2a,c). Using a method similar to [28], ‘point clouds’ were generated for the flagella of 10 distinct linear swimming cells and 10 distinct turning cells during the recovery stroke. Polynomials were fitted to the point clouds at 10 evenly spaced time intervals to generate an average flagella beat pattern for both linear swimming and turning. A comparison of the average flagella beating pattern to a single cell displaying either linear swimming or turning can be seen in the top frame of the electronic supplementary material, movies S3 and S4. When comparing the duration of each anterior flagellum beat for turning, it was determined that the free flagellum beat with a shorter duration than the stalked flagella (table 1). Additionally, stalked flagella 1 and 2 (referred to as stalked 1 and stalked 2 from this point forward) were found to beat together, resulting in the same duration throughout the turning motion (table 1 and the electronic supplementary material, movies S3 and S4). By contrast, for linear swimming, propulsion from each flagellum occurred over a different time interval. Another key difference between the anterior flagella during linear swimming and turning was that the two stalked flagella beat on opposite sides of the body for linear swimming, having opposing angular contributions, whereas they beat on the same side of the body and sum together to generate a larger angular change during turning (figure 2a,c and the electronic supplementary material, movies S3 and S4). Commensurate with this change, the two stalked flagella appeared to have a much more rigid beating form during turning.

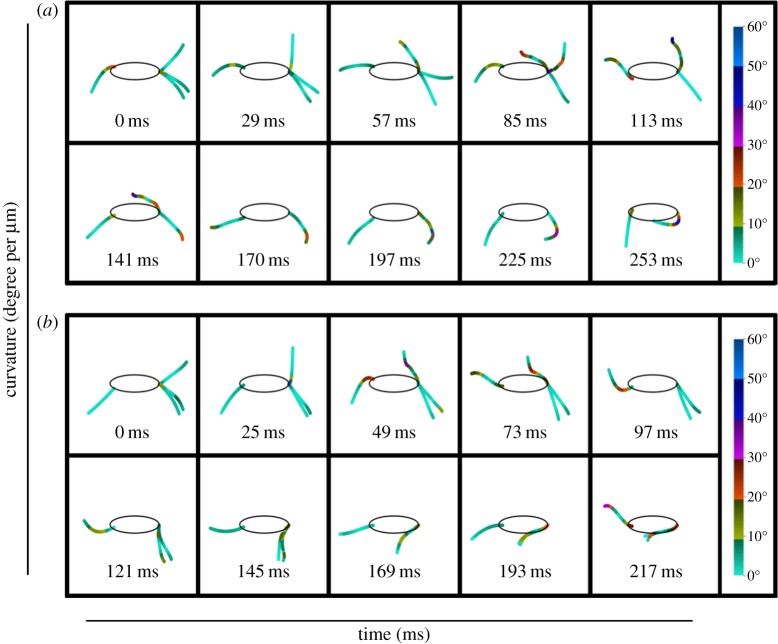
In order to analyse the curvature changes in the average flagella at each time point, over the length of the flagella, each flagellum was divided into 10 distinct regions. The first region spanned from the point of exit from the cell body to 10% of the flagellum length, followed by further segmentation for every 10% increase in length (10–20, 20–30%, etc.). The curvature of these regions was calculated at each time point using the method of Okuno et al. [29]. Briefly, by taking the angle formed by two tangents at the points before and after the point of interest and dividing it by the length of that section, curvature was calculated. In figure 3, a colour gradient is used to represent the degree of curvature in the different regions along the length of the flagella. Quantitative analysis of the curvature change revealed similar trends to those observed from the video microscopy analysis. In both linear swimming and turning, the free flagellum has little curvature at the first time instant, followed by a gradual increase in the first 20% at the second time interval. More pronounced curvature was observed for the rest of the free flagellum beat, with the curvature increasing along the length of the flagellum. The most obvious difference between linear swimming and turning was the lack of curvature in both stalked 1 and 2 throughout the entire beat cycle. In linear swimming, both of the stalked flagella had regions where the curvature exceeded 40°; however, during turning neither stalked flagellum exceeded 30°. In fact, for the first 97 ms of turning, the stalked flagella had almost no curvature. This was in opposition to linear swimming, where stalked 1 had significant curvature at 85 ms. Analysis of the curvature also supported the observation from video microscopy that during linear swimming the anterior flagella beat out of phase with each other, whereas stalked 1 and 2 beat in phase for turning. Further, because the curvature of the anterior flagella did not decrease monotonically along their lengths, this analysis demonstrated that they move with a ciliary waveform rather than with a sinusoidal beat [30,31]. Analysis of the recurrent flagella between linear swimming and turning did not reveal any significant differences in the magnitude of curvature, which was not surprising owing to the similarity of the beats between the two motions. In addition to curvature, this analysis highlights the timing and coordination necessary for T. foetus to effectively use these two distinct beating patterns for effective propulsion. To further characterize the motion of the flagella between the two beating patterns, quantitative analyses of the flagella mechanics were conducted.

Figure 3.

Curvature changes along the length of each flagellum during the entire recovery stroke of linear swimming and turning. The zero point of each flagellum was the point of exit from the cytoplasm. Curvature was then calculated at equally distributed intervals along the length of the flagella (10% increments). The magnitude of curvature at each increment is shown by the gradient colour bar. When comparing the changes in curvature between linear swimming (a) and turning (b), it is apparent that differences exist between the strokes, both in the magnitude of the curvature and the time phase of bending.

2.2. Mechanics analysis

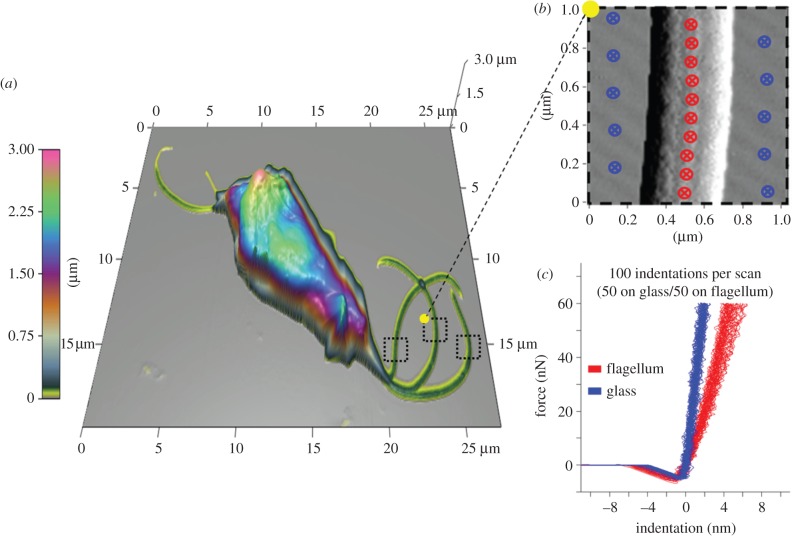
While several studies have used atomic force microscopy to image various protozoa [32–35], none have applied nanoindentation to experimentally determine the mechanical properties of the flagella of these microorganisms. Using nanoindentation, we determined that the Young modulus for the flagella of T. foetus was 11.96±3.51 GPa (figure 4). Considering that the cells were fixed with glutaraldehyde prior to analysis, the measured modulus is expected to be higher than in the natural biological state. Unfortunately, limited data exist on the extent to which fixation affects the Young modulus values obtained from nanoindentation. In a recent study, the stiffness of cartilage was found to increase by one order of magnitude after fixation with paraformaldehyde [36]; however, it is unknown the degree to which the stiffness of flagella will change after fixation.

Figure 4.

Determination of the Young modulus for T. foetus's flagella using nanoindentation. (a) A three-dimensional topographical image of T. foetus used to visualize the location and orientation of each flagellum. (b) A 1 µm² scan over the selected region used for the placement of indentation points (20 total, 10 on glass and 10 on flagellum) shown in blue (glass) and red (flagellum). (c) Resulting force versus indentation curves from the selected points in (b), along with the calculated averages of the Young modulus for both glass and flagellum (65.91±13.16 and 11.96±3.51 GPa).

Assuming the same moment of inertia (I) as a typical (9 + 2) eukaryotic axoneme [29], the flexural rigidity of the flagella in T. foetus was estimated to be 1.55×10⁻²¹ N m², within the range of other eukaryotic flagella. While similar values have been reported for sperm flagella (0.3–5.8 × 10⁻²¹ N m²) [37], when compared with typical (9 + 2) cilia (3–13 × 10⁻¹⁸ N m²) [38] and bacterial flagella (1.0 × 10⁻¹⁴ N m²) [39], the flagella of T. foetus are considerably more flexible. Recent studies have reported that primary mammalian cilia (9 + 0), however, are considerably more flexible (1.4–3.9 × 10⁻²³ N m²) than the flagella of T. foetus, which would be expected due to the lack of central pair microtubules in primary cilia [40]. After obtaining a value for the flexural rigidity of the flagella and the curvature change along the length of the flagella, it was possible to calculate the bending moments along the length of the flagella. Briefly, by multiplying the flexural rigidity by the curvature at a particular point on the flagella, the bending moments were calculated; however, the trends are identical to those shown for curvature alone, thus only curvature is shown in figure 3. Next, a dynamics model was created to further characterize the differences in these strokes, and identify the role of each flagellum in propulsion.

2.3. Dynamics analysis of swimming

2.3.1. Model validation

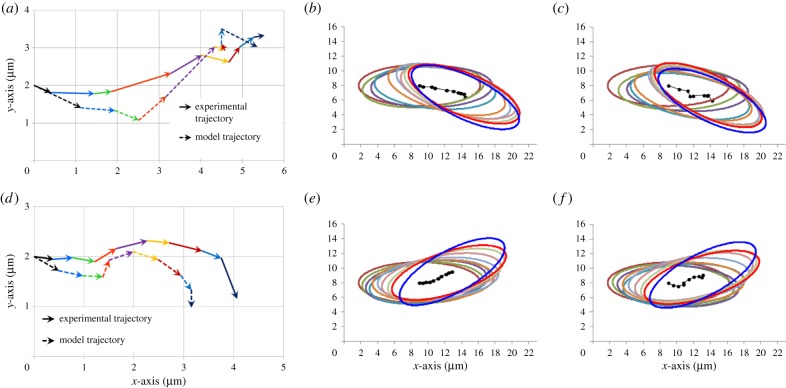
The input to the model was the flagella traces obtained from the experimental platform; however, to ensure the same distance between points along the length of the flagella, polynomials were fitted to the flagella traces (figure 2b,d). As shown in figure 2 and the electronic supplementary material, movies S3 and S4, the polynomial fits accurately represent the average flagella traces, and therefore can be used to calculate the flagellar forces. The first step in determining the forces generated by the flagella during both linear swimming and turning was to determine the ratio of the tangential and normal drag coefficients on the flagella (C_T/C_N). Considering the complexity associated with modelling a multi-flagellated microorganism, we chose to set the C_T/C_N ratio to 0.5, the optimum ratio for a smooth cylinder [41]. Previous studies have found that C_T/C_N ratios range from 0.44 to 0.7 for microorganisms with either cilia or flagella as the primary motile structure [10,42–48]. The only microorganisms known to have a C_T/C_N ratio outside of this range, and greater than 1, are the hispid flagellates such as Euglena [49]. In these microorganisms, the flagella are modified with mastigonemes, stiff filaments that extend perpendicular to the flagella surface, providing the necessary force to achieve this high C_T/C_N ratio. Considering these constraints, the approximation of the C_T/C_N ratio at 0.5 for T. foetus was reasonable. While the C_T/C_N ratio can be easily approximated, following the approach used in [10], the magnitudes of C_N and C_T were determined based on a minimization of the normal mean-squared error in the instantaneous velocity in x and y (E_x and E_y) between the experimental trajectory, and the model-derived trajectory of the cell in the body-aligned frame. Using this optimization method, it was possible to determine C_N and C_T for both linear swimming and turning, as shown in table 2. The optimized C_N and C_T values were within the range of values typically reported for flagellated microorganisms, 1.226–2.46 pN s μm⁻² [10,43,46–48]. Using the optimized values of C_N and C_T, trajectories generated by the model in the body-aligned frame were compared with the experimental trajectories. Based on the comparison of the trajectories in the body-aligned frame, it can be seen that with the optimized values of C_N and C_T, the magnitude and direction of the vectors from each time point closely match the model trajectory (figure 5a,d). In early attempts at modelling linear swimming, the model trajectories showed similar trends in the direction of vectors; however, the magnitude of the vectors was reduced. This problem was not encountered in the analysis of turning. The reduced magnitude of the initial vectors for linear swimming and the fluid dynamics associated with this reduction are extensively addressed in section Discussion.

Table 2.

Results from modelling analysis of propulsive stroke.

	model
	linear	turning
propulsive force (pN)
free	2.91	4.86
stalked 1	6.62	6.53
stalked 2	4.11	6.34
recurrent	7.05	8.37
total propulsive force (pN)	20.69	26.09
CN (pN s μm−2)	1.85×10−3	1.75×10−3
CT (pN s μm−2)	0.93×10−3	0.88×10−3
α	2.76	5.94
EVx	0.48	0.16
EVy	0.39	0.43
ER	0.42	0.49
flexural rigidity (N m2)	1.55×10−21

Figure 5.

Experimental and model-derived trajectories for linear swimming and turning in both the body-aligned frame and laboratory frame. (a) Comparison of the experimental and optimized model-derived trajectories for linear swimming in the body-aligned frame. The vectors from each time point are shown as a different colour throughout the course of the stroke. The shape of the trajectories is similar and the trajectories end at similar points. (b) Experimental trajectory of an average cell displaying the linear swimming pattern with its flagella. Ellipses have been superimposed around the centre of mass to indicate the angular change of the cell. All cells start at the same position and travel in the positive x-direction. Despite variations around a central line, the cell proceeds along a linear path with minimal angular changes from the starting and ending points. (c) Model trajectory in the laboratory frame using the flagella input from the average linear swimming flagella traces. (d) Comparison of the experimental and optimized model-derived trajectories for turning in the body-aligned frame. Note that there is a slight reduction in the x-component of the trajectory, with an increased y-component. (e) Experimental trajectory of an average cell using the turning beating pattern. During turning, the cell has reduced motion in the forward (positive x) direction and has a large angular change of approximately 30° from its starting orientation. (f) Model trajectory in the laboratory frame using the flagella input from the average turning flagella traces. Note that over the course of each stroke the cell follows the same trajectories and angular changes as the experimental trajectories.

The ability of the model-derived, body-aligned frame trajectories to follow the experimental trajectories, within a tolerable error, validates the C_N and C_T magnitudes identified by the model. However, when considering the angular component of the trajectories that are required to translate the body-aligned frame into the laboratory frame (defined as the actual trajectory of the cell), the values of C_N and C_T identified by the model have a reduced angular velocity. In [10], a correction factor, α, was applied to increase the magnitude of C_N and C_T to provide enough force to correct for the reduced angular velocity. However, in that work, a unicellular mutant of Chlamydomonas was modelled, and the correction factor was used to account for the poor swimming ability of the cell, leading to a large boundary effect. In the case of T. foetus, these boundary conditions were minimized owing to the swimming ability of this cell. Instead, the correction factor, α, was applied directly to the net moment (Material and methods) to provide the necessary increase in angular velocity. In terms of the fluid dynamics of the system, the application of α to the net moment means that the forces generated by the flagella are correct, as demonstrated with the body-aligned frame comparison; however, how these forces influence the rotation of the body cannot be accurately described without a correction factor. Considering the complex fluid dynamics at the interface between the cell body and flagella, it was not surprising that a correction factor was necessary to account for the actual rotation of the cell body. It should be noted that the normal mean-squared error for angular velocity (E_R) before correction was 0.73 for turning and 0.56 for linear swimming. In essence, this low error demonstrates that the instantaneous angular velocity generated from the flagella created the correct angular changes, but with a reduced magnitude. When α was applied to correct for the low angular velocity, the error was reduced to 0.47 for turning and 0.41 for linear swimming. Comparisons of the model-derived and experimental trajectories in the laboratory frame of reference are shown in figure 5b,c,e,f. At the start of each simulation, the cells were oriented the same as figure 2a,c, with the undulating membrane at the bottom of the cell. After validating the model, in terms of both instantaneous angular and linear velocities, as well as the ability to maintain a similar trajectory to the average experimental cells, the model was used to analyse the thrust generated by the flagella during each motion.

2.3.2. Analysis of multi-flagellated propulsion

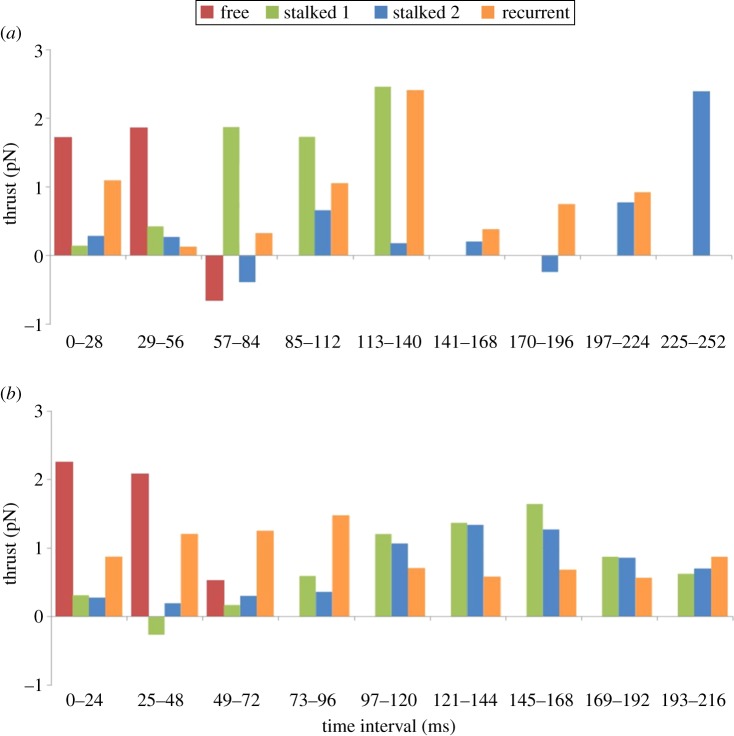
One of the key contributions from the implementation of the proposed RFT model was the ability to determine the thrust generated by each flagellum. During linear swimming, 20.69 pN of thrust was generated by all of the flagella. The anterior flagella were responsible for 87% of the thrust in the forward direction (along the x-axis of the body-fixed frame), with the recurrent flagellum contributing 70% of the thrust along the y-axis in the body-fixed frame. Cumulatively, the free flagellum provides the smallest amount of total thrust, as it is only involved in the first three time intervals, whereas stalked 1 and the recurrent flagella generate similar thrust values (table 2). In addition to the thrust generated by each flagellum, the timing or phase of beating was shown to have a significant effect on propulsion. As shown in figure 6a, during the first 56 ms, the free flagellum provides the majority of the thrust, followed by stalked 1 over the next 84 ms, and finally the thrust over the last 112 ms is split between the recurrent flagellum and stalked 2 (as illustrated by the force vectors in the electronic supplementary material, movie S1). Thus, for linear swimming, propulsion is generated through a highly coordinated beating of each of the anterior flagella over a distinct time interval.

Figure 6.

Thrust generated during each time interval of the recovery stroke. (a) Thrust generated by each flagellum for linear swimming shows the cyclic nature of this stroke. From 0 to 56 ms, the free flagellum contributed 56% and 69% of the propulsive force. From 57 to 140 ms, stalked 1 contributed >50% of the propulsive force. After this interval, the propulsive force was generated by a combination of the recurrent and stalked 2. Over the course of the entire stroke, the recurrent flagellum generated the greatest propulsive force (7.04 pN); however, as mentioned in the text, this force was predominantly along the y-axis. The majority of the forward propulsive force was generated by stalked 1 (6.61 pN). Combined, the total thrust generated from all four flagella during the recovery stroke was 20.69 pN. (b) Thrust generated by each flagellum for turning. Similar to linear swimming, over the first 48 ms, the free flagellum provided the majority of the propulsive force (62.5%). For the rest of the stroke, however, stalked 1 and 2 contributed relatively equally to propulsion. This is further confirmed by the total propulsive force generated by stalked 1 and 2 (6.53 and 6.33 pN). The total thrust generated during the course of the turning motion was 26.09 pN, 1.26 times larger than the force generated during linear swimming.

Similar to the analysis of thrust generation for linear swimming, the thrust generated by each flagellum during turning was highly coordinated. Over the first 56 ms, the free flagellum generated the majority of the thrust; however, unlike linear swimming, the rest of the beat had similar thrust values for both stalked 1 and stalked 2 (as illustrated by the force vectors in the electronic supplementary material, movie S2). Considering that these two flagella have a similar beat and orientation during turning, this result was not surprising. Another distinction between linear swimming and turning was the contribution of the recurrent flagellum throughout the entire beat motion during turning (figure 6b). Although both strokes appear to have cyclic or periodic contributions from the recurrent flagellum, the thrust generated during turning is much more consistent in magnitude (0.56–1.46 pN) when compared with linear swimming which covers a broader range of thrust values (0.13–2.39 pN). In general, the thrust generated during turning is larger, 26.09 pN, than linear swimming. In fact, only stalked 1 has a similar value for both strokes, 6.61 and 6.53 pN (table 2). The ability to predict the thrust generated from multi-flagellar beating not only allows comparison of propulsion between linear swimming and turning in T. foetus, but also allows for comparison of propulsion across a wide range of microorganisms using various swimming strategies.

3. Discussion

In this work, we combined high-speed, high-contrast video microscopy, nanoindentation and an RFT model to analyse multi-flagellated propulsion using T. foetus as a test case. Significant insights into the motion of T. foetus, beating characteristics of its flagella and thrust generation were elucidated. Further, the resulting changes in the fluid dynamics associated with the ‘spinning’ of the cell body are discussed. Based on these results, we have gained greater insights into the biology of T. foetus, and more generally into multi-flagellated propulsion.

The first major finding of this work was that T. foetus was capable of generating two distinct flagellar beating motions to adjust its trajectory from linear swimming to turning. The ability of T. foetus to generate multiple waveforms from the same flagellar structure has implications for the underlying biology of the flagella and behaviour of the cells. In an effort to further understand potential structural modifications in the flagella of T. foetus, and physiological factors that contribute to the change in waveform, examples of other microorganisms capable of generating multiple waveforms are discussed below. One example is the unicellular algae Chlamydomonas, which is capable of generating a forward swimming motion through ciliary beating of its flagella, or backward swimming by changing to an undulating waveform [50]. Previous studies have demonstrated that the flagellar membranes of Chlamydomonas play a role in the regulation of calcium to the flagella, which can reversibly alter the flagella motion from ciliary to sinusoidal [50,51]. Further analysis of the central pair microtubules during forward and backward swimming showed that the generation of the different waveforms leads to differential twisting of the central pair with each beat form [52]. In Chlamydomonas and Paramecium, the central pair rotates parallel to the bend plane of the flagella; however, in Opalina, the central pair rotates perpendicular to the bend plane [52]. In general, the twisting of the central pair can occur through modification of the flagella structure, where relaxed flagella have an inherent twist, or through activation of specialized dynein motors that initiate twisting [52]. In other microorganisms, such as T. brucei, the orientation of the central pair remains fixed throughout beating; however, this organism has a more rigid paraflagellar rod that may prevent free rotation of the central pair [53]. Because no paraflagellar rod exists in T. foetus, we hypothesize that central pair twisting provides the underlying force for the generation of the two waveforms exhibited by the anterior flagella. Further analysis would be necessary to confirm this hypothesis.

In addition to the structural implications of the multiple flagella waveforms, behaviourally, this fine control over direction suggests that the microorganism is responding to environmental cues and adjusting its trajectory to reach a target destination. Similar strategies are used by Escherichia coli and Chlamydomonas, where the cells change the waveform of their flagella to alter their trajectory in response to a chemical gradient, or photophobic response [54,55]. A recent study on the flagella membrane of T. foetus revealed that the anterior flagella have rosettes of integral membrane proteins along their length, which were hypothesized to contribute to active exo- and endocytosis [56]. These specialized integral membrane proteins may be involved in active sensing of environmental parameters that provide cues for the cell to change direction. Further, the abundance of these proteins along the length of the anterior flagella may play a key role in controlling local calcium levels, which could initiate the rapid switching between the different flagella waveforms through modification of the central pair, or other unknown mechanisms. In this study, the cells were grown in a nutrient-rich medium, preventing analysis of any kind of targeted motion. However, T. foetus has shown the ability to invade fetal tissue [57] and to actively adhere to and phagocytose sperm cells [23]. It is possible that the highly specialized linear and turning motion evolved as a means to rapidly track and capture its motile prey, sperm.

Associated with the ability of cells to sense environmental changes is the ability of the cell to ‘search’ for desired chemical gradients, and then follow the gradient to reach its target. In bacteria, this sort of searching and directed movement is conducted using the well-studied ‘run and tumble’ mechanism [8,58–61]. More recently, ‘run and tumble’ behaviours have been discovered in the eukaryote Chlamydomonas, where cells grown in the dark oscillate between nearly straight swimming and abrupt large reorientations in search of nutrients or light [13]. Similar ‘run and tumble’ strategies have been hypothesized for Trypanosoma brucei, although this has not been confirmed [62,63]. More recently, a mechanical model was proposed to investigate the potential for ‘run and tumble’ in a migrating amoeboid cell [64]. In this work, we identified a ‘run and tumble’ type of motion in T. foetus, similar to bacteria and Chlamydomonas, leading to the hypothesis that T. foetus has the ability to sense and track molecular or chemical gradients. While further studies are necessary to validate this hypothesis, this study provides support for the ubiquity of this strategy in microorganisms in general, despite the majority of focus in prokaryotic cells. The discovery of a ‘run and tumble’ mechanism in T. foetus has further implications for the treatment of disease, and if the chemotactic agent(s) can be identified, it may be possible to reduce the pathogenesis associated with this organism.

Another strength of the combined experimental and theoretical modelling approach used in this work was the ability to identify key changes in the fluid dynamics that were not evident from the experimental analysis. While the first iteration of the model for linear swimming generated velocity vectors with similar direction, the magnitude of the vectors was roughly half that of the experimental data. For turning, however, the magnitude and direction of the velocity vectors generated from the model were similar to those measured from experimental trajectories. This suggested that there was a significant difference in the fluid dynamics associated with linear swimming and turning. Considering that the body spins around the longitudinal axis during linear swimming and not turning, it can be hypothesized that there are key changes in the resulting fluid dynamics associated with this type of motion. As noted previously, with the introduction of the correction factor α, current models applying similar methods have been unable to accurately characterize the resulting torque on the cell body at low Reynolds number [10]. Considering that the complex fluid dynamics at the interface between the cell body and flagella are still unknown, it is likely that there are significant boundary effects that cannot be directly accounted for using the current approach. Similarly, in this work, the fluid dynamics associated with the spinning of the cell body around the longitudinal axis cannot be accounted for. One hypothesis that would explain the reduced magnitude of the velocity vectors predicted by the model for linear swimming is that the spinning of the cell body effectively reduces the drag experienced by the body. While this has not been demonstrated for a prolate ellipsoid at low Reynolds number, recent work has shown that the rotation of other uniquely shaped structures or bodies under similar conditions have increased propulsion efficiency [65,66]. While it was necessary to model T. foetus as a prolate ellipsoid, because irregular shapes are too complex, in actuality an undulating membrane wraps around its body from the anterior to posterior region, and it is possible that this structure generates a reduction in drag upon spinning. Further, owing to the motion and position of the flagella and undulating membrane during linear swimming in T. foetus, it is reasonable to hypothesize that the viscoelastic properties of the localized fluid could be altered as a result of interactions occurring at this interface, as reported for other microorganisms [67]. In the work done by Spagnolie et al. [65], it was shown that viscoelasticity can either increase or decrease both the swimming speed and/or swimming efficiency of helical bodies depending on geometry, fluid properties and rotation rate. Another study regarding the formation of chiral ribbon trajectories of sperm was able to show that the three-dimensionality of sperm swimming generates a situation in which the surface area is minimalized, further stating that this could potentially lead to energy minimization corresponding to maximal propulsion efficiency [68]. The three-dimensionality of linear swimming in T. foetus could therefore be a similar strategy in which the spinning of the body creates a minimal surface leading to an increase in propulsion not evident during the turning motion. Although the direct cause and degree to which spinning might affect the propulsion of T. foetus during linear swimming cannot be determined, the results from this study provide additional evidence that this type of rotation could be an efficient strategy for maximizing propulsion at low Reynolds number.

The ‘spinning’ of the cell body around the longitudinal axis also has significant implications for the control of the trajectories. As illustrated in figure 1a, during linear swimming, the 180° rotation of the cell around the longitudinal axis allows the cell to correct for the approximately 15° change in angle observed for a single recovery stroke. In essence, in the first beat of the linear swimming, the cell will turn approximately 15° away from the linear trajectory; however, after rotation in the second beat, the cell will turn approximately 15° towards the overall linear trajectory, resulting in a net angle change of 0°. Unlike linear swimming, the lack of ‘spinning’ around the longitudinal axis during turning, as shown by the position of the axostyle in figure 2b, allows the cell to make a sharp angular change or turn, before initiating linear swimming again. Considering the two-dimensional nature of the model and experimental technique, we were not able to conclusively elucidate the structure that provided the initial force to start the cell ‘spinning’. However, based on the differences in the active stroke for turning and linear swimming, we hypothesize that the force for ‘spinning’ is generated by the three-dimensional motion of the active stroke. Further analysis is necessary to analyse this hypothesis.

The final contribution from this work was the ability to analyse the multi-flagellated propulsion of T. foetus in the context of other known microorganisms with varying strategies for generating low Reynolds number propulsion. The net propulsive force generated by the flagella in T. foetus during the recovery stroke (20–26 pN) was similar to the values obtained for other eukaryotic flagellates. Despite the sinusoidal motion of the flagella in sperm compared with the ciliary beating of the flagella in Chlamydomonas and T. foetus, the propulsive forces for linear swimming from all of these organisms fall within a similar range of magnitude, 13.5–25 pN [69–71]. When compared with the propulsive force generated from the rotary flagella of the bacteria E. coli and Salmonella typhimurium, 0.37–0.57 pN, the eukaryotes have much greater force, although the body size of bacteria is much smaller, thus drag is lower [72,73]. By far the propulsive strategy that generates the most force is the ciliated swimming of Paramecium, which generates 7000 pN of force [74]. However, Paramecium are much larger than the other eukaryotic cells provided for comparison, and the number of cilia is in the thousands. In addition to the overall thrust generated by T. foetus, the propulsive force per flagellum is within the range of other eukaryotic cells: the flagella of sperm, 6.5–11.1 pN [75], Chlamydomonas reinhardti, 2.4 pN [76], and Volvox carteri, 0.3–0.8 pN [76]. Considering that the total propulsive force generated by the four flagella of T. foetus is similar to the force generated by the biflagellate Chlamydomonas and uniflagellated sperm, we hypothesize that the multi-flagellated state may have evolved for a separate purpose beyond simple propulsion. A similar hypothesis has been put forward for E. coli, where flagellar bundles have been shown to generate similar thrust values compared with individual flagella [77]. Similarly, as indicated previously for G. lamblia, the presence of multiple flagella pairs may aid in precise steering, orientation and stability [14]. For T. foetus, a similar trend has been observed, where the recurrent flagella controls angular deviation, while contributing less directly to forward propulsion. Additionally, an increased number of flagella may aid in sensing, attachment or other key biological functions independent of propulsion.

4. Material and methods

4.1. Experimental

Tritrichomonas foetus cultures were purchased from the American Type Culture Collection (ATCC; strain BP-4 ATCC no. 30003) and cultured axenically in Diamond's medium. Microscopic analysis was conducted using the CytoViva (Aetos Technologies, Inc., Auburn, AL) illumination and imaging system described previously for the analysis of the flagella motion of G. lamblia [14]. Using this system, the flagella motion of T. foetus was captured at 167 fps, far superior to previous studies [24,26]. Manual traces of the flagella motion over 10 complete beat cycles were conducted in the ImageJ software package (following inversion of the image colours), and the x–y coordinates of the flagella traces were exported to generate ‘point clouds’ from which the average beat motion was analysed, similar to the methods outlined in [28]. Using the point clouds, it was possible to generate a representation of the flagella motion at 10 different time-points for the recovery strokes. Polynomial fits were used to smooth the average traces and to extrapolate points along the flagella. The polynomials were then used to obtain the velocities of the flagella, and used as the input to the model.

In order to experimentally obtain a value for the Young modulus of the flagella in T. foetus, the cells were fixed with 2.5% glutaraldehyde in Millonig's buffer and dehydrated using an ascending series of ethanol, prior to air-drying onto coverslips. Nanoscale imaging and nanoindentation of T. foetus were performed using an Asylum MFP/3D atomic force microscope. Cells were first imaged in AC mode using AC240TM cantilevers with a spring constant of 2 N m⁻¹ and frequency of 70 kHz (figure 4a). After imaging, 1 µm² scans were taken on individual flagella (figure 4b). Twenty points were then selected (10 points equally distributed over the coverslip surface and 10 points equally distributed along the centre line of the flagellum) and a series of indentations (five at each point) were performed. A 60 nN trigger force was selected to indent 5–10% into the flagellum to ensure that there were no effects from the underlying glass substrate. This procedure was repeated for 10 different flagella from multiple cells, yielding 1000 total force curves (500 taken on the glass substrate and 500 taken on the flagella) from which the Young modulus was calculated using the Hertzian model provided in the MFP/3D software.

4.2. Modelling

In both linear swimming and turning, the flagella have a planar beating motion, which allows the flagella to be traced. In turning, the lack of rotation of the cell body around the longitudinal axis maintains the planar beat motion of the flagella. During linear swimming, the cell body spins around the longitudinal axis; however, because the flagella are projected in front of the cell, each flagellum beats within the plane of the microscopic system during the recovery stroke, allowing for precise flagella tracing. Similarly, only the two-dimensional trajectory of the cell body was determined, because any three-dimensional deviations in trajectory could not be measured. Owing to the two-dimensional nature of the microscopic platform, and thus the experimental data, a modified two-dimensional RFT model was implemented to measure the viscous forces on the flagella of T. foetus [10]. In this two-dimensional model, only rotation of the body in the x–y plane can be accounted for numerically, whereas spinning of the cell body around the longitudinal axis cannot be accurately represented. The methods and equations shown here follow closely the analysis in [10], and are reproduced here for convenience. First, the experimental velocity of the cell body (v_G) was measured using the microscopic platform. In the laboratory frame, the linear and angular velocity of the cell body can be differentiated from the linear and angular displacements of the cell body recorded by the microscopic platform. In order to translate these kinematic variables into forces acting on the cell body, the cell body was transformed to the body-fixed frame with the centre of the body as the origin. In the body-fixed frame, the frame translates with velocity, v, and rotates with angular velocity, ω. This is coincident with the body-aligned frame; however, in the body-aligned frame, the frame is stationary. To calculate the components of the linear velocity of the cell body, v_x and v_y, with respect to the body-aligned frame, straightforward transformation of the coordinates was conducted.

The cell body was modelled as a prolate ellipsoid, with a major axis (a), minor axis (b) and eccentricity (e), where  Using this approximation, the viscous drag and torque on the cell body can be calculated from the following equations [10,78]:

4.1a

4.1b

and

4.1c

where

4.1d

4.1e

and

4.1f

and μ is the viscosity of water. Equations (4.1a,b) govern the viscous drag of the body, whereas equation (4.1c) shows the relationship between the torque and rotation of a prolate ellipsoid around its minor axis. Equations (4.1d,e) are the linear drag coefficients of a prolate ellipsoid, and equation (4.1f) is the drag coefficient of rotation of a prolate ellipsoid around its minor axis [78].

The viscous drag (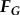) and net moment (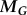) on the body must be balanced by the fluid forces of the flagella ( 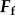and 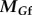), as shown below:

4.2a

and

4.2b

Considering that T. foetus has four flagella, the fluid forces and net moment generated from the flagella can be expanded to the following form:

4.2c

and

4.2d

To accurately derive the flagellar forces in the laboratory frame, the absolute velocity (laboratory frame of reference) was calculated from the following equation:

4.3

where 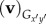 is the velocity of each point along the flagella in respect to the body-fixed frame,  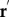is the position of the flagella element in the body-fixed frame,  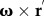is the velocity due to the rotation of the frame and  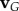is the velocity of the body in the laboratory frame. Next, the velocity was expressed in terms of normal, and tangential coordinates:

4.4

In equation (4.4), 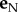 is the normal unit vector, v_N is the component of the velocity in the normal direction,  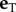is the tangent unit vector and v_T is the component of the velocity in the tangential direction. The force of the fluid on an element of the flagella was then calculated using RFT [10,41,45]. In RFT, the force/unit length in the normal and tangential direction, f_N and f_T, respectively, are obtained by multiplying the velocity components in the normal and tangential direction by the drag coefficients C_N and C_T. The drag–velocity equations for the force from the fluid on a particular point on the flagella in the laboratory frame are

4.5a

and

4.5b

It should be noted that the forces exerted by the flagella on the fluid leading to propulsion are equal and opposite to the forces of the fluid on the flagella as described by equations (4.5a,b). By integrating the force at each point along the length of the flagella, the net force and moment generated by the flagella in respect to the centre of mass of the body (F_xf, F_yf, M_Gf) were estimated using the following equations:

4.6a

4.6b

and

4.6c

By using the above net forces and torque, the linear and angular velocities of the cell body were calculated from [10]

4.7a

4.7b

and

4.7c

The C_T/C_N ratio was then set to the optimum value for a smooth cylinder, 0.5, as described in §2.3.1. The magnitude of C_N and C_T was estimated using the optimization procedure described in Bayly et al. [10]. Essentially, the predicted linear velocities of the cell body for each C_N and C_T value were validated against the experimental trajectories to get the normal mean-squared error in x and y:

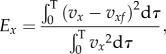4.8a

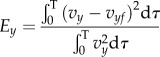4.8b

and

4.8c

The values with the minimum error were chosen for the simulations. To account for the reduced angular velocity a correction factor, α, was applied to the net moment, as shown in equation (4.9) and discussed in §2.3.1:

4.9

Funding statement

This work was supported by the Office of Naval Research Young Investigator Programme award (ONR-N00014-11-1-0622 and ONR-N00014-13-1-0667) under the supervision of Dr T. McKenna. S.N.-V. was also supported by the Programme for Excellence and Equity in Research, National Institutes of Health. The authors are grateful for the support.