Abstract
Large scale simulations of electrically coupled neuronal oscillators often employ the phase coupled oscillator paradigm to understand and predict network behavior. We study the nature of the interaction between such coupled oscillators using weakly coupled oscillator theory. By employing piecewise linear approximations for phase response curves and voltage time courses, and parameterizing their shapes, we compute the interaction function for all such possible shapes and express it in terms of discrete Fourier modes. We find that reasonably good approximation is achieved with four Fourier modes that comprise of both sine and cosine terms.
1 Introduction
The Kuramoto model of phase coupled oscillators is the most popular model to study the collective states among diverse groups of oscillators found in nature [1, 2]. The interaction between the coupled oscillators is described by a sinusoidal function, and is designed to exhibit oscillator phase-locking when the frequency disparity between the oscillators is smaller than the coupling between them. While the Kuramoto model provides a simple way of modeling the coupled oscillators [3, 4, 5, 6], the simple sinusoidal interaction function that is employed in it may not be a typical functional form one could find in wide ranges of experimental situations [7, 8, 9, 10]. For example, when Hodgkin-Huxley model neurons representing real spiking neurons of the brain are coupled electrically, a simple sinusoidal function is not sufficient, but at least three Fourier modes are necessary [11]. Although many neuronal models are based on the original Hodgkin-Huxley formulation, there are in use as many number of neuronal models as there are neuronal types in the nervous system [12, 13, 14]. For a modeler who wishes to apply standard mathematical techniques to investigate neuronal populations in somewhat generic manner [15, 16], the diversity in the neuronal models comes as a difficult hurdle to pass. But phase-coupled oscillator theory [17], like that of Kuramoto model, offers a simple starting point that lays generic formulation. Still, since the interaction function changes from model to model, and experiment to experiment, the modeler has no clue as to what the general nature of the interaction function is that could describe as many neuronal interactions as possible. As is stated above, the Kuramoto model’s interaction function is insufficient. There is also no evidence of a pure odd function or pure even function describing any brain neuronal network. Here we address the question: what is the nature of the interaction function in general for coupled oscillating neurons? The coupling is assumed to be electrical which is also often termed diffusive coupling. This question, however, is more inconvenient than what it appears to be because it seeks to address all possible electrically coupled neurons despite the fact that almost each type of brain neuron that is electrically coupled is characterized by a unique set of underlying model equations (see some modeling studies in [18, 19, 20, 21]). Thus we need to parameterize the underlying model itself as well as identify the critical parameters in it such that some degree of generalization is achieved.
One way of obtaining the interaction function is appealing to the theory of weakly coupled oscillators [22, 23, 24, 25, 26] that explicitly provides a method of relating the interaction function to an intrinsic property of the oscillator, the phase response curve, and the coupling mechanism between any two such identical oscillators [27, 28, 29]. Once the interaction function is available it could be used to study not only neuronal oscillators with identical frequencies, but also those with slight heterogeneity. When applied to regularly oscillating electrically coupled neurons, the coupling mechanism is easily specified: it is proportional to the difference of the voltage time course, and it is sufficient to formulate a model for the voltage and parameterize its shape. The voltage in general has three segments: a spike profile that consists of spike upstroke and a downstroke, and the rest of the voltage segment that is simply a depolarizing phase. Voltage time courses can indeed be more complex than this, but we confine to such a simple description which fits the well known Hodgkin-Huxley model equations [30] as will be explained in the next section where we parameterize this shape such that the lengths of the three segments can be altered. An important parameter is the width of the spike. When it is zero, the spike resembles a pulse, and when it is very broad the time course becomes less spiky, and more like a regular sinusoidal oscillation. The spike width will be varied in all its available range.
The phase response curve (PRC) relates the temporal location of a brief stimulus placed during the ongoing oscillation to the ensuing change of the oscillator’s phase [31, 32, 33, 34]. Except in special or simple cases, the PRC is in general difficult to compute analytically [35, 33, 36], and is often computed numerically [37, 38]. Examining the PRC again of the classical Hodgkin-Huxley model reveals five distinct segments: two nearly unresponsive regimes at the edges, and three other regimes that have finite response. But the PRCs of most neurons can be completely positive, i.e. their response can be completely phase-advancing or both phase-advancing for part of the oscillation cycle (mostly for late phases) and phase-delaying for part of the cycle (mostly for early phases). These two kinds of curves are termed type-1 and type-2 [11, 39], and our model contains a single parameter that could impart either a type-2 or type-1 nature to the PRC. Usually the PRCs have their peak (maximum phase advancement) positions occurring at longer phases. We term this tendency the PRC skewness, and the skewness is varied in all its available range.
Using the voltage and PRC shapes described above, we vary their shape parameters freely to span all possible parameter sets. In real experiments, the PRC and the voltage of course are tightly related, although the PRC depends on all the internal variables of the system including the voltage. But as the relationship between them is model dependent, there is no simple way to construct a single dynamical model that retains their exact relationship, while still giving the advantage of variable shape parameters. In other words, there is no single dynamical model that could be tuned in a simple manner to result in all possible PRC and voltage shapes. Thus our approach that segments these shapes into piecewise linear and independent curves sacrifices the exact relationship between the PRC and the voltage for the advantage we will obtain by making their shapes freely variable. Thus we span more parameter ranges than necessary.
Even within our approach obtaining analytical expressions becomes quite an involved task. We will present analytical expressions for the interaction function when the spike width parameter is zero, and present numerical results for non-zero spike width. We also numerically compute the interaction function in all the available parameter spaces, and quantify the contribution of the first few Fourier modes to the interaction function. We will find that simple interaction functions such as sinusoidal (as in Kuramoto model) must be very rare. We will also show that completely odd or completely even interaction functions must be rare, but four Fourier modes in the interaction function appear to accurately account for large ranges of the parameters.
2 Model
Using the weakly coupled oscillator theory, the interaction function is computed from the phase response curve and the coupling mechanism between the neurons. The coupling mechanism in the present case of electrical coupling depends only the voltage time course during a single oscillation cycle of the oscillating neuron. In this section we present models for the PRC shape and the voltage time course shape, and then review how the interaction function is computed from them. We have chosen to model these shapes using piecewise linear curves due to the fewest number of free parameters sufficient to describe them. We have used such shapes recently to study in-phase and anti-phase states [40] of coupled neurons, but in the current study our focus is on the nature of the interaction function, and not the existence and stability of steady and dynamic states. The interaction function will further be expressed as a series of Fourier terms, and based on the Fourier coefficients a quantity that determines the total strength of the first N number of Fourier modes on a scale from 0 to 1 is defined. This quantity will be used later to determine the number of Fourier modes that could accurately describe the interaction function.
Model of the PRC
PRCs can have both phase advancement for part of the oscillation cycle and phase delay for the rest of the cycle. The phase response curves that are recorded from most neurons are often classified into type-1 or type-2 [11] depending on whether the phase response excludes phase delay (i.e the PRC is non-negative) or not (i.e. the PRC is negative part of the time and then becomes positive). The PRCs are periodic with the period same as that of the oscillation cycle of the neuron, T. Broadly speaking, most of the PRCs have essentially five segments. Two of the segments correspond to the regimes of minimal or no response near the early and the late phases. These two segments represent the responses of the neuron, respectively in the absolute refractory period and the spike rise regime. In some reduced one and two-dimensional models such as integrate and fire and FitzHugh-Nagumo these assumptions are not valid. But our empirical observation is based on models such as the Hodgkin-Huxley whose PRC is illustrated in Fig. 1(a, bottom, thin curve). The other three segments are required to represent the regime reaching the maximum phase delay, maximum phase advancement and the regime in between. The five segments as a function of time t are illustrated in Fig. 1(a, top, thick curves) and are given by the following expressions.
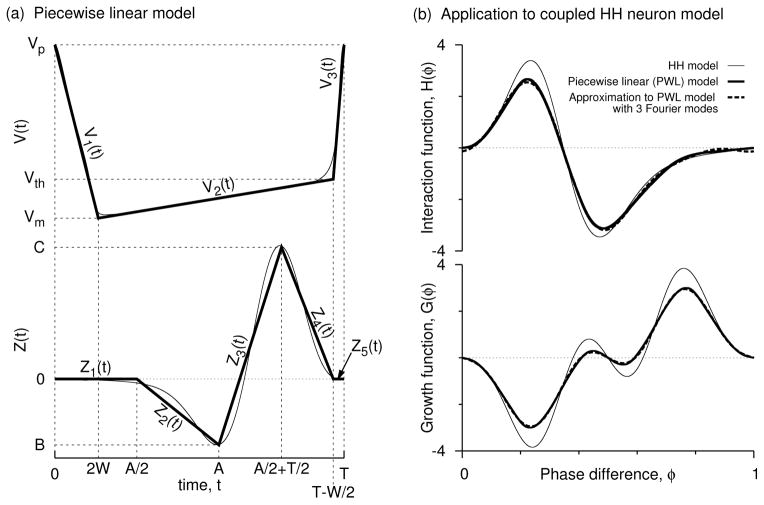
Figure 1.
Parameterizing the PRC and the voltage shapes. (a) The voltage (top) and the PRC (bottom) of the HH model (thin lines) at an applied current of 10μA/cm2 are taken as empirical models to construct parameterized and piecewise linear shapes (thick lines; displayed here for A′ = 0.567, B′ = −0.5, and W′ = 0.075) formulated using Eqs. 1 and 2. Parametrization of these curves allows for consideration of very general PRCs and voltage forms. (b) Comparing the interaction function and the growth function obtained from the full model (thin lines) and those obtained from piecewise linear approximations (thick lines). Fourier expansion approximations using first few modes to the H(φ) that is computed using the piecewise linear formulation are shown in dashes. The growth function, G(φ), is simply H(−φ) − H(φ), and its intersections are the phase-locked solutions of the coupled system. The negative slopes at the intersections indicate stability. The piecewise model and the Fourier approximation predicted the in-phase (φ = 0) and antiphase (φ = 1/2) states and their stability accurately. The stability of the other phase locked states is also accurately predicted.
| (1) |
The shape of the PRC can now be altered by using A (that can range from 0 to T), the skewness parameter that defines the amount of tilt the PRC has toward late phases, the type parameter B that causes the PRC to be either of type-1 (when B ≥ 0) or type-2 (while B < 0), and the maximum phase advancement C (> 0). Altering the magnitude of B with respect to the level of C affects the interaction function, but scaling both of them with a positive constant only introduces a multiplication factor (C) for the resultant interaction function. We can also see this fact from Eq. 1 where C can be taken out as a multiplication factor from each of the right hand side expressions while replacing B with B/C. Hence the PRC shape is altered by the independent parameter B/C and the skewness A which can also be normalized by the period T. As we will see below, the spike rise time is W/2. The spike downstroke may be even bigger than W/2, and in our case it is 2W. Thus the total spike width could be up to 5W/2, but for ease of reference we term W the spike width. For the HH model depicted in Fig. 1, the PRC can be approximated using A = 8.3 ms, B = −0.25, C = 0.5, T = 14.636 ms, and W = 1.1 ms.
The initial segment [Z1(t)] that spans a time of A/2, and the final segment [Z5(t)] that spans a window of spike rise time (W/2) are set to zero. The second segment Z2(t) can be either positive or negative. (For the HH model example, it is negative). It connects the time point A/2 and the maximum delay B of the PRC at t = A. The fourth segment Z4(t) is always positive, and connects the maximum advancement (C) at time T/2 + A/2 and the time point T − W/2. The middle segment Z3(t) connects the maximum delay point B and maximum advancement point C. As the skewness is increased from 0 to T, the position of the maximum phase advancement increases from T/2 to T. Most experimental and computational PRCs indeed display such skewness that shows a preferential tilt of the maximum phase advancement toward late phases.
Model of the voltage time course
The voltage time course can be imagined to be traversing from the spike peak (Vp) to a minimum hyperpolarized voltage level (Vm), then to a value (Vth) near spike threshold, and then to the spike peak. The HH model voltage time course depicted in Fig. 1(a, top, thin curve) can be represented with piecewise linear curves Fig. 1(a, bottom, thick curves) that represent these three segments with Vp = 35 mV, Vm = −72 mV, and Vth = −48 mV. Vm occurs at a time value of 2W, and Vth at T − W/2. Based on this empirical observation, we parameterize the voltage profile by the following set of three curves [Fig. 1(a, bottom)]:
| (2) |
where a1 = Vp − Vth, a2 = Vp − Vm, and a3 = Vth − Vm. With the stated V(t) and Z(t) applied to the HH model, the computed interaction function matches satisfactorily with the one computed directly from Z(t) and V(t) of the actual model [Fig. 1(b, top)]. In particular the number of phase-locked equilibria for two coupled neurons (zero-crossings of the “growth function”) and their stability (indicated by the negative slope at the corresponding zero-crossing) are predicted accurately by the piecewise linear approach [Fig. 1(b, bottom)]. In the following sections, we will use the above formulas for Z(t) and V(t) and compute either analytically or numerically the interaction functions as all the main parameters A′ = A/T, W′ = W/T, and B′ = B/C are altered.
Method of computing the interaction function
Given the functional forms of the voltage and the PRC of any oscillating neuron, the interaction of a pair of such identical oscillating neurons can be understood in terms of the evolutions of their phases θ1, θ2 by studying the following two phase evolution equations [23, 24, 25, 26]:
| (3) |
| (4) |
where ω0 is the oscillating frequency of each of the neurons in the absence of coupling, K is the conductance coupling coefficient, and H(φ) is the interaction function (IF) which is given by the following expression for electrical coupling,
| (5) |
where the phase difference φ ranges from 0 and T. Once the functional form of the IF is known, it is straightforward to either numerically or analytically analyze the collective behavior of the coupled system of either two or more identical neurons. In the following we compute H(φ) analytically in simple cases, and numerically in other cases.
Quantifying the Fourier coefficients of the interaction function
The IF will be expressed using its discrete Fourier transform while exploring the available parameter spaces of skewness, type parameter, and spike width. Specifically H(φ) takes the following form.
We are interested in limiting the number of these modes such that the resultant expression would still be a good approximation for the actual H(φ) computed using Eq. 5 in predicting the phase-locked states, and their stability. Thus the H(φ) that is computed using Eq. 5 is approximated by the first few modes in its Fourier expansion. In order to quantify such an approximation, we weigh the coefficients of the modes that are being used in the approximation against the coefficients of all the available modes. Thus we define a weight coefficient FN as the ratio of the sum of the absolute values of the first N modes to such a sum carried over all the available modes:
| (6) |
where N is the maximum number of modes used in the approximation. We consider this term representing the fractional power contained in the first N modes (though no squared sums are used in its definition). Thus FN × 100 will represent the percentage power contained in those modes. The modes that are included in the above expression are not necessarily in the order of their dominance. Defining a similar quantity using such an ordering would be more complicated, and difficult to understand. With the above definition, if the H(φ) is described completely by a sine, cosine or a combination of them with a fundamental mode, then F1 would become 1. Similarly if the first four modes represent H(φ) accurately, then F4 would become close to 1. We later show that F4 > 0.9 in most of the parameter spaces. Our numerical evidence suggests that including large number of Fourier modes does not always improve FN rapidly with N, partly also because of the numerical errors accumulated in carrying out the discrete Fourier transform. Thus achieving a higher value of FN may not necessarily achieve more accuracy. We find in general that using N modes where FN > 0.9 offers more than satisfactory prediction of the stability of the phase-locked equilibria. For the HH example mentioned earlier (with an applied current of 10 μA/cm2), the first three Fourier modes (with F3 = 0.95) as below provide excellent agreement with the H(φ) computed from our model Z(t) and V(t) [Fig. 1(b, dashed curve)]:
where T is the time period of oscillation (14.636 ms). Including only the first mode results in F1 = 0.54, and including the first two modes results in F2 = 0.85 and both these cases would result in differences in the H(φ) and its odd part (that predicts the stability) from those computed from original voltage and PRC.
3 Interaction function when spike width is zero
In this section we give analytical expressions for the interaction function when W = 0. The analysis depends only on one parameter from the voltage profile which is the slope of the depolarizing branch, a3. As we will see, a3 appears as a multiplication coefficient in the expressions derived for the IF. Thus the results are applicable to general class of voltage profiles as long as there is only one depolarizing branch with constant slope. In this and later sections, the analysis and computation is done in normalized units: Time is normalized with the period T. Hence the phase φ runs from 0 to 1, and the voltage and PRC shapes are periodic with period 1.
When W = 0, the length of the last segment of the PRC [Z5(t)] also becomes zero, and the voltage time course is defined by just one segment [V2(t)] in the entire period of oscillation, and consequently analytical expressions for H(φ) can be computed easily. Hence the integration in Eq. 5 can be carried out from 0 to 1. The single discontinuity of the function V (t + φ) − V (t) between 0 and 1 can occur in either of the four remaining segments of the PRC, leading to four different cases (limits on φ) that together contribute to the interaction function. Using the formula in Eq. 5, we obtain the following analytical expression for H(φ):
| (7) |
where the expressions H1(φ), H2(φ), H3(φ), and H4(φ) are derived below.
In the first regime defined for small φ such that 0 ≤ φ < (1 − A′)/2, the interaction function integral (Eq. 5) is computed as follows:
| (8) |
This simplifies to a quadratic expression in φ:
In the second regime defined by (1 − A′)/2 ≤ φ < 1 − A′, the first and second integrals in Eq. 8 remain the same, but the third, fourth, and fifth integrals will have the integrands, respectively, Z3(t)a3φ, Z3a3(φ − 1), and Z4(t)a3(φ − 1), and the limits of these integrals will be A′ to 1 − φ, 1− φ to (1 + A′)/2, and (1 + A′)/2 to 1. Computing the integrals and simplifying, we get
In the third regime defined by 1 − A′ ≤ φ < 1 − A′/2, the first and fifth integrals remain the same as in the second regime above, but the second, third, and fourth integrals have the integrands, respectively, Z2(t)a3φ, Z2a3(φ − 1), and Z3(t)a3(φ − 1), and the limits of these integrals will be A′/2 to 1 − φ, 1 − φ to A′, and A′ to (1 + A′)/2. Computing the integrals and simplifying, we get
And finally in the fourth regime defined by 1 − A′/2 ≤ φ < 1, the fourth and fifth integrals of the third regime above remain the same, and the first and second integrals become zero because the discontinuity in V(t + φ) occurs during the length of Z1(t). The third integral then has the integrand given by Z2(t)a3(φ − 1), and the limits are from A′/2 to A′. Computing the integrals and simplifying, we get a very simple linear expression for H(φ) in this regime:
We can clearly see the continuity of the slopes of H(φ) at phases 0 and 1 by noting that the derivative of H1(φ) obtained from the expression in the first regime a3C(−2A′ + B′ + 2)/4 at φ = 0 is the same as that obtained from the expression of H4(φ) from the fourth regime at φ = 1. The slopes at the boundaries of the disjoint curves similarly match. Thus the piecewise linear nature of the voltage and the PRC did not result in any discontinuities or discontinuous derivatives in H(φ).
A sample of type-1 and type-2 PRCs are illustrated in Fig. 2(a1, b1), and their interaction functions using the expressions in Eq. 7 are illustrated in Fig. 2(a2, b2). The expressions become even simpler for B′ = 0:
| (9) |
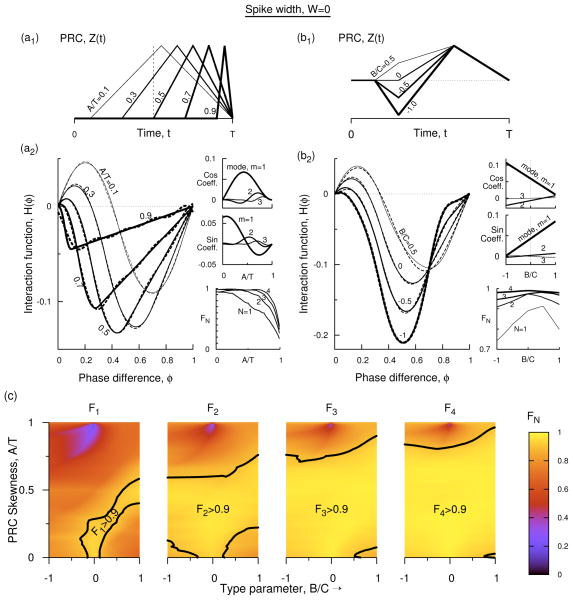
Figure 2.
(Color online) Interaction function at zero spike width. (a1) Profile of type-1 PRC with B′ = 0, at five different skewness values. (a2) Analytically determined H(φ) (Eq. 9) for the five PRCs of (a1). The dashed curves for A′ = 0.1, 0.3, 0.5, and 0.7 are Fourier approximations in Eq. 11. For A′ = 0.9 up to eight modes are needed, but the curve is plotted using only four modes in order to compare with the other curves. In the side panels the coefficients of cosine terms [cos(m2πφ]), and the sine terms [sin(m2πφ)] in the discrete Fourier spectrum of H(φ) for the first three modes are displayed for all levels of skewness. The side panel also displays FN for N = 1, 2, 3, and 4 as a function of normalized skewness. (b1) Profile of type-2 PRC at four different levels of B′, and fixed skewness of A′ = 0.3. (b2) H(φ) for the PRCs in b1 using Eq. 7 (solid) and Fourier approximations (dashed, Eq. 12). The side panels are similar to those in b2 but as a function of type parameters at A′ = 0.3. (c) The weight factor FN that captures the relative Fourier power in modes 1 to N in the parameter space of skewness and B′ as incrementally more number of modes are included in an expression for H(φ) in terms of its Fourier expansion terms. The black dots indicate the contour lines on which FN = 0.9. The brighter yellow parameter regimes bordering the dotted boundaries can be represented by the given or fewer number of Fourier modes, and contain 90% or more total power in them. For example, in the region marked F4 > 0.9 in the last panel the interaction function could be approximated by either 4 or fewer modes.
Further, in the absence of skewness (A′ = 0) the type-1 PRC becomes symmetric with two piecewise linear components. The resultant H(φ) becomes a3C(φ/2 − φ2) in the interval 0 ≤ φ < 1/2 and a3C(1/2 − 3φ/2 + φ2) in the interval 1/2 ≤ φ < 1, which is symmetric crossing at φ = 1/2, and can be expressed a single sinusoidal with F1 > 0.9. As the skewness is increased, the zero crossing of H(φ) shifts toward smaller phases. To see this, let V1(t) and V2(t) be the voltage time courses of the first and the second oscillator, and let Vd ≡ V2(t + φ) − V1(t) be the voltage difference at a given phase shift φ between the two oscillators. Small φ shifts V2(t + φ) left of V1(t), and thus always leads to a positive Vd = a3φ. Hence the interaction function is positive at such φ values. At φ near 1, V2(t + φ) shifts right of V1(t), and thus Vd = a3(φ − 1) becomes negative leading to a negative value of the interaction function, H(φ). A transition occurs between the positive and negative values right at φ = 1/2 if the PRC has no skewness (A/T = 0), but with finite A/T, the positive contribution at small φ is diminished due to small PRC value at small phases, whereas the negative contribution at large phases remains. Thus the transition from positive to negative H(φ) occurs at increasingly smaller φ giving its shape at large skewness. Consequently we can expect higher Fourier modes to arise.
3.1 Fourier modes
The interaction functions computed above will now be approximated with discrete Fourier components. The resultant expressions that include only the first few modes are shown as dashed curves in Fig. 2(a2, b2). The actual coefficients of these modes (both sine and cosine components), and the combined power carried by them as the number of modes is increased from 1 to 4 are also displayed in the side-panels of Fig. 2(a2, b2). Except the curve for A′ = 0.9, which is an example of a PRC with extremely large skewness (and also a rare occurrence) all other curves (dashed lines) can be approximated by truncations of the Fourier expressions with four or fewer number of modes.
Type-1 PRCs
As the skewness is increased the power in the first mode rapidly decreases [F1 in the side panel of Fig. 2(a2)], and thus it is necessary to include higher order modes in order to have accurate representation of H(φ). The first Fourier mode is still the most dominant of all the modes. The cosine term of the first mode dominates all other cosine terms at any given skewness, whereas the sine coefficient of the first mode becomes weaker than that of the second mode in the parameter region surrounding A′ = 0.5 and stronger outside that region. Together the sine and cosine terms of the first mode continue to hold the maximum power at any skewness, but the power falls below 90% for slightly large skewness (for A′ > 0.29), thus making it clear that representation of H(φ) by a single Fourier mode becomes quickly inadequate with skewness. Adding the second mode extends such skewness regime by two fold: F2 > 0.9 when A′ < 0.61. Further addition of higher modes extends it further to higher skewness levels, but the upper skewness boundary that marks the 90% power increases only moderately. We can see this in Fig. 2(c). The Fourier approximations are displayed as dashed curves in Fig. 2(a2) and all these approximations when A′ < 0.9 use three or less number of Fourier modes. At larger skewness values, many more Fourier modes are required, and in particular at A′ = 0.9, we require the first eight modes in order to achieve FN > 0.9. Increasing B′ further (toward positive) makes representation by the first mode insufficient. But there still is a narrow parameter space [Fig. 2(c)] that extends from B′ = 0 and A′ = 0 to a finite skewness and finite positive B′ that can be represented by just the first Fourier mode. A third mode expands the region a little more, leaving a small regime in the lower right hand corner, but the region extends up to A′ = 0.7. Inclusion of the fourth Fourier mode expands it up to A′ = 0.81 and above, and leaving only a very small region in the lower right hand corner. Inclusion of the fifth mode expands it up to A′ = 0.84 (near B′ = 0) and above, inclusion of the sixth mode expands it up to A′ = 0.87 (near B′ = 0) and above, inclusion of the seventh mode expands it up to A′ = 0.89 (near B′ = 0) and above, and so on. Thus the parameter region covered by inclusion of higher modes above 4 expands only moderately.
Type-2 PRCs
We now consider type-2 PRCs. Skewness has similar effect on H(φ) as in type-1 PRCs [see the slightly leftward movement of the curves between the curve marked A′ = 0.3 in Fig. 2(a2) and that marked B′ = 0 in Fig. 2(b2)]. Decreasing the type parameter B′ (i.e. by making the PRCs more type-2 like) has similar effect on the skewness exhibited by H(t); the transition point of H(t) from positive to negative has shifted toward left with increasing B′. The positive contribution of the H(φ) integral due to positive Vd is now multiplied by the negative levels in the PRC. Thus while skewness decreases the positive contribution to the integral, the negative type-parameter increases the negative contribution, effectively exhibiting a similar effect on the interaction function in this regime. At any given A′, decreasing B′ has two noticeable effects on the interaction function. First, there is a phase at which H(φ) becomes independent of B′ [see Fig. 2(b2), the non-zero phase at which all H(φ) intersect], and second, as B′ is decreased, H(φ) that is to the left of the above intersection becomes more negative, and the segment that is to the right of this intersection becomes less negative.
The first observation arises because the integral expression for H2(φ) [or even H3(φ)] of the expression in Eq. 7 becomes −a3CA′(1 − A′)/2, and is independent of B′ at φ = 1 − A′. This is again because of the five sub integrals that contribute to H3(φ), the first and the third become zero at φ = 1− A′, the fifth becomes a3CA′(A′+W′ −1)/4, and the second and fourth integrals become respectively a3B′A′(1 − A′)/4 and a3(B′ + 1)A′(A′ − 1)/4. Thus when combined the expression becomes independent of B. The last integrals arise when convolving Z2(t) with a3φ and Z3(t) with a3(1 − φ). The geometrical arrangement of these two (Z2 and Z3) segments leads to this property. But a finite W′ could disturb this relationship. The second observation above holds for all A′. At small A′ this intersection is near large φ and hence decreasing B′ makes H(φ) look more like a negative cosine (ignoring the increment of H(φ) to the right of the intersection). Thus at small A′ decreasing B′ make the interaction function less odd and thus more even [Fig. 2(b2, side panels)]. As A′ is increased more complicated interaction function emerges. At large A′ and large B′, H(φ) is more even than odd because the intersection point mentioned above occurs at very small φ, and large A′ already makes H(φ) more negative. Decreasing B′ now pushes the segment to the left of the intersection upward and that to the right further downward causing it to have more oddness at large negative B′ [Fig. 2(b2)]. The Fourier expansions of the interaction functions displayed in Fig. 2(b2) are displayed there in dashes. With just four or less number of Fourier modes we can achieve FN bigger than 0.9. As before, increasing the skewness [Fig. 2(c)] requires higher order modes to achieve the same levels of FN.
4 Interaction function at non-zero spike width
Finite spike width makes the derivation of IFs more complicated. Thus we explore this case numerically and present exhaustive results for the specific voltage profile (Fig. 3(a1, left) derived from the HH model described earlier, but the PRC parameters (the skewness A′, and the type parameter B′) are freely varied. And of course we alter W′ freely. For the sample type-1 and type-2 PRCs displayed in Fig. 3(a1, b1), the interaction functions are shown in Fig. 3(a2, b2).
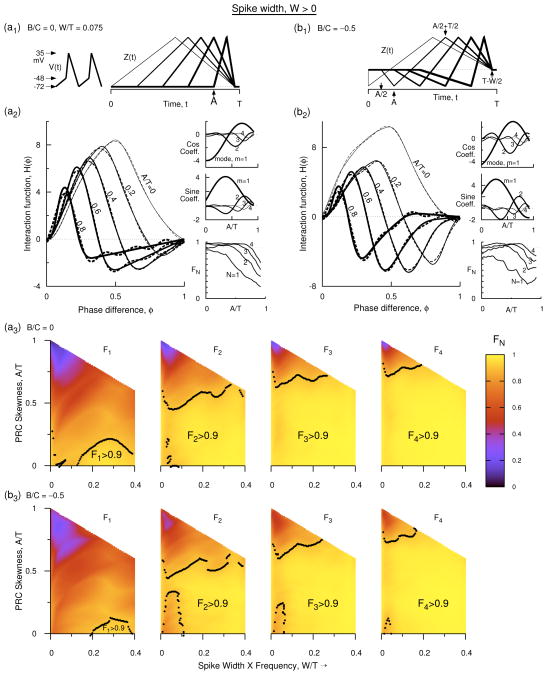
Figure 3.
(Color online) Interaction function at non-zero spike width. (a1) Voltage time course with W′ = 0.075 used in all the figure panels, and profile of type-1 PRC with B′ = 0 at five different skewness values. (a2) Numerical H(φ) (solid) for PRCs in a1, and Fourier approximations for four of the curves as in Eq. 13. The approximation for A′ = 0.8 requires 5 modes but only four modes are used for comparison with the other curves. The side panels are similar to those in Fig. 2. (b1) Profiles of five type-2 PRCs at a fixed skewness of A′ = 0.3. (b2) Same as that in a2 but for the type-2 PRCs described in b1. The Fourier approximations are as in Eq. 14. (a3, b3) Fourier weight coefficient (FN) shown in the parameter space of skewness and B′ as incrementally more number of modes are included in an expression for H(φ) in terms of its Fourier modes. The black dots indicate the contour lines on which FN = 0.9 for the corresponding N. The brighter yellow parameter regimes bordering the dotted boundaries (FN > 0.9) can be represented by the given number of Fourier modes that contain 90% or more total power in them. Type-1 PRC is illustrated with B′ = 0 in a3 and type-2 PRC with B′ = −0.5 in b3.
Spike width can alter the shape of the IF significantly. For W′ = 0.075, the IF still has a single zero crossing at non-zero phase for most values of skewness. This crossing is pushed toward smaller phases as the skewness is increased, whereas increasing W′ pushes it toward longer phases. But for very large skewness and very large negative B′, the IF could develop more than one zero-crossing. But such parameter regimes may not be physiological. As in the previous section we find that with four Fourier modes, H(φ) can be represented satisfactorily by achieving F4 > 0.9 in most of the parameter space. We also find that even the first Fourier mode, just as in the case for W′ = 0, could satisfactorily represent some parameter regime with F1 > 0.9 although this region shrinks with increasingly negative type parameter.
As the skewness is increased, in general, the IF develops a negative lobe near φ = 1 for both type-1 and type-2 PRCs [Figs. 3(a2), 3(b2)], i.e. the leading neuron slows down its frequency at that phase. Whereas near φ = 0 it continues to be positive. Increasing the spike width has the effect of speeding up the leading neuron at small phases and counters the decrement in frequency caused by the skewness at those phases, and thus displaying increasingly positive values of the IF in both type-1 and type-2 neurons. At a qualitative level the type of the PRC (B′ slightly positive or negative) has less effect on the IF than the skewness or the spike width. When expressed in Fourier series, The cosine and sine coefficients of the first mode dominate the other modes [Figs. 3(a2, side panels), 3(b2, side panels)] such that the first mode remains the dominant mode for most of the skewness values. For most skewness values, the second mode is the second highest mode. At large skewness higher order modes contribute significantly to the total power. Altering the type parameter, B′ brings in some quantitative differences in the contribution of these modes.
Spike width works counter to the skewness in positioning the transition of the IF from positive to negative in both type-1 and type-2 neurons. For type-1 neurons, and for small φ, spike width introduces a large negative Vd = Vd1 during the spike, positive Vd = Vd2 during the depolarizing part, and then a larger positive Vd = Vd3 during the spiking portion near φ = 1. But if A/2T is larger than 2W/T, which is true for most realistic skewness values, then the effect of Vd1 will be suppressed by the zero phase of Z(t). Thus H(φ) acquires a large positive lobe owing to the large effect of Vd3. At large φ, however, the downstroke of V2(t + φ) falls below V1(t), thus a negative factor Vd = Vd4 as well as another negative factor that is due to the depolarizing phase of V2(t+φ) grow bigger bringing H(φ) back to negative level.
4.1 Fourier modes
Type-1 PRCs
Fourier expansions for the five IFs displayed in Fig. 3(a2, solid) are shown there in dashes. FN > 0.9 for four of them (A′ = 0, 0.2, 0.4, and 0.5) when N ≤ 3. Including four Fourier modes can account for A′ up to 0.72. To achieve FN > 0.9 for the curve with A′ = 0.8, we require N = 5 Fourier modes.
The weight coefficient FN is computed in the two parameter space of skewness and spike width for type-1 PRCs [Fig. 3(a3)], and for one level of negative type parameter for type-2 PRCs [Figs. 3(b3)]. The contours representing FN = 0.9 are shown in dots in these figures. Symmetric type-1 (A′ = 0, B′ = 0) PRCs have very simple IFs, and are representable by a single mode to a high level of F1. This ability to retain the power in the first mode persists for slightly bigger A and W [the small region near the bottom left corner of the first panel in Fig. 3(a3)]. In this region the H(φ) is more like sinusoidal, but as the spike width is increased (equivalently as the frequency of oscillation is increased), H(φ) transforms into more like a cosine like function, and for still larger W′ like a negative sine function. In the transition region between these two regimes H(φ) requires more modes to achieve a good FN. When the H(φ) does become more cosine like or negative sine like a single mode achieves FN > 0.9 [region to the bottom right in the first panel of Fig. 3(a3)]. With second mode added, there still are a few small regions that require higher modes for achieving FN > 0.9. But three Fourier modes account for significant amount the parameter region and with four Fourier modes most of the parameter region in (A′, W′) space will have FN > 0.9. However, very large skewness [the top region in the corner of last panel of Fig. 3(a3)] requires a very large number of Fourier modes, because in this regime the IF itself looks very skewed with its peak shifted to very small φ. Such skewness values may not be very common in neuron models and experiments.
Type-2 PRCs
For an example of type-2 PRC, we compute H(φ) for B′ = −0.5, at W′ = 0.075 at five different values of A′ as displayed in Fig. 3(b2). An important feature that we observe in Fig. 3(b2) that is absent in such diagrams presented before is that for large skewness the IF begins to have a second zero-crossing at a non-zero phase difference value. When expanded in Fourier series we will see that this H(φ) also requires up to five Fourier modes to achieve FN > 0.9. Decreasing B′ raises the segment of H(φ) near late phases and decreases it near early phases. But achieving a second-crossing was lot harder when W′ = 0 (Fig. 2) even at large skewness, but with finite spike width it can be achieved. The numerics suggest that such second-crossing is easily achieved if the spike width is very small, skewness is very large, or the type-2 parameter is large negative.
H(φ) essentially is the instantaneous increment in a neuron’s frequency as the other neuron leads its phase. The increment, because of the electrical coupling, can have different contributions from the spike portion and from the rest of the voltage time course. Suppose V1(t) and V2(t) represent the voltage time courses of the first and the second neuron. When the second neuron is slightly leading the first neuron (φ small but near zero), the term Vd ≡ V2(t + φ) −V1(t) becomes negative during most of the spike duration of V1(t) [from t = 0 to t = t* < 2W, where t* is the intersection of the spike down stroke of V1(t) and the depolarizing segment of V2(t)], but is positive for the rest of the time course. When convolved with the PRC, the positive and negative factors will have different weights, and thus determine the sign of the IF. The curves using the Fourier expansions of H(φ) are displayed as dashed curves in Fig. 3(a2, b2). Four of the curves (A′ = 0, 0.2, 0.4, 0.6) again use three or less number of Fourier modes. Including the fourth mode extends the region of FN > 0.9 up to A′ = 0.73. To achieve similar FN for A′ = 0.8, we require 5 Fourier modes.
When the PRC becomes type-2 [B′ < 0, Figs. 3(b3)], the symmetric PRC at A′ = 0 quickly develops a negative regime due to B′, imparting an extra dip in the IF near large φ. As B′ is increased, the negative peak at larger φ increases and the rising branch of H(φ) develops a slight convex shape. As W′ is increased, however, the intersection point of H(φ) with the horizontal axis moves rightward, thus making it more like a sinusoidal function. The transition into this regime requires a sufficiently long W′, leaving a small region in the parameter space that requires higher modes for achieving FN > 0.9 [small reddish regions near small W′ and small A′ in Figs. 3(b3)]. This region becomes bigger with decreasing B′. But with four Fourier modes only very small such regions are left even at B′ = −1 level. These regions are confined to very small A′ and very small W′. The regions that still cannot be approximated with four Fourier modes are located at very large skewness and very small W′ (top regions). Both these parameter regions perhaps lie outside of most of the neuroscience models, and thus for most practical parameter values, four Fourier modes give a good estimate of H(φ).
5 Oddness of the interaction function
The previous two sections asserted that a simple sinusoidal function like that of the Kuramoto type is far insufficient to model the interaction function of coupled neurons. But they did not completely rule out the possibility of a pure even or a pure odd function that might perhaps represent portions of the available parameter space. Here we examine this issue. Considering the modulation of the cosine and sine terms for the few example parameters displayed in the cases of zero and finite spike width, it may indeed appear that the regions of purely odd or purely even IFs must be sparse. To examine the overall oddness of the IF, we specifically ask how likely a purely odd or purely even IF is an accurate assumption in the parameter space of skewness (A′) and type-parameter (B′). We define an oddness coefficient that weighs all the coefficients of the odd terms in the Fourier expansion against all the coefficients of both odd and even terms:
| (10) |
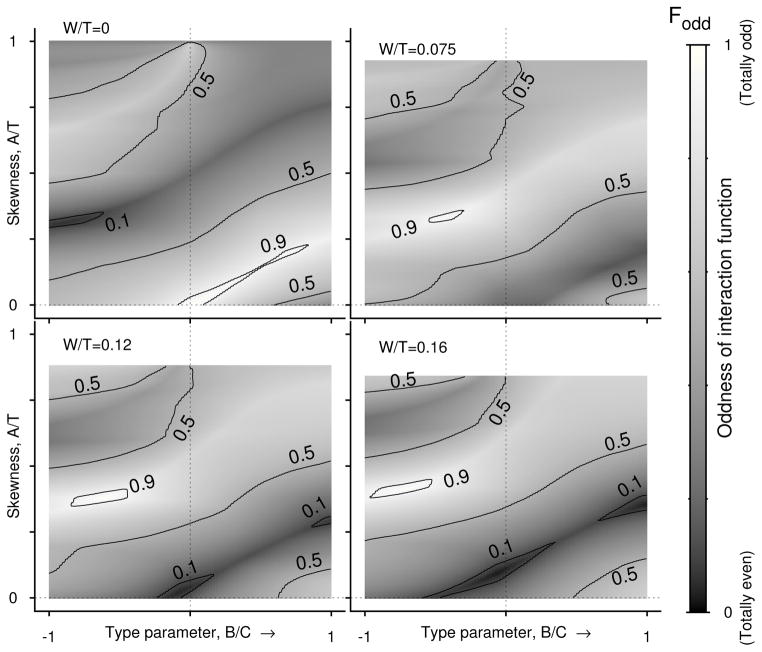
which can range from 0 (that represents a completely even IF) to 1 (that represents a completely odd function). We computed Fodd in (B′, A′) parameter space for four levels of W′ (Fig. 4). Contours defining discrete levels of Fodd are overlaid, and they confirm our observation that when B′ = 0 and A′ = 0, H(φ) is mostly odd, but such regime occupies only a narrow parameter space. Likewise, the parameter regime that can be described by mostly even terms (Fig. 4, W′ = 0, the regime inside the contour of 0.1) is also very small. The dark and bright shades run across the parameter space indicating that regimes that are predominantly odd or predominantly even are also confined to narrow parameter regimes. The entire map looks moved upward when spike width becomes non-zero, but for non-zero spike width, the map itself does not show significant qualitative changes as W′ is increased. Most importantly in either case, the regions where the IF can be represented by either purely odd function (Fodd = 1) or purely even function (Fodd = 0) are confined to very small regions and perhaps are single points in the plane.
Figure 4.
Proportion of odd components in H(φ). Oddness factor Fodd in the plane of skewness (A′ that ranges from 0 to its maximum allowed value of 1 − W′) and type parameter (B′ shown here between −1 and 1) at four different values of spike width. The interaction function is rarely totally even or totally odd. Even predominantly evenness (Fodd < 0.1) or predominantly oddness (Fodd > 0.9) occurs in tiny pockets of the parameter space. For most of the type parameter and skewness values H(φ) is a mixture of both even and odd modes.
6 Discussion and Conclusions
Finding the interaction functions that pertain to given class of systems is usually a difficult task. Very few studies reported the actual measurement of the interaction functions. In an electrochemical experiment [41] interaction functions that deviate substantially from simple sinusoid were discovered. In a modeling study of coupled Hodgkin-Huxley neurons [42], an interaction function that has not only the complete first mode (both sine and cosine) but also the sine component of the second mode was found. Our study addresses the question of what the nature of the interaction function is for electrically coupled oscillatory neurons as a whole. To address this, we relied on the theory of weakly coupled oscillators, which asserts that the phase response curve and the voltage time course are sufficient to determine the interaction function. But the PRC and the voltage are tightly related in any realistic neuronal model, and this fact makes it hard to address the main question in any general manner. Since there are indeed a large number of neuronal models that address not only the neuronal type, but also the variations in the effective ionic channels present under given conditions, any single model that uses differential evolution equations cannot provide sufficient insight into the generality of the interaction functions across the neuronal models. Such generality can be achieved by parameterizing the PRC and the voltage shapes.
Parameterizing the PRC and the voltage independently has the unpleasant effect that any given realistic neuronal model, under the effect of some tuning parameter, traverses an unspecified curve in the two-parameter spaces depicted in Figs. 2 3, and 4. Also, some of the parameter combinations would be physiologically unrealistic. For example, the parameter regimes closer to A′ = 1 in Figs. 2(c), 3(a3, b3) are indeed extremely rare in experiments and models. However, the approach covers a number of realistic PRCs and the voltages. We have already depicted and also based our empirical model on the Hodgkin-Huxley model. A number of other models and experiments are also covered within the parameter spaces we explored [40]. Using this method we were able to arrive at some general conclusions that are valid for coupled neurons across the field.
Piecewise linear approximations were introduced for PRC shape and voltage time courses. In particular the PRC shape uses five piecewise linear curves. Our observation shows that this kind of shape can account for a large array of model PRCs, but evidently this may not cover all possible PRC shapes, particularly those that may have sharp drop at the edges, or modulations other than a single maximum and a single minimum. The voltage time course is modeled along the HH voltage time course although we have freely varied the spike width. Though the HH model is perhaps the most famous and successful of the neuronal models, the shape we have used is not universal in its applicability. Addition of extra currents than those incorporated into this model may distort the qualitative shape of the voltage time course, and in electrical coupling, more so than in other synaptic couplings, such changes in shape can have important consequences in the stability of the phase-locked states. The effect of such currents on the shape of the IF can also be significant.
The principal motivation behind using piecewise linear models is to reduce the number of parameters to as few as possible while retaining the ability to obtain realistic PRC and voltage shapes. A single skewness parameter for the PRCs and a single independent type parameter are sufficient to describe the PRC. We incorporated the spike width in the voltage time course in an efficient manner by coupling the spike rise time (W/2) and the spike downstroke time (2W). This is based on our empirical observation of the Hodgkin-Huxley model, and it is possible to find model and experimental observations that disobey this relationship. The positions of the maximum phase delay and maximum phase advancement of the PRC are also linked such that they are separated by less than half an oscillation period. This again is based on an empirical observation. Significant variations of the shapes from these empirical observations would require a reformulation of the model.
Given these limitations, we have fully explored the available parameter spaces, and obtained analytical expressions for the interaction functions when the spike width is zero, and discussed in detail the case of non-zero spike width numerically. The interaction functions were expressed in discrete Fourier series that is curtailed by examining the absolute sum of the included Fourier coefficients against the absolute sum of all the coefficients in the expansion; This quantity is given by FN where N is the number of included modes. Similar conclusions can be obtained by using a quantity that depends on the summed squares of the Fourier coefficients, but would not be necessary for our purpose. The test of the accuracy of the Fourier expansion is its ability to correctly predict the phase-locked states. We found that including N number of modes such that FN > 0.9 is more than sufficient to achieve the needed accuracy. The overall oddness of the interaction function was also computed that pictorially depicted the regimes of maximum oddness or evenness in the parameter space of skewness and type parameter. We summarize below our main conclusions.
Pure sine or cosine interaction functions are rare, and inclusion of both sine and cosine is essential
Nearly symmetric (A′ near 0) type-1 PRCs (with B′ = 0) have mostly odd H(φ), and in particular can be approximated by a single sine function with FN > 0.9 similar to the well-known Kuramoto phase coupled oscillator model [1, 2, 43]. But on the other hand, in the context of the current study of electrically coupled neurons, this is a very rare case because such parameter regimes must exist within the dotted areas in Figs. 2(c, F1), and 3(a3, F1). Similarly one can obtain a pure even function H(φ) for a specially constructed PRC that resembles those of leaky integrate and fire models. Even in this case, for achieving FN > 0.9 many higher order cosine terms must be included. However presence of finite spike width makes things slightly better [Fig. 3(a3, F1)] in that for small enough skewness values and for large enough spike width or spike frequency there is a region of parameter space where the first mode that includes both cosine and sine terms, or written succinctly as
where H0 is a constant, r and α are non-zero constants, approximates the IF with the desired accuracy. There is also a small parameter region for near symmetric PRCs (A′ near 0, and B′ = 0) and small spike width or frequency where the above relation is a good approximation. Ermen-trout [7] computed discrete Fourier expansion for the interaction functions based on Hoppensteadt and Izhikevich [26] for some simple coupled neuronal networks, and they are expressed in terms of both the components of the first Fourier mode. Interaction function that uses both the components of the first Fourier mode can produce a variety of cluster states [44].
Completely even or completely odd interaction functions are also rare
In the parameter spaces of PRC skewness and type parameter we have not found extended regions where the oddness of the IF, Fodd, is either completely odd (1) or completely even (0) (Fig. 4). But nearly odd (Fodd > 0.9) or nearly even Fodd < 0.1 IFs could exist in some thin ranges of parameters. Such ranges for nearly even functions may exist either in type-1 (B′ ≥ 0) or type-2 (B′ < 0) PRC parameters. In the parameter range that we examined, the nearly odd H(φ) is found for type-2 PRCs (Fig. 4) with finite spike width, and for zero spike width such range can occur for both type-1 and type-2 PRCs. By increasing or decreasing skewness and type parameter together similar oddness or evenness of H(φ) may be achieved.
Four Fourier modes can account for most of the parameter space
With finite or zero spike width (Figs. 2, 3) inclusion of two Fourier modes can account of a large region in the parameter space of skewness and spike width. Accuracy of F2 > 0.9 is achieved by using the approximation
where again α1, α2, r1, and r2 are constants. Three Fourier modes expand the region of F3 > 0.9 to larger skewness (still A/T < 0.7), but when the spike width is small, there are regions where F3 < 0.9 at large B′. Approximating the IFs with the first two modes was earlier done in an experimental preparation of thalamo-cortical circuits [8]. The authors were able to fit “any of the measured PRCs” by altering the coefficients of the first two modes. Four Fourier modes extend the region of F4 > 0.9 to skewness levels of A′ bigger than 0.7 and nearly all levels of frequency. Inclusion of still higher modes provides a better approximation for skewness levels still higher, but the upper boundary moves only moderately. Extremely large skewness levels are also rare to find in experiments and models. Thus H(φ) can be accurately represented in most of the parameter space when the first four modes are included,
that gives F4 > 0.9, where rn, αn, n = 1, …, 4 are constants. Some of the coefficients rn and αn can indeed be zero, but such a specific choice only represents very isolated parameter points.
Phase response curve transition from type-1 to type-2 does not critically affect the interaction function
The Fourier coefficients computed as a continuous function of the type parameter B′ (figure not shown) reveal that while changing the PRC from type-1 (B′ ≥ 0) to type-2 (B′ < 0) altered the coefficients of the modes comprising H(φ) quantitatively, there is no criticality or sudden change of character of these coefficients at B′ = 0. As can also be seen from Fig. 4, the oddness of the IF changes gradually as B′ is altered across 0. But there is a significant difference between large positive B′ and large negative B′. Large negative B′ when paired with large skewness does indeed change the shape of H(φ) in a significant way.
For most parameter values H(φ) has either none or one intersection with the horizontal axis at a non-zero φ
The type-1 PRCs that resulted in near sinusoidal IFs in the absence of spike width obviously lead to a single intersection at a non-zero φ, but at very large skewness values [curve for A′ = 0.9 in Fig. 2(a2)], such an intersection disappears. Similarly we get no non-zero intersection at large negative B′ [Fig. 2(b2)]. Very small skewness coupled with symmetric type-1 PRCs [Fig. 3(a2)] also leads to no non-zero intersection. But in most of the parameter spaces we find one non-zero intersection. However there can be two such intersections in some windows of parameter spaces. One such window we found is when B′ is large negative and the skewness and spike width are favorable [Fig. 3(b2)]. In general skewness appears to move the intersection toward early phases.
We have not focused in this study on the steady or dynamical solutions that emerge from the interaction functions reported. Such a study between two coupled neurons confining to synchronous and antisynchronous states are being reported elsewhere [40]. But the complete dynamics that emerge from these interaction functions either in the case of two coupled oscillators or in a larger network are still unknown. We expect that future studies of phase coupled oscillators will take advantage of the interaction functions reported here.
Acknowledgments
The work was supported by NIH grant NS047085. We thank Texas Advanced Computing Center at University of Texas, Austin, and Computational Systems Biology Core at University of Texas at San Antonio for computational facilities.
Appendix. Fourier expansions of the interaction functions
The following expressions are the expansions of the analytically or numerically computed inter-action functions displayed in Figs. 2(a2, b2), and Figs. 3(a2, b2). Each expression, except for A′ = 0.9, achieves FN > 0.9 for the number of modes N (≤ 4) used in it. Employing the notation that Sn = sin(2nπφ) and Cn = cos(2nπφ), the Fourier terms that together constitute at least 90% of the power in the expansion of the interaction functions displayed in Fig. 2(a2) are as below.
| (11) |
Similar expressions for the curves displayed in Fig. 2(b2) are
| (12) |
The following expansions are obtained from the numerically computed H(φ) for B′ = 0 at W′ = 0.075 [Fig. 3(a3)], at five different values of skewness. Except for A′ = 0.8, the number of modes included are the least number necessary to obtain a value of FN that is at least 0.9 when N number of modes as displayed are included. For A′ = 0.8 five Fourier modes are needed to accurately represent the interaction function.
| (13) |
The following expressions for H(φ) are computed at B′ = −0.5 and W′ = 0.075 [Fig. 3(b3)], and are the least number necessary to obtain a value of FN that is at least 0.9 with the exception for A′ = 0.8 as in the above expressions.
| (14) |
References
- 1.Kuramoto Y, Nishikawa I. Statistical macrodynamics of large dynamical-systems - case of a phase-transition in oscillator communities. Journal of Statistical Physics. 1987;49:569–605. [Google Scholar]
- 2.Acebrón JA, Bonilla LL, Vicente CJP, Ritort F, Spigler R. The Kuramoto model: A simple paradigm for synchronization phenomena. Reviews of Modern Physics. 2005;77:137–185. [Google Scholar]
- 3.Yeung MKS, Strogatz SH. Time delay in the Kuramoto model of coupled oscillators. Physical Review Letters. 1999;82:648–651. [Google Scholar]
- 4.Strogatz SH. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D: Nonlinear Phenomena. 2000;143:1–20. [Google Scholar]
- 5.Filatrella G, Nielsen AH, Pedersen NF. Analysis of a power grid using a Kuramoto-like model. The European Physical Journal B. 2008;61:485–491. [Google Scholar]
- 6.Chowdhury D, Cross MC. Synchronization of oscillators with long-range power law interactions. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82:016205. doi: 10.1103/PhysRevE.82.016205. [DOI] [PubMed] [Google Scholar]
- 7.Ermentrout B. Neural networks as spatio-temporal pattern-forming systems. Reports of Progress in Physics. 1998;61:353–430. [Google Scholar]
- 8.Perez Velazquez JL, Galán RF, Garcia Dominguez L, Leshchenko Y, Lo S, Belkas J, Erra RG. Phase response curves in the characterization of epileptiform activity. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76:061912. doi: 10.1103/PhysRevE.76.061912. [DOI] [PubMed] [Google Scholar]
- 9.Rusin CG, Johnson Sarah E, Kapur J, Hudson JL. Engineering the synchronization of neuron action potentials using global time-delayed feedback stimulation. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84:066202. doi: 10.1103/PhysRevE.84.066202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhu Y, Hsieh YH, Dhingra RR, Dick TE, Jacono FJ, Galán RF. Quantifying interactions between real oscillators with information theory and phase models: Application to cardiorespiratory coupling. Phys Rev E Stat Nonlin Soft Matter Phys. 2013;87:022709. doi: 10.1103/PhysRevE.87.022709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hansel D, Mato G, Meunier C. Synchrony in excitatory neural networks. Neural Computation. 1995;7:307–337. doi: 10.1162/neco.1995.7.2.307. [DOI] [PubMed] [Google Scholar]
- 12.McCormick DA, Huguenard JR. A model of the electrophysiological properties of thalamocortical relay neurons. Journal of Neurophysiology. 1992;68:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- 13.Liu Z, Golowasch J, Marder E, Abbott LF. A model neuron with activity-dependent conductances regulated by multiple calcium sensors. The Journal of Neuroscience. 1998;18:2309–2320. doi: 10.1523/JNEUROSCI.18-07-02309.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Purvis LK, Butera RJ. Ionic current model of a hypoglossal motoneuron. Journal of Neurophysiology. 2005;93:723–733. doi: 10.1152/jn.00703.2004. [DOI] [PubMed] [Google Scholar]
- 15.Daido H. Generic scaling at the onset of macroscopic mutual entrainment in limit-cycle oscillators with uniform all-to-all coupling. Physical Review Letters. 1994;73:760–763. doi: 10.1103/PhysRevLett.73.760. [DOI] [PubMed] [Google Scholar]
- 16.Daido H. Multibranch entrainment and scaling in large populations of coupled oscillators. Physical Review Letters. 1996;77:1406–1409. doi: 10.1103/PhysRevLett.77.1406. [DOI] [PubMed] [Google Scholar]
- 17.Kuramoto Y. Chemical Oscillations, Waves, and Turbulence. Springer-Verlag; Berlin: 1984. [Google Scholar]
- 18.Chow CC, Kopell N. Dynamics of spiking neurons with electrical coupling. Neural Computation. 2000;12:1643–1678. doi: 10.1162/089976600300015295. [DOI] [PubMed] [Google Scholar]
- 19.Lewis TJ, Rinzel J. Dynamics of spiking neurons connected by both inhibitory and electrical coupling. Journal of Computational Neuroscience. 2003;14:283–309. doi: 10.1023/a:1023265027714. [DOI] [PubMed] [Google Scholar]
- 20.Nomura M, Fukai T, Aoyagi T. Synchrony of fast-spiking interneurons interconnected by gabaergic and electrical synapses. Neural Computation. 2003;15:2179–2198. doi: 10.1162/089976603322297340. [DOI] [PubMed] [Google Scholar]
- 21.Pfeuty B, Mato G, Golomb D, Hansel D. Electrical synapses and synchrony: the role of intrinsic currents. Journal of Neuroscience. 2003;23:6280–6294. doi: 10.1523/JNEUROSCI.23-15-06280.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Winfree AT. Biological rhythms and the behavior of populations of coupled oscillators. Journal of Theoretical Biology. 1967;16:15–42. doi: 10.1016/0022-5193(67)90051-3. [DOI] [PubMed] [Google Scholar]
- 23.Neu JC. Coupled chemical oscillators. SIAM Journal on Applied Mathematics. 1979;37:307–315. [Google Scholar]
- 24.Neu JC. Chemical waves and the diffusive coupling of limit cycle oscillators. SIAM Journal on Applied Mathematics. 1979;36:509–515. [Google Scholar]
- 25.Ermentrout GB, Kopell B. Multiple pulse interactions and averaging in systems of coupled neural oscillators. Journal of Mathematical Biology. 1991;29:195–217. [Google Scholar]
- 26.Hoppensteadt FC, Izhikevich EM. Weakly Connected Neural Networks. Springer; New York, NY 10013, USA: 1997. [Google Scholar]
- 27.van Vreeswijk C, Abbott LF, Ermentrout GB. When inhibition not excitation synchronizes neural firing. Journal of Computational Neuroscience. 1994;1:313–321. doi: 10.1007/BF00961879. [DOI] [PubMed] [Google Scholar]
- 28.Smeal RM, Ermentrout GB, White JA. Phase-response curves and synchronized neural networks. Philos Trans R Soc Lond B Biol Sci. 2010;365:2407–2422. doi: 10.1098/rstb.2009.0292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiological Reviews. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Winfree AT. The Geometry of Biological Time. 2nd edition. Springer; New York, NY 10013: 2000. [Google Scholar]
- 32.Reyes AD, Fetz EE. Two modes of interspike interval shortening by brief transient depolarizations in cat neocortical neurons. Journal of Neurophysiology. 1993;69:1661–1672. doi: 10.1152/jn.1993.69.5.1661. [DOI] [PubMed] [Google Scholar]
- 33.Gutkin BS, Ermentrout GB, Reyes AD. Phase-response curves give the responses of neurons to transient inputs. Journal of Neurophysiology. 2005;94:1623–1635. doi: 10.1152/jn.00359.2004. [DOI] [PubMed] [Google Scholar]
- 34.Tateno T, Robinson HP. Phase resetting curves and oscillatory stability in interneurons of rat somatosensory cortex. Biophysical Journal. 2007;92:683–695. doi: 10.1529/biophysj.106.088021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Brown E, Moehlis J, Holmes P. On the phase reduction and response dynamics of neural oscillator populations. Neural Computation. 2004;16:673–715. doi: 10.1162/089976604322860668. [DOI] [PubMed] [Google Scholar]
- 36.Fujita T, Fukai T, Kitano K. Influences of membrane properties on phase response curve and synchronization stability in a model globus pallidus neuron. Journal of Computational Neuroscience. 2012;32:539–553. doi: 10.1007/s10827-011-0368-2. [DOI] [PubMed] [Google Scholar]
- 37.Ermentrout GB. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Society for Industrial and Applied Mathematics; 2002. [Google Scholar]
- 38.Ladenbauer J, Augustin M, Shiau L, Obermayer K. Impact of adaptation currents on synchronization of coupled exponential integrate-and-fire neurons. PLoS Computational Biology. 2012;8:e1002478. doi: 10.1371/journal.pcbi.1002478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Computation. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- 40.Dodla R, Wilson CJ. Effect of phase response curve skewness on synchronization of electrically coupled neuronal oscillators. Neural Computation. 2013;25:2545–2610. doi: 10.1162/NECO_a_00488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kiss IZ, Zhai Y, Hudson JL. Predicting mutual entrainment of oscillators with experiment-based phase models. Phys Rev Lett. 2005;94:248301. doi: 10.1103/PhysRevLett.94.248301. [DOI] [PubMed] [Google Scholar]
- 42.Hansel D, Mato G, Meunier C. Phase dynamics for weakly coupled hodgkin-huxley neurons. EPL (Europhysics Letters) 1993;23:367–372. [Google Scholar]
- 43.Hong H, Strogatz SH. Kuramoto model of coupled oscillators with positive and negative coupling parameters: an example of conformist and contrarian oscillators. Physical Review Letters. 2011;106:054102. doi: 10.1103/PhysRevLett.106.054102. [DOI] [PubMed] [Google Scholar]
- 44.Kiss IZ, Rusin CG, Kori H, Hudson JL. Engineering complex dynamical structures: sequential patterns and desynchronization. Science. 2007;316:1886–1889. doi: 10.1126/science.1140858. [DOI] [PubMed] [Google Scholar]