Information-limited parallel processing in difficult heterogeneous covert visual search

Abstract

Difficult visual search is often attributed to time-limited serial attention operations, although neural computations in the early visual system are parallel. Using probabilistic search models (Dosher, Han, & Lu, 2004) and a full time-course analysis of the dynamics of covert visual search, we distinguish unlimited capacity parallel versus serial search mechanisms. Performance is measured for difficult and error-prone searches among heterogeneous background elements and for easy and accurate searches among homogeneous background elements. Contrary to the claims of time-limited serial attention, searches in heterogeneous backgrounds instead exhibited nearly identical search dynamics for display sizes up to 12 items. A review and new analyses indicate that most difficult as well as easy visual searches operate as an unlimited-capacity parallel analysis over the visual field within a single eye fixation, which suggests limitations in the availability of information, not temporal bottlenecks in analysis or comparison. Serial properties likely reflect overt attention expressed in eye movements.

Introduction

Visual search for a target among distractor elements – finding a particular object among many others – is of both theoretical and practical significance. Neural computations in early visual cortex represent visual inputs simultaneously at distinct retinal locations. Visual search for a specific target in the visual field requires the further analysis and identification of each display element as a target or distractor, a process reflecting both attention and decision (Treisman & Gelade, 1980; Verghese, 2001). One of the most widely studied paradigms in cognitive science, visual search has also been investigated in neurophysiology (Chelazzi, Miller, Duncan, & Desimone, 2001; Reynolds & Desimone, 2001), in computational neuroscience (Corchs & Deco, 2001), and in cognitive psychology (Neisser, 1967; Treisman & Gelade, 1980; Treisman & Gormican, 1988; Sperling, Budiansky, Spivak; Johnson, 1971; Wolfe & Friedman-Hill, 1992; Wolfe, 2003) and has applications to practical situations in screening and human operator environments.

One central theoretical issue is whether human observers are characterized by serial or parallel search processing architectures, often associated with the processing of complex and basic visual features respectively (Treisman & Gelade, 1980; Dosher, 1998). Most behavioral assays of search efficiency evaluate either search time in freely viewed displays (i.e., Treisman & Gelade, 1980) or search accuracy in time-limited displays (i.e., Palmer, 1994). Search times that increase substantially with added display elements are usually associated with a covert serial processing architecture (Sternberg, 1966), yet in fact are ambiguous and may reflect parallel processes (Townsend & Ashby, 1983, Theois, 1973). Mathematical analyses show that increased average response time (and/or decreased accuracy) for larger displays do not, by themselves, distinguish the serial or parallel architecture of visual analysis (Palmer, Verghese, & Pavel, 2000; Sperling & Dosher, 1986, for reviews). On the other hand, some search accuracy experiments express the performance as thresholds (either contrast or feature differences) corresponding to a criterion accuracy (e.g., Allen & Humphreys, 2007), and focus on the relationship between thresholds and display size. Search accuracy and thresholds can be directly related to one another within theoretical contexts of observer model (e.g., Lu & Dosher, 2008), and are considered briefly in the discussion. These studies provide important insights into processing capacity (limited vs unlimited) but not the temporal architecture (parallel vs serial) of search. Detection theory-based analyses of decision uncertainty may test for whether ultimately – perhaps at a delayed processing time – accuracy is consistent with unlimited capacity. However, such analyses cannot answer questions about the time course of processing.

A true test of the full architecture of visual search requires joint evaluation of both the accuracy and the temporal properties of search. Here, speed-accuracy tradeoff methods (e.g., Reed, 1973; Dosher, 1976) were used to trace the full time course of processing and assess the serial or parallel nature of visual search. Two previous studies (Dosher, Han, & Lu, 2004; McElree & Carrasco, 1999) measured the full time course of visual search for different display sizes in demanding searches and made conflicting claims. McElree & Carrasco (1999) argued that search for a conjunction target defined by color and form (i.e., red triangle among red squares and green triangles), often associated with serial search, was consistent with a limited-capacity parallel process. In contrast, the time-course of a difficult asymmetry search (Dosher et al., 2004), also often associated with serial search, was consistent with an unlimited capacity parallel processes. A recent study of isoluminant color search (Sahti & Reeves, 2004) used a model and response time analysis and also argued for parallel processing. Which result is the more typical? Is pure parallel processing only rarely characteristic of difficult search, or do most cases of difficult visual search engage capacity-limited parallel or serial processes?

This paper focuses on time-course measurements, and concludes that the classification of individual elements as target or distractors is carried out in parallel across the visual field within any single episode of information acquisition (eye fixation), even in many very difficult searches. Here we study difficult heterogeneous distractor search and easy homogeneous distractor search to evaluate the generality of unlimited capacity parallel mechanisms. The time-course accuracy functions, hits and false alarms, as well as the previous results on asymmetry searches (Dosher et al., 2004), and a reanalysis of conjunction search data (McElree & Carrasco, 1999) all show that – within a single eye fixation – unlimited capacity parallel processing characterized visual search for a wide class of tasks. These results are consistent with an analysis of multiple-target search (Thornton & Gilden, 2007) and with recent computational models of eye fixations in search that assume parallel processing across the field within a single glance (Najeminik & Geisler, 2005).

Parallel and Serial Visual Search

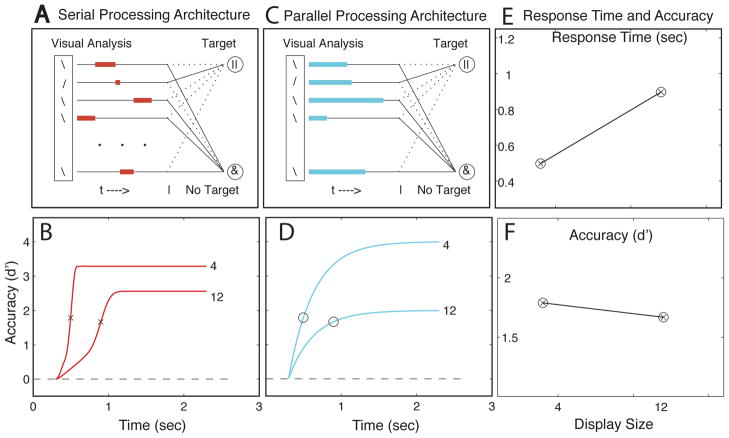
In serial architectures (Fig. 1A), as the number of elements in a visual display increases, more elements must be searched one after the other in sequence to find a target. The visual search terminates as soon as a target is found, or continues through the entire display to decide that a target is not present. Serial searches show reduced accuracy and slowed time course (Fig. 1B) for displays with more objects, as well as slower response times and lower accuracies in a standard response time measurements (x symbols). Many models of visual search invoke serial processes associated with the capacity-limited deployment of attention, including feature integration theory (Treisman & Gelade, 1980), selective search models (Dosher, 1999; Egeth, Virzi, & Garbart, 1984), guided search models (Cave & Wolfe, 1990; Wolfe, 1994, 2003), and others. In unlimited capacity parallel architectures (Fig. 1C) (e.g., Townsend & Ashby, 1973; Dosher, Han, & Lu, 2004; McElree & Dosher, 1989; Ratcliff, 1978), all objects are processed simultaneously, but with variable completion times. Again, search terminates when a target is found or after all items are evaluated when a target is not found. Parallel searches may or may not show noticeable reductions in ultimate accuracy, but exhibit very similar time courses (Fig. 1D) for larger and smaller displays. Even if standard response times and error rates (o symbols) show increases with display size, especially if the target is absent, they may nonetheless be consistent with a parallel time-course.

Figure 1.

Temporal processing architectures for serial (A) and parallel (C) visual search, corresponding time-course functions for display sizes of 4 and 12 for serial (B) and parallel (D) visual search, and standard single-point response time (E) and accuracy (F). The identical results in a response time paradigm (E and F) are compatible with serial (A, B) or parallel (C, D) architectures of visual analysis.

Pairs of response times and accuracies (RT, d′) for different display sizes can be consistent with either a serial or an unlimited parallel architecture. Figures 1E and F illustrate this point, graphing serial and parallel time-courses of search. (This is meant to be illustrative; consideration of additional display sizes may provide added constraints.) Measuring the full time course of visual search is a very direct way to distinguish the two temporal architects, although analysis of response time distributions (Townsend & Nozawa, 1997), and of multiple-target paradigms (Thornton & Gilden, 2007), also provide converging evidence. Identical or nearly identical time courses for different display sizes support a conclusion of parallel processing. Some slowing in time course may still be compatible with unlimited capacity parallel models. Significant slowing in time course with larger displays requires formal models to evaluate the adequacy of different serial or capacity limited models.

The full time course of visual search is measured in a speed-accuracy tradeoff paradigm in which processing time of the observer is manipulated and performance accuracy is the dependent measure. In the cued-response speed-accuracy tradeoff (SAT) paradigm (e.g., Dosher, 1976), the observer is interrupted by a cue to respond – such as a brief tone – and required to respond as quickly as possible. Usually 6 to 8 interruption times, or cue lags, are used to measure the full time course of information accumulation. Performance accuracy, usually d′ (a bias-free measure of discrimination accuracy) is measured as a function of processing time (average time from the onset of the display to the response, or average total processing time). A condition that leads to faster response times and higher accuracy in an RT paradigm may actually differ only in limiting accuracy and not in temporal dynamics when measured by SAT time-course functions (see Dosher, 1984; Dosher & McElree, 1990; McElree & Dosher, 1989, Reed, 1973).

Probabilistic Models of Visual Search

The time course data are evaluated using a probabilistic serial search model and a probabilistic parallel search model of visual search (Dosher, Han, & Lu, 2004), illustrated schematically in Figures 1A and C, respectively. The models are analogous in all respects save the temporal scheduling of evaluations of display elements. Observers begin a visual search trial in a neutral, or no-information, state. If any item, correctly (for targets) or incorrectly (for distractors) is classified as a target, the observer enters a positive information state. If all items, correctly (for distractors) or incorrectly (for the target) are classified as distractors, the observer enters a negative information state. If the observer is interrupted early in the search, s/he is likely to be in the neutral state, and will guess. Later in the search, more responses will be based on informed classifications, though some may be erroneous. These models are a significant extension of previous analyses because they incorporate the consequences of possible errors in identification of display elements into time course predictions. For example, misclassification of the target as a distractor may prolong the search processes in target-present displays, while misclassification of a distractor (as a target) in a target-absent display shortens search times.

The limiting accuracy for each condition depends on the probability of correctly classifying the target, P_T, the probability of correctly classifying a distractor, P_D, and a guessing probability g. Correct classifications of individual display elements are shown as solid lines while dashed lines indicate possible classification errors (Figures 1A and C). For both the serial and parallel models, the time course of search reflects a probabilistic mixture of completion times – the first target present classification (OR) or the last target absent classification (AND). In the serial model, the completion times are approximated by the Gamma distribution G(t|τ,a), with a stages determined by the number of serial evaluations, and a time constant τ. In the parallel model, the time to evaluate each element, beginning simultaneously, is drawn from a fixed Gamma distribution G(t|τ,a), where variation in τ and a control the mean and skew. The probabilities of yes or no responses and search times are computed from the combinatorics over individual element decisions (e.g., a distractor false alarm in the third evaluation following the correct rejection of two previous distractors in serial search, etc.). The equations for these models, developed in Dosher, Han, & Lu (2004), are detailed in Appendix A. These models are fit directly to the time course data.

While time-accuracy (or SAT) functions may reflect either a continuous accrual of information over time, or the cumulative distribution of completion times of a discrete process (e.g., Dosher, 1976, 1979, 1981), the probabilistic parallel and serial models of visual search are developed here as completion time models. However, this analysis is also consistent with continuous diffusion information accumulators where information becomes available only when a decision or classification boundary is reached (i.e., Ratcliff, 1998; Thornton & Gilden, 2007) in which case the distribution G(t|τ,a) approximates the completion time distribution of individual comparisons.

Heterogeneous and Homogeneous Search

Duncan and Humphreys (1989) were among the first to systematize the observation that search efficiency depended both upon the similarity of the target and distractors and on the heterogeneity of different distractors. In homogeneous conditions, all distractor elements are identical. In heterogeneous conditions, distractor elements are of at least two types. Homogeneous visual search is usually associated with pre-attentive parallel evaluation. Even when the target is known, as in the current case, heterogeneous visual search is usually claimed to involve attention-demanding serial search processes (Duncan & Humphreys, 1989; Wolfe, et. al, 1992; Rosenholtz, 2001). In order to guarantee that only covert information processing is evaluated, the SAT study uses time-limited displays to guard against eye movements during search. All the experiments and analyses testing signal detection accounts of search accuracy (without reaction time) also use brief time-limited displays (e.g., Palmer, 1994; Palmer, Verghese, & Pavel, 2000).

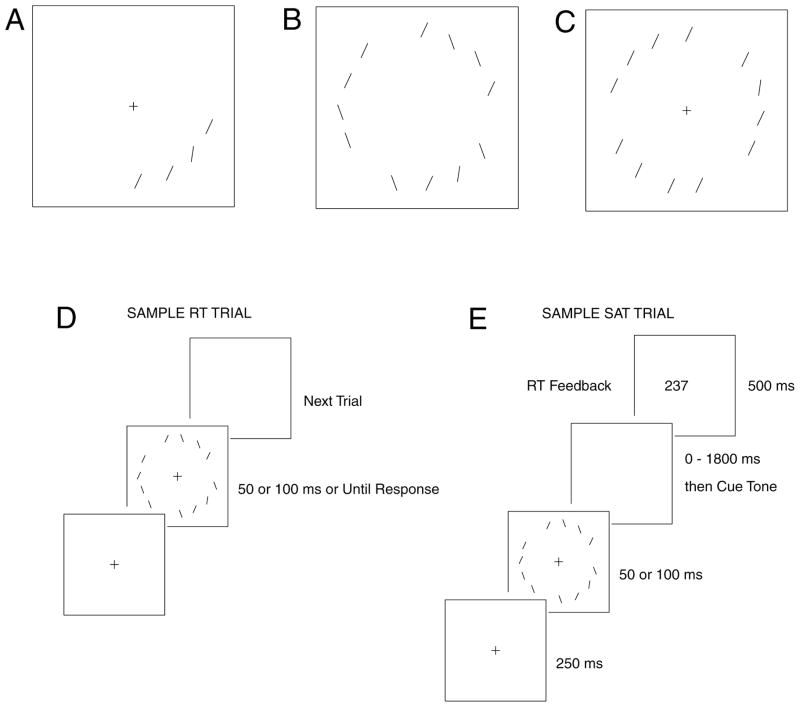
In these experiments, the target was always a line of shallow right tilt (8° clockwise of vertical). In homogeneous search, all distractors had a sharper right tilt (25° clockwise of vertical). In heterogeneous search, distractors were equally often tilted sharp right or somewhat left (25° clockwise or 15° counter-clockwise of vertical). So, a single boundary in orientation space separated the target and distractors in the homogeneous condition; the heterogeneous condition required multiple or non-linear boundaries in orientation space, although some researchers might claim a unique category for the target as a steep angle (Wolfe et al., 1992). Annular search layouts controlled for eccentricity (Carrasco, Evert, Chang & Katz, 1995; Carrasco, McLean, Katz, & Frieder, 1998) and density effects (see Dosher, Han, & Lu, 2004). A sample trial and layout are illustrated in Figure 2.

Figure 2.

Stimulus layouts and sample trial sequences. (a) Homogeneous distractor display of size 4. (b) Homogeneous distractor display of size 12; (c) Heterogeneous distractor display of size 12. Display elements appear on an annulus at 4.12 deg of visual angle, grouped with spaces to equate the local interactions of display elements. (d) Trial sequence for response time paradigm. The stimulus appeared for 100 ms or 50 ms (time-limited condition) or until response (unlimited display conditions). (e) Trial sequence for the speed-accuracy tradeoff paradigm.

Experiment 1 documented the typical reaction time effects of display size for heterogeneous search in a standard response time paradigm with display until response (Wolfe, et. al, 1993). Experiment 2 evaluated time-course of heterogeneous and homogeneous visual search using the cued-response SAT paradigm for brief displays of 100 ms or 50 ms. Experiment 3 measured response times for the practiced observers of Experiment 2 in standard response time and in brief displays.

General Methods

Observers

In Experiment 1, 10 observers participated in a one-hour session for undergraduate course credit. Four new observers participated in Experiments 2–3 and were paid for their service. Experiment 2 required a series of 10–12 sessions, while Experiment 3 required 4 sessions. Observers reported normal or corrected to normal vision.

Stimuli

The target was a shallow line tilted 8° clockwise of vertical. Homogeneous distractors were tilted 25° clockwise of vertical. Heterogeneous distractors were either tilted 25° clockwise of vertical or tilted 15° counter-clockwise of vertical, with equal probability. These values were chosen based on piloting to optimize asymptotic accuracies in the SAT data. The dark tilted lines were rendered as gray scale images with anti-aliasing on a 32 × 32 pixel grid displayed on a Leading Edge Technology 1230V monitor controlled by a Vista image board on a PC computer. A special circuit combined two output channels to produce 4096 grey levels (12 bits), linearized to yield 256 programmable luminance levels. The tilted lines were specified as the minimum luminance (1 cd/m²) with the background luminance of 71 cd/m² (luminance range 1 cd/m² to 144 cd/m²). The lines were rendered in regions subtending 0.98 × 0.98 degrees at a viewing distance of approximately 60 cm, and were arranged on a 4.12 deg radius with fifteen possible equally spaced positions on the annulus, randomly rotated on each trial. Elements of displays of size 4, 8 and 12 consisted of 1, 2, or 3 sets of 4 adjacent locations, with a space between sets (Figure 2A–C), thus equating eccentricity and the density for all displays (one half of elements are adjacent to a space, and one half are internal items). Lastly, the position of each element was randomly “jittered” (a uniform distribution from −4 to +4 pixels) in the horizontal and vertical directions to introduce some irregularity into global contour cues.

Design

Homogeneous and heterogeneous displays were tested in separate blocks and alternated. For all display sizes, half the trials included a target and half did not. In heterogeneous trials, the two types of distractors appeared in randomized locations in the display; a target replaces one of these items when it is present. Trials with different display size and target presence/absence were presented in a random order within blocks.

Experiment 1 tested display sizes of 4, 8, and 12 for target present and target absent conditions for separate blocks of heterogeneous and homogeneous displays. Blocks were 480 trials with 80 trials per condition per subject. The displays remained on until the observer responded.

Experiment 2 tested display sizes of 4 and 12 for target present and target absent conditions for separate blocks of heterogeneous and homogeneous displays. Processing time was manipulated with 7 cue delays of 0.0, 0.050, 0.150, 0.300, 0.500, 1.150 and 1.800 s after display offset, for net cue delays from stimulus onset of these values plus the display duration. All trial types within a block were tested in random order. Following one or two sessions of SAT training with display duration set at 150 ms, observers participated for 6 sessions (n=60 trials in each of the 28 conditions, or 1680 trials) with display duration of 100 ms, followed by 6 sessions with a display duration of 50 ms.

Experiment 3 tested display sizes of 4, 8, and 12 for target present and target absent conditions for separate blocks of heterogeneous and homogeneous displays. In one condition, the displays remained on until the observer responded. In another, a brief display of 50 ms was used. Observers ran one session each of the homogeneous and heterogeneous search tasks, four sessions total, to yield a sample size per observer per condition of 80 in each condition.

Procedure

On each trial, a fixation plus appeared for 250 ms, followed by the test display. For Experiment 1 and the free response version of Experiment 3, the display remained available until the observer responded by pressing the “j” key with the right hand for target present trials, and the “f” key with the left hand for target absent trials; the handedness of the observers was not controlled. In the brief-display version of Experiment 3, the array was displayed for 50 ms. Observers were instructed to respond “as quickly and accurately as possible” in the response time paradigms. For Experiment 2, the cued-response SAT task, the display was presented briefly (150 ms in practice, then 100 ms or 50 ms) and a tone occurred at a delay of 0–1.8 s after display offset, and finally, the response time after the tone cue was displayed for 500 ms. Observers were instructed to respond as quickly as possible following the tone cue, and also that cued response times less than 90 ms suggested anticipation of the cue while cue response times greater than 400 ms were too slow. Sessions lasted slightly less than one hour.

Analyses

Percent yes (target present) responses and mean response times (from display onset) were tabulated for each display size, cue delay, and target present/absent condition. For the cued-response data, the discrimination measure, d′, was calculated from the percent yes data (d′ = z_hit −z_fa). Probabilities of zero or one were corrected (Macmillan & Creelman, 1991) by 1/(2n)to yield measurable d′ values. Time-course functions graph d′ as a function of total processing time, the average time between display onset and response.

Both the probabilistic serial and parallel search models (Appendix A) and an exponential models were fit to time-accuracy d′ data by minimizing the squared deviations between the model and the data ${\displaystyle \sum _{i=1}^n}{\left(d_i-{\widehat{d}}_i\right)}^2$, where the d_i are the observed d′ value and the d̂_i are the predicted d′ values. The exponential approach to a limit, d′ = λ(1 − e^{−β(t−δ)})for t > δ; and 0 otherwise, provides an excellent empirical summary of time-accuracy functions and also allows comparison to other published data (Dosher, 1976; Sutter & Graham, 1995; Sutter & Hwang, 1999). In this equation, λ is the asymptotic (maximal) accuracy, the intercept δ is the point where accuracy first rises above chance, and the rate β describes the speed of rise from chance to asymptote. Error minimization was programmed in Matlab using fminsearch. The quality of fit was summarized by: $R^2=1-\frac{\left({\displaystyle \sum _{i=1}^n}{\left(d_i-{\widehat{d}}_i\right)}^2/(n-k)\right)}{\left({\displaystyle \sum _{i=1}^n}{\left(d_i-\overline{d}\right)}^2/(n-1)\right)}$, where d_i and d̂_i are as described above, d̄ is the observed mean, n is the total number of predicted data values, and k is the number of model parameters. The fidelity index r² is the proportion variance accounted for by the model (replace (n − k) in the R² equation by (n − 1)). R² is the percent variance accounted for by the model, adjusted by the number of free parameters. Nested models are tested for significance using nested-F tests (Wannacott & Wannacott, 1981): $F=\frac{({\mathit{RSS}}_{\mathit{reduced}}-{\mathit{RSS}}_{\mathit{full}})}{(k_{\mathit{full}}-k_{\mathit{reduced}})}/\frac{({\mathit{RSS}}_{\mathit{full}})}{(k_{\mathit{full}})}$ with degrees of freedom k_full − k_reduced and n − k_full, where RSS is the residual sum of squared errors for the model. Model comparisons used r², R² and nested F-tests. The probabilistic parallel model was fit to the percent yes data by maximizing the likelihood of the proportion yes data over all curves simultaneously: $L={\displaystyle \prod _{i=1}^N}\frac{n_i!}{c_i!(n_i-c_i)!}{p}_i^{c_i}{(1-p_i)}^{n_i-c_i}$ where ${\displaystyle \prod _{i=1}^N}$ is the product over N observed percent yes points over all conditions, p_i is the predicted percent yes n_i is the number of trial per point, c_i is the number of yes trials and so n_i − c_i is the number of no trials.

Results

Experiment 1 Results

Response times increased with display size for the heterogeneous condition, while display size had minimal effects in the homogeneous condition (Figure 3A). All main effects and interactions of distractor condition, number of display elements, and target presence were significant for response times (all p < .01 except p<.05 for the main effect of target presence) and errors (all p < .01, except p < .08 for the interaction of target presence and display size). The details of the analysis of variance for response times are: distractor condition F(1,9) = 66.22, p < .001, η² = 0.761, partial ${\eta }_p^2=0.880$; target presence F(1,9) = 6.43, p < .05, η² = 0.022, ${\eta }_p^2=0.412$; display size F(2,18) = 70.40, p < .001, η² = 0.108, ${\eta }_p^2=0.887$; distractor condition × target presence F(1,9) = 9.18, p < .01, η² = 0.016, ${\eta }_p^2=0.505$; distractor condition × display size F(2,18) = 58.57, p < .001, η² = 0.079, ${\eta }_p^2=0.867$; target presence × display size F(2,18) = 15.82, p < .001, η² = 0.009, ${\eta }_p^2=0.638$; and the three way interaction F(2,18) = 5.64, p < .013, η² = 0.023, ${\eta }_p^2=0.385$. The details of the analysis of variance for errors are: distractor condition F(1,9) = 23.95, p < .001, η² = 0.427, ${\eta }_p^2=0.727$; target presence F(1,9) = 19.81, p < .002, η² = 0.321, ${\eta }_p^2=0.688$; display size F(2,18) = 11.51, p < .001, η² = 0.024, ${\eta }_p^2=0.520$; distractor condition × target presence F(1,9) = 11.08, p < .01, η² = 0.149, ${\eta }_p^2=0.552$; distractor condition × display size F(2,18) = 20.98, p < .001, η² = 0.036, ${\eta }_p^2=0.700$; target presence × display size F(2,18) = 2.78, p < .09, η² = 0.009, ${\eta }_p^2=0.236$; and the three way interaction F(2,18) = 4.68, p < .05, η² = 0.012, ${\eta }_p^2=0.342$. The ${\eta }_p^2$, or partial etas, divide the sum of squares for each factor by the relevant sum of squares plus sum of squared errors for that factor in the multi-way analysis of variance. The ${\eta }_p^2$ reflects the percent variance accounted for by any factor holding constant all remaining factors, and is similar to a partial correlation coefficient.

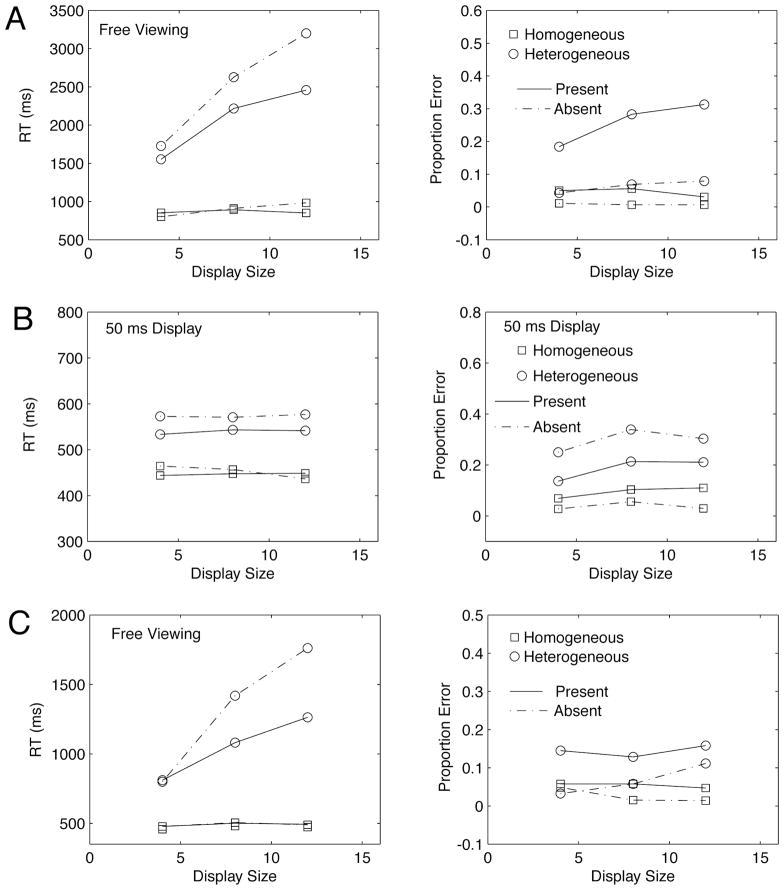
Figure 3.

Average correct RT and error rates as a function of display size for search with free viewing of unlimited-time displays in Experiment 1. (A) RT (left) and proportion errors (right) in target present and target absent conditions of homogeneous and heterogeneous displays for unpracticed observers with free viewing. (B) RT (left) and proportion errors (right) in target present and target absent conditions of homogeneous and heterogeneous displays for practiced (SAT) observers for 50 ms brief displays. (C) RT (left) and errors (right) in target present and target absent conditions of homogeneous and heterogeneous displays for practiced (SAT) observers with free viewing.

The slopes of heterogeneous target present and target absent displays were 113 ms and 184 ms per item, respectively. The slopes of homogeneous displays were 0 ms and 22 ms, respectively. Homogeneous search was more accurate than heterogeneous search, with display sizes of 4, 8, and 12 yielding 83.8 and 97.3 and 83.8 percent correct, and 92.8, 89.7 and 89.2 percent correct, respectively. With the exception of the relatively high error rates for the target-absent heterogeneous distractor conditions, the primary differences were reflected in reaction times.

These results replicate in annular displays the previous reports for distractor heterogeneity conditions (e.g., Wolfe, et. al, 1993). The high slopes in the heterogeneous distractor condition would typically be interpreted as the consequence of attention demanding serial processing. The small slopes of the homogeneous condition would typically be associated with pre-attentive parallel processing. The results in this free-viewing condition may in part reflect overt information acquisition through movement of the eyes.

Experiment 2 Results

Speed-accuracy tradeoff functions

Experiment 2 tested the full time course of visual search using cued-response speed-accuracy tradeoff. The average time-accuracy functions (d′ vs. total processing time) are shown in Figure 4. The data for 100 ms displays and for 50 ms displays are displayed separately. The average data are representative of the individual observer data. In these SAT functions, accuracy is graphed as a function of total processing time, which is the average time from display onset to response, or the lag to the cue to respond plus the average response times. Total processing time includes stimulus registration and motor response time, which is also true for standard reaction time. The average response times to the response cues were unaffected by display size or search difficulty, but varied slightly over the shortest few cue delays, as is typical in the SAT paradigm (e.g., Dosher, 1976; Dosher, Han, & Lu, 2004).

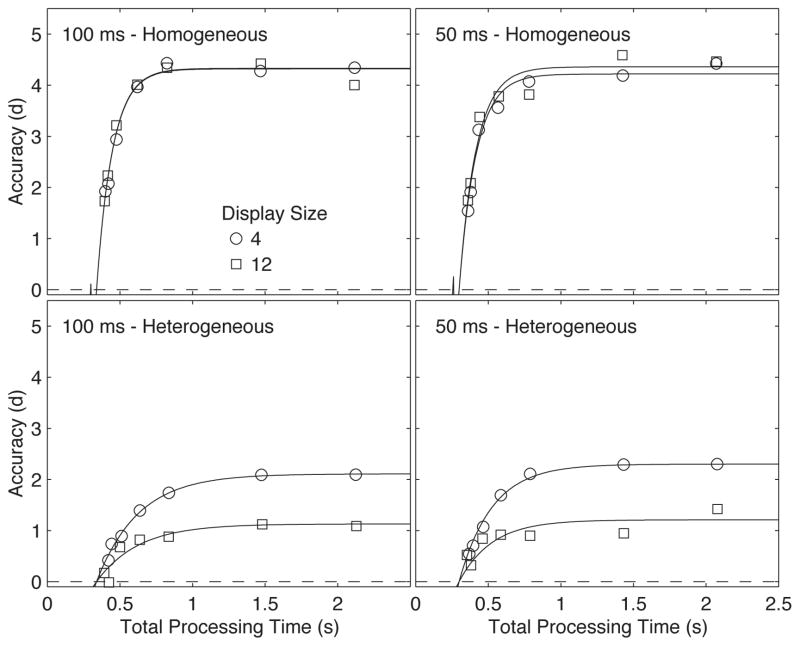
Figure 4.

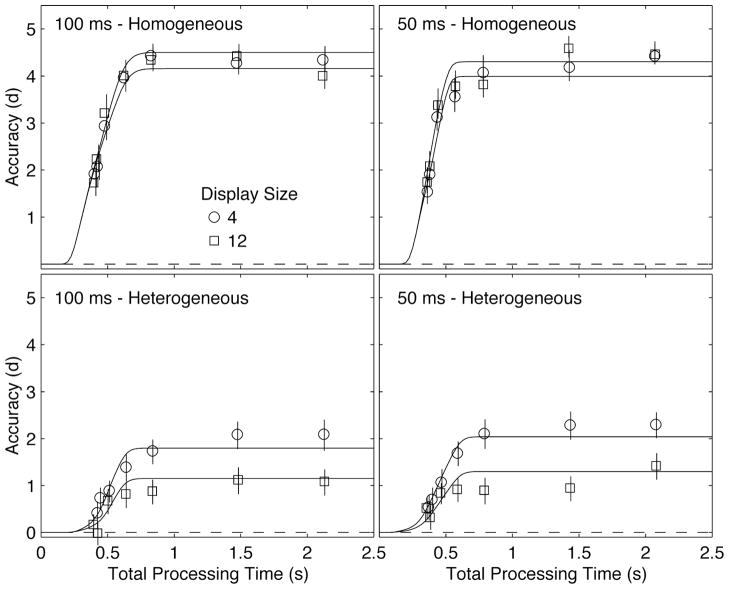
Discrimination performance (d′) as a function of total processing time (test onset to response) for display sizes of 4 and 12 from Experiment 2 for (upper left) 100 ms display homogeneous searches; (lower right) 100 ms display heterogeneous searches; (upper right) 50 ms display homogeneous searches, and (lower right) 50 ms display heterogeneous searches. The symbols are observed data points and the smooth curves are best fitting descriptive exponential functions.

The data for the 100 ms (performed first) and 50 ms (performed second) display conditions are quite similar. These conditions may differ slightly as they reflect different display durations, and hence visual availability, but also different stages of practice. The 50 ms display duration allows earlier cues to respond. We treat the two sets of data as independent replications. Exponential fits of time-accuracy data (d′ vs. total processing time) provide a standard descriptive analysis, and allow comparisons with previously reported data. The exponential fits minimized least-squared error. The best fitting exponential models (smooth functions in Figure 4) are listed in Table 1. Exponential models describe each function with an asymptote (λ), a rate (β), and an intercept (δ) (see Analysis section). A lattice of models with different constraints was considered to account for the four conditions, homogeneous set sizes 4 and 12 and heterogeneous set sizes 4 and 12. A (4λ, 2β, 1δ) model with asymptotic accuracy estimated independently for each condition, two rates (one for homogeneous and one for heterogeneous), and a single intercept fit the data very well, yielding R² for the average data of 0.991 [range over observers 0.916–0.976] for 100 ms displays and 0.977 (0.908–0.968) for 50 ms displays. Nested model F-tests evaluated whether reduced models, which hold certain parameters constant across conditions, caused significant losses in quality of fit. Eliminating the rate difference between homogeneous and heterogeneous conditions significantly reduced the quality of fit for 4 of 5 observers in each of the 100 ms and 50 ms display conditions (see Table 1). Homogeneous search conditions yielded both higher asymptotic accuracies and slightly faster temporal dynamics in most cases than heterogeneous search conditions.

Table 1.

Exponential Descriptive Parameters Experiment 2

Parameter	AV	KC	RC	SM	SP
100 ms Display
Homogeneous - 4 λ	4.32	4.10	3.92	4.50	4.81
Homogeneous - 12 λ	4.33	4.54	4.10	4.26	4.51
Heterogeneous - 4 λ	2.11	2.81	2.25	1.55	2.82
Heterogeneous - 12 λ	1.13	0.50	1.01	1.16	1.91
Homogeneous β	9.11	9.81	7.53	6.20	10.0
Heterogeneous β	3.48	0.93	2.35	3.71	5.60
Common δ	.339	.351	.327	.289	.314
Adjusted-R2	.992	.957	.979	.959	.916
Test	*	*	*	≈	*
50 ms Display
Homogeneous - 4 λ	4.21	4.22	4.17	4.27	4.37
Homogeneous - 12 λ	4.35	4.12	4.21	4.25	4.98
Heterogeneous - 4 λ	2.30	1.78	2.15	2.30	3.13
Heterogeneous - 12 λ	1.21	0.51	0.96	1.23	2.14
Homogeneous β	8.45	6.54	8.14	10.0	6.75
Heterogeneous β	4.42	2.32	3.68	4.03	5.27
Common δ	.300	.300	.295	.323	.254
Adjusted-R2	.977	.954	.968	.913	.908
Test	*	*	*	*	≈

NOTE: Parameters for a (4 λ, 2 β, 1 δ) exponential model. Each condition has a separate asymptote λ, rate β may vary for homogeneous and heterogeneous searches, and the intercept δ is common. The symbol ≈ indicates that the rate difference is not-significant (p > .10);

^*indicates that the rate for homogeneous searches is significantly faster than the rate for the heterogeneous searches (p<.05, p <.01 in most cases).

Importantly, in no case did the quality of fit significantly improve by allowing the larger display size to slow the search speed (exponential rate parameter) (p values for all relevant model comparisons > .3). These results are qualitatively consistent with parallel search processing architectures and qualitatively inconsistent with serial search processing architectures. These observations are directly evaluated next using the probabilistic serial and parallel search models. These models describe the time course of visual search, but they also provide constrained fits of the asymptotic accuracies.

Probabilistic Parallel Search Models

In the probabilistic parallel search model, visual search involves identifying each element of the display as a target or distractor. The items are processed in parallel – starting simultaneously and with a common time dnistribution. At any given time, the observer will respond “yes” if at least one item has been identified (correctly or in error) as a target or “no” if all items have been (correctly or in error) identified as distractors, or may guess “yes” in the absence of information. The predicted time course of the target-present decision is controlled by the distribution of times for individual comparisons (drawn from an a-stage Gamma distribution with time parameter τ, probabilities of correctly classifying targets (P_T) and distractors (P_D), and the decision rule, with guessing probability g. See Appendix A for a full description and derivation of the model. The models fit d′ using least-squared methods, and nested models in the lattice of models were compared with the nested F-test. Models were fit to average data because a lattice of models with different numbers of free parameters was extremely time consuming to process due to the computation of the combinatorics of comparison orders across items.

The probabilistic parallel search models were fit separately to average d′ data for the 100 ms and 50 ms exposure durations, averaged over observers, for homogeneous and heterogeneous search. The model provided an excellent account of the time course of both homogeneous and heterogeneous search. While homogeneous visual search is generally associated with parallel search processes, heterogeneous search is generally associated with the operation of some form of serial search architecture.

An 8-parameter (plus one pre-set parameter) model, (4 P, 2τ, 2 g, a = 25), provided an excellent fit to the time course data for homogeneous and heterogeneous searches, as good a fit as a fully saturated model. The values of the four Ps specify the probabilities of correct target and distractor identification in the homogeneous and heterogeneous conditions. The two parameters of the Gamma distribution, τ and a, specify the completion time distribution for each individual item; in this context, a could be set without loss to 25 (see Dosher, Han, & Lu, 2004, for a discussion).

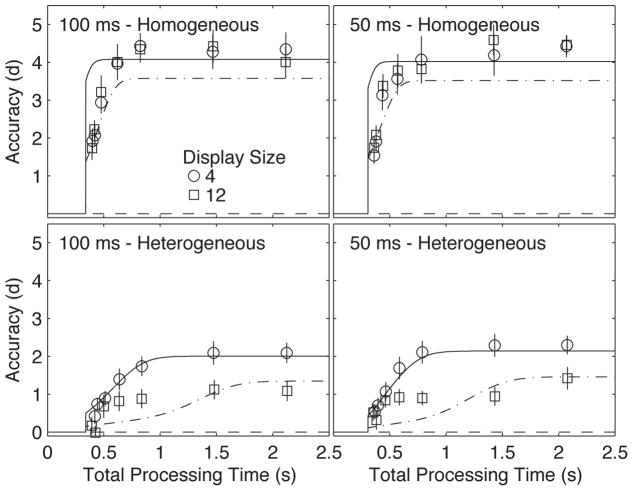
For the 100 ms data, the estimated parameters were: identification probabilities P_T and P_D for targets and distractors of 0.967 and 0.999, respectively, time constant τ of 0.014 and guessing parameter g of 0.100 in the homogeneous condition; identification probabilities of 0.970 and 0.815, τ of 0.020 and guessing probability of 0.102 for the heterogeneous condition. This model yields an R² of 0.986. The independently estimated parameters for the 50 ms data were closely similar: identification probabilities for target and distractors of 0. 961 and 0.999, τ of 0.013, and guessing parameter of 0.202 in the homogeneous condition; and identification probabilities of 0.983 and 0.817, τ of 0.016 and guessing probability of 0.053 for the heterogeneous condition. This yields an R² of 0.966. This model was compared with a lattice of both less constrained and more constrained models that set various parameters to be equal in the homogeneous and heterogeneous search conditions. Model variants equating the P_T and P_D or τ in the homogeneous and heterogeneous conditions provided a statistically inferior fit to the data. A model with separate time constants τ’s for the homogeneous and heterogeneous provided a slightly better fit by a nested F-test (p < .01), consistent with the exponential fits. The fit of the probabilistic parallel model is shown in Figure 5. This parallel model makes the standard simplifying assumption of all of the uncertainty models of unlimited capacity visual search, namely that the criteria for false alarms are identical in the 4-item and 12-item displays, or that the two set sizes are fit with a common P_T and P_D. In a later section, we consider an elaborated model for percent yes data, which can also be used to regenerate an excellent equivalent fit of the parallel model to the d′ data.

Figure 5.

Fit of the probabilistic parallel search model to the discrimination data in Figure 4 for 100 ms and 50 ms displays for homogeneous and heterogeneous searches. The symbols are observed data points and the smooth curves are best fitting model functions.

The probabilistic parallel search model constrains the relationships of the asymptotic search accuracies of the two display sizes because the asymptotic accuracies are derived from the probabilities of correct identification of the single target and the numbers of distractors for display sizes of 4 and 12. In the descriptive exponential model, the asymptotic accuracies for the display sizes of 4 and 12 were simply estimated independently to maximize fit. The asymptotic accuracy for display sizes 4 and 12 are well fit by the decision model in the probabilistic model, which embodies the classic uncertainty calculations for these display sizes in search accuracy experiments (Palmer et al., 2000; Eckstein, 1998).

Distractor identification in the heterogeneous displays was estimated to be notably poorer than that of the homogeneous displays, although all the heterogeneous distractors were at least as dissimilar from the target (see Hodsoll & Humphreys, 2005; Rosenholtz, 2001 for related discussions). The probabilistic parallel search model applies directly to homogeneous search, but could be an approximation to heterogeneous search. If the two types of distractors in heterogeneous search were to differ substantially in identification accuracy or temporal parameters, then a more complex model that distinguishes the two would be required. Counting all of the combinatoric instances of such a model would be so complex that it would likely be implemented by simulation rather than derivation. That the probabilistic parallel search model fit the data from the heterogeneous condition quite well suggests that the two types of distractor were similar in identification time and accuracy.

In sum, the probabilistic parallel search model provided a good account of the time course and asymptotic accuracies of visual search not just for homogeneous search generally associated with parallel processes – but also in the case of heterogeneous search – generally cited as a classic example of serial search.

Probabilistic Serial Search Models

In this section, the complementary test evaluates the probabilistic serial search model and its ability to fit the time-course data. The probabilistic serial model is an exact analog to the probabilistic parallel model, except that the identification of items occurs in series, one after the other, in random order. All of the model parameters remain the same, except that the temporal properties of the search are determined by the Gamma distribution with time parameter τ characterizing the processing of each individual item, and a variable number of stages determined by the (random) order of processing each item, and the probabilities of doing so accurately. See Appendix A for details and equations. The probabilistic serial model, which incorporates the consequence of identification errors into the time course predictions, moderates the strongly slowed time course predictions of previous versions of the serial model in visual search (e.g., McElree & Carrasco, 1999).

We gave the probabilistic serial model every possible chance to work by fitting a fully saturated serial model with all different parameters for homogeneous and heterogeneous searches, allowing the greatest possible freedom to this model (4 independent probabilities of element identification accuracy, independent estimates of guessing bias, independent time constants, and independent time intercepts for the homogeneous and heterogeneous conditions, 4 P, 2 τ, 2 g, 2 t0 – or 10 model parameters free to vary), the model yielded consistently poorer quality of fits compared to that of the probabilistic parallel search model, with an R² of 0.789 for the 100 ms data and of 0.721 for the 50 ms data (Unconstrained, the serial model tried to overcome a poor fit by vastly overestimating the asymptotic accuracy so that the display size difference occurred largely after the last measured data point. However, we know from the shape of the time-accuracy functions and from pilot data for selection of the interruption times which tested times as long as 4 s, that the curves were already at asymptote at 2.3 s. Therefore, the fit was constrained not to overshoot the observed asymptotic levels by a substantial amount.) Any model that includes a saturating monotonically increasing time-course fits the data about as well as this probabilistic serial model; the systematic misfits of this model were clear. The best fitting fully saturated probabilistic serial model is shown in Figure 6.

Figure 6.

Fit of the probabilistic serial search model to the discrimination data in Figure 4 for 100 ms and 50 ms displays for homogeneous and heterogeneous searches. The symbols are observed data points and the smooth curves are best fitting model functions.

Further relaxing the relationship in asymptotic levels, in which the modeled asymptotic performance is constrained by the signal detection uncertainty relationship between the two displays sizes, still failed to achieve the quality of fit of the parallel models. This 8 P, 2 τ, 2 g, 2 t0, 14-parameter model has full flexibility in fitting asymptotic levels (with 8 accuracy parameters to account for different target and distractor identification probabilities in the different set sizes and distractor conditions), yet only marginally improved the quality of fit, with an R² of 0.849 for the 100 ms data and of 0.796 for the 50 ms data (compare with R²’s of 0.986 and 0.966 for the 8-parameter parallel model).

Even assuming that homogeneous displays reflect parallel search while heterogeneous displays reflect a standard serial search would not solve the poor fit of the serial model because the fit to the heterogeneous data is independent of the fit of the homogeneous data. The sum of squared errors for the mixed homogeneous-parallel, heterogeneous serial model exceeded that of the parallel model by a factor of more than 2 for both 100 ms data and 50-ms data. The parallel search model provides a good account of both homogeneous and homogeneous search, while serial search gives a poor account of both. These results were independently replicated in the data for the 100 ms displays and the data for the 50 ms displays.

Compensatory-Rate Serial Model

Is there any condition under which a serial model could account well for the time-course data? One such case, suggested by a reviewer, might be a paradoxical compensatory-rate probabilistic serial model in which the rate of processing each item is increased in larger displays to compensate for the effect of increasing numbers of items in a serial process. This model is counter-intuitive – if it is possible to process items three times as fast in a 12-element display as in a 4-element display, then why not process the 4-element display at the faster rate? The compensatory model violates the fulcrum of all standard tests of serial processing, which assume either equivalent processing time for each item regardless of the number of elements, or that added items slow the rate of processing each one.

It seems obvious, however, that such a paradoxical compensatory processing model should overcome the incompatibility in time courses of display sizes 4 and 12. We implemented the compensatory-rate probabilistic serial model by incorporating not just independent speeds of processing for the two search types (homogeneous and heterogeneous), but also for each display size within search type. All other aspects of the probabilistic serial model are retained. Thus, the model includes 4 independent probabilities of element identification accuracy, independent estimates of guessing bias, independent time constants for the homogeneous and heterogeneous conditions and for display sizes 4 and 12, and independent time intercepts for the homogeneous and heterogeneous conditions (4 P, 4 τ, 2 g, 2 t0). The ratio of the processing times per item should be about 3 to 1 because the faster times in larger displays are accounting for a 12 to 4 (3 to 1) ratio of the number of elements to yield a common time course. As expected, the compensatory rate serial model estimated the two rate parameters, τ, to be 20 ms and 7 ms (ratio 2.9) and 82 ms and 22 ms (ratio 3.7) for the homogeneous and heterogeneous 100 ms displays (respectively), and to be 21 ms and 6 ms (ratio 3.5) and 87 ms and 22 ms (ratio 3.9) in the homogeneous and heterogeneous 50 ms displays. As intuitively expected, the compensatory model fits to the speed-accuracy data approached (though did not quite match) those of the parallel probabilistic model, with R² of 0.964 for the 100 ms data and of 0.930 for the 50 ms data for the 12-parameter model. This compares to R² of .986 and .966 for the 8-parameter parallel search model. These residual differences reflect differences in time course shape for the two set sizes in the serial and parallel models.

Probabilistic Parallel Model and Percent Yes Data

The previous sections documented that the probabilistic parallel model of processing provided a good account of the time course of discrimination (d′) in both relatively easy homogeneous search conditions and in relatively difficult heterogeneous search conditions. In this section, the data for percent yes (hits and false alarms) are considered. The changes in hit and false alarm rates over processing time are intrinsically more complex to model than the bias-free discrimination measures, because hits and false alarms will be sensitive to time-dependent changes in bias as well as discrimination. For this reason, the hit and false alarm rates have not been modeled in any previous analyses of speed-accuracy tradeoff data. In this case, however, it was possible to provide a good account of these data, which provide additional constraints on the probabilistic parallel model. However, we do not necessarily expect this simple model to account for the percent yes data in all experiments, because criteria and guessing strategies may change over the time-course of decision.

The fact that the 8P version of the serial model for d′, where the asymptotes were fit freely, did not provide a competitive fit to the data implies that the corresponding serial model would not provide a competitive fit to the percent yes data, where the same model would need to fit not just the d′s but the more constraining pattern of hits and false alarms. For this reason, we focus on the ability of the probabilistic parallel model to fit percent yes (hit and false alarm) data.

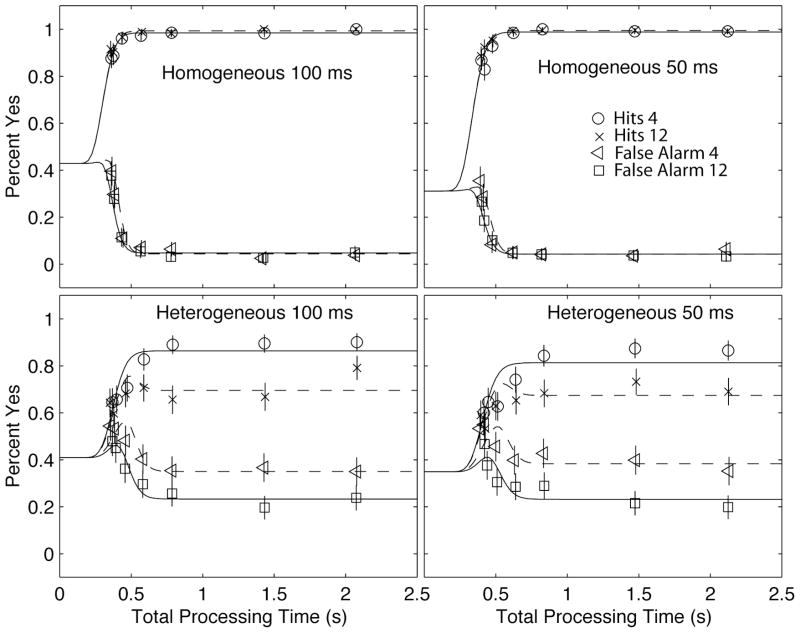
The best fitting probabilistic parallel model for the average hit and false alarm data are shown in Figure 7. The percent yes (hit and false alarm) data were fit with maximum likelihood methods. Different identification probabilities for display sizes of 4 and 12 were required to account for these data. The different identification probabilities for display size are necessary because display size 12 provides additional opportunities to false alarms compared to display size 4, yet the observed false alarm rates are only slightly worse in the 12-item conditions. The best-fitting probabilistic parallel model is a 12-parameter model (with one fixed parameter) (8P, 2τ, 2g, a=25). Overall, the P_T and P_D values were about 0.99 for all homogeneous conditions, but ranged from 0.50 – 0.96 for the heterogeneous condition, with the guessing parameter about 30%. For the 100 ms condition, the best fitting parameter values are (8P = 0.99, 0.99, 0.99, 0.99, 0.77, 0.94, 0.50, 0.96, τ = 0.013 for homogeneous search, and τ = 0.017 for heterogeneous, g = .311 for homogeneous, g = .348 for heterogeneous, and a = 25, R² = .982). (The 8P are given, respectively, in the order: P_T and P_D for display size 4, then P_T and P_D for display size 12 for the homogeneous searches, and then the same order for the heterogeneous searches). For the 50 ms condition, the best fitting parameter values are (8P = 0.98, 0.99, 0.99, 0.99, 0.93, 0.94,0.55, 0.96, τ = 0.013 and 0.016, g = .429 and 0.409, a = 25, R² = .986). These fits to the percent yes data can, in turn, be used to generate predictions for d′ that are comparable to the earlier fits of the probabilistic parallel model to the d′ data. As in those fits, the 100 ms and 50 ms provide quite consistent independent estimation of parameter values.

Figure 7.

Fit of the probabilistic parallel search model to the percent yes data for 100 ms and 50 ms displays for homogeneous and heterogeneous searches. The symbols are observed data points and the smooth curves are best fitting model functions.

The identification probabilities for the homogeneous condition are essentially identical (and very high) for the two display sizes, so the differences focus on the heterogeneous condition. The four independent identification probabilities for the heterogeneous conditions (targets and distractors in display sizes 4 and 12) can be equivalently remapped in terms of a signal detection situation with four free parameters. The mean and standard deviation of the evidence distribution for distractors are set to 0 and 1, respectively, corresponding with standard scaling assumptions of the signal detection theory. The mean of the evidence distribution for targets is D, and the standard deviation is σ. There are different criteria for classification of an item as a target for display sizes 4 and 12: c₄ and c₁₂. For the 100 ms displays, the best fitting Ps can be remapped as D = 1.76, σ = 0.31, c₄ = 1.52, c₁₂=1.76. For the 50 ms displays, the best fitting Ps can be remapped as D = 1.84, σ = 0.34, c₄ = 1.52, c₁₂=1.81. The different identification probabilities for 4-element and 12-element heterogeneous displays reflect a change in criterion for identification that reduces the false alarm rates for the 12-element displays. The variation in evidence is estimated to be smaller for target elements than for distractor elements, which may reflect a special coding status for the target item, or intrinsically larger variance in the distractor distribution in this heterogeneous case.

In summary, the probabilistic parallel search model provided an excellent account of the hit and false alarm data over the full time course of visual search as well as an excellent account of the d′ time-course data.

Experiment 3 Results

Time-Limited Display RT Data

The response time and errors for the 50 ms time-limited displays under a response time protocol are shown in Figure 3B for the practiced observers who had previously participated in Experiment 2. Response times were relatively fast for these time-limited displays. Reaction time slopes were all −1 ms to 1 ms, however the response time levels were sensitive to both distractor type and target presence. Error rates in the time-limited displays also depend on distractor type and target presence, and there is a modest increase in errors of about 0.4% per display element in homogeneous condition and of about 0.8% in heterogeneous conditions. The level of performance is consistent with the performance in the 50-ms time-limited time course data. Indeed, the relevant response time/accuracy points from these data are very close to points generated in the time-controlled testing protocol. These relatively flat functions of display size seem to differ for similar brief displays of Santhi & Reeves (2004) for isoluminant color stimuli. The reasons for this difference are not clear.

The details of the analysis of variance for response times are: distractor condition F(1,3) = 5.13, p < .11, η² = 0.936, ${\eta }_p^2=0.631$; target presence F(1,3) = 4.87, p < .11, η² = 0.033, ${\eta }_p^2=0.619$; display size F(2,6) = 0.24, p > .5, η² = 0.000, ${\eta }_p^2=0.072$; distractor condition × target presence F(1,3) = 24.14, p < .02, η² = 0.017, ${\eta }_p^2=0.889$; distractor condition × display size F(2,6) = 19.47, p < .002, η² = 0.005, ${\eta }_p^2=0.886$; target presence × display size F(2,6) = 15.78, p < .01, η² = 0.005, ${\eta }_p^2=0.840$; and the three way interaction F(2,6) = 17.03, p < .01, η² = 0.004, ${\eta }_p^2=0.850$. The details of the analysis of variance for errors are: distractor condition F(1,3) = 146.06, p < .001, η² = 0.737, ${\eta }_p^2=0.979$; target presence F(1,3) = 0.39, p > .5, η² = 0.017, ${\eta }_p^2=0.115$; display size F(2,6) = 11.20, p < .01, η² = 0.056, ${\eta }_p^2=0.789$; distractor condition × target presence F(1,3) = 11.84, p < .05, η² = 0.164, ${\eta }_p^2=0.798$; distractor condition × display size F(2,6) = 12.25, p < .01, η² = 0.012, ${\eta }_p^2=0.800$; target presence × display size F(2,6) = 1.57, p > .2, η² = 0.005, ${\eta }_p^2=0.342$; and the three way interaction F(2,6) = 0.15, p > .5, η² = 0.000, ${\eta }_p^2=0.042$.

Free Viewing RT Data

Figure 3C shows the response times and error rates for standard response time conditions, in which the stimulus was available until response, for the practiced observers of Experiment 2. The performance of the practiced observers is faster and more accurate than that of the unpracticed observers in Experiment 1, yet the general pattern of the data was equivalent. With only four observers, all main effects and interactions, including those assessing the effects of display size, were significant in the response time data (p < .05). In the accuracy data, the differences were smaller, and fewer main effects and interactions were significant. The details of the analysis of variance for response times are: distractor condition F(1,3) = 14.48, p < .05, η² = 0.676, ${\eta }_p^2=0.828$; target presence F(1,3) = 11.55, p < .05, η² = 0.026, ${\eta }_p^2=0.794$; display size F(2,6) = 10.20, p < .02, η² = 0.124, ${\eta }_p^2=0.727$; distractor condition × target presence F(1,3) = 10.10, p < .05, η² = 0.026, ${\eta }_p^2=0.771$; distractor condition × display size F(2,6) = 9.34, p < .01, η² = 0.113, ${\eta }_p^2=0.757$; target presence × display size F(2,6) = 12.05, p < .01, η² = 0.016, ${\eta }_p^2=0.800$; and the three way interaction F(2,6) = 13.03, p < .01, η² = 0.016, ${\eta }_p^2=0.813$. The details of the analysis of variance for errors are: distractor condition F(1,3) = 8.00, p < .07, η² = 0.441, ${\eta }_p^2=0.727$; target presence F(1,3) = 10.10, p < .05, η² = 0.281, ${\eta }_p^2=0.770$; display size F(2,6) = 1.35, p > .3, η² = 0.022, ${\eta }_p^2=0.310$; distractor condition × target presence F(1,3) = 5.71, p < .10, η² = 0.060, ${\eta }_p^2=0.657$; distractor condition × display size F(2,6) = 4.44, p < .07, η² = 0.084, ${\eta }_p^2=0.596$; target presence × display size F(2,6) = 0.68, p > .5, η² = 0.008, ${\eta }_p^2=0.188$; and the three way interaction F(2,6) = 1.89, p > .2,η² = 0.039, ${\eta }_p^2=0.387$.

The response time slopes were 2 ms and 1.5 ms for homogeneous conditions, respectively, for target present and target absent displays; and were 57 ms and 120 ms for heterogeneous conditions, respectively, for target present and target absent conditions. Practice improves, but does not fundamentally alter, the processes for visual search.

General Discussion

Empirical Summary

Experiment 1 documented the classic heterogeneity effect in a standard, free-viewing reaction time paradigm in annular displays controlling for target and distractor eccentricity. Response times increased substantially with the number of distractors in heterogeneous distractor conditions, but only slightly in homogeneous conditions. Attention-demanding serial search processes is widely associated with the pattern of performance in heterogeneous displays.

In Experiment 2, the time course of visual search was measured using speed-accuracy tradeoff methods in time-limited displays (100 ms or 50 ms). A probabilistic parallel model provided an excellent account of both the constrained relation of the asymptotic performance and the common time course of visual search with display sizes of 4 and 12. The probabilistic parallel model also provided an excellent fit to the hit and false alarm pattern underlying the d′ time-course data. The model for the hits and false alarms required distinct probabilities for the two display sizes, but these probabilities were well fit by a consistent signal detection model with a higher criterion in the 12 item displays in order to compensate for the high levels of false alarms otherwise engendered by location uncertainty.

In contrast, a fully elaborated 10-parameter probabilistic serial search model provided a relatively poor account of the data. The parallel model is consistent with closely equivalent temporal dynamics over the various conditions, with a small slowing regardless of display size due to heterogeneity. The serial model predicts slowing in dynamics for larger displays, a phenomenon that was not observed in the data. Even adding to the freedom of this model to allow unconstrained fits to the asymptotic levels for display sizes 12 and 4, with 14-parameters, failed to substantially improve the quality of the fits and isolated the failures firmly in dynamic aspects of the time-course functions.

Relatively high asymptotic levels in homogeneous search and much lower accuracy in heterogeneous search were related to differences in item identification probabilities. The relative accuracies of the display sizes of 4 and 12, however, were then fully constrained by these estimates in both models.

A compensatory-rate serial model in which each item is processed approximately 3 times more quickly in 12-element displays than in 4-element displays provided nearly but not quite as good a fit as the parallel model. This paradoxical model violates the assumptions of all common tests of serial models of equal efficiency in all display sizes, or lower efficiency in larger display sizes if capacity limits are evoked. Even if this model achieved an equal fit, the parallel model would be preferred on the grounds of simplicity. The simpler parallel model accounts for the data with 8 free parameters rather than the 12-parameter compensatory serial model. However, certain unusual serial models such as the compensatory rate model cannot be completely ruled out.

Experiment 3 documented that highly practiced SAT observers showed the same pattern of performance as that of unpracticed observers in a standard response time paradigm. There was no evidence that the extended practiced altered the form or mechanisms of search, although those mechanisms became somewhat more efficient with faster response times and fewer errors. The data from the time-limited response time paradigm were consistent with the SAT data.

Relation to Other Findings

The probabilistic parallel search model provided a good quantitative fit of the time course data, consistent with the suggestive analysis based on descriptive exponential models. The explicit model is important because it assesses the constraints on performance for different display sizes, incorporating asymptotic constraints and the effects of classification errors on the time-course of visual search. The model accounts well for the asymptotic accuracies for display size of 4 and 12 using the same parameters P_T and P_D.

The current asymptotic accuracy effects are consistent with a series of findings focused on search accuracy in time-limited displays (Palmer, 1994, 1995; Palmer et. al, 1993, 2000). In that literature, effects of display size were consistent with statistical uncertainty within the framework of a signal detection framework, and not consistent with models that proposed capacity limitations, for a wide range of searches with targets defined by primary features such as line length, brightness, or orientation. This is also true for the portion of the search accuracy literature (e.g., Palmer 1994) measuring the effects of display size as feature or contrast thresholds – the difference needed to achieve a given accuracy. These are two different ways of expressing the same accuracy effects, which can be directly related via observer models such as the perceptual template model (see Lu & Dosher, 2008, for a review).

Overall, then, the uncertainty constraints of the search accuracy experiments of Palmer and others are consistent with the asymptotic accuracies of the current and other time-accuracy studies. The current results go beyond the search accuracy literature in providing a consistent account of the temporal properties of visual search, not just the ultimate, asymptotic accuracy levels.

The current results join our earlier results on the time-course of visual search asymmetries (O in C’s) (Dosher, et al., 2001). This difficult search asymmetry also generated large display size effects in standard response time, yet the probabilistic parallel model of visual search gave an excellent account of the time-course of search for brief displays. The current results extend the parallel model from a simple case of feature search to the more complex heterogeneous search conditions.

Thus, parallel processing has been documented in two cases that have classically been associated with serial deployment of covert attention. However, the previous study of McElree and Carrasco (1999), the first to apply cued-response speed-accuracy tradeoff methods to visual search, argued that a pure unlimited capacity parallel model cannot account for the temporal dynamics of conjunction search, and suggested instead that conjunction search invoked a limited-capacity parallel search.

Combining the results of the current study, the results of Dosher et al. (2004), and the results of McElree & Carrasco (1999) could suggest a qualitative difference between difficult search conditions of heterogeneous search and difficult asymmetric search that exhibit parallel search processes on the one hand, and conjunction searches that exhibit some form of capacity limitations on the other hand. The definition of this boundary between purely parallel processes and other forms as involving conjunction search would be complicated under Wolfe’s (Wolfe et. al., 1994) suggestion that some cases of heterogeneous search are implicitly conjunction searches in which the target is the conjunction of being tilted right and having steep (or shallow) tilt. However, the conclusions of McElree and Carrasco (1999) were based on the presence of small but significant slowing in dynamics of conjunction search as assessed in exponential fits rather than a direct fit of an explicit parallel model. We fit the data of McElree & Carrasco (provided by the authors) with the probabilistic parallel and serial search models, and found that, counter to the initial interpretation, the probabilistic parallel search model provided quite a good account of these time course data and asymptotic accuracy data for conjunction search. The fit of the probabilistic parallel search model to the McElree and Carrasco conjunction data is shown in Figure 8.

Figure 8.

Fit of the probabilistic parallel model to the time-course data of McElree and Carrasco (1999), including a feature and conjunction searches. The symbols are observed data points and the smooth curves are best fitting model functions.

This new finding, based on direct fitting of explicit models, considerably simplifies the meta-pattern of results. All cases in which the full time-course of visual search has been measured, for brief visual displays that eliminate eye movements, are consistent with parallel processing architectures, although the difficult conditions may yield low accuracies. We are not claiming that all difficult visual searches will exhibit unlimited-capacity parallel processing, although we have yet to find a documented case of clear serial processing using time-course analysis. There may however be some cases in future investigations that do show covert serial processes.

These time-course results and the probabilistic parallel and serial models (Dosher, et al., 2004) are closely related to the modeling development and observations of Thornton and Gilden’s (2007) in a multi-target search paradigm. Their analysis used four-location search, varied the number of targets, and examined the response time and error patterns of search within the context of an unlimited capacity parallel processing model. This model simulated the various outcomes based on independent parallel accumulation of evidence to a criterion for each display element, and is essentially equivalent to the probabilistic parallel model with the distribution of element comparison times (Dosher, Han & Lu, 2004). The analysis of the multi-target paradigm also led Thornton and Gilden to conclude that a wide range of difficult search tasks were consistent with parallel search. The multi-target data, together with the time-course investigations, provide converging evidence for the widespread explanatory adequacy of parallel processes in visual analysis. This is also generally consistent with recent analyses of increasing d′ per unit second of response time estimated for near-isoluminant color visual searches (Santhi & Reeves, 2004).

Models that routinely incorporate attention-demanding serial processing architectures face challenges in accounting for the visual search data in time-limited displays. This includes the feature integration model (Treisman, 1993; Treisman & Gelade, 1980; Treisman & Gormican, 1988), selective search models (Dosher, 1999; Egeth, Virzi, & Garbart, 1984) and guided search models (Cave & Wolfe, 1990; Wolfe, 1994, 1996). Each of these models ascribes effects of display size on reaction time to the serial deployment of covert attention over the display in free viewing conditions. The feature integration model (Treisman & Gelade, 1980) assumes serial search over the display elements, or groups of elements, and is directly tested with the probabilistic serial search model here. Selective search models (Dosher, 1999; Egeth, Virzi, & Garbart, 1984) restrict serial searches to particular subsets of stimuli (e.g., the red items). The guided search models (Wolfe, 1994, 1996) also serially search selected subsets of stimuli, in this case defined by a more complex salience ordering. Finally, recursive rejection models (Humphreys and Muller, 1993) would require elaboration or modification to account for full time course data. In short, a number of models of covert attention, especially those involving serial search operations, appear to be simply inconsistent with the time course results, and others would require elaboration and further evaluation.

Visual search models are often applied to the response times and accuracies of free-viewing search paradigms, yet make claims about covert attention processes. A comparison of the search reaction times in freely viewed displays and those in time-limited displays leads us to believe that eye movements must play a considerable role in the former (e.g., Geisler & Chou, 1995; Motter & Belky, 1998). The current analysis of the temporal properties of search in time-limited displays suggests that processing within a single episode of information acquisition is parallel, at least for the clear (unmasked) displays used in these studies.

This conclusion is consistent with all the data on time-course of visual search, with the data in a multiple-target paradigm, and it is also consistent with recent proposed models of eye movements during search for small targets in cluttered fields (Najeminik & Geisler, 2005). These models are based on an assumption of parallel uptake of information across the visual field, modulated by eccentricity, and compute a region that is expected to yield the most new information as the location of the next eye fixation. The eye movement system works together with visual processing of the information available over the visual field.

Conclusions

Covert attention is deployed in parallel over the items in the visual field in heterogeneous searches studied here, in asymmetry searches (Dosher, et al., 2004), and in conjunction search (McElree & Carrasco, 1999). A probabilistic parallel search model (Dosher, et al., 2004) provided an excellent account of the time course and asymptotic accuracy of search in all these cases. The time-course of search for different displays sizes is consistent with the combination of classifications, some of them errors, of all the display items embodied in the probabilistic parallel model. Visual search is information limited, not limited with temporally serial processing within an eye movement. These results converge with an analysis of multiple-target searches (Thornton & Gilden, 2007) and with recent analyses of eye movements in visual search (Najeminik & Geisler, 2005). Some extremely difficult versions of search, or of search within masked or noisy displays (e.g., Dosher & Lu, 2000) may require close scrutiny of the targets and hence serial processes, but whether even such examples would engender serial processes within a single eye fixation or information acquisition episode is an open question.

Appendix A: Models of Visual Search

This appendix presents the equations for probabilistic serial and parallel search models developed by Dosher, Lu, & Han (2001). These model predictions include a single identification accuracy for non-targets. As such, these models are directly applicable to homogeneous search conditions, and are a first-order approximation for heterogeneous search conditions. See Dosher, Han, & Lu (2001) for a more detailed model development.

Figure 1A illustrates a probabilistic serial search model in which each item in a display is searched successively in a random order. The serial model implements a probabilistic weighting rule that incorporates errors – both misses of the target and false alarms to distractor items – and determines both the completion time and accuracy of the search. Observers begin in a neutral information state. A positive information state is entered when an item, correctly or incorrectly, is identified as a target. The negative information state is entered when all items, correctly or incorrectly, are identified as distractors.

Let P_T and P_D be the probability of correctly identifying a target and a distractor, respectively, and N be the display size. Finally, G(t|τ,a), the Gamma distribution with time constant τ and number of stages α (defined later), characterizes the finishing time distributions as a function of time from the onset of the display, t.

For target present displays, the probability of entering the positive information-state (correctly or in error) by time t following display onset is:

$$\begin{array}{l}{P}^{+}(t)=\left[\frac{1}{N}\sum _{m=1}^N{p}_D^{m-1}{p}_{T}G(t\mid \tau ,m)\right]\\ +\left[\frac{1}{N}\sum _{m=2}^N\sum _{k=0}^{m-2}{p}_D^k(1-p_D)G(t\mid \tau ,k+1)\right]\\ +\left[\frac{1}{N}\sum _{m=1}^{N-1}\sum _{k=0}^{N-m-1}{p}_D^{m-1}(1-p_T)p_D^k(1-p_D)G(t\mid \tau ,m+k+1)\right].\end{array}$$

Here, m is an index for the order or position in which the location containing the target is searched, and k is an index for calculating the combinatorics of errors at various positions.

For target present displays, the probability of entering the negative information-state is:

$$P^{-}(t)=P_d^{N-1}(1-p_t)G(t\mid \tau ,N).$$

For target absent displays, the probability of entering the positive information-state is:

$$P^{+}(t)=\sum _{m=1}^N{P}_D^{m-1}(1-p_D)G(t\mid \tau ,m).$$

where m is the first process where a distractor is incorrectly identified as a target.

For target absent displays, the probability of entering the negative information state is:

$$P^{-}(t)=p_d^{N}G(t\mid \tau ,N).$$

Figure 1C illustrates a probabilistic parallel search model in which each item in a display is searched in parallel, beginning at the same time but with independent finishing times drawn from a distribution G(t|τ,a). P_T and P_D are the probabilities of correct target and distractor identification. This is a parallel model with unlimited-capacity dynamics, in that the speed of processing individual items does not depend upon the number of elements in the display.

For the target present displays, the probability of entering a positive information state is:

$$\begin{array}{l}{P}^{+}(t)=\sum _{m=0}^{N-1}\left[\frac{(N-1)!}{m!(N-m-1)!}{p}_T{p}_D^{N-m-1}{(1-p_D)}^m(1-{(1-G(t\mid \tau ,\alpha ))}^{m+1})\right]\\ +\sum _{m=1}^{N-1}\left[\frac{(N-1)!}{m!(N-m-1)!}(1-p_T)p_D^{N-m-1}{(1-p_D)}^m(1-{(1-G(t\mid \tau ,\alpha ))}^m)\right].\end{array}$$

where m is the number of distractors that are misidentified as targets and the weighting factors reflect the combinatorics on the completion order of those processes.

For the target present displays, the probability of entering a negative information state is:

$$P^{-}(t)=(1-p_T)p_D^{N-1}G{(t\mid \tau ,\alpha )}^N.$$

For target absent displays, the probability of entering a positive information state is:

$$P^{+}(t)=\sum _{m=1}^N\frac{N!}{m!(N-m)!}{p}_D^{N-m}{(1-p_D)}^m(1-{(1-G(t\mid \tau ,\alpha ))}^m).$$

For target absent displays, the probability of entering a negative information state is:

$$P^{-}(t)=p_D^{N}G{(t\mid \tau ,\alpha )}^N.$$

For both parallel and serial models, the probabilities of yes and no responses is used to calculate a composite (overall) d′ performance accuracy. The probability of “yes” and “no” responses is calculated by assuming that the observers say “yes” when in the positive information state, say “no” when in the negative information state, and otherwise guess with probability g:

$$P_{\mathit{yes}}(t)=P^{+}(t)+g(1-P^{+}(t)-P^{-}(t)),$$

and

$$P_{no}(t)=P^{-}(t)+(1-g)(1-P^{-}(t)-P^{-}(t)).$$

A predicted measure of bias-fee accuracy, d′ for the model is derived from the predicted hit and false alarm rates as a function of processing time, d′ = Z(P_yes) − Z(1 − P_no).

The cumulative density function of the gamma distribution, G(t|τ,a), in the time-course equations is:

$$P(T<t)=\frac{{\tau }^{\alpha }}{(\alpha -1)!}\underset{0}{\overset{t}{\int }}{e}^{-\tau t^{\prime }}{t^{\prime }}^{\alpha -1}{dt}^{\prime },t>0;\text{else}0.$$

(This may be generalized to include a shift by a base time δ.)