Lung Parenchymal Mechanics

Abstract

The lung parenchyma comprises a large number of thin-walled alveoli, forming an enormous surface area, which serves to maintain proper gas exchange. The alveoli are held open by the transpulmonary pressure, or prestress, which is balanced by tissues forces and alveolar surface film forces. Gas exchange efficiency is thus inextricably linked to three fundamental features of the lung: parenchymal architecture, prestress, and the mechanical properties of the parenchyma. The prestress is a key determinant of lung deformability that influences many phenomena including local ventilation, regional blood flow, tissue stiffness, smooth muscle contractility, and alveolar stability. The main pathway for stress transmission is through the extracellular matrix. Thus, the mechanical properties of the matrix play a key role both in lung function and biology. These mechanical properties in turn are determined by the constituents of the tissue, including elastin, collagen, and proteoglycans. In addition, the macroscopic mechanical properties are also influenced by the surface tension and, to some extent, the contractile state of the adherent cells. This article focuses on the biomechanical properties of the main constituents of the parenchyma in the presence of prestress and how these properties define normal function or change in disease. An integrated view of lung mechanics is presented and the utility of parenchymal mechanics at the bedside as well as its possible future role in lung physiology and medicine are discussed.

Introduction

The lung is an organ with complex internal structure that evolved to serve the gas exchange needs of the organism. For efficient gas exchange, the internal surface area should be maximized, while the distance traveled by O₂ and CO₂ between alveolar air and capillary blood should be minimized (274, 275). Furthermore, the functional needs of an organism also require a significant reserve capacity of the lung and hence a large surface area for gas exchange. These constraints, together with the shape of the thorax, place severe limitations on the internal structure of the lung. First, the gas exchanging regions need to be connected with the airway opening that defines the airway structure. Second, for efficient overall gas exchange, different regions should be supplied uniformly with fresh air (135). The three-dimensional structure that can satisfy such constraints is a fractal branching tree (136). The terminal branches of the tree supply air to the acinus that is composed of thousands of alveoli where the actual gas exchange occurs via diffusion (215). The thickness of the septal walls is only 4 to 5 μm and the diameter of the alveoli in the human lung at total lung capacity (TLC) is approximately 200 μm. The parenchymal structure is thus a huge collection of tiny and fine balloons that pack an enormous surface area (close to that of a tennis court) into the chest cavity (275).

Gas exchange in the lung is maintained via the rhythmic process of inspiration and expiration. The acini are connected to the airway opening and consequently, the pressure in the alveoli is near atmospheric most of the time. Since the thin-walled compliant alveoli easily collapse, they must be held open by a positive transmural pressure. This pressure, called transpulmonary pressure (P_tp), is generated by a negative pressure around the lung in the thoracic cavity. Because of the mechanical connectedness of the lung parenchyma, the distending action of P_tp produces a tensile stress, or prestress, throughout the parenchyma. The extent to which the alveoli become distended by the cyclic variation of prestress during breathing depends upon the mechanical properties of the parenchyma. Thus, the efficiency of gas exchange is inextricably linked to three fundamental features of the lung: the structural organization of the parenchyma, the mechanical properties of its components, and the prestress.

There are several important consequences of the fact that the parenchyma is prestressed. First, the mechanical forces generated by the prestress will ultimately be transmitted to pulmonary cells that adhere to the parenchymal tissue, affecting thereby many essential cell functions and hence general lung biology (76, 264). Second, the prestress also contributes to lung deformability itself, which influences a host of other macroscopic and microscopic processes such as local ventilation, regional blood flow, smooth muscle contractility, surface tension, fluid balance, and alveolar stability (234). The main pathway of stress transmission is, however, through the extra-cellular matrix (ECM). Thus, the mechanical properties of the ECM also play a key role both in lung function and biology. These mechanical properties in turn are determined by the constituents of the tissue including elastin, collagen and the “ground substance” composed mostly of proteoglycans (252). In addition to the prestress and the ECM, the macroscopic mechanical properties are also influenced by adherent cells, the surface tension of the air-liquid interface and the organization of the parenchyma. The field of biomechanics attempts to uncover how the elementary properties of biological constituents and their organization determine the specific microscopic and macroscopic properties of an organ or tissue (80).

This article focuses on the biomechanical and structural properties of the lung parenchyma in the presence of prestress and how these properties define function in the normal and diseased lung. First, we present a brief review of the biomechanics of soft tissues. Next, we summarize the constituents of the connective tissue of the lung and their structural organization. We will then describe how the mechanical properties of the parenchyma at the macroscale arise from the properties of its constituents that include fibers, ground substance, surface film and cells, as well as their structural organization. In places where there is a lack of experimental data on specific ECM properties of the lung, we will use results from other tissues or organs. The importance of prestress is highlighted throughout. Next, we examine how the most important load-bearing elements of the parenchyma transmit the prestress down to the level of cells since these stresses are critical in determining the homeostasis and cellular responses to lung injury. We also discuss lung stability since it is an important determinant of normal gas exchange. Finally, we provide an integrated view on lung mechanics and speculate on the utility of parenchymal mechanics at the bedside as well as on its possible future role in lung physiology and pulmonary medicine.

Biomechanics of Soft Tissues

Biomechanics can be defined as the application of the principles of mechanics to biology and physiology. According to Fung (80), “Biomechanics aims to explain the mechanics of life and living. From molecules to organisms, everything must obey the laws of mechanics.” Beyond its power to explain the mechanical behavior of the living, biomechanics is now recognized to be part of mechanobiology (192, 264) in that the mechanical properties of biological tissues, also called biomechanical properties, play fundamental roles in the normal functioning of virtually all connective tissues, organs, and organisms. Indeed, these biomechanical properties are critical determinants of how mechanical interactions of the body with the environment produce physical forces at the cellular level. Mechanobiology is particularly relevant for the lung since it is an open system cyclically stretched by external forces generated by the respiratory muscles (76, 252, 264).

In the lung, mechanical forces can directly influence physiological function via cellular signaling (283) such as during lung development (260), surfactant release by alveolar epithelial cells (282), contraction of airway smooth muscle cells (74) and tissue remodeling (144). It is now well recognized that mechanical interactions between cells and the ECM have major regulatory effects on cellular physiology and cell-cycle kinetics, which can lead to the reorganization and remodeling of the ECM (30, 43). This in turn influences the macroscopic biomechanical properties and hence the functioning of the lung.

Linear Elastic Behavior

Traditional biomechanics (80) has focused on characterizing the macroscopic structural and mechanical properties of living tissues and organs by establishing mathematical relations, called the constitutive equations, that describe how mechanical stresses (force per unit area) change in response to a change in the size and/or shape of a body usually given in terms of strain (relative change in dimension). The simplest constitutive equation is Hooke's law that relates a small uniaxial length change to the corresponding stress (σ) in the material via the following equation:

$$\sigma =Y\epsilon$$ (1)

where Y is the Young's modulus of elasticity. Here the strain ε is defined as the relative change in length, ε = (l − l₀)/l₀ with l and l₀ being the deformed and resting length, respectively, and the stress is equal to the stretching force F applied to the material divided by the initial cross-section A₀, σ = F/A₀. Equation 1 describes a static linear relationship between stress and strain in simple uniaxial elongation that has often been used in parenchymal tissue strip experiments (3, 21, 31, 65, 67, 69, 73, 122, 129, 154, 172, 177, 182, 208, 213, 256, 286). Note that Eq. 1 presumes that prior to the application of F, the material is stress-free. However, many biological tissues, including lungs, are not stress-free but rather are prestressed and their elastic properties depend on the level of the prestress, as discussed in the next section.

The mechanical properties of an ideal isotropic linearly elastic material, are completely characterized by two elastic moduli. One of them can be Y and the other can be one of the following: the shear modulus, the Poisson's ratio or the bulk modulus. The shear modulus (μ) describes the material's ability to resist shape distortion without volume changes, and is defined as the ratio of the shear stress (shear force divided by the area it applies to) and the corresponding shear strain. During uniaxial stretch of a tissue strip, the lateral dimensions of the strip decrease. This decrease can be characterized by the Poisson's ratio that is defined as the negative ratio of the strains perpendicular and parallel to the elongation. Finally, the bulk modulus (κ) measures the resistance of the material to uniform volume change and is given by the change in pressure divided by the relative change in volume of the sample.

The various moduli are a function of the constituents and their organization in the material tested. For parenchymal tissue strips measured in tissue bath, Y depends on the elastin, collagen, and proteoglycan content of the strip (3, 31, 45, 64, 67, 69, 177, 255, 287), alveolar diameters (31), anatomic makeup (214), tonicity of the bath (45, 172), to some extent cellular contractile state (65, 73, 182, 286), and even genetic make-up (8). As we shall see below, small mechanical strains can be superimposed on a prestressed state; hence the moduli can also depend on the prestress. These dependencies will be discussed later in the article.

Nonlinear elastic behavior

While the simple linear constitutive equation of Eq. 1 can be useful in various applications particularly when the modulus can be related to composition and microstructure, in reality constitutive equations of biological materials are invariably nonlinear within the physiological ranges of stress and strain (80). Figure 1A shows the stress-strain curves of lung parenchymal tissue strips from a normal rat and one that had been treated with elastase that causes functional changes in the lung akin to pulmonary emphysema (138). It can be seen that with increasing strain, the relationship deviates from linearity, especially in the normal lung; the slope dσ/dε increases with increasing ε, which is called strain-hardening. Clearly, Eq. 1 is not applicable to describe such a behavior. However, for small variations around a given strain, Eq. 1 can still be a useful descriptor and Y becomes the incremental modulus of the tissue that is a function of the operating point around which the slope of the curve is evaluated. To illustrate this, consider a general nonlinear elastic constitutive equation:

$$\sigma =f\left(\epsilon \right)$$ (2)

where f is a nonlinear continuous function of its argument that often takes an exponential form (242). It is useful to approximate f with a series expansion around a given operating strain, ε₀:

$$\sigma =f\left({\epsilon }_0\right)+f^{\prime }\left({\epsilon }_0\right)(\epsilon -{\epsilon }_0)+(1∕)f^{″}\left({\epsilon }_0\right){(\epsilon -{\epsilon }_0)}^2+\dots$$ (3)

Figure 1.

(A) Stress-strain curves of parenchymal tissue strips from a normal rat and a rat that had been treated with elastase-mimicking pulmonary emphysema. (B) Pressure-volume curves measured by injecting 2 ml of air starting from functional residual capacity in a normal and an elastase-treated rat. Adapted from Ref. (138) with permission.

Here f′ (ε₀) and f″(ε₀) are the first and second derivatives of f, respectively, evaluated at ε₀. The first term on the right-hand side of Eq. 3, σ₀ = f(ε₀), represents the prestress. It is thus evident that for small deviations of ε from ε₀, the higher order terms become negligible and the stress around the operating point, σ* = σ − σ₀, becomes a linear function of the strain ε* = ε − ε₀. Thus, we obtain σ* = f′ (ε₀)ε* which is analogous to the linear stress-strain relation in Eq. 1. The main difference is that f′ (ε₀) now represents the incremental modulus of the material that depends on the operating strain ε₀. By inverting the relation σ0 = f (ε₀), that is, ε = f⁻¹ (σ₀), the incremental modulus can also be obtained in terms of the prestress σ₀.

For isotropic inflation of the lung, a nonlinear constitutive equation similar to Eq. 3 is obtained by replacing σ and ε with P_tp and the fractional change in lung volume, respectively. In isolated lungs, P_tp = 0 cmH₂O corresponds to zero gas volume in the lung, whereas in situ, it is more convenient to choose residual volume (RV) as the reference lung volume. The operating point in lung mechanics is often chosen to be a specific value of P_tp that can be experimentally set by the positive end-expiratory pressure (PEEP) that is superimposed on the functional residual capacity (FRC). Figure 1B compares the pressure-volume (P-V) curves of a normal and an emphysematous lung with inflation starting from FRC as the operating point (138). In this case, PEEP 0 cmH₂O and both P and V are taken to be zero at FRC. Consequently, the first term on the right-hand side of Eq. 3 now corresponds to P_tp at FRC and f′ in the second term is the incremental bulk modulus that can be related to the more familiar static lung elastance (E_L,S) as the bulk modulus normalized by absolute lung volume. The value of E_L,S can be determined simply as the change in P_tp divided by the volume slowly injected into the lung. It can be seen from Figure 1 that emphysema reduces the ability of the lung parenchyma to resist stretching both at the tissue strip level during uniaxial strain (Fig. 1A) as well as in the whole lung during isotropic three-dimensional expansion (Fig. 1B).

Viscoelasticity

When the constitutive equation includes at least one term that depends on the rate of change of deformation or the rate of change of stress, the tissue is referred to as viscoelastic. All living tissues display viscoelastic behavior (80), which is characterized by time- and frequency-dependent behavior of the material responses. Unlike elastic materials, which attain equilibrium instantaneously following the application of external loading, in viscoelastic materials this process is delayed and impeded by internal viscous stresses. Consequently, viscoelastic materials exhibit creep (i.e., continuous deformation in response to a constant stress) and stress adaptation (i.e., continuous change in stress in response to a constant strain). During cyclic loading, a phase lag develops between stress and strain due to the impeding effects of viscous forces that in turn leads to hysteresis between the loading and unloading limbs of the stress-strain curve.

One approach to mathematically deal with systems that exhibit hysteretic behavior is to define a separate elastic-like stress-strain relation for the loading and unloading limbs of the hysteresis loop (80). A more general description of nonlinear viscoelastic materials is given by a functional series expansion of the output (stress or pressure) in terms of the time history of the input (strain or volume) (246). In the frequency domain, the Fourier transform of the output P is related to the Fourier transform of the input V via a series expansion involving convolutions (246):

$$P\left(\omega \right)=E_1\left(\omega \right)V\left(\omega \right)+\int E_2(\omega ,\omega -{\omega }^{\prime })V\left(\omega \right)V(\omega -{\omega }^{\prime })d{\omega }^{\prime }+\dots$$ (4)

Here ω is the circular frequency, E₁ is the first order kernel and E₂, … are the higher order kernels incorporating nonlinear viscoelastic effects. In general, these kernels are complex numbers and depend on ω. The expansion in Eq. 4 is not valid if the system displays static hysteresis or discontinuities. For simplicity, we will assume that the kernels are smooth functions of ω, which allows us to linearize Eq. 4 around an operating point. If P denotes the pressure measured above a given PEEP and V is the corresponding change in lung volume, then E₁ is the complex modulus of the lung. The linear impedance Z of the lung is defined as the pressure divided by the flow and is given by Z = E₁/(jω) where j √−1 is the imaginary unit indicative of the out-of-phase behavior between pressure and flow.

Lung tissue was recognized to be viscoelastic as early as 1939 by Bayliss and Robertson (22) and later by Mount (179) in 1955. Subsequently, Hildebrandt and co-workers demonstrated in a series of studies (102–104,108,109, 244) that the frictional component of stress in the lung tissue depends on the amount but not the rate of expansion, a finding that appears to contradict the notion that frictional losses are caused by viscous dissipation. Importantly, the relationship between the frictional and elastic stresses in the lung tissue turns out to be nearly invariant; the frictional stress is invariably between 10% and 20% of the elastic stress. The ratio of viscous and elastic stresses is referred to as the structural damping coefficient, or “hysteresivity” (77). This fixed relationship holds at the level of the whole lung (100), isolated lung parenchymal tissue strips (73), isolated smooth muscle strips (75), and even isolated living cells (68). The coupling between frictional and elastic stresses is known in the structural mechanics literature as the structural damping law (55), whereas in the physiological literature it is often referred to as the constant phase model (100), which is described below. The structural damping law is an empirical relation which implies that frictional energy loss and elastic energy storage are tightly coupled (77). In the context of linear viscoelasticity theory, it simply means that viscoelastic responses are characterized by a broad spectrum of time constants (80, 248).

If we limit the analysis to the lung tissues, the bulk mechanical properties of the parenchyma can be well described by the so-called constant phase model of tissue impedance (Z_ti) proposed by Hantos et al. (100,101):

$${\mathrm{Z}}_{\text{ti}}=(G-jH)∕{\omega }^{\alpha }$$ (5)

The parameters G and H are the coefficients of tissue damping and elastance, respectively, and being incremental moduli, they depend on the operating point defined either by the PEEP or lung volume. The parameter α is a dependent quantity, given by 2/π) tan⁻¹(H/G). It is noteworthy that this model also provides a good description of tissue behavior at the tissue strip level during cyclic uniaxial deformation (286). Both in tissue strips and whole lungs, the first term in Eq. 5, R_ti = G/ω^α , is the tissue resistance and the second written as E_ti = Hω^{1 − α} is the dynamic lung tissue elastance. The power-law dependence of R_ti and E_ti on ω is consistent with a power-law type of stress relaxation of the tissue that is detailed in the article “Complexity and emergence in Comprehensive Physiology.” Furthermore, as indicated above, the constant phase model is closely related to the structural damping law; the tissue hysteresivity can be obtained from Eq. 5 simply as η = G/H which shows that the phase angle of Z_ti is independent of frequency and consequently, the dissipative portion of Z_ti is a constant fraction of its elastic portion. Experimental studies confirm these model predictions and show that viscosity changes very little with frequency and tidal volume in whole lungs or tissue strips indicating that damping and elastic stresses are tightly coupled (17, 77, 177, 182, 287). However, several more recent studies indicated that at higher PEEP levels viscosity decreases possibly due to the increased contribution of collagen (31, 229) and that subtle changes in the coupling between viscous and elastic stresses reflect biological remodeling of the ECM of the parenchyma (3, 31, 64, 67, 69, 128, 197).

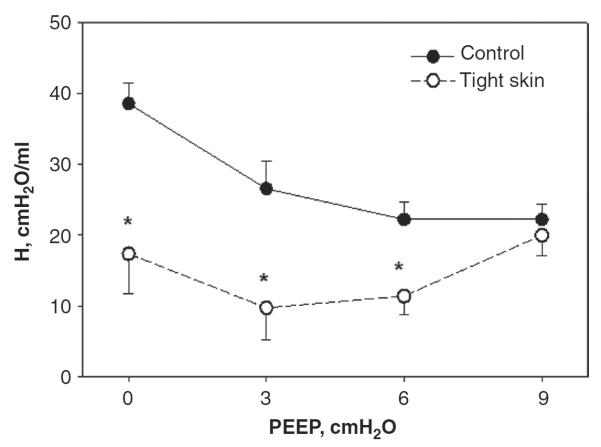
Numerous studies have evaluated the PEEP dependence of E_ti or H and G in a variety of conditions including emphysema (31, 124, 126, 127), fibrosis (64, 181), and adult respiratory distress syndrome (ARDS) (5, 132, 141, 258). Such linear analyses around an operating point can be useful since the way E_ti and H depend on PEEP carries information about the underlying pathology. For example, in anesthetized animals, lung volume decreases significantly in the supine position. Consequently, alveoli become unstable and collapse, a phenomenon that will be discussed later. Therefore, in healthy anesthetized animals H decreases when PEEP is increased from 0 to about 6 cmH₂O due to alveolar recruitment in several species (94) including mice (99, 127, 128). Beyond a PEEP of about 10 cmH₂O, H increases with PEEP due to the dominating contribution of stiff collagen. However, in various mouse models of emphysema such as the tight skin mouse (126), the rate of increase of H with PEEP is much stronger than in normal mice. Indeed, despite the much lower H in the tight skin than in the normal mice at low PEEP, H is similar in magnitude at a PEEP of 9 cmH₂O in the two groups (Fig. 2), implying abnormal ECM organization and collagen function in the tight skin mouse (126).

Figure 2.

Mean and SD of dynamic lung elastance coefficient (H) as a function of positive end-expiratory pressure (PEEP) in groups of normal and tight skin mice. *denotes significance. Adapted from Ref. (126) with permission.

Although the incremental analysis discussed above is useful, the full nonlinear dynamic stress-strain curve or P-V relation carries more information about the structure and composition of the parenchyma than the incremental modulus. Indeed, the incremental analysis is limited to mapping the values of the moduli as a function of the operating point and neglects all higher order components. While powerful, such nonlinear analysis is complicated and only a few studies have applied it to the lung (155, 157, 246, 250, 288). Nevertheless, the natural way the lung functions is similar to the incremental analysis since breathing involves relatively small amplitude tidal oscillations superimposed on an operating point, P_tp at FRC. Furthermore, some information about the nonlinearity can be extracted from forced oscillatory data when breathing amplitudes are employed (289). In this case, nonlinear distortion of the waveforms can be analyzed which can provide information on collagen function (126, 128).

The precise link between the viscoelastic behavior of the lung tissue and its microstructure is still poorly understood, although various theories have been proposed. For example, stress relaxation may occur through cascades of microruptures within the tissue (18) or as a result of slow undulation of fibers (248) or fiber-fiber kinetic interaction (173). In any case, the constitutive equations are commonly determined from measured dynamic stress-strain or P-V curves. These relations generally reflect behavior that emerges from the mechanical properties of the individual constituents as well as their structural arrangement in the tissue. This article focuses mostly on the elastic behavior of the lung tissue. Viscoelasticity will be treated only briefly and mostly for the purposes of identifying the roles or the changes in the roles of certain components of the tissue following a given intervention or disease condition. Some possible mechanistic insight into the viscoelastic behavior of the ECM of the normal lung tissue is presented in the article on “Complexity and Emergence,” whereas the rheological behavior of cells is treated in the “Material Properties of the Cytoskeleton” article in Comprehensive Physiology.

Structure-function relations

One of the primary goals of biomechanics is to develop quantitative relationships between the biochemical composition and microstructure of the tissue and its functional properties, usually characterized by the constitutive equation. For example, functional properties can be given by the elastic modulus such as Y at the tissue strip level or lung elastance at the organ level. The dependence of the functionality on the composition and microstructure is called the structure-function relation. Quantitative understanding of structure-function relations in the normal lung can help identify structural defects from noninvasive functional measurements at the organ level in diseases. To develop such structure-function relations, it is necessary to determine the bulk composition of the tissue and to gain understanding of the structure and interaction of the components.

Generally, connective tissues are composed of cells and ECM that includes water and a variety of biological macromolecules. The macromolecules that are most important in determining the mechanical properties of these tissues are collagen, elastin, and proteoglycans. Among these macromolecules, the most abundant and perhaps the most critical for structural integrity is collagen. One might expect therefore that the amount of collagen in a tissue is the primary determinant of its mechanical properties. However, different connective tissues with similar collagen content can exhibit different viscoelastic behavior (80). During the last decade, the advent of novel imaging techniques (54) and quantitative computational modeling (205) have allowed the study of micromechanics of specific components of tissues and hence improved our understanding of the relationships between tissue composition, microstructure, and macrophysiology. In particular, it has become evident that macrophysiology reflects both the mechanical properties of the individual components of the tissues, as well as the complexity of its structure (19, 252). Consequently, an understanding of lung parenchymal mechanics and function requires the integration of the physical properties of the constituent molecules with their organization into fibrils, fibers, ground substance, and cells. The next section provides an overview of the most important components of the ECM of the lung and other determinants of lung mechanical function including interstitial cells and surfactant.

Main Constituents of the Parenchyma

The lung parenchyma consists of a large collection of near spherical gas exchanging units, the alveoli. The internal surface of the alveoli is lined by a layer of cells, the epithelium, which is covered by a thin liquid film. There is a surface tension at the air-liquid interface that contributes to lung elastic recoil. The alveolar septal walls are composed of interstitial cells and the ECM. Cells can modulate the local tension on the ECM. Alternatively, mechanical forces of breathing are transmitted to the cells via the ECM fibrils and fibers such as collagen and elastin that are embedded in a soft gel called the proteoglycan matrix. Figure 3 depicts the general organization of the parenchyma from the scale of tens of alveoli surrounding an alveolar duct to cell-ECM interactions within the septal wall. Below, we describe in detail the structure and basic mechanical properties of the constituents of the alveolar wall tissue.

Figure 3.

Structure and complexity of the parenchyma at three length scales. The top panel shows a terminal bronchiole (TB) leading to an alveolar duct (AD). The bottom left is a zoom into a single air-filled alveolus (A) with type I (E1) and type II (E2) alveolar epithelial cells covered by a thin liquid layer. The dots represent surfactant (S) molecules at the air-liquid interface. Secretion of lamellar bodies (LB) by the E2 cell is also shown. The right panel is a schematic representation of the extracellular matrix of the alveolar septal wall with various components including amorphous elastin (El), wavy collagen (C), complex proteoglycans (PG), basement membrane (BM) and fibroblast cells (F). (Drawing by E. Bartolák-Suki).

Extracellular matrix

The collagen system

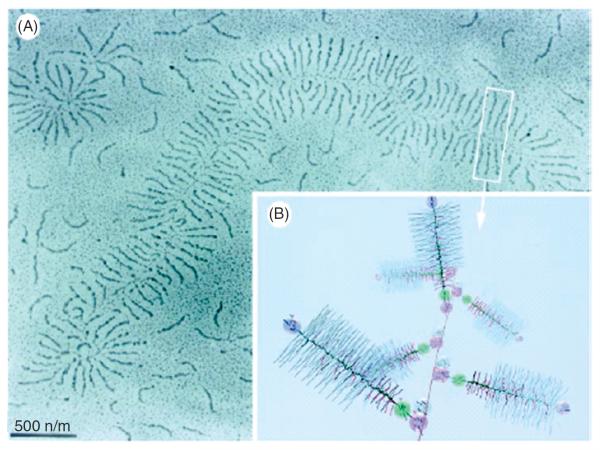
There are nearly 30 different types of collagen molecule. Most interstitial collagens (I, II, III, V, and XI) are helical that provides them with a basic structure supporting role. The helices consist of three polypeptide chains each of which is a left-handed coil of approximately 1000 amino acids, with the three chains forming a right-handed super helix (34). These helical molecules are rod-like rigid structures with length and diameter of about 300 nm and 1.5 nm, respectively, and capable of spontaneous fibril forming (226). The helical subunits are first assembled in the endoplasmic reticulum of the cell in precursor forms called procollagens that have amino and carboxyl terminal globular regions known as propeptides. These serve to solubilize the procollagen, and correctly align the individual peptide chains to facilitate helix formation (226). Following secretion, the propeptides are enzymatically cleaved, which allows the collagen molecules to associate both axially and laterally and start forming fibrils. Apparently, type I collagen is thermally unstable at body temperature and folding of the least stable microdomains can trigger self-assembly of fibrils where the helices are protected from complete unfolding (146). The fibril structure itself also shows tremendous hierarchical complexity. For example, the lateral packing of molecules can exhibit significant fluid-like disorder (106, 117). The collagen fibrils can further organize into thicker fibers through cross-linking of lysine and hydroxylysine residues present within the overlapping terminal helical and teleopeptide regions of the molecules (226). Figure 4A summarizes the hierarchical complexity of the collagen system. These fibrils and fibers may be arranged either in a randomly oriented manner (e.g., in lung tissue or cartilage) or as quasi-deterministic networks (e.g., in tendon) within an organ. In the lung, the collagen fibers are wavy at low inflation and become straight at higher lung volumes (Fig. 4B).

Figure 4.

(A) Structure of collagen. Top left: single alpha helix; bottom left: collagen molecule comprising a triple helix; top right: cross-linked collagen; bottom right: schematic view of 5 molecules; with permission from Ref. (117). (B) Collagen network in the rat lung is wavy at low transpulmonary pressure (left) and at a medium inflation level (right). AE denotes alveolar entrance. Scale bar is 10 μm. Adapted from Ref. (261) with permission.

The interstitium of the lung parenchyma contains mostly types I and III collagen that provide the structural framework for the alveolar wall. Fiber thickness ranges from several hundred nanometers to well over a micron (232). The distribution of fiber thickness is skewed, and has a long “tail” (232) similar to a power law (245), indicating broad variability of fiber structure. This blend of deterministic order (exact amino sequence and axial packing) and random disorder (from fluid-like lateral packing to random networks) may partly be responsible for the existence of a broad range of time constants that characterizes the viscoelastic properties of the connective tissue of the lung (21, 248). These collagen fibers in the parenchyma are further organized to form an axial fiber network extending down from the central airways to the alveolar ducts, a peripheral fiber network extending centrally from the visceral pleura, and a parenchymal interstitium that connects the two (273). Variations in the collagen content of the parenchyma during development (255, 256), in fibrosis (64) or following in vitro digestion (287) have suggested an important role for these protein fibers in the biomechanical properties of the parenchyma. In addition to the fibrillar types I and III collagen, type IV collagen is more sheet like and is part of the basement membrane to which epithelial cells adhere. The role of type IV collagen in the mechanical properties of the ECM of the lung is currently unknown.

The Young's modulus of the type I collagen molecule has been estimated to be between 3 and 9GPa (217, 226). The elasticity of a single collagen molecule has been attributed to the existence of amino acid sequences along the triple helix that lack proline and hydroxyproline (227). These regions are more flexible than other regions of the helix. Such variation of rigid and flexible regions likely has a significant effect on the fibril-forming ability and hence the elasticity of the fibrils. Additionally, the unfolding of thermally activated molecular kinks or “crimps” along the molecule may also contribute to elasticity (175). The stress-strain curve of fibrils appears reasonably linear up to 3% to 5% strain with a modulus in the order of 0.5 to 5 MPa (226).

The elastic fiber system

Elastin is another essential load bearing component of the ECM. Elastin is known for its resilience over a large range of strains, and hence its ability to provide elasticity to tissues. Consequently, tissues and organs that need elasticity because they undergo cyclic stretching throughout the life time of an organism can generally be expected to contain a significant amount of elastin. Elastin is synthesized in a soluble precursor form called tropoelastin with a molecular weight of 72 kDa by smooth muscle cells, endothelial cells, and fibrob-lasts (40, 167, 185). In contrast to collagen, which is rich in hydrophylic amino-acid residues, the amino acid composition of elastin is rich in hydrophobic residues including glycine and proline (211). The hydrophobic residues together with the dense interchain crosslinking make elastin highly stable and insoluble. Tropoelastin is capable of self-assembly under physiological conditions (24) to form insoluble fibrils and fibers with a half-life of 70 years (201). Because heparan sulfate, a glycosaminoglycan (GAG) and an essential component of the proteoglycans, interacts with tropoelastin, it also plays a role in elastic fiber formation (88).

Elastic fibers are composed of elastin and microfibrils. The three most important groups of microfibrils that are closely associated with elastin include fibrillins, fibulins, and the microfibril-associated glyoproteins (56, 206, 211). The microfibrils also play a role in elastogenesis by regulating the deposition of tropoelastin onto the developing elastic fiber (176). The elasticity of microfibrils is controversial and their role in lung elasticity has not been studied. Values of the Young's modulus of microfibrils have been reported to be as low as 0.2 MPa (259), which is about 3 to 5 times lower than the stiffness of elastin (80, 223), and as high as 96 MPa (224), which is closer to that of collagen (80). The microfibrils often form a fibrous outer mantle surrounding the more amorphous elastin. While the 3D molecular structure of elastin fibers is not as well understood (117, 139), elastin organizes itself into easily extensible fibers and has a linear stress-strain relation up to 200% strain (80). The elastin molecules organize themselves into cross-linked fibers. The distributions of the diameters and lengths of elastin fibers in the lung are skewed with long “tails,” and appear similar to the distribution of collagen fiber properties (232). Thus, the elastic fibers exhibit significant structural heterogeneity and are also known to be mechanically connected to the collagen (35) via microfibrils and/or proteoglycans (117, 133, 204).

It is notable that the stiffness of elastin is at least 2 orders of magnitude smaller than that of collagen (80). This is likely a result of the amorphous nature of elastin compared to the more regular organization of collagen fibers. The elastic resistance of elastin is thought to be of entropic origin. Figure 5A shows the stretch-induced conformational changes in elastic fibers. However, this is not simply the entropic elasticity of a random chain. The tropoelastin has two major types of alternating domains, the hydrophilic helical domains and the hydrophobic lysine-rich domains. These nonrandom, regularly repeating structures exhibit dominantly entropic elasticity by means of a damping of internal chain dynamics on extension (266). In the lung, elastin forms a complete network of fibers (Fig. 5B). Traditionally, elastin is thought to dominate parenchymal elasticity at normal breathing lung volumes (221), while collagen becomes progressively more important as volume approaches TLC. However, comparing the effects of elastin and collagen digestion on the constitutive equation of parenchymal strips suggests that collagen and elastin may be equally important even at lower lung volumes (287).

Figure 5.

(A) Longitudinal sections of elastin-rich extracellular matrix sheet stained with acid Orcein at 0% strain (top) and 30% uniaxial strain in the horizontal direction (bottom). Note the straightening and thinning of the elastin fibers with increased strain. The scale bar denotes 10 μm. With permission from Ref. (29). (B) Structure of elastin in the parenchyma. V, AS, and AD denote vessel, alveolar sack, and alveolar duct, respectively. The scale bar is 200 μm. Adapted with permission from Ref. (261).

The proteoglycans

Within the lung, collagen and elastin fibers of the connective tissues are embedded in a hydrated gel, the ground substance. The composition of the matrix and the ratio of fiber to gel vary among tissues (117) and change during maturation and with disease states (131). Critical constituents of this matrix are the GAGs that are long chains of repeating disaccharide units that are variably sulfated and highly charged (117). There are several different types of GAGs (e.g., hyaluronic acid, chondroitin sulfate, heparan sulfate, dermatan sulfate, and keratan sulfate) whose molecular weights vary over three orders of magnitude implying that the polymer chains can contain as many as 10⁴ units with a huge variability in size and structure (36, 220). Within the lung parenchyma, the most abundant GAGs are heparan sulfate and chondroitin sulfate. Except for hyaluronic acid, GAGs covalently attach to a PG core protein via a link tetrasaccharide to form proteoglycans. Similar to collagen, GAGs can also have secondary and tertiary structures by forming helical and randomly organized regions depending on the ionic environment and pH of the matrix (220). Images of the proteoglycans obtained by electron microscopy reveal an extraordinarily complex structure (36, 71). Proteoglycans can also associate ionically with one another to form large aggregates that exhibit an even higher level of hierarchical organization. Usually, the hyaluronic acid forms a long core to which various proteoglycans attach (Fig. 6).

Figure 6.

Proteoglycan structure on a larger scale (A) and at a smaller scale zoom-in (B). Different colors represent various groups; for example, blue is chondroitin sulfate, red is keratan sulfate, pink spheres are hyaluronan-binding sites. From Ref. (209) with permission.

Proteoglycans have a number of important biological roles (41, 209). For example, they can act as receptors on the cell surface and hence influence intracellular signaling (42). Proteoglycans on the cell surface can bind to growth factors and various other proteins and this binding can regulate the secretion of proteins, such as proteolytic enzymes that are involved in cell migration and tissue remodeling (125). Furthermore, the lateral and axial growth of collagen fibrils appears to be, in part, determined through interactions with the proteogly-cans (117,118, 204). Proteoglycans have also been reported to influence elastic fiber assembly (112). Thus, through a variety of indirect mechanisms, proteoglycans can significantly alter lung mechanics. As we shall see below, their elastic behavior can also directly influence the macroscopic stress-strain curve.

The majority of studies on proteoglycan mechanics have been carried out in cartilage. The elastic modulus of the cartilage tissue measured using the indentation atomic force microscopy appears to depend on the size of the probe (241). At the millimeter to micrometer scale, values in the order of 2 MPa were obtained, whereas at the nanometer scale a 100-fold lower modulus similar to that of simple agarose gel was seen. The reason is that at the millimeter scale, the elastic modulus includes contributions from both collagen and proteoglycans and the value is dominated by the properties of the collagen. In contrast, at the nanometer scale individual elements, mostly GAGs, appear to dominate elasticity (241). Little is known about the mechanics of the proteoglycans in the lung. It is likely that their role in lung function has been underestimated. Indeed, only a few studies have examined their role in lung mechanics (3, 45, 84).

Lung cells

The lung parenchyma, prestressed by the P_tp, is a habitat of up to 40 different cell types. The prestress within the parenchymal tissue that is transmitted to the cells through the ECM adhesions influences cellular mechanical responses and mechanotransduction. On the other hand, forces generated within cells directly and indirectly affect the mechanical properties of the parenchyma.

From the point of view of mechanics, the most important cells are the contractile cells. Although recent findings suggest that both epithelial (263) and endothelial (137) cells can also contract, their contractile force is small. The stronger contractile cell types include smooth muscle cells in the alveolar duct and mouth and blood vessel walls and the myofibroblasts and fibroblasts (147). Beside airway and blood vessel walls, the protein α-actin associated with contractile force generation has been found in septal ends and bends but not in septal walls (187). Stimulation of the contractile machinery of these cells with different agonists induces local internal stresses in the fiber network of the ECM that can lead to changes in the viscoelastic properties of the lung tissue (65, 73, 182, 286). However, during contractile challenge, the mechanical properties of excised parenchymal tissue strips have also been found to vary with the number of medium-size airways in the sample (214). Thus, it is possible that part of the previously observed changes in the mechanical response during agonist challenge were in fact related to smooth muscle contraction and airway-parenchymal interaction. Nevertheless, the viscoelastic properties of the lung parenchyma are only moderately affected by the active tone of the interstitial cells (65, 286). A more important function of the interstitial cells is to actively remodel and repair the connective tissue during growth or after injury. For example, transforming growth factor beta (TGF-β), which is the main cytokine that stimulates fibroblasts to produce and secrete ECM molecules, is upregulated by mechanical stretch (97). Tensile forces also regulate the connective tissue growth factor that is able to stimulate ECM protein release through a TGF-β-independent pathway (218). As a result of such cellular processes, the nonlinear viscoelastic properties of the lung tissue can significantly change both at the organ and the alveolar wall levels (31). Thus, while cellular mechanical properties contribute little to the mechanical properties of the parenchyma in response to physical (e.g., deformation) or chemical stimuli (e.g., histamine challenge) over a short time period, they are responsible for the longer term homeostatic maintenance as well as the remodeling of the composition and structure of the ECM. Below we provide a short summary of the mechanical properties of cells and the reader is referred to a more complete account in the “Mechanics of the Cell” section.

Mechanical properties of cells

The cellular response to mechanical perturbation such as the prestress in the lung is governed by the cytoskeleton (CSK), an intracellular molecular network composed of filamentous biopolymers (actin filaments, microtubules, and intermediate filaments) and a number of actin binding and crosslinking proteins. The CSK is the site of the actomyosin contractile machinery that generates mechanical forces through ATP-dependent processes. Furthermore, the CSK also transmits forces across the cytoplasm. Many signaling molecules are immobilized in the CSK network and are very highly sensitive to mechanical deformation. In other words, the deformable cytoskeletal network provides a physical scaffold for mechanotransduction. To understand how mechanical forces regulate cellular function, it is necessary to know how cells develop mechanical stresses as they deform under applied mechanical forces. This mechanical response of the CSK is determined by the passive material properties of the molecules of the CSK, by the contractile forces generated within the CSK and by changes in biochemistry that modify cytoskeletal composition and structure through remodeling. It was found that the actin network has the bulk contribution to cell stiffness (>50%), whereas the contributions of microtubules and intermediate filaments are substantially lower (236, 270, 271). It was also found that measured cell stiffness (0.1–10 kPa) is much lower than the Young's modulus of any of the cytoskeletal filament or stress fibers (16, 68, 70), indicating that the network properties of the CSK play an important role in cell deformability. The roles of cytoskeletal filaments and cytoskeletal architecture on cellular mechanical behaviors are discussed in detail in articles “Stress Transmission within the Cell” and “Material Properties of the Cytoskeleton” in Comprehensive Physiology.

Microrheological measurements on living cells have shown that their mechanical behavior is governed by two major principles: (1) the CSK exists in a state of tension, that is, the prestress, which is critical for stabilizing cell shape and regulating cell rigidity; and (2) cellular rheological behavior is driven by very slow dynamics such that global viscoelastic responses of cells scale with time and frequency of loading according to a weak power law. Various theories have been proposed to explain the experimentally observed mechanical behaviors of cells, but there is a lack of consensus between those theories about the biophysical mechanisms that govern cell mechanical behaviors. Currently, none of those theories can provide a complete description of cellular mechanical responses that include both prestress-dependent and power-law behaviors. These models are discussed in detail in the articles “Stress Transmission within the Cell” and “Material Properties of the Cytoskeleton in Comprehensive Physiology”

Cell-ECM interactions

Force transmission between the CSK and the ECM is not continuous. Forces are transmitted across the cell membrane at discrete sites of focal adhesion composed of integrin receptors with their extracellular domain attached to the ECM and their cytoplasmic domain to a cluster of proteins (α-actinin, paxillin, vinculin, talin, zxyin, etc.) that are physically linked to the cytoskeletal actin (52, 130). Therefore, the mechanical properties of the ECM and the focal adhesions also play an important role in mechanical behaviors of cells. More importantly, these mechanical properties together with biochemical cues influence intracellular signaling that in turn determines the type and amount of remodeling enzymes and load bearing ECM components produced and secreted by interstitial cells (47). Thus, cells maintain the composition and architecture of the ECM of the lung, while the prestress related to P_tp and the local mechanical properties of the ECM are key regulators of essential cellular processes (249). Figure 7 shows a small region of the lung tissue fixed in formalin and immunohistochemically labeled for types I and III collagen as well as cell nuclei. It can be seen that some nuclei appear rounded (green arrow), whereas some appear to be stretched in a direction parallel with the alveolar wall (blue arrow). One may speculate that forces in the wall primarily carried by the collagen at the high fixation pressure were transmitted to the nucleus.

Figure 7.

Double-label immunohistochemistry of mouse lung tissue. The blue labels type I collagen, the brown corresponds to type III collagen, and the pink is cell nucleus. It can be seen that some fibers comprises almost exclusively type I or type III collagen (black arrows), whereas at several locations, the two collagen types also appear to colocalize suggesting that they mix and form composite fibers (red arrow) where the color is intermediate between blue and brown. Green arrow shows a round nucleus, whereas the blue arrow points to an elongated nucleus suggesting that the nucleus is under mechanical tension. From Ref. (249) with permission.

Although the mechanical properties of cells contribute less to the macroscopic mechanical properties of the parenchyma than those of the ECM, there are striking similarities between cellular and parenchymal tissue mechanics. Indeed, the mechanical properties of both cells and the parenchyma are characterized by a weak-power-law viscoelasticity and by strain hardening with increasing levels of the prestress. While these similarities may reflect common biophysical mechanisms that are reiterated at different length scales (76), it is not clear whether they occur by mere chance or have some functional advantages. For example, matching the viscoelastic responses of cells and the parenchyma would ensure that cells and the tissue matrix deform synchronously during breathing. This in turn would facilitate efficient stress transmission from the tissue to adhering cells which is important for mechanotransduction. On the other hand, there are phenotypic differences in alveolar epithelial cell stiffness that likely contribute to the observed heterogeneity of alveolar cell deformation during lung inflation and hence help better understand stretch-induced surfactant release (13).

Surfactant and surface tension

The airways and alveoli are lined with a thin liquid film containing pulmonary surfactant which derives from type II epithelial cells. During volume excursions between FRC and TLC, the P-V curves of air-filled and liquid-filled lungs have remarkably different hysteretic behaviors; on the inflation limb, the recoil pressure is substantially higher in the air- than in the saline-filled lungs, whereas along the deflation limb this difference is much smaller (15, 90, 166, 231, 240, 269). The greater hysteresis in the air-filled lung is attributed to the hysteretic behavior of the alveolar surface film and associated phenomena such as airway opening as discussed later. The specific mechanical behavior of the surface film arises from changes in film composition and from asymmetry in the adsorption-desorption kinetics during the expansion-compression cycle (49, 92, 231). In addition to its direct effects on lung recoil, the surfactant also influences lung macrophysiology by ensuring alveolar stability, and preventing collapse at low lung volume by reducing the surface tension (11). Among the various components of the surfactant, phospholipids, and low-molecular weight hydrophobic surfactant proteins play a critical role in determining its biophysical properties that help maintaining low surface tension (123). The amount and composition of surfactant released by the type II epithelial cells into the air-liquid interface are largely determined by the dynamic stretching pattern of the lung parenchyma (10, 184, 282). Type II cells respond to the proximity of an air-liquid interface by a graded calcium response, which results in lamellar body secretion, implying that the physical environment in the vicinity of cells can initiate a complex biological response which, in turn, modulates the physical environment of the cell via a feedback loop (200).

Pulmonary surfactant must adsorb rapidly to the air-liquid interface to form a surface active film. Recent models suggest that phospholipid adsorption is mediated by pores that bridge the gap between the vesicular bilayer and the air-liquid interface (111). Proposed mechanisms are akin to vesicle-plasma membrane fusion during neurotransmission and are thought to require hydrophobic surfactant proteins to aid in bending of the outer lipid leaflet (212). Moreover, it appears that the adsorption and transformation of lamellar body lipids to the air-liquid interface is surface tension dependent and does not require tubular myelin as intermediary structure (26). Classic models assume that alveolar stability at low lung volumes requires the presence of a highly DPPC (Dipalmitoyl-phosphatidylcholine)-enriched monolayer, implying the “squeeze out” of unsaturated phospholipids during film compression (49). More recent studies combining fluorescence microscopy and atomic force microscopy have invoked the formation of multilayers during film compression, which may act as a surface-associated surfactant reservoir (290).

Surface tension has various effects on lung mechanics. First, surface tension directly contributes to the overall recoil stress of the parenchyma. Second, it distends the alveolar ducts and by distorting duct geometry, it indirectly alters the elastic properties of the associated connective tissues (234, 281). For small deformations, similar to those that occur during normal tidal breathing, the hysteresis of the surface film is negligible and surface film viscoelasticity may be less important than lung tissue viscoelasticity (219). Indeed, tissue hysteresivity, as defined above, was found to be very similar in isolated lungs with an intact air-liquid interface and in lung tissue strips that lack an air-liquid interface (213). While interfacial phenomena may not contribute greatly to energy dissipation during quiet breathing, they do exert a profound effect on lung recoil under conditions when lung expansion is limited by neuromuscular disease, obesity, or chest wall restriction (243). Moreover, the invariable need to call upon the lungs' reserve capacity during activities of daily living and the devastating consequences of impaired surfactant function in disease, underscore its critical role in lung biology as well as lung mechanics. A more detailed review of surface tension and surfactant biology may be found in the articles “Air-liquid interface and Alveolar” surface tension and lung surfactant as well as in the section on alveolar duct mechanics below.

Mechanical Properties of the Normal Lung

In this section, we will overview the elasticity of the normal lung parenchyma at several length scales. We will start with the elasticity of collagen molecules, fibrils, and fibers followed by elastin fibers. We will then examine the elastic behavior of the alveolar wall and how these fibers fold within the ground substance of the wall. The parenchyma is a network of alveolar walls and hence it is also important to understand its network behavior. Next, we present various models of the tissue strip. Even though the tissue strip and the uniaxial stretching condition are not physiological, the tissue strip is a viable preparation and many important physiological and biological questions can be and have been answered at the level of the tissue strip. Finally, we present a comprehensive picture of the mechanics of the entire parenchyma of the normal lung during breathing.

Molecular, fibril, and fiber elasticity

The structure of the lung is largely determined by the connective tissue network. The complex organization and the nonlinear viscoelastic properties of these tissue components lead to complex mechanical behavior. One of the main load-bearing components of the parenchyma is collagen. As discussed above, molecular kinks or crimps contribute to collagen elasticity. Crimps also exist at the fibril and fiber level (226). When thicker fibers in the tissue are stretched, it is the crimps along the fibers that first unfold followed by an unfolding of the crimps in the fibrils (175). Further stretching the fibers results in stretching of the triple helices and the cross-links which also raises the possibility of slipping of molecules and fibrils within the fiber (72). In addition to the elasticity of a single molecule, collagen fiber stiffness may depend on the number of fibrils through a given cross section, that is, the diameter as well as the type of cross-linking between molecules and fibrils. Both increasing diameter and cross-linking tend to increase fiber stiffness in normal collagen (7, 226). Furthermore, fibril length as well as small proteoglycan bridges between fibrils can contribute to the stiffness of collagen fibers (205).

The stress-strain curve of tendon composed of many fibrils arranged in parallel is nonlinear with a toe and a steep region (216, 242). The toe region is usually attributed to the crimps along the fibrils which, upon stretching, become straight (91) (Fig. 8). The composition of the fibrils and fibers is also important because fibers can contain a mixture of different collagen types (see Fig. 7). It has been argued that type I collagen is stiffer than type III (227) implying that fiber stiffness can depend on the relative amounts of type I and type III collagen within the fiber. Furthermore, there are notable species-related differences. A small amount (5–10%) of variation in amino acid composition between bovine and equine collagen can lead to a 2- to 3-fold difference in elastic modulus of in vitro cross-linked collagen gels (7). All these factors can give rise to significant inter- and intra-species variability in the mechanical properties of the alveolar walls. However, as both mechanical and biochemical factors contribute to collagen production and assembly, it is likely that there is a significant regional variability in collagen fiber properties within the lung. For example, even though not studied systematically, it is possible that fiber properties are different near the sharp edges of the lobes, where increased stability is required, compared to regions deeper inside the parenchyma. This variability is in addition to the different fiber content and mechanical properties of alveolar ducts and alveolar walls (60, 168). The former has been argued to be stiffer and hence contribute more to lung elasticity at higher lung volume based on relative volume changes along the P-V curve (170) as well as the larger concentration of fibers in ducts than in septal walls (168).

Figure 8.

Stress-strain curve of collagen in tendon. Nonlinearity characterized by the heel region originates from the crimp (a) unfolding with stretching. From Ref. (72) with permission.

As discussed earlier, elastin is thought to behave as a linearly elastic material. However, thin ECM sheets containing elastin and proteoglycans do exhibit some mild nonlinear behavior during uniaxial stretch (29). The reason for this mechanical behavior is as follows. Elastin fibers in the tissue are not parallel. There is a distribution of angles relative to the direction of macroscopic strain. When the tissue is stretched, elastin fibers change shape and gradually reorient into the direction of macroscopic strain. This is a recruitment-like process in which more and more fibers become aligned with the strain and contribute more to stiffness. Nevertheless, elastin is still significantly softer than collagen and hence in a tissue containing both fiber types, the recruitment of collagen would ultimately dominate macroscopic elasticity. Figure 9 shows the stretch-induced shape change and recruitment of elastin together with the recruitment of collagen toward the direction of macroscopic strain in thin ECM sheets (28).

Figure 9.

Electron microscope images of ECM sheets containing both collagen and elastin at 0% (A) and 30% (B) uniaxial strain. Images were taken at 12,500×. Arrows denote collagen fibers and the white regions are elastin. Scale bar represents 0.5 μm. From Ref. (28) with permission.

Elasticity of the alveolar wall and the tissue strip

The stress-strain curve of individual tissue fibers may become linear once the crimps are unfolded (Fig. 8). However, for larger lung tissue samples that contain many fibers, the stress-strain curve often exhibits exponential-like stiffening (79, 172, 174, 182, 287). During uniaxial stretching, the non-linear stress-strain curve (Eq. 2) of the tissue strip can be written as:

$$\sigma =a\epsilon e^{b_{\epsilon }}$$ (6)

where a is the amplitude of the stress-strain curve and can be related to the incremental elastic modulus near zero strain. Indeed, with ε₀ = 0 it follows from Eqs. (3) and (6) that the first term disappears and we obtain:

$$\sigma =a\epsilon +c{\epsilon }^2+\dots$$ (7)

The parameter c = ab characterizes thus the strength of the nonlinearity which is thought to reflect the progressive recruitment of collagen fibers. In other words, at low strains, most of the stress in the tissue is borne by the relatively compliant elastin fibers and hence a in Eq. (6) would primarily be a function of the volume fraction of elastin. As the applied strain increases, the initially flaccid collagen fibers start to straighten (Fig. 4B), fold into the direction of strain and gradually take up the load-bearing role. As progressively more of the stiff collagen fibers are recruited in this way, the bulk stiffness of the tissue increases commensurately. The parameter c is therefore a function of the volume fraction of both elastin and collagen as well as their ability to fold toward the direction of strain. As we shall see below, the folding and the recruitment of the fibers is related to the third major ECM component, the proteoglycans. Macroscopic tissue stiffness thus arises largely because of the way in which the various constituent fibers are organized with respect to each other, rather than being a reflection of the constitutive properties of any particular fiber type. Maksym and Bates (154) modeled this behavior analytically in terms of a linear chain of pairs of parallel spring and string units. If the springs (representing extensible elastin fibers) are all identical then the overall stress-strain behavior of the model is determined by the length distribution of the strings (representing inextensible collagen fibers). Alternatively, the model can be constructed using strings of equal length and springs with distributed stiffness. They found that the exponential nonlinearity in Eq. (6) could be explained by a power-law distribution of collagen fiber properties, which is compatible with morphometric assessment of collagen in the lung (168, 232).

Maksym et al. (156) also extended their model into two dimensions by using a triangular network of line elements each containing a parallel combination of a crimped collagen fiber and an elastin fiber. The force-transmission through such a model displays an interesting heterogeneous spatial distribution similar to the phenomenon known as percolation suggesting a complex network behavior (see article “Complexity and Emergence” in Comprehensive Physiology). When the microstrain in a material follows the macrostrain, the deformation is called affine. This is the case in a homogeneous continuum. In a network, however, the heterogeneous viscoelastic properties of neighboring segments can significantly contribute to a given segment's microscopically observed mechanical behavior. The deformation and folding of an isolated segment can thus behave differently from a segment that is part of a network. Using diffuse light scattering, Butler et al. (39) estimated that the microstrain followed the macrostrain during externally imposed isovolumetric uniaxial deformation of the lung. In contrast, Brewer et al. (31) directly imaged individual alveolar walls of lung tissue strips during uniaxial stretching and found that alveolar walls did not follow the macroscopic deformation (Fig. 10). The former study superimposed the uniaxial deformation on a uniformly prestressed state of the air-filled lung, which homogenizes the system, whereas in the latter study, tissue strips submerged in fluid were stretched starting from the relaxed state. Additionally, Butler et al. (39) considered length scales of 1 to 2 cm sampled by an optical probe, and their data may correspond to the average behavior of several hundred alveoli. In the study by Brewer et al. (31), the authors examined the mechanics of individual alveolar walls at length scales of about two orders of magnitude smaller than those of Butler et al. (39). The results in Figure 10 suggest that continuum analysis cannot be used to evaluate the configurations of individual alveolar walls and that network models must be used to describe the behavior instead. As we shall see in the next section, such network effects can have significant impact on the focal development of lung diseases. Here it is sufficient to point out that these network effects also represent recruitment processes at the level of alveolar walls at a length scale of about 2 orders of magnitude larger than those in Figure 9.

Figure 10.

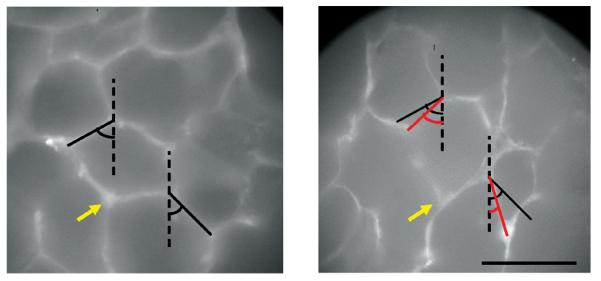
Fluorescent images of the same alveolar region labeled for collagen in a normal rat lung. Left: before deformation; Right after 30% uniaxial stretching vertically. The black lines show alveolar walls and the red lines are their new length and orientation after stretching. The yellow arrow points to the same septal wall junction. Note the significant change in angle between the two septal walls. Scale bar denotes 100 μm. From Ref. (31) with permission.

To describe the deformation of individual alveolar walls, it is thus necessary to include a realistic geometry such as a hexagonal network in a model as originally proposed by Mead et al. (165). Such hexagonal network models of the lung parenchyma have since been developed (31, 45, 277). Simulations using the hexagonal network to mimic the microscopically observed deformation of the alveoli in normal, hypotonic, and hypertonic solutions suggest that the folding of the alveolar wall and collagen during uniaxial stretching is elastically limited by the proteoglycan matrix (45). The reason is that the proteoglycans are highly sensitive to the osmolarity of the bath, whereas collagen and elastin are much less sensitive. In hypertonic solution, the negatively charged proteoglycans collapse resulting in low stiffness, whereas in hypotonic solution they become inflated and their stiffness increases. Thus, the proteoglycans by their compressive resistance hinder the folding of fibers into the direction of the macroscopic strain and so contribute to the elastic behavior of the tissue. A simple hexagonal model without prestress would be unable to mimic the exponentially increasing stress-strain curve of lung tissue strip [e.g., Eq. (6)] because without external constraints such a model is unstable and angles of the hexagons collapse upon stretching that leads to zero elasticity. However, this is not observed experimentally in the tissue strip as Figure 1A demonstrates.

Accordingly, a structurally reasonable model of the tissue strip needs to include both line element elasticity and a mechanism that hinders the collapse of angles. This can be achieved by using an angular spring or bond bending that resists the folding of two neighboring line elements (9). The analysis of such a system needs to include the energy associated with stretching the springs and bending the angle θ between two springs:

$$U=\sum _i(a_i{\epsilon }^2∕2+c_i{\epsilon }^2∕3)+\sum _j{q}_j\Delta {\theta }_j^2∕2)$$ (8)

where ε is the macroscopic strain and Δθ indicates the local change in angle between adjacent springs. The first and second summations in Eq. (8) go through all the springs and all the nodes, respectively. The a_i and c_i are the linear and nonlinear parameters of an individual spring based on Eq. (7) and the q_j are the bond-bending constants. The equilibrium configuration of the network following deformation corresponds to minimum of U. Such a model is shown in Figure 11 for two network configurations corresponding to two values of q (taken to be the same throughout the network) while the line element parameters were kept constant (45). Notice that the minimum energy configuration of the same exact structure is very different when the bond-bending is low (left panel) or high (right panel). This means that (1) the Poisson's ratio of the network is significantly influenced by the mechanical interaction between collagen and proteoglycans; and (2) the deformation pattern of the alveolar wall network does not follow the macroscopic deformation, that is, it is not affine. However, by incorporating this mechanical interaction between collagen and proteoglycans into the hexagonal network model and comparing its stress-strain curve to measured data, the average Young's modulus of a single alveolar wall could be calculated and it was estimated to be about 5 kPa. Furthermore, by taking into account the volume fraction of collagen fibers in the alveolar walls, a lower limit of collagen fiber stiffness in the alveolar wall was also estimated and a value of 300 kPa was obtained when tissue was stretched to 30% uniaxial macroscopic strain (45).

Figure 11.

Effects of the bond-bending parameter q on the configu-ration of the elastic network model at 30% strain in the vertical direction. A: stiff network with bond-bending constant q 100. B: soft network with q = 0.01. Color is proportional to energy carried by the springs. The maximum energy values corresponding to dark red on A and B are different. From Ref. (45) with permission.

The tissue strip preparation is simple and popular partly because of its easy manipulation and partly because the complexities associated with surface tension and circulation are eliminated. The lack of circulation does not pose a technical problem. The tissue strip can be placed in cell culture media that keeps the cells alive. The lack of surface tension is probably also not a serious limitation because the recoil due to surface tension can be restored by applying a prestress, albeit uniaxial in the strip as opposed to the uniform three-dimensional deformation in the lung. Despite these limitations, mechanobiology of lung cells can be conveniently studied in the tissue strip preparation since the cells are in their native ECM. While the study by Cavalcante et al. (45) offered novel insight into the mechanics of the tissue strips at multiple scales, it is still based on a two-dimensional analysis, and the mechanical influence of the alveolar ducts were neglected. Hence a more realistic three-dimensional model of the tissue strip integrating the detailed mechanics of the alveolar wall ECM with the mechanobiology of the interstitial cells embedded in a network of alveoli will eventually be needed.

Mechanics of the lung parenchyma

The mechanical properties of the parenchyma in situ are different from those of the tissue strip due to the presence of prestress related to P_tp and surface tension at the air-liquid interface. Both of these factors also influence the three-dimensional architecture of the parenchyma and the corresponding mechanical properties that are considered next.

Mechanics of the alveolar ducts

Pressure-volume measurements on air- and liquid-filled lungs (15, 90, 166, 231, 240, 269) led to the conclusion that the lung tissue and alveolar surface tension are major stress-bearing components of the lung. Orsós (189) and Weibel and Gil (273) described the lung tissue as comprising three interconnected tissue systems (Fig. 12): (1) a peripheral tissue system consisting of the pleural membrane and the interlobular membranes and their extensions into the parenchyma; (2) an axial tissue system comprising sheaths enveloping airways and pulmonary arteries into the acini, where they form a network of the alveolar duct tissue; and (3) a parenchymatous tissue system of delicate septa that links the axial and the peripheral tissue systems. The appearance of the tissues obtained from scanning electron micrographs of air-filled, saline-filled, and detergent-rinsed air-filled lungs suggested that at a given lung volume, the bore of the alveolar duct is the greatest in the detergent-rinsed lungs and the smallest in the saline-filled lungs. Furthermore, the alveolar septa of air-filled and detergent-rinsed lungs appear taut and tensed, whereas in the saline-filled lungs they are flimsy and slack (14, 90). These differences were attributed to the variation in the alveolar surface tension among the conditions that was the highest in the detergent-rinsed and the smallest (zero) in the saline-filled lungs.

Figure 12.

Schematic drawing of the connective tissue systems in the parenchyma according to the Wilson and Bachofen model showing the alveolar duct with its axial tissue fibers organized in a helical structure, as well as the septal and peripheral fibers. The heavy arrows indicate the distending action of surface tension that exerts radially outward pull on the axial fibers of the alveolar duct. Adapted from Ref. (281) with permission.

Modeling the lung parenchyma as a two-compartment system composed of tissue and surface film acting mechanically “in parallel” has not been satisfactory. For example, Bachofen et al. (15) assumed that the difference in the recoil pressures P_tp of air-filled and saline-filled (P_s) lungs can be entirely attributed to surface forces, that is, P_tp − P_s = 2γ S/3 V, where γ is the surface tension, S is the alveolar surface area, and V is the lung volume. If this were the case, then during uniform lung expansion, S would be proportional to V^2/3, and hence (P_tp − P_s)/γ ∝ V^−1/3. However, experimental data on lungs in which γ was maintained constant showed that (P_tp − P_s)/γ is nearly independent of V below γ = 20 dyn/cm and increases with V for γ > 20 dyn/cm (231, 238). This discrepancy suggested that during lung expansion, S does not change uniformly with V^2/3 and that the reason for this behavior may be due to the distortion of S caused by surface tension. Subsequently, several investigators pointed out that γ acts in two ways: directly, by providing a recoil pressure equal to 2γ S/3V, and indirectly, by distorting parenchymal geometry and thus providing an additional tissue component of the recoil pressure (153, 279). These observations as well as the morphometric studies by Weibel and co-workers (14, 90) led to the development of a novel microstructural model of the alveolar duct by Wilson and Bachofen (281).

According to this model, the peripheral tissue network predominantly provides P_s of the saline-filled lung. Increasing γ at a given V has a minor influence on this network. The axial tissue network of the alveolar duct and the septal tissue network are not affected by volume changes in the saline-filled lung, but they are distended by γ in the air-filled lung. Wilson and Bachofen (281) assumed that the tension carried by the alveolar septal tissue is much smaller than the tension carried by the alveolar duct tissue and thus they neglected the contribution of the septal tissue. An analysis of the mechanics of the model yielded the following relation between recoil pressure, alveolar surface area, surface tension, and lung volume

$$P_{\text{tp}}-P_s=\frac{2\gamma S}{3V}+\frac{nFL}{3V}$$ (9)

where n and L are the number and the length of fibers forming the alveolar duct lattice and F is the force on the fibers. The axial fibers are described as a system of intersecting helices (Fig. 12). The first term on the right-hand side of Eq. (9) is due to surface tension, whereas the second term is indicative of the indirect contribution of surface forces through distortion of the alveolar duct lattice. It was found (281) that Eq. (9) can fairly accurately predict data for P − P_s versus S relationships for lung volumes up to 80% of TLC, which were obtained from P-V and morphometric measurements on air-filed, saline-filled, and detergent-rinsed lungs (14, 90). For higher lung volumes, the authors suggested that the contribution of the alveolar septal tissue might need to be included.

While the Wilson and Bachofen model was very successful because it was capable of predicting the quasi-static P-V behavior of the lung, it also has several limitations. First, more recent electron microscopic imaging results predict larger changes in epithelial basement membrane surface area with lung volume (265) than the original studies (14, 90) which the model was based on. Second, the model does not include separate mechanical properties of the collagen and elastic fibers and their contribution cannot be understood during lung inflation. Third, the model considers only the average properties of the parenchyma and it cannot be used to infer the effects of regional heterogeneities on overall mechanics. Finally, the model is elastic and hence it is unable to predict lung mechanics during breathing. With regard to structure, several newer models of the alveolar duct were proposed subsequently. In all these models, alveolar geometry was described as a collection of space filling 14-sided regular polyhedra (tetrakaidecahedron) and the ducts and alveoli are formed by opening specific common faces between the polyhedra (58–62, 82). While these models provided a description of the alveolar duct morphology which is consistent with average morphometric data, they are limited to a single acinus and hence do not incorporate the variability in structure. A stochastic model of a large collection of irregular polyhedra that incorporated viscoelastic effects was also proposed (145). With regard to the mechanical properties of the structural elements, a refined deterministic model of the acinus was introduced more recently by Denny and Schroter (61). These authors developed a three-dimensional model of the acinus that also included separate and realistic viscoelastic properties of the collagen and elastin fibers together with surface tension properties of the air-liquid interface. They used the structure as a representative model of the acinus and calculated its resistance and elastance as a function of frequency. The model predicted little difference in R_ti between the air-filled and lavaged lungs. Additionally, surface tension contributed significantly to both R_ti and E_ti in the air-filled lung. Interestingly, the surface tension tended to amplify any existing tissue hysteresis despite the fact that the surface area-tension curve itself exhibited very little hysteresis during small amplitude tidal oscillations. Future efforts could incorporate the effects of proteoglycans, interstitial cells and, given the ever increasing computational power, multiple acini and gravity to explore the effects of heterogeneity and mechanical interaction among the acini.

Experimentally, different studies appear to provide a somewhat controversial picture of the role of surface tension. For example, Stamenovic and Barnas (235) found that the dissipative properties of the lung's ECM are the major determinants of R_ti, whereas the elastic properties of both the tissue and surface film are important determinants of E_ti. In contrast, Navajas et al. (183) found that E_ti was smaller in isolated liquid-filled lungs than in air-filled lungs, whereas η was similar in both lungs. Hence, they concluded that surface tension accounts for a considerable part of both elastance and resistance of the air-filled lung within the volume range of normal breathing. Sakai et al. (213) reported similar values of viscosity in isolated lungs and tissue strips despite different deformation and the lack of surface film in the latter. Additionally, for breathing frequencies, the energy loss in the lung parenchyma is a much smaller fraction of the stored elastic energy in shear than during isotropic volumetric oscillations and it is P_tp and not the properties of the surface film that primarily determines the lung's dynamic properties in shear (53). Furthermore, dynamic oscillations invoking small changes in surface area of a surfactant monolayer have shown negligible hysteresis in the surfactant itself (219). Others also argued that parenchymal mechanics are largely dominated by the connective tissues for tidal-like oscillations (286). It is also possible that the contribution of the surface film to parenchymal mechanics during breathing is species dependent since the average size of the alveolus shows a moderate increase with body mass while minimum surface tension appears to be independent of size suggesting that the role of surface tension may be less important in larger species (150). On the other hand, septal wall thickness and the amounts of collagen and elastin fibers in the wall increase linearly with alveolar diameter (171) suggesting a species-specific fine balance between surface and tissue forces. Nevertheless, it appears now that during breathing, surface film mechanics contribute much more to E_ti than to R_ti. More experimental studies are needed to better understand the role of surface film and surfactant and their interaction with tissue elasticity in the lung during tidal breathing.

Parenchymal interdependence

Mead and co-workers (165) introduced the concept of mechanical interdependence into pulmonary mechanics to explain how the parenchyma resists nonuniform deformation. They pointed out that P_tp acting on the pleural surface is transmitted into deeper regions of the lung by the interconnected parenchymal network. Specifically, they showed that if the parenchymal network is homogeneous and alveolar gas pressure is uniform, then the stress at any point in the parenchyma equals P_tp and thus “all distensible regions could be thought of as being exposed to transpulmonary pressure.” If, however, gas pressure in one region of the lung is lower than in the surrounding tissue, the net inward pressure would cause the lower pressure region to shrink. Through mechanical interdependence, however, this shrinkage would be resisted by the distortion of the surrounding parenchyma that produces an outward stress and hence counterbalances the net inward pressure. The authors identified three mechanisms by which the parenchymal network resists deformation: change in the spacing of the network elements, change in their orientation and change in the forces carried by those elements. The first two mechanisms are purely kinematic and are determined by the topological arrangement of the microstructure. The third mechanism depends on the material properties of tissue elements and surface film. These notions are consistent with the network modeling of Cavalcante et al. (45) discussed above.

As described earlier, the bulk modulus represents the lung's ability to resist uniform volume change and is defined as κ = VdP_tp/dV. The value of κ can be obtained from the local slope of the P-V curve (238, 240) and was found to increase faster than linearly with increasing P_tp, for example, from 3 P_tp to 6 P_tp between 40% and 90% TLC for dog lungs (142). The shear modulus micron representing the lung's ability to resist shear deformation cannot be inferred from P-V measurements but rather from measurements where a nonuniform deformation is applied to the lung. Values of micron were obtained from local indentations applied to the lung surface via a cylindrical punch (98, 142, 143, 238, 240). It was found that micron increases approximately linearly with increasing P_tp; for example, for dog lungs μ ≈ 0.7 P_tp over a wide range of volumes (142). Two conclusions can be drawn from these results. First, since κ is much larger than micron, the lung responds to a force applied locally by changing shape more than by changing volume, and therefore the gas volume per unit mass of tissue remains uniform in the deformed region. Second, since micron depends only on P_tp, the material properties of the parenchymal tissue and the surface film seem to have little effect on micron. This, in turn, suggests that the lung resists shape distortion primarily by reorientation and changes in spacing of its tissue and surface film elements, and not by deforming those elements.

The linear shear modulus versus prestress relationship is characteristic of the so-called stress-supported structures. In the absence of prestress, these structures become unstable since rigidity and connectedness of their structural elements are insufficient to fully constrain their freedom to move and deform. Consequently, these structures do not have intrinsically stable shape (like, e.g., rocks, beams, or rubber), and thus they require the prestress for shape stabilization. When an external force is applied to a prestressed structure, its taut structural elements undergo primarily reorientation and change in spacing, and to a lesser degree extension/shortening, until a new equilibrium configuration is attained. The greater the prestress, the smaller the configurational changes are, that is, the greater the stiffness of the structure. Indeed, in such structures micron can remain finite and small even if the stiffness of its members becomes very large. This explains why micron is small despite the relatively stiff connective tissue fibers that comprise the alveolar walls and why it must be a nearly constant fraction of P_tp (37, 78, 234). Microstructural models of the lung parenchyma that incorporated the above principles successfully predicted the observed linear dependence of micron on prestress, regardless of whether they used very simple line-element networks (38, 277) or morphologically more realistic surface-element networks (59, 134). Thus, the structural connectedness and the stabilizing role of the prestress appear to be key features of parenchymal mechanics that lead to the linear μ-P_tp relationship, whereas the geometrical and material properties of the structural elements may be secondary.

The situation, however, appears to be different at low lung volumes. Cavalcante et al. (45) studied the contribution of proteoglycans to parenchymal elasticity as described earlier. The authors found that proteoglycans contribute to the stress-strain properties as well as to the macroscopic shear modulus of parenchymal tissue strips. Microscopic imaging measurements showed that at the level of individual alveoli, bath tonicity, which only influences proteoglycans (and pulmonary cells) but not elastin or collagen, does change the configuration of the alveolar wall network. Importantly, they showed that stretching of relaxed strips causes an immediate buildup of stress, that is, the tissue exhibits a finite elastic modulus at zero stress. This finding appears to be at odds with the idea that in the whole lung resistance to shear is conferred to the parenchyma by P_tp and that if P_tp = 0, resistance to shear should be lost. If the parenchyma indeed behaved as an unstable structure in the absence of prestress, then uniaxial stretching of a relaxed parenchymal strip should develop no stress until all alveolar walls become aligned with applied strain and individual walls begin to stretch. The results of Cavalcante et al. (45) therefore suggest that the parenchymal structure is not unstable even if P_tp = 0 and that proteoglycans provide stability and resistance to shear at low lung volumes. The authors argued that at the scale of the alveolar wall ECM, proteoglycans, due to their large negative surface charge density, resist compression and shear and hence they serve as a bond-bending spring producing elastic resistance against alignment of fibers and alveolar walls with the direction of macroscopic strain (Fig. 11).

Data from punch indentation experiments show that at low P_tp, the relationship between micron and P_tp deviates from the observed linear relation at medium and higher P_tp (237, 240). While this could be a result of air-trapping that occurs at low lung volumes, it can also indicate the increasing contribution of proteoglycans as discussed above. In fact, this deviation is even more pronounced in liquid-filled lungs where there is no effect of air trapping (240). Taken together, the picture that emerges is that at low P_tp, where surface tension is low and alveolar architecture is not fully recruited, proteoglycans in the ECM may play a major role in resisting lung distortion. With increasing P_tp, the alveolar network becomes fully recruited and the contribution of structural mechanisms becomes predominant.

Contributions of non-parenchymal and cellular structures

It should be also mentioned that non-parenchymal structures may play role in pulmonary mechanics. For example, using indentation tests, it was determined that the pleural membrane contributes ~20% to recoil pressure during uniform expansion of the lung (98, 188) and at least 30% to the resistance to shear (119, 233). However, tissue hysteresivity of the pleura was estimated to be small (251). The deformation of the parenchyma associated with the axial forces along the airways may locally distort the parenchyma. It was inferred that the parenchyma stabilizes airway length against transmitted axial forces, and perhaps even forces on airway plugs (107). Interestingly, the elasticity of the bronchial and vascular trees was found to contribute to lung recoil pressure only up to 10% (230).

Other potentially important contributors to lung elasticity include cellular structures. Initial studies found that activation of the airway smooth muscle can cause a decrease in lung compliance in vivo (51, 284, 285). Among the four major alveolar cell types, alveolar type I and type II epithelial cells, endothelial and fibroblasts, the latter cells are the most contractile and have the highest elastic modulus (13). Additionally, there are smooth muscle and perhaps contractile myofibroblast cells in the alveolar ducts (147, 187) that are highly contractile. Therefore, it is possible that the contraction of these cells modulates lung elasticity. However, at the whole lung level, it is important to partition the bronchoconstriction response into separate airway and tissue properties because airway heterogeneities can produce apparent increases in estimated lung properties. Indeed, using gases of different viscosities, it has been demonstrated that airway smooth muscle activation mainly causes time constant heterogeneities and little change occurs in R_ti and E_ti at least in small animals (152). This finding is also in agreement with tissue strip studies that reported only a modest 5% to 20% increase in stiffness during contractile stimulation depending on the concentration of the agonist (65, 182, 286). Interestingly, a recent study reported that the overall mechanical behavior of the lung may be sensitive to a specific cytoskeletal intermediate filament protein, desmin, which is expressed in smooth muscle cells of the lung. Specifically, desmin-null mice showed lower lung stiffness and recoil pressure both at baseline and following induced airway constriction than control mice (222). However, as discussed earlier, it is generally thought that the most important structural element of the CSK that dominates cell stiffness is actin (236, 270, 271). Furthermore, it is unclear whether the ECM of the desmin knockout mice is comparable to that of the wild-type mice. Nevertheless, this area at the interface of lung biology and parenchymal mechanics warrants more attention and further studies are needed to determine the specific role of various proteins as well as the effect of different biological interventions. Before physiological conclusions can be drawn from any biological intervention, it is crucial to understand the role of heterogeneities in the whole lung response. Besides using gases of different viscosities, another possibility is model-based partitioning of heterogeneities from physical changes in tissue properties (127, 254). Alternatively, the tissue strip can be studied in isolation as it is minimally sensitive to airway heterogeneities.

Stability of the Lung

Generally, a thermodynamic system responds to an applied load by developing a restoring force. For example, when air is pumped into a rigid chamber, the pressure inside the chamber increases monotonically. However, during inflation of the collapsed lung, the lung does not always develop an increasing restoring force; instead, the pressure inside the lung can decrease intermittently due to the sudden opening of airways and alveolar airspaces. Thus, the local slope of the P-V curve of the lung can become negative indicating the presence of instabilities. Lung parenchymal stability is closely associated with collapsing of the airways and air spaces known as atelectasis. In normal lungs, atelectasis is present only during abnormal conditions such as the first inflation of degassed lungs, ventilation with pure oxygen, pressing on lung surface at low lung volumes or ventilation of anesthetized subjects. Figure 13 shows a series of images of a region of an isolated lung during inflation from the collapsed state. It can be seen that the atelectatic regions gradually disappear as P_tp increases. Conversely, when the regional distending pressure of the parenchyma decreases below some critical value, the region can collapse hindering gas exchange. In lungs with abnormally high surface tension, atelectasis can occur spontaneously with the lungs inflated by small but uniformly positive P_tp (50, 231). The occurrence of atelectasis in prematurely born infants (32, 33) is associated with abnormally high and nearly constant surface tension (11). In this section, we will examine instabilities associated with surface tension and with the dynamics of airway opening and closing.

Figure 13.

Images of a region of an isolated lung at successive inflation pressures. The inflation was started from the collapsed state and the bottom, middle, and top images correspond to transpulmonary pressure of approximately 25, 27, and 30 cmH₂O. Dark red corresponds to collapsed regions. Notice that as inflation progresses, the pink aerated regions gradually penetrate into the atelectatic region by pulling the underlying alveoli open (Z. Hantos and B. Suki; unpublished data).

Analysis of static instability

The earliest models of parenchymal stability depicted the alveolar structure as a collection of independent spherical balloons connected to a common airway tree (203, 269). The tension in the balloon wall was assumed to be the sum of the surface tension γ and tissue tension T. Using the law of Laplace, the transmural pressure p that keeps each balloon inflated is

$$p=2\frac{T+\gamma }{r}$$ (10)

where r is the radius of the balloon and T and possibly γ depend on r. As the lung expands, r increases and, according to Eq. (10), p tends to decrease unless the total wall tension increases faster than linear with increasing r. Since the alveolar septal tissue exhibits exponential-like nonlinear tension-extension behavior (79, 182, 287), it is reasonable to assume that T/r increases with increasing r. If γ were constant, then γ/r would decrease with increasing r and if γ were sufficiently high, then p would reach a maximum and start to decrease as r further increases. The first balloon with decreasing p would set up an unstable situation: all balloons with smaller r and higher p would empty into the balloon with a bigger r and lower p. This implies that if the alveoli had slightly different size, constant and elevated γ would make the lung intrinsically unstable. In the normal lung, this instability is, however, avoided because type II alveolar epithelial cells secret surfactant that reduces γ and makes it dependent on r such that γ/r increases with increasing r (81, 239).

In his conceptual model of stability, Mead (164) identified three mechanisms of parenchymal stability which he referred to as geometrical stability, surface film stability, and tissue stability. As a criterion of stability, Mead employed the notion that an increase in P_tp must be accompanied by an increase in lung volume, that is, a positive slope of the P-V curve and thus a positive κ. Fung (81) and Wilson (278, 280) formalized Mead's idea as follows. Because the lung's recoil pressure equals the sum of all tissue and surface forces transmitted across any plane through the parenchyma per unit area of the plane, the rate of increase of these forces (i.e., tissue and surface stability) during lung expansion must exceed the rate of increase in spacing between the force-bearing components of the parenchyma (i.e., geometrical stability) to have increasing recoil pressure. Because the contribution of γ to the recoil pressure depends on the alveolar surface-to-volume ratio (S/V) [the first term on the right-hand side of Eq. (9)], Wilson (279) concluded that if γ were constant and high enough, this term would decrease with increasing V leading to a decrease in P_tp and thus κ < 0, which implies instability. Stamenovic and Smith (237) studied the P-V behavior of lungs with constant and elevated γ and did not observe negative P-V slopes. Instead, they observed very small slopes accompanied by regional atelectasis at low volumes. They argued that these atelectatic regions occur as V decreases, with most of the expiring volumes from the collapsing regions being transferred to the remaining expanded regions. Fung (81, 83) analyzed regional collapsing of the air spaces and concluded that if a region that tends to collapse is entirely surrounded by the parenchyma, then its collapsing will be prevented through the stabilizing effect of mechanical interdependence. A planar regional collapse would be marginally stabilized by the surrounding parenchyma and would be susceptible to collapse if a small local compression force is applied. However, this analysis did not take into account the effect of alveolar surface film properties. Similar conclusions were also reached by Graves et al. (95). Stamenovic and Wilson (239) attempted to reconcile the different results obtained from the various models. Using both continuum and microstructural analysis, they showed that in a homogeneous lung, the parenchyma would be stable and local atelectasis would not occur at any positive P_tp. If, however, the alveolar S/V ratio is inhomogeneous, regions of higher S/V ratio would collapse if surface tension is elevated and constant. This may explain the observed atelectatic regions at low volumes of lungs where surface tension is high and insensitive to changes in alveolar surface area.

Dynamic instabilities

As described in the previous section, alveolar stability during a small deformation is determined by the relation among the local shear and bulk moduli and surface tension. The analysis of stability can be extended to include airways and gas flows during slow inflation as follows.

Figure 14A depicts the P-V curve of an isolated rat lung during inflation from the collapsed and degassed state to TLC (4). The lung's recoil pressure P_tp was measured with respect to atmospheric pressure as a function of the volume displacement V of a piston that slowly inflated the lung. It can be seen that with increasing V, P_tp also increases, but this increase is not monotonic and P_tp intermittently decreases. Therefore, the elastance E = dP_tp/dV can take both negative and positive values. Successive values of E were estimated as the local slope of a straight line fit within a short moving window along the P-V curve. The magnitudes E_neg of elastance with negative values show fluctuations and the distribution Π of E_neg was found to be exponential:

$$\Pi {\left(E_{neg}\right)}^{~}{e}^{-E_{neg}∕E_0}$$ (11)

where E₀, the characteristic value of E_neg, increased with inflation rate (Fig. 14B). It was found that the pattern of E_neg varied from inflation to inflation, but the distribution in Eq. (11) was reproducible. This excludes the possibility that E_neg arises from tissue rupture.

Figure 14.

(A) P-V curve during the inflation of a degassed rat lung. The inset shows a magnification of a region with many local negative elastance patterns. (B) Distributions of negative elastance from 10 inflations at rates of 2.0 ml/s (triangles) and 0.5 ml/s (circles). The regression line fits to the measured distributions are shown by dashed lines. The solid lines correspond to the distributions of negative elastance from 1000 simulated inflations of an 18-generation symmetric binary tree. (C) An example of the P-V curve from the inflation of the model. The inset shows a magnification of a region with many local negative elastance patterns similar to those in Fig. 14A. The red line in the inset traces an avalanche shock. Adapted from Ref. (4).

To understand the existence and fluctuations of the negative elastance, a dynamical model of a system consisting of a piston chamber and a lung was developed (4). The lung was modeled as a binary tree terminating in elastic alveoli (4). The root of the tree, the trachea, was connected to the chamber containing air at atmospheric pressure, corresponding to the experimental conditions. Inflation was then simulated by increasing V at a constant rate. At the beginning of the inflation, all airways were closed and no alveoli are connected to the root, so a small increase in V increased P_tp. A closed airway opens when P_tp exceeds the airway's critical opening threshold pressure (86) P_th, which was assumed to be a random variable uniformly distributed between 0 and 40 cmH₂O (the pressure at TLC). When a segment opens, the pressure propagates deeper into the lung. If the P_th of either daughter airway is also smaller than P_tp, then this daughter opens together with its parent. This process leads to an avalanche of openings involving a large number of airways and alveoli (247). The newly opened airways and alveoli increase the volume of the lung, the gas suddenly redistributes in a larger volume and consequently the pressure decreases according to Boyle's law. The reduction in P_tp, however, can terminate the propagation of the avalanche and P_tp increases again due to the steady influx of air. This phenomenon of the decrease in P_tp following a single avalanche and the subsequent rise in P_tp was termed an avalanche shock (Fig. 14C inset), which is not a traditional propagating shock wave. The time course of an avalanche shock is smoothed by relaxation processes due to flow resistance of the airways such as regional airway resistance and viscoelasticity of the parenchymal tissue. The decreasing part of an avalanche shock corresponds to instabilities characterized by negative elastance. The continuous increase in P_tp is intermittently interrupted by avalanche shocks of different sizes until all air in the piston chamber is injected into the lung.

Simulations using the above model with an 18-generation airway tree ending in elastic alveoli produced P-V curves (Fig. 14C) that are similar to the P-V curves observed experimentally (Fig. 14A). The local E_neg was then determined in the same way as for the measured data. The distributions Π (E_neg) from the simulations fit the experimentally ob tained distributions for both slow and fast inflation rates (Fig. 14B). These results indicate that inflating the lung from a state in which a considerable part of the gas exchange region is collapsed is a complex, nonequilibrium dynamical process characterized by regions of instabilities that manifest macroscopically as negative elastance. For slow inflation, the system has enough time following each avalanche to reach equilibrium, so the individual avalanche shocks are distinct and nonoverlapping. With increasing inflation rate, however, avalanche shocks due to separate avalanches increasingly overlap, resulting in smoother P-V curves with fewer regions of negative elastance. Thus, the mechanism for the paradoxical negative elastance and its distribution arises from the avalanche shocks involving the sudden recruitment and subsequent relaxation of a large number of airways and alveoli.

It can be concluded that the instabilities that were attributed to a combination of the static properties of the alveolar liquid lining (50) and the nonuniform deformation of the lung tissue (239) can be dynamic in nature. These simulations also suggest that both airways and alveoli are inextricably involved in the processes producing macroscopic instabilities of the lung during inflation. Since the topological properties of the airway tree are also involved in these instabilities, the associated phenomena can become very complex due to the avalanches (see article on “Complexity and Emergence” in Comprehensive Physiology). Furthermore, it appears that the rate of deformation plays an important role in the formation of instabilities and their contribution to the global mechanical properties of the lung. Next, we examine the influence of taking into account the rate of deformation of individual airway opening and closing on dynamic lung elastance.

Instabilities during cyclic deformations

Opening and closing of lung units are not processes that occur instantaneously once critical pressure thresholds have been crossed. A closed airway takes a finite amount of time to open when it is subjected to sufficient pressure (86), and the same is true for an open airway that closes when pressure is reduced enough (44). This is also evident from the progressive decrease in lung compliance seen during mechanical ventilation following a recruitment maneuver (6). Both the opening and closing processes together with the time to open and close are significantly influenced by the presence of surfactant. The precise biophysical mechanisms governing these processes are beyond the scope of this article and here we concentrate on a simple and more phenomenological description that can be used to simulate whole lung behavior. Such a model was developed by Bates and Irvin (20). The temporal dynamics of recruitment and derecruitment in the lungs have been simulated by representing the lungs as a parallel collection of compliant units each served by an airway that connects to a common entry point. Each lung unit is associated with a virtual trajectory, parameterized by the quantity x that can take values between 0 and 1. Each unit can exist in one of two states, either fully open or fully closed, with the transition between the two states governed by the behavior of x, as follows. If the pressure, P, applied to an airway exceeds the airway's critical opening pressure, P_o, then x increases toward 1 with a speed proportional to the difference P − P_o and a constant of proportionality s_o. Similarly, movement toward 0 occurs with speed s_c(P 7#x2212; P_c), where P_c is a critical closing pressure, s_c is another constant of proportionality, and P_c < P_o. It is assumed that x does not change for P_c ≤ x ≤ P_o. If an airway is closed and its value of x reaches 1, the airway immediately opens. Conversely, if the airway is open and x reaches 0, the airway closes. The quantity x thus does not correspond to anything physical in particular; the virtual trajectory is merely an empirical mechanism that allows each airway to exhibit hysteretic opening and closing as the pressure applied to it varies in time. Even so, the airway behavior produced by the virtual trajectory mechanism shows similarities to that observed experimentally in in vitro models of elastic conduits that open and close as a result of bridging across the lumen by a fluid lining layer (86, 190, 194,195).

This computational model has been fit to data obtained in mice with acute lung injury (ALI) caused by intratracheal instillation of hydrochloric acid (161). The mice were given a recruitment maneuver (deep lung inflation) to recruit closed lung regions and then ventilated with a normal tidal volume and frequency for several minutes during which time lung elastance was monitored. This procedure was repeated at three different levels of PEEP. The model was able to fit the experimental data closely (Fig. 15) when the values of P_o and P_c were normally distributed. While P_o and P_c had the same variance, the mean P_o was about 4 cmH₂O greater than mean P_c. Furthermore, the speeds of opening and closing were hyperbolically distributed, with the speed of opening being about an order of magnitude greater than the speed of closing. The best-fit model parameters for the acid-injured mice were the same as for control (uninjured) mice except that the mean values of P_o and P_c were both increased by about 5 cmH₂O, which is consistent with an increase in surface tension at the air-liquid interface in the lung (86, 194, 195). An analytical version of this model was also used to account for the derecruitment dynamics of rats injured by saline lavage (6). Again, the model simulated the lung stiffness data accurately, but the rate of rise of elastance following a recruitment maneuver in the rats was much greater than in the acid-injured mice in Figure 15. This shows that recruitment and derecruitment dynamics may be species dependent and are greatly influenced by the type and degree of lung injury.

Figure 15.

Fits of a computational model of recruitment and derecruitment in the lung (lines) to experimental measurements of respiratory elastance (symbols) in mice with various degrees of acid-induced injury ventilated at three different PEEP levels. Elastance was measured as a function of time following a recruitment maneuver. From Ref. (161) with permission.

In summary, we have reviewed three different approaches to lung stability. The corresponding mechanisms are not exclusive. For example, the local shear and bulk moduli of the parenchyma could be incorporated into the model of dynamic instabilities via avalanches by making the critical opening pressures dependant on the local moduli. Also, the velocity of opening could be taken into account in avalanche dynamics. Alternatively, gas redistribution and possibly avalanche dynamics likely occur during cyclic breathing-like deformation of the injured lung during mechanical ventilation. Furthermore, the bulk and shear moduli of the parenchyma should also influence the speed of opening and closing. Understanding these processes may become critical in determining the nature of ventilator-induced lung injury such as repetitive opening and collapse induced by high shear and normal stresses on the epithelium during mechanical ventilation.

Biomechanics of the Lung Parenchyma in Diseases

Elastin, collagen, and mechanics in interstitial diseases

Using scanning electron microscopy, the three-dimensional microstructure of normal lung parenchyma has recently been visualized in extraordinary detail (see also Fig. 4B and Fig. 5B) and shows complex intermingled networks of elastin and collagen (261). In diseases of the parenchyma, these structures become remodeled (149, 268). While the detailed cellular machinery behind this remodeling is not well understood, it has significant consequences for the structural and mechanical properties of the parenchyma. In mouse models of emphysema, for example, these elastin and collagen fiber networks show tortuous and substantially damaged structures (186). Cultures of cells exposed to elastase exhibit damaged elastic fibers with a frayed, porous appearance, and a granular texture (178). Following 7 days of repair, the granular texture of damaged fibers disappears and the porous areas become filled in. By 22 days following elastase exposure, the elastic fibers are indistinguishable from fibers in control cultures. Nevertheless, this repair is likely to be aberrant because elastase treatment has been shown to lead to progressive airspace enlargement in rat lungs despite normal levels of elastin (169).

A recent study characterized the force-extension curves of collagen fibrils and whole tendons from rats that had been pretreated with β-APN, which inhibits the formation of cross-links among fibrils (202). In the absence of cross-links, the stress required to stretch the tendon decreased dramatically almost 10-fold from 120 MPa in the normal to 15 MPa in the tendon from the treated rats. Furthermore, the stress quickly reached a plateau and in certain samples actually started to decrease beyond a critical stretch, indicating the breakdown of the tendon. It has also been shown that the collagen in the alveolar walls, and indeed the walls themselves, mechanically fail at a lower stress in emphysematous lungs than in normal lungs (128, 138). Since the failure stress of the alveolar wall is determined by the strength of collagen, this could indicate abnormal cross-linking of the collagen in emphysematous lungs as a consequence of inflammation and remodeling. Enzymatic digestion of fibers makes them susceptible for mechanical failure. Ultimately, it is not the digestion that generates failure but the mechanical force on the fibers (253). When actual fiber rupture occurs, fragments of the molecules forming the original fiber are exposed. Such fragments do have an important biological effect; for example, elastin fragments have chemotactic activity, they attract monocytes (110) which in turn can prolong local inflammation with further tissue deterioration. The progression of the functional decline of the lung due to cascades of failure is discussed in detail in the article “Complexity and Emergence” in Comprehensive Physiology.

During fibrosis, there is significant collagen deposition in the lung that is accompanied by stiffening of the lung tissue (64, 67, 69, 198). Interestingly, while both the elastin and collagen contents increase, changes in the overall viscoelastic properties of the lung tissue appear to correlate with the contents of collagen (64) or proteoglycans (67), suggesting that it is the reorganization of the fibers that is most responsible for the altered mechanical properties of the tissue. However, little is known about the organization and stiffness of individual collagen fibrils and fibers in fibrosis, making this an important area for future research. In cardiovascular tissues, the fibrotic increase in stiffness is attributed to the deposition of extra collagen and also to increased collagen cross-linking associated with the formation of advanced glycation end-products (228). If the maturation of cross-linking is faster than the turnover of collagen itself, then fibrotic lesions develop and lead to an increased local stiffness, a process similar to aging (12). It is unclear, however, how the locally formed fibrotic lesions influence organ level function. Indeed, the few published studies in the lung are somewhat contradictory in their accounts of the correlation between mechanical properties and collagen content (67, 93). Using network modeling of the lung, it has been show that collagen content alone cannot account for the organ level functional properties of the lung (19). Instead, of key importance is how the remodeled tissue is organized spatially. Additionally, the stiff fibrotic tissue can alter the character of the residing cells such as fibroblasts by promoting cell differentiation into more fibrogenic myofibroblasts. This can then set up a vicious circle since the myofibroblasts start secreting the excessive stiff ECM component which in turn cause more phenotypic change in fibroblasts (105).

In summary, various microscopic alterations in the ECM of the lung parenchyma result in changes in the mechanical properties of fibrils, fibers, and the alveolar walls. These microscopic pathological alterations are invariably heterogeneous and the extent to which they influence organ level lung function critically depends on the spatial organization these lesions (19). In the case of emphysema, the missing alveolar walls together with the reduced elasticity of individual walls lead to lower stiffness and recoil pressure (Fig. 1) as well as an altered PEEP dependence of lung elastance (Fig. 2). In fibrosis, opposite changes occur, tissue strip stiffness and lung elastance increase. In both cases, changes in lung mechanics can severely compromise the functionality of the parenchyma as a gas exchanger.

Surfactant, edema, and mechanics in acute lung injury

The syndrome ALI and its more severe form the ARDS are characterized by the accumulation of an inflammatory exudate in small airways, alveolar ducts, and air sacs. The edema fluid contains many bioactive molecules with complex, interdependent, and incompletely understood effects on parenchymal remodeling and repair (272). Serum proteins, phospholipases and cholesterol among them exert profound effects on adsorption and spreading kinetics of pulmonary surfactant, effectively inactivating it, and thereby contributing to alveolar instability, additional flooding, gas absorption atelectasis and alveolar derecruitment. (96). It is one of the reasons why, in contrast to children with immature lungs, surfactant replacement in adults with ARDS has been disappointing. The effects of edema and surfactant inhibition are not only an important source of the increased mechanical load resisting lung inflation, but they also place airway and alveolar epithelial cells at risk for wounding by interfacial stress (27, 115). This injury mechanism is thought to operate in so-called atelect-trauma, a form of mechanical ventilation-induced lung injury associated with the cyclic recruitment and derecruitment of unstable alveolar units (180).

The advent of computed tomography provided the important insight that parenchymal mechanics of the injured lungs are regionally heterogeneous (85). This in turn had a profound impact on the practice of mechanical ventilation insofar as it motivated clinical trials, which established that minimizing parenchymal stress and strain can be life saving (1). Initial models of the regional mechanics of injured lungs viewed dependent airspaces as compressed by the increased weight of the overlying edematous tissue (193). This interpretation was subsequently challenged in favor of a model that considered the dependent lung units as airless, but with normal tissue dimensions on account of unit expansion by foam and liquid (113, 159). Figure 16 compares subpleural alveoli in a normal and an injured rat lung. It can be seen that gas bubbles of different sizes and shapes are surrounded by flooded alveoli indicating nonuniform surface tensions and/or regional pressures. These images then suggest that following injury, liquid bridges form at the level of the alveolar ducts that trap air in some alveoli while others can be partially or completely flooded.

Figure 16.

Optical sections of a normal (left) and a ventilator-injured (right) rat lung 20 mm below the pleural surface. Because the injured lung had been perfused with a Fluorescein Dextran alveolar edema appears white on this image. Note that some alveoli are completely filled with edema fluid, while others retain trapped gas (dark ovals). From Ref. (113) with permission.

At the macroscale, the global P-V curve of injured lungs is characterized by substantial hysteresis and a prominent lower inflection point, a nonlinearity marking a volume-dependent increase in lung compliance along the inflation limb (Fig. 17). Impaired surfactant function, effects of edema on interfacial forces and the corresponding reduction in the number of recruitable lung units all contribute to the increased resistance of the injured lung to inflation (158). Furthermore, these abnormalities are regionally heterogeneous and consequently the regional P-V curves of the lung can be quite different from each other (23). The focus of this article precludes a comprehensive review of the literature devoted to the P-V curve of injured lungs. Nevertheless, we consider liquid and foam in alveoli and peripheral airways as central to this issue. For small applied forces, foam is an elastic material. Foam yields and begins to flow at a critical shear stress. Typical values of critical stresses in foam are of the order of a few tenths of a cmH₂O (140). However, flow of foam through an airway branch requires simultaneous yield of more than one surface, and the pressure required to drive foam through a branch may be many times the yield stress of a single liquid plug. The theory of plasticity shows that the pressure required to drive flow of a perfectly plastic material is independent of the scale of the flow. Thus, the pressure drop across a branch may be almost the same for all-sized airways. Therefore, the pressure drop required to drive flow through a self-similar branching network of n generations is n times the pressure drop required to drive flow across a single branch, and the pressure drop that would be required to drive flow through the bronchial tree may be quite large (160). Figure 17 underscores the importance of interfacial forces as determinants of the elastic resistance of the lung during inflation. A comparison of P-V curves between an air-filled and a completely fluid-filled canine lower lobe shows the expected differences in compliance and hysteresis. However, the P-V characteristics drastically change when a fluid-filled lobe is inflated with air. Note that the pressure required to advance but a few presumably surfactant poor air-liquid interfaces in lobar and segmental bronchi is considerable as is reflected in the prominent lower inflection point of the inflation curve. Thus, while the P-V curve of degassed lungs also show apparent similarities and instabilities (Fig. 14), the mechanisms contributing to the P-V curve of an edematous lung appear to be different.

Figure 17.

Pressure-volume curves of a canine caudal lobe containing air only, saline only, and an air-saline mixture. Note the high initial impedance when air is injected into a saline-filled lung. Adapted with permission from Ref. (158).

Mechanical Force Transmission in the Parenchyma

Mechanical forces and mechanotransduction in the normal lung

As discussed earlier, lung tissue is constantly under a prestress which is a result of the distension of the lung by the P_tp. The regional distribution of prestress is determined by gravity-related hydrostatic pressure in the pleural space and the shape of the chest cavity (113, 276). As a consequence, alveoli are somewhat bigger at the apex than at the base of the lung. Prestress also changes cyclically and irregularly with breathing. Again, due to the smaller alveoli at the base, regional tidal volumes are also bigger at the base. The mechanical tension in the alveolar walls is transferred through the ECM fibers to the adhering cells with important consequences for cellular biophysics, biochemistry and phenotype (89). Such mechanical interactions between cells and the matrix are known to modulate cell contractility and myosin light chain phosphorylation (199), cell rheology (210), and focal adhesion assembly (46), all of which are critical for control of cell adhesion, migration, growth, contractility, and viability (63). Additionally, the mechanical properties of the ECM may influence angiogenesis (121), as well as connective tissue homeostasis itself (48). The direct interaction between the ECM and cellular biochemistry also has important implications for the biomechanical properties of the connective tissues.

Cells in the interstitium sense mechanical forces via the integrin adhesion receptors that connect the CSK to the ECM (120). In addition to collagen, integrin receptors can also anchor to other ECM molecules such as fibronectin or laminin. However, since collagen is the main load-bearing component in connective tissue, any prestress in the lung would likely be transferred from the collagen to the other ECM molecules. Although the exact molecular mechanisms by which this mechanotransduction occurs are not entirely clear (225), it has been found that modulation of stresses on the cell surface leads to a dynamic remodeling of focal adhesions (57). Thus, integrins serve as a mechanotransduction device and can activate various cellular processes (89) when the forces along the collagen network change. For example, integrins have been shown to downregulate collagen alpha-1(I) and upregu-late interstitial collagenase when fibroblasts were grown on a collagen matrix without prestress (144). However, mechanical forces can also induce direct secretion of various growth factors that accelerate the remodeling of the matrix. For example, tensile force-mediated upregulation of the alpha-1(I) procollagen gene was found to depend on the release of TGF-β (97). Tensile force also appears to regulate the connective tissue growth factor that is able to stimulate extracellular protein release through a TGF-β independent pathway (218). Additionally, fibroblasts appear to respond differentially to various types of mechanical stimuli (e.g., uniaxial vs. biaxial deformation) (25).

It is clear that the presence of specific types of mechanical forces and various signaling cues in the ECM jointly regulate how the cells create their microenvironment to maintain an optimal structure and biomechanical properties of an organ (116). Thus, cells and the prestressed ECM live in a dynamic balance in which about 10% of total lung collagen is newly synthesized each day, 40% of which is immediately degraded, resulting in continuous remodeling of the matrix (162). A schematic diagram of the hierarchical transmission of mechanical stimuli from the level of the whole lung down to single cells, and the various possible feedback loops controlling ECM remodeling and ultimately organ level mechanics, are shown in Figure 18. We note, however, that there are several other important mechanisms related to the effects of mechanical forces on lung biology such as surfactant secretion (282) and smooth muscle contractility (74, 199) or mechanical ventilation-induced cellular injury (267) which are not considered in Figure 18.

Figure 18.

Schematic diagram of force transmission from the level of the whole lung to single cells with various feedback mechanisms influencing ECM composition and lung mechanics. Dotted lines show external or internal influences as well as various possible feedback loops in disease states (see text for explanation). Adapted from Ref. (252) with permission.

Mechanical forces in the diseased lung

ECM-related diseases

In disease, the biochemical cues within the alveolar walls change either because of the expression of enzymes and/or cytokines, or secondary to injury caused by external agents such as cigarette smoke. This can drastically change the turnover half-time of matrix molecules. For example, increased collagen mRNA expression in the lung was detected within 6 h of elastase treatment of hamsters (149). In this case, matrix remodeling was directly initiated by the acute injury caused by elastase. It is conventional to think that diseases such as emphysema or fibrosis develop as a result of the changes in the biochemical microenvironment. However, as soon as the composition of the ECM is altered, either because of direct injury or cellular remodeling, corresponding changes occur in the biomechanical properties of the matrix and consequently of the alveolar wall. Such changes affect the local deformation of the alveolar wall, causing the wall network to reorganize itself to re-establish mechanical equilibrium. Thus, it is conceivable that diseases can change local prestress on the alveolar wall which, in turn, can have a positive feedback effect on cell signaling, leading to further assembly of matrix molecules or release of digestive enzymes. In this way, the initiation of a disease process has the potential to lead to chronic and progressive tissue remodeling in which mechanical forces and ECM stiffness can play a regulatory role.

While virtually nothing is known about the remodeling effects of mechanical forces in the fibrotic lung, the possibility that mechanical forces contribute to the progression of emphysema has been put forth as early as 1971 by West (276) who showed that the topological distribution of emphysema scores closely resemble the regional distribution of mechanical stresses in the lung due to its own weight. Consequently, West argued that mechanical forces should contribute to tissue pathophysiology. In a two-dimensional finite element model of the alveolar structure, Gefen et al. (87) demonstrated that alterations in the elastic properties of the alveolar wall in emphysema can lead to a stress concentration up to 6 times higher than in the normal lung tissue. Such high stresses might lead to rupture of remodeled fibers (87). This idea was further explored by imaging of alveolar walls coupled with simultaneous measurement of the mechanical properties of tissue strips during uniaxial stretching (138). It was found that the alveolar walls from elastase-treated rats can break under the influence of mechanical forces akin to those likely occur in vivo. The notion that mechanical forces might contribute to tissue destruction is also consistent with lung CT images of patients with emphysema (174).

The breakdown of the alveolar wall network driven by mechanical forces has been shown to lead to significant heterogeneities in structure at the parenchymal tissue level, with collagen expected to play a major role in this process since it is the most important load-bearing constituent of the alveolar wall (253). At high lung volumes, collagen in the alveolar wall normally protects the parenchyma from rupture. Therefore, rupture of alveolar walls observed in the emphysematous lung at strains corresponding to normal breathing suggests that the yield stress of collagen must be weaker following remodeling (138). This notion is supported by a recent study reporting that tissue strips from elastase-treated mice failed at ~ 50% less stress than control even though the treated animals had a 50% increase in total collagen content of the lung (128). It is important to note, however, that the mean linear intercept, an index that is often invoked as a measure of airspace enlargement (191), was also increased, indicating that the number of alveolar walls available to support the stress per cross-sectional area perpendicular to the direction of stretching was reduced. One may be tempted to conclude that the reduction in failure stress was simply due to the larger stress per alveolar wall in the emphysematous tissue. However, it has also been argued that the increase in mean linear intercept cannot fully explain the decrease in failure stress, especially when the collagen content per alveolar wall is increased (128). Therefore, despite the increased collagen content of alveolar walls in the emphysematous lung, wall stiffness is still smaller than in healthy animals.

These findings suggest that the normal dynamic equilibrium between matrix turnover and mechanical forces is disturbed in emphysema, which can lead to the additional positive feedback mechanisms reinforcing disease progression as shown by dotted lines in Figure 18. For example, direct injury to the alveoli might lead to an alteration in matrix turnover and reduction in collagen failure strength that ultimately results in the breakdown of alveolar walls, which then causes further stress on the remaining walls so that they themselves can break. Such positive feedback loops can cause a continuous deterioration of lung function and may explain the progressive nature of emphysema (253). One might also speculate that positive feedback loops would persist in fibrosis. One possibility is that chemical or genetic influences stimulate fibroblasts to secrete more collagen and hence the stiffness of the local ECM increases. The regional expansion of the lung during breathing would be altered and hence mechanical forces on the ECM and the fibroblasts would also change. Abnormal levels of mechanical force can then further stimulate cells to produce stiff ECM components that would eventually lead to focal development of fibrotic lesions. Indeed, ECM stiffening has recently been shown to shift fibroblasts toward a more fibrogenic myofibroblast phenotype with increased matrix synthesis and reduced matrix proteolytic gene expression (148). In any case, the finding in emphysema that increased collagen content is accompanied by decreased stiffness is in stark contrast to the mechanics of the fibrotic lung in which total collagen content also increases but is accompanied by an increase in stiffness (64). The conclusion is thus inescapable that, following the remodeling process, the internal structural organization of the collagen fibers in the alveolar wall is drastically different in emphysematous and fibrotic lungs. If, as is widely suspected, both emphysema and fibrosis are triggered by an aberrant cellular repair response to an initial insult, the grossly different mechanical and structural fates of the parenchyma in these two diseases could be due to a bifurcation at some point in the process of tissue repair. To further complicate matters, however, there is evidence to suggest that emphysema and fibrosis can co-exist, so it may be that different repair processes can take place concurrently within the same lung (151).

Acute lung injury

Physiologists have long realized that in healthy lungs, the vertical in situ gradients in pressure and volume do not scale with lung density (2, 114). They concluded that the topographical distribution of parenchymal stress resulted from a shape matching constraint between two gravitationally deformed solids, the lungs and the thorax (207). One can conclude then that next to the gravitational deformation of the thorax/abdomen, the resistance of the lungs to a shape change, as reflected in the lung's shear modulus, is an important determinant of the topographical distribution of stresses and strains. As mentioned earlier, based on punch indentation measurements, Hajji et al. estimated that the shear modulus of the normal canine lung scales as 0.7 P_tp (98). Magnetic resonance-elastography-derived measurements of parenchymal shear wave propagation characteristics (163) indicate that the shear moduli of injured rat lungs are an order of magnitude larger, that is, between 1 and 2 kPa at volumes near FRC (McGee et al. unpublished observations). It is therefore likely that the gray scale gradients in CT images of human lungs with ARDS reflect gradients in regional alveolar edema as opposed to gradients in parenchymal prestress and alveolar size.

In the injured lung, edema usually collects in the gravitationally dependent, normally well-perfused paraspinal regions of the lower lobes. When such a lung undergoes mechanical ventilation, regional tidal volumes are generally delivered into the low resistance and high compliance regions of “open” nondependent lung zones. Unless tidal volume is adjusted, the open regions will experience substantial mechanical forces compared to the regions that are occluded by liquid plugs. This results in overdistension of alveolar units in the open regions. Consequently, matrix adherent cells, foremost the epithelium and endothelium of the thin part of the blood gas barrier, may experience stress failure of the CSK and plasma membranes, which in turn trigger innate pro-inflammatory immune responses (66, 262, 267). On the macroscale, hyperinflation has been inferred from the grayscale patterns of thoracic CT images. Specifically, some patients with severe ARDS have lung regions with end-inspiratory grayscale values corresponding to air/tissue ratios that exceed those observed in maximally inflated normal lungs (257). However, it cannot be known from imaging alone whether the parenchyma surrounding such regions experiences abnormally high mechanical stresses, or perhaps these regions are overdistended because they have low bulk moduli on account of prior stress failure and/or tissue remodeling. While a contribution from mechanotransduction in shaping this injury manifestation is likely, it is not clear that the observation in and of itself establishes a cause and effect relationship or that airway inflation pressure safety limits can be derived from it. Nevertheless, it is clear that regional mechanics have to be considered in ALI and cellular responses to regional mechanical stresses play an important if not dominating role in the development, progression, and resolution of this pathophysiological condition of the lung.

An integrated View of Parenchymal Mechanics

The experimentally determined quasi-static stress-strain curve of lung tissue strips can be completely accounted for by various phenomenological models such as Eq. (6). However, despite the considerable progress described in this article, the relationship between the molecular organization of collagen-elastin fibers or potentially other ECM structures embedded in the proteoglycan gel and the stress-strain curve is not fully understood. Furthermore, the picture is even less clear in the in vivo lung where surface tension and cellular contraction-induced airway phenomena can further complicate the understanding of the quasi-static P-V curve or the dynamic impedance spectrum of the lung. A mechanistic link between molecular features at the nanoscale, atelectasis, and opening phenomena at the microscale and organ level function that incorporates the effects of heterogeneities would obviously be valuable. Indeed, such a link would help to better understand the pathophysiology observed in emphysema, fibrosis, and ALI, the main diseases in which the mechanical properties of the lung change in a manner that implies alteration in collagen and elastin elasticity or surface tension properties. In this section, we attempt to provide such a mechanistic link for the tissue strip as well as separately for the whole lung to the extent current knowledge allows it. Since some of the links are missing, the interpretation necessarily contains speculative elements. While future studies will fill in the missing links, generating structure-function relations with current knowledge is still a useful exercise since function can be easily measured, whereas structure and composition are available only to a limited resolution (e.g., CT imaging) or extent (biopsy).

Before going into the details of these structure-function relations, we must point out their relation to the concept of prestress that has been emphasized throughout this article. Since FRC represents the elastic equilibrium between the outward pulling of the chest and the inward pulling of the lung recoil, the externally imposed prestress is borne out by the various components of the lung parenchyma. Therefore, when discussing how these components contribute to the stress-strain or the P-V curve, it should also be realized that these are exactly the constituents that carry the prestress at a given strain or lung volume.

In Figure 19, we show a conceptual stress-strain curve of a lung parenchymal tissue strip during uniaxial stretching in a tissue bath. In region 1, the strip appears soft and the stress builds up slowly. The fibers are wavy and stretching causes them to start aligning with the direction of macroscopic strain. The alignment process is opposed by the compressibility and shear resistance of the proteoglycan matrix. It is also possible that some wavy elastin fibers that are much softer than the collagen fibers start to become straight. It is a balance between fiber stiffness in elongation and proteoglycan stiffness in compression and shear that determines their relative contribution to stress. As stretching proceeds, the fibers become progressively more aligned with macroscopic strain and their waviness begins to unfold in region 2. Here the crimps along the fibers produce a disproportionately larger stress and hence the stress-strain curve becomes nonlinear. In this region, proteoglycans may still contribute to this nonlinearity. Indeed, if all springs in a network are linear but their alignment is opposed by bond-bending, gradual recruitment occurs which causes the stress-strain curve to become more nonlinear as a consequence of more springs operating in parallel. Hence nonlinearity of a network does not necessarily reflect nonlinearity of its constituent elements. In region 3, most fibers are aligned and become progressively less wavy. The stress increases rapidly and eventually when all fibers are aligned, the stress-strain curve becomes linear again. This region is dominated by the stiff collagen especially at the highest strains. Because the tissue strip is in fluid bath, surface tension forces do not contribute to the stress. Also, there is no circulation in the tissue strip so that the vessels are likely collapsed. While this phenomenon has not been studied extensively, at low P_tp, lung elastance in isolated lungs is sensitive to perfusion due to altered organization of elastin fibers around the alveoli in the absence of perfusion (196).

Figure 19.

Schematic representation of the stress-strain curve in arbitrary units of a lung tissue strip during uniaxial stretch in tissue bath. The regions labeled 1, 2, and 3 correspond approximately to regions of different mechanisms contributing to the stress (see text for explanation).

The mechanisms contributing to whole lung behavior are considerably more complex than those at the tissue strip level. Furthermore, the shape of the P-V curve depends on the volume history of the lung. A schematic representation of the P-V curve is shown in Figure 20. First, the lung is inflated from the collapsed state to TLC. The primary mechanism contributing to the P-V curve can be summarized as follows. In region 1, P_tp increases but little change occurs in lung volume. This is due to the massive airway and alveolar collapse and the slight increase in volume is likely a result of the expansion of the larger airways. As P_tp further increases in region 2, the critical opening pressures of airways are gradually exceeded and around P_tp = 10 cmH₂O airways start to open in avalanches which recruit substantial alveolar airspaces and hence lung volume increase accelerates. The open regions now begin to expand and consequently surface film expansion and possibly proteoglycan compression and shear contribute to the curve. The slope of the curve here can be significantly steeper depending on the initial amount of collapse and the inflation rate. Next, in region 3, surface film and alveolar tissue elasticity dominate the rate of change of lung volume. Local fiber alignment and crimp unfolding can occur together with stretching of the elastin. Finally, once almost all alveoli are recruited and the fiber crimps are eliminated, collagen fiber recruitment starts to dominate region 4 with a sharp increase in the bulk modulus of the whole lung. During deflation these processes are likely reversed, although the adsorption-desorption kinetics of the surfactant are quite different during deflation than inflation that gives rise to lower closing pressures than opening pressures and a prominent hysteresis. Thus, airway and alveolar collapse happen at a P_tp much lower than 10 cmH₂O and the amount of air trapped behind the collapsed segments will determine RV.

Figure 20.

Schematic representation of the P-V curve of a lung during inflation from the collapsed state (black solid line) to total lung capacity (TLC), deflation (dashed line) to residual volume (RV), and during breathing with tidal volume (VT) from functional residual capacity (FRC). The regions labeled 1, 2, 3, and 4 correspond approximately to regions of different mechanisms contributing to the curve (see text for explanation).

During breathing, the situation is drastically different. In the normal lung, no airway or alveolar collapse occurs. The surface film undergoes much smaller stretches than during inflation from RV to TLC. Consequently, most of the hysteresis area is a result of the viscoelastic properties of the ECM. However, surface tension toward end-expiration is low due to the active role of pulmonary surfactant. Thus, the low stiffness of the lung along the P-V curve during tidal breathing is determined both by the efficiency of the surfactant and the mechanics of the ECM of the tissue. The latter is in turn dominated by the alignment processes of elastin and collagen, the stretching of elastin and perhaps to a smaller extent stretching of collagen with small contribution from compressing and shearing the proteoglycans. Additionally, the basal tone of interstitial and airway smooth muscle cells can mildly modulate the slope of the loop.

During diseases, these processes as well as their contribution to parenchymal mechanics can significantly change and some of these alterations have been described in this article. The characteristic changes in the stress-strain and the P-V curve are specific to the given disease state. For example, in the fibrotic lung parenchyma, the stress at any strain along the stress-strain curve would be higher than in the normal tissue. Similarly, in the ARDS, the P-V curve even starting from FRC significantly deviates from the small loop shown in Figure 20 and may be more similar to the air/saline curve in Figure 17. It is important to understand the specific mechanisms contributing to lung mechanics during breathing in the diseased lung and this is an area for future research. Specifically, new computational models will be necessary that incorporate not only the mechanics of the ECM and surface film, but the home-ostasis of lung cells during cyclic deformation over prolonged time periods. Such models should ultimately be able to predict changes in cellular phenotype and the associated alterations in ECM composition and structure and hence provide clinical insight into the progression or resolution of diseases.

Conclusion

Currently, we have a reasonable understanding of the mechanical and functional properties of the lung parenchyma at the macroscale both under normal and diseased conditions. This understanding stems from the mechanics of the surface film, the ECM and, to some extent, the mechanics and contractility of lung cells at the micro scale. A more fundamental understanding based on theories of the mechanics of molecules, their interaction in the surface film and in fibrils and fibers is still lacking and likely require novel experiments and multi-scale analyses. Prestress appears to play a major role both in the mechanics and function of the parenchyma. The effect of prestress on the homeostasis of a wide variety of cells is just beginning to receive attention.

The act of breathing generates cyclic variations in prestress and undoubtedly shapes the lung's response to noxious stimuli. The recognition of mechanical ventilation-associated lung injury and the recent insights regarding parenchymal stress failure in experimental models of emphysema underscore the delicate interplay between deforming stress and the biologic response of the lung to it. In the normal lung, these responses are generally considered adaptive, while following external or internal biological, biochemical and/or mechanical insults they are viewed as maladaptive. To a clinician or translational scientist, these distinctions are not always straightforward because adaptive and maladaptive processes often share the same biomarkers. Yet, their meaning can vary a great deal regionally in the lung as well as over time. It is easy to think of inflammation or apoptosis as injury manifestations, but it is hard to imagine effective tissue repair and return of normal function without them. Many have lamented that there is no specific treatment for a given parenchymal disease condition because single molecule/mediator-targeted interventions have not proven efficacious. But this notion is missing the point: every breath generates innumerable mechanotransduction events in the lung which are fundamental for the pathogenesis of the syndrome and likely for the repair as well. These mechanotransduction events can neither be understood nor influenced unless their relation to lung mechanical properties is identified. Thus, any future attempt to prevent the development, stop the progression or improve the conditions of parenchymal diseases will have to incorporate the influence of prestress and the mechanical properties of the parenchyma at the ECM and cellular levels.

In conclusion, understanding parenchymal mechanics has entered a new phase; it is now clear that mechanics, physiology, and cell biology are all involved in maintaining normal lung function and responding to injury or disease. Many aspects of this complex interaction have to be further studied both at the small scale and at the organ level because this is the only way a comprehensive understanding can be obtained. In this effort, both novel experimental and improved computational studies will play a significant role.