Abstract
Objective: The goal of this research was to position all the standardized 361 acupuncture points on the entire human body based on a 3-dimensional (3D) virtual body.
Materials and Methods: Digital data from a healthy Korean male with a normal body shape were obtained in the form of cross-sectional images generated by X-ray computed tomography (CT), and the 3D models for the bones and the skin's surface were created through the image-processing steps.
Results: The reference points or the landmarks were positioned based on the standard descriptions of the acupoints, and the formulae for the proportionalities between the acupoints and the reference points were presented. About 37% of the 361 standardized acupoints were automatically linked with the reference points, the reference points accounted for 11% of the 361 acupoints, and the remaining acupoints (52%) were positioned point-by-point by using the OpenGL 3D graphics libraries. Based on the projective 2D descriptions of the standard acupuncture points, the volumetric 3D acupoint model was developed; it was extracted from the X-ray CT images.
Conclusions: This modality for positioning acupoints may modernize acupuncture research and enable acupuncture treatments to be more personalized.
Key Words: : Acupuncture Points, Digital Korean Data, X-Ray Computed Tomography, Surface Reconstruction, 3-Dimensional Image Process
Introduction
Recent advances in technology in the computer hardware and software industries are now making it possible to address many issues that could not be addressed several decades ago. One of the most active research subjects is the human body, and, in medical science, vast amounts of data are being produced in qualitative and quantitative forms of images. In addition, many novel ways of representing medical knowledge have been introduced by integrating concepts of computer graphics and artificial intelligence as the data on the human body have accumulated, and medical knowledge definitely includes therapeutic experiences with old traditional medical systems.1,2
Recently, traditional medicine has set off in a quest for modernization through collaborations between different regions (interregional), different business sectors (intersectoral), and different areas of knowledge (interdisciplinary).3 As one of major treatment modalities in traditional medicine, acupuncture has been accepted for thousands of years in East Asia, and uses of this modality have spread all over the world.4 Although acupuncture has become a global therapeutic method in recent decades, controversies have been reported among acupuncturists regarding the locations of approximately one-fourth of the standard acupuncture points, raising doubts and uncertainty concerning the efficacy and the safety of acupuncture treatments, as well as causing difficulties in the fields of acupuncture research and education.5 To meet a growing international demand for standardization of acupuncture-point locations for education, research, and clinical practice, the World Health Organization (WHO) Western Pacific Regional Office started a project to reach a consensus on acupuncture-point locations.5 As a final result of the project, guidelines for the locations of the standard acupuncture points stipulated the methodology to be used to locate 361 acupoints on the skin's surface of the human body.
The lack of consensus on the specific locations of the acupoints may result from a lack of proper tools for specifying the acupoints. Precise localization of acupoints is a key issue in acupuncture research. Books and atlases for acupuncture usually describe the positions of acupoints in a two-dimensional (2D) projected plane. Almost a decade ago, computerized three-dimensional (3D models), such as the VOXEL-MAN system, were introduced as a useful way to localize the acupoints on the head, based on a virtual body.6 The use of such models is expected to advance learning and teaching of acupuncture and to contribute substantially to acupuncture research.
In this article, the positioning of all the standardized acupoints over the entire human body is extended to a 3D space. Using Korean digital data, a 3D virtual body was constructed with a skeletal structure and a skin surface in space from cross-sectional images generated by using computed tomography (CT). For locating acupoints on the skin's surface, the principles and methods, the WHO's standard acupuncture point location guidelines5 was adopted according to the WHO's descriptions, in which three combined methods were used to locate acupoints: (1) the anatomical landmark method; (2) the proportional bone (skeletal) measurement method; and (3) the finger–cun measurement method. Based on those methods, this research was particularly focused on how to position the anatomical landmarks from the skeletal structure and the skin's surface and how to represent the proportional features between the acupoints and the anatomical landmarks.
Materials and Methods
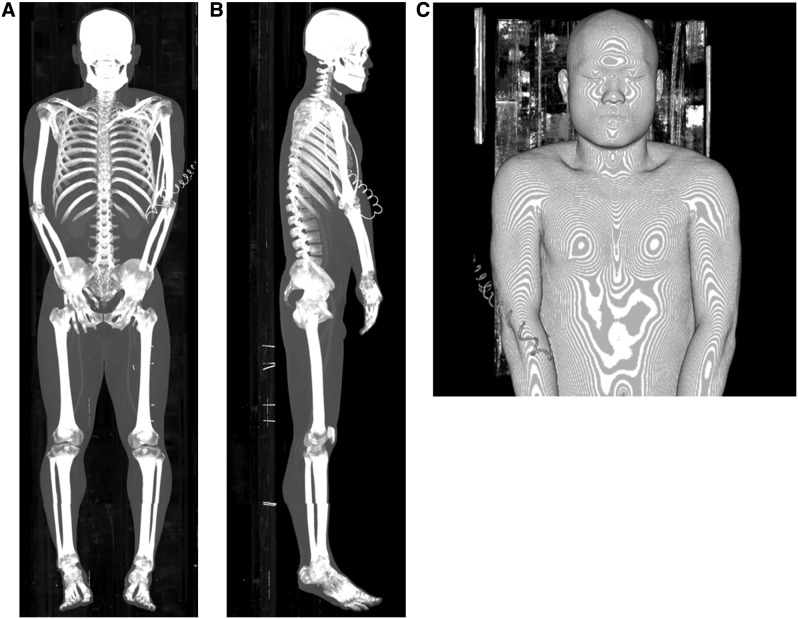
In 2003, Digital Korean data were constructed at the Catholic Institute for Applied Anatomy, College of Medicine, Catholic University of Korea, in Seoul, Korea. The data were managed and distributed by the Korean Institute of Science and Technology Information (KISTI).7 These data, developed through the use of CT, are composed of numerous sets of images from hundreds of cadavers, as well from as 6 living human beings (visit: http://dk.kisti.re.kr). Each body was X-ray scanned from head to foot with a CT machine in 1-mm spatial intervals. The CT-scanned images were saved in a DICOM file format with 512×512, 16-bit resolution. The current authors contracted with the KISTI and obtained permission to download the image data for use. The data for the current research were from healthy Korean males with normal body shapes. Figure 1 shows 2D side views of the data and a 3D image taken from the 3D viewer of ImageJ (http://rsbweb.nih.gov/ij/).
FIG. 1.
Digital Korean data: (A) coronal view and (B) sagittal view obtained by using maximum intensity projection with combined stacks of two-dimensional images. (C) A three-dimensional (3D) image of the data was constructed by using a 3D viewer from ImageJ.
For construction of the 3D surface models for the skin and the bones, serial DICOM files were transformed to corresponding 8-bit BMP files, which were put in binary form with the threshold values 10 and 110 for skin and bones, respectively. The binary images were subsequently inputted to the subroutine for binary dilations with a 3×3 structuring element to fill the holes inside the surface for skin or bones. Unnecessary areas were also cut in this process. After the borders of the objects in the serial images had been obtained, the target surface was isolated by using a connected component counting method. The counting method can be performed by examining the connectivity of voxels with their neighbors and assigning a unique label to each connected set found.8 The connected component-labeling algorithm is recursive and assumes 26-connectivity for the foreground voxels. After overlapping the original 8-bit gray BMP files with those of boundary 2-bit black-and-white images for the surface, the Marching Cube algorithm was applied for polygonizing the surface with triangle-shaped grids.9 Smoothed surfaces were obtained by calculating vectors normal to the surfaces of the triangles. The obtained 3D surface models were made viewable on a computer by using the OpenGL program.
All the processes for getting 3D surface models were carried out with a Microsoft Visual Studio 2008 software package installed on a personal computer with a Windows 7, 64-bit operating system. For convenience and to avoid computer memory problems, the entire human body was divided into eight parts: (1) head; (2) trunk; (3) pelvis; (4) leg; (5 and 6) left and right hands; and (7 and 8) left and right foot. For the head, half of the skull was exposed through the opaque skin for a visual effect. The opacity of OpenGL was used properly in the other parts to visualize the relationships between the acupuncture points and the skeletal structure. Zooming in and out, translating, and 3D rotating of the model were also performed by using the conventional graphic libraries from OpenGL.
For a given part of the body, the Cartesian coordinate system with its origin at the center of mass was chosen for the 3D image of the model. Based on that system, all the position values for the acupoints were determined and/or calculated. In 3D space, the position of a point can be specified with three values such as the x-, y-, and z-coordinates. Because the acupoints are distributed on the skin's surface, a constraint should be imposed in such a way that the acupoints reside on the skin's surface. Although the three values were introduced for positioning acupoints, that restriction made only two of the three positions' values independent.
All the 361 acupoints can be labeled by using the names of 14 meridians: Lung Meridian (LU); Large Intestine Meridian (LI); Stomach Meridian (ST); Spleen Meridian (SP); Heart Meridian (HT); Small Intestine Meridian (SI); Bladder Meridian (BL); Kidney Meridian (KI); Pericardium Meridian (PC); Triple Energizer Meridian (TE); Gall Bladder Meridian (GB); Liver Meridian (LR); Governor Vessel (GV); and Conception Vessel (CV). In Table 1, the forty-two reference points are shown with short descriptions of the anatomical features for their positioning. Just three of them (Yintang, apex of the patella [AP], and medial malleolus [MM]) do not have corresponding acupoints, but they show anatomical structures for landmarks on the body. Almost all the other reference points (10.8% among all the standardized acupoints) were chosen to be acupoints themselves.
Table 1.
Reference Points Positioned from the Anatomical Structures and Their Corresponding Acupoints
| Acupoint | Anatomical structure & position | Acupoint | Anatomical structure & position |
|---|---|---|---|
| CV 1 | Midpoint between the anus and genital organ | CV 2 | Pubic symphysis |
| CV 8 | Umbilicus | CV 16 | Xiphisternal junction |
| CV 22 | Suprasternal fossa | CV 23 | Hyoid tubercle |
| CV 24 | Mentolabial sulcus | ST 17 | Nipples |
| ST 35 | Patellar ligament | ST 41 | On the anterior aspect of the ankle |
| KI 3 | On the posteromedial aspect of the ankle | KI 10 | On the posteromedial aspect of the knee |
| GV 3 | In the depression inferior to the spinous process of L4 | GV 4 | In the depression inferior to the spinous process of L2 |
| GV 5 | In the depression inferior to the spinous process of L1 | GV 6 | In the depression inferior to the spinous process of T11 |
| GV 7 | In the depression inferior to the spinous process of T10 | GV 8 | In the depression inferior to the spinous process of T9 |
| GV 9 | In the depression inferior to the spinous process of T7 | GV 10 | In the depression inferior to the spinous process of T6 |
| GV 11 | In the depression inferior to the spinous process of T5 | GV 12 | In the depression inferior to the spinous process of T3 |
| GV 13 | In the depression inferior to the spinous process of T1 | GV 14 | In the depression inferior to the spinous process of C7 |
| BL 40z | On the posterior aspect of the knee | BL 60z | On the posterior aspect of the ankle |
| LU 5 | On the anterior aspect of the elbow | LU 9 | On the anterolateral aspect of the wrist |
| HT 1 | In the center of the axillary fossa | HT 3 | Anterior to the medial epicondyle of the humerus |
| HT 7 | On the anteromedial aspect of the wrist | SP 9 | On the tibial aspect of the leg |
| PC 3 | On the anterior aspect of the elbow | PC 7 | On the anterior aspect of the wrist |
| LI 5 | On the posterolateral aspect of the wrist | LI 11 | On the lateral aspect of the elbow |
| SI 5 | In the depression between the triquetrum bone & the ulnar styloid process | SI 8 | In the depression between the olecranon & the medial epicondyle of the humerus bone |
| Yintanga | Between the eyebrows | GV 17 | External occipital protuberance |
| b | Apex of the patella (AP) | b | Medial malleolus (MM) |
This point is not among the 361 acupuncture points.
AP and MM do not have corresponding acupoints, but show anatomical structures for landmarks on the body.
The subscript z is the z-component of the vector in the frame coordinates.
Determining the reference points started with putting a sphere, in the 3D virtual model, that could be moved to any position by pressing some character buttons on the computer's keyboard. After the sphere had been positioned onto a reference point as described in by the WHO,5 the three coordinate values in the model were recorded for later use. During this process, full advantage was taken of OpenGL's capacity for precise positioning on the skin's surface by rotating and translating the models and by zooming in and out on the models.
With the reference points, the positions of nearby acupoints could be calculated based on some formulae that were obtained from the pictorial and the textual descriptions by the WHO.5 Table 2 presents the formulae for the positions of 135 acupoints and shows the proportionalities between any two reference points. These points account for ∼37.4% of all the standardized acupuncture points. The main portions of the acupoints, in which the formulae are applicable, reside on three areas of the body: (1) the top of the head and (2 and 3) the front and the back parts of the trunk. The acupoints in these areas can be automatically positioned by determining the reference points. The formulae look like those in linear algebra, but have restrictions that the points be on the skin's surface. Some of the formulae are shown to be applicable in terms of the coordinates in the reference frame. For positioning acupoints in the other areas without formulae (51.8% of all acupoints), the same method was applied point-by-point as that for the case of determining the reference points.
Table 2.
Formulae for Positioning Acupoints with Reference Points
| Meridian | Formula for acupoints | ||
|---|---|---|---|
| CV | CV 3=(4×CV 2+CV 8)/5 | CV4=(3×CV 2+2×CV 8)/5 | CV 5=(2×CV 2+3×CV 8)/5 |
| CV 6=(1.5×CV 2+3.5×CV 8)/5 | CV 7=(CV 2+4×CV 8)/5 | CV 9=(7×CV 8+CV 16)/8 | |
| CV 10=(6×CV 8+2×CV 16)/8 | CV 11=(5×CV 8+3×CV 16)/8 | CV 12=(4×CV 8+4×CV 16)/8 | |
| CV 13=(3×CV 8+5×CV 16)/8 | CV 14=(2×CV 8+6×CV 16)/8 | CV 15=(CV 8+7×CV 16)/8 | |
| CV17=(7×CV 16+2×CV 22)/9 | CV 18=(5×CV 16+4×CV 22)/9 | CV 19=(3×CV 16+6×CV 22)/9 | |
| CV20=(2×CV 16+7×CV 22)/9 | CV 21=(CV 16+8×CV 22)/9 | ||
| ST | ST 19 y=ST 17y/2, ST 19z=CV 14z | ST 20 y=ST 17y/2, ST 20z=CV 13z | ST 21y=ST 17y/2, ST 21z=CV 12z |
| ST 22 y=ST 17y/2, ST 22z=CV 11z | ST 23 y=ST 17y/2, ST 23z=CV 10z | ST 24y=ST 17y/2, ST 24z=C V9z | |
| ST 25 y=ST 17y/2, ST 25z=CV 8z | ST 26 y=ST 17y/2, ST 26z=CV 7z | ST 27y=ST 17y/2, ST 27z=C V5z | |
| ST 28 y=ST 17y/2, ST 28z=CV 4z | ST 29 y=ST 17y/2, ST 29z=CV 3z | ST 30y=ST 17y/2, ST 30z=CV 2z | |
| ST 36=(13×ST 35+3×ST 41)/16 | ST 37=(10×ST 35+6×ST 41)/16 | ST 38=(8×ST 35+8×ST 41)/16 | |
| ST 39=(7×ST 35+9×ST 41)/16 | ST 40=(8×ST 35+8×ST 41)/16 | ||
| KI | KI 7=(13×KI 3+2×KI 10)/15 | KI 8=(13×KI 3+2×KI 10)/15 | KI 9=(10×K I3+5×KI 10)/15 |
| KI 11y=CV2y+0.5 Bcun, KI 11z=CV 2z | KI 12y=CV 3y+0.5 Bcun, KI 12z=CV3z | KI 13y=CV 4y+0.5 Bcun, KI 13z=CV 4z | |
| KI 14y=CV5y+0.5 Bcun, KI 14z=CV 5z | KI 15y=CV 7y+0.5 Bcun, KI 15z=CV7z | KI 16y=CV 8y+0.5 Bcun, KI 16z=CV 8z | |
| KI 17y=CV10y+0.5 Bcun, KI 17z=CV 10z | KI 18y=CV 11y+0.5 Bcun, KI 18z=CV 11z | KI 19y=CV 12y+0.5 Bcun, KI 19z=CV 12z | |
| KI 20y=CV13y+0.5 Bcun, KI 20z=CV 13z | KI 21y=CV 14y+0.5 Bcun, KI 21z=CV 14z | KI 22y=CV 16y+2.0 Bcun, KI 22z=CV 16z | |
| KI 23y=CV17y+2.0 Bcun,KI 23z=CV 17z | KI 24y=CV 18y+2.0 Bcun, KI 24z=CV 18z | KI 25y=CV 19y+2.0 Bcun, KI 25z=CV 19z | |
| KI 26y=CV20y+2.0 Bcun, KI 26z=CV 20z | KI 27y=CV 21y+2.0 Bcun, KI 27z=CV 21z | ||
| SP | SP 13y=(0.7×CV 8y+4.3×CV 2y)/5–4 Bcun, SP 13z=(0.7×CV8z+4.3×CV 2z)/5 | SP 14y=(3.7×CV 8y+1.3×CV2y)/5×4 Bcun, SP 14z=(3.7×CV 8z+1.3×CV 2z)/5 | SP 15y=CV 8y – 4 Bcun, SP 15z=CV 8z |
| SP 16y=CV 11y+4 Bcun, SP 16z=CV 11z | SP 17y=CV 16y+6 Bcun, SP 17z=CV16z | SP 18y=CV 17y+6 Bcun, SP 18z=CV 17z | |
| SP 19y=CV18y+6 Bcun, SP 19z=CV 18z | |||
| LR | LR 7x=SP9x – 1 Bcun, LR 7z=(13×(AP)z+2×(MM)z)/15 | LR 12y=CV2y+2.5 Bcun, LR 12z=CV 2z | LR 14y=ST 19y+4 Bcun, LR 14z=ST 19z |
| GV | GV 18=(11.0×GV 17+1.5×Yintang)/12.5a | GV 19=(9.5×GV 17+3.0×Yintang)/12.5a | GV 20=(7.5×GV 17+4.5×Yintang)/12.5a |
| GV 21=(6.0×GV 17+6.5×Yintang)/12.5a | GV 22=(4.5×GV 17+8.0×Yintang)/12.5a | GV 23=(3.5×GV 17+9.0×Yintang)/12.5a | |
| GV 24=(3.0×GV 17+9.5×Yintang)/12.5a | |||
| BL | BL 3a | BL 4a | BL 5a |
| BL 6a | BL 7a | BL 8a | |
| BL 9a | |||
| BL 11y=GV 13y+1.5 Bcun, BL 11z=GV 13z | BL 13y=GV 12y+1.5 Bcun, BL 13z=GV 12z | BL 15y=GV 11y+1.5 Bcun, BL 15z=GV 11z | |
| BL 16y=GV 10y+1.5 Bcun, BL 16z=GV 10z | BL 17y=GV 9y+1.5 Bcun, BL 17z=GV 9z | BL 18y=GV 8y+1.5 Bcun, BL 18z=GV 8z | |
| BL 19y=GV 7y+1.5 Bcun, BL 19z=GV 7z | BL 20y=GV 6y+1.5 Bcun, BL 20z=GV 6z | BL 22y=GV 5y+1.5 Bcun, BL 22z=GV 5z | |
| BL 23y=GV 4y+1.5 Bcun, BL 23z=GV 4z | BL 25y=GV 3y+1.5 Bcun, BL 25z=GV 3z | BL 37=(8×BL 36+6×BL 40)/14 | |
| BL 41y=BL 12y+1.5 Bcun, BL 41z=BL 12z | BL 42y=BL 13y+1.5 Bcun, BL 42z=BL 13z | BL4 3y=BL 14y+1.5 Bcun, BL 43z=BL 14z | |
| BL 44y=BL 15y+1.5 Bcun, BL 44z=BL 15z | BL 45y=BL 16y+1.5 Bcun, BL 45z=BL 16z | BL 46y=BL 17y+1.5 Bcun, BL 46z=BL 17z | |
| BL 47y=BL 18y+1.5 Bcun, BL 47z=BL 18z | BL 48y=BL19y+1.5 Bcun, BL 48z=BL 19z | BL 49y=BL 20y+1.5 Bcun, BL 49z=BL 20z | |
| BL 50y=BL 21y+1.5 Bcun, BL 50z=BL 21z | BL 51y=BL 22y+1.5 Bcun, BL 51z=BL 22z | BL 52y=BL 23y+1.5 Bcun, BL 52z=BL 23z | |
| BL 53y=BL 28y+1.5 Bcun, BL 53z=BL 28z | BL 54y=BL 30y+1.5 Bcun, BL 54z=BL 30z | BL 55z=(14×BL 40z+2×BL 60z)/16 | |
| BL 56z=(11×BL 40z+5×BL 60z)/16 | BL 57z=(8×BL 40z+8×BL 60z)/16 | BL 58z=(7×BL 40z+9×BL 60z)/16 | |
| BL 59z=(3×BL 40z+13×BL 60z)/16 | |||
| LU | LU 6=(7×LU 5+5×LU 9)/12 | LU 8=(LU 5+11×LU 9)/12 | |
| HT | HT 2=(3×HT 1+6×HT 3)/9 | HT 4=(1.5×HT 3+10.5×HT 7)/12 | HT 5=(HT 3+11 HT 7)/12 |
| HT 6=(0.5×HT 3+11.5×HT 7)/12 | |||
| PC | PC 1=(SP 18+ST 17)/2 | PC 4=(5×PC 3+7×PC 7)/12 | PC 5=(3×PC 3+9×PC 7)/12 |
| PC 6=(2×PC 3+10×PC 7)/12 | |||
| LI | LI 6=(9×LI 5+3×LI 11)/12 | LI 7=(7×LI 5+5×LI 11)/12 | LI 8=(4×LI 5+8×LI 11)/12 |
| LI 9=(3×LI 5+9×LI 11)/12 | LI 10=(2×LI 5+10×LI 11)/12 | ||
| SI | SI 7=(7×SI 5+5×SI 8)/12 | SI 15y=2 Bcun from the posterior median line, SI 15z=GV 14z | |
| GB | GB 15a | GB 16a | GB 17a |
| GB 18a | GB 19a | ||
Acupoints on the surface of the top of the head. Refer to Fig. 2 for diagram representation.
The subscripts x, y, and z are the x-, y-, and z-components, respectively, of the vectors in the frame coordinates.
Bcun, unit of length on the body; the distance between the left and the right nipples corresponds to 8 Bcun, AP apex of the patella; MM, medial malleolus.
Results
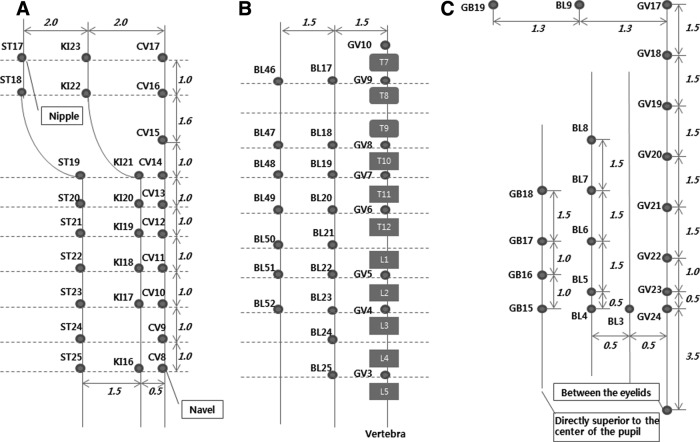
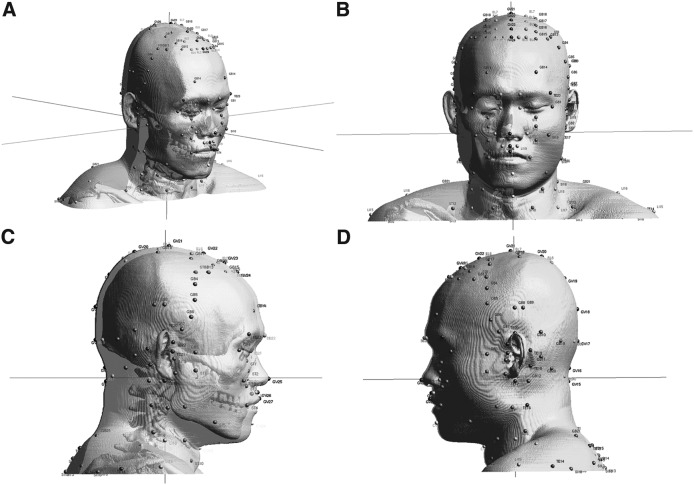
The acupoints around the top of the head were determined by using two reference points: (1) the external occipital protuberance in the back of the head (GV 17) and (2) the Yintang (the central point between the eyelids) on the face. The proportionalities between the acupoints are pictorially presented in Figure 2. Most acupoints in the face and on the side of the head were determined point-by-point following the descriptions used for the skin's surface and the skull's structure. All the acupoints on the head are depicted from various views, as shown in Figure 3. The right side of the head's skin was made to be nonopaque so that the skull's structure could be seen. The acupoints on the left side were obtained by using the left–right symmetry of the body. However, if some deviations from coordinate space exist in the midsagittal plane of the body, a proper adjustment can be made in the future.
FIG. 2.
A diagram for positioning acupoints on the corresponding area of the (A) anterior and the (B) posterior aspects of the trunk, and the (C) head. The acupoints on the anterior and the posterior aspects of the trunk are depicted in the projected two-dimensional (2D) plane. Because the shape of head is spherical, the acupoints are positioned in a flattened 2D plane in a way similar to that used to mark latitude and longitude coordinates on a world map. The numbers in the diagrams represent the ratios of the distances between the acupoints and the reference points.
FIG. 3.
Three-dimensional views with positioned acupoints around the head from various sides: (A) general view; (B) front view; (C) right view; and (D) left view.
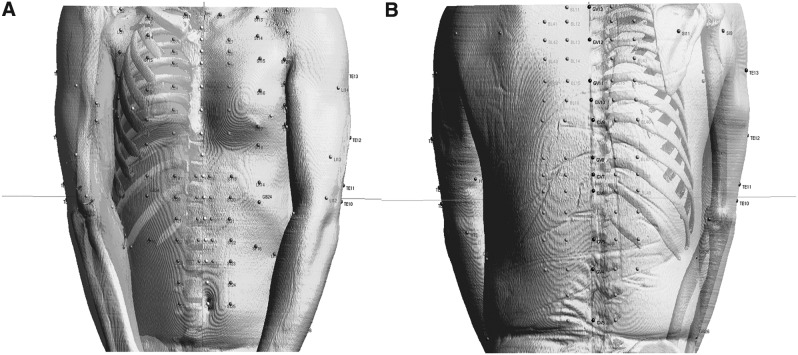
The distributions of acupoints on the anterior and the posterior aspects of the trunk show simple patterns, such as a lattice on the skin's surface (Fig. 2). As for the acupoints on the anterior aspect, the three reference points on the surface of the thoracic and the abdominal parts were chosen: two nipples (ST 17) and a navel (CV 8). The nearby acupoints in the KI and the ST meridians were distributed like a web, connecting the points with specified proportional distances from the anterior median line of the CV meridian. Most positions of the acupoints on the posterior aspect were determined by using the positions of the spinal vertebra, information that can be extracted from the skeletal structure. The nearby acupoints in the BL meridian were also distributed along the posterior median line with the GV acupoints, as shown in Figure 4.
FIG. 4.
Three-dimensional views with positioned acupoints on the (A) anterior aspect and the (B) posterior aspect of the trunk.
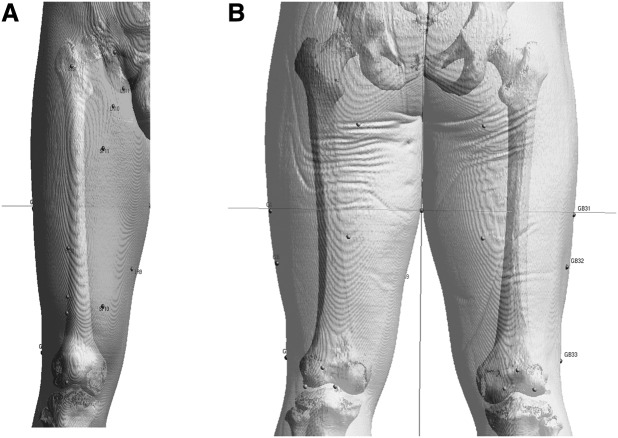
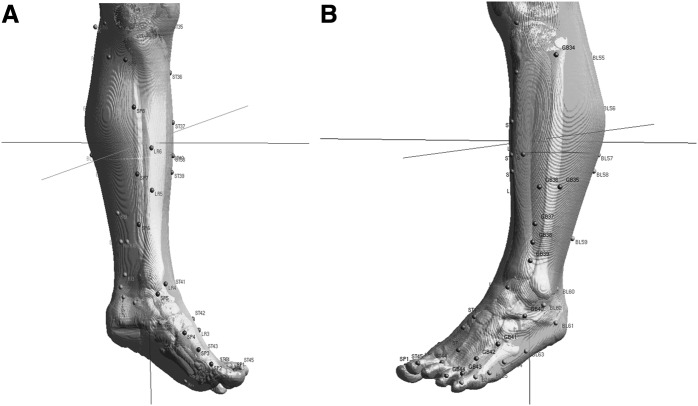
The acupoints in the other areas—such as the pelvis, leg, hands, and feet—were also positioned on the 3D virtual body. These regions have such large spatial curvatures in the shape of the body's skin that they do not show the systematic structures shown in the anterior and the posterior aspects of the trunk and the top of the head. The positions of many acupoints in the sacral region depend on the structure of the pelvic bones and the posterior sacral foramina, as shown in Figure 5. Most acupoints of the Bladder meridian in this region are distributed over the back down to the posterior aspect of the knee (Fig. 6). The acupoints on the left hand and the left foot are presented in Figures 7 and 8. One of the most frequently used acupoints is ST 36 (Zusanli) on the anterior aspect of the leg between the two reference acupoints ST 35 and ST 41.
FIG. 5.
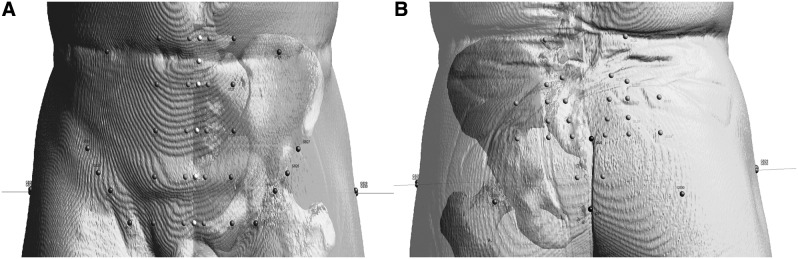
Three-dimensional views with positioned acupoints on the (A) anterior aspect and the (B) posterior aspect of the pelvis.
FIG. 6.
Three-dimensional views with positioned acupoints on the (A) anterior aspect and the (B) posterior aspect of the upper leg.
FIG. 7.
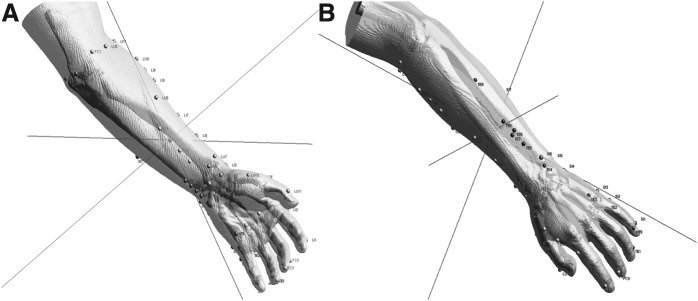
Three-dimensional views with positioned acupoints on the (A) anterior aspect of the forearm and palm, and on the (B) posterior aspect of the wrist and the dorsum of the hand.
FIG. 8.
Three-dimensional views with positioned acupoints from the (A) medial aspect of the foot to the tibial aspect of the leg and on the (B) fibular aspect of the leg.
Discussion
Acupuncture meridians in traditional Oriental medicine are known to be channels connecting specific points on the surface of the body to corresponding internal organs. The meridians have been considered to reflect a systematic network of empirical knowledge that functions as the basis for acupuncture treatment.10 The therapeutic effects of acupuncture meridian treatments are being increasingly accepted worldwide,11 so it is imperative to elucidate the mechanism of acupuncture's effects in terms of modern scientific concepts and terminologies.12,13
Recently, many research laboratories, as well as clinical institutes and hospitals, have been carrying out acupuncture research with various types of setups equipped with modern instruments and advanced technologies, such as magnetic resonance imaging (MRI), functional MRI, synchrotron radiation phase-contrast X-ray CT imaging, and positron emission tomography.14–17 In the clinical research, imaging from CT has been used to investigate the acupuncture points in relation to the body's anatomical landmarks and structures.18,19 A clinical study was performed to investigate acupuncture treatment regimens for a specific disease, low-back pain, and that study suggested a new model for the visualization of a data-driven 3D meridian system of biomedical information about meridians and acupoints.20 All this information can be used to formulate a modern basis for understanding the structure and the function of the acupuncture meridian network on the human body.
The partial positioning of acupuncture points and the visualization of the blood-vessel networks under the skin have been achieved with the image datasets of the Visible Human Project.21 With the digitalized anatomical cryosection images and the CT images of humans, the color variations under the skin were investigated at the acupoints on the anterior and the posterior aspects of the trunk. Color localizations at the acupoints and directional patterns along the meridians were presented at specific depths under the skin by comparisons with the nearby surrounding points. This kind of study was suggested as a unique method for gaining a systematic understanding of acupuncture-meridian–related anatomy in 3D space.
One limit of this current research with images of X-ray CT may be the result of difficulties in visualizing the distributions of the blood vessels, muscles, and tendons, which are important anatomical landmarks for positioning certain acupoints. This positioning method can be applied to any group of images taken from other techniques, such as magnetic resonance tomography, and/or from imaging tools combined with CT. The method can also be used as a computerized medical tool for designing personalized medicine, considering the condition of each patient. Including the depth information at the acupuncture points, precise positioning may be possible so that meridians can be used as drug-delivery pathways for pharmacoacupuncture therapy. A second limitation of this current research is that the method may not cover some acupuncture protocols, for example, the Hara diagnosis in which the acupoints are located by radial pulse changes. With more combined efforts from basic and clinical research, biomedical information on the acupuncture and meridian system should be complete in the near future. The third limitation is that the 3D correlations do not, at this stage, explain the deep extensions of the meridian systems as described in classical or empirical acupuncture.
Conclusions
3D mapping of the human body by X-ray CT provides a novel method of tracing the meridian systems, hence providing useful knowledge toward the modernization of clinical acupuncture practice.
Acknowledgments
The author (J.K.) would like to thank K.S. Soh, PhD, and M.S. Chung, MD, PhD, for helpful advice. The current authors used the Digital Korean data that were produced and distributed by the Catholic Institute for Applied Anatomy, College of Medicine, Catholic University of Korea and the Korean Institute of Science and Technology Information.
Disclosure Statement
No financial conflicts of interest exist.
References
- 1.Höhne K, Pflesser B, Pommert A, et al. . A new representation of knowledge concerning human anatomy and function. Nature Med. 1995;1:506–511 [DOI] [PubMed] [Google Scholar]
- 2.Pommert A, Höhne K, Pflesser B, et al. . Creating a high-resolution spatial/symbolic model of the inner organs based on the visible human. Med. Image Anal. 2001;5:221–228 [DOI] [PubMed] [Google Scholar]
- 3.Xu Q, Bauer R, Hendry B, et al. . The quest for modernization of traditional Chinese medicine. BMC Complement Altern Med. 2013;13:132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.National Institutes of Health (NIH) Consensus Development Panel on Acupuncture Acupuncture—NIH consensus conference. JAMA. 1998;280:1518–15249809733 [Google Scholar]
- 5.World Health Organization (WHO) WHO standard acupuncture point location. In: WHO Standard Acupuncture Point Locations in the Western Pacific Region. Geneva: WHO Western Pacific Region; 2008:1–14 [Google Scholar]
- 6.Zheng L, Qin B, Zhuang T, Tiebe U, Höhne K. Localization of acupoints on a head based on a 3D virtual body. Image and Vision Computing. 2005;23:1–9 [Google Scholar]
- 7.Lee SH, Lee SB. Production and usage of Korean human information in KISTI. J Korea Contents Assn. 2010;10(5):416–421 [Google Scholar]
- 8.Nikolaidis N, Pitas I. 3-D Image Processing Algorithms. New York: John Wiley & Sons; 2000 [Google Scholar]
- 9.Lorensen W, Cline H. Marching cubes: A high resolution 3D surface construction algorithm. Computer Graphics. 1987;21:163–169 [Google Scholar]
- 10.Yin C, Koh H. What's the original concept of meridian and acupuncture point in Oriental medicine?—a perspective of medical history [in Korean]. Uisahak. 2005;14:137–150 [PubMed] [Google Scholar]
- 11.Han J, Ho Y. Global trends and performances of acupuncture research. Neurosci Biobehav Rev. 2011;35(3):680–687 [DOI] [PubMed] [Google Scholar]
- 12.Soh K. Bonghan circulatory system as an extension of acupuncture meridians. J Acupunct Meridian Stud. 2009;2(2):93–106 [DOI] [PubMed] [Google Scholar]
- 13.Longhurst J. Defining meridians: A modern basis of understanding. J Acupunct Meridian Stud. 2010;3(2):67–74 [DOI] [PubMed] [Google Scholar]
- 14.Kim J, Bae K, Hong K, Han S, Soh K. Magnetic resonance imaging and acupuncture: A feasibility study on the migration of tracers after injection at acupoints of small animals. J Acupunct Meridian Stud. 2009;2(2):152–158 [DOI] [PubMed] [Google Scholar]
- 15.Liu H, Xu J, Li L, Shan B, Nie B, Xue J. fMRI evidence of acupoints specificity in two adjacent acupoints. Evid Based Complement Alternat Med. 2013;2013:932581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang D, Yan X, Zhang X, et al. . Synchrotron radiation phase-contrast X-ray CT imaging of acupuncture points. Anal Bioanal Chem. 2011;401(3):803–808 [DOI] [PubMed] [Google Scholar]
- 17.Liu H, Shen X, Tang H, Li J, Xiang T, Yu W. Using microPET imaging in quantitative verification of the acupuncture effect in ischemia stroke treatment. Sci Rep. 2013;3:1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Groenemeyer D, Zhang L, Schirp S, Baier J. Localization of acupuncture points BL25 and BL26 using computed tomography. J Altern Complement Med. 2009;15(12):1285–1291 [DOI] [PubMed] [Google Scholar]
- 19.Koo S, Kim S, Kim Y, Kang S, Choi S. Measuring the location of PC8 acupuncture point using X-ray radiography in healthy adults [in Korean]. Korean J Oriental Med. 2010;16:123–126 [Google Scholar]
- 20.Lee I, Lee S, Kim S, Lee H, Park H, Chae Y. Visualization of the meridian system based on biomedical information about acupuncture treatment. Evid Based Complement Alternat Med. 2013;2013:872142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kim J, Kang D, Soh K, Kim S. Analysis on postmortem tissues at acupuncture points in the image datasets of visible human project. J Altern Complement Med. 2012;18:120–129 [DOI] [PubMed] [Google Scholar]