Is Memory Search Governed by Universal Principles or Idiosyncratic Strategies?

Abstract

Laboratory paradigms have provided an empirical foundation for much of psychological science. Some have argued, however, that such paradigms are highly susceptible to idiosyncratic strategies and that rather than reflecting fundamental cognitive principles, many findings are artifacts of averaging across participants who employ different strategies. We develop a set of techniques to rigorously test the extent to which average data are distorted by such strategy differences and apply these techniques to free recall data from the Penn Electrophysiology of Encoding and Retrieval Study (PEERS). Recall initiation showed evidence of subgroups: the majority of participants initiate recall from the last item in the list, but one subgroup show elevated initiation probabilities for items 2–4 back from the end of the list and another showed elevated probabilities for the beginning of the list. By contrast, serial position curves and temporal and semantic clustering functions were remarkably consistent, with almost every participant exhibiting a recognizable version of the average function, suggesting that these functions reflect fundamental principles of the memory system. The approach taken here can serve as a model for evaluating the extent to which other laboratory paradigms are influenced by individual differences in strategy use.

Much of psychological research relies on laboratory paradigms that have been designed to measure specific cognitive processes. Each area of research has its own set of laboratory paradigms, for example, psychologists studying perception use detection and discrimination tasks (Chun & Wolfe, 2001), psychologists studying memory use list recall and recognition tasks (Kahana, 2012), psychologists studying language use word naming and lexical decision tasks (Balota et al., 2007), and those studying decision making use preference and temporal discounting tasks (Loewenstein & Prelec, 1993). An assumption of such paradigm-centric research is that participants’ performance on laboratory tasks reflects the operation of the targeted cognitive processes. However, all but the simplest task is likely to rely on multiple processes. Moreover, many researchers have argued that performing a task involves selecting strategies from a cognitive toolbox to create ad hoc solution to challenges posed by the task (Gigerenzer, 2008; Gigerenzer, Hoffrage, & Goldstein, 2008; Marewski & Schooler, 2011; Rieskamp & Otto, 2006; Simon, 1956) and that the particular strategy a person selects can be highly sensitive to their individual goals and preferences (Carstensen, Isaacowitz, & Charles, 1999).

Indeed, there has been much intrest in the extent to which strategy use accounts for major findings in many areas including decision making (Payne, Bettman, & Johnson, 1988), frequency judgment (Tversky & Kahneman, 1973), students’ study habits (Hartwig & Dunlosky, 2011), working memory (Cusack, Lehmann, Veldsman, & Mitchell, 2009; Ericsson & Kintsch, 1995; Turley-Ames & Whitfield, 2003), and long-term memory (Delaney, Spirgel, & Toppino, in press; Kahneman & Wright, 1971; Paivio & Yuille, 1969; Wright & Kahneman, 1971) as well as for differences between individuals (Bailey, Dunlosky, & Kane, 2008; Coyle, Read, Gaultney, & Bjorklund, 1998) and groups of individuals such as younger and older adults (Dunlosky & Hertzog, 1998, 2000; Mata, Schooler, & Rieskamp, 2007). These views, while not generally framed as direct criticisms of using laboratory tasks to study particular cognitive systems (but see, Hintzman, 2011), raise the question of whether performance on a laboratory task is so contaminated by individual differences in strategy as to be uninformative or even misleading about underlying cognitive processes.

To answer this question it is not enough to qualitatively describe individual differences in task behavior; rather, one must show quantitatively that individuals deviate from the average in a way that substantially distorts the average pattern. Such quantitative tests are rare. Yet, given that data from laboratory paradigms provide the empirical foundation for much of psychological science, it is critical that the influence of idiosyncratic strategies be rigorously assessed. Here we develop an approach for distinguishing idiosyncratic contributes relatively strategies from core cognitive processes and apply it to a classic memory paradigm—free recall of word lists. We choose free recall both because it reveals a very detailed empirical pattern that has deeply influenced moderen theories of memory (Davelaar, Goshen-Gottstein, Ashkenazi, Haarmann, & Usher, 2005; Farrell, 2012; Polyn, Norman, & Kahana, 2009) and because, of all the major memory tasks, it provides participants with the most opportunity to develop idiosyncratic encoding and retrieval strategies (Dalezman, 1976; Delaney & Knowles, 2005; Delaney et al., in press; Hintzman, 2011; Murdock & Metcalfe, 1978; Sahakyan & Delaney, 2003; Stoff & Eagle, 1971).

Free Recall and The Dynamics of Memory Search

Many laboratory memory tasks require participants to retrieve very specific information, thereby imposing strong constraints on the scope of memory search. For example, serial recall forces participants to reconstruct the temporal order of events. Recognition provides a very strong external retrieval cue that constrains the scope of memory search as does the paired associates task. The great advantage of these tasks is that the strong constraints allow researchers to study specific memory processes while controlling other factors. Outside the laboratory, however, we must often search memory without strong external retrieval cues. If I ask you what you did last weekend, you are likely to search your memory for the various things you did, but the question itself does not provide any strong cues to guide you to a particular activity, nor does it constrain the order in which you recall your activities. Instead, you must take the vague cue of “what you did last weekend” and elaborate it to retrieve a specific activity. Once a first activity is retrieved associations between various activities are likely to govern their order of recall.

Many aspects of this natural memory search are captured by the free recall task, which allows participants to recall the studied items in any order. Therefore, the order of a sequence of recalls provides a window on memory search, allowing researchers to study search processes with precision and rigor. Free recall has helped illuminate important principles of memory search such as recency (recent events tend to be more memorable than distant events; Murdock, 1962), primacy (the first events in a sequence tend to be more memorable; Murdock, 1962), temporal contiguity (items that were experienced close together in time tend to be recalled contiguously; Kahana, 1996), and semantic proximity (items that are semantically related tend to be recalled together; Bousfield, Sedgewick, & Cohen, 1954; Howard & Kahana, 2002; Romney, Brewer, & Batchelder, 1993).

We focus on four functions that provide a summary of the dynamics of memory search in free recall: The Serial Position Curve (SPC), the Probability of First Recall (PFR) function, the Lag-Conditional Response Probability (Lag-CRP) function, and the Semantic-Conditional Response Probability (Semantic-CRP) function. To illustrate the functions we use data from The Penn Electrophysiology of Encoding and Retrieval Study. The study is described in detail in the methods section, but briefly, participants studied multiple lists, each composed of 16 words, for immediate free recall.

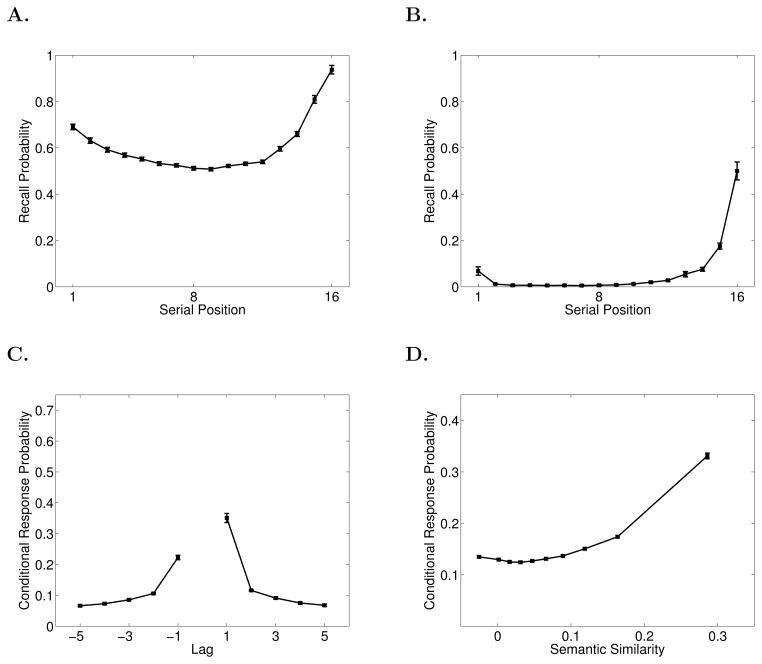
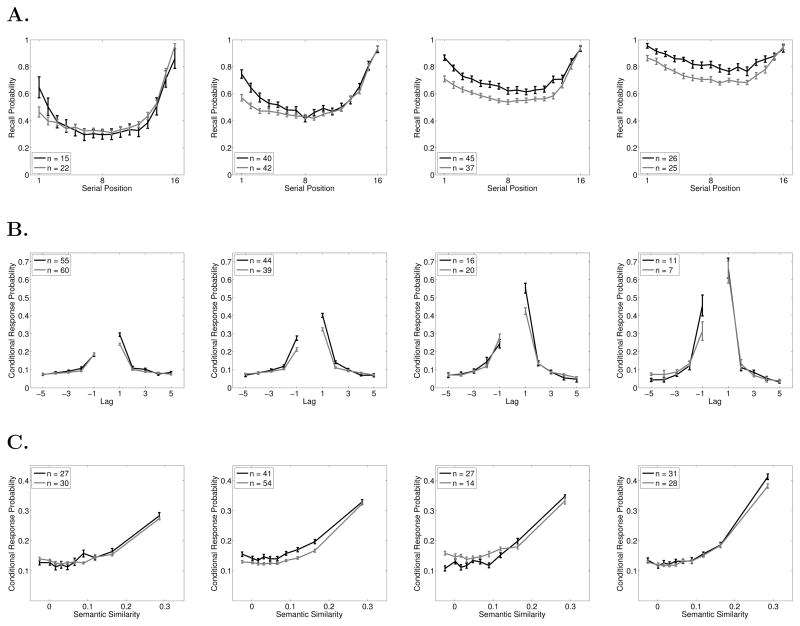
The first function we consider is the classic SPC, which breaks down overall probability of recall by serial position at presentation. The SPC reveals the primacy and recency effects (Figure 1A). In immediate free recall, recency dominates and the primacy effect is modest. The remaining functions we consider provide a detailed picture of the dynamics of memory search by measuring how participants initiate recall and how they transition among items after initiation.

Figure 1.

Data from the Penn Electrophysiology of Encoding and Retrieval Study. A. Serial Position Curve. B. Probability First Recall function. A. Lag-Conditional Response Probability function. D.Semantic-Conditional Response Probability function. See the text for details on how these functions are computed. Error bars are 95% within-subject confidence intervals (Loftus & Masson, 1994).

Recall initiation can be examined by looking at which item participants tend to recall first and computing a PFR function; a SPC based only on the very first item recalled (Hogan, 1975; Howard & Kahana, 1999; D. Laming, 1999). As seen in Figure 1B, participants tend to initiate recall from the last serial position (Deese & Kaufman, 1957).

After recall initiation, subsequent recalls are driven by associations between the just-recalled word and other words in the lexicon (Kahana, Howard, & Polyn, 2008). Both preexisting semantic associations and newly formed episodic, or temporal, associations exert a powerful influence on recall transitions. In general if a participant has just recalled item i from the list, we can measure how i’s associations with other items influence which item, j, is recalled next. To measure the influence of temporal associations we can compute the probability that i is followed by j conditional on the distance, or lag, between i and j in the original list. For example, if i = 5 and j = 6 we would have a lag, j-i, of +1. Lag-CRP functions give these probabilities for a variety of lags and are computed by dividing the number of times a transition of a given lag was actually made by the number of times it could have been made (Kahana, 1996). Note that lags that would lead outside the list boundaries are not considered possible (e.g., a +2 lag is impossible after recalling the 15^th item in a 16–item list), nor are transitions to items that have already been recalled. Lag-CRP functions (Figure 1C) reveal the contiguity effect: transitions are most likely between temporally adjacent items and decrease in probability with increasing lag. In immediate free recall, the contiguity effect tends to be larger for the first few items recalled than for later output positions due to the strong recency effect (Davelaar et al., 2005; Sederberg, Howard, & Kahana, 2008). Therefore we exclude the first two outputs from the Lag-CRP analyses in this paper. The Lag-CRP also shows a forward asymmetry such that forward transitions are more likely than backward transitions for small absolute values of lag.

Lag-CRPs show how the probability of transitioning between two items is influenced by the proximity (i.e., lag) of those items along a temporal associative dimension, but semantic associations also exert a powerful influence on memory search (Bousfield, 1953; Romney et al., 1993). To measure the influence of semantic associations on transition probabilities we can employ the same procedure used for temporal associations but replace temporal lag with a measure of semantic proximity. We use Latent Semantic Analysis (LSA; Landauer & Dumais, 1997) to measure semantic proximity. LSA allows one to measure the semantic relationship between two words as the cosine of the angle between the words’ representations in a multidimensional model of semantic space. Using LSA values we can compute the semantic similarity between item i and all other items in the list. We can then bin pairs of items based on their semantic similarity and calculate the probability of making a transition from i to j based on the similarity bin of that pair. As seen in the resulting Semantic-CRP function (Figure 1D), there is a strong tendency to make transitions between semantically related words (Howard, Addis, Jing, & Kahana, 2007; Howard & Kahana, 2002; Sederberg, Miller, Howard, & Kahana, 2010).

These effects are quite robust. To our knowledge there is no published failure to find a temporal contiguity effect in a standard free recall task (but see McDaniel, Cahill, Bugg, & Meadow, 2011, for a failure to find contiguity in recall of lists composed of orthographically distinct items), and the effect also emerges in a variety of other tasks such as high confidence old/new recognition responses(Schwartz, Howard, Jing, & Kahana, 2005) and intrusions in paired-associate recall (Davis, Geller, Rizzuto, & Kahana, 2008). Robust semantic clustering effects in recall of categorized lists have been widely reported (Bousfield et al., 1954; Romney et al., 1993). While the semantic proximity effect in uncategorized lists revealed by using LSA to construct Semantic-CRPs has not been investigated as extensively, the effect is quite consistent across multiple independent datasets (Bridge, 2006; Howard & Kahana, 1999; Kahana & Howard, 2005; Kahana, Howard, Zaromb, & Wingfield, 2002; Sederberg et al., 2006; Zaromb et al., 2006) as illustrated by the meta-analyses of Sederberg et al. (2010). Recency, as noted above, is somewhat more variable, being sensitive to the ratio of the length of the delay between successive items to the length of the delay between the final item and recall (Glanzer & Cunitz, 1966; Postman & Phillips, 1965), and other factors such as presentation modality (Murdock & Walker, 1969). Primacy also varies, being closely tied to the frequency, recency, and spacing of rehearsals (D. Laming, 2008; D. L. Laming, 2006; Marshall & Werder, 1972; Modigliani & Hedges, 1987; Rundus, 1980; Tan & Ward, 2000; Ward, 2002). But the variables that influence primacy and recency are well understood and many of their effects are predicted by several contemporary models of episodic memory (e.g., Farrell, 2012; Polyn et al., 2009).

Free recall data have played a major role in development of memory theory over the past 50 years. For example, the presence of recency in immediate free recall, and the absence of recency when there is a delay between the last item and recall (Glanzer & Cunitz, 1966; Postman & Phillips, 1965), is one of the strongest pieces of evidence supporting the distinction between immediate and secondary memory (Atkinson & Shiffrin, 1968; Glanzer & Cunitz, 1966; Waugh & Norman, 1965). The temporal contiguity effect helped solidify the role that context has long played in episodic memory theories (Bower, 1972; Estes, 1955; McGeoch, 1932), and is now a benchmark effect that any model of episodic memory must account for (Davelaar et al., 2005; Farrell, 2012; Polyn et al., 2009).

Principles of Memory or Artifacts of Strategy

Despite the contributions of free recall, there remains some question as to whether the task actually captures fundamental principles of the memory system. Some scholars have expressed concern that free recall requires searching memory in a way that is alien to how memory is accessed outside the laboratory, which encourages use of idiosyncratic strategies. For example, Hintzman (2011) argued that participants in a free recall experiment are obligated to devise ad hoc mnemonic strategies and that individual differences in the type of strategy devised are likely to overlay and obscure more general memory processes:

“Allowing subjects to recall the words in any order they wish encourages them to explore various encoding and retrieval strategies.” (Hintzman, 2011, p. 255)

“But the overlay of study and retrieval strategies makes the task a grotesque, neither-fish-nor-fowl creature of the laboratory—corresponding to nothing people do in everyday life and too complex to be of much use for scientific analysis..” (Hintzman, 2011, p. 255)

Others have made similar, if less sweeping, claims that various aspects of free recall performance are either artifacts of strategy use or are modulated by strategy use (e.g., Dalezman, 1976; Delaney et al., in press; Hasher, 1973; McDaniel & Bugg, 2008).

Without doubt, participants will adopt strategies to help them perform free recall or any other laboratory task. The issue we wish to address here is whether variation across individuals in strategy use accounts for the shape of the average curves shown in figure 1. Specifically, are the curves the result of averaging across subgroups of participants who are using different strategies, in which case they would tell us little about memory principles. Before describing how we will address this issue, it is important to clarify the distinction between strategies and principles of memory.

Performance on laboratory memory tasks is not a pure measure of memory. Rather, performance represents a complex interaction between characteristics of the participants, stimuli, the encoding conditions, and the retrieval conditions (Jenkins, 1979; Roediger, 2008). More generally, we can think of laboratory tasks like puzzels that require the participant to find the optimal way to use memory to meet the task requirements. For example, free recall and serial recall both rely on the same underlying memory system (Solway, Murdock, & Kahana, 2012) but serial recall requires participants to place more weight on newly learned temporal associations and less weight on long-standing semantic associations.

A rough analogy can be made to chess playing: chess is like a laboratory task, with the rules of the game placing constraints on how it can be played; the brain of the chess player is not pre-equipped with any “chess processes”, just as there are no “free recall” processes. Instead the player must take existing perception, memory, and executive processes and devise a strategy to deploy these processes in a way well-suited to the rules of the game. If we were to find patterns in how people play the game, for example that they tend to plan only x moves ahead, those effects could arise either from the particular strategies people adopt or from more fundamental principles of the cognitive systems those strategies deploy.

This view of task performance as an interaction between task–specific strategy selection and domain–general memory processes is captured by several influential theories in cognition. The notion of “working with memory” (Moscovitch & Winocur, 2002), for example, proposes that frontal executive processes must determine how best to deploy medial temporal lobe memory processes to meet the demands of the particular task. A similar view of task performance underlies the idea of the multiple-demand system (Duncan, 2010), which suggests that complex behavior depends on a network of frontal regions that break a task into smaller sub–components that can be processed by other cognitive systems such as memory and perception. Similarly, the idea of general purpose cognitive systems being recruited in novel ways to address new tasks lies at the heart of production systems such as ACT-R (Anderson et al., 2004).

Characteristics of both the task and the participants will influence the balance between the strategy and memory process components of free recall performance. A variety of task characteristics such as presentation rate, presentation modality, and list length, have been shown to influence the shape of free recall functions. More generally if we consider task parameters such as list length to be a continuum, there are likely to be points along this continuum where the optimal strategy shifts (Grenfell-Essam & Ward, 2012). Indeed, Grenfell-Essam and Ward (2012) have shown that for short list lengths many participants tend to initiate recall from the beginning of the list rather than from the end of the list as seen with the longer lists we use here (Figure 1). Therefore, studies designed to capture the memory component should avoid crossover points at which the strategy component is likely to be highly influential.

An important characteristic of participants that will affect the balance between the strategy and memory process components is the amount of practice they have with the task. When first introduced to a new task strategy differences are likely to be prominent, as participants explore different strategies in an attempt to find an optimal one. Indeed, the findings that recall initiation patterns change with practice (Dallett, 1963; Goodwin, 1976; Hasher, 1973; Huang, 1986), and that memory task performance tends to improve with practice (i.e., the “learning to learn” effect, Postman, 1969) may stem partly from participants optimizing strategies to meet the needs of the tasks (we revisit this suggestion in the discussion and make an important cavet).. Therefore, we examine the performance of participants with extensive experience with the free recall task.

However, using well–practiced participants is not enough to ensure that the effects shown in Figure 1 reflect general memory processes. It is possible that even after many trials of practice, differences in strategy use between individuals may remain and that these differences may be obscured when looking at averaged data. In this manuscript, we develop an analytical framework for detecting such strategy differences.

Establishing Consistency Across Individuals

In developing this analytical framework we start by identifying differing predictions of the strategy–difference and memory–process accounts of free recall effects. One guiding principle is that if the functions in Figure 1 reflect fundamental principles of the memory system then they should be universal in the sense that every cognitively intact individual should exhibit a similar function, just as every healthy individual shows markers of fundamental physiological processes. There will, of course, be individual differences but they should be quantitative rather than qualitative. By contrast, a strategy account predicts that the shape of a participant’s function will depend on the strategy they use.

Specifically, if any of the effects described above are the result of averaging across subgroups of participants who are using different strategies, each subgroup should correspond to a distinct and identifiable cluster in the data. Assume, for example, that the average curves actually disguise a “primacy” subgroup who adopt the strategy of initiating recall with items from early serial positions and a “recency” subgroup who adopt a strategy of initiating with end–of–list items, similar to the two initiation patterns identified by Grenfell-Essam and Ward (2012). We should be able to identify these two clusters by examining the PFR functions of individual participants. One could imagine many other ways in which strategy use could influence PFR functions. And similar strategy–based accounts could be made for contiguity and proximity effects (e.g., there may be a cluster of participants that shows strong contiguity and another that shows weak contiguity). We develop a generalizable strategy detection procedure that is based on identifying clusters in the data but does not require specifying the particular strategies, the number of clusters, or how strategies change the shape of the functions.

In addition to the cluster detection procedure, we use the strategy-free Context Maintenance and Retrieval (CMR) model of free recall (Polyn et al., 2009) to test the strategy account. Unsworth, Brewer, and Spillers (2011) point out that while several existing models fit a wide range of free recall effects, they do so at the level of average data and do not model individual differences in strategy use. This view implies that existing models would be unable to fit data at the individual level without being modified to incorporate a strategy component. However, whether models need to include strategy components to account for individual data has not been extensively investigated. The issue actually suggests a strong test of the claim that free recall effects cannot be explained apart from reference to strategy: if a model without a strategy component can fit individual difference data, it constitutes a suffciency proof – conclusively showing that reference to strategy is unnecessary to account for the existing data.

Methods

Participants

The data reported here are from The Penn Electrophysiology of Encoding and Retrieval Study (PEERS). PEERS aims to assemble a large database on the electrophysiological correlates of memory encoding and retrieval. The present analyses are based on the 126 young adult (age 18–30) participants who had completed Experiment 1 of PEERS as of December 2012. Participants were recruited through a two–stage process. First, we recruited right-handed native English speakers for a single session to introduce participants to EEG recordings (EEG data are not reported here) and the free recall task. Participants who completed this introductory session were invited to enroll in the full study, on the condition that they did not make an excess of eye movements during item presentation epochs of the experiment and their probability of recall was less than 0.8. Approximately half of the subjects recruited for the preliminary session agreed to participate in the multi-session study. Participants were consented according the University of Pennsylvania’s IRB protocol and were compensated for their participation.

PEERS Experiment 1

Participants performed a free recall experiment consisting of 1 practice session and 6 subsequent experimental sessions. Each session consisted of 16 lists of 16 words presented one at a time on a computer screen. Each study list was followed by an immediate free recall test and each session ended with a recognition test. Half of the sessions were randomly chosen to include a final free recall test before recognition, in which participants recalled words from any of the lists from the session.

Words were either presented concurrently with a task cue, indicating the judgment that the participant should make for that word, or with no encoding task. The two encoding tasks were a size judgment (“Will this item fit into a shoebox?”) and an animacy judgment (“Does this word refer to something living or not living?”), and the current task was indicated by the color and typeface of the presented item. Using the results of a prior norming study, only words that were clear in meaning and that could be reliably judged in the size and animacy encoding tasks were included in the pool. There were three conditions: no-task lists (participants did not have to perform judgments with the presented items), single-task lists (all items were presented with the same task), and task-shift lists (items were presented with either task). The first two lists were task-shift lists, and each list started with a different task. The next fourteen lists contained four no-task lists, six single-task lists (three of each of the task), and four task-shift lists. List and task order were counterbalanced across sessions and participants.

Each word was drawn from a pool of 1638 words. Lists were constructed such that varying degrees of semantic relatedness occurred at both adjacent and distant serial positions. Semantic relatedness was determined using the Word Association Space (WAS) model described by Steyvers, Shiffrin, and Nelson (2004). WAS similarity values were used to group words into four similarity bins (high similarity: cos θ between words > 0.7; medium high similarity, 0.4< cos θ <0.7; medium-low similarity, 0.14< cos θ < 0.4; low similarity, cos θ <0.14). Two pairs of items from each of the four groups were arranged such that one pair occurred at adjacent serial positions and the other pair was separated by at least two other items.

For each list, there was a 1500 ms delay before the first word appears on the screen. Each item was on the screen for 3000 ms, followed by jittered 800 – 1200 ms inter-stimulus interval (uniform distribution). If the word was associated with a task, participants indicated their response via a keypress. After the last item in the list, there was a 1200 – 1400 ms jittered delay, after which a tone sounded, a row of asterisks appeared, and the participant was given 75 seconds to attempt to recall any of the just-presented items.

If a session was selected for final free recall, following the immediate free recall test from the last list, participants were shown an instruction screen for final free recall, telling them to recall all the items from the preceding lists. After a 5 s delay, a tone sounded and a row of asterisks appeared. Participants had 5 minutes to recall any item from the preceding lists.

After either final free recall or the last list’s immediate recall test was a recognition test, indicated by an instruction screen. Target/lure ratio was variable by session, where targets made up 80, 75, 62.5, or 50 percent of the total items. Participants were told to respond verbally by saying “pess” for old items and “po” for new items and to confirm their response by pressing the space bar. This was done so that both response types would initiate with the same stop consonant (or plosive) so as to assist in automated detection of word onset times. Following the old/new judgment, participants made a confidence rating on a scale of 1 to 5, with 5 being the most confident. Recognition was self-paced though participants were encouraged to respond as quickly as possible without sacrificing accuracy. Participants were given feedback on accuracy and reaction time.

The first session was identical to the experimental sessions except that this session always had final free recall. To make it easier for participants to adjust to the encoding task lists were not presented randomly in the first session. Rather, lists 1–4 were no task lists, lists 5–8 were single-task lists of one randomly selected judgment type, lists 9–12 were single-task lists using the other judgment, and lists 13–16 were task-shift lists. The number of item presentations for each judgment type were counterbalanced across lists.

Results

Overview of Data

In determining whether the free recall effects are consistent across participants, it is useful to examine the free recall functions for individual participants. As described in the methods, PEERS includes an encoding task manipulation; task trials require participants to make either a size or an animacy judgment about each word as it is presented, whereas no-task trials have no encoding task. The requirement to perform a specific task during encoding may influence a participant’s choice of strategy. Therefore we analyse task and no-task conditions separately.

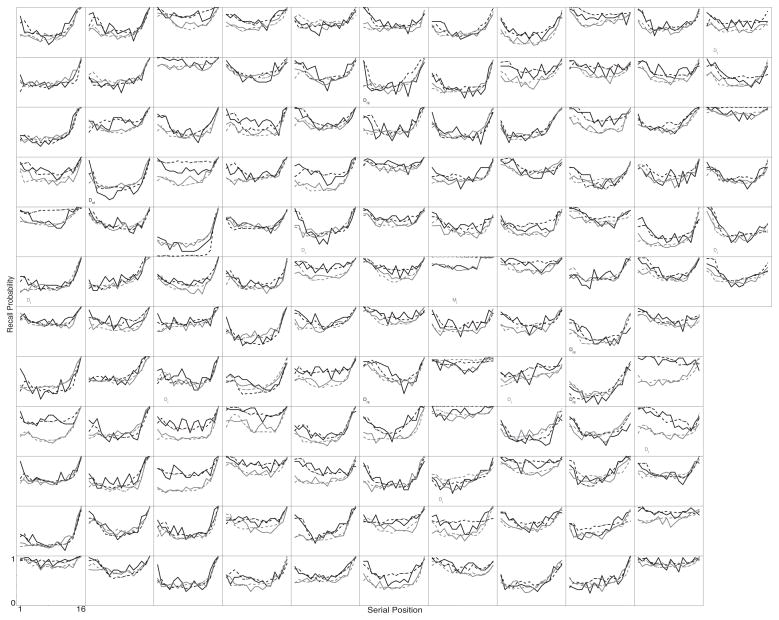
Figures 2–5 show SPC, PFR, Lag-CRP, and semantic-CRP functions respectively. In the figures, a separate panel is devoted to each participant. Each panel displays four curves. The black curves show No-Task lists and the grey curves show Task lists. The solid curves show the participant’s data and the dotted curves show the fit of the Context Maintenance and Retrieval model to their data (see below for details on the model and how it was fit to the data). The ordering of participants is consistent across figures, so that a given participant appears in the same panel in each figure¹. We present detailed quantitate analyses below, but the data are suffciently clear to begin with a visual inspection and descriptive overview.

Figure 2.

Individual participants’ Serial Position Curves. Each panel shows the data from one participant. Participants are displayed in the same order in each of Figures 2–5. Black lines show the No-Task lists, grey lines show the Task lists. Solid lines are each participant’s actual data. Dotted lines are fits of CMR to the participant’s data. A “D” in the lower left of a participant’s panel indicates that they differed significantly from the average function, an “M” indicates that CMR failed to provide a good fit to their data (see the text for details on how these determinations were made). Subscripts on “D’s” and “M’s” indicate list type: “t” indicates Task lists, “nt” indicates No-Task lists.

Figure 5.

Individual participants’ Semantic-Conditional Probability functions. Each panel shows the data from one participant. Participants are displayed in the same order in each of Figures 2–5. Black lines show the No-Task lists, grey lines show the Task lists. Solid lines are each participant’s actual data. Dotted lines are fits of CMR to the participant’s data. A “D” in the lower left of a participant’s panel indicates that they differed significantly from the average function, an “M” indicates that CMR failed to provide a good fit to their data (see the text for details on how these determinations were made). Subscripts on “D’s” and “M’s” indicate list type: “t” indicates Task lists, “nt” indicates No-Task lists.

Figure 2 shows each participant’s SPC. While there are clearly individual differences, every participant’s function resembles a classic SPC. If we define recency as a higher average recall probability for the final 6 serial positions than for positions 5–10 (mid–list positions), then on both No-Task and Task lists, 90% of participants show recency. If we define primacy as higher average probabilities for items 1–4 than for mid–list positions, then for both No-Task and Task lists, 93% of participants show primacy.

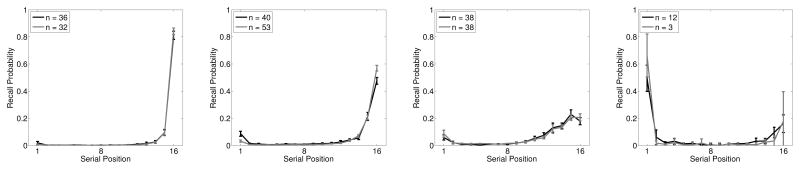
Individual PFR functions are shown in figure 3. The PFR peaks at the final item for 64% of participants on No-Task lists and for 79% participants on Task lists. The PFR is uniformly near zero for mid-list positions: across all participants the average initiation probability for items 5–10 is less than 1% for both No-Task and Task lists. No participants show an average initiation probability of more than 5% for mid–list items on No-Task lists (1 participant does so on Task lists). Individual PFRs do, however, vary somewhat from the average. First, on No-Task lists, 27% of participants (16% on Task lists) are more likely to initiate recall from an item 1–3 back from the final item than from the final item itself. Second, 44% (27% on Task lists) of participants initiate recall from the beginning of the list on more than 5% of trials, producing an uptick in the PFR at the first item. Overall, the PFR average function is a reasonable description of the modal participant. A substantial number of participants do depart from this modal function, but they do not greatly distort the average (with the possible exception of a small uptick for the first item, which is visible in the average function).

Figure 3.

Individual participants’ Probability First Recall functions. Each panel shows the data from one participant. Participants are displayed in the same order in each of Figures 2–5. Black lines show the No-Task lists, grey lines show the Task lists. Solid lines are each participant’s actual data. Dotted lines are fits of CMR to the participant’s data. A “D” in the lower left of a participant’s panel indicates that they differed significantly from the average function, an “M” indicates that CMR failed to provide a good fit to their data (see the text for details on how these determinations were made). Subscripts on “D’s” and “M’s” indicate list type: “t” indicates Task lists, “nt” indicates No-Task lists.

The individual participant lag-CRP functions (Figure 4) show remarkable consistency. Defining a contiguity effect as the CRP for lag 1 being greater than the CRP for lag 2 and the CRP for lag −1 being greater than the CRP for lag −2, 96% of participants show a contiguity effect on No-Task lists and 100% show contiguity on Task lists. As a more stringent test, we created a 6-point Lag-CRP function composed of lag 1, the averages of lags 2 and 3, the averages of lags 3 and 5, and the corresponding points for negative lags. These functions decline monotonically with increasing absolute value of lag for 98% of participants on No-Task lists and 100% of participants on Task lists. The asymmetry effect is also highly consistent with 95% of participants showing higher recall probabilities for lag 1 than for lag -1 on No-Task lists (96% of participants show asymmetry on Task lists). There are, of course, individual differences with some participants showing large asymmetries and others show very small asymmetries. However, these differences are quantitative rather than qualitative as would be expected if all participants’ asymmetry effects were drawn form a normal distribution centered above zero with a left tail close to zero.

Figure 4.

Individual participants’ Lag-Conditional Response Probability functions. Each panel shows the data from one participant. Participants are displayed in the same order in each of Figures 2–5. Black lines show the No-Task lists, grey lines show the Task lists. Solid lines are each participant’s actual data. Dotted lines are fits of CMR to the participant’s data. A “D” in the lower left of a participant’s panel indicates that they differed significantly from the average function, an “M” indicates that CMR failed to provide a good fit to their data (see the text for details on how these determinations were made). Subscripts on “D’s” and “M’s” indicate list type: “t” indicates Task lists, “nt” indicates No-Task lists.

The semantic proximity effect also shows striking consistency across participants (Figure 5). For all participants, conditional recall probability peaks at the highest similarity bin and decreases as semantic similarity decreases. No participants show a flat or negatively sloped function.

Even though it is not our primary focus, it is useful to compare the No-Task and Task conditions. On average, SPC curves tend to be lower for the task lists and primacy is more pronounced for no-tasks lists. Temporal contiguity also tends to be lower on the task lists. These differences suggest the encoding task influences how participants approach the task, however it is not clear whether this reflects differences in the strategy component or the memory component. We return to this issue in the discussion.

Figures 2–5 reveal an impressive level of consistency across participants and strongly suggest that a common set of memory processes underlie the functions. Yet, few individuals show a pattern that is identical to the average. Of course, visual inspection does not tell us wether we can reject the null hypothesis that a given participant’s curve actually deviates significantly from the average. Therefore, we turn to a series of analyses that provide a more rigorous test.

Detailed Analyses

We develop a two step procedure for detecting such strategy subgroups. The first step, is a cluster detection algorithm and is suited to situations in which participants fall into clear subgroups. The second step is to test each individual’s deviance from the average, and is intended for cases in which the fist step fails to detect large clusters.

We will use the PFR curve to illustrate the frist step in our approach. We created simulated “strategy” dataset composed of two distinct groups of simulated participants; the first group shows a strong recency effect but no primacy (Figure 6A), the second shows strong primacy but no recency (Figure 6B). By combining these two groups in a 75:25 ratio, we get an average PFR function that resembles real data (Figure 6C). We can test the null hypothesis that the dataset contains a single cluster by calculating the mean squared deviation of observations from the overall mean and then determining how much we can reduce the this deviation by assigning the data to k clusters and getting the deviation of each point from its cluster mean rather than the overall mean. The challenge for cluster detection algorithms is that mean squared error is a monotonically decreasing function of k, and approaches zero as k approaches the number of observations (i.e., each datapoint is its own cluster).

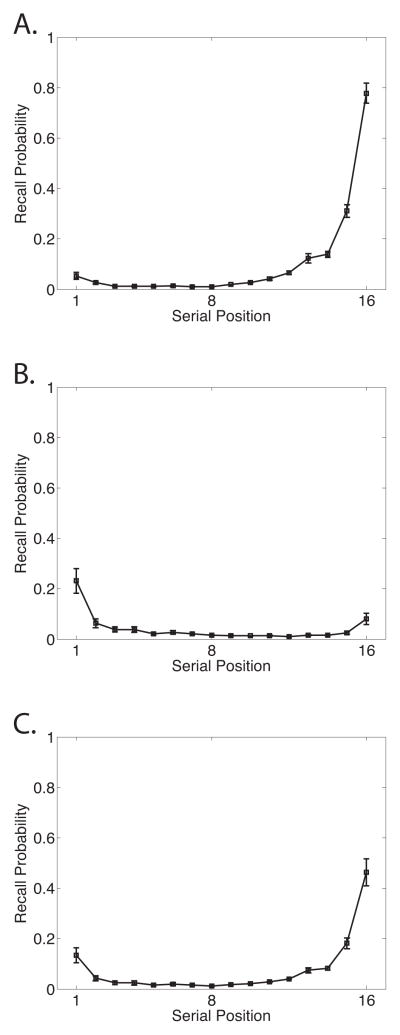
Figure 6.

Probability of First Recall curves from simulated participants. A. Data from 95 simulated participants, all showing recency but no primacy. B. Data from 31 simulated participants, all showing primacy but no recency. C. The average function from all 126 simulated participants shows strong recency and weaker primacy. Error bars are 95% within-subject confidence intervals (Loftus & Masson, 1994).

There are many existing cluster detection algorithms (Garrido, Abad, & Ponsoda, 2012; Pelleg & Moore, 2000; Pham, Dimov, & Nguyen, 2005; Sugar & James, 2003), however most deal with this overfitting problem by relying on arbitrary rules of thumb (e.g., looking for an “elbow” or inflection point in a plot of error against values of k) or on generic corrections for overfitting (e.g., the Akaike and Bayesian Information Criteria). Instead we use a principled method (Sugar & James, 2003) based on the intuition that the correct number of clusters should provide a greater decrease in error than any other value of k. The algorithm starts by assigning the data to k clusters (here we use k-means for cluster assignment) for a range of values of k (here we use 1—4)². Then for each value of k it computes, d_k, the average mahalanobis distance of datapoints from their cluster centers divided by the number of dimensions in the data:

$$d_k=1/p\frac{{\displaystyle \sum _{i=1}^n}{(X_i-c_{x_i})}^T{S}^{-1}(X_i-c_{x_i})}{n}$$

Where p is the number of dimensions in the data, X_i is a the i^th participant’s data as a column vector, S is the covariance matrix, n is the number of subjects, and c_xi is the center of the i^th participant’s cluster. The next step is to raise d_k to a small negative power, −Y, so that it is an increasing function of k with a fairly shallow slope, which reduces differences between adjacent values of k. The final step is to calculate the reduction in error, or “jumps”, created by moving from k − 1 to k for each value of k. Specifically:

$$J_k=d_k^{-Y}-d_{k-1}^{-Y}$$

Note that when k = 1, d_k−1 is taken to be zero so that a jump value can be calculated for one cluster. The largest jump should occur for the true value of k, which can easily be seen in a plot of J_k, against k. Sugar and James (2003) have shown that this method is highly effective recovering the true value of k in many simulated and real data sets both with normal and non-normal underlying distributions. We ran the algorithm for values of k between 1 and 4 and take the k with the largest jump to be the appropriate number of clusters. Noise in the data can blur the boundaries between true clusters, making them hard to detect. We overcame this challenge by performing the above fitting procedure on 5000 bootstrap samples; the reported jump values are the averages over all samples. Bootstrapping also allows us to create confidence intervals around the values of J_k, which provides an natural test for the presence of significant clustering: if the data contains k true clusters, J_k should fall outside the 95% confidence interval for J₁.

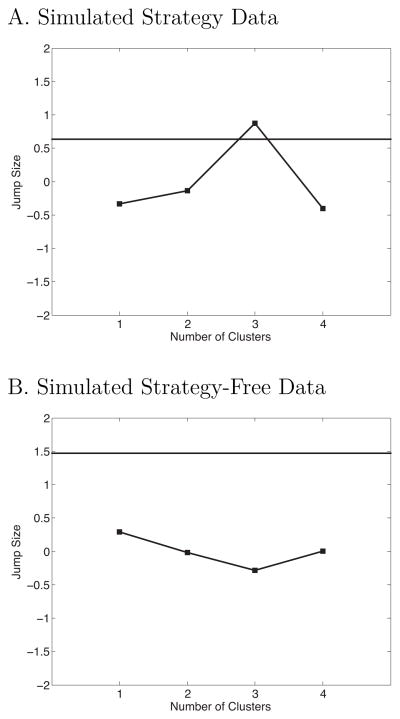
We applied this procedure to the both the simulated strategy dataset and to a no-strategy control set that has the same means as the strategy set but contains a single cluster. Figure 7 shows that cluster detection procedure correctly determined that simulated strategy data contains clusters but that the no-strategy does not. To establish the effectiveness of this cluster detection procedure, we tested its ability to detect clusters in simulated data with ratios of recency to primacy simulated participants of 55:45, 65:35, 75:25, and 85:15. For each ratio we generated 1000 samples of 126 simulated participants; the algorithm correctly identified all of these datasets as having more than one cluster, and tended to overestimate the actual value of k. That is the procedure is highly accurate at detecting the presence of clusters composed of as little as 15% of the sample. The tendency to overestimate the value of k makes it a conservative test of the claim that k = 1. We explored a variety of other clustering algorithms such as Monte Carlo methods that compare multivariate distributions implied by k clusters with the actual data, and found that these methods tended to underestimate the true value of k.

Figure 7.

Results of cluster detection analyses for simulated participants. A. The results of the procedure applied to a sample composed of 31 simulated primacy participants and 95 simulated recency participants. B. The results of the procedure applied to a sample composed of 126 participants all drawn from a distribution that shows both primacy and recency. The solid horizontal lines show the upper bound of a 95% confidence interval on the jump value for k = 1, if the jump value for any k exceeds this bound, we can reject the hypothesis that the data contains a single cluster, with the peak of the function indicating the appropriate number of clusters.

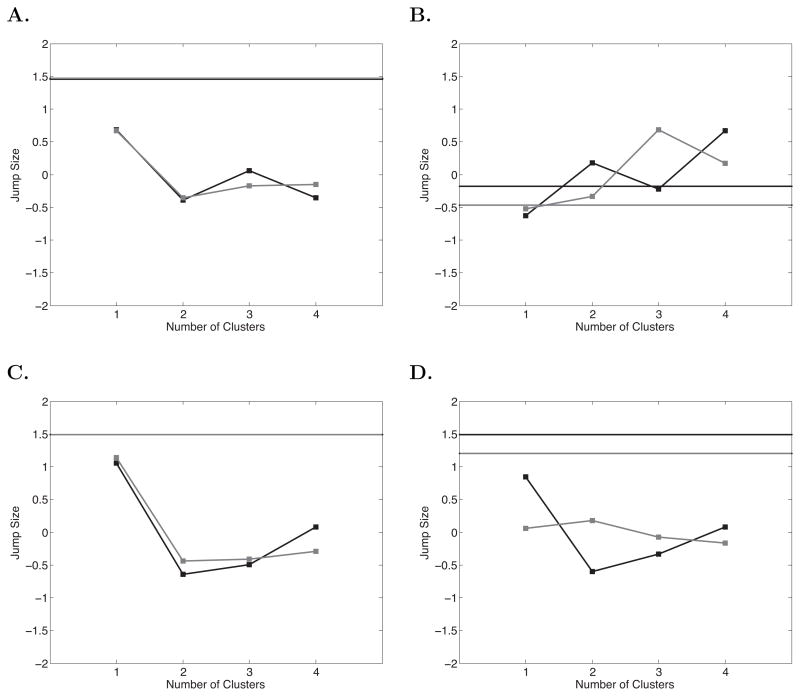
We applied the same analysis to the free recall curves of the actual participants. For the actual SPC, Lag-CRP, and Semantic-CRP curves, the results in Figure 8 closely resemble the pattern shown by the no-strategy simulations. For each of these curves we were unable to reject the null hypothesis that the data contained a single cluster. By contrast, the PFR curves showed evidence of clustering: The null of k = 1 was rejected for both the No-Task and Task lists, and the jump functions peaked at k = 3 and k = 4 for each list type. To understand the differences in initiation patterns between the clusters, we used k-means clustering to assign each participant to one of 4 clusters and plot the average curves for each cluster in Figure 9.

Figure 8.

Results of cluster detection analyses for actual participants. A. Serial Position Curve. B. Probability First Recall function. C. Lag-Conditional Response Probability function. D. Semantic-Conditional Response Probability function. Black lines are No-Task lists, grey lines are Task lists. Jump values were normalized across values of k to place each plot on a common scale. The solid horizontal lines show the upper bound of a 95% confidence interval on the jump value for k = 1, if the jump value for any k exceeds this bound, we can reject the hypothesis that the data contains a single cluster, with the peak of the function indicating the appropriate number of clusters.

Figure 9.

Means of clusters for PFR functions. K-means with k = 4 was used to assign each participant to a cluster. Black lines show the No-Task lists, grey lines show the Task lists. The legend gives the number of participants assigned to each cluster.

The fist two clusters show the same basic shape as the average PFR curve, and likely represent an artificial division of a continuous distribution at an arbitrary point. That is, both clusters show a “end-first” initiation pattern and simply differ quantitatively. The next two clusters, however, show qualitative deviation from the average curve. The third cluster represents participants who follow a “beginning-first” initiation pattern. This subgroup of participants resembles the initiation pattern found by Grenfell-Essam and Ward (2012) with short lists. It appears that even with long lists, a substantial number of participants retain the “beginning-first” pattern (note, however, that the number of participants showing this pattern is substantially smaller for Task lists than No-Task lists, suggesting an influence of encoding task on initiation pattern). The last cluster represents participants who tend to initiate at some point near, but not exactly at, the end of the list. This may reflect chunking (Farrell, 2012) in which participants encode trains of 3–4 successive items into a chunk and recall in forward order within chunks. Thus, the PFR function exhibits evidence of qualitative variation that may reflect individual differences in strategy. We stress, however, that these qualitative variations do not substantially distort the average function, which provides a very good description of the modal participant. It is not the case that the average PFR gets its shape from averaging across subgroups that do not resemble the average. Rather it is the case that the average disguises two subgroups while accurately describing the largest group.

To provide a visual check on the claim that the SPC, Lag-CRP, and Semantic-CRP curves do not show clustering, we can use k-means to force the data into clusters and plot the cluster means as we did for PFR. In the absence of true clusters, (i.e., if the data are drawn from a single distribution) we would expect k-means to simply divide the distribution into quantiles, which should be apparent as systematic variation of the curves across clusters (as opposed to the qualitatively different curves seen across clusters for PFR). For the SPC curve such variation should appear as a lowering of the curve, for the contiguity curves, we would expect some clusters to have steeper contiguity effects than others, but for all to show the same functional form (i.e., CRP changes non-linearly with both temporal and semantic proximity, thus we would not expect a simple raising and lowering of the curves, but a change in slope). As can be seen in Figure 10, this is exactly the pattern we observe; each cluster shows the same basic shape as the average curve but with the level or slope differing systematically.

Figure 10.

Means of data clusters for A. SPC B. Lag-CRP, and C. Semantic-CRP curves. K-means with k = 4 was used to assign each participant to a cluster. Black lines show the No-Task lists, grey lines show the Task lists. The legend gives the number of participants assigned to each cluster.

The foregoing clustering analyses confirm what is obvious from inspecting individual participants’ data: for the SPC, Lag-CRP, and Semantic-CRP curves that the average effects are not due to substantial subgroups of participants performing the task in qualitatively different ways. The PFR curve provides an accurate description of the modal participant who follows a “end-first” recall initiation pattern, but disguises two subgroups who adopt a “beginning-first” and a “clustering” initiation pattern respectively. The clustering analyses, however, do not tell us whether a particular individual is well described by the average. That is, even though coherent groups of participants do not deviate from the average pattern, individual participants may. This is an important point, as under the assumption that free recall is capturing something fundamental about the memory system, we would expect the functions to capture the performance of every healthy adult, just as we expect an anatomy textbook to qualitatively capture the anatomy of any healthy individual.

How do we test whether an individual’s function is well described by the average function? Using the SPC as an example, one could examine each serial position and determine if the participant’s score for that position deviated from the average. However, this approach ignores the fact that performance across serial positions is correlated. For example, it might not be unusual for a participant to be 1 SD below the average at all serial positions, but it would be unusual for someone to be 3 SDs above the mean on the first few serial positions and 1 SD below average for all other positions. That is, we want to know whether a participant’s function taken as a whole is unusual.

Therefore, we started with the null hypothesis that each participant’s function for a particular effect is the result of a random draw from a multivariate distribution described by the means and covariance matrix for that effect (e.g., the covariance of the subjects × serial position matrix). For each participant we followed several steps designed to test if this null hypothesis could be rejected; rejection of the null would suggest that the participant’s data were not drawn from the average distribution. First, we computed the covariance matrix using the data from all participants except the one currently being considered (so that participants did not bias the results in their favor) and used the matrix to generate 100,000 simulated serial position curves with the same means, distributions, and covariance structure as the actual data. Next, for each simulated function we calculated its Mahalanobis distance from the rest of the simulated functions, providing us with a distribution of distances for functions actually drawn from the same underlying distribution. Finally, to determine if the participant in question was likely to also be drawn form that distribution, we calculated the Mahalanobis distance of their function from the simulated functions. If the participant’s Mahalanobis distance was greater than 95% of the simulated Mahalanobis distances, that participant was designated as deviant³.

The same procedure was repeated for each effect for the SPC, Lag-CRP (we do not consider the PFR as we have already established that subgroups deviate from the average). To avoid giving too much weight to noise in the individual curves, we averaged across certain data points. Specifically, we created reduced curves consisting of the following data points for each function: SPC: positions 1, 2, 3, 4, the average of positions 5–8, the average of positions 9–12, and positions 13, 14, 15, 16; Lag-CRP: lag 1, the average of lag 2–3, the average of lags 4–5, and the corresponding negative lags; Semantic-CRP: each of the individual bins. Participants who were designated as deviant are marked by an ‘D’ in their panel in Figures 2, 4, and 5.

For SPC, Lag-CRP, and Semantic-CRP only 4%, 4.8%, and 7.14% of cases respectively (6.3%, 4.8%, and 5.56% on Task lists) were classified as deviant. Visual inspection of these cases suggests they do not differ qualitatively from the average functions (see the marked cases in Figures 2 and 5), rather deviant participants show the same qualitative pattern as the non-deviant subjects, but are near the tails of the non-deviant distribution (e.g., relatively steep or relatively shallow contiguity effects). Because of this qualitative similarity and the fact the these deviance rates are very near or below the 5% false detection rate for the procedure, we assume they are false alarms and do not consider them further.

To determine if a participant’s distance from the average of one function predicts their distance from the other functions, we correlated participants’ Mahalanobis distances for each of the four functions. Mahalanobis distances are expected to be highly skewed, therefore, we used the non-parametric Spearman’s Rho rather than Pearson’s r. The results are displayed in Table 1. In general, a participant’s distance from the average of one function was not strongly correlated with their distance from the average of the other functions. However, distance from the Lag-CRP was moderately but significantly correlated with distance from both Semantic-CRP and PFR.

Table 1.

Correlations (Spearman’s Rho) between Mahalanobis distances for the four free recall functions.

Variable	1	2	3	4
1. SPC	–
2. PFR	0.11	–
3. Lag-CRP	0.11	0.2	–
4. Semantic-CRP	0.029	0.03	0.26	–

Correlations in bold are significant at α = .05

Modeling Individual Participants’ Data

As a final test of the claim that free recall effects arise from individual differences in strategies rather than core memory processes, we attempt to fit individual participant data using a model of episodic memory that does not include a strategy component. Most existing models of free recall assume that the SPC, PFR, and CRP functions are produced by fundamental memory processes. Thus, modelers have focused on identifying and modeling those processes, but generally do not model strategic elements of the task. The ability of a “strategy free” model to capture free recall data is in principle an excellent way of determining whether strategies are a necessary part of accounting for free recall effects: if a strategy free model can fit the effects, there is no need to posit strategic elements. However, most previous modeling work does not provide such a decisive test because the models generally have been fit to averaged data. It is possible that a strategy free model can capture averaged data but fail to capture individual participants’ data (Unsworth et al., 2011). Therefore, we attempt to model individual participants’ data with the Context Maintenance and Retrieval (CMR) model (Polyn et al., 2009), a model that has successfully accounted for a range of free recall effects including those considered here.

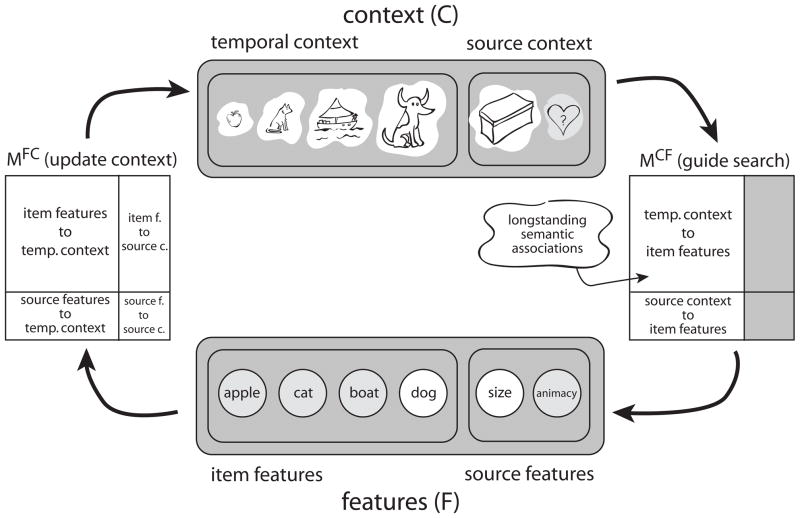
Before discussing the simulations we provide an outline of the CRM model; for a full formal description of the model see (Polyn et al., 2009). In CMR, two types of cognitive representations interact: (a) the feature representation (F), in which the features of the current list item are activated, and (b) the context representation (C), in which the current state of context is activated. Hebbian associative matrices connect these representations, one connecting features to context (M^FC), and one connecting context to features (M^CF). Each association matrix is a weighted sum of a pre-experimental component that reflects longstanding semantic relationships (derived using LSA) and an experimental component that reflects new learning that occurs during the experiment.

In Figure 11, the words boat, cat, and apple have already been studied and the next word, dog, has just been presented. Studying dog activates the corresponding features, f_i, which in turn retrieve the context states to which dog has previously been associated: c^IN_i = M^FCf_i. This retrieved context, c^IN_i, is incorporated into the context representation according to: c_i = ρ_ic_i−1 + βc^IN_i. Here, β is a model parameter governing how quickly context changes (ρ_i is chosen such that |c_i| = 1).

Figure 11.

Schematic of CMR. When an item is studied, a set of features (F) are activated, corresponding to the item’s identity. This set of features is then used to update a context representation (C) by projecting through the feature-to-context associative weight matrix (M^FC). Hebbian learning creates links between co-active features and context elements (on both M^FC and M^CF). During recall, context is used to reactivate the features of studied items by projecting through M^CF.

During recall, the current contextual state is used to cue retrieval via the M^CF associations: f^IN_i = M^CFc_i. The resulting f^IN_i gives the degree of support for each item in the model’s vocabulary. This vector of support values is used as the starting point for a set of competitive accumulators, one for each word, according to the leaky competitive accumulator model of Usher and McClelland (2001). The first word to accumulate enough activation to cross a threshold is recalled. When an item wins the recall competition, its representation is reactivated on F, allowing the model to retrieve the contextual state associated with the item. Context is updated using the same mechanism used during the study period (although the rate of context updating β can differ between study and recall). This updated state of context activates a different set of features (a new f^IN) and another recall competition begins. This series of competitions continues until the end of the recall period is reached, at which point the next trial begins.

Critically, under CMR all the free recall effects derive from memory processes that are assumed to be qualitatively invariant across healthy adults. Recency occurs because the context at the end of the list, which is used as a retrieval cue, most closely matches items presented near the end of the list. Contiguity occurs because each recalled item retrieves a new context that is similar to the contexts associated with its neighbors in the list and less similar to its more distant neighbors. Semantic proximity occurs because recalled items retrieve a context representation that is similar to the contexts associated with its semantic associates.

To prevent overfitting noise in participants’ curves, we fit the model to the reduced curves described in the previous section (for the PFR, which was not considered in the previous section the reduced curve consisted of position 1, the average of positions 2–13, and positions 14, 15, and 16). For each participant, a genetic algorithm was used to minimize the deviation between model simulations and the participants’ data across these 30 data points using Root Mean Square Deviation (RMSD) as the measure of deviation. No-Task and Task lists were fit independently⁴

The resulting fits are shown by the dotted lines in Figures 2–5. A visual inspection indicates that the model fits quite well for almost all of the participants. To test whether the model provided an adequate fit for a given participant and a given curve, we tested whether the deviation between the best–fitting model curve and the participant’s curve was greater than would be expected had the two curves been drawn from the same distribution. In principle, we could use the same Mahalanobis distance test we used above when testing if individual participants deviated from the average functions. However, the Mahalanobis test requires computing covariances and 7 sessions per participant is too few to provide stable estimates of covariance. Therefore, we adopted a slightly different procedure that does not require covariances. Specifically, for a given participant and a given curve we computed an RMSD, RMSD_model, for the deviation between model and data. We then created 100,000 simulated curves with the same means and standard deviations as the participant’s data (computed across sessions). For each simulated curve we calculated a RMSD for the deviation between the simulated curve and the participant’s actual curve, providing us with a distribution of RMSD_data values for curves drawn from the same distribution. The model was said to provide an adequate fit if RMSD_model fell below the 95^th percentile of the RMSD_data distribution.

Participants for whom the model failed to provide an adequate fit are designated by an ‘M’ in their panel in Figures 2–5. For SPC, Lag-CRP, and Semantic-CRP, the number of poorly–fit subjects was below the 5% false detection rate at 0%, 0%, and 0% respectively (0.79%, 0%, and 0% for Task lists). For PFR, the model failed to fit 4.8% (11% for Task lists) of participants. These poorly fit PFRs tended to be from participants in the “chunking” cluster, which suggests these participants’ initiation patterns may reflect strategy use. It is notable, however, that CMR captures the initiation pattern of most participants in the “beginning-first” cluster, which suggests this pattern may reflect a difference in the parameterization of memory processes rather than differences in strategies (we return to this claim in the Discussion). Overall, CMR captures the recall initiation of most participants, and after recall initiation, CMR captures the recall dynamics of essentially all participants.

Discussion

Laboratory tasks designed to measure specific cognitive processes are a staple of psychological research and have provided much of the empirical foundation of our science. For this prominent position to be justified, we must be sure that the key measures derived from such tasks are not contaminated by differences across individuals in idiosyncratic strategy use (Hintzman, 2011). Here we have taken up this challenge for free recall, a task that has played a key role in memory research and theory development. Contrary to predictions of a strategy–difference account of free recall, serial position functions, lag-CRP functions, and semantic-CRP functions showed no evidence of subgroups of participants employing different strategies. The average PFR curve accurately described the modal participant, but disguised two qualitatively different subgroups. These results suggest that free recall effects, especially those describing post–initiation dynamics, are not substantially contaminated by different participants employing different strategies. We hope that the approach we have taken here can serve as a model for assessing the influence of strategy on important paradigms in other research areas.

Stability and Variability in Free Recall

Serial position functions, lag-CRP functions, and semantic-CRP functions were all extremely consistent across participants and did not show the multi-modal distributions one would expect with strategy differences. These data provided absolutely no evidence that the average function distorts individual participants’ behavior. Instead, the functions of most participants could be characterized as a sample from a multivariate distribution described by the average function - that is, generated by the same underlying processes. A model of these underlying processes, CMR, provided a very good fit to individual participants. In the case of temporal contiguity and semantic proximity, 126 out of 126 showed the effect. This level of consistency suggests that temporal contiguity and semantic proximity are universal principals in the sense that every healthy adult shows them. Indeed, the contiguity and proximity effects were so consistent across individuals that one is tempted to rename them contiguity and proximity laws.

Most participants’ PFR functions were flat through early list items and began a steep, monotonic increase a few items back from the end of the list, mirroring the average function. However, we found evidence of two subgroups that showed patterns quite different from the average PFR. The first subgroup showed a “beginning-first” pattern reminiscent of the average initiation pattern seen on early trials (Dallett, 1963; Goodwin, 1976; Hasher, 1973; Huang, 1986) and with short lists (Grenfell-Essam & Ward, 2012). The second subgroup showed a tendency to initiate recall from a variety of positions from the second half of the list rather than the strong tendency to initiate at the last item. Notably, the PFR of this subgroup is non-monotonic, peaking about 1 item back from the end of the list (Figure 9D), suggesting items are chunked and recalled in forward order within chunks (Farrell, 2012).

Strategies Versus Processes

As detailed in the introduction we view task performance as an interaction between task–specific strategy selection and domain–general memory processes. Under this view strategy plays a important role in memory tasks; it allows a common set of memory processes to be intelligently deployed to meet the demands on a wide range of tasks. Moreover, there is no doubt that there are differences between participants in the strategies they adopt. Our analyses show, however, regardless of any variation among participants in strategy use, there is a set of effects that are highly consistent across participants, which we suggest reflect the operation of a common set of memory processes.

Throughout the paper we have built a case that differences among participants in strategy use cannot account for the shape of average free recall functions, and suggested that these curves instead represent the operation of core memory processes. Of course, the fact that differences in strategy use do not account for the shape of the curves does not logically preclude the possibility that all participants adopt a common strategy, and that the common strategy determines the shape of the curves. For example, the constraints of the task may force all participants in to a common, but still ad hoc, strategy that tells us little about the memory system. Such a common–strategy account borders on unfalsifiable if we limit ourselves to examining behavioral performance on a single task (indeed, one could argue that almost any effect in psychology represents a strategy rather than a cognitive process). Luckily we can gain some traction in separating common–strategy and core–process accounts if a few ways. First, we can resort to models of the cognitive system. We have shown that CMR, a model of core memory processes which has previously been used to account for a wide range of empirical findings without simulating strategy use, can account for the data of almost all individuals. These simulations show conclusively that the effects can be accounted for without strategies. Second, we can attempt to generalize the effects beyond a single task. The contiguity effect is observed on a variety of other tasks that do not obviously have the same strategy–affordances as free recall, such as high confidence old/new recognition responses (Schwartz et al., 2005), intrusions in paired-associate recall (Davis et al., 2008), and more naturalistic recall of autobiographical events (Moreton & Ward, 2010).

The claim that core cognitive processes are not hopelessly obscured by strategy use should not be surprising: A good strategy must operate within the constraints of how the memory system operates. For example, a strategy that ignores the powerful effect of semantic proximity on the memorability of items is a bad strategy. This view suggests that when participants are exposed to a new task, they likely explore different strategies, abandoning ineffective ones as they gain practice, and converging on those that take best advantage of core memory processes. Therefore, a first hurdle in attributing an effect to a core memory processes is showing that it does not disappear with practice. We cleared that hurdle by examining free recall functions in participants who are highly practiced with the free recall task having completed many trials over multiple sessions. In typical single-session laboratory studies, early trials constitute a much higher percentage of the total number trials, and therefore likely confound learning-to-learn effects with underlying memory processes.

However, even in the case of learning a new task, we should not overestimate the importance of strategy. If we view task performance as reflecting both a strategy–component and a memory–component, there is no reason to assume that only the strategy–component is optimized with practice. Just as participants will explore different strategies when first exposed to a task, participants likely go through a “tuning period” in which they attempt to optimize the parameters of their memory system to fit the demands of the task. To use CMR as an example, participants may tune the parameters that control the weighting of pre-experimental semantic associations versus newly learned temporal associations to optimally balance the influence of the two types associations in guiding recall. Tuning parameters is not the same as exploring strategies; two participants may have the same strategy but different parameter settings. The distinction can be clarified by asking if the effect in question could be captured by varying the parameters of a strategy-free model. If so it may be a case of parameter tuning, if not strategy differences may be the cause. For example, a weakening of semantic clustering and a strengthening of temporal clustering with repeated exposure to the same list (Klein, Addis, & Kahana, 2005) could naturally be modeld by gradually increasing the CMR parameter that controls the weighting of new temporal associations. By contrast, the difference introduced by asking participants to encode deeply or shallowly, would likely require some addition to the model to account for selective attention to stimuli features.

This logic suggests that the beginning-first and end-first recall initiation clusters do not necessarily reflect a difference in strategy. The fact that CMR can fit the beginning–fist cluster, suggests that it is in fact a difference in parameter tuning as one woud expect CMR to be unable to fit individuals who are using different strategies. A similar analysis could be applied to the recently reported that beginning-first initiation becomes less likely as list length increases (Grenfell-Essam & Ward, 2012). Such an effect could occur because different list lengths encourage the use of different strategies, but it could also result from a strategy-free model under which both a primacy gradient and a recency gradient influence the accessibility of list items. If we assume that both primacy and recency decay with temporal separation between an item and the retrieval cue then, all else being equal, we expect participants to initiate with an item from near the end of the list. If, however, primacy is stronger than recency, then as list length decreases and the proximity of early items to the end of the list increases there will be a point at which primacy overcomes the temporal-proximity advantage of recency and participants shift to a beginning-first initiation pattern. Moreover, there will also be individual differences in the shift point if there are any systematic or stochastic differences between individuals in their recency and primacy parameters.

Individual Differences in Recall Dynamics

While there is some work on individual differences in strategy selection (Bailey et al., 2008; Coyle et al., 1998), the notion of parameter tuning has received little attention. Thus, the extent to which differences between individuals on early trials are due to strategy exploration versus parameter tuning should be an important target for individual differences researchers. For example, some variables, such as orthographic distinctiveness of list items, can influence and possibly eliminate the contiguity effect (McDaniel et al., 2011) among participants with limited practice, but it remains to be seen whether these variables influence contiguity directly by disrupting memory processes or indirectly by encouraging participants to explore strategies that obscure contiguity.

Similarly, analyses reported by Unsworth et al. (2011) could be seen as showing an effect of individual differences in strategy on the shape of the SPC. They found three distinct clusters of participants, which they labeled “Recency”, “Primacy” and “Both”. However, the (Unsworth et al., 2011) participants completed only 10 free recall lists (compared with 112 lists for the participants reported here), and therefore the subgroups may represent variation in strategy exploration and parameter tuning and not variation in core processes. Moreover, (Unsworth et al., 2011) reported results only from dividing the data into three clusters and did not report parsimony corrected fit values for other numbers of clusters. Indeed, inspecting the SPCs of these clusters suggests they vary quantitatively rather than qualitatively; each group seems to show both a recency and a primacy effect but to varying degrees. Therefore, we argue their findings are consistent with our own.

The analyses presented here suggest that individual differences in SPC, PFR, Lag-CRP, and Semantic-CRP functions are largely due to quantitative variations in the effciency of the same underlying memory processes, rather than qualitative differences in strategies employed. The claim that individual diferences are quantitative rather than qualitative should not be mistaken for the claim that individual differences are unimportant. Indeed, we think individual differences have been neglected in memory research in general, and free recall research in particular. By contrast, researchers investigating working memory have a long and productive tradition of studying individual variation in memory processes and the relation of those processes to other aspects of cognition (e.g., Hasher, Lustig, & Zacks, 2007; Kane, Poole, Tuholski, & Engle, 2006; McCabe, Roediger, McDaniel, Balota, & Hambrick, 2010; Miyake et al., 2000).

There is growing interest in individual differences in long-term memory tasks (Mogle, Lovett, Stawski, & Sliwinski, 2008; Unsworth & Engle, 2007) driven by accumulating evidence that the tasks used to study working memory actually measure, at least partly, long-term memory (Healey & Miyake, 2009; Unsworth & Engle, 2006). We have recently shown that four sources of variation underly individual differences in recall dynamics, corresponding to primacy, recency, and temporal and semantic contiguity (Healey, Crutchley, & Kahana, Submitted). We expect that the emerging literature on individual differences in long-term memory will have a major impact on the field, but it is important to understand the nature of those individual differences: quantitative variation in a common set of memory processes.

Conclusions

Laboratory paradigms have been the most important tools in developing an understanding of human cognition. Concerns that the key measures provided by these paradigms do not reflect core cognitive processes, but are in fact artifacts of averaging across individuals who employ different strategies (e.g., Hintzman, 2011) must be taken seriously. But the solution is not to abandon existing paradigms. Rather, the solution is to rigorously test their validity. Here we found that four key free recall measures are highly consistent across individuals, with only recall initiation showing signs of qualitative differences among individuals. This level of consistency, and the fact that individual participants data are well–characterized by a computational model of core memory processes that makes no use of strategy, suggest that these free recall effects reflect fundmental principles of the memory system. We hope that the analytical techniques we have introduced here can be used test the validity of other key laboratory paradigms.