Magnetic resonance temperature imaging validation of a bioheat transfer model for laser-induced thermal therapy

Abstract

Purpose

Magnetic resonance-guided laser-induced thermal therapy (MRgLITT) is currently undergoing initial safety and feasibility clinical studies for the treatment of intracranial lesions in humans. As studies progress towards evaluation of treatment efficacy, predictive computational models may play an important role for prospective 3D treatment planning. The current work critically evaluates a computational model of laser induced bioheat transfer against retrospective multiplanar MR thermal imaging (MRTI) in a canine model of the MRgLITT procedure in the brain.

Methods

A 3D finite element model of the bioheat transfer that couples Pennes equation to a diffusion theory approximation of light transport in tissue is used. The laser source is modelled conformal with the applicator geometry. Dirichlet boundary conditions are used to model the temperature of the actively cooled catheter. The MRgLITT procedure was performed on n = 4 canines using a 1-cm diffusing tip 15-W diode laser (980 nm). A weighted L₂ norm is used as the metric of comparison between the spatiotemporal MR-derived temperature estimates and model prediction.

Results

The normalised error history between the computational models and MRTI was within 1–4 standard deviations of MRTI noise. Active cooling models indicate that the applicator temperature has a strong effect on the maximum temperature reached, but does not significantly decrease the tissue temperature away from the active tip.

Conclusions

Results demonstrate the computational model of the bioheat transfer may provide a reasonable approximation of the laser–tissue interaction, which could be useful for treatment planning, but cannot readily replace MR temperature imaging in a complex environment such as the brain.

Introduction

The rate of occurrence of brain and CNS tumours has remained steady over the past 20 years [1] and accounted for>22,000 new cases and>12,000 deaths in the USA in 2009 [2]. Recent key advances in technology have made a significant impact in realising the potential of MR-guided laser-induced thermal therapies (MRgLITT) as a clinical alternative or adjuvant to conventional surgery in brain. MRgLITT is a minimally invasive interstitial thermal ablation technique whereby tissue is heated to high temperatures (>5°C) leading to thermal necrosis of tissue between 24–72 h post ablation [3]. Applicators are navigated under stereotactic image guidance into the target tissue through a keyhole in the skull. Once in place, MR temperature imaging (MRTI) [4–6] is used during delivery of therapy to quantitatively monitor the laser induced temperature changes in a volumetric region of interest. Recently, commercialisation of the equipment and infrastructure needed to perform this procedure and deliver a desired dosimetry under closed loop MR guidance has made these systems clinically available [7]. Actively cooled applicator technology further helps prevent vaporisation and charring of adjacent tissue [8] and facilitates higher powers and exposure times to be used for faster treatment delivery over larger volumes (≈90 s for a 2-cm diameter lesion in brain). Closed-loop software utilises MRTI feedback to monitor the temperature near critical structures, lesion borders, and the applicator surface to minimise the potential for vaporising and charring of tissue; thus adding an essential level of safety and efficacy to the procedure.

While temperature-monitoring feedback provided during therapy makes LITT procedures safe and feasible in the brain, realistic predictive computational techniques for prospective pretreatment planning and intra-operative model-assisted filtering can also significantly improve the safety and efficacy of the procedure. Three-dimensional predictive modelling can provide invaluable insight into the outcome of difficult clinical procedures when irregularly shaped lesions are targeted, applicator trajectories become oblique with respect to the anatomy, multiple applicators are used, or nearby convective sources of heat transfer (ventricles, vessels, tissue perfusion, interfaces, etc.) lead to unexpectedly asymmetric temperature distributions. For these purposes, a fundamental model that couples the Pennes bioheat equation [9] to the diffusion theory of light transport in tissue [10, 11] is rigorously derived and critically evaluated against MR-derived thermal imaging data in a canine brain model. Similar to previous investigators, the presented model attempts to capture the geometrical effects of the cylindrical applicator [12, 13] and effects of the actively cooled applicator on the maximum temperature distribution [14]. The current study utilises isotropic constitutive parameters to evaluate the computer model of the laser–tissue interaction against real-time MR temperature imaging. The computational framework is intended as the infrastructure for further work to derive and validate computer models using temperature and thermal dose-dependent constitutive parameters [15].

Materials and methods

Animal model and fibre placement

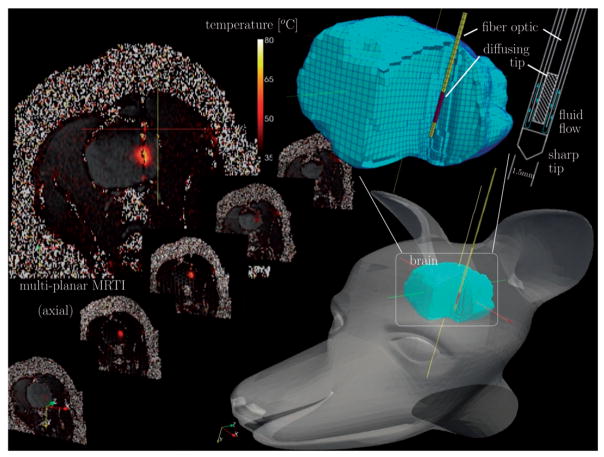
The experimental set-up of a MRgLITT procedure in brain is shown in Figure 1. The procedure was part of a MRgLITT safety and feasibility study in a canine model using multiplanar MR thermal monitoring with pre- and post-applicator 3D T1-weighted treatment planning images. All experiments (n = 4) were performed under institutional protocol. Mixed breed hounds were anaesthetised with ketamine/midazolam (Versed) solution (ketamine, 10 mg/kg; midazolam, 0.5 mg/kg; and glycopyrrolate, 0.01 mg/kg), incubated, and maintained with a 2% isoflurane/oxygen mixture. A water-cooled diffusing tip applicator was introduced percutaneously several cm into the brain tissue through a small burr hole in the parietal bone. Applicators were introduced coplanar with an axial plane of the animal. The actively cooled applicator consisted of two clear, concentric tubes for water flow, the central of which contains a 1-cm (axial) diffusing tip 4000-μ diameter silica fibre-optic (BioTex, Houston, TX). The fibre was attached to a near infrared 980 nm 15-W diode laser (Photex 15, BioTex, Houston, TX). For the interstitial laser application, the flow rate of the water was set to 15 mL/min for the water-cooled diffusing tip fibre-optic applicator. Applicators were secured using a skull bolt from planning images. A 3D fast spoiled gradient echo sequence was used to acquire the planning images as well as confirm the placement of a laser fibre using a separate set of coronal images. Prior to treatment delivery, the final fibre position within the brain was verified by a low power test pulse delivered under MRTI guidance. The power delivery history varied as the result of manual laser power control to achieve a desired lesion size from a single exposure. The exact power history for each canine in this study is provided in Figure 2. Safety mechanisms to prevent the possibility of charring monitored the temperature near the fibre, and laser power was turned off to keep temperatures below 90°C.

Figure 1.

Schematic diagram of in vivo MR-guided LITT procedure in a canine model of brain. A 1.5-mm diameter water-cooled diffusing tip applicator was introduced percutaneously through the parietal bone. The applicator consisted of two clear, concentric tubes for water flow, the central of which contains an active 1-cm diffusing tip 400 μm diameter silica fibre-optic. Delivery of the photothermal energy is monitored using a multiplanar EPI sequence for MR temperature imaging.

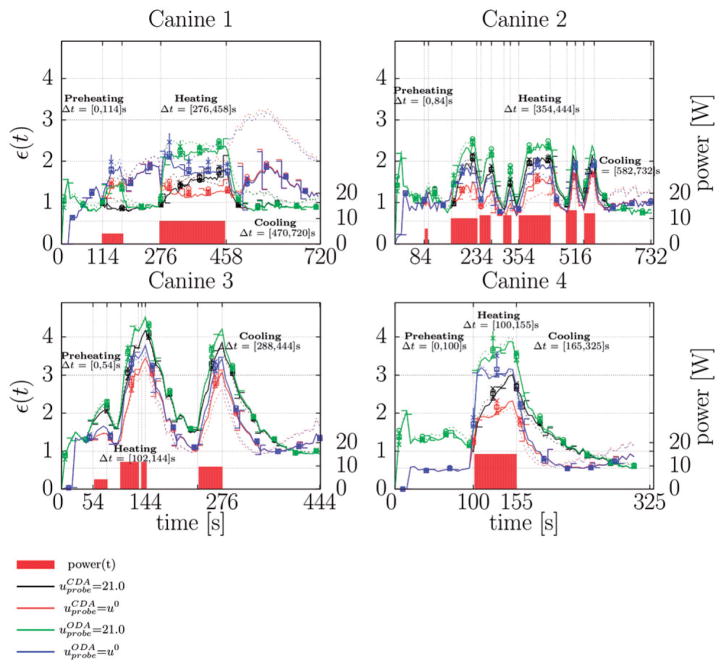
Figure 2.

Normalised error history. The history of the L₂ error normalised by the measured multiplanar temperature image noise (4), ε(t), is shown for each canine in this study. The normalised error is dimensionless. Data is plotted at $\omega =6.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$. The error bars shown provide the error range for the perfusion values considered; error bars left and right of the vertical axis plot ω = 3:0, $12.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$, respectively. Dotted lines plot ω = 0.0 for comparison. Permutations of laser (CDA, ODA) and cooling model u_probe = (21°C, u⁰) are shown for each canine. The power history of the thermal dose deliver is plotted against the right axis as a reference. Power is provided in W. The labelled time intervals highlight three regimes of interest: prior to heating, during heating, and during cooling. The corresponding pointwise maximum error plots during each of the regimes is provided for the centre plane of the multiplanar data in Figures 3–4. The -×-□- ○-Δ sequence shown illustrates the convergence of the finite element numerical solution throughout the thermal dose history. The -×-□- ○-Δ plots values of the error metric (4) at $\omega =6.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$ when monotonically increasing the mesh resolution (decreasing element diameter from 2 mm to 0.5 mm).

Additional fluoroptic probe devices for direct temperature measurement were not used during this procedure as they would interfere with the treatment delivery to the animals, add susceptibility artefact to the images, and unnecessarily complicate the craniotomy procedure. This was deemed excessive to obtain a point measurement, given that the MR temperature imaging technique and associated SNR-based uncertainty estimate were previously validated against independent measurement [16, 17] and is an often utilised methodology for in vivo monitoring of spatiotemporal temperature changes during therapy delivery. Ex vivo calibration of the temperature sensitivity coefficient in canine brain using a 980-nm laser resulted in a temperature sensitivity coefficient of $-0.0102\pm 0.0005\left[\frac{\text{ppm}}{°\mathrm{C}}\right]$ over the range of 25–60°C.

Multiplanar magnetic resonance thermal imaging

MR temperature imaging was performed on a 1.5T MRI (ExciteHD^®, GE Healthcare Technologies, Waukesha, WI) using an 8-channel, receive-only phased-array head coil (MRI Devices, Gainesville, FL) and a 2D multi-slice 8-shot EPI sequence [17] (FA = 60°, FOV = 20 × 20 cm, slice thickness 4 mm, TR/TE = 544/20 ms, encoding matrix of 256 × 128, with 5 s per update). Temperature images were reconstructed as a linear combination of the individual coil images weighted by the measured coil sensitivities. Image space parallel imaging techniques [18, 19] were used with an acceleration factor of two in canine 2. No acceleration factor was used in canines 1, 3, and 4. The centre slice of the multi-planar data contained the fibre for all canines. A time series of images was taken; imaging commenced prior to heating and continued throughout heating and cooling of the tissue. The complex-valued demodulated MR signal was captured in quadrature; one real and one imaginary image were acquired at each time point. The water proton frequency is assumed to chemically shift to lower frequencies with higher temperatures (caused by rupture, stretching, bending of hydrogen bonds) [20]. Thus, a phase change that corresponds to a decrease in the Larmor frequency implies a positive temperature change. The total temperature change, Δu, is proportional to the measured phase change, δφ:

$$\mathrm{\Delta }u=\frac{\delta \phi }{2\pi \alpha ·\gamma B_0·\text{TE}}$$

where α is the temperature sensitivity coefficient, γ is the gyromagnetic ratio of water, B₀ is the static magnetic field strength, and TE is the echo time. Computation of the accumulated phase difference to avoid phase wrap artefacts is discussed in the Appendix. Potential phase change measurement error due to temperature and spatially dependent temperature gradient-induced changes in magnetic susceptibility [21, 22] are not considered in this measurement model. However, as presented in the discussion, this approximation is expected to have a minimal impact on the results of this work due to the error metric (4) used. The measured body temperature of the canines, u⁰ = 34.6° ± 0.7°C is used to obtain an absolute temperature.

Computational methods

The thermal effects are expected to be confined to a region near the applicator. Consequently, the boundary conditions of a conformal canine-specific 3D volumetric hexahedral FEM mesh, shown in Figure 1 are expected to have no effect on the results. Thus, a single template FEM mesh was used to investigate each canine data set. Magnitude images were used to manually register the mesh template to the thermal imaging data. The objective of this study was to investigate modelling error in an ROI about the active tip of the applicator.

The ROI for each canine, Ω ⊂ R³ (FOV = 1.95 × 2.38 cm ± 0.21 × 0.19 cm) was chosen large enough to encompass the extent of the heating region but small enough to minimise bias of the error metric (4) where no heating occurred. Individual regions of the brain were not segmented due to the localised nature of the heating study. To ensure convergence, five FEM mesh resolutions were considered for each ROI (min/median/max number of elements = 896/3693/11978, min/median/max number of nodes = 1349/4674/13874). Within the ROI, the mesh size element diameter ranged between 0.5 mm and 2 mm. As a reference, 1 mm is in the order of the pixel size.

Geometric details of the applicator were closely modelled according to the manufacturer’s design and details provided in Figure 1. The active cooling of the applicator was modelled using Dirichlet boundary conditions to fix the temperature along the axial length of the 1.5-mm diameter catheter. The temperature of the catheter was studied at both ambient room temperature, 21°C, and body temperature, 34.6° ± 0.7°C. The 400-μm core diameter active region of the fibre-optic was modelled as Ω_tip, a cylindrical 1.5 mm diameter, 1 cm axial region, at a distance of 5 mm from the catheter tip. Modelling at the level of the 400-μm core diameter active tip is not expected to produce significant differences in the computations. The finite element basis functions are continuous across the applicator tissue interface.

The optical photon source of the laser–tissue interaction was rigorously derived from a diffusion theory approximation to the light transport equation [10]. The resulting photon source is referred to as the conformal discretisation approximation (CDA) in this manuscript. The CDA model is similar to fully analytic attempts to capture the cylindrical geometry of the interstitial fibre-optic [13] but exploits the underlying finite element discretisation of the computational domain to evenly distribute the laser power amongst the axial length and finite diameter in the active tip region. An analogous discretisation approach was implemented on structured grids [12] and results in multiple individual optical diffusion approximation (ODA) along the centre line of the applicator. The CDA accounts for the finite diameter of the applicator. Within the diffusion theory assumptions, the resulting conformal discretisation approximation is expected to provide a fluence source comparable to direct numerical solutions to the light transport equation [14, 11].

The diffusion model for light transport is built from the assumption that light is scattered more than absorbed, μ_a ≪ μ_s, where μ_a and μ_s give probability of absorption and scattering of photons, respectively. An applied volumetric power density, $P^{\ast }\left[\frac{W}{m^3}\right]$, provides a photon flux throughout the active region of the interstitial laser fibre, Ω_tip. Huygens superposition principle [13] is used to treat each position in the domain, x̂ ∈ Ω_tip, as an isotropic differential point source of irradiance, dE,

$$\mathrm{d}E(x,\widehat{x})=\frac{P^{\ast }(t)\mathrm{d}\widehat{x}}{4\pi {\Vert x-\widehat{x}\Vert }^2}exp({\mu }_t\Vert x-\widehat{x}\Vert )\widehat{\mathrm{s}}=\frac{x-\widehat{x}}{\Vert x-\widehat{x}\Vert }x\in \mathrm{\Omega }\backslash {\mathrm{\Omega }}_{\mathit{tip}}$$

The total attenuation is denoted μ_t = μ_a + μ_s. The propagation direction, ŝ, is the unit vector from the primary source of unattenuated photons to the position x. The light transport is assumed quasi-static and a stationary diffusion model is used at each time point of interest to relate the scattered fluence, z, to the known irradiance, dE, emitted from point source x̂ ∈ Ω_tip

$$\begin{array}{l}-{\mu }_{a}z+{\mu }_s\mathrm{d}E(x,\widehat{x})=\nabla ·\left(-\frac{\nabla z}{3{\mu }_{tr}}+\frac{{\mu }_{s}g}{3{\mu }_{tr}}\mathrm{d}E(x,\widehat{x})\widehat{\mathrm{s}}\right)\\ {\mu }_{tr}={\mu }_a+{\mu }_s(1-g)x\in \mathrm{\Omega }\backslash {\mathrm{\Omega }}_{\mathit{tip}}\end{array}$$ (1)

The anisotropic factor is denoted g. A conformal discretisation approximation (CDA) of the integral of the differential irradiance over the domain of the active tip, Ω_tip, is used to obtain an analytical expression for the scattered light, z

$$\begin{array}{l}E={\int }_{{\mathrm{\Omega }}_{\mathit{tip}}}\mathrm{d}E(x,\widehat{x})\mathrm{d}\widehat{x}={\int }_{{\mathrm{\Omega }}_{\mathit{tip}}}\frac{P^{\ast }(t)}{4\pi {\Vert x,\widehat{x}\Vert }^2}exp({\mu }_t\Vert x-\widehat{x}\Vert )\mathrm{d}\widehat{x}\\ \approx \sum _{e\in {\mathrm{\Omega }}_{\mathit{tip}}}{E}_{\mathrm{e}}(x,t)=\sum _{e\in {\mathrm{\Omega }}_{\mathit{tip}}}\frac{\mathrm{\Delta }{V}_{\mathrm{e}}{P}^{\ast }(t)}{4\pi {\Vert x-{\widehat{x}}_e\Vert }^2}exp({\mu }_t\Vert x-{\widehat{x}}_e\Vert )\end{array}$$

where ΔV_e is the volume and x̂_e is the centroid of the elements within the FEM mesh of the active tip. Here, conformal refers to a discretisation such that the finite elements adhere to the boundary of the active tip, Ω_tip. Similarly for the flux,

$$\begin{array}{l}{\int }_{{\mathrm{\Omega }}_{\mathit{tip}}}\mathrm{d}E(x,x)\widehat{\mathrm{s}}\mathrm{d}\widehat{x}={\int }_{{\mathrm{\Omega }}_{\mathit{tip}}}\frac{P^{\ast }(t)}{4\pi {\Vert x,\widehat{x}\Vert }^2}exp({\mu }_t\Vert x-\widehat{x}\Vert )\frac{x-\widehat{x}}{\Vert x-\widehat{x}\Vert }\mathrm{d}\widehat{x}\\ \approx \sum _{e\in {\mathrm{\Omega }}_{\mathit{tip}}}{E}_{\mathrm{e}}(x,t){\widehat{\mathrm{s}}}_e\\ =\sum _{e\in {\mathrm{\Omega }}_{\mathit{tip}}}\frac{\mathrm{\Delta }{V}_{\mathrm{e}}{P}^{\ast }(t)}{4\pi {\Vert x,{\widehat{x}}_e\Vert }^2}exp({\mu }_t\Vert x-{\widehat{x}}_e\Vert )\frac{x-{\widehat{x}}_e}{\Vert x-{\widehat{x}}_e\Vert }\end{array}$$

By linearity, each element in the discretisation may be treated as an uncoupled and independent source in the light diffusion equation.

$$-{\mu }_a{z}_e+{\mu }_s{E}_e=\nabla ·\left(-\frac{\nabla z_e}{3{\mu }_{tr}}+\frac{{\mu }_{s}g}{3{\mu }_{tr}}{E}_e\frac{x-{\widehat{x}}_e}{\Vert x-{\widehat{x}}_e\Vert }\right)\forall e\in {\mathrm{\Omega }}_{\mathit{tip}}$$

The total fluence resulting from each element source, (φ_t)_e = z_e + E_e, may be obtained from the classical isotropic point source solution [10] as the sum of the light scattered from the element, z_e, and the element-wise primary source, E_e. The total emanating fluence, φ_t(x, t), is the superposition of the element-wise solutions and reduces to a volume-weighted sum over the elements.

$$\begin{array}{l}{\phi }_t(x,t)=\sum _{e\in {\mathrm{\Omega }}_{\mathit{ttp}}}{P}^{\ast }(t)\mathrm{\Delta }{V}_e\left(\frac{3{\mu }_{tr}exp(-{\mu }_{\mathit{eff}}\Vert x-x_e\Vert )}{4\pi \Vert x-x_e\Vert }-\frac{exp(-{\mu }_t\Vert x-x_e\Vert )}{2\pi {\Vert x-x_e\Vert }^2}\right)\\ \approx \sum _{e\in {\mathrm{\Omega }}_{\mathit{ttp}}}{P}^{\ast }(t)\mathrm{\Delta }{V}_e\frac{3{\mu }_{tr}exp(-{\mu }_{\mathit{eff}}\Vert x-x_e\Vert )}{4\pi \Vert x-x_e\Vert }\\ {\mu }_{\mathit{eff}}=\sqrt{3{\mu }_a{\mu }_{tr}}x\in \mathrm{\Omega }\backslash {\mathrm{\Omega }}_{\mathit{tip}}\end{array}$$ (2)

A single point source ODA of the photon source at the centroid of the active tip, x₀, is used as a control and comparison against previous work [23].

$${\phi }_t(x,t)=P(t)\frac{3{\mu }_{tr}exp(-{\mu }_{\mathit{eff}}\Vert x-x_0\Vert )}{4\pi \Vert x-x_0\Vert }x\in \mathrm{\Omega }\backslash {\mathrm{\Omega }}_{\mathit{tip}}$$ (3)

A linear Pennes model was used to simulate the bioheat transfer [9]. The fluence, φ_t, provides the thermal source in the bioheat equation and couples the diffusion theory model of light transport in tissue to Pennes model. The laser powers and exposure times for each canine shown in Figure 2 were modelled using piecewise continuous step functions of the wattage. The model considers the optical and thermal properties of the tissue as well as a highly simplified model of the micro-vasculature heat sink consisting of a linear temperature difference between the heated region and the arterial temperature, u_a. The Pennes bioheat equation has been shown to accurately model heating in areas absent of major vasculature [24].

$$\begin{array}{l}\rho c_p\frac{\partial u}{\partial t}-\nabla ·(k\nabla u)+{wc}_{\mathit{blood}}(u-u_a)={\mu }_a{\phi }_t\text{in}\mathrm{\Omega }\\ -k\nabla u·\mathbf{n}=0\text{on}\partial \mathrm{\Omega }u=u_{\mathit{probe}}in{\mathrm{\Omega }}_{\mathit{probe}}\end{array}$$

The initial temperature field, u(x, 0) = u⁰ = 34.6° ± 0.7°C, is taken as the measured baseline body temperature. The density of the continuum is denoted ρ and the specific heat of blood is denoted $c_b\left[\frac{1}{\text{kg}·\mathrm{K}}\right]$. The boundary of the mesh template is far enough away from the heating region such that zero heat flux may be considered as the Neumann boundary condition on ∂Ω. The scalar-valued coefficient of thermal conductivity and perfusion are denoted k and ω. Within the region of the mesh that represents the applicator, Ω_probe, a Dirichlet boundary condition is imposed such that the cooling water of the applicator is held at body temperature, u_probe = u⁰, or ambient temperature, u_probe = 21°C, throughout the procedure. The temperature evolution predicted by the bioheat equation was computed using the finite element method with linear polynomials and a Crank-Nicholson time stepping scheme.

Constitutive data

The bio-thermal and optical parameters were obtained from literature [10, 25, 26] and were modelled as homogeneous throughout the delivery region of interest, Table I. An average value of the range of scattering, μ_s, and absorption, μ_a, values quoted in the literature was used. A range of perfusion values ω = 0.0,3.0,6.0, $12.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$ were simulated to capture physically realistic values of brain tissue perfusion found in literature and as a first order study of temperature-dependent perfusion. Empirical models of the temperature dependence of the constitutive data [27, 28, 25], k(u), ω (u), μ_a(u), will be considered in future validation studies. Statistics were collected comparing the thermal imaging data for each animal against each permutation of laser model, cooling model, and perfusion value, a total of 64 simulations at each mesh resolution considered.

Table 1.

Constitutive data [9, 23, 24]

$k\frac{\mathrm{W}}{\mathrm{m}·\mathrm{K}}$	$\omega \frac{\text{kg}}{{\mathrm{m}}^3\mathrm{s}}$	g	${\mu }_s\frac{1}{\text{cm}}$	${\mu }_a\frac{1}{\text{cm}}$	$\rho \frac{\text{kg}}{{\mathrm{m}}^3}$	$c_{\mathit{blood}}\frac{1}{\text{kg}·\mathrm{K}}$	$c_p\frac{1}{\text{kg}·\mathrm{K}}$
0.527	0.0, 3.0, 6.0, 12.0	0.862	47.0	0.45	1045	3840	3600

Error metric and thermal image noise

The temperature-dependent relaxation properties of tissue are expected to adversely affect the MR temperature signal and cause artefacts. Time varying and spatially dependent maps of the temperature image noise, σ(x, t), are used to pointwise normalise unrealistic discrepancies between the measured temperature data, u^MRTI, and the model predicted temperature, u. The resulting metric of comparison, ε(t), is a weighted space L₂ norm within the time interval of interest, [0, T], and normalised by the volume of the ROI, Ω ⊂ R³

$$\begin{array}{l}\epsilon (t)={\left(\frac{{\Vert u-u^{\mathit{MRTI}}\Vert }_{\sigma }^2}{{\int }_{\mathrm{\Omega }}\mathrm{d}x}\right)}^{1/2}\\ ={\left(\frac{{\int }_{\mathrm{\Omega }}{\left(\frac{u(x,t)-u^{\mathit{MRTI}}(x,t)}{\sigma (x,t)}\right)}^2\mathrm{d}x}{{\int }_{\mathrm{\Omega }}\mathrm{d}x}\right)}^{1/2}t\in [0,T]\end{array}$$ (4)

The SNR is assumed sufficiently large (SNR>10) such that the noise in the real and imaginary images may be approximated as Gaussian and the temperature image noise may be obtained from the measured SNR of the MR signal.

$$\sigma (x,t)=\underset{\tau \in [0,t]\subseteq [0,T]}{max}\frac{1}{2\pi \alpha ·\gamma B_0·\text{TE}}\frac{\sqrt{2}}{\text{SNR}(x,\tau )}$$

The current time maximum, max_τ∈[0,t], is needed to normalise unrecoverable phase changes following T1-related signal loss due to large temperature changes. The pointwise SNR was obtained as the ratio of corresponding magnitude image intensity I(x, t) to the measured system noise, σ_system.

$${\sigma }_{\mathit{sustem}}=\frac{{\langle \delta I\rangle }_{\mathit{ROI}}}{0.655\sqrt{2}}$$

A difference method [29] was used to compute the system noise in the corresponding magnitude images. The difference image standard deviation in the small volume of interest, 〈δI〉_ROI, in air is measured in initial magnitude images. A factor of 0.655 is needed to approximate the low SNR Raleigh distributed signal in air as a Gaussian distribution [30]. The $\sqrt{2}$ arises from the difference method.

Results

Representative time-dependent statistics of the error history collected for all 320 simulations comparing the thermal imaging data for each animal against each permutation of finite element mesh resolution, laser model, cooling model, and perfusion value is shown in Figure 2. The laser exposure history for each canine is provided as a reference. The wattage versus time specific to each canine was the result of manual laser power control to achieve a desired lesion size from a single exposure. The time history of the normalised error metric (4) indicates average errors between 1–4 standard deviations with respect to the temperature image noise. The error metric (4) is unaffected as the finite element mesh resolution reaches the pixel resolution.

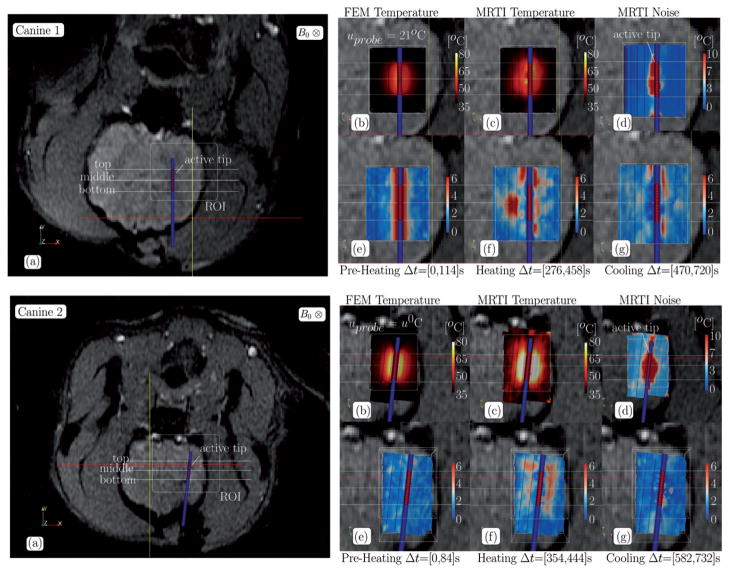
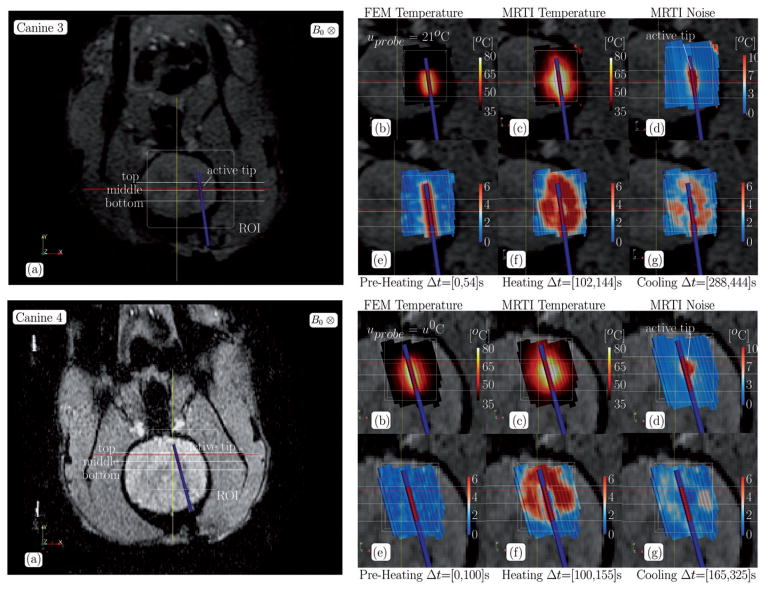
Representative individual results using the fluence obtained from the conformal discretisation approximation (CDA) of the light transport equation (2) for each canine are shown for $\omega =6.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$ in Figures 3–5. Canine 1 and Canine 3 are shown for with u_probe = 21°C. Canine 2 and Canine 4 are shown for with u_probe = u⁰. Individual results for the optical diffusion approximation (ODA) control (3) are not shown but, in general, the ODA model [23] predicts unrealistic excessive heating near the centroid of the active tip and spherical isotherms as expected from the isotropic point source heating a homogeneously modelled tissue. For each canine, the anatomical position of the ROI and spatial profiles are illustrated on magnitude images of the anatomy. Profiles illustrate the maximum over time of the MR temperature data, computational prediction, and MR temperature noise in °C. The applicator is near the centre of the profiles for all canines and is characterised by the 1.5-mm constant temperature region enclosed within the highest temperature regions. Cut-planes coplanar with the applicator and through the ROI of the finite element data used in Figure 2 are also shown. The pointwise maximum over time for the FEM predicted temperature, MR temperature data, and MR temperature noise is provided in °C. The pointwise maximum normalised error

Figure 3.

Canine 1–2 data summary, CDA, $\omega =6.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$ (a) The anatomical position of the ROI and the spatial profiles used in Figure 5 are illustrated on magnitude images of the anatomy. Cutplanes through the ROI of the finite element data used in Figure 2 is shown in (b–g). Cutplanes are coplanar with the applicator. The pointwise maximum over time for the (b) FEM predicted temperature, (c) MR temperature data, and (d) MR temperature noise is provided in °C. The pointwise maximum normalised error (5) over time for the (e) pre-heating, (f) heating, and (g) cooling regimes labelled in Figure 2 are provided.

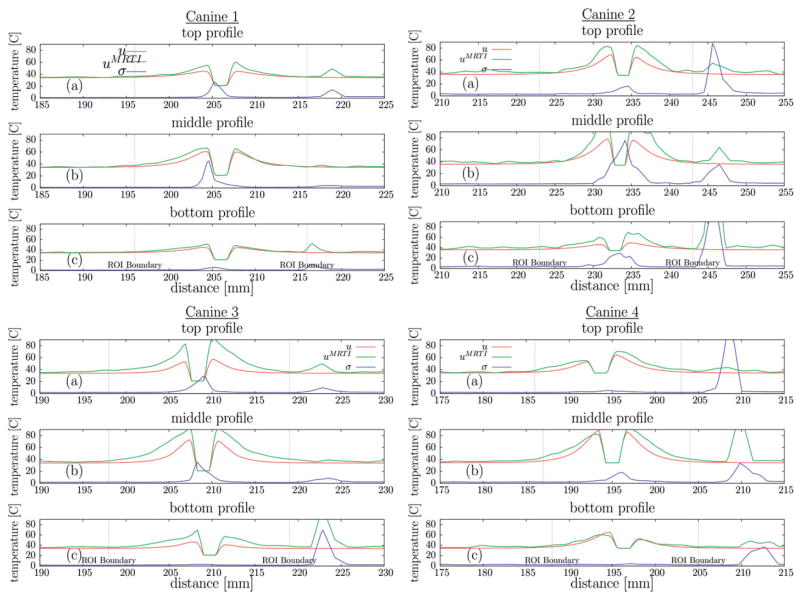
Figure 5.

Canine 1–4 spatial profiles summary, CDA, $\omega =6.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$ The (a) top, (b) middle, and (c) bottom profiles illustrated in Figures 3, 4(a) plot the maximum over time of the MR temperature data (°C), computational prediction (°C), and MR temperature noise (°C) against distance (mm). Profiles extend beyond the ROI used in normalisation in Figure 2; the boundary of the ROI is denoted on the profiles.

$$\underset{\tau \in \mathrm{\Delta }t}{max}\sqrt{{\left(\frac{u(x,\tau )-u^{\mathit{MRTI}}(x,\tau )}{\sigma (x,\tau )}\right)}^2}$$ (5)

over time for the pre-heating, heating, and cooling regimes labelled in Figure 2 is also provided. Cooling time intervals were chosen slightly offset from the heating time intervals to distinguish the regimes and avoid overlapping error.

Discussion

The multiplanar MR thermal imaging reflects the applied laser exposure and reveals significant variability in the heating profiles amongst the four canine experiments. During the period prior to laser exposure, modelling error is approximately one standard deviation, which is within the measured thermal image noise as would be expected (Figure 2). In all canines the initial three multiplanar imaging data instances (18 s) in the time sets are not used to allow the bulk magnetisation to reach a steady state precession. This results in immediate initial discrepancies between the u_probe = u⁰, 21°C models in the preheating regime. Initial errors with the u_probe = 21°C cooling model are due to the model predicted diffusion of the cooled temperature of the applicator into tissue; this phenomenon is not seen in MR thermal images at these early times. Insignificant error in the u_probe = u⁰ models during the preheating regime also implies that potential susceptibility-induced temperature measurement artefact due to the presence of the applicator in the tissue appears to be negligible. Over the permutations of laser models and cooling models considered, the CDA of the light transport equation model combined with the u_probe = u⁰ consistently provided the least error during heating. Immediately after laser exposure, there is a recurring trend of the u_probe = u⁰ cooling model providing less modelling error during the initial stages of tissue cooling followed by the u_probe = 21°C cooling model providing less error at later times. This suggests that the active cooling fluid is mildly heated during the thermal delivery. As MR thermal imaging is unreliable in the applicator region, further work incorporating a thermal sensor internal to the applicator would provide useful temperature information to compare to the assumed model values. As expected of the Pennes bioheat perfusion model, the error, ε(t) (4), is most sensitive to the perfusion value when temperatures have deviated furthest from body temperature. The greatest deviations are consistently seen immediately after the laser is stopped. Effects from scattering, absorption, and thermal conductivity parameters dominate during heating phase.

The spatial time-wise maximum error contours, Figures 3–4(e–g), over the pre-heating, heating, and cooling regimes illustrated in Figure 2 indicate that the applicator active cooling does not significantly decrease the tissue temperature. During the preheating time regime, Figures 3–4(e), the ambient temperature, u_probe = 21°C, cooling model shows significantly more modelling error than the body temperature, u_probe = u⁰, cooling model. A similar phenomenon is seen during the heating and cooling regime, however: recall that the heating and cooling plots, Figures 3–4(f, g), are biased by the maximum MRTI noise, Figures 3–4(d), and areas with a history of low SNR are effectively excluded. The pointwise errors seen in the maximum temperature comparison are recapitulated in the maximum error plots over the time interval of heating, Figures 3–4(f). Isotherms of the ODA model (not shown) are spherical about the point source due to the isotropic constitutive parameters and the error reflects the geometrical inconsistencies with the cylindrical applicator. Isotherms of the CDA model are elliptical and conform to the active tip of the applicator.

Figure 4.

Canine 3–4 data summary, CDA, $\omega =6.0\left[\frac{\text{kg}}{{\text{sm}}^3}\right]$ (a) The anatomical position of the ROI and the spatial profiles used in Figure 5 are illustrated on magnitude images of the anatomy. Cutplanes through the ROI of the finite element data used in Figure 2 are shown in (b–g). Cutplanes are coplanar with the applicator. The pointwise maximum over time for the (b) FEM predicted temperature, (c) MR temperature data, and (d) MR temperature noise is provided in °C. The pointwise maximum normalised error (5) over time for the (e) pre-heating, (f) heating, and (g) cooling regimes labelled in Figure 2 are provided.

Significant canine-specific variability in the heating profiles of the MR thermal imaging data cutplanes is seen, Figure 5; maximum values range between 65–110°C. Variability results from the applied laser exposure and the local biothermal parameters of the tissue. The maximum temperature noise in the regions of interest is between 20–30°C, temperature history dependent, and correlates with the maximum temperature values of the heating. Asymmetries in the maximum noise indicate spatially dependent relaxation properties of the tissue. In regions of large heating, the MR temperature signal is not expected to recover from the signal loss due to the temperature-induced T1 increase, the normalisation introduced in (4) effectively excludes these regions from the error history presented in Figure 2. Further, normalisations due to the error metric used (4) significantly reduces the weighting of errors in regions where the temperatures and temperature gradients will have the most profound effects on spatially dependent susceptibility-induced artifact [21] in the MR temperature measurement. Spatial profiles outside the ROI also show high temperature noise at the brain boundary due to susceptibility effects at the tissue interface. Maximum temperature pointwise agreement between the first order finite element models and the MR thermal imaging data is heavily tissue property-dependent, is affected by thermal image noise, and varies substantially, 1–30°C. There may also be potential errors due to out of plane mis-registration. Heat is diffused several more mm into the tissue when using the body temperature, u_probe = u⁰, cooling model as compared to the ambient temperature, u_probe = 21°C, cooling model but still diffuses less into the tissue than is seen in the MR thermal images. The results agree with the observed tissue thermal conductivity increase with temperature [28].

Alone, the developed models may be potentially useful for 3D prospective treatment planning with the primary aim of providing a more optimal assessment of the number of applicators required, the impact of applicator location and, most importantly, the approximate range of thermal damage. However, to achieve patient-specific predictions of the bioheat transfer, canine-specific variability in the temperature isotherms clearly indicates a need for modelling biothermal heterogeneities of the tissue [23, 31] and non-linear temperature-dependent effects on the constitutive parameters. In spite of the inability of the models to capture patient-specific details for independent prospective pretreatment planning, the developed models are first order accurate, and could easily serve as the foundation for many future personalised modelling efforts. Pretreatment imaging could be used to incorporate higher level details of the biothermal model by identifying large vessel boundaries and even measuring the perfusion directly [32, 33]. Techniques to propagate uncertainties [34, 35] in the model parameters and quantitatively predict confidence intervals of treatment success could also be directly used to provide clinically useful planning information. Higher order modelling of further details of the MR thermal image acquisitions, such as the effect of multi-channel receive arrays on the measurement uncertainty [36], may prove significant to uncertainty propagation methods. Additionally, the first order accurate models are expected to be computationally efficient and ideal for model-assisted filtering techniques to synergistically improve the fidelity of monitoring. Further studies are needed to rigorously investigate the computational performance of the developed model and the applicability to real-time application software. In addition to the computational speed, the set-up time required to treatment-time generate a FEM mesh that is conformal with one or multiple applicators must be considered. Under the current CDA approach, interactive movement of multiple applicators would require a rapid FEM mesh for each configuration. Rapid conformal mesh generation techniques within isogeometric analysis [37] framework may be of potential use. Future work may also incorporate the class of δP approximations into the fluence derivation to model recent advances in photonics and nanotechnology [38, 39].

In conclusion, results presented here demonstrate that the derived fundamental model of Pennes bioheat equation coupled with light transport diffusion theory is a reasonable approximation of laser–tissue interaction and heating in a canine brain model (n = 4) and therefore may be a useful foundation for 3D prospective treatment planning of laser ablation in brain when additional monitoring, such as MR temperature imaging, is employed to ensure safety and efficacy. During the period with the laser power source active, the conformal discretisation approximation (CDA) of the light transport equation model was significantly more accurate than the point source ODA model but, in general, the finite element models are only able to reproduce the temperature variability to first order accuracy. The observed time histories of the error pattern also indicate that incorporating the added complexity of modelling the convective heat transfer of the active cooling fluid flow may not substantially add to the temperature prediction with respect to the L₂ norm as the metric.

Appendix

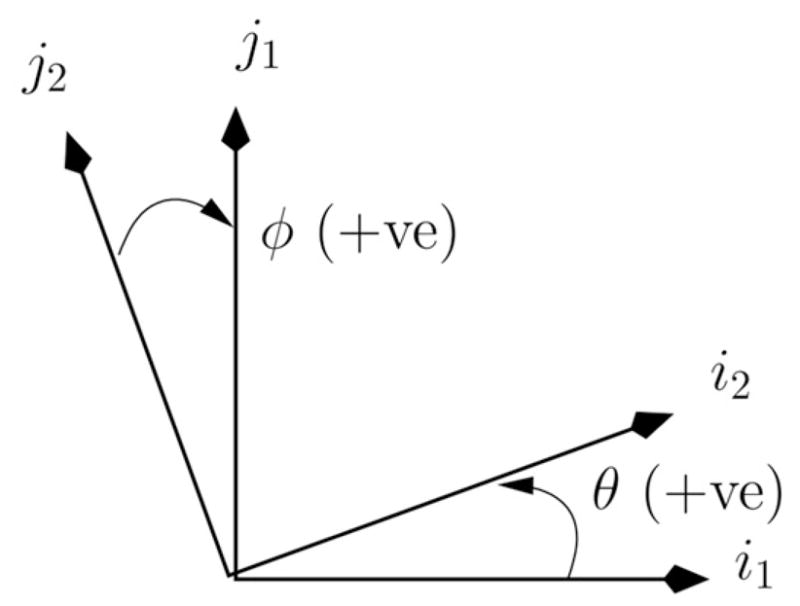
For the heating regime of interest, phase wrap artefacts are expected and are removed by incrementally summing the phase of the MR signal between time t_k, S^k = |S^k|e^iθk, and the signal at time t_k+1, S^k+1 = |S^k+1|e^iθk+1. This is equivalent to an R3 transformation of the frame of reference such that the signal at time t_k is along the x-axis, i₂, in the new frame of reference. The original coordinates in this frame of reference are given as

$$i_1=cos{\theta }^k{i}_2-sin{\theta }^k{j}_2{j}_1=sin{\theta }^k{i}_2+cos{\theta }^k{j}_2$$

The new signal in this reference frame is

$$\begin{array}{l}{S}^{k+1}=S_x^{k+1}{i}_1+S_y^{k+1}{j}_1\\ =S_x^{k+1}\left(cos{\theta }^k{i}_2-sin{\theta }^k{j}_2\right)+S_y^{k+1}\left(sin{\theta }^k{i}_2-cos{\theta }^k{j}_2\right)\end{array}$$

and the phase change is given by the angle with the i₂ axis. Within the usual conventions for the right handed polar coordinate system, Figure 6, the rotating frame of reference of the bulk magnetisation is in the negative z-direction.

Figure 6.

Polar convention.

Consequently, positive θ (increase with the angle from x-axis) corresponds to a negative phase change and a positive phase shift in the rotating frame corresponds to an increase in frequency and thus negative theta in the usual convention.

$$\begin{array}{l}\delta \phi =-\delta \theta =\text{atan}\left(\frac{\left(S_y^{k+1}cos{\theta }^k-S_x^{k+1}sin{\theta }^k\right)}{\left(S_y^{k+1}cos{\theta }^k+S_x^{k+1}sin{\theta }^k\right)}\right)\\ =\text{atan}\left(\frac{\left(S_y^{k+1}{S}_x^k-S_x^{k+1}{S}_y^k\right)}{\left(S_y^{k+1}{S}_x^k+S_x^{k+1}{S}_y^k\right)}\right)\\ =\text{atan}2(Im,Re)\\ =\text{atan}2\left(S_y^{K+1}{S}_x^k-S_x^{k+1}{S}_y^k,S_x^{k+1}{S}_x^k+S_y^{K+1}{S}_y^k\right)\end{array}$$

The method is equivalent to complex phase difference techniques [16] such that the accumulated phase difference, φ_N, is given by

$$\delta \phi =\sum _{k=1}^N\angle {\overline{S}}^k·S^{k+1}=\sum _{k=1}^N\text{atan}\left({\overline{S}}^k·S^{k+1}\right)$$

where N is the number of temperature measurements.