Optimising biometry for best outcomes in cataract surgery

Abstract

Biometry has become one of the most important steps in modern cataract surgery and, according to the Royal College of Ophthalmologists Cataract Surgery Guidelines, what matters most is achieving excellent results. This paper is aimed at the NHS cataract surgeon and intends to be a critical review of the recent literature on biometry for cataract surgery, summarising the evidence for current best practice standards and available practical strategies for improving outcomes for patients. With modern optical biometry for the majority of patients, informed formula choice and intraocular lens (IOL) constant optimisation outcomes of more than 90% within ±1 D and more than 60% within ±0.5 D of target are achievable. There are a number of strategies available to surgeons wishing to exceed these outcomes, the most promising of which are the use of strict-tolerance IOLs and second eye prediction refinement.

Introduction

On 29 November 1949, Harold Ridley implanted the first prosthetic intraocular lens (IOL) into a human eye. Ridley's 1952 paper describes the new technique and documents the first ever audit of refractive outcomes after cataract surgery with IOL implantation.¹ In the first audit cycle, comprising two patients, both were found to have highly myopic outcomes (−21 and −15 dioptres spherical equivalent, DSE), resulting from excessive power of the first IOL design. This was modelled on the natural crystalline lens with a radius of curvature for the anterior and posterior surfaces of 10 and 6 mm, respectively. Unfortunately, the higher refractive index of the polymethyl methacrylate material in comparison to the crystalline lens was overlooked and the IOL was more powerful than intended. A new design with a power of +24 dioptres (D) was developed, and the next 25 patients all received this standard IOL. The second audit cycle found that with this lens the median post-operative refractive error was -2.25 DSE (range −10.5 to +4.5 DSE).

For the next two decades, IOL implantation remained controversial because of ‘chaotic experimentation and defective IOL design and manufacture' and efforts were focussed on reducing the complications of IOL implantation.² During this period, surgeons typically implanted the same power IOL into every eye with the intention of restoring the patient's pre-cataract refractive status, and although this approach worked well for many patients, large refractive surprises were common³ with poor correlation between pre- and post-operative refractive error.⁴ As IOL implantation became accepted as the standard of care for cataract surgery attention turned to improving refractive outcomes using IOL power prediction algorithms based on biometric measurements of individual patients' eyes,³ resulting in around 70–80% achieving a post-operative refraction within ±1 D of the intended target.^{3, 5} The superior clinical outcomes of phakoemulsification over previous surgical procedures, particularly in relation to post-operative astigmatism,⁶ the improved accuracy and repeatability of measurements provided by devices such as the IOL Master (Carl Zeiss Meditec AG, Oberkochen, Germany) and Lenstar LS-900 (Haag-Streit AG, Koeniz, Switzerland), ⁷ and modern third- and fourth-generation IOL power prediction formulas, which use up to seven pre-operative variables,⁸ have improved the predictability of refractive outcomes and transformed routine cataract surgery from a procedure intended simply to restore sight to a refractive procedure.

Biometry has become one of the most important steps in modern cataract surgery.⁹ Gale et al. found that with appropriate formula selection, optical axial length measurement, and optimisation of IOL constants 87% of patients achieved an outcome within ±1 D of target.¹⁰ The Royal College of Ophthalmologists, in its most recent Cataract Surgery Guidelines,¹¹ has adopted a standard of 85% within ±1 D of target and 55% within ±0.5 D of target.

This paper is aimed at the NHS cataract surgeon and intends to be a critical review of the recent literature on biometry for cataract surgery, summarising the evidence for current best practice standards and available practical strategies for improving outcomes for patients. It is assumed that both optical and ultrasound axial length measurement devices are available, appropriate measurement protocols and quality control procedures are established, and that a mechanism for ascertaining refractive outcomes and performing audit is in place.

Theoretical limits to biometry

If biometry and IOL power prediction were perfect, then the prediction error (PE) for every eye would be zero, and the mean error (ME) and mean absolute error (MAE) for all patients having cataract surgery would also be zero (see Appendix). In reality, biometric measurements are not perfectly accurate and it is not yet possible to measure all of the physiological variability between eyes; the measurements and IOL prediction algorithms therefore rely upon a large number of assumptions, and which are not accurate in every case.

Norrby evaluated the effect of the variability of the input parameters on refractive outcome and estimated their relative contribution to the final PE.¹² The biggest source of error (35.5%) is inaccuracy in the IOL formulas' predictions of the post-operative IOL position. Inaccuracies in axial length and keratometry measurements, either arising from the measurements themselves or associated underlying assumptions, account for 17.0% and 10.1% of the error, respectively. It might seem surprising that post-operative refraction is a significant contributor to the PE (27.0%), but the standard deviation for a subjective refraction is 0.39 D¹² indicating wide variability in the measurement of refractive outcome.

Norrby estimated that the lowest MAE achievable with current methods is between 0.36 and 0.40 D,¹² implying a maximum proportion within ±1 D of target of between 95 and 97%.¹³ Norrby's limits are not absolute, however, and many of the strategies outlined below allow improved predictions by implicitly refining systematic errors or biometric assumptions, thereby reducing the magnitude of their contribution to the final PE. Although the goal of zero PE for all eyes remains distant, it is a realistic objective to improve outcomes by reducing the spread of PEs.

Axial length measurement

The axial length of the eye may be measured by ultrasound (either contact or immersion) or by optical means (IOL Master or Lenstar). Non-contact optical biometry has become the gold-standard because of its ease of use, accuracy, and reproducibility.⁹ The main disadvantage of the optical methods is their inability to obtain axial length measurements in approximately 10% of eyes, typically those with dense posterior subcapsular cataracts.^{7, 14} For these eyes ultrasonic axial length measurement is required, and in the UK contact ultrasound is the method of choice with immersion methods rarely used.¹⁵ In general, however, immersion ultrasound produces more accurate predictions than contact ultrasound,⁸ approaching or matching those of the optical methods.^{16, 17} If immersion ultrasound was adopted as the second-line investigation for eyes in which optical biometry fails, then outcomes could be improved from 82.5% within ±1 D of target¹⁰ to between 85.7 and 94.3%.^{18, 19} The impact of such improvement on the patient population as a whole is dependent upon the proportion requiring ultrasound biometry; assuming a rate of 10% then between 0.3 and 1.2% more eyes overall could achieve within ±1 D of target as a result of this change in practice.

Formula choice

The formulas in widest use utilise two biometric measurements (axial length and keratometry) and a single IOL constant²⁰ (Hoffer Q,²¹ Holladay 1,²² and SRK/T²³). The Haigis formula uses three measurements (axial length, keratometry, and pre-operative anterior chamber depth) and three IOL constants,¹⁸ Olsen's formula five uses measurements (those used for the Haigis, plus pre-operative refraction and lens thickness) and one IOL constant,²⁴ and the Holladay 2 formula uses seven measurements (those used by Olsen, plus patient age, and the horizontal white-to-white measurement) and one IOL constant.⁸

There is presently no single formula that is suitable for all eyes.⁹ There are many studies comparing the performance of various formulas in different patient groups, but often the number of eyes analysed is small. The most authoritative comparison to date is that of Aristodemou et al, which evaluated the performance of the Hoffer Q, Holladay 1, and SRK/T formulas in 8108 eyes.²⁵ The authors concluded that the Hoffer Q was best for axial lengths below 21.5 mm and the SRK/T for those above 26.0 mm. For the intervening range, there was no statistically significant difference between the formulas, although the Holladay 1 showed a modest performance advantage over the others.

The T2 formula is a modification of SRK/T, which corrects for systematic non-physiological behaviour in the latter, and which results in a 10% improvement in PE.²⁶ The Haigis formula is reported to give accurate predictions for both short²⁷ and long eyes,²⁸ but Olsen's formula may produce results slightly better than Haigis'.²⁹ The Holladay 2 formula is suggested to be ‘one of the more accurate formulas available',⁸ but there is little systematic evidence for this assertion.³⁰ In the absence of compelling comparative evidence of the superiority of these formulas, it is justifiable to continue using an appropriate combination (according to axial length) of the two variable single constant formulas.

IOL constant selection and optimisation

The term ‘IOL constant' is a misnomer as it does not relate solely to the IOL and is not necessarily a constant. It is best considered as a ‘fudge factor' that adjusts IOL predictions for systematic errors arising from the entire clinical environment, including those arising from the biometry measurement devices (and combinations thereof), patient population, and surgical technique.^{29, 31}

The estimated IOL constant published by manufacturers is typically intended for use with contact ultrasound biometry, although increasingly constants specific to optical biometry are also provided. It is well established that, as a result of corneal indentation, contact ultrasound produces shorter AL measurements than the immersion technique³² and optical biometry.³³ The use of a contact ultrasound-specific IOL constant with either immersion or optical biometry will result in outcomes more hyperopic than intended.³¹

If an IOL constant specific for immersion or optical biometry is not available, then a suitable value may be listed at the User group for Laser Interference Biometry (ULIB);³⁴ at the time of writing, IOL constants for over 250 IOL models are available, derived from the outcomes of over 50 000 patients, although caution should be exercised when using constants optimised on other patient populations (eg, inspection of the ULIB data shows differences in constants for the same IOL model between Japanese and non-Japanese eyes), and by other surgeons. Furthermore, in some cases, the ULIB data reflect a mixture of optical and immersion axial length measurements, and automated and manual keratometry.³¹ Despite these caveats a constant obtained from the ULIB database is likely to be a better starting point for optical biometry than the manufacturer's published contact ultrasound constant when introducing a new IOL into practice, provided that the IOL constant is then optimised according to local clinical outcomes.

Constant optimisation is the process by which the IOL constant is adjusted to minimise the systematic errors listed above, as indicated by a ME of zero.²⁹ The process of constant optimisation has little effect on the dispersion of outcomes around the mean (ie, the standard deviation, SD),²⁹ but maximises the proportion of eyes within a particular target range and minimises the MAE (see Appendix for a discussion of the relationship between ME, MAE, and SD). IOL constant optimisation has been shown to improve substantially prediction accuracy for contact ultrasound (from 79.7 to 82.5% within ±1 D),¹⁰ immersion ultrasound (from 60% to 65% within ±0.5 D),¹⁶ and with optical biometry (from 76–89% to 92–94% within ±1 D, dependent upon IOL model and formula).³¹ The latter study used constants intended for contact ultrasound as the baseline,³¹ and in practice, the magnitude of the improvement to be gained from IOL constant optimisation depends on how close the optimised and baseline constants are found to be.

IOL constant optimisation may be performed by entering refractive outcome data into the IOL master, or by using one of the online services provided by Dr Haigis³⁵ or Dr Hill.³⁶ Haigis recommends using data from more than 50 eyes,³⁵ and Hill more than 200.³⁶ Aristodemou et al evaluated the clinical significance of different degrees of error in the IOL constant and estimated that a minimum of 86 eyes is required to optimise the pACD for the Hoffer Q formula and around 250 for the SRK/T A constant and Holladay 1 Surgeon Factor.³¹

All eyes included for optimisation should have a stable refractive error and best-corrected visual acuity of 6/12 or better,²² and as wide a range of axial length as possible,³⁵ and preferably all eyes should have been measured using the same devices for keratometry and axial length. Although the optical biometry devices were calibrated against immersion ultrasound measurements and correlate well with them¹⁷ and with each other,³⁷ and therefore the IOL constants for the different methods should be very similar, inspection of ULIB data suggests that this may not be the case.³⁴ It is not clear whether the observed differences are due to random or systematic errors, due to differences between populations or surgeons, or represent true differences between the devices, but optimisation should perhaps distinguish between immersion ultrasound, IOL master, and Lenstar axial lengths.

Surgeon-specific lens constants

It has long been suggested that there is sufficient variation between surgeons' refractive outcomes after cataract surgery to justify the use of individually optimised surgeon-specific IOL constants, although much of the variation in early studies resulted from differences in biometry measurement devices and IOL model, in addition to variation in surgical technique.²² Modern optical biometry with its low inter-observer variability⁹ means that two surgeons measuring the same eye with the same device are likely to acquire almost identical measurements. Small-incision phakoemulsification techniques, with continuous curvilinear capsulorhexis and in-the-bag IOL placement, may reduce inter-surgeon variability and its effects on refractive outcome.

Aristodemou et al examined the variation in optimised IOL constant in a group of 27 surgeons³¹ and concluded that for the majority of surgeons (25 out of 27, 93%) there was no clinically meaningful difference that would justify the use of surgeon-specific IOL constants. For two surgeons (7%), the differences in the surgeon-specific constants from the mean IOL constant for the entire group were clinically relevant. The authors were not able to identify reasons for the systematic differences these surgeons exhibited in comparison to their peers because data collection was anonymous, but in day-to-day practice if an individual surgeon demonstrates a ME in their refractive outcomes that is different from that of other surgeons using the same IOL, or clinically different from zero, then they may benefit from using a surgeon-specific IOL constant. It may be demonstrated that a surgeon with a ME of ±0.15 D compared with another with a ME of zero will achieve 1% fewer eyes within ±1 D of target, and 2.1% fewer within ±0.5 D; conversely optimisation of the first surgeon's IOL constant will correct the ME to zero with corresponding improvements in the proportions within ±1 D and ±0.5 D of target.

Axial length- and keratometry-specific lens constants

Since the introduction of the SRK II formula, it has been recognised that the IOL constant may vary with axial length.³⁸ Aristodemou et al confirmed that this remains true of the three principal third-generation formulas, with clinically significant deviations from the mean IOL constant at both short and long axial lengths, although the magnitude and pattern of the variation differed by formula and IOL model.³¹ The authors did not evaluate the potential performance gain from using AL-specific IOL constants, but as the largest variations in lens constants were observed at ALs less than 21 mm (42 of 8108 eyes, 0.5%) or greater than 26 mm (288 eyes, 3.6%),²⁵ the benefit of doing so is likely to be small. A practical implication of the findings, however, is that if a formula is to be used for a restricted range of ALs (eg, Hoffer Q for ALs less than 21.5 mm), then the IOL constant should be optimised using only eyes with ALs within that range.

More recently Eom et al. demonstrated that the SRK/T A constant varies with corneal power, such that eyes with flatter than average corneas require a higher A constant and those with steeper corneas a lower constant.³⁹ The use of a keratometry-specific IOL constant improved the proportion of eyes achieving within ±1 D of target by 2.3% and within ±0.5 D of target by 6.2%. This was a small study of 257 eyes and further work is required to confirm the findings and to determine whether other IOL formulas show the same behaviour.

Second eye prediction refinement

There is high inter-ocular correlation between biometric measurements and subsequent PEs after cataract surgery, but early attempts to use the refractive outcome after first eye surgery to improve the prediction accuracy for the second eye failed.^{40, 41} Subsequently, Covert et al discovered that correcting the second eye target by 50% of first eye PE (using the Holladay 1 and SRK II formulas) improved the proportion of second eyes achieving within ±1 D of target by 3.4% and ±0.5 D of target by 7.8%.⁴² Olsen confirmed that partial correction of the second eye prediction improved its accuracy, but found that the correction factor was dependent upon the formula used (eg, 0.38 for SRK/T and 0.27 for the Olsen formula).¹³

Aristodemou et al reported a series of 2129 patients who had undergone bilateral sequential cataract surgery, and confirmed that a 50% correction factor improved the accuracy of the prediction for the second eye such that 4% more eyes achieved within ±1 D of target and 19% within ±0.5 D.⁴³ In this study, the authors used the formula most appropriate to axial length (Hoffer Q for ALs <21.5 mm, Holladay 1 for ALs between 21.5 mm and 26 mm, and the SRK/T for ALs ≥ 26 mm), and recommended that the 50% correction factor could be applied when the inter-ocular axial length and keratometry differences were less than 0.7 mm and 0.6 D, respectively, the first eye PE 1.5 D or less, and when using the same IOL in each eye.

The studies outlined above are theoretical and based upon retrospective data analysis. Jivrajka et al conducted a prospective study of 250 patients undergoing bilateral sequential surgery, which confirmed a significant improvement in second eye outcome when the second eye IOL selection was adjusted using a 50% correction factor for first eye PE (ie, if the first eye was found to be 1 D more hyperopic than intended, then the second eye was targeted 0.5 D more myopic than suggested by the IOL formula).⁴⁴

It should be remembered that not all second eyes are suitable for this technique and that, by definition, at most 50% of eyes will be second eyes, therefore, the magnitude of the improvement resulting from this procedure, when considering all eyes operated upon, will be less than half the figures reported, that is, a maximum of 2% more eyes within ±1 D and 9% within ±0.5 D of target.

IOL design and manufacture

When designing IOLs manufacturers are obliged to follow the standards set out in ISO 11979-2.⁴⁵ This defines, among many other parameters, the tolerances that IOLs should meet. For an IOL labelled between 0 and 15 D, its true power must be within ±0.3 D of the labelled power, between 15.5 and 25 D the allowed tolerance is ±0.4 D, between 25.5 and 30 D it is ±0.5 D, and above 30 D the true power is permitted to be up to ±1 D from the labelled power. For the lowest power IOLs, the resulting error at the spectacle plane may be up to ±0.2 D, but for IOLs greater than 30 D the error resulting from manufacturing tolerance may be as high as ±0.7 D. Norrby, however, suggests that ‘the error should be even smaller because a conscientious manufacturer should apply an internal tolerance of ±0.25 D',¹² and estimates that the proportion of the PE because of IOL manufacturing is just 1.2% and therefore clinically insignificant.

Zudans et al. compared the refractive outcomes of eyes with two different IOLs, the first of which was manufactured to a tolerance of ±0.11 D and a second for which manufacturing tolerances were not known.⁴⁶ The authors found significantly more accurate outcomes with the first IOL than the second (85% within ±0.5 D of target vs 69%), suggesting that IOL manufacturing tolerances, at least for some IOLs, are of clinical significance. Unfortunately, most manufacturers do not make this information routinely available to clinicians.

Discussion

The Royal College of Ophthalmologists Cataract Surgery Guidelines state ‘what matters most in biometry is achieving excellent results, which can be presented in terms of the percentage of eyes within 0.5 or 1.0 D of the target refraction', and ‘with the routine use of optical biometry when possible, modern IOL calculation formulas and optimisation of lens constants busy NHS departments with a variety of surgeons and biometry technicians should be able to achieve a refractive outcome within ±1 D of the target in 85% of cases'.¹¹ More recent studies than those available at the time the guidelines were written suggest that this target is easily achievable, and that more than 90% within ±1 D and 60% within ±0.5 D would not be unreasonable expectations.^{10, 16, 31} Many departments and surgeons would be very satisfied with such results.

For surgeons wishing to improve outcomes for their patients further, there are options available that do not entail major changes in practice or investment in new equipment. The effort required to realise performance gains, however, appears to follow the Pareto Principle, an empirical rule of thumb used in many settings that states that 80% of the outcome results from 20% of the input,⁴⁷ that is, each additional 1% beyond 80% within ±1 D of target requires more and more effort to realise.

Of the possible strategies outlined about the greatest gain appears to result from using an IOL manufactured to stricter tolerances than required by the ISO standard, resulting in 16% more eyes within ±0.5 D of target,⁴⁶ although this was a single study and the comparator IOL was unidentified. However, switching to a known tolerance IOL would be very straightforward, and simply require informed selection of the IOL constant to use initially, followed by a cycle of audit and optimisation. IOL manufacturers could help surgeons make an informed choice by publishing the manufacturing tolerances for their IOLs.

The next largest gain is to introduce refinement of second eye predictions according to first eye refractive outcome in the expectation of up to 2% more eyes achieving within ±1 D and 9% ±0.5 D of target. This would require patients to be refracted 4–6 weeks after first eye surgery, with a potential delay to the second procedure. Furthermore, the studies cited above all relied upon subjective refraction,^{13, 42, 43} which may not be practical in all settings; it remains to be established whether the 50% correction factor would be applicable to auto-refraction data.

With respect to optimisation of constants, a surgeon with a ME greater than ±0.15 D may benefit from using a personal surgeon-specific constant rather than the local average, and expect at least 1% more patients to achieve within ±1 D and 2.1% within ±0.5 D of target. The value of the use of axial length and keratometry-specific constants remains uncertain. It is likely that the susceptibility of the different formulae to AL-dependent changes is reflected in the recommendations about formula choice for different AL ranges^{25, 31} and the use of AL-specific constants in addition is unlikely to lead to further significant performance improvements. If particular formulas are to be used for only particular subsets of ALs, the variability of IOL constant with AL suggests that it would be prudent to optimise the constant using eyes with ALs from the range of intended use. The improvement in the performance of the SRK/T formula by using keratometry-specific constants is promising,³⁹ but further work is required to determine its importance in relation to axial length and whether other formulas demonstrate similar behaviour.

The switch from contact to immersion ultrasound for the 10% of eyes that fail optical biometry may lead up to 1.2% more patients achieving ±1 D of target. Devices such as the Prager Shell (ESI Inc., Plymouth, MN, USA) and EZ-immersion tip (Micro Medical Devices Inc., Calabasas, CA, USA) may facilitate the procedure for patients and biometry technicians, but some may consider the potential gains insufficient for the additional training required.

Finally, it is unlikely that each of the strategies described delivers results independently of the others; therefore, the gains from using a strict-tolerance IOL and second eye prediction refinement together is likely to be less than the sum of the gains reported by the individual studies. Furthermore, the number of eyes required for a study to have sufficient power to detect a statistically significant difference is very large; to detect a difference between 90 and 91% within ±1 D of target would require nearly 27 000 eyes, well beyond the reach of individual surgeons or departments. The Royal College Guidelines state ‘given the number of cataract operations performed and the amount of data required for each operation audit is only practical with electronic medical record systems that collect the cataract national data set',¹¹ and it is only by combining the outcomes from multiple departments will sufficient numbers be collected to answer some of the outstanding unknowns, and to develop further improvements to biometric predictions.

Conclusions

With modern optical biometry for the majority of patients, informed formula choice and IOL constant optimisation outcomes of more than 90% within ±1 D and more than 60% within ±0.5 D of target are achievable. There are a number of strategies available to surgeons wishing to exceed these outcomes, the most promising of which are the use of strict-tolerance IOLs and second eye prediction refinement.

Appendix

Prediction error (PE)

PE is the difference in dioptres between the actual and intended refractive outcome in a particular patient, and is usually calculated such that the PE is negative for an outcome more myopic that intended and positive for a hyperopic outcome:

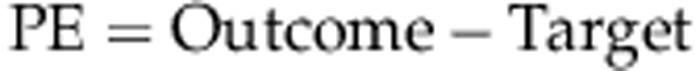Mean error (ME)

ME is the arithmetic mean of the prediction errors from a cohort of patients:

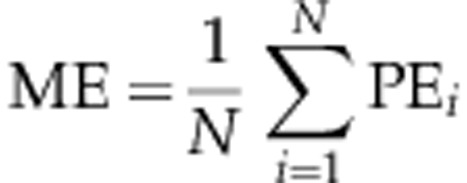ME indicates on average how close the outcome is to the intended target; a negative value indicates that outcomes tend to be more myopic than intended and a positive ME indicates a hyperopic tendency.

Mean absolute error (MAE)

MAE is the mean of the absolute prediction errors in a cohort (ie, the prediction errors ignoring the sign):

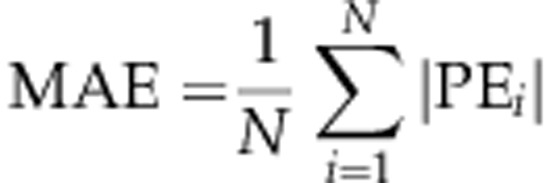The MAE is often used as an indicator of the spread (or dispersion) of refractive outcomes, and if the ME of the data is zero and the prediction errors are normally distributed, then the MAE is approximately 80% of the standard deviation.¹³ If, however, the ME is non-zero, then this relationship does not hold and it is difficult to infer the dispersion of the outcomes from the MAE in this case. The standard deviation, interquartile range, or the proportion of eyes within a particular range may be a better indicator of the spread of outcomes. Despite its shortcomings MAE has become established in the literature, and may be a useful single figure for comparing data sets as long as its limitations are understood.

The author declares no conflict of interest.