Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2013 Oct 3;8(3):504–514. doi: 10.1038/ismej.2013.169

Dispersal network structure and infection mechanism shape diversity in a coevolutionary bacteria-phage system

Michael Sieber 1, Matthew Robb 2, Samantha E Forde 3,*, Ivana Gudelj 1,*
PMCID: PMC3930312  PMID: 24088626

Abstract

Resource availability, dispersal and infection genetics all have the potential to fundamentally alter the coevolutionary dynamics of bacteria–bacteriophage interactions. However, it remains unclear how these factors synergise to shape diversity within bacterial populations. We used a combination of laboratory experiments and mathematical modeling to test how the structure of a dispersal network affects host phenotypic diversity in a coevolving bacteria-phage system in communities of differential resource input. Unidirectional dispersal of bacteria and phage from high to low resources consistently increased host diversity compared with a no dispersal regime. Bidirectional dispersal, on the other hand, led to a marked decrease in host diversity. Our mathematical model predicted these opposing outcomes when we incorporated modified gene-for-gene infection genetics. To further test how host diversity depended on the genetic underpinnings of the bacteria-phage interaction, we expanded our mathematical model to include different infection mechanisms. We found that the direction of dispersal had very little impact on bacterial diversity when the bacteria-phage interaction was mediated by matching alleles, gene-for-gene or related infection mechanisms. Our experimental and theoretical results demonstrate that the effects of dispersal on diversity in coevolving host–parasite systems depend on an intricate interplay of the structure of the underlying dispersal network and the specifics of the host–parasite interaction.

Keywords: coevolution, diversity, dispersal, host–parasite, mathematical model, spatial heterogeneity

Introduction

Microbial diversity is key to many ecosystem processes (Naeem and Li, 1997; Bell et al., 2005; Madsen, 2011), and coevolution among microbes has been suggested as one of the major drivers of biodiversity (Buckling and Rainey, 2002; Forde et al., 2008a). Coevolution is an inherently spatial process that depends not only on the traits of the interacting species but also on the environment in which those interactions take place (Thompson, 1999, 2005; Forde et al., 2004; Parchman and Benkman, 2008; Piculell et al., 2008; Laine, 2009; Craig and Itami, 2010; King et al., 2011; Lorenzi and Thompson, 2011).

There are many ways in which the environment can be spatially structured, but variation in resource input is likely to be one of the major factors influencing coevolutionary dynamics (Hochberg et al., 2000). In particular, experimental studies using bacteria and bacteriophages have demonstrated that the rate of coevolution can increase with increased resources (Forde et al., 2004; Lopez-Pascua and Buckling, 2008), whereas bacterial diversity peaks at intermediate resource levels (Forde et al., 2008a).

High dispersal and the cosmopolitan distribution of bacteria (Brodie et al., 2007; Fahlgren et al., 2010; Yamaguchi et al., 2012) and phages (Breitbart et al., 2004; Angly et al., 2006) across a wide range of environments add additional complexity and the potential to greatly influence microbial diversity (Brockhurst et al., 2007; Vogwill et al., 2008, 2009, 2010). If the abiotic environment does not vary in space, theoretical and experimental studies indicate that dispersal, or gene flow, homogenizes genetic variation (Gandon and Michalakis, 2002; Vogwill et al., 2011). Theory suggests that the same result holds if the abiotic environment varies in space. In particular, Hochberg and van Baalen (1998) predicted that gene flow across spatial gradients in productivity can lead to a decrease in overall diversity summed across the gradient. However, this theoretical prediction remains experimentally untested.

In the present study, we evaluated how the structure of the dispersal network across a spatial resource gradient affects patterns of bacterial phenotypic diversity in a coevolutionary system consisting of the bacteriophage T3 and its bacterial host Escherichia coli. Bacteriophage T3 uses lipopolysaccharides (LPS) as receptors for adsorption to the host cell, and resistance to T3 is conferred through mutations that truncate LPS (Tamaki et al., 1971; Lenski, 1988; Qimron et al., 2006), which can lower bacterial fitness through pleiotropic effects on outer membrane proteins (OMPs) involved in the uptake of resources (Sen and Nikaido, 1991). This bacteria-phage interaction forms the molecular basis for a coevolutionary system conforming to the terminology of the ‘Kill the Winner' (KtW) hypothesis (Winter et al., 2010) in the sense that phenotypes with intact LPS structure correspond to competition specialists, whereas truncated LPS structures are a hallmark of a defense specialist.

Our previous work with E. coli and phage T3 coevolution in experimental microcosms showed that low resource environments supported more diverse communities than high resource environments (Forde et al., 2008a). Both high and low resource environments contained highly resistant bacterial phenotypes (defense specialists) and highly infective generalist phage. However, whereas these dominated high resource environments leading to low diversity, low resource environments additionally contained sensitive bacterial phenotypes (competition specialists) and their more specialist phage, and as such, were more diverse (Forde et al., 2008a).

Here we considered how the above patterns of bacterial diversity changed when symmetric and asymmetric movement of both bacteria and phage was introduced across the resource gradients. For symmetric (bidirectional) gene flow, we expected the fitness of a given phenotype to be the weighted average of the local fitness it experiences in all habitats along the gradient (Kawecki and Holt, 2002). This should only favor bacteria and phage found in both low- and high-resource habitats, namely defense specialists and highly infective generalist phages (Forde et al., 2008a). This in turn is expected to decrease overall diversity. However, it is less clear a priori how unidirectional dispersal should affect bacterial diversity.

In accordance with expectations, we found that bidirectional dispersal decreased diversity compared with when communities were closed. Somewhat surprisingly, however, we found that unidirectional dispersal from high to low resources increased host diversity. Extending the mathematical model in Forde et al. (2008a), we showed that these unexpected outcomes are predicted when bacteria-phage interactions follow modified gene-for-gene infection genetics (Forde et al., 2008a).

To further test how the observed dispersal-induced patterns of host diversity depended on the genetic underpinning of the bacteria-phage interactions, we expanded our mathematical model to include different infection mechanisms. This was motivated by the findings in Forde et al. (2008a), which showed that the precise nature of the relationship between diversity and resources depended on the infection genetics between bacteria and phages.

Curiously, although in the case of modified gene-for-gene mechanism the different dispersal directions gave rise to different patterns of bacterial diversity, this was not the case for matching alleles (Gandon and Michalakis, 2002; Morgan et al., 2005; Weitz et al., 2005; Forde et al., 2008a), gene-for-gene (Morgan et al., 2005; Forde et al., 2008a; Gandon and Nuismer, 2009) or related infection mechanisms (Nuismer and Otto, 2005; Fenton et al., 2009). These results could be explained by the fact that the modified gene-for-gene mechanism gives rise to ‘KtW' dynamics (Winter et al., 2010), whereas the other tested infection mechanisms do not. Our paper illustrates that the effect of dispersal on microbial diversity depends on the intricate interplay of the structure of the dispersal network and precise nature of coevolutionary interactions.

Materials and methods

Experimental design

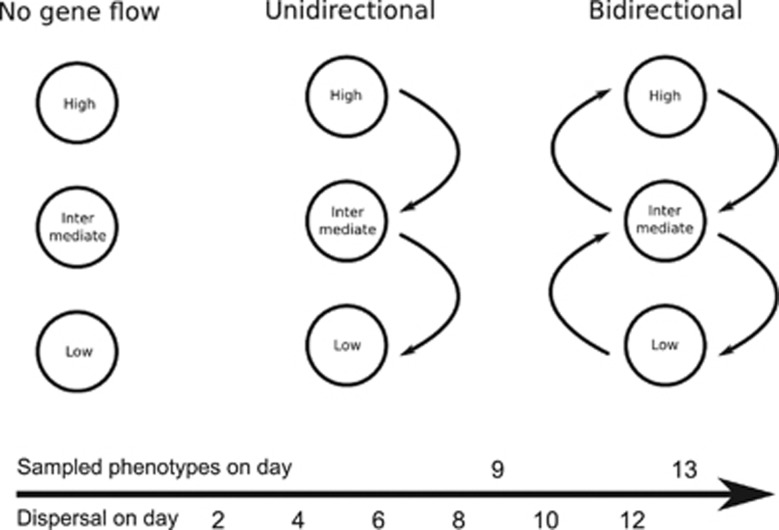
We coevolved E. coli and phage T3 in continuous culture devices known as chemostats (Bohannan and Lenski, 1997) which were connected by dispersal. All chemostats were initially inoculated with isogenic strains of bacteriophage T3 (obtained from the American Type Culture Collection) and E. coli (strain REL 607; Bohannan and Lenski, 1997). The volume of each community was maintained at 30 ml, with a washout rate of 0.2 turnovers per h. We directly manipulated resource input and dispersal of T3 and E. coli to test how the direction of dispersal along a resource gradient affected local adaptation and diversity. Three levels of resource input were used (high=1000 μg ml−1, intermediate=100 μg ml−1 or low=10 μg ml−1 glucose), whereas the dispersal treatments consisted of unidirectional, bidirectional and no dispersal of the bacteriophages and bacteria together (Figure 1).

Figure 1.

Figure 1

Open in a new tab

The structure of the dispersal network, labels indicate the different resource levels. Timeline of dispersal and sampling events are shown at the bottom.

Chemostats were sampled every 48 h, concordant with the imposition of the dispersal treatments. For the unidirectional and bidirectional dispersal treatments, ∼7.5 ml were removed from each chemostat before imposition of the dispersal treatments. Thus, the same volume, containing the entire bacteria-phage community, was removed from each chemostat regardless of the direction of the flow. A portion of each sample was used for the dispersal treatments and to evaluate the phenotypic diversity of the hosts.

In the unidirectional dispersal treatment, 3 ml of the bacteria-phage community were dispersed from the high resource environment to the intermediate environment, and likewise 3 ml from the intermediate to the low resource environment. Three milliliters of sterile saline solution were added to the high resource environment to control for the input volume across treatments (totaling 10% of the total community). In the bidirectional dispersal treatment, 1.5 ml were dispersed from the high into the intermediate environment, and 3 ml from the intermediate into the low resource environment. In the other direction, 1.5 ml were dispersed from the low into the intermediate environment, and 3 ml from the intermediate into the high resource environment. Thus, each community received an input volume totaling 3 ml, regardless of the direction of the flow. Each treatment was replicated three times. The experiment ran for 13 days, or ∼200 bacterial generations and 1000 generations of the bacteriophage. During this period, there were seven bouts of dispersal among communities.

Three different reference phage (T2, Tu1a and K3) that attack LPS and different OMPs were used to evaluate phenotypic diversity of the hosts. The three reference phages utilize distinct mechanisms to attack the host, and resistance to them requires different counter-adaptations. For instance, OMPF is the most common OMP of E. coli and is involved in osmoregulation and nutrient uptake (Datta et al., 1977; Travisano and Lenski, 1996). Phage T2 uses both OMPF and a part of LPS distal to the T3 receptor to infect E. coli cells (Lenski, 1984), so that resistance to T2 indicates that the LPS mutation has also affected the assembly or function of OMPF. Resistance to Tu1a also indicates effects on OMPF (Schwartz, 1980). Resistance to K3 on the other hand indicates that the truncation of LPS has also affected the assembly or function of OMPA (Schwartz, 1980), which is involved in amino-acid transport and the structural integrity of the outer membrane (Morona et al., 1985; Heller, 1992).

Approximately 20 colonies were isolated from the high- and low-resource communities on days 9 and 13 of the experiment each. We did not evaluate host diversity in the intermediate productivity communities. Twenty microliters of each of the three bacteriophages from the screen were then dried on an agar plate and each bacterial isolate was streaked across the bacteriophages to assess whether bacteria were sensitive, partially resistant or completely resistant. Further details on the methodology and cellular biology associated with the phenotypic screen are given in Forde et al. (2008b).

This specific screening procedure allowed us to identify up to 27 distinct phenotypes, as for each of the three reference phage exactly three different outcomes of the infection assay were possible. Of those 27 potential phenotypes, a total of 15 were actually observed across all populations (Table 1). The observed frequencies of each phenotype within a population were averaged across replicate chemostats.

Table 1. Identified phenotypes.

Phenotype T2 Tu1a K3 Resistance score
1 s s s 0
2 s pr s 0.16
3 s s pr 0.16
4 s r s 0.33
5 s s r 0.33
6 pr r s 0.5
7 pr s r 0.5
8 s pr r 0.5
9 s r pr 0.5
10 r pr pr 0.66
11 pr r pr 0.66
12 s r r 0.66
13 r r pr 0.83
14 r pr r 0.83
15 r r r 1
Open in a new tab

Abbreviations: S, sensitive; pr, partially resistant; r, resistant.

Based upon these considerations, phenotypic diversity was calculated using the Shannon-Wiener index in the form

graphic file with name ismej2013169e1.jpg

where pi is the proportion of phenotype i in the focal host population. Note, that we sum over all 15 observed phenotypes and set piln(pi)=0 for phenotypes that were not present in the focal community. The results shown throughout the paper are the diversity measures averaged over time. Data were analyzed using analysis of variance with fixed effects (direction of dispersal and resource level) and their interaction.

We also obtained the total number of phenotypes for each dispersal treatment and each resource environment. This measure of phenotype richness and degree of endemicity gives an indication of whether diversity was mediated by phenotypes specific to a resource environment or by phenotypes shared between environments.

In addition, we quantified the resistance of each observed bacterial phenotype against the reference phages (Table 1). For each phenotype, we summed up the level of resistance rn,i(0=sensitive, 0.5=partially resistant and 1=resistant) against each of the three reference phages, such that after rescaling the resistance score 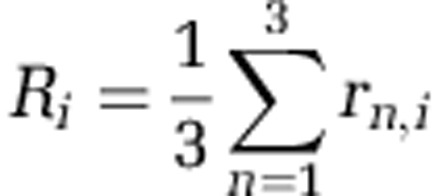Inline graphic of a phenotype can range from 0 (universally sensitive) to 1 (universally resistant).

We then calculated the population level of resistance against reference phages in each treatment by multiplying the average local proportions of each phenotype with its resistance score and summing over all phenotypes: 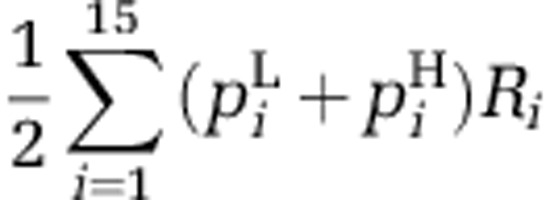Inline graphic, where the superscripts L and H denote proportions in the low and high productivity environments, respectively. This average population resistance against reference phages is a measure of the probability that a randomly picked cell from either resource environment is resistant against a randomly picked reference phage.

The model

The mathematical model was based on the one developed in Forde et al. (2008a) and was designed specifically to capture the biology of microbial coevolution. The deterministic model tracks evolution in initially isogenic populations of co-occurring clonally reproducing bacteria (B0) and phages (P0) in the chemostat. Mutations occurred with a small but prescribed probability, and the fitness of mutant bacteria and phages depends on every component of the system (a genotype-by-genotype-by-environment interaction).

T3 phages have higher adsorption rates to wild-type E. coli than to contemporary hosts (Chao et al., 1977; Forde et al., 2004; Qimron et al., 2006). Thus, in our initial model, we assumed that the binding probabilities between bacteria and phages are graded (see Sasaki and Godfrey, 1999). As in Forde et al. (2008a), we also assumed that there are two character states at two diallelic loci, L and O, in wild-type bacteria (B0). We incorporated pleiotropy between LPS and OMPs by assuming that mutations at these loci regulate the biosynthesis of LPS polymers such that the length of the LPS O antigen correlates with the phenotype T=4−(2 × L+O), yielding four phenotypes: B0(L=0,O=0) with T=4; B1(0,1) with T=3; B2(1,0) with T=2; and B3(1,1) with T=1.

We assumed that mutations in the bacteria occurred as point mutations at either L or O locus with rate ɛ. Mutations in wild-type phages (P0) occur at one locus with four possible alleles giving rise to one of three types, denoted Pi (where i is from 1 to 3) and the rate of mutations from one phage type to another, ɛ, is independent of the type of phage. The matrices Mb and Mp modeling mutations between the four bacterial types and the four phage types, respectively, are given in Appendix A.

The core of the E. coli–T3 model is a 4 × 4 matrix that defines the relative infectivities of each phage strain to each bacterial type:

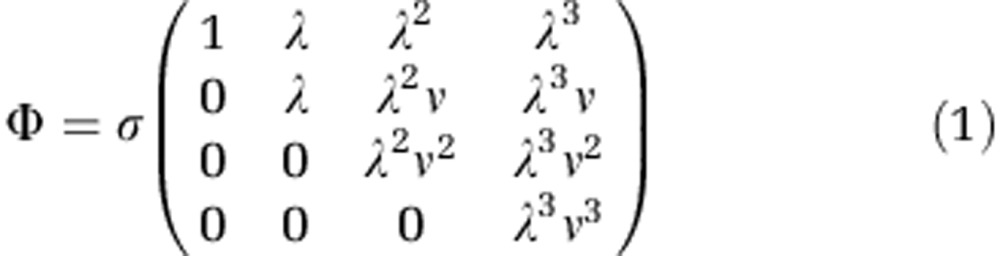graphic file with name ismej2013169e4.jpg

This infection matrix is based on a mechanistic understanding of the attachment process of T3 to its host and as such it is specific to the system under consideration (Forde et al., 2008a). Each column represents one of the four phage types and the respective interactions with the different host strains. For example, the first column corresponds to the wild-type T3 that can only infect wild-type E. coli, hence there is a single entry in the first row of this column. Here σ stands for the attachment rate of the wild-type phage, λ represents the change of adsorption rate caused by alterations in the structure of phage tail-fiber protein and ν represents the change in adsorption rate caused by the loss of a single sugar from the bacterial LPS complex with constraints λ<1, ν<2, respectively. Because of its resemblance to the classical gene-for-gene model (Morgan et al., 2005; Gandon and Nuismer, 2009), this specific model has been termed modified gene-for-gene infection mechanism (Forde et al., 2008a).

In complete analogy to the experimental methods, we can define a resistance score for each bacterial phenotype as the number of phage phenotypes against which it is resistant. This means that the resistance score in the model is simply given by the number of zeros in each row of the infection matrix divided by the total number of phage phenotypes. For the modified gene-for-gene infection mechanism in (1), the resistance score thus ranges from 0 for the wild-type B0 (competition specialist) to 0.75 for the most, but not completely, resistant type B3 (defense specialist).

We extended the model in Forde et al. (2008a, 2008b) to include dispersal between chemostats of different productivity. Following from the experimental design shown in Figure 1, we considered a scenario in which three chemostats contain different resource levels, resulting from different concentrations of resources in the chemostat input vessels. The rates of change over time in the resource concentration Si, bacterial densities Bi and phage densities Pi in high-, intermediate- and low resource environments are given by

graphic file with name ismej2013169e5.jpg

where the subscript i=L, I, H represents the low, intermediate and high resource environments, respectively. Here, 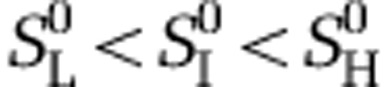Inline graphic denote the resource concentrations in the input vessels, whereas Bi and Pi denote the vectors of the four bacterial and phage densities in the different resource environments. The matrix ΦT is the transposed of the infection matrix. The operators · and * denote the scalar product and component-wise multiplication, respectively.

The first equation of (2) describes the rate of change in resource concentration in the three chemostats, where the constant D represents the chemostat washout rate. Resource consumption is modeled using a Michaelis–Menten bacterial growth vector function μ and resource conversion rate c. The phage production is represented by a vector of burst sizes β; however, latent period was not explicitly modeled. Bacterial costs for resistance are mediated by phenotype-specific maximal growth rates, which are incorporated into the growth vector function μ. Similarily, an increase in phage host range is traded-off with a decrease in burst size, described by the burst size vector β (Ferris et al., 2007; Poullain et al., 2008). For a further description of the model in the absence of spatial structure see Appendix A.

Unidirectional and bidirectional dispersal between high (i=H), intermediate (i=I) and low resource (i=L) environments was incorporated into the model in the following way. After a simulated time of N hours, the simulation was stopped and the densities of resources, bacteria and phages in the three chemostats were reduced by 25%, representing the removal of 7.5 ml of the total chemostat volume of 30 ml. Then the dispersal treatment was imposed by increasing the densities in the receiving chemostats by the appropriate amount, which depends on the predispersal densities in the source chemostat and the dispersal treatment. For example, in the unidirectional treatment, the low productivity chemostat received a sample of 10% of the whole resource-bacteria-phage community of the intermediate productivity chemostat, corresponding to 3 ml of volume. After this procedure, the simulation of system (2) was started again and run until the next dispersal event. In this way, complete analogy with the experiments was maintained. All parameters in model (2) are from Forde et al. (2008a) and are shown in Table 2.

Table 2. Parameter values for model (2).

Parameter Description Value
μimax Maximal growth rate of bacterial type i μ0max=1.18 h−1, μ1max=1.009 h−1, μ2max=0.89 h−1, μ3max=0.66 h−1
K Bacterial half saturation constant 0.06 μg ml−1
βi Burst size of phage i β0=306, β1=153, β2=99, β3=72 virions per cell
D Chemostat dilution rate 0.2 h−1
ɛ Rate of point mutations 10−4
c Resource conversion rate 2.3 × 10−5 μg per cell
Si0 Resource in parameter SH0=103 μg ml−1, SI0=102 μg ml−1, SL0=10 μg ml−1
σ Wild-type T3 attachment rate 2 × 10−8 ml h−1
ν,λ Infectivity parameters fitted in Forde et al. (2008a, 2008b) ν=0.677, λ=0.94
Open in a new tab

To test how the model results depend on the form of host–parasite interactions, we also included matching alleles, gene-for-gene, inverse matching alleles and inverse gene-for-gene infection genetics in our analysis. The detailed forms of these infection matrices can be found in Appendix A.

Results

Experiment

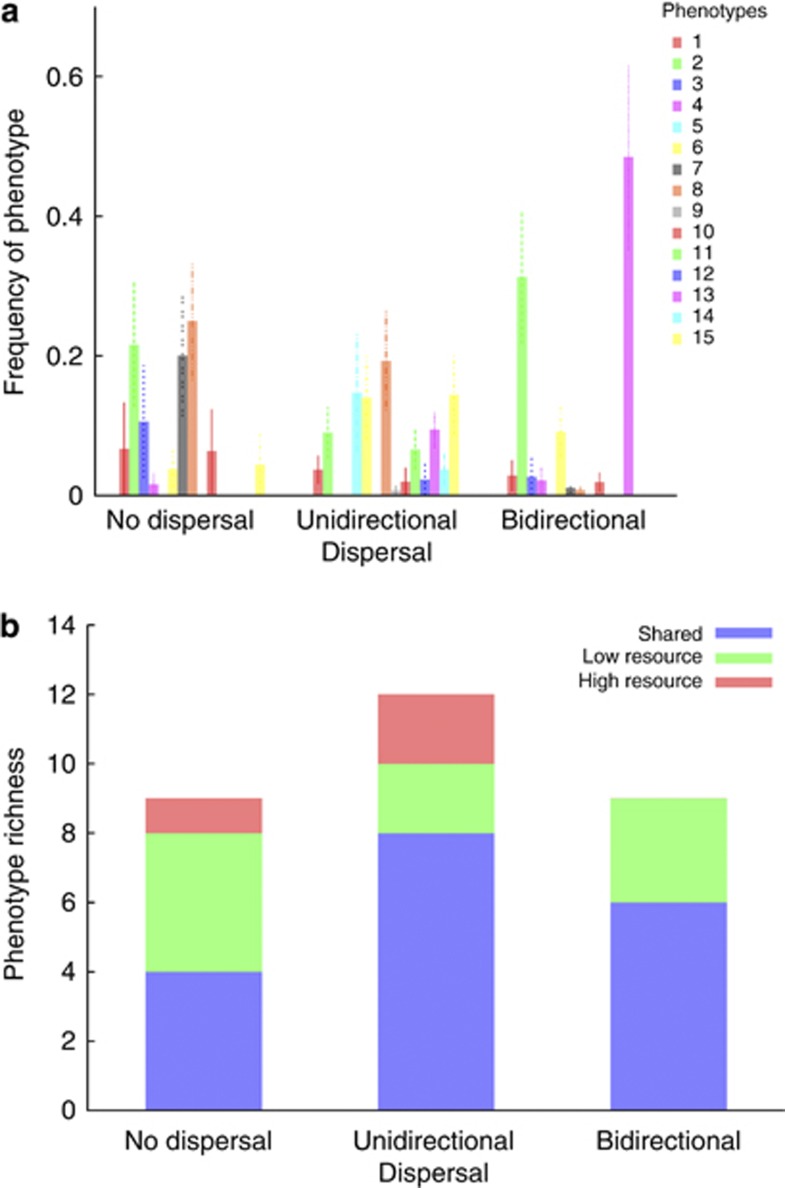
The results of the phenotypic diversity assay are displayed in Figure 2a. Diversity differed markedly among the dispersal treatments and an analysis of variance showed that the direction of dispersal had a significant effect on diversity, whereas there was no effect of resource level or interaction between factors (Table 3). Unidirectional dispersal increased diversity compared with no dispersal (P-value=0.045), in particular in the high resource environment. Bidirectional dispersal on the other hand had an overall negative effect on diversity compared with no dispersal (P-value=0.01) and unidirectional dispersal (P-value<0.0001).

Figure 2.

Figure 2

Open in a new tab

(a) Host diversity (Shannon-Wiener index ±s.e.m.) in the high (dark grey) and low (light grey) resource environments for the three different dispersal treatments. Dotted lines were used to guide the eye highlighting host diversity levels in high (dark grey dots) and low (light grey dots) resource environments in the absence of dispersal. (b) Population resistance against reference phages as a proxy for bacterial resistance against the wild-type T3 phage. Bar length gives the average population resistance for each dispersal treatment. Phenotypes have been grouped according to their average resistance against the reference phage, and the partitioning of each bar indicates the contribution of each group to the mean population resistance.

Table 3. Analysis of variance for experimental results of host diversity.

Source Sum square d.f. Mean square F Probability>F
Gene flow direction 2.17816 2 1.08908 17.89 <0.0001
Resource 0.03859 1 0.03859 0.63 0.4363
Gene flow × resource 0.18694 2 0.09347 1.54 0.2423
Error 1.09592 18 0.06088    
Total 3.65280        
Open in a new tab

Abbreviation: d.f., degree of freedom.

For the no dispersal and bidirectional treatments, an equal total number of phenotypes were identified, whereas the highest total number of phenotypes was observed in the unidirectional treatment (Figure 3). The fraction of locally specific types was highest for the no dispersal treatment and lower in the unidirectional and bidirectional treatments (Figure 3b).

Figure 3.

Figure 3

Open in a new tab

(a) Proportions of identified host phenotypes (Table 1) for the three different dispersal treatments across both resource environments. For each dispersal treatment, the phenotypes are placed on the x axis in order of ascending resistance against the reference phages, from the universally sensitive type 1 on the left to the universally resistant type 15 on the right (see text for details). (b) Phenotype richness and endemicity. Each bar indicates the total number of identified phenotypes for each of the three dispersal treatments, partitioned into the number of phenotypes that were present in both resource environments (blue); only in the low resource environments (green); only in the high resource environments (red).

The global proportions of identified phenotypes within each dispersal treatment were obtained as the average frequency of each type across resource environments (Figure 3a). In contrast to the no dispersal and unidirectional flow treatments, the meta-population in the bidirectional treatment is dominated by just two phenotypes, which explains the lower level of diversity in this treatment.

The average level of resistance against reference phage for each treatment, along with the relative contribution of each phenotype to the population level resistance against reference phage, is shown in Figure 2b. This serves as a proxy for assessing the resistance to the wild-type T3 phage. For example, resistance to the reference phages signifies changes in LPS, OMPF and/or OMPA which can be used to infer whether a given phenotype has mostly intact LPS structure (low resistance score) or truncated LPS (high resistance score) required for the resistance to T3 (Tamaki et al., 1971; Lenski, 1988; Qimron et al., 2006). Although the average level of resistance is similar in all three dispersal treatments, the contribution of different phenotypes is consistent with the differing levels of diversity (Figure 2b). In the no dispersal and unidirectional treatments, the population level resistance is mediated by several different types with varying degrees of resistance, whereas the level of resistance in the bidirectional treatment can mainly be attributed to one single highly resistant phenotype.

Model

Using deterministic simulations of model (2), we calculated diversity for each directional treatment (see Materials and methods for details) and to maintain consistency with the experiments, diversity was averaged over time.

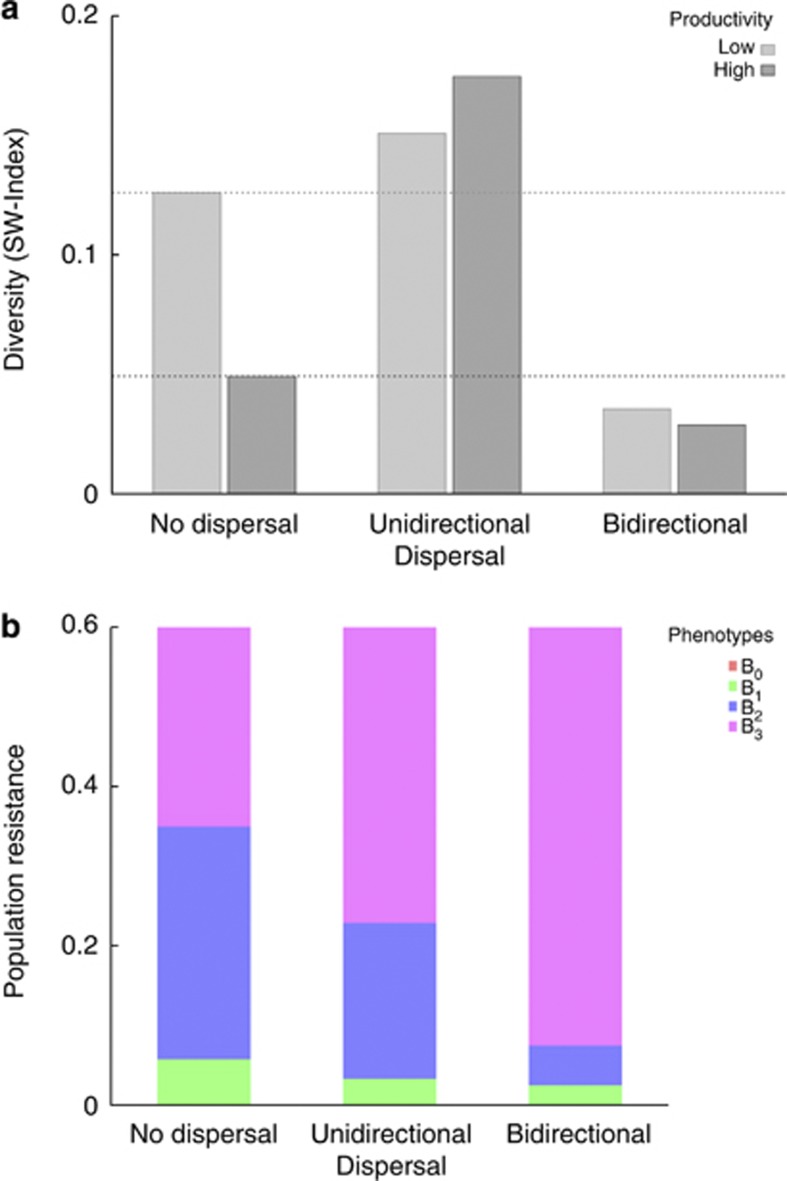
In order to relate theoretical predictions to experimental data of E. coli–T3 interactions, we first considered the modified gene-for-gene mechanism (1). In the absence of dispersal, the model predicted greater host diversity in low resource environments compared with high resource environments (Figure 4a), which was in agreement with the experimental results (Figure 2a).

Figure 4.

Figure 4

Open in a new tab

(a) Bacterial diversity as predicted by model (2) with modified gene-for-gene infection mechanism in high (dark grey) and low (light grey) resource environments. Dotted lines highlight host diversity levels in high (dark grey) and low (light grey) resource environments in the absence of dispersal. Dispersal rate was set to 6 h. (b) Average population resistance against the wild-type T3 phage as predicted by model (2) with modified gene-for-gene infection mechanism. Each color represents one of the four phenotypes from the theoretical model.

We fine-tuned the dispersal rate in the model by using the experimentally observed patterns of phenotypic diversity (Figure 2a). Model predictions (Figure 4a) aligned with the experimental results (Figure 2a) for dispersal rates higher than those used in the experiment. This discrepancy could be due to the relative simplicity of the model that combines bacterial diversity into four phenotypes. This naturally also led to consistently lower absolute levels of diversity (Figure 4a) than observed experimentally (Figure 2a). However, it is the simplicity of the model that enabled us to interpret experimental findings in a broader context as explained in the Discussion.

Turning to the population level of resistance, the model predicted that resistance against wild-type T3 under the bidirectional treatment is conferred almost exclusively through the dominance of the most resistant type (Figure 4b). This is in agreement with experimental results in Figure 2b, which depict bacterial resistance against reference phages and supports our use of population resistance against reference phage as a proxy for bacterial resistance against the wild-type T3. Under the other two modes of dispersal, the model predicted that a significant proportion of a less resistant type was maintained in the population, which is broadly in agreement with the experimental results (Figure 2b). The model does not capture the precise population composition observed in the experiments due to its simplification of grouping bacterial diversity into four phenotypes.

Model predictions did not change when we removed the intermediate resource environment from our model and instead only considered low and high resource environments linked by dispersal. This could be explained by the observation that in the absence of dispersal, the intermediate resource environment followed the pattern of diversity observed in the high resource environment (Supplementary Figure B1, Appendix B).

We next tested our hypothesis that the effect of dispersal across productivity gradients on host diversity depends not only on the structure of the dispersal network but also on the infection genetics of bacteria and phages. Therefore, we replaced the modified gene-for-gene interaction matrix (1) with the matching alleles, gene-for-gene, inverse matching alleles and inverse gene-for-gene models described in the Appendix B.

In line with previous results, in the absence of dispersal, the model with matching alleles infection mechanism predicted coexistence of all four bacterial types at similar densities in both resource environments (Forde et al., 2008a). As a consequence, we observed markedly higher levels of diversity independent of habitat productivity (Figure 5a). Moreover, neither unidirectional nor bidirectional dispersal had a visible impact on bacterial community composition and the observed levels of diversity (Figure 5a).

Figure 5.

Figure 5

Open in a new tab

Bacterial diversity in high (dark grey) and low (light grey) resource environments as predicted by model (2) with matching alleles infection mechanism (a) and gene-for-gene infection mechanism (b). Dotted lines highlight host diversity levels in high (dark grey dots) and low (light grey dots) resource environments in the absence of dispersal.

The results with the classical gene-for-gene infection mechanism were very similar to the matching alleles model. Bacterial populations were dominated mainly by equal proportions of the two host types with intermediate resistance, such that diversity was higher overall and there was no difference between resource environments (Figure 5b). In addition, diversity did not change in response to different dispersal modes (Figure 5b). Note, that similar marginal effects on diversity were also obtained with inverse matching alleles and inverse gene-for-gene infection genetics.

Discussion

We combined experimental coevolution of bacteria and phages with mathematical modeling to determine the effects of dispersal across a productivity gradient on bacterial diversity. We found that dispersal of bacteria and phages had a marked effect on overall host diversity compared with diversity in the absence of dispersal, but patterns of diversity depended on the structure of the dispersal network. When communities were connected by bidirectional dispersal, bacterial diversity decreased in all habitats across the productivity gradient (Figure 2), as expected from previous results (Hochberg and van Baalen, 1998; Vogwill et al., 2011). Unexpectedly, unidirectional dispersal from high to low productivity habitats increased bacterial diversity in the source habitat and had only a small effect on the downstream community (Figure 2), leading to an overall increase in diversity.

This differential effect of the two dispersal networks can be understood within the framework of the ‘KtW' hypothesis (Winter et al., 2010). KtW assumes that bacterial phenotypes employ evolutionary strategies ranging from competition specialists (efficiently growing, but phage-sensitive) to defense specialists (slower growing, but phage-resistant). The modified gene-for-gene infection mechanism mediating the interaction between E. coli and T3 (Forde et al., 2008a) conforms to the assumptions of KtW. Here wild-type bacteria with intact LPS structures correspond to competition specialists, whereas phenotypes with one or several LPS truncations are at the defense specialist end of the strategy spectrum, as truncations in LPS can have pleiotropic effects on OMPs involved in the uptake of nutrients (Sen and Nikaido, 1991).

In accordance with central predictions of KtW and previous results (Bohannan and Lenski, 2000; Forde et al., 2008a), we found that without dispersal, low resource environments allowed the coexistence of competition specialists and a smaller fraction of defense specialists, whereas in high resource environments, costly mutations conferring resistance against phages were effectively mitigated by abundant resources and thus allowed defense specialists to dominate (Forde et al., 2008a). As a consequence, low resource environments were more phenotypically diverse compared with high resource environments (Figure 2).

When bacteria and phages were dispersed together bidirectionally across the resource gradient, the defense specialists, which were able to persist under both environmental conditions, became the dominant phenotype in all habitats. Thus, as expected from theoretically predictions (Hochberg and van Baalen, 1998; Kawecki and Holt, 2002), overall diversity decreased when dispersal was bidirectional (or symmetrical) across the heterogeneous landscape.

In contrast to the prediction by Hochberg and van Baalen (1998) that dispersal across a resource gradient should decrease diversity, we found that unidirectional dispersal from high to low resource environments increased overall diversity. A possible explanation for our result is that although the high productivity community did not receive any input of non-endemic phenotypes, the repeated loss of a fraction of the microbial population during dispersal events may have opened up a niche for the competition specialists. Our theoretical model suggests that the decrease in density of defense specialists and the associated lower rates of phage predation after a dispersal event can allow a small subpopulation of competition specialists to temporarily reach high population densities. If dispersal is not too infrequent, this transient effect is enough to allow the competition specialists to persist in the high productivity environment. Thus, a decrease in density-dependent competition as a side-effect of the dispersal process itself led to the observed increase in diversity in the upstream high resource environment, rather than any actual dispersal-mediated gene flow.

Our theoretical study of different infection mechanisms further suggests that the presence of different phenotypic strategies in different environments is in fact necessary for dispersal to have a marked effect on diversity. The matching-alleles infection mechanism, for example, led to a higher overall bacterial diversity, but in this case the different phenotypes all represent the same evolutionary strategy with equal competitive abilities and resistance against phages. Thus, all phenotypes coexist in similar proportions in all environments across the productivity gradient and dispersal between habitats can have no effect on local phenotypic diversity.

A similar rationale applies to the gene-for-gene and related infection mechanisms, such as inverse matching alleles and inverse gene-for-gene. Whenever the infection mechanism mediating the bacteria-phage interaction does not promote the emergence of a locally specific set of phenotypic strategies, in the sense of the KtW hypothesis, the effect of dispersal on local diversity can only be marginal.

The form of dispersal we considered in our study is typical for, but not limited to, aquatic habitats, where bacteria and phages are passively transported together with the surrounding aquatic environment. The effect of riverine network structure on biodiversity is of great importance in freshwater ecology (Nelson et al., 2009; Brown et al., 2011), but its effects on microbial diversity are under-researched. Our results shed light on how local selection for distinct phenotypic strategies and dispersal work together to shape microbial diversity in aquatic networks. We further illustrate that dispersal events can pose significant perturbations of upstream communities, which allow the local rare biosphere (Sogin et al., 2006) to fill newly opened niches and flourish temporarily. This is a usually overlooked aspect of dispersal with the potential to alter the course of coevolution and induce a permanent shift in microbial community composition.

Our theoretical model further predicts that dispersal rates have an effect on bacterial community composition (Supplementary Figure B2, Appendix B), in line with dispersal experiments involving freshwater bacteria in their natural lake water environments (Lindström and Östman, 2011). Our model also suggests that unidirectional dispersal tends to increase overall bacterial diversity, regardless of the strength of the transport flow (Supplementary Figure B2a, Appendix B). Interestingly, the relationship between dispersal strength and diversity is more complex in bidirectional networks, suggesting that high dispersal rates have a negative impact on overall diversity, whereas low to moderate dispersal rates tend to increase diversity (Supplementary Figure B2b, Appendix B). These theoretical results have implications for the potential impact of altered flow regimes (Bunn and Arthington, 2002) on microbial community composition.

In summary, our combination of in vitro experiments and mathematical models suggests that the effect of dispersal on microbial diversity depends on an intricate interplay of the abiotic characteristics of habitats within a dispersal network and the specific mechanism mediating the interaction of the coevolutionary players. If the heterogeneous landscape supports the formation of locally distinct ecological strategies following a KtW pattern, bidirectional dispersal tends to favor defense specialist strategies and thus decreases diversity. Unidirectional dispersal, on the other hand, can increase diversity in high productivity upstream communities by disturbing the resident defense specialists, thereby opening up niches for competition specialists. These findings could be taken further and used to shed light on why are certain marine bacteria so successful (Zhao et al., 2013).

Acknowledgments

We thank JN Thompson for editorial comments on the manuscript. IG was supported by a NERC Advanced Fellowship, SEF was funded by the National Science Foundation DEB 0515598 and MR was supported by a NERC PhD studentship. IG, SEF and MS were also funded by a BBSRC/NSF EEID grant.

Footnotes

Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)

Supplementary Material

Supplementary Material
Click here for additional data file. (602.5KB, doc)

References

  1. Angly FE, Felts B, Breitbart M, Salamon P, Edwards RA, Carlson C, et al. The marine viromes of four oceanic regions. PLoS Biol. 2006;4:2121–2131. doi: 10.1371/journal.pbio.0040368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bell T, Newman JA, Silverman BW, Turner SL, Lilley AK. The contribution of species richness and composition to bacterial services. Nature. 2005;436:1157–1160. doi: 10.1038/nature03891. [DOI] [PubMed] [Google Scholar]
  3. Bohannan BJM, Lenski RE. The effect of resource enrichment on a chemostat community of bacteria and phage. Ecology. 1997;78:2303–2315. [Google Scholar]
  4. Bohannan BJM, Lenski RE. The relative importance of competition and predation varies with productivity in a model community. Am Nat. 2000;156:329–340. doi: 10.1086/303393. [DOI] [PubMed] [Google Scholar]
  5. Breitbart M, Miyake JH, Rohwer F. Global distribution of nearly identical phage-encoded DNA sequences. FEMS Microbiol Lett. 2004;236:249–256. doi: 10.1016/j.femsle.2004.05.042. [DOI] [PubMed] [Google Scholar]
  6. Brockhurst MA, Buckling A, Poullain V, Hochberg ME. The impact of migration from parasite-free patches on antagonistic host-parasite coevolution. Evolution. 2007;61:1238–1243. doi: 10.1111/j.1558-5646.2007.00087.x. [DOI] [PubMed] [Google Scholar]
  7. Brodie EL, DeSantis TZ, Moberg Parker JP, Zubietta IX, Piceno YM, Anderson GL. Urban aerosols harbor diverse and dynamic bacterial populations. PNAS. 2007;104:299–304. doi: 10.1073/pnas.0608255104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Brown BL, Swan CM, Auerbach DA, Campbell Grant EH, Hitt NP, Maloney KO, et al. Metacommunity theory as a multispecies, multiscale framework for studying the influence of river network structure on riverine communities and ecosystems. J N Am Benthol Soc. 2011;30:310–327. [Google Scholar]
  9. Buckling A, Rainey PB. Antagonistic coevolution between a bacterium and bacteriophage. Proc R Soc B. 2002;269:931–936. doi: 10.1098/rspb.2001.1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bunn SE, Arthington AH. Basic principles and ecological consequences of altered flow regimes for aquatic biodiversity. Environ Manage. 2002;30:492–507. doi: 10.1007/s00267-002-2737-0. [DOI] [PubMed] [Google Scholar]
  11. Chao L, Levin BR, Stewart FM. A complex community in a simple habitat: an experimental study with bacteria and phage. Ecology. 1977;58:369–378. [Google Scholar]
  12. Craig TP, Itami KJ. Divergence of Eurosta solidagninis in response to host plant variation and natural enemies. Evolution. 2010;65:802–817. doi: 10.1111/j.1558-5646.2010.01167.x. [DOI] [PubMed] [Google Scholar]
  13. Datta DB, Arden B, Henning U. Major proteins of the Escherichia coli outer cell envelope membrane as bacteriophage receptors. J Bacteriol. 1977;131:821–829. doi: 10.1128/jb.131.3.821-829.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fahlgren C, Hagström A, Nilsson D, Zweifel UL. Annual variations in the diversity, viability, and origin of airborne bacteria. Appl Environ Microbiol. 2010;76:3015–3025. doi: 10.1128/AEM.02092-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fenton A, Antonovics J, Brockhurst MA. Inverse-gene-for-gene infection genetics and coevolutionary dynamics. Am Nat. 2009;174:230–242. doi: 10.1086/645087. [DOI] [PubMed] [Google Scholar]
  16. Ferris MT, Joyce P, Burch CL. High frequency of mutations that expand the host range of an RNA virus. Genetics. 2007;176:1013–1022. doi: 10.1534/genetics.106.064634. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Forde SE, Thompson JN, Bohannan BJM. Adaptation varies through space and time in a coevolving host-parasitoid interaction. Nature. 2004;431:841–844. doi: 10.1038/nature02906. [DOI] [PubMed] [Google Scholar]
  18. Forde SE, Beardmore RE, Gudelj I, Arkin S, Thompson JN, Hurst LD. Understanding the limits to generalizability of experimental evolutionary models. Nature. 2008;455:220–224. doi: 10.1038/nature07152. [DOI] [PubMed] [Google Scholar]
  19. Forde SE, Thompson JN, Bohannan BJM, Holt RD. Coevolution drives temporal changes in fitness and diversity across environments in a bacteria-bacteriophage interaction. Evolution. 2008;62:1830–1839. doi: 10.1111/j.1558-5646.2008.00411.x. [DOI] [PubMed] [Google Scholar]
  20. Gandon S, Nuismer SL. Interactions between genetic drift, gene flow and selection mosaics drive parasite local adaptation. Am Nat. 2009;173:212–224. doi: 10.1086/593706. [DOI] [PubMed] [Google Scholar]
  21. Gandon S, Michalakis Y. Local adaptation, evolutionary potential and host–parasite coevolution: interactions between migration, mutation, population size and generation time. J Evol Biol. 2002;15:451–462. [Google Scholar]
  22. Heller KJ. Molecular interaction between bacteriophage and the gram negative cell envelope. Arch Microbiol. 1992;15:235–248. doi: 10.1007/BF00245239. [DOI] [PubMed] [Google Scholar]
  23. Hochberg ME, van Baalen M. Antagonistic coevolution over productivity gradients. Am Nat. 1998;152:620–634. doi: 10.1086/286194. [DOI] [PubMed] [Google Scholar]
  24. Hochberg ME, Gomulkiewicz R, Holt RD, Thompson JN. Weak sinks could cradle mutualisms - strong sources should harbor pathogens. J Evol Biol. 2000;13:213–222. [Google Scholar]
  25. Kawecki TJ, Holt RD. Evolutionary consequences of asymmetric dispersal rates. Am Nat. 2002;160:333–347. doi: 10.1086/341519. [DOI] [PubMed] [Google Scholar]
  26. King K, Delph LF, Jokela J, Lively CM. Coevolutionary hotspots and coldspots for host sex and parasite local adaptation in a snail-trematode interaction. Oikos. 2011;120:1335–1340. [Google Scholar]
  27. Laine AL. Role of coevolution in generating biological diversity: spatially divergent selection trajectories. J Exp Bot. 2009;60:2957–2970. doi: 10.1093/jxb/erp168. [DOI] [PubMed] [Google Scholar]
  28. Lenski RE. Experimental studies of pleiotropy and epistasis in Escherichia coli I. Variation in competitive fitness among mutants resistant to virus T4. Evolution. 1988;42:425–432. doi: 10.1111/j.1558-5646.1988.tb04149.x. [DOI] [PubMed] [Google Scholar]
  29. Lenski RE. Two-step resistance by Escherichia coli B to bacteriophage T2. Genetics. 1984;107:1–7. doi: 10.1093/genetics/107.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lindström ES, Östman Ö. The importance of dispersal for bacterial community composition and functioning. PloS One. 2011;6:e25883. doi: 10.1371/journal.pone.0025883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lopez-Pascua LDC, Buckling A. Increasing productivity accelerates host–parasite coevolution. J Evol Biol. 2008;21:853–860. doi: 10.1111/j.1420-9101.2008.01501.x. [DOI] [PubMed] [Google Scholar]
  32. Lorenzi MC, Thompson JN. The geographic structure of selection on a coevolving interaction between social parasitic wasps and their hosts hampers social evolution. Evolution. 2011;65:3527–3542. doi: 10.1111/j.1558-5646.2011.01403.x. [DOI] [PubMed] [Google Scholar]
  33. Madsen EL. Microorganisms and their roles in fundamental biogeochemical cycles. Curr Opin Biotechnol. 2011;22:456–464. doi: 10.1016/j.copbio.2011.01.008. [DOI] [PubMed] [Google Scholar]
  34. Morgan AD, Gandon S, Buckling A. The effect of migration on local adaptation in a coevolving host-parasite system. Nature. 2005;437:253–256. doi: 10.1038/nature03913. [DOI] [PubMed] [Google Scholar]
  35. Morona R, Krämer C, Henning U. Bacteriophage receptor area of outer membrane protein OmpA of Escherichia coli. J Bacteriol. 1985;164:539–543. doi: 10.1128/jb.164.2.539-543.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Naeem S, Li S. Biodiversity enhances ecosystem reliability. Nature. 1997;390:507–509. [Google Scholar]
  37. Nelson CE, Sadro S, Melack JM. Constrasting influences of stream inputs and landscape position on bacterioplankton community structure and dissolved organic composition in high-elevation lake chains. Limnol Oceanogr. 2009;54:1292–1305. [Google Scholar]
  38. Nuismer SL, Otto SP. Host-parasite interactions and the evolution of gene expression. PloS Biol. 2005;3:e203. doi: 10.1371/journal.pbio.0030203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Parchman TL, Benkman CW. The geographic selection mosaic for ponderosa pine and crossbills: a tale of two squirrels. Evolution. 2008;62:348–360. doi: 10.1111/j.1558-5646.2007.00295.x. [DOI] [PubMed] [Google Scholar]
  40. Piculell BJ, Hoeksema JD, Thompson JN. Interactions of biotic and abiotic environmental factors on an ectomycorrhizal symbiosis, and the potential for selection mosaics. BMC Biol. 2008;6:23. doi: 10.1186/1741-7007-6-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Poullain V, Gandon S, Brockhurst MA, Buckling A, Hochberg ME. The evolution of specificity in evolving and coevolving antagonistic interactions between a bacteria and its phage. Evolution. 2008;62:1–11. doi: 10.1111/j.1558-5646.2007.00260.x. [DOI] [PubMed] [Google Scholar]
  42. Qimron U, Marintcheva B, Tabor S, Richardson CC. Genomewide screens for Escherichia coli genes affecting growth of T7 bacteriophage. PNAS. 2006;103:19039–19044. doi: 10.1073/pnas.0609428103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sasaki A, Godfray HCJ. A model for the coevolution of resistance and virulence in coupled host-parasitoid interactions. Proc R Soc B. 1999;266:455–463. [Google Scholar]
  44. Schwartz M.1980Interaction of phages with their receptor proteinsIn: Randall LL, Philipson L edsVirus Receptors, Part 1 Bacterial Viruses Chapman Hall: New York, NY, USA; 59–94. [Google Scholar]
  45. Sen K, Nikaido H. Lipopolysaccharide structure required for in vitro trimerization of Escherichia coli OmpF porin. J Bacteriol. 1991;173:926–928. doi: 10.1128/jb.173.2.926-928.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Sogin ML, Morrison HG, Huber JA, Welch DM, Huse SM, Neal PR, et al. Microbial diversity in the deep sea and the underexplored 'rare biosphere'. PNAS. 2006;103:12115–12120. doi: 10.1073/pnas.0605127103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tamaki S, Tomoyasu S, Matsuhashi M. Role of lipopolysaccharides in antibiotic resistance and bacteriophage adsorption of Escherichia coli K-12. J Bacteriol. 1971;105:968–975. doi: 10.1128/jb.105.3.968-975.1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Thompson JN. Specific hypotheses on the geographic mosaic of coevolution. Am Nat. 1999;153:S1–S14. [Google Scholar]
  49. Thompson JN. The Geographic Mosaic Theory of Coevolution. Chicago Univ Press: Chicago, IL, USA; 2005. [Google Scholar]
  50. Travisano M, Lenski RE. Long-term experimental evolution in Escherichia coli. IV. Targets of selection and the specificity of adaptation. Genetics. 1996;143:15–26. doi: 10.1093/genetics/143.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Vogwill T, Fenton A, Brockhurst MA. The impact of parasite dispersal on antagonistic host-parasite coevolution. J Evol Biol. 2008;21:1252–1258. doi: 10.1111/j.1420-9101.2008.01574.x. [DOI] [PubMed] [Google Scholar]
  52. Vogwill T, Fenton A, Buckling A, Hochberg ME, Brockhurst MA. Source populations act as coevolutionary pacemakers in experimental selection mosaics containing hotspots and coldspots. Am Nat. 2009;173:171–176. doi: 10.1086/597374. [DOI] [PubMed] [Google Scholar]
  53. Vogwill T, Fenton A, Brockhurst MA. How does spatial dispersal network affect the evolution of parasite local adaptation. Evolution. 2010;64:1795–1801. doi: 10.1111/j.1558-5646.2009.00937.x. [DOI] [PubMed] [Google Scholar]
  54. Vogwill T, Fenton A, Brockhurst MA. Coevolving parasites enhance the diversity-decreasing effect of dispersal. Biol Lett. 2011;7:578–580. doi: 10.1098/rsbl.2011.0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Weitz JS, Hartman H, Levin SA. Coevolutionary arms races between bacteria and bacteriophage. PNAS. 2005;102:9535–9540. doi: 10.1073/pnas.0504062102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Winter C, Bouvier T, Weinbauer MG, Thingstad TF. Trade-offs between competition and defense specialists among unicellular planktonic organisms: the “Killing the Winner” hypothesis revisited. Microbiol Mol Biol Rev. 2010;74:42–57. doi: 10.1128/MMBR.00034-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Yamaguchi N, Ichijo T, Sakotani A, Baba T, Nasua M. Global dispersion of bacterial cells on Asian dust. Sci Rep. 2012;2:525. doi: 10.1038/srep00525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zhao Y, Temperton B, Thrash JC, Schwalbach MS, Vergin KL, Landry ZC, et al. Abundant SAR11 viruses in the ocean. Nature. 2013;494:357–360. doi: 10.1038/nature11921. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material
Click here for additional data file. (602.5KB, doc)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES