Abstract
A study was conducted to test the hypothesis that instruction with graphically integrated representations of whole and sectional neuroanatomy is especially effective for learning to recognize neural structures in sectional imagery (such as MRI images). Neuroanatomy was taught to two groups of participants using computer graphical models of the human brain. Both groups learned whole anatomy first with a three-dimensional model of the brain. One group then learned sectional anatomy using two-dimensional sectional representations, with the expectation that there would be transfer of learning from whole to sectional anatomy. The second group learned sectional anatomy by moving a virtual cutting plane through the three-dimensional model. In tests of long-term retention of sectional neuroanatomy, the group with graphically integrated representation recognized more neural structures that were known to be challenging to learn. This study demonstrates the use of graphical representation to facilitate a more elaborated (deeper) understanding of complex spatial relations.
Neuroanatomy is a scientific discipline that describes the structure and operation of nervous systems. It is a fundamental discipline with applications in many areas of biological, social, and clinical science. Expertise in neuroanatomy includes recognition of parts of the human brain in sectional representation. Sectional representation is the two-dimensional (2-D) spatial representation of a three-dimensional (3-D) structure in terms of planar slices sampled from its interior. Images from computed tomography (CT) and magnetic resonance imagery (MRI) are familiar examples (Mai, Paxinos, & Voss, 2007). Neuroanatomy is a challenging topic to learn, and sectional neuroanatomy is particularly challenging (Chariker, Naaz, & Pani, 2011, 2012; Drake, McBride, Lachman, & Pawlina, 2009; Oh, Kim, & Choe, 2009; Ruisoto, Juanes, Contador, Mayoral, & Prats-Galino, 2012).
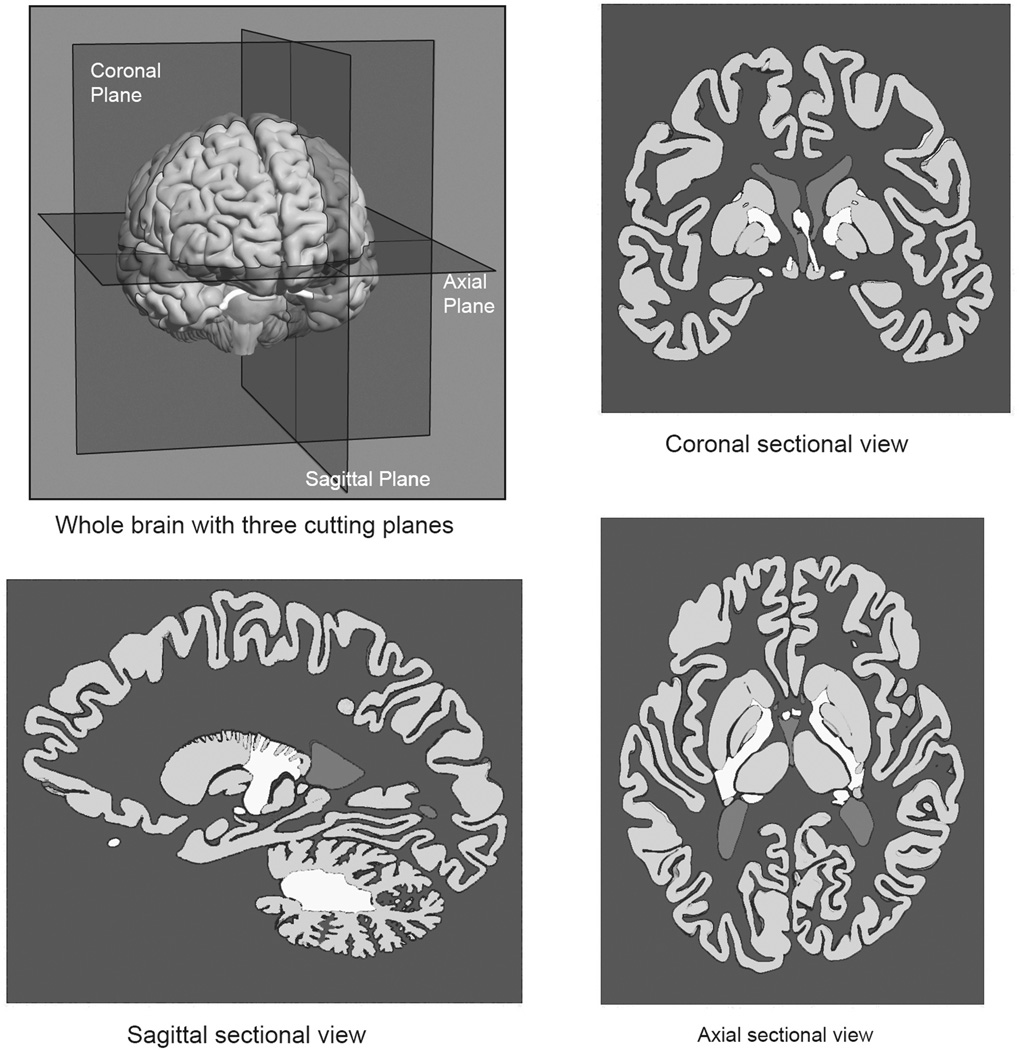
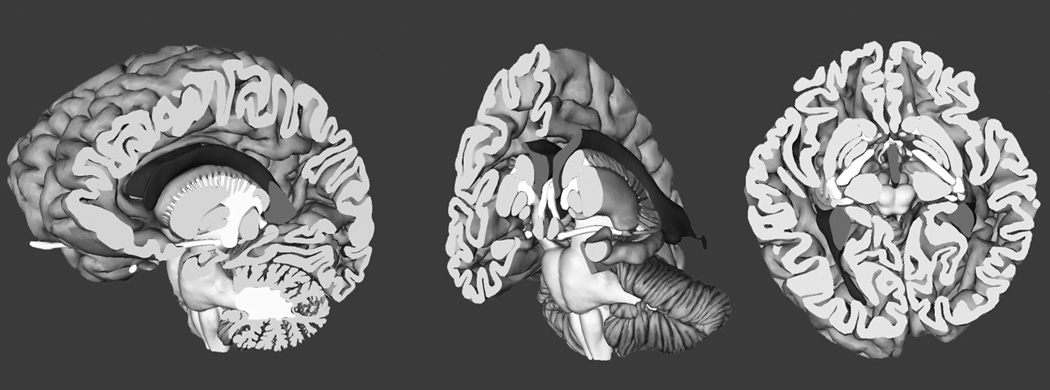
Learning to recognize neural structures in sectional representation can be described as an effort to establish a mapping between different sets of representations. Briefly, the neural structures can be understood as a set of whole structures, with 3-D form, and as sets of planar samples taken in a coronal (frontward), sagittal (sideways), or axial (horizontal) orientation. As illustrated in Figure 1, sectional samples generate representations with a great deal of variation in how individual structures appear. A primary challenge for the learner is to develop a coherent understanding of the mapping among the various spatial representations. The present research tested the hypothesis that learning sectional neuroanatomy in more challenging cases would be facilitated by the explicit illustration of the spatial relations between whole and sectional anatomy, as illustrated in Figure 2.
Figure 1.
Illustration of the whole brain with three cutting planes and three sectional views of the brain sampled at the cutting planes.
Figure 2.
Screen images showing sectional representation of neuroanatomy as a cut through the whole brain.
The context for this hypothesis is a project aimed at developing effective methods of computer-based instruction of human neuroanatomy (Chariker et al., 2011, 2012; Pani, Chariker, & Naaz, 2013). The project has been guided by an effort to develop instructional methods appropriate for the unique challenges presented by this domain. In the first place, the human brain is a complex spatial structure, and its anatomy will be learned most efficiently through study of spatial representations that present critical concepts directly (e.g., Felten & Shetty, 2010; Mai et al., 2007; Nolte & Angevine, 2007). Modern computer graphics have become an excellent platform for representing spatial structures, and they are being incorporated into instruction in a variety of STEM disciplines, including geoscience, astronomy, and chemistry (e.g., Reynolds, 2001).
Two further considerations have been critical to the development of computer-based learning environments. The first is a goal to incorporate graphics into an active learning environment in which study, test, and feedback can be cycled quickly and repetitively (see also Koedinger & Corbett, 2006). Adaptive exploration was developed to be a method that incorporates flexible graphical exploration in the context of repeated testing and feedback (Chariker et al., 2011; Pani et al., 2013). The second consideration is that neuroanatomy is a very large and complex domain that requires extensive self-study. The capabilities for information management provided by computers are well suited to support self-study in a large domain.
Specific hypotheses about how to design computer-based instruction of neuroanatomy have come from an effort to incorporate into instruction the general principles of organization and integration of knowledge that have been explored in the study of learning and memory (Bower, Clark, Lesgold, & Winzenz, 1969; Bransford, 1979; Tulving & Donaldson, 1972). A basic hypothesis was that 3-D whole anatomy is a form of representation that can be used efficiently to construct a unified understanding of sectional representations (Chariker et al., 2011). If whole anatomy is mastered first, learners will have a mental model(s) of the brain that will support transfer of learning to mastering sectional anatomy.
In general, this hypothesis was confirmed. When experimental participants learned the anatomy of the human brain from computer graphical models, whole anatomy was learned relatively efficiently (Chariker et al., 2011). Later learning of sectional anatomy began at a high level of performance, compared to a control group that began learning with sectional anatomy. Moreover, when participants learned whole anatomy first, they learned sectional anatomy in fewer trials, demonstrated superior long-term retention, and were better able to generalize knowledge to biomedical images not seen before (Chariker et al., 2012). In a later study, interleaving learning trials for whole and sectional anatomy further increased the efficiency of learning sectional anatomy (Pani et al., 2013).
The present hypothesis, that a more explicit graphical integration of whole and sectional anatomy will improve learning, arises from two additional points. One concerns data from these prior studies, and the other concerns theory. In regard to data, there was large variation in the success with which neural structures were learned (Chariker et al., 2012). Several structures were mastered in the first trial of learning. Other structures consistently required many more trials to learn, and this disadvantage carried over to long-term retention and to generalization. The most consistent set of difficult structures included six items: hypothalamus, mammillary body, nucleus accumbens, subthalamic nucleus, substantia nigra, and red nucleus. In a hierarchical cluster analysis of patterns of error over learning trials, these structures formed the single most differentiated cluster. Early in learning, these structures were omitted from test answers. Later in learning, they were confused with each other.
In regard to theory, the basic task to master in learning sectional neuroanatomy is visual recognition of structures that have unique names, properties, and concepts associated with them. A neurologist, for example, must be able to look at an MRI image and say, “This is the tail of the caudate nucleus.” In achieving perceptual recognition, the cognitive system often can use categorical spatial terms, such as surrounds, curved, runs through, thin, nodular, and behind (e.g., Biederman, 1987; Kosslyn, 1994; Stevens & Coupe, 1978; Tversky, 1981). Such categorical terms are very often applicable to basic knowledge in neuroanatomy. The putamen, for example, is a medium-sized ovoid shape flattened in a sideways direction located just inside the cortex near the middle of the brain.
It was implicit in the prediction of transfer of learning from whole to sectional neuroanatomy that there is invariance of categorical spatial descriptions across these representations. For example, the cerebral cortex is a large convoluted surface running around the outside of the brain both in whole and in sectional representations (Figure 1). Small structures at the middle of the brain in whole anatomy are small structures at the middle of the brain in sectional anatomy.
Of course, this invariance across whole and sectional anatomy does not apply to all spatial properties of the brain. Thus, a movement from front to back through a series of coronal sections maps to a movement from left to right within a single sagittal section. However, knowledge of whole anatomy in conjunction with a global knowledge of spatial transformations will provide a clear basis for organization and integration of sectional anatomy. Moving through coronal slices and finding the amygdala at the front, the putamen in the middle, and the cerebellum at the back should be easy to map to a sagittal image where the amygdala is seen to the left, the putamen is at the middle, and the cerebellum is at the right. Spatial reasoning is involved in understanding the relationship, but it would seem to be fairly simple if knowledge of whole anatomy can be used to guide and reinforce the reasoning.
With these ideas made explicit, it becomes clear why certain anatomical structures presented a challenge to learning. They are similar to each other in being small, ovoid, and relatively near to each other in the middle of the brain. Simple categorical descriptors such as “small” or “near the middle” do not differentiate them. If such descriptors do not uniquely characterize the anatomical structures, they also cannot be used in integrating knowledge of whole and sectional anatomy. Moreover, confusion among similar structures would have increased the uncertainty in reasoning about global spatial relations among the different sectional views of the brain (e.g., coronal and sagittal views). Easier structures to learn, such as the amygdala, the putamen, and the cerebellum, have different shapes and sizes that help to guide and constrain spatial reasoning about them. If individual structures are not confidently recognized, it is a more complex problem to discover how they are spatially related across different views.
These challenges for learning may be significantly reduced by providing an explicit illustration of the spatial relations between whole and sectional anatomy. The information provided in a sectional sample is a small subset of the spatial information that comprises the structure of the brain. If identifiable parts of the 3-D brain remain visible while the section is viewed, the information in the section can be related more explicitly to the whole brain than would be possible with application of a mental model retrieved from memory. With the additional perceptual support, the sectional information could be related more completely, in greater detail, and more confidently to the whole brain. It could be seen, for example, that a coronal section occurs toward the front of the brain, just ahead of the hippocampus, with the brainstem located a certain distance behind. If the individual also is able to move the plane at which sectional information is sampled while parts of the 3-D anatomy remain visible, it should be possible to develop an understanding of the ordering of sectional samples from front to back, top to bottom, and side to side. The individual can learn to describe the structure of the brain in terms of a spatial matrix of sectional samples that is well defined in relation to the structure of the whole brain (consider Novick & Hurley, 2001).
Such integration of whole and sectional information would clarify the spatial relations of the neural structures and their sectional samples to each other. At the same time, the additional cognitive context for individual structures should further differentiate them. It should become more obvious, for example, how the hypothalamus and the red nucleus are different. Both of these outcomes should be valuable in later recognition of sectional representations. From the point of view of research on memory (Craik & Tulving, 1975), this method encourages a more elaborated encoding of critical spatial relations among the neuroanatomical structures and the various representations of them.
In turning to the larger experimental literature, an argument can be made that explicit illustration of the relations between whole and sectional anatomy might not improve learning. Several studies have demonstrated cases in which sophisticated graphics do not facilitate learning (Mayer, Hegarty, Mayer, & Campbell, 2005; Tversky, Morrison, & Betrancourt, 2002). In direct comparisons between methods of computer-based learning, the more compelling graphics are often not the most effective method for learning (Chariker et al., 2011; Pani, Chariker, Dawson, & Johnson, 2005). Another body of work suggests that people with low spatial ability do not always benefit from computer graphics made available during learning (Keehner, Hegarty, Cohen, Khooshabeh, & Montello, 2008; Levinson, Weaver, Garside, McGinn & Norman, 2007).
It has been important to show that the new computer-based technologies are not a panacea. In the long term, however, there will be domains in which computer-based learning environments are especially valuable for instruction. The domains are very likely to include disciplines such as neuroanatomy, where physical demonstration and graphical illustration have long been mainstays of instruction. It is a question for research as to which instructional designs will be effective in the deployment of computer-based technology.
Whether individuals with low spatial ability are disadvantaged in the use of computer graphics will depend on the instructional system that is used (see Keehner et al., 2008; Stull, Hegarty, & Mayer, 2009). Moreover, in a complex spatial domain such as neuroanatomy, there is a question whether people with low spatial ability are at a disadvantage for every form of demonstration or illustration (Lufler, Zumwalt, Romney, & Hoagland, 2012). Indeed, it is possible that computer graphics will disadvantage this group least of all, depending on how the system is designed (Hegarty, 2004). Finally, most studies of spatial ability and learning have focused on learners’ initial contact with spatial material, but outcomes in the short term may not predict outcomes in the long term (see Uttal & Cohen, 2012). In longitudinal studies of computer-based learning of neuroanatomy, people with low spatial ability begin in the first trial of learning at a lower level of test performance (Chariker et al., 2011; Pani et al., 2013). However, their learning takes place at a rate comparable to other individuals. Across all of learning, they require only a few additional trials.
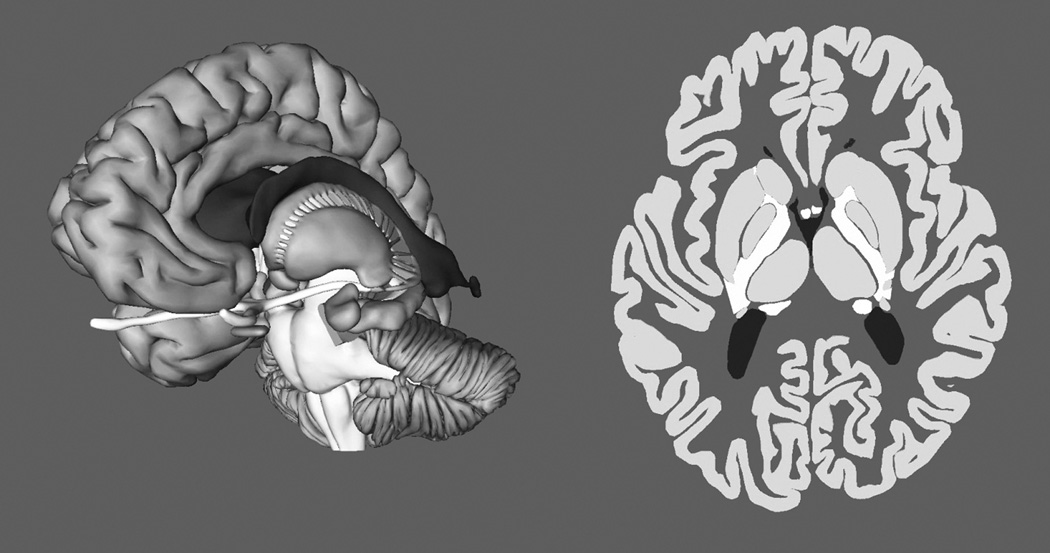
Overall, it was an empirical question whether explicit illustration of the relations between whole and sectional neuroanatomy would improve learning. The possibility was tested with an experimental condition in which the learner could move a cutting plane continuously through the brain to generate either a coronal, sagittal, or axial sequence of sectional views. As the cutting plane was moved with a slider, the part of the brain in front of the plane disappeared, while the part behind the plane remained visible (Figure 2). Learning began with mastery of whole anatomy, shown on the left side in Figure 3, as that has been shown to be an efficient method for gaining basic expertise in neuroanatomy. Thus, instruction with the moving cutting plane was a way to learn sectional anatomy in the context of familiar whole anatomy. A control group also learned whole anatomy first. They then learned sectional anatomy with a more standard presentation, shown on the right side in Figure 3. For this group, movement of the slider changed the section through the brain that was displayed on the screen. There was no further display of whole anatomy. Due to the critical importance of testing and feedback in the instructional method, both of the experimental groups were tested and were provided feedback only with sectional anatomy. Thus, the difference in the instructional method between the two groups was in the graphical tools available for study of sectional anatomy.
Figure 3.
Screen images showing exploration of the whole brain and sectional imagery from the axial view.
Because the control group used a method that was known to lead to efficient learning (Chariker et al., 2011), we did not expect that the experimental group would learn more efficiently. As discussed earlier, it was also known that many neural structures would be learned well with either method. Questions for research concerned whether the experimental group would have better performance in long-term retention and in generalization to new sectional imagery for neural structures that were known to be difficult to learn.
Method
Participants
Sixty-four volunteers between 16 and 34 years of age were recruited for the study through paper and online advertisements posted throughout the University of Louisville campus. A detailed survey assessed knowledge of neuroanatomy. Only volunteers with minimal or no knowledge of neuroanatomy were included in the study.
Participation in the study required coming to the laboratory for an hour session at least twice a week. Sixteen participants did not complete the study due to unanticipated scheduling conflicts, because they did not comply with instructions, or because they dropped out without explanation. On average, participants took 12 hours to complete the study. On completion, participants were compensated 100 dollars.
Participants were randomly assigned to learning groups with the constraint that the means and distributions of spatial ability were balanced between the groups (see Psychometric tests in Materials section). After data were collected, a further balancing procedure was used to match the groups on a pretest of sectional neuroanatomy identification. This pretest was given after whole anatomy learning (in which individuals in the two groups were treated identically) but prior to sectional anatomy learning. The balancing procedure was used because it has been shown that in studies of learning in challenging domains there is extreme variation in the performance of paid volunteers due to motivation and work habits (Pani, Chariker, Dawson, et al., 2005). To better control this variability, participant data were excluded from all statistical analyses if a participant’s combination of spatial ability and pretest score did not match with individuals in the other experimental group. In particular, spatial ability and pretest scores were treated as dimensions in a Euclidean space. The standard Euclidean distance formula was used to calculate the distance between participants in the space. A recursive algorithm was developed to find the best matching pair of participants between the two experimental groups, the next best match, and so on. When the worst matching pair of participants was identified, their data were removed from the sample of participants. This process was repeated until the differences between the two groups on both spatial ability and pretest performance had p > .5. Several papers have suggested that two groups should be considered matched on a variable when the p obtained from comparing the groups is above .5 (Frick, 1995; Mervis & Klein-Tasman, 2004). After application of the matching algorithm, twenty participants were included in each group.
Materials
Psychometric tests
Before learning neuroanatomy, participants were tested on their spatial ability and the capacity of their short-term memory for visuospatial patterns. The Differential Aptitude Test: Space Relations (DAT: SR; Bennett, Seashore, & Wesman, 1989) was used to measure spatial ability. The DAT: SR is a multiple-choice test of mental paper folding. Short-term memory for visuospatial patterns was measured with the Designs I test for immediate recall from the Wechsler Memory Scale IV (Wechsler, 2009). The test of visuospatial memory did not yield results relevant to the main topic of this article and will not be discussed further.
Neuroanatomical model
An accurate 3-D computer graphical model of the human brain (Figure 3) was adopted from Chariker et al. (2011). The model consisted of 19 major neuroanatomical structures, including amygdala, brainstem, caudate nucleus, cerebellum, cortex, fornix, globus pallidus, hippocampus, hypothalamus, mammillary body, nucleus accumbens, optic tract, pituitary, putamen, red nucleus, subthalamic nucleus, substantia nigra, thalamus, and ventricles. Dense sectional representation of the 3-D model was available in the three standard planes for use in the sectional anatomy learning programs (Figure 3). There were 60 coronal sections, 50 sagittal sections, and 46 axial sections.
Learning programs
Three computer programs were used for instruction in this study: one for learning whole anatomy and two for learning sectional anatomy. The basic structure of learning trials was the same across all three programs. During an initial 4-minute study period, participants could freely explore the brain model using the graphical tools available for that program. Clicking on a structure with a computer mouse highlighted the structure, and its name appeared prominently at the bottom of the screen. In a self-timed test period, participants named the structures they had learned by clicking on each structure and selecting its name from a virtual button panel that represented all 19 structures. Participants could omit naming structures if they wished, and a name could be used more than once. After a structure was named, it turned blue to help the participant keep track of what already had been named. Immediately after the test, there was a 2-minute feedback period. This had two parts: a numerical feedback screen and subsequent graphical feedback. The numerical feedback indicated the number of structures that were named correctly, the number of structures named incorrectly, and the number of structures omitted. The graphical feedback consisted of a color coding of the brain model: the structures that had been named correctly appeared in green, the structures named incorrectly appeared in red, and the structures that were omitted appeared in their original color. During the feedback period, participants could interact with the color-coded structures using the same tools available in study. Participants could click on structures, highlight them, and see their correct names. The feedback stage ended with the appearance of an exit screen, which displayed the participant's percentage correct score on the test.
Whole anatomy program
The program for learning whole anatomy featured the 3-D model of the brain (Figure 3). Both of the groups learned whole anatomy using this program. During the study period, participants could explore the model freely with the help of tools provided for rotation, zooming, and virtual dissection. As described earlier, clicking on structures highlighted them and displayed their names. Participants engaged in virtual dissection of the brain by selecting structures and removing them one by one, using buttons on the button panel at the right side of the screen. Participants also could restore the structures that had been removed, either one by one or all at once. The brain model initially appeared from a front, side, or top view, but participants could rotate the brain by any amount.
In testing, the orientation of the brain model was restricted to angles within 45 degrees of the view in which the brain was first presented in the study period. The tools for exploring the brain remained available. Participants were asked to name as many structures as they could by selecting structures and clicking on their names in the button panel. With 19 structures in the 3-D model of the brain, this test of whole anatomy recognition consisted of 19 items.
Sections only program
After learning whole anatomy, one experimental group, called the whole then sections group, learned sectional anatomy using a program that permitted exploring the series of 2-D sections taken from the 3-D model of the brain (Figure 3). During the study period, the participants saw thin sections of the brain in a single view (coronal, sagittal, or axial). The participants could move from one section to another by using the computer mouse to move a slider at the bottom of the screen. In the coronal view, for example, moving the slider successively displayed all of the coronal sections of the brain from front to back. At each section, participants could click on individual structures to highlight them and learn their names. Structures remained highlighted during navigation through the sections.
In testing of sectional anatomy recognition, a subset of the available sections (12–15) was used in each test. Between one and five structures were indicated by arrows in each of the sections. The participants were to name each structure indicated by an arrow. They did this by clicking on the structure, selecting its name from the button panel, and submitting the answer. The arrows were adopted for testing because asking for the names of all structures in multiple sections would have comprised a test that was too long. Numbers were displayed on the screen to show the number of structures to be named in a section, how many structures had been named in that section, and the number of test sections remaining. Participants moved from one test section to the next by clicking on a button. They could not go back to a previous test section. Sectional samples of structures were varied across tests, and longer structures were sampled twice in each test. There were 29 test items for the coronal and sagittal views of sectional anatomy and 27 test items for the axial view.
The graphical feedback for sectional anatomy was similar to the presentation during the study period. All of the sections of the brain were available to be explored. The test sections were clearly marked as "Test Section," and the arrows indicating the test items remained. The test items again were color coded to reflect the performance on the test. The feedback stage allowed participants to go freely through all of the sections and to locate the test sections among them. Participants could select structures and see their correct names.
2-D/3-D program
After learning whole anatomy, a second experimental group, called the explicit 2-D/3-D group, learned sectional anatomy using a program that permitted moving a cutting plane through the model of whole neuroanatomy (Figure 2). During the study period of a trial, participants could explore the 3-D model using all the tools they used earlier in the whole anatomy program, including tools for rotation, zooming, and virtual dissection. In addition, the 3-D model could be sliced to view sectional anatomy by using the computer mouse to move a slider at the bottom of the screen. On moving the slider from left to right, a virtual cutting plane appeared to move through the brain and to remove the part of the brain in front of the plane. This exposed the 2-D cross-sections of the 3-D structure from one end of the brain to the other. In the axial view, for example, moving the slider from left to right made a horizontal cutting plane move from the top of the brain to the bottom, removing the part of the brain above the plane. Beyond the cutting plane, the 3-D structures remained visible, allowing the participants to see the transformation from 3-D to 2-D. Participants could move the slider back and forth to see how these 3-D structures would appear in sections from different depths in the brain. The test and feedback stages were identical to the test and feedback stages of the sections only program.
Tests of generalization
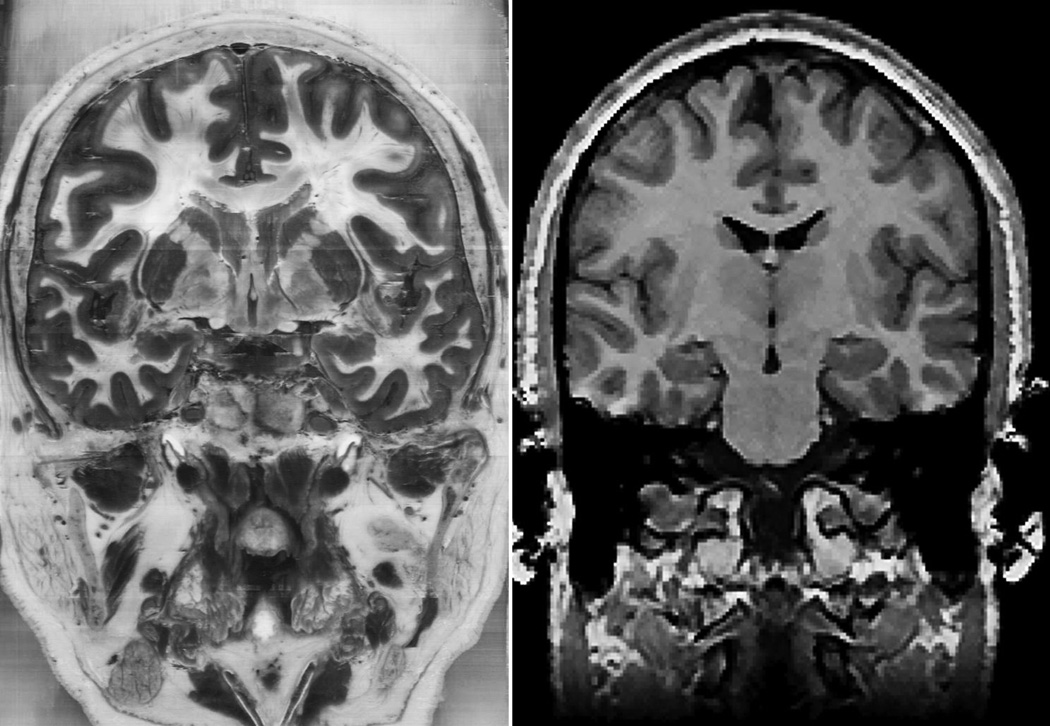
Three tests of generalization were created using biomedical images to test the transfer of knowledge to new representations of sectional neuroanatomy. The biomedical images were MRI images (from the SPL-PNL Brain Atlas; Kikinis et al., 1996) and color photographs from the Visible Human 2.0 dataset (Figure 4; Ackerman, 1995). Compared to the Visible Human (VH) images, MRI images have low resolution, low contrast, and relatively few clear boundaries between structures. Both sets of images showed many structures, such as bones, muscles, additional neural structures, and blood vessels that were not shown during learning. Both sets of images were presented from all three standard anatomical views. Tests of generalization were always blocked by image type (VH or MRI) and anatomical view. Test items were selected to match the testing in the sectional anatomy learning programs. Thus, there were 29 test items for coronal and sagittal views, and 27 test items for the axial view. No feedback was given for the tests of generalization.
Figure 4.
Examples of biomedical images used in the tests of generalization. A Visible Human image is shown at the left and an MRI image is shown at the right. In the study, the Visible Human image was in color.
In a test of generalization called Global Cues, participants were asked to name all recognizable structures in each image. The participants received two global cues to orient them for this test. A visual cue consisted of a brain icon at the upper left corner of the screen with a line going through it to indicate the orientation and position of the plane of section. A numeric cue was presented below the brain icon to indicate the number of identifiable structures in the image. The participant indicated the location of a learned structure in the image by clicking on it with the mouse. A red dot appeared on the image at that location. The participant then indicated the name of the structure by selecting the name from the standard button panel. When the participant was confident he had his best answer, he submitted it by clicking on a virtual button.
In a test of generalization called Submit Structure, the name of a single neural structure appeared at the bottom of the screen for each image. The participant’s task was to indicate the location of the named structure by clicking it with the mouse. Clicking on the image caused a red dot to appear at that location. When the participant was confident he had his best answer, he submitted it by clicking on a virtual button. He then proceeded to the next image.
In a test of generalization called Submit Name, a red arrow on each image indicated a single structure. The participant named the indicated structure by selecting the name from the button panel and submitting the answer.
Sections pretest and test of long-term retention
The sections pretest and test of long-term retention were tests of knowledge of sectional anatomy with the same format as those in sectional anatomy learning trials. However, the tests were administered without study or feedback periods.
Instruction programs
Practice programs were created for learning the options for user interaction with each of the learning programs and the generalization tests. A mock brain model was created for use in the practice programs. The mock brain model contained several geometric structures in a variety of shapes and spatial relations. The structures were given pseudobiological names. Demonstration videos were created for the practice programs. These included visual demonstration of user interaction along with simultaneous verbal descriptions. After watching a video, the participant used a practice program with the mock brain to demonstrate to a member of the research team an understanding of how to use the program. The experiment did not proceed until the participant could successfully demonstrate complete use of the relevant programs in study, test, and feedback. The practice programs for the generalization tests used biomedical images (MRI and VH images) that were not part of the actual tests.
Apparatus
The study was conducted using individual workstations with high capacity graphics cards and sufficient RAM for smooth presentation of the neuroanatomical models and images. The programs were displayed on 24-inch LCD color monitors at a resolution of 1920×1200 pixels. The participants were seated approximately 60 cm from the monitors (arm’s length). Participants used the learning programs by themselves in quiet rooms. They were provided with headphones for use with the instructional videos.
Design and Procedure
The primary hypothesis of the study was evaluated using two learning groups: whole then sections (WtS) and explicit 2-D/3-D (2-D/3-D). The participants in the two learning groups received identical treatment except for the program used to learn sectional anatomy.
The psychometric tests were conducted immediately after informed consent was obtained. Participants were then assigned to a learning condition and were given instruction videos to watch in a quiet room with headphones. After watching the videos, the participants used the practice programs until they could demonstrate to an experimenter a competent use of the interactive tools.
All participants learned whole anatomy first. Whole anatomy was learned from the three different views (front, side, and top) in alternating trials. The order of presentation of the views was counterbalanced over participants. Participants continued cycling through trials until they reached at least 90% correct test performance on three successive trials.
After participants completed learning whole anatomy, they were given the sectional anatomy pretest for all three views of sectional anatomy (coronal, sagittal, and axial). After taking the pretest, participants learned sectional anatomy using one of the two learning programs (sections only or 2-D/3-D), based on their group assignment. Participants learned sectional anatomy in the three standard views in alternating trials. Participants continued learning until they reached at least 90% correct test performance on three successive trials.
The three tests of generalization of knowledge were given as soon as possible after learning was completed (although not the same day). The order of the generalization tests was counterbalanced over participants. Tests of long-term retention of sectional anatomy were administered for all three anatomical views four to eight weeks after completion of the learning trials, depending on the participant’s schedule.
Scoring
Two of the generalization tests (Global Cues and Submit Structure) required manual scoring of the locations of mouse clicks on images. The scoring was done with versions of the biomedical images that had explicit boundaries drawn for each structure. The individual who scored the responses was blind to the participants’ identities and group assignment.
Item difficulty
Because the primary hypothesis concerned learning neuroanatomical structures that were particularly difficult to learn, the data were divided according to the difficulty of individual test items. This was done in two ways. First, on the basis of the prior work, the six neural structures discussed earlier were designated a priori to be difficult items to learn. Three different sectional views of those structures generated 18 difficult test items.
The second method was a statistical procedure developed by Chariker et al. (2012). For each of the two groups (WtS and 2-D/3-D), the mean proportion correct on each test and the upper and lower bounds of the mean at the 95% confidence interval were determined by binomial logistic regression applied over the complete set of tests (e.g., the three tests of long-term retention). The next step was to define the raw measure of item difficulty as the proportion of the participants in a group that identified an item correctly on a particular test. Then, for each test, test items with proportions correct above the lower bound of the confidence interval were categorized as typical. Test items with proportions correct below the lower bound of the confidence interval were categorized as difficult. Items categorized as difficult also had to have less than 75% of the sample identifying them correctly. For each test, items identified as difficult in either of the two groups were categorized as difficult test items. Finally, mean performance of each participant on the typical and the difficult test items was calculated for each test.
Results
Long-Term Retention
The two methods for determining item difficulty led to statistical outcomes that were close approximations to each other. The two sets of results were identical for the sets of comparisons that were statistically significant, and the effect sizes were very similar. For sake of brevity, we report here only the analyses from use of the statistical method for identifying difficult test items.
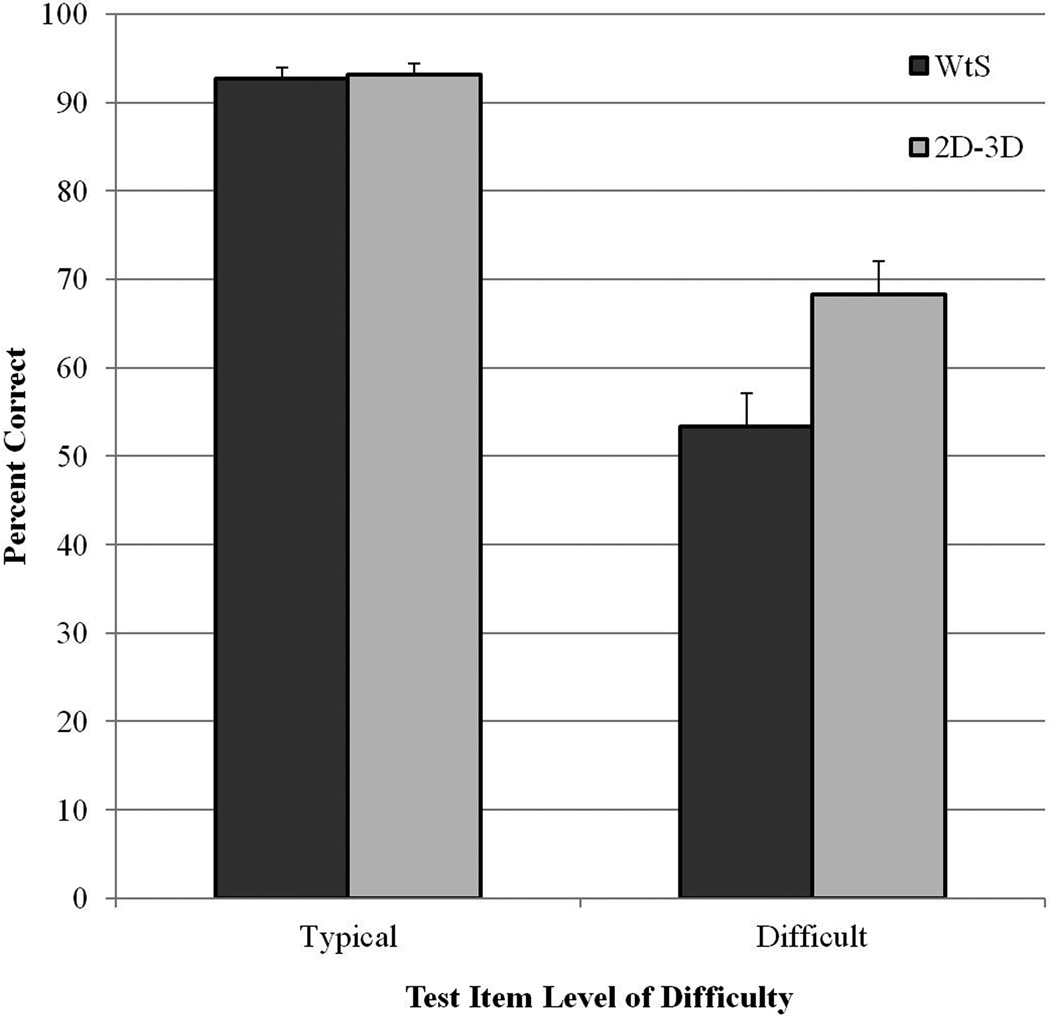
The analysis of item difficulty in long-term retention of sectional neuroanatomy led to categorization of 65 test items as typical (76.5% of the test items) and 20 as difficult (23.5% of the items). Mean retention of the two learning groups on typical and difficult test items is shown in Figure 5. A 2×2 mixed randomized ANOVA was conducted using item difficulty as a repeated measure variable and learning condition as a between group variable. There were significant main effects of item difficulty, F(1, 38) = 197, p < .001, np2 = .839, and learning condition, F(1, 38) = 5.396, p = .026, np2 = .124. Most importantly, there was a clear interaction between item difficulty and learning condition, F(1, 38) = 10.205, p = .003, np2 = .212. A planned pair-wise comparison showed a significant effect of condition for difficult test items, t(1, 38) = 2.797, p = .008, Cohen’s d = 0.89. The 2-D/3-D group scored 16 percentage points higher than the WtS group in identifying difficult test items in the test of long-term retention.
Figure 5.
Mean percentage correct for the two learning groups on the test of long-term retention of sectional anatomy, broken down by typical and difficult test items. Error bars show standard error of the mean.
Spatial ability and long-term retention
Spatial ability did not correlate with performance in long-term retention for either group (WtS: r = .332, p = .152; 2-D/3-D: r = -.023, p = .922). To test more directly whether spatial ability affected learners’ ability to benefit from the 2-D/3-D learning condition, the participants in each condition were divided by spatial ability into two groups using a median split. The two higher ability groups had a mean DAT: SR of 90.6, and the two lower ability groups had a mean DAT: SR of 58.2. Because the mean percentile for the lower group was near 50, this group should be considered average on spatial ability. A 2×2×2 mixed randomized ANOVA was conducted to analyze the role of spatial ability in learning. Learning condition, item difficulty, and DAT: SR were used as independent variables.
There was no interaction of spatial ability with learning condition, F(1, 36) = 0.209, p = .650. All participants had similar performance on typical test items (accuracy of approximately 93% for all four groups). Both the higher and lower spatial ability groups in the 2-D/3-D condition retained difficult test items at a numerically higher level than their counterparts in the WtS condition (Higher spatial ability: WtS M = 58.5%, SD = 15.99; 2-D/3-D M = 71.0%, SD = 16.80; Lower spatial ability, WtS M = 48.0%, SD = 11.83; 2-D/3-D M = 65.5%, SD = 21.40).
Tests of Generalization to Interpreting Biomedical Images
There were no effects of learning group on any of the tests of generalization to interpreting biomedical images. There also were no significant correlations between spatial ability and generalization performance.
Effect of test order on generalization
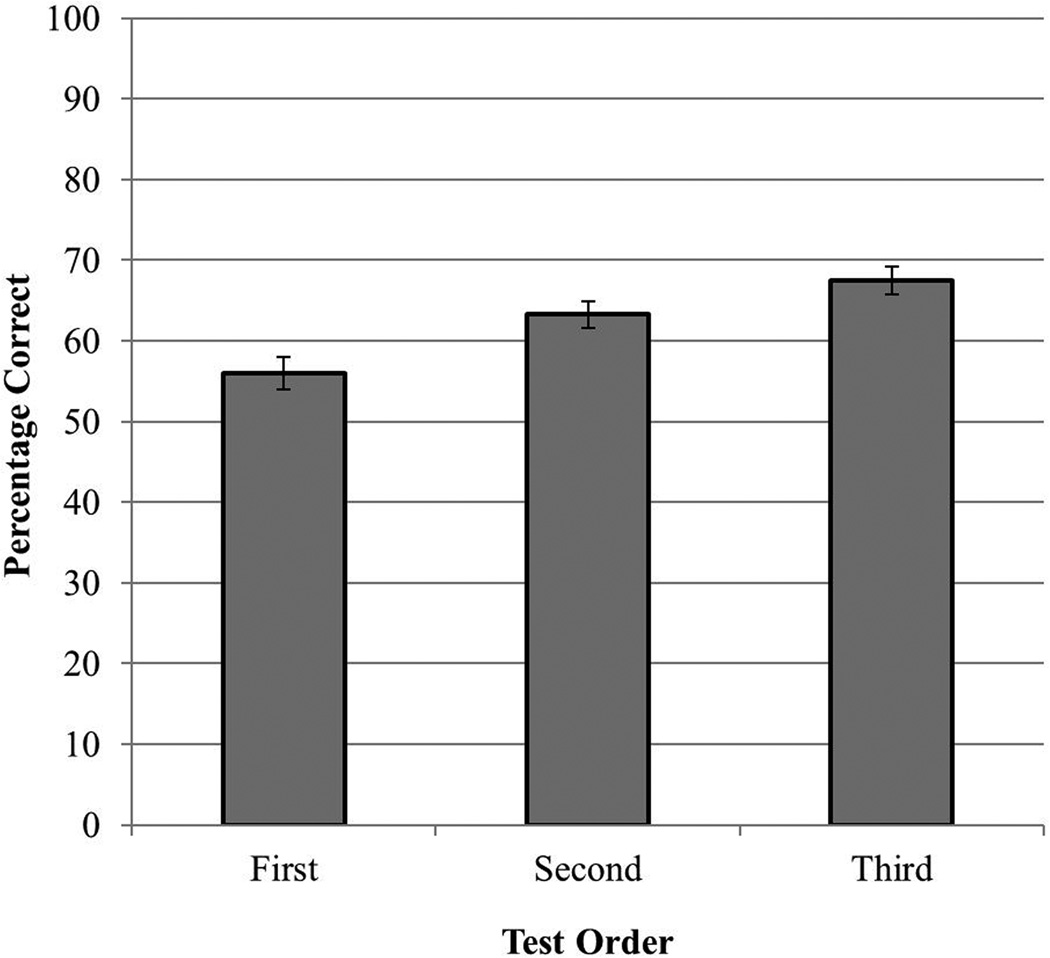
Improvement in performance across the three counter-balanced tests of generalization would suggest that the computer-based methods had established a preparation for future learning (Bransford & Schwartz, 1999). To test for the effects of test order on generalization, the score of each participant on each of the three generalization tests was categorized according to the ordinal position in which the test occurred (i.e., first, second, or third). A one-way repeated measure ANOVA revealed a significant effect of test order, F(2,78) = 12.034, p < .001, np2 = .236. As shown in Figure 6, performance improved as participants moved through the tests (first test M = 56.0, SD = 12.77; second test M = 63.2, SD = 10.7; third test (M = 67.5, SD = 11.2). Pair-wise comparisons of the three test positions were conducted with Bonferroni correction. Performance on the second and third tests was significantly better than the performance on the first test (first vs. second: t(39)= 3.51, p = .001, d = 0.62; first vs. third: t(39) = 4.50, p = .001, d = 0.96).
Figure 6.
Mean percentage correct for the tests of generalization, broken down by test order. Error bars show standard error of the mean.
Effect of test type (cues)
The mean test performances for the three tests of generalization were 70% for Submit Name (SD = 9.09), 64% for Submit Structure (SD = 11.71), and 52% for Global Cues (SD = 9.17). A repeated measures ANOVA revealed a significant main effect of test type, F(2, 78) = 52.589, p < .001, np2 =.574. Performance on the Submit Name test was significantly better than performance on both the Global Cues, t(39) = 10.92, p = .00, d = 1.96, and the Submit Structure test, t(39) = 3.15, p = .003, d = 0.59. Performance on the Submit Structure test was significantly better than performance on the Global Cues test, t(39) = 6.89, p = .00, d = 1.11.
Effect of image type
Replicating previous work, performance on VH images was significantly better than performance on MRI images in all of the tests of generalization, Submit Name: t(1,39) = 15.2, p < .001, d = 1.6; Submit Structure: t(1,39) = 14.9, p < .001, d = 1.4; Global Cues: t(1,39) = 5.1, p < .001, d = 0.55. In the Submit Name test, for example, mean generalization performance was 77.9% for VH images (SD = 9.6) and 62.6% for MRI images (SD = 9.6).
Learning Efficiency
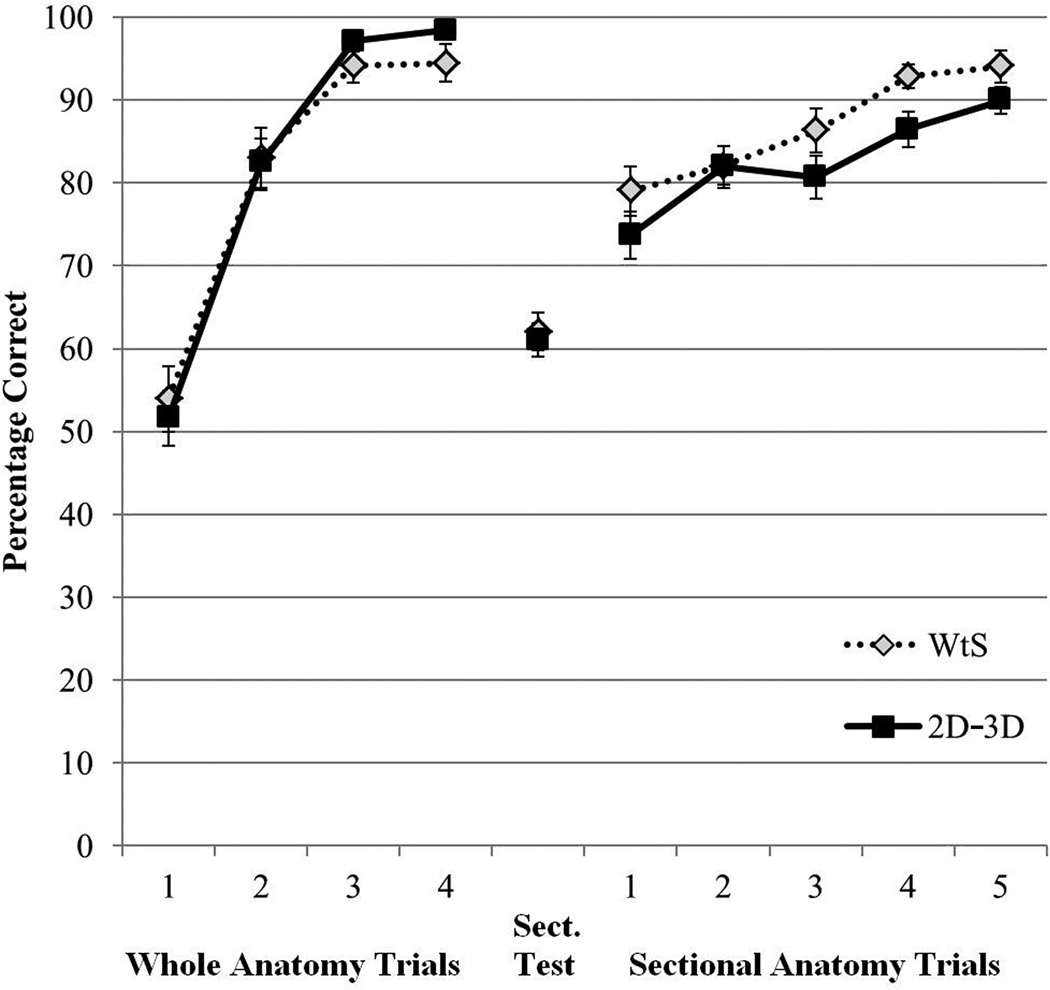
Mean percent correct test performance during learning is presented in Figure 7, broken down by trial and learning condition. Participants learned whole neuroanatomy to criterion in about five trials (M = 4.98 trials, SD = 1.48). The mean number of trials to complete learning of sectional anatomy was 7.8 trials for the WtS condition (SD = 4.83) and 9.35 trials for the 2-D/3-D condition (SD = 3.82).
Figure 7.
Mean percentage correct test performance for the two learning groups during the learning phase of the study. The data are broken down by whole anatomy learning trials, the Sections Test, and the sectional anatomy learning trials. Error bars show standard error of the mean. Where some participants finished learning in fewer trials than are indicated, their performance was extrapolated forward to contribute to the displayed means.
There were no statistical differences between the two groups in the efficiency of learning. For sectional anatomy learning, comparisons were tested for mean percent correct in Trial 1, t(38) = 1.30, p = .203, mean percent correct over the first five trials, F(1, 38) = 2.58, p = .116, np2 =.064, and the number of trials to complete learning, t(38) = 1.13, p = .267.
Spatial ability and the efficiency of learning
There were clear effects of spatial ability on the efficiency of learning neuroanatomy. There was a correlation of spatial ability with the number of trials required to learn whole anatomy, r = -.581, p < .001, and with performance on the sectional anatomy pretest, r = .345, p < .05. In addition, spatial ability correlated with the number of trials to learn sectional anatomy for both learning groups, although the statistical significance was marginal for the 2-D/3-D group (WtS: r = -.526, p < .05; 2-D/3-D: r = -.404, p = .086).
Discussion
Neuroanatomy is a scientific discipline in which people learn a large amount of information about a complex spatial structure. As a consequence, instruction in this discipline depends on spatial representation and extended self-study. Methods of instruction that take advantage of the capabilities of modern computer graphics are likely to be valuable in learning such a discipline. This raises the question: how should instruction be designed so that the technology is deployed effectively?
With a focus on learning sectional neuroanatomy, prior research has shown that a transfer of learning from whole to sectional anatomy has many benefits for learning. However, there was substantial variation in the difficulty of learning different neural structures, and this variation persisted into tests of long-term retention and generalization.
To address this problem, the present study moved farther into the use of integrative computer graphics for representing the relations between whole and sectional neuroanatomy. It was shown that explicit graphical demonstration of the spatial relations between 3-D whole anatomy and 2-D sectional anatomy improved long-term retention of sectional neuroanatomy that was known to be challenging to learn. Spatial ability did not correlate with levels of long-term retention, and the benefit of the integrative condition did not depend on levels of spatial ability.
There are several ways in which such integrative graphics might improve learning of sectional anatomy. For the materials in this study, we believe that the ability to view sectional representations of the brain at the same time that much of the 3-D anatomy remained visible permitted a more elaborated encoding of the spatial relations between the sectional representations and the 3-D structure of the whole brain. This elaboration was no doubt facilitated by the relatively easy recognition of whole structures during learning of the sectional representations. It probably was facilitated also by the ability to move the sectional planes continuously through the whole brain, allowing an exploration of spatial relations in single episodes of learning. Overall, the improved understanding of spatial relations would provide better cognitive differentiation of individual structures, including their sectional samples, and this would facilitate recognition and retention.
If this account is correct, explicit illustration of spatial relations will be useful in many instances where spatial material is difficult to learn (e.g., challenging rotational motions; Pani, Chariker, Dawson, et al., 2005; Stull et al., 2009; see Mayer, 2005). We wish to emphasize, however, that this graphical illustration of neuroanatomy was not just a mode of illustration. It occurred in the context of detailed testing, immediate feedback, and continuous learning that proceeded until a demanding performance criterion was met. It was illustration that helped to meet the immediate cognitive goals of an active learner who was focused on a particular set of learning outcomes.
Although the integrative 2-D/3-D condition improved retention, it is important to consider that it was not more effective for learning most of the neuroanatomical structures. Participants in the whole then sections condition tested at 79% correct in Trial 1 of sectional anatomy learning. Moreover, long-term retention for typical test items was 92.7% correct for this condition. It is also important to consider that the 2-D/3-D condition was not a more efficient method of learning than the pure transfer of learning used in the whole then sections condition. In contrast, a different study showed that interleaving trials of whole and sectional anatomy was a more efficient method of learning, although it did not improve retention (Pani et al., 2013). Anecdotally, we have seen two graduate students who were using the learning programs for neuroscience coursework seek out a member of the lab and request to use the sections only program (from the whole then sections condition) rather than the 2-D/3-D program. Apparently these students found the rich graphics in 2-D/3-D to be distracting when they were trying to learn sectional anatomy. The overall pattern of results from several studies suggests that neuroanatomy learning should begin with whole anatomy and then interleave trials of whole and sectional anatomy using the sections only program. The explicit illustration in the 2-D/3-D method should be available to permit more elaborated understanding of spatial relations when that is needed for structures that are particularly challenging to learn. More generally, it seems likely that different interactive methods of instruction will be best suited to individual domains, levels of expertise, tests of performance, and sets of items to be learned.
The results of this study are relevant in several ways to more general considerations of science instruction. First, we think it is important to note that when psychology has considered spatial cognition, the primary emphasis has been on relatively simple and abstract tasks, such as mental rotation (see Atit, Shipley, & Tikoff, 2013). Such tasks are solved in seconds, while a biology or medical student will puzzle for weeks over the surprising complexity of the human skull. Work on learning neuroanatomy will help to grow a subdiscipline of educational science focused on real world problems of spatial learning (Liben, Kastens, & Christensen, 2011; Pani, Chariker, & Fell, 2005; Stull, Hegarty, Dixon, & Stieff, 2012). Such a focus will enable insights about learning and instruction in spatial domains that cannot be obtained in simple laboratory studies.
In regard to an evaluation of interactive graphics in computer-based learning, there were reasonable levels of generalization of knowledge to interpreting biomedical images. When structures in VH images were cued with arrows, for example, mean recognition performance was 78% correct. This occurred even though the biomedical images had a very different appearance from the graphical models used in learning, and the images contained many structures that were not in the models (for other tests of generalization from interactive graphics, see Chariker et al., 2011; Pani, Chariker, Dawson et al., 2005). In addition, generalization performance improved over testing, even though there was no explicit feedback in the tests of generalization. Thus, computer-based instruction provided a preparation for future learning (Bransford & Schwartz, 1999). Participants were able to use their existing knowledge of neuroanatomy together with the cues provided in the tests of generalization to work out recognition of structures that had not been possible when testing began.
The results of this study also support recent statements that differences in spatial ability are evident in the early stages of spatial learning but may diminish in later stages (Uttal & Cohen, 2012). For example, spatial ability clearly correlated with the number of trials required to learn whole anatomy at the beginning of the study, but it was not correlated with long-term retention or generalization of sectional anatomy at the end of the study.
Finally, this study replicated work that points to a wide-ranging set of factors that will have to be addressed by educational systems aimed at biomedical disciplines. The clear superiority of recognition for VH images over MRI images demonstrated that problems for recognition could be due to the visual information in the images rather than the knowledge of the person viewing the images. The superiority of image recognition with specific cues, such as arrows pointing to structures, indicated that more should be done to help learners to reason about what they see in the images.
In summary, this study investigated the use of interactive graphics in computer-based learning of a complex spatial domain. It was found that explicit graphical illustration of the spatial relations between 3-D whole neuroanatomy and 2-D sectional neuroanatomy improved long-term retention of sectional representations of neural structures that were known to be particularly difficult to learn. We interpret this finding to show that interactive computer graphics can be designed to provide an opportunity for greater elaboration of knowledge in an intrinsically spatial domain. On the other hand, the particularly rich graphical displays in the present method should be reserved for times when simpler forms of representation are not effective.
Acknowledgments
Primary support for this research came from grant R01 LM008323 from the National Library of Medicine, NIH. The research also was supported by grant IIS-0650138 from the National Science Foundation and the Defense Intelligence Agency.
We thank the Surgical Planning Lab in the Department of Radiology at Brigham and Women's Hospital and Harvard Medical School for use of MRI images from the SPL-PNL Brain Atlas (supported by NIH grants P41 RR13218 and R01 MH050740). We thank the National Library of Medicine for use of the Visible Human 2.0 photographs. We thank Ronald Fell, Keith Lyle, Carolyn Mervis, and Pavel Zahorik for their comments on drafts of this manuscript.
Contributor Information
Farah Naaz, Department of Psychological and Brain Sciences, University of Louisville..
Julia H. Chariker, Department of Psychological and Brain Sciences, University of Louisville.
John R. Pani, Department of Psychological and Brain Sciences, University of Louisville.
References
- Ackerman MJ. Accessing the Visible Human Project. D-Lib Magazine [On-line] 1995 Retrieved from http://www.dlib.org/dlib/october95/10ackerman.html.
- Atit K, Shipley TF, Tikoff B. Twisting space: Are rigid and non-rigid mental transformations separate spatial skills? Cognitive Processes. 2013;14:163–173. doi: 10.1007/s10339-013-0550-8. [DOI] [PubMed] [Google Scholar]
- Bennett GK, Seashore HG, Wesman AG. Differential aptitude tests for personnel and career assessment: Space relations. San Antonio, TX: The Psychological Corporation, Harcourt Brace Jovanovich; 1989. [Google Scholar]
- Biederman I. Recognition-by-components: A theory of human image understanding. Psychological review. 1987;94:115–147. doi: 10.1037/0033-295X.94.2.115. [DOI] [PubMed] [Google Scholar]
- Bransford JD. Human cognition: Learning, understanding, and remembering. Belmont, CA: Wadsworth; 1979. [Google Scholar]
- Bransford JD, Schwartz DL. Rethinking transfer: A simple proposal with multiple implications. Review of Research in Education. 1999;24:61–100. [Google Scholar]
- Bower GH, Clark MC, Lesgold AM, Winzenz D. Hierarchical retrieval schemes in recall of categorized word lists. Journal of Verbal Learning and Verbal Behavior. 1969;8(3):323–343. [Google Scholar]
- Craik FIM, Tulving E. Depth of processing and the retention of words in episodic memory. Journal of Experimental Psychology: General. 1975;104(3):268–294. [Google Scholar]
- Chariker JH, Naaz F, Pani JR. Computer-based learning of neuroanatomy: A longitudinal study of learning, transfer, and retention. Journal of Educational Psychology. 2011;103(1):19–31. doi: 10.1037/a0021680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chariker JH, Naaz F, Pani JR. Item difficulty in the evaluation of computer-based instruction: An example from neuroanatomy. Anatomical Sciences Education. 2012;5(2):63–75. doi: 10.1002/ase.1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake RL, McBride JM, Lachman N, Pawlina W. Medical education in the anatomical sciences: The winds of change continue to blow. Anatomical Sciences Education. 2009;2:253–259. doi: 10.1002/ase.117. [DOI] [PubMed] [Google Scholar]
- Felten DL, Shetty AN. Netter’s atlas of neuroscience. 2nd ed. Philadelphia: Saunders/Elsevier; 2010. [Google Scholar]
- Frick RW. Accepting the null hypothesis. Memory & Cognition. 1995;23(1):132–138. doi: 10.3758/bf03210562. [DOI] [PubMed] [Google Scholar]
- Hegarty M. Dynamic visualizations and learning: Getting to the difficult questions. Learning and Instruction. 2004;14:343–351. [Google Scholar]
- Keehner M, Hegarty M, Cohen C, Khooshabeh P, Montello DR. Spatial reasoning with external visualizations: What matters is what you see, not whether you interact. Cognitive Science. 2008;32(7):1099–1132. doi: 10.1080/03640210801898177. [DOI] [PubMed] [Google Scholar]
- Kikinis R, Shenton ME, Iosifescu DV, McCarley RW, Saiviroonporn P, Hokama HH, Jolesz FA. A digital brain atlas for surgical planning, model driven segmentation and teaching. IEEE Transactions on Visualization and Computer Graphics. 1996;2:232–241. [Google Scholar]
- Koedinger KR, Corbett A. Cognitive tutors: Technology bringing learning sciences to the classroom. In: Sawyer RK, editor. The Cambridge handbook of the learning sciences. New York: Cambridge University Press; 2006. pp. 61–77. [Google Scholar]
- Kosslyn SM. Image and brain. Cambridge, MA: MIT Press; 1994. [Google Scholar]
- Levinson AJ, Weaver B, Garside S, McGinn H, Norman GR. Virtual reality and brain anatomy: A randomised trial of e-learning instructional designs. Medical Education. 2007;41(5):495–501. doi: 10.1111/j.1365-2929.2006.02694.x. [DOI] [PubMed] [Google Scholar]
- Liben LS, Kastens KA, Christensen AE. Spatial foundations of science education: The illustrative case of instruction on introductory geological concepts. Cognition and Instruction. 2011;29:45–87. [Google Scholar]
- Lufler RS, Zumwalt AC, Romney CA, Hoagland TM. Effect of visual–spatial ability on medical students’ performance in a gross anatomy course. Anatomical Sciences Education. 2012;5:3–9. doi: 10.1002/ase.264. [DOI] [PubMed] [Google Scholar]
- Mai JK, Paxinos G, Voss T. Atlas of the human brain. 3rd Edition. San Diego, CA: Academic Press; 2007. [Google Scholar]
- Mayer RE, editor. The Cambridge handbook of multimedia learning. New York: Cambridge University Press; 2005. [Google Scholar]
- Mayer RE, Hegarty M, Mayer S, Campbell J. When static media promote active learning: Annotated illustrations versus narrated animations in multimedia instruction. Journal of Experimental Psychology: Applied. 2005;11:256–265. doi: 10.1037/1076-898X.11.4.256. [DOI] [PubMed] [Google Scholar]
- Mervis CB, Klein-Tasman BP. Methodological issues in group-matching designs: Alpha levels for control variable comparisons and measurement characteristics of control and target variables. Journal of Autism and Developmental Disorders. 2004;34(1):7–17. doi: 10.1023/b:jadd.0000018069.69562.b8. [DOI] [PubMed] [Google Scholar]
- Nolte J, Angevine JB. The human brain in photographs and diagrams. 3rd ed. Philadephia: Mosby/Elsevier; 2007. [Google Scholar]
- Novick LR, Hurley SM. To matrix, network, or hierarchy: That is the question. Cognitive Psychology. 2001;42(2):158–216. doi: 10.1006/cogp.2000.0746. [DOI] [PubMed] [Google Scholar]
- Oh C-S, Kim J-Y, Choe YH. Learning of cross-sectional anatomy using clay models. Anatomical Sciences Education. 2009;2:156–159. doi: 10.1002/ase.92. [DOI] [PubMed] [Google Scholar]
- Pani JR, Chariker JH, Dawson TE, Johnson N. Acquiring new spatial intuitions: Learning to reason about rotations. Cognitive Psychology. 2005;51(4):285–333. doi: 10.1016/j.cogpsych.2005.06.002. [DOI] [PubMed] [Google Scholar]
- Pani JR, Chariker JH, Fell RD. Visual cognition in microscopy. In: Bara BG, Barsalou L, Bucciarelli M, editors. Proceedings of the 27th Annual Conference of the Cognitive Science Society; Cognitive Science Society. 2005. pp. 1702–1707. [Google Scholar]
- Pani JR, Chariker JH, Naaz F. Computer-based learning: Interleaving whole and sectional representation of neuroanatomy. Anatomical Sciences Education. 2013;6:11–18. doi: 10.1002/ase.1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds SJ. Virtual worlds, virtual field trips, and other virtual reality files. [Online] 2001 Retrieved from http://reynolds.asu.edu/virtual_reality.htm. [Google Scholar]
- Ruisoto P, Juanes JA, Contador I, Mayoral P, Prats-Galino A. Experimental evidence for improved neuroimaging interpretation using three-dimensional graphic models. Anatomical Sciences Education. 2012;5:132–137. doi: 10.1002/ase.1275. [DOI] [PubMed] [Google Scholar]
- Stevens A, Coupe P. Distortions in judged spatial relations. Cognitive Psychology. 1978;10:422–437. doi: 10.1016/0010-0285(78)90006-3. [DOI] [PubMed] [Google Scholar]
- Stull AT, Hegarty M, Dixon B, Stieff M. Representational translation with concrete models in organic chemistry. Cognition and Instruction. 2012;30:404–434. [Google Scholar]
- Stull AT, Hegarty M, Mayer RE. Getting a handle on learning anatomy with interactive three-dimensional graphics. Journal of Educational Psychology. 2009;101:803–816. [Google Scholar]
- Tulving E, Donaldson W. Organization of memory. New York: Academic Press; 1972. [Google Scholar]
- Tversky B. Distortions in memory for maps. Cognitive Psychology. 1981;13:407–433. [Google Scholar]
- Tversky B, Morrison JB, Betrancourt M. Animation: Can it facilitate? International Journal of Human Computer Studies. 2002;47:247–262. [Google Scholar]
- Uttal DH, Cohen CA. Ross BH, editor. Spatial thinking and STEM education: When, why, and how? Psychology of Learning and Motivation. 2012;Vol. 57:147–181. [Google Scholar]
- Wechsler D. Wechsler memory scale. 4th ed. San Antonio, Texas: Pearson Education, Inc.; 2009. [Google Scholar]