Simplification of Reversible Markov Chains by Removal of States With Low Equilibrium Occupancy

Abstract

We present a practical method for simplifying Markov chains on a potentially large state space when detailed balance holds. A simple and transparent technique is introduced to remove states with low equilibrium occupancy. The resulting system has fewer parameters. The resulting effective rates between the remaining nodes give dynamics identical to the original system’s except on very fast timescales. This procedure amounts to using separation of timescales to neglect small capacitance nodes in a network of resistors and capacitors. We illustrate the technique by simplifying various reaction networks, including transforming an acyclic four-node network to a three-node cyclic network. For a reaction step in which a ligand binds, the law of mass action implies a forward rate proportional to ligand concentration. The effective rates in the simplified network are found to be rational functions of ligand concentration.

1. Introduction

Markov chain models (MCM) have numerous important applications in biology, chemistry, computer science, and engineering systems (Norris, 1997). In biology for example, Markov models have contributed a great deal towards understanding the function and structure of ion channels, enzymes, ligand-binding proteins, and population process. A common problem with Markov chains is the large state space that these models span in many applications. State aggregation is perhaps the most straight forward way to deal with such large chains when some sets of states can be treated as indistinguishable (Stewart, 1991; Deng et al., 2009). Spectral methods have become popular for aggregating states and model simplification (Huisinga et al., 2004). However, the requirement to compute eigenvectors of the Markov transition matrix for a large dimensional space makes spectral methods hard to implement, and results in a complex mapping between the original states and the resulting aggregated states. This motivates a simpler method for model simplification, the subject in this paper.

In many cases, Markov chains contain states that have relatively low probability of being occupied, but may serve as important transition gateways between high occupancy states. We show that it is possible to simplify these models so that low-occupancy states do not appear in the simplified chain, but their effect is included in the model. The elimination of the low occupancy states affects the rates between the remaining states. This reduction can yield complicated reaction rates that reflect the physics of the eliminated states. For example, it can introduce non-trivial ligand dependence into the rates of the reduced model.

Understanding this class of simplified models can be important for interpreting results of fitting data with Markov chains. Colquhoun has argued that one should never fit data to the Hill equation (defined below) because it represents a “physical impossibility” (Colquhoun, 2006), in that integer Hill coefficients greater than unity suggest simultaneous binding of multiple ligands, with no intermediate steps. We agree that there is no physical justification for a priori fits to the usual Hill equation, but we show that the Hill equation with any positive integer coefficient does represent a physical situation. It might happen that the statistical best fit (based on, for example, the AIC (Akaike, 1974) or BIC (Schwarz, 1978) criteria which penalize for overfitting) of the ligand dependent probability of occupancy, p, of some state of interest yields a Hill equation with coefficient four: p = d L⁴/(1 + d L⁴) where L is the concentration of the ligand. Uncovering such a Hill equation does not imply that four ligands bind simultaneously. Rather we will show that it implies the intervening states with 1 – 3 ligands bound have relatively low occupancy compared to the states with 0 and 4 ligands bound. That is, although the “true” occupancy might be given by p = dL⁴/(1 + aL + bL² + cL³ + dL⁴) it can happen that using nonzero values for a, b, and c does not improve the statistical quality of the fit. Colquhoun did not address the question of how to proceed if one uncovers a Hill equation during the fitting process but we suspect he would agree that one ought not to introduce parameters for which there is no statistical evidence (such as a, b, c).

This raises a question. If a Hill equation with a Hill coefficient greater than one is found to provide the statistical best fit for the ligand concentration dependence of the equilibrium occupancy of some observable state, what ligand dependent rates should be used to connect the unbound and fully bound states? A maximum likelihood fit to time series data keeping all the states will be found to have neutral directions in the space of parameters because the model is over-parameterized relative to what the experimental data can constrain. One might try to resolve the issue experimentally by collecting more data, but this will likely be time-consuming, expensive, and not practicable. The low-occupancy states can add unnecessary complexity to Markov models. However, completely ignoring the low occupancy states is not appropriate either as they can introduce non-trivial ligand dependence for the experimentally inferred rates. The ligand dependence of the rates can provide crucial insight into the structure and function of the system under consideration. In essence we are disgarding processes with fast time scales. The mathematics of “multi-scale” methods goes back at least to the late 19th century (Lindstedt, 1882). The purpose of the current manuscript is simply to point out that for reversible Markov chains a nonstandard parameterization renders the elimination of the fast processes trivial. We show that in many cases, it is easy to write down the correct ligand-dependent rates, essentially by inspection.

The rest of this paper is organized as follows. In the next section, we discuss detailed balance and reversible Markov chains and show how to simplify a 3 state reversible Markov chain with a low occupancy state to a two state Markov chain. We also discuss the energy landscape of the full and simplified chains. We then show that reversible Markov chains are equivalent to resistor-capacitor networks, and that our simplification amounts to neglecting small capacitances. We show how to construct the equivalent circuit for the general problem using a known result from circuit theory. In section “Examples” we work through several cases that we think ought to be of general interest, one a linear 5-state chain which runs from 0 to 4 ligands bound, a chain with multiple ligands dependence, the simplification of a 4 state model with no cycles to a 3 state model connected in a loop, and finally the well-studied Monod, Wyman, and Changeux (hereafter referred to as MWC) model (Monod et al., 1965) in the Hill equation limit. We simplify the MWC model to a two state chain and compare the distribution of first passage times to go from one high occupancy state to another in both the full model and in the simplified 2-state model. The approximation is singular; at any finite time the probability of making the transition converges for the two models but for infinitesimal times the distributions do not converge. The details of these calculations are addressed in the Appendices. Finally, we summarize the main findings of the paper in the conclusions section.

2. Reversible Markov Chains

Finite state Markov chains obey an evolution equation of the form:

$$\frac{dp}{dt}=pQ$$ (1)

where p is a vector with p_i(t) being the probability that state i is occupied at time t. The generator matrix Q contains the transition rates from state i to state j. The diagonal entries of Q satisfy Q_ii = −Σ_j≠i Q_ij. We assume that there is a unique equilibrium vector of steady state occupancies, w which satisfies:

$$wQ=0.$$ (2)

Note also that the vector containing all ones, which we denote by u, satisfies Qu = 0. Our primary goal in the present work is to show how to construct an approximate chain to the “true chain” that obeys an evolution equation:

$$\frac{d\stackrel{\sim }{p}}{dt}=\stackrel{\sim }{p}\stackrel{\sim }{Q}$$ (3)

where p̃ and Q̃ are the reduced probability vectors and generator matrices. This is straightforward for reversible Markov chains in the case that some of the states have very low equilibrium probabilities (or occupancies). In particular we will show that reduced generator, Q̃ can be constructed using known methods from circuit theory.

In this work we are considering only the important special case of chains which obey “detailed balance” or microscopic reversibility, also known as “reversible” chains. If one starts from an arbitrary rate matrix and tries to impose this condition loop by loop, detailed balance seems to introduce great complexity. Detailed balance reflects time reversal symmetry, and if the system is expressed in a way that manifestly satisfies detailed balance (Yang et al., 2006; Fredkin et al., 1985; Kolmogorov, 1936; Onsager, 1931) then the equations become simpler rather than more complex. A chain is reversible if and only if w_iQ_ij = w_jQ_ji for all i, j. We define a diagonal matrix W by

$$W_{ii}=w_i$$ (4)

in terms of which the reversible condition can be written WQ = (WQ)^T.

The matrix WQ gives the directional probability flux at equilibrium from state i to state j, by which we mean the equilibrium occupancy of state i times the rate from state i to j. For example for the two state chain $A\underset{k_r}{\overset{k_f}{\rightleftharpoons }}B,W=\frac{1}{Z}\left(\begin{array}{cc}{w}_A& 0\\ 0& w_B\end{array}\right)$, where w_A = 1 and w_B = k_f /k_r are the unnormalized occupancies of states A and B relative to A. Z = w_A + w_B and $Q=\left(\begin{array}{cc}-k_f& k_f\\ k_r& -k_r\end{array}\right)$ so that $WQ=\frac{1}{Z}\left(\begin{array}{cc}-k_f& k_f\\ k_f& -k_f\end{array}\right)$. At equilibrium, there are equal and opposite fluxes of magnitude k_f /Z between the two states.

2.1. Equilibrium Flux

Because of its fundamental importance we denote the symmetric matrix WQ by

$$J\equiv WQ$$ (5)

where J_ij (i ≠ j) is the equilibrium flux of probability between states i and j and J_ii = −Σ_j≠iJ_ij.

In the remainder of this paper we use “state occupancy” and “equilibrium flux” parameters to parameterize the Markov chain as suggested in (Yang et al., 2006) instead of reaction rates. The two approaches are mathematically equivalent but the occupancy-equilibrium flux parameter approach automatically satisfies detailed balance and is more intuitive because it separates thermodynamic quantities (equilibrium occupancies, or state energies) from kinetic quantities (equilibrium reaction fluxes, or transition state energies). Thus we can write:

$$Q=W^{-1}J$$ (6)

so that Eq. (1) can be written:

$$\frac{dp}{dt}={pW}^{-1}J.$$ (7)

We will see that states for which the occupancy is very low can be eliminated by taking the limit w_i → 0 while maintaining finite fluxes through state i.

2.2. Reduction of a 3 state chain to 2 states and the energy landscape

To explain our approach, we reduce the following 3-state chain to a 2-state chain by discussing the energy landscape of this reaction.

$$A\underset{k_{BA}}{\overset{k_{AB}}{\rightleftharpoons }}B\underset{k_{CB}}{\overset{k_{BC}}{\rightleftharpoons }}C$$ (8)

where k_AB is the reaction rate from state A to state B, etc. If the occupancy of B is vanishingly small, one would expect that replacing the full chain by an effective chain:

$$A\underset{k_{CA}}{\overset{k_{AC}}{\rightleftharpoons }}C$$ (9)

with effective rates should be legitimate on time scales long compared to the equilibration of the B state. In the low occupancy limit¹, the rates out of B become fast and the B equilibration time goes to zero. As the limit is approached, the time spent in B becomes negligible compared to the mean time to go between A and C. If the effective chain is to approximate the full chain, the mean times to make the transitions from A to C and C to A should agree in the two chains.

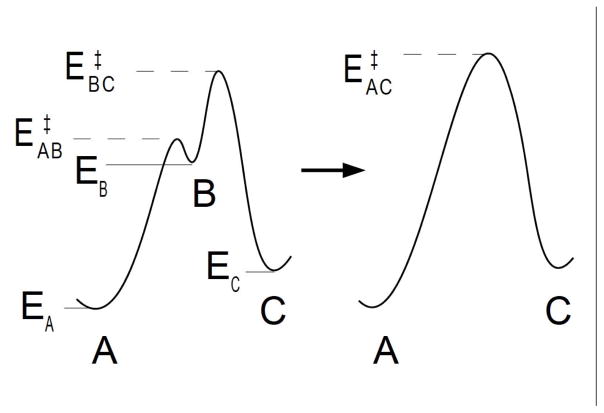
Energetically, low occupancy states are local minima high in the energy landscape. In Figure 1 we show the energy landscape corresponding to the reaction given by equation 8. Our parameterization does not require Arrhenius temperature dependence for the reaction rates but Arrhenius kinetics allows for a more intuitive understanding of the equilibrium flux/occupancy parameterization. We write:

$$\begin{array}{l}{k}_{AB}=k_0{e}^{-\frac{(E_{AB}^{‡}-E_A)}{k_{B}T}}\\ k_{BA}=k_0{e}^{-\frac{(E_{AB}^{‡}-E_B)}{k_{B}T}}\\ k_{BC}=k_0{e}^{-\frac{(E_{BC}^{‡}-E_B)}{k_{B}T}}\\ k_{CB}=k_0{e}^{-\frac{(E_{BC}^{‡}-E_C)}{k_{B}T}}\end{array}$$

for the rates where k_B is Boltzmann’s constant and T is the absolute temperature. The energy E_A is the energy of state A etc. The energy $E_{AB}^{‡}$ is the energy of the unstable transition state between A and B (which can be defined as the state with maximum energy state along the most probable trajectory connecting A with B, as illustrated in Figure 1). The rate, k₀, is the number of attempts to cross a barrier per unit time. For simplicity, we take this to be the same for all reactions, but differences could be absorbed into the transition state energies.

Figure 1.

Removal of a low-occupancy, high-energy intermediate state. The middle state has high energy and therefore low equilibrium occupancy. The double barrier is replaced by a single, slightly taller barrier (taller by an energy ranging from nearly zero to ln(2) * k_BT). This results in a very good approximation to the dynamics, if the intermediate state occupancy is low and its relaxation dynamics are fast (barriers not too high) compared to the timescales of interest.

Denoting the flux at equilibrium from A to B by J_AB etc., and the occupancies for state A, B, and C, by w_A = e^{−E_A/(k_BT)}/Z, etc., with Z = e^{−E_A/(k_BT)}+e^{−E_B/(k_BT)}+ e^{−E_C/(k_BT)} we have:

$$\begin{array}{l}{J}_{AB}=w_A{k}_0{e}^{-\frac{(E_{AB}^{‡}-E_A)}{k_{B}T}}=\frac{k_0}{Z}{e}^{-\frac{E_{AB}^{‡}}{k_{B}T}}\\ J_{BA}=w_B{k}_0{e}^{-\frac{(E_{AB}^{‡}-E_B)}{k_{B}T}}=\frac{k_0}{Z}{e}^{-\frac{E_{AB}^{‡}}{k_{B}T}}\\ J_{BC}=w_B{k}_0{e}^{-\frac{(E_{BC}^{‡}-E_B)}{k_{B}T}}=\frac{k_0}{Z}{e}^{-\frac{E_{BC}^{‡}}{k_{B}T}}\\ J_{CB}=w_C{k}_0{e}^{-\frac{(E_{BC}^{‡}-E_C)}{k_{B}T}}=\frac{k_0}{Z}{e}^{-\frac{E_{BC}^{‡}}{k_{B}T}}\end{array}$$

for the fluxes. The fluxes are confirmed to be symmetric: J_AB = J_BA, J_BC = J_CB, which shows that Arrhenius kinetics on an energy landscape obey detailed balance, as expected. The generator matrix is:

$$Q=W^{-1}J=\left(\begin{array}{ccc}{e}^{\frac{E_A}{k_{B}T}}& 0& 0\\ 0& e^{\frac{E_B}{k_{B}T}}& 0\\ 0& 0& e^{\frac{E_C}{k_{B}T}}\end{array}\right)\left(\begin{array}{ccc}-e^{-\frac{E_{AB}^{‡}}{k_{B}T}}& e^{-\frac{E_{AB}^{‡}}{k_{B}T}}& 0\\ e^{-\frac{E_{AB}^{‡}}{k_{B}T}}& -e^{-\frac{E_{AB}^{‡}}{k_{B}T}}-e^{-\frac{E_{BC}^{‡}}{k_{B}T}}& e^{-\frac{E_{BC}^{‡}}{k_{B}T}}\\ 0& -e^{-\frac{E_{BC}^{‡}}{k_{B}T}}& e^{-\frac{E_{BC}^{‡}}{k_{B}T}}\end{array}\right)k_0.$$ (10)

Note the separation between thermodynamic quantities (E_A,E_B,E_C) and kinetic ones (k₀ and transition state energies). The generator matrix for other topologies takes this same general form, with the inverse occupancy of state i being proportional to e^E_i/(k_BT) and the flux between states i and j being proportional to $e^{-E_{ij}^{‡}/(k_{B}T)}$. The exact mean first passage time to go from A to C, τ_AC, is given by (Fredkin et al., 1985):

$${\tau }_{AC}^{\mathit{exact}}=-(1,0)·Q_{\mathcal{A}\mathcal{A}}^{-1}{u}_{\mathcal{A}}$$

where 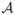represents the two states A and B aggregated together, and Q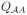_A denotes that part of Q that connects states within 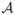to each other (in this case 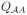is the first two columns of the first two rows of Q), so that:

$$Q_{\mathcal{A}\mathcal{A}}=k_0\left(\begin{array}{cc}\frac{1}{w_A}& 0\\ 0& \frac{1}{w_B}\end{array}\right)\left(\begin{array}{cc}-e^{-\frac{E_{AB}^{‡}}{k_{B}T}}& e^{-\frac{E_{AB}^{‡}}{k_{B}T}}\\ e^{-\frac{E_{AB}^{‡}}{k_{B}T}}& -e^{-\frac{E_{AB}^{‡}}{k_{B}T}}-e^{-\frac{E_{BC}^{‡}}{k_{B}T}}\end{array}\right)$$ (11)

and 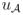= (1, 1)T is just u confined to the subspace 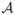, and (1, 0) is the initial state. So,

$${\tau }_{AC}^{\mathit{exact}}=\frac{1}{k_0}\left(\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)e^{-\frac{E_A}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}{e}^{-\frac{E_B}{k_{B}T}}\right).$$ (12)

Similarly, the exact mean time to go from C to A, τ_CA is given by:

$${\tau }_{CA}^{\mathit{exact}}=\frac{1}{k_0}\left(\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)e^{-\frac{E_C}{k_{B}T}}+e^{\frac{E_{AB}^{‡}}{k_{B}T}}{e}^{-\frac{E_B}{k_{B}T}}\right)$$ (13)

The low occupancy limit (of the B state) obtains when E_B − E_A ≫ k_BT and E_B − E_C ≫ k_BT. In this case, the mean times to go from A to C and C to A simplify to:

$${\tau }_{AC}\approx \frac{1}{k_0}\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)e^{-\frac{E_A}{k_{B}T}}$$ (14)

$${\tau }_{CA}\approx \frac{1}{k_0}\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)e^{-\frac{E_C}{k_{B}T}}.$$ (15)

These are the approximate mean transition times. Thus we define effective (approximate) rates

$$k_{AC}\equiv \frac{1}{{\tau }_{AC}}\approx k_0{e}^{\frac{E_A}{k_{B}T}}{\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)}^{-1}={\left(\frac{1}{k_{AB}}+\frac{e^{(\frac{E_B-E_A}{k_{B}T})}}{k_{BC}}\right)}^{-1}$$ (16)

$$k_{CA}\equiv \frac{1}{{\tau }_{CA}}\approx k_0{e}^{\frac{E_C}{k_{B}T}}{\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)}^{-1}={\left(\frac{1}{k_{CB}}+\frac{e^{(\frac{E_B-E_C}{k_{B}T})}}{k_{BA}}\right)}^{-1}.$$ (17)

and effective fluxes:

$$J_{AC}\equiv w_A{k}_{AC}=w_A{k}_0{e}^{\frac{E_A}{k_{B}T}}{\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)}^{-1}=\frac{k_0}{Z}{\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)}^{-1}.$$ (18)

Note that

$$J_{AC}={(J_{AB}^{-1}+J_{BC}^{-1})}^{-1}$$ (19)

This is an important general result that applies whenever a low occupancy state connects to only two other states, as will become clear in section “Reversible Chains are Equivalent to RC networks”. We can interpret equation 18 in terms of an effective barrier height between states A and C, $E_{AC}^{‡}$, such that:

$$J_{AC}=\frac{k_0}{Z}{e}^{-\frac{E_{AC}^{‡}}{k_{B}T}}\equiv \frac{k_0}{Z}{\left(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}}\right)}^{-1}$$ (20)

by defining

$$E_{AC}^{‡}=E_{BC}+k_{B}Tlog(1+e^{-\frac{E_{BC}^{‡}-E_{AB}^{‡}}{k_{B}T}})$$ (21)

which simplifies in two limits. If $\frac{E_{BC}^{‡}-E_{AB}^{‡}}{k_{B}T}\gg 1$ then $E_{AC}^{‡}\approx E_{BC}^{‡}$ to good approximation. In words, this limit simply means that if the difference in the barrier heights $E_{AB}^{‡}$ and $E_{BC}^{‡}$ is large compared to k_BT, then the presence of the lower barrier has negligible effect.

The other simplifying limit is when $\frac{E_{BC}^{‡}-E_{AB}^{‡}}{k_{B}T}\approx 0$ in which case we find $E_{AC}^{‡}\approx E_{BC}^{‡}+k_{B}Tlog(2)$ which at first glance might not appear particularly intuitive. However, noting that the effective flux is written: $J_{AC}=\frac{k_0}{Z}{e}^{-\frac{E_{AC}^{‡}}{k_{B}T}}\approx \frac{k_0}{2Z}{e}^{-\frac{E_{BC}^{‡}}{k_{B}T}}$ we find that $J_{AC}=\frac{1}{2}{J}_{BC}\approx \frac{1}{2}{J}_{AB}$ which says that the fluxes from A to B and from B to C are equal, and the effective flux from A to C is half as much. The mean number of A–B transitions the system makes while transitioning from A to C is 2 in this case because once the sytem is in B it has equal odds of hopping to A or C.

The exact distribution of first passage times to go from A to C, f(t) can be shown to be:

$$f^{\mathit{exact}}(t)=-(1,0)e^{Q_{\mathcal{A}\mathcal{A}}t}{Q}_{\mathcal{A}\mathcal{A}}{u}_{\mathcal{A}}=\frac{e^{-{\lambda }_{s}t}-e^{-{\lambda }_{f}t}}{\frac{1}{{\lambda }_s}-\frac{1}{{\lambda }_f}}$$ (22)

for small w_B the fast and slow decays (λ_f and λ_s respectively) are given by: ${\lambda }_s\approx \frac{{Zk}_0}{w_A}{(e^{\frac{E_{AB}^{‡}}{k_{B}T}}+e^{\frac{E_{BC}^{‡}}{k_{B}T}})}^{-1}$ and ${\lambda }_f\approx \frac{k_{0}Z}{w_B}(e^{-\frac{E_{AB}^{‡}}{k_{B}T}}+e^{-\frac{E_{BC}^{‡}}{k_{B}T}})$. Note that as w_B → 0 we have λ_s → k_AC and λ_f ~ ∞. At t = 0 the exact distribution function is identically zero:f ^exact(0) = 0 while the approximate distribution function, k_ACe^−k_ACt is simply k_AC at t = 0. At any finite time the exact and approximate distributions converge as w_B → 0.

2.3. Reversible Chains are Equivalent to RC networks

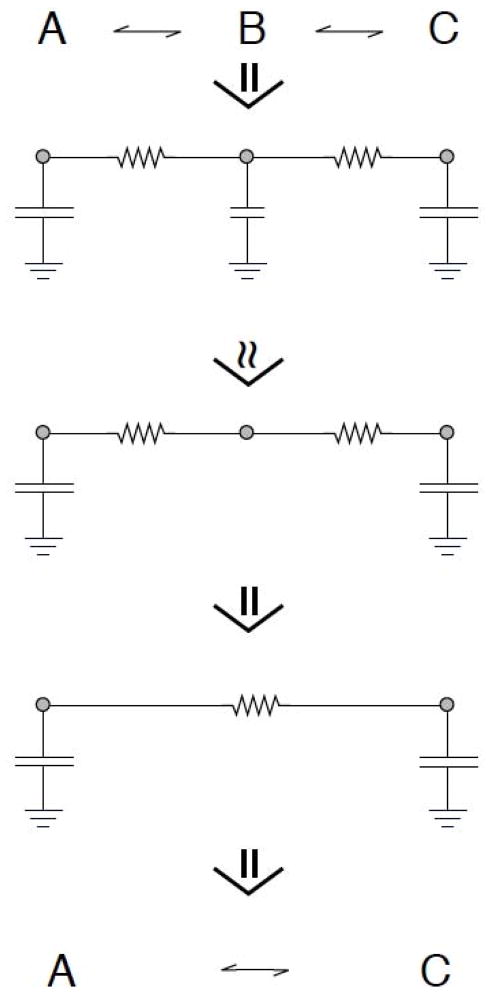
Equation 7 is formally equivalent to Kirchoff’s law for an RC circuit in which a collection of capacitors are connected to ground on one side and to each other via a network of resistors on the other side with p_i the charge on the i^th capacitor which has capacitance w_i and J_ij is the conductivity between the i^th and j^th nodes (which is symmetric) (Figure 2). The condition J_ii = −Σ_j≠i J_ij is Kirchoff’s junction rule which states that the sum of the currents into a node must be zero. Detailed balance follows from the fact that the conductivity of a passive resistor is the same in either direction which follows from Ohm’s law. At steady state no current flows in an RC circuit. The voltage across the i^th capacitor is q_i/C_i where q_i is the charge on the i^th capacitor (which has capacitance C_i). As an initial charge distribution relaxes to equilibrium, current flows until the voltage across each capacitor is the same. This voltage is the total charge ( 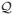) over the total capacitance ( 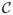), 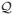/C which we take to be one volt. The analog to voltage in the Markov case is p_i/w_i. The energy stored in the capacitors initially is $1/2{\sum }_i{q}_i{V}_i=1/2{\sum }_i{q}_i^2/C_i$. As time goes by this is dissipated via joule heating in the resistors until it reaches 1/2 Σ_i qi ×1 volt = 1/2 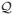× 1 volt. In the Markov case with initial probability p_i for being in the i^th state, the “energy” is initially $1/2{\sum }_i{p}_i^2/w_i$ which dissipates until it reaches $1/2{\sum }_i{w}_i^2/w_i=1/2{\sum }_i{w}_i=1/2$. In the Markov case, as an initial probability distribution relaxes to equilibrium, probability flows until the “voltage” for each state is unity. Note that, provided all the capacitors in the RC network are actually connected, the final charge distribution is independent of the network. For the Markov case, the final probability distribution is independent of the network. One cannot use equilibrium probability distributions to infer the network and one cannot use the final charge distribution to infer the connectivity of the capacitors. Just as information on the time dependent flow of charge is required to make inferences regarding the resistor network, information on the time dependent flow of probability is required to make inferences regarding the connectivity of reversible Markov chains.

Figure 2.

RC circuit analogy of a 3-state Markov chain. The states and probability fluxes are represented by nodes and resistors respectively. The simplification of 3-state model to a 2-state model is equivalent to replacing the two resistors by a single resistor which has an effective conductance of both resistors.

The crux of this paper is that small capacitors (small occupancies) can be neglected. Any node that has a very small capacitance can be removed from the network. After these capacitors are removed, the low capacitance nodes can be removed by connecting the remaining nodes with resistors having the correct resistances. Equation 19 is a corollary based on the fact that the resistances of resistors in series add. I.e., the inverse of the effective flux through a linear chain is just the sum of the inverse node to node fluxes along the chain, since flux is analogous to electrical conductance (or inverse resistance). Another corollary is that for parallel paths the fluxes add, just as conductances do for parallel resistors. Although this approximation may cause large errors on very short timescales, the duration of the errors is often so short as not to be noticed. For example, any connection between two resistors can hold some tiny amount of charge and therefore has some capacitance relative to ground. Yet, formulas for adding resistors in series or parallel are taught without concern for the violations that must be present on very short time scales.

We will see later that the flux matrix, J̃ for the simplified chain (equation 3) can easily be constructed by a series of “Y − Δ” transformations that have been used in circuit theory since the late 19th century (Kennelly, 1899; Akers Jr, 1960; Knudsen and Fazekas, 2006; Van Lier and Otten, 1973). The resulting network can then be simplified so that some links are replaced by combinations of rates (or flux parameters). With the states ordered so that the high occupancy ones come first followed by the low occupancy ones the reduction can be achieved by the following sequence of transformations which in essence removes the low occupancy states one state at a time (the transformations will be explained further with examples in section 3.2).

$${\stackrel{\sim }{J}}_{ij}^k=({\stackrel{\sim }{J}}_{ij}^{k-1}+{\stackrel{\sim }{J}}_{i{t}_k}^{k-1}{BF}_{{jt}_k}^{k-1})\text{for}i\ne j;i,j=1,2,\dots ,t_k-1$$ (23)

$${BF}_{{jt}_k}^{k-1}=\frac{{\stackrel{\sim }{J}}_{{jt}_k}^{k-1}}{{\sum }_{m\ne t_k}{\stackrel{\sim }{J}}_{m{t}_k}^{k-1}}$$ (24)

$$t_k=n_{\mathit{low}}+n_{\mathit{high}}-k+1$$ (25)

$$k=1,2,\dots n_{\mathit{low}}$$ (26)

$$\stackrel{\sim }{J}={\stackrel{\sim }{J}}^{n_{\mathit{low}}}$$ (27)

where n_low is the number of low occupancy states, n_high is the number of high occupancy states, and J̃⁰ = J. The diagonal entries at any point in the sequence are of course given by ${\stackrel{\sim }{J}}_{ii}^{k-1}=-{\sum }_{j\ne i}{\stackrel{\sim }{J}}_{ij}^{k-1}$. In the preceding, t_k indexes the low occupancy states. The quantity ${BF}_{{jt}_k}^{k-1}$ is the “branching fraction” and denotes the fractional flux between state j and the low occupancy state t_k. In essence this transformation removes each low occupancy node one at a time and interconnects all the states that were previously linked to the removed node. If the high occupancy states are renormalized so that w̃_i = w_i/z̃ with z̃ set by the normalization condition: ${\sum }_{i=1}^{n_{\mathit{high}}}{\stackrel{\sim }{w}}_i=1$, the transformed flux matrix must also be renormalized J̃ → J̃/z̃. Finally the reduced system obeys:

$$\frac{d\stackrel{\sim }{p}}{dt}=\stackrel{\sim }{p}{\stackrel{\sim }{W}}^{-1}\stackrel{\sim }{J}$$ (28)

A Mathematica program that performs this reduction on random flux matrices is in the online supplement. While the reaction steps in the original process can be considered as “elementary”, the reaction rates in the reduced process are not elementary. Consequently, the reduction procedure can give complicated ligand dependence for reaction rates between the remaining states. For example, in the full model discussed in section 3.1 (equation 29), the transition rates from E₄ to S₀ along the chain are ligand independent. However the effective rate from E₄ to S₀ in the reduced 2 states system is ligand dependent.

3. Examples

In this section we perform 3 simplifications on models that we think might be of general interest. We begin by discussing a 5 state linear chain in which the states have 0, 1, 2…4 ligands bound but only the unliganded and quadruply liganded states have high occupancy. We then consider the MWC model for a tetrameric molecule which binds ligand. We consider the MWC model in the Hill limit, for which only the states with 0 and 4 ligands bound have high occupancy. Finally we consider a 4 state acyclic model in which three states are all connected to the same low occupancy state. The resulting 3 state model has a cycle but still automatically obeys detailed balance.

3.1. A linear chain

Here we consider the following chain:

$$S_0\underset{j_{01}L/K_{1}L}{\overset{j_{01}L/K_0}{\rightleftharpoons }}{t}_1\underset{j_{12}{L}^2/K_2{L}^2}{\overset{j_{12}{L}^2/K_{1}L}{\rightleftharpoons }}{t}_2\underset{j_{23}{L}^3/K_3{L}^3}{\overset{j_{23}{L}^3/K_2{L}^2}{\rightleftharpoons }}{t}_3\underset{j_{34}{L}^4/K_4{L}^4}{\overset{j_{34}{L}^4/K_3{L}^3}{\rightleftharpoons }}{E}_4.$$ (29)

As shown in (Yang et al., 2006), we have written the rate from state X_l to X_m equal to the ratio of flux between X_l and X_m and occupancy of X_l where l and m is the number of ligands bound in X_l and X_m respectively. The (unnormalized) flux between states X_l and X_m is j_lmL^max(l,m) and the (unnormalized) occupancy of state X_l is written as K_lL^l. Only energy differences are relevant, so we can give unit unnormalized occupancy to the unliganded state, S₀ (i.e. K₀ = 1). Denoting the normalized occupancies of state X_l by w_l, we have w_l = K_lL^l/Z with Z = 1 + K₁L + K₂L² + K₃L³ + K₄L⁴. If the occupancies of the intermediate states, t₁, t₂, and t₃ are negligible compared to max(w₀, w₄), then the mean times to go from S₀ to E₄, τ_S0E4, and back, τ_E4S0 are given by:

$$\begin{array}{l}{\tau }_{S_0{E}_4}=\frac{1}{j_{01}L}+\frac{1}{j_{12}{L}^2}+\frac{1}{j_{23}{L}^3}+\frac{1}{j_{34}{L}^4}\\ {\tau }_{E_4{S}_0}=K_4{L}^4(\frac{1}{j_{01}L}+\frac{1}{j_{12}{L}^2}+\frac{1}{j_{23}{L}^3}+\frac{1}{j_{34}{L}^4})\end{array}$$

Details of reaching these expressions using generator matrix theory are given in Appendix A. In Appendix B, we demonstrate the simplification of an example where the states have binding sites for multiple ligands.

3.2. Reduction of an Acyclic Model to a Cyclic Model: Application of the “Y − Δ” Transformation

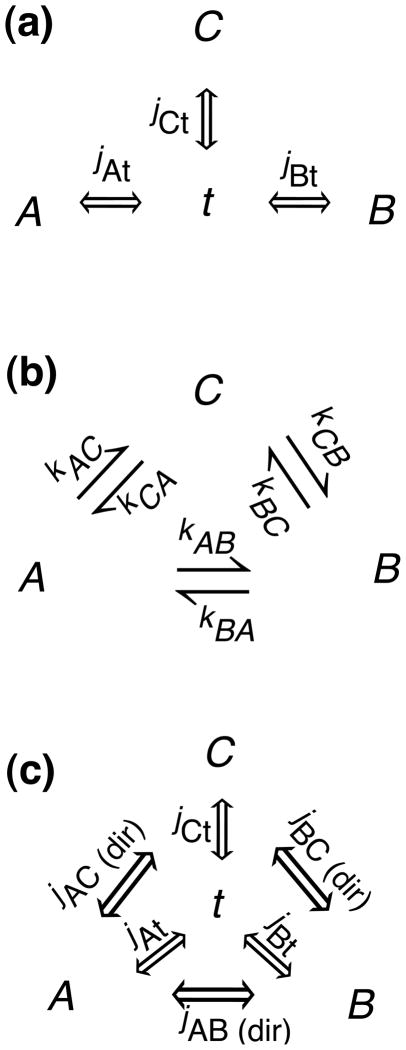
Next, we consider the case where the chain has more than one branch. An example of such case is shown in Figure 3a. If the state labeled “t” represents a low-occupancy state then the system can be simplified to the chain shown in Figure 3b via the “Y − Δ” transformation discussed in section 2.3. We denote the (unnormalized) occupancies of the states (A, B, C) by K_A, K_B, K_C respectively. The effective probability flux from A to B, J_AB, is the product of probability flux from A to t, J_At, and the fractional probability flux flowing from t to B (see equation 23). Notice that there are no direct fluxes between the high occupancy states in the full scheme (Figure 3a) therefore, the first term on the right hand side of equation 23 is zero. Thus, the effective fluxes between high occupancy states, A, B, and C are given by:

$$J_{MN}=J_{Mt}\times B{F}_{Nt}$$ (30)

where M, N = A, B, and C. The branching fraction of probability flux from state N to t given by equation 24 is $B{F}_{Nt}=\frac{J_{Nt}}{{\sum }_i{J}_{it}}$, i = A, B, and C. The denominator in BF_Nt is the total probability flux out of t.

Figure 3.

Simplification of acyclic to cyclic chain. (a) Full scheme with three high occupancy states, A, B, and C and one low occupancy state, t. (b) Simplified three state scheme after aggregation. (c) An example of modified “Y” chain where there are direct links between high occupancy states in addition to the links through low occupancy state. j_MN and k_MN stand for the flux parameter and transition rate between states M and N respectively. J_MN(dir) in panel (c) represents the direct flux between high occupancy states M and N.

The effective rates from M to N (with M ≠ N), k_MN, are given by: $k_{MN}=\frac{J_{Mt}{J}_{Nt}}{K_M{\sum }_i{J}_{it}}$. For example in Figure 3b,

$$k_{AB}=\frac{J_{At}{J}_{Bt}}{K_A{\sum }_i{J}_{it}}={\left(\frac{1}{k_{Bt}}\frac{K_A}{K_B}+\frac{1}{k_{At}}+\frac{1}{k_{At}}\frac{k_{Ct}}{k_{Bt}}\frac{K_C}{K_B}\right)}^{-1}$$ (31)

The reader can check that detailed balance is satisfied.

In situations where the high occupancy states in the “Y” chain are linked directly in addition to the links through the low occupancy state (see Figure 3c for an example), the first term on the right hand side of equation 23 is non-zero (Akers Jr, 1960; Knudsen and Fazekas, 2006; Van Lier and Otten, 1973). For example, the effective flux between the high occupancy states after simplifying the chain in Figure 3c to a “Δ” loop is given by

$$J_{MN}=J_{MN(\mathit{dir})}+\frac{J_{Mt}{J}_{Nt}}{{\sum }_i{J}_{it}}$$ (32)

where J_MN(dir) is the probability flux for the direct link between high occupancy states M and N.

Any complex network can be reduced by applying equation 23 to all branches involving low occupancy states. The simplification would result in a fully connected (△, □, , , .....) loop depending on the number of high occupancy states (3, 4, 5, 6, .....) in the original (Y, X, , , .....) branch. Each state in the resultant loop would be directly connected to all other states.

3.3. The Tetrameric MWC Model

The MWC model was developed by Monod, Wyman, and Changeux as a model for allostery in hemoglobin (Monod et al., 1965). For historical continuity we use the original MWC notation except that we use L for ligand concentration (instead of their F) and Λ (instead of their L) for the occupancy of the “tense” state, T₀, relative to the “relaxed” state R₀. The original MWC model considered only thermodynamics, not kinetics, so we must make a few assumptions regarding the dynamics. For the usual tetrameric case, we write the MWC model as follows:

$$\begin{array}{ccc}{R}_0& \underset{j_{rt}}{\overset{j_{rt}\mathrm{\Lambda }}{\rightleftharpoons }}& T_0\\ j_{rr}⥮j_{rr}\frac{4L}{K_R}& & j_{tt}⥮j_{tt}\frac{4L}{K_T}\\ R_1& \underset{j_{rt}}{\overset{j_{rt}\mathrm{\Lambda }c}{\rightleftharpoons }}& T_1\\ 2j_{rr}⥮j_{rr}\frac{3L}{K_R}& & 2j_{tt}⥮j_{tt}\frac{3L}{K_T}\\ R_2& \underset{j_{rt}}{\overset{j_{rt}\mathrm{\Lambda }{c}^2}{\rightleftharpoons }}& T_2\\ 3j_{rr}⥮j_{rr}\frac{2L}{K_R}& & 3j_{tt}⥮j_{tt}\frac{2L}{K_T}\\ R_3& \underset{j_{rt}}{\overset{j_{rt}\mathrm{\Lambda }{c}^3}{\rightleftharpoons }}& T_3\\ 4j_{rr}⥮j_{rr}\frac{L}{K_R}& & 4j_{tt}⥮j_{tt}\frac{L}{K_T}\\ R_4& \underset{j_{rt}}{\overset{j_{rt}\mathrm{\Lambda }{c}^4}{\rightleftharpoons }}& T_4.\end{array}$$

As in MWC K_R and K_T are the dissociation constants for ligand unbinding from the relaxed and tense monomers and c = K_R/K_T. The flux parameters, j_tt, j_rr, and j_rt, set the rates of tense-tense, relaxed-relaxed, and tense-relaxed transitions respectively. MWC did not discuss dynamics but only equilibrium and so had need for equilibrium constants but not for flux parameters, or equivalently, reaction rates. MWC did not specify whether there are transitions between R_i and T_i present for states i > 0. We assume there are such links. For simplicity, we use a single flux parameter j_rt for all R_i to T_i transitions. Relaxing the previous assumption has little effect. Similarly we use the same flux parameters j_rr and j_tt for each R_i to R_i+1 and each T_i to T_i+1 transition in the spirit of the original MWC model in which the monomers are unaffected by ligand binding. The Hill limit corresponds to Λ → ∞, c → 0, and Λc⁴ → 0. The exact expected fraction of sites with ligand bound (MWC’s Ȳ_F), ${\overline{Y}}_F^{ex}$ is given by:

$${\overline{Y}}_F^{ex}=\frac{\mathrm{\Lambda }cx{(1+cx)}^3+x{(1-x)}^3}{\mathrm{\Lambda }{(1+cx)}^4+{(1-x)}^4}$$ (33)

Which reduces to ${\overline{Y}}_F^{\mathit{lim}}$ in the Hill limit (large Λ and small c)² i.e.

$${\overline{Y}}_F^{ex}\approx \frac{x{(1+x)}^3}{\mathrm{\Lambda }+{(1+x)}^4}\approx \frac{x^4}{\mathrm{\Lambda }+x^4}$$ (34)

$${\overline{Y}}_F^{\mathit{lim}}=\frac{x^4}{\mathrm{\Lambda }+x^4}$$ (35)

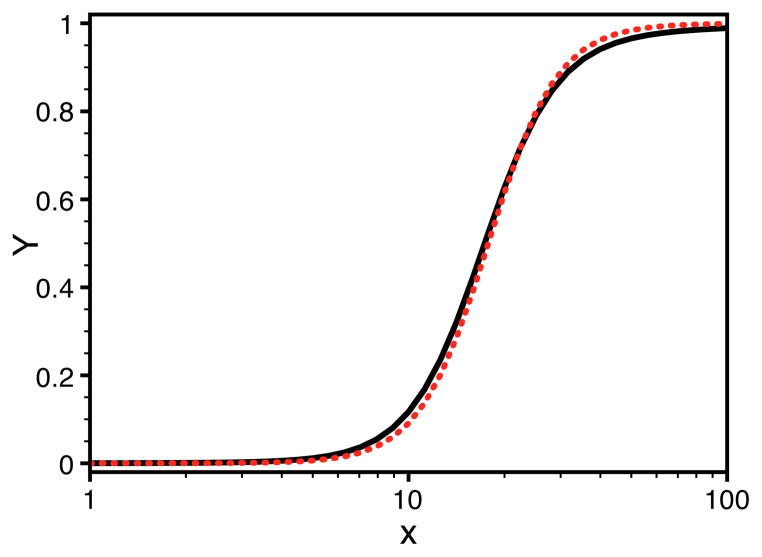
where x ≡ L/K_R is MWC’s “α”. Thus a Hill equation with coefficient greater than one can be physically meaningful. But we can also make use of these equations without taking the Hill limit. We consider parameter values that are in a physically plausible range: Λ = 10⁴ and c = 10⁻⁶ with K_R = 1nM and K_T = 1mM. In Figure 4 we plot ${\overline{Y}}_F^{ex}$ and ${\overline{Y}}_F^{\mathit{lim}}$. The (unnormalized) occupancies of the relaxed and tense states, are given by $w_{R_i}=\left(\begin{array}{c}4\\ i\end{array}\right)x^i$ and $w_{T_i}=\mathrm{\Lambda }\left(\begin{array}{c}4\\ i\end{array}\right){(cx)}^i$ respectively (see Appendix C). For small x, T₀ is the only state with significant occupancy and for large enough x R₄ is the only significantly occupied state. T₀ and R₄ have equal occupancy at x = Λ^1/4 = 10. At this value of x, the (unnormalized) occupancy of R₃ is 4, 000 while that of R₄ and T₀ are each 10, 000 which gives a normalized probability for R₃ (at x ≈ 13) of about .18 so if one were able to glean this from observation one could keep the state R₃ and reduce the system to a “Δ” loop involving T₀, R₃, and R₄ using the “Y − Δ” transformation. We show this towards the end of Appendix C. But first we reduce the full MWC model to a two-state model involving T₀ and R₄ states.

Figure 4.

Comparison between the exact (solid curve) and approximate (dotted curve) Ȳ_F given by equations 33 and 35 respectively.

To find the effective rates between T₀ and R₄ in the reduced two-states MWC model, one can perform the matrix algebra (as done in Appendix C). Here we point out that for large Λ and sufficiently small c using the analogy with RC circuits and the definition of flux (occupancy x rate) gives the effective flux from T₀ to R₄ by inspection. Since the tense states T₁, T₂, T₃, T₄ have negligible occupancy for small enough c we simply have a chain from T₀ ⇌ R₀ ⇌ R₁ ⇌ R₂ ⇌ R₃ ⇌ R₄ with (unnormalized) occupancies of Λ, 1, 4x, 6x², 4x³, x⁴ respectively. Unnormalized means we drop the normalization factor Z. The normalized fluxes are the unnormalized fluxes divided by Z, and the rates work out the same as long as the fluxes and the occupancies are both unnormalized or both normalized. By inspection we find (in the small c limit):

$$\begin{array}{l}\frac{1}{J_{T_0{R}_4}}=\frac{1}{J_{T_0{R}_0}}+\frac{1}{J_{R_0{R}_1}}+\frac{1}{J_{R_1{R}_2}}+\frac{1}{J_{R_2{R}_3}}+\frac{1}{J_{R_3{R}_4}}\\ =\frac{1}{\mathrm{\Lambda }{j}_{rt}}+\frac{1}{j_{rr}4x}+\frac{1}{4x{j}_{rr}3x}+\frac{1}{6x^2{j}_{rr}2x}+\frac{1}{4x^3{j}_{rr}x}\\ =\frac{1}{\mathrm{\Lambda }{j}_{rt}}+\frac{1}{j_{rr}4x}\left(1+\frac{1}{3x}+\frac{1}{3x^2}+\frac{1}{x^3}\right)\end{array}$$ (36)

The mean transition time from T₀ to R₄ is the occupancy of T₀ (Λ) times 1/J_T0R4 and the transition time from R₄ to T₀ is the occupancy of R₄ (x⁴) times 1/J_T0R4. That is for small c

$${\tau }_{T_0{R}_4}=\frac{1}{j_{rt}}+\frac{\mathrm{\Lambda }}{j_{rr}4x}\left(1+\frac{1}{3x}+\frac{1}{3x^2}+\frac{1}{x^3}\right).$$ (37)

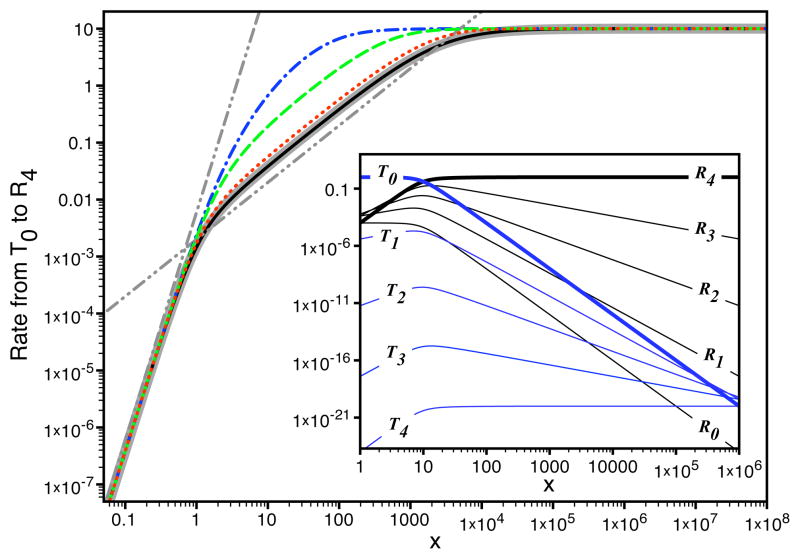
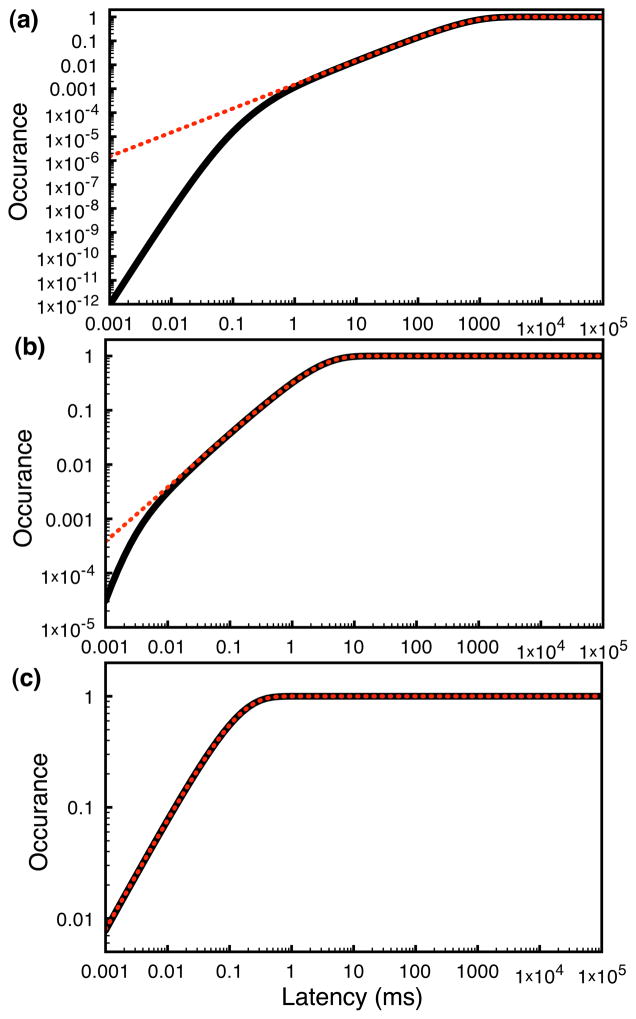
In Figure 5 we plot the exact and effective (approximate) transition rate from T₀ to R₄, (the inverse of τ_T0R4 given by equation 37), as a function of x, for j_rr = j_rt = j_tt = 10 (in arbitrary time units). The exact rate is given by the inverse of equation C.12. There are 3 distinct regimes: small x in which the rate goes as x⁴, intermediate x in which the rate goes as x, and large x in which the rate becomes constant and equal to j_rt. As clear from Figure 5, the exact transition rate converges to the approximate rate as we decrease the value of c. In Figure 6, we compare the exact and approximate cumulative probabilities that the MWC model has reached the state R₄ given that it was in state T₀ at time 0 for three different values of x. The exact and approximate cumulative probabilities are given by equations C.16 and C.17 respectively. The dotted curves show the approximate solution and the solid curves show the exact solution. We notice that for short times there can be significant deviation between the two, but that the probabilities begin to converge in all three cases by the time that the probability exceeds roughly 0.001.

Figure 5.

The approximate (thick gray line) and exact transition rate from state T₀ to state R₄ in MWC model for c = 10⁻⁶ (black solid line), c = 10⁻⁴ (red dotted line), c = 10⁻³ (green dashed line), and c = 10⁻² (blue dotted-dashed line). The gray dotted-dotted-dashed and dotted-dotted-dashed-dashed lines are plotted to represent x and x⁴ behaviors of the transition rate respectively. In the inset, we show the occupancies of all ten states in the MWC model and are given by equation C.4 at c = 10⁻⁶. The occupancies of relaxed (tensed) states are shown in black (blue). The thick (thin) lines represent the high (low) occupancy states.

Figure 6.

Comparison between the exact (solid curves) and approximate (dotted curves) cumulative probabilities that the MWC model has reached the state R₄ given that it was in state T₀ at time 0. (a) x = 1, (b) x=100, (c) x=10,000. Λ = 10⁴, c = 10⁻⁶, and j_rr = j_rt = j_tt = 10 for all panels.

4. Conclusions

In this paper we developed a rigorous technique for simplifying reversible Markov chains in the case that some of the states have very low occupancy relative to the other states. Using the analogy between reversible Markov chains and RC-networks we showed that analytic formulae for the reduced models can be obtained by inspection in many cases including linear chains, the Hill equation limit of the tetrameric MWC model, and the 4 state acyclic model which reduces to 3 states connected in a loop.

The motivation behind our study was to develop a simple and transparent procedure for reducing Markov chains with low occupancy states in order to (1) avoid over-parameterization when fitting a model to a given data set and (2) acquire a better understanding of the underlying dynamics of the system from which the data is collected. Nevertheless, our simplification procedure would also enhance the computational efficiency when simulating such systems. The reduction in computational time would depend on the number of low occupancy states eliminated and the probability flux between low and high occupancy states. We illustrate the improvement in computational time by considering the following example.

$$A\underset{j_{At}L/\epsilon L}{\overset{j_{At}L}{\rightleftharpoons }}t\underset{j_{Bt}{L}^2/K{L}^2}{\overset{j_{Bt}{L}^2/\epsilon L}{\rightleftharpoons }}B$$ (38)

where A and B are the high occupancy states with occupancy 1 and KL² respectively, and t is the low occupancy state having occupancy εL. j_At and j_Bt are the flux parameters for A ⇔ t and t ⇔ B transitions respectively. After eliminating the low occupancy state t, the chain in equation 38 reduces to

$$A\underset{k_{BA}}{\overset{k_{AB}}{\rightleftharpoons }}B$$ (39)

k_AB and k_AB are the effective transition rates from A to B and vice versa. In Appendix D, we calculate the expected number of random numbers, N_rand, needed to perform a Gillespie simulation (Gillespie, 1976) of the full model for one transition from A to B and back to A. We find N_rand = 3(p_A/p_B + p_B/p_A + 2), where p_A and p_B are the probabilities of transition from t to A and t to B respectively. The minimum value of N_rand = 12. As the ligand concentration, L, varies, p_A/p_B or p_B/p_A will become large so N_rand can increase arbitrarily. For the reduced model, only two random numbers are ever required to simulate a transition from A to B and back to A. Thus for this simple example the amount of computational work required to simulate the full model is at least 6 times (and potentially much more than) that needed for the reduced model.

Any Markov chain can be reduced by applying the “Y − Δ” transformation (equation 23) and other simplification methods from circuit theory. There is a large body of work, both ongoing and older, for performing these transformations efficiently on large circuits (see for example (Akers Jr, 1960; Knudsen and Fazekas, 2006; Van Lier and Otten, 1973)). These techniques carry over directly to the important case of reversible Markov chains.

Nodes with very small occupancy compared to all of the remaining nodes can certainly be removed for the purposes of longer time dynamics. It can be desirable to keep some small occupancy nodes, if they correspond to initial states or only have small occupancy for a certain range of ligand concentration or other parameter. In this case it can happen that other nodes can be removed that don’t have small occupancy compared to these nodes. This will still be a good approximation if the equilibration time for the latter nodes is short compared to the time-scales of interest (typically, the equilibration times of the high occupancy nodes). More generally the early time dynamics could be treated via matched asymptotics but this would require additional parameters while our primary goal in this paper is the elimination of parameters that are difficult to estimate from data.

We have attempted to use the ideas sketched here to help with the development of a data-driven model of the IP₃ receptor/Ca²⁺-channel(Ullah et al.). The standard approach to fitting single molecule data with Markov chains involves first selecting a chain and then maximizing the likelihood of a data set by varying the parameters in the selected chain. However, there are an enormous number of possible chains and one is unlikely to guess the correct chain. Our approach allows one to construct models that have as many decay constants as can be distinguished by experiments, yet can also give correct dependence on ligand concentration. Ideally the data-driven construction of reaction networks would proceed iteratively from data collection to model construction, analysis, and refinement and ultimately additional data collection. During the course of the modeling process the modeler could gain the ability to provide estimates of some of the missing parameters. Even so the approximations discussed here provide a useful arrow for the modeler’s quiver.

Highlights.

• A simple technique for simplifying Markov chains on large state space.

• The approach is illustrated by several analogies from physics.

• The technique is presented by several examples.

• Our method works for multi-ligand dependent molecules as well.

• Our study will have a broad impact in the field of single-molecule dynamics.

Appendix A

In this Appendix we use generator matrix theory to reduce the 5-state chain to 2-state chain discussed in section “A linear chain”. The 5-state chain has 2 high occupancy states, S₀ and E₄ and 3 low occupancy states, t₁, t₂, and t₃. The goal is to aggregate this 5 state model into a 2 state model by eliminating the 3 low occupancy states. We will derive the mean time to go from one state to another. The effective transition rates between the high occupancy states are simply the inverse of mean times to transition between those states. To simplify this chain we first write it in terms of probability fluxes

$$S_0\stackrel{j_{01}L}{\iff }{t}_1\stackrel{j_{12}{L}^2}{\iff }{t}_2\stackrel{j_{23}{L}^3}{\iff }{t}_3\stackrel{j_{34}{L}^4}{\iff }{E}_4$$ (A.1)

W in the generator matrix Q (equation 6) is the diagonal matrix whose entries are the unnormalized equilibrium occupancies of the five states, S₀, t₁, t₂, t₃, and E₄.

$$W=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& K_{1}L& 0& 0& 0\\ 0& 0& K_2{L}^2& 0& 0\\ 0& 0& 0& K_3{L}^3& 0\\ 0& 0& 0& 0& K_4{L}^4\end{array}\right)$$ (A.2)

where K₁L, K₂L², K₃L³, and K₄L⁴ are the occupancies of states t₁, t₂, t₃, and E₄ respectively relative to state S₀ having an occupancy of 1. J in equation 6 is the symmetric generator matrix with element J_xy corresponding to the equilibrium probability flux from state x to y. The diagonal entries of J are given by J_xx = −Σ_y≠x J_xy which is an expression of conservation of probability (Bruno et al., 2005).

$$J=\left(\begin{array}{ccccc}-j_{01}L& j_{01}L& 0& 0& 0\\ j_{01}L& -j_{01}L-j_{12}{L}^2& j_{12}{L}^2& 0& 0\\ 0& j_{12}{L}^2& -j_{12}{L}^2-j_{23}{L}^3& j_{23}{L}^3& 0\\ 0& 0& j_{23}{L}^3& -j_{23}{L}^3-j_{34}{L}^4& j_{34}{L}^4\\ 0& 0& 0& j_{34}{L}^4& -j_{34}{L}^4\end{array}\right)$$ (A.3)

Putting equations A.2 and A.3 in equation 6 gives

$$Q=\left(\begin{array}{ccccc}-j_{01}L& j_{01}L& 0& 0& 0\\ \frac{j_{01}}{K_1}& -\frac{j_{01}+j_{12}L}{K_1}& \frac{j_{12}L}{K_1}& 0& 0\\ 0& \frac{j_{12}}{K_2}& -\frac{j_{12}+j_{23}L}{K_2}& \frac{j_{23}L}{K_2}& 0\\ 0& 0& \frac{j_{23}}{K_3}& -\frac{j_{23}+j_{34}L}{K_3}& \frac{j_{34}L}{K_3}\\ 0& 0& 0& \frac{j_{34}}{K_4}& -\frac{j_{34}}{K_4}\end{array}\right)$$ (A.4)

We first aggregate S₀, t₁, t₂, and t₃ states and represent the aggregated state by 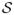. The exact distribution of first passage time to go from 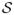to E₄ is given by

$$f_{\mathcal{S}{E}_4}^{\mathit{exact}}={\mathrm{\Pi }}_{\mathcal{S}}{e}^{Q_{\mathcal{S}\mathcal{S}}t}{Q}_{\mathcal{S}{E}_4}{u}_{E_4}$$ (A.5)

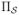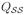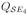where = (1, 0, 0, 0) is the row matrix whose elements are initial probabilities of states S₀, t₁, t₂, and t₃ and u_E4 is a unit column matrix with dimension equal to the number of final states to which the system is about to transition, in this case one state (E₄). , and are the sub-matrices of Q

$$Q^{\mathcal{S}\mathcal{S}}=\left(\begin{array}{cccc}-j_{01}L& j_{01}L& 0& 0\\ \frac{j_{01}}{K_1}& -\frac{j_{01}+j_{12}L}{K_1}& \frac{j_{12}L}{K_1}& 0\\ 0& \frac{j_{12}}{K_2}& -\frac{j_{12}+j_{23}L}{K_2}& \frac{j_{23}L}{K_2}\\ 0& 0& \frac{j_{23}}{K_3}& -\frac{j_{23}+j_{34}L}{K_3}\end{array}\right)$$ (A.6)

$$Q^{\mathcal{S}{E}_4}=\left(\begin{array}{c}0\\ 0\\ 0\\ \frac{j_{34}L}{K_3}\end{array}\right)$$ (A.7)

We can calculate the exact mean time to go from aggregated state 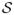to E₄, ${\tau }_{S_o{E}_4}^{\mathit{exact}}$, by integrating equation A.5 and is given by

$${\tau }_{S_0{E}_4}^{\mathit{exact}}={\mathrm{\Pi }}_{\mathcal{S}}{(Q_{\mathcal{S}\mathcal{S}})}^{-2}{Q}_{\mathcal{S}{E}_4}{u}_{E_4}$$ (A.8)

$${\tau }_{S_0{E}_4}^{\mathit{exact}}=\frac{1}{j_{01}L}+\frac{1+K_{1}L}{j_{12}{L}^2}+\frac{1+K_{1}L+K_2{L}^2}{j_{23}{L}^3}+\frac{1+K_{1}L+K_2{L}^2+K_3{L}^3}{j_{34}{L}^4}$$ (A.9)

$${\tau }_{S_0{E}_4}=\frac{1}{j_{34}{L}^4}+\frac{1}{j_{23}{L}^3}+\frac{1}{j_{12}{L}^2}+\frac{1}{j_{01}L}$$ (A.10)

The last expression is the approximate mean transition time to go from 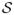to E₄ and is reached by assuming that the occupancies of the states t₁, t₂, and t₃ are negligible as compared to states S₀ and E₄. If the low occupancy states have small but finite occupancy then the mean transition time to go from aggregated state 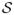to E₄ is given by equation A.9.

Similarly, the exact distribution of first passage time to go to S₀ from 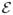, which represents the aggregate of t₁, t₂, t₃, and E₄ states is given by

$$f_{\mathcal{E}{S}_0}^{\mathit{exact}}={\mathrm{\Pi }}_{\mathcal{E}}{e}^{Q_{\mathcal{E}\mathcal{E}}t}{Q}_{\mathcal{E}{S}_0}{u}_{S_0},$$ (A.11)

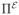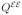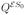where = (0, 0, 0, 1) is the row matrix having the initial probabilities of states t₁, t₂, t₃, and E₄ respectively, u_S0 is a 1 × 1 identity matrix, , and are the sub-matrices of Q

$$Q^{\mathcal{E}\mathcal{E}}=\left(\begin{array}{cccc}-\frac{j_{01}+j_{12}L}{K_1}& \frac{j_{12}L}{K_1}& 0& 0\\ \frac{j_{12}}{K_2}& -\frac{j_{12}+j_{23}L}{K_2}& \frac{j_{23}L}{K_2}& 0\\ 0& \frac{j_{23}}{K_3}& -\frac{j_{23}+j_{34}L}{K_3}& \frac{j_{34}L}{K_3}\\ 0& 0& \frac{j_{34}}{K_4}& -\frac{j_{34}}{K_4}\end{array}\right)$$ (A.12)

$$Q^{\mathcal{E}{S}_0}=\left(\begin{array}{c}\frac{j_{01}}{K_1}\\ 0\\ 0\\ 0\end{array}\right)$$ (A.13)

Integrating equation A.11 gives us the exact mean time to go from state 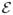to S₀ as

$${\tau }_{E_4{S}_0}^{\mathit{exact}}={\mathrm{\Pi }}^{\mathcal{E}}{(Q^{\mathcal{E}\mathcal{E}})}^{-2}{Q}^{\mathcal{E}{S}_0}{u}_{S_0}$$ (A.14)

$${\tau }_{E_4{S}_0}^{\mathit{exact}}=\frac{K_4}{j_{34}}+\frac{K_3+K_{4}L}{j_{23}}+\frac{K_2+L(K_3+K_{4}L)}{j_{12}}+\frac{K_1+L(K_2+L(K_3+K_{4}L))}{j_{01}}$$ (A.15)

$${\tau }_{E_4{S}_0}=K_4{L}^4\left(\frac{1}{j_{34}{L}^4}+\frac{1}{j_{23}{L}^3}+\frac{1}{j_{12}{L}^2}+\frac{1}{j_{01}L}\right)$$ (A.16)

where the last expression follows from the assumption that states t₁, t₂, and t₃ have negligible occupancies.

Appendix B

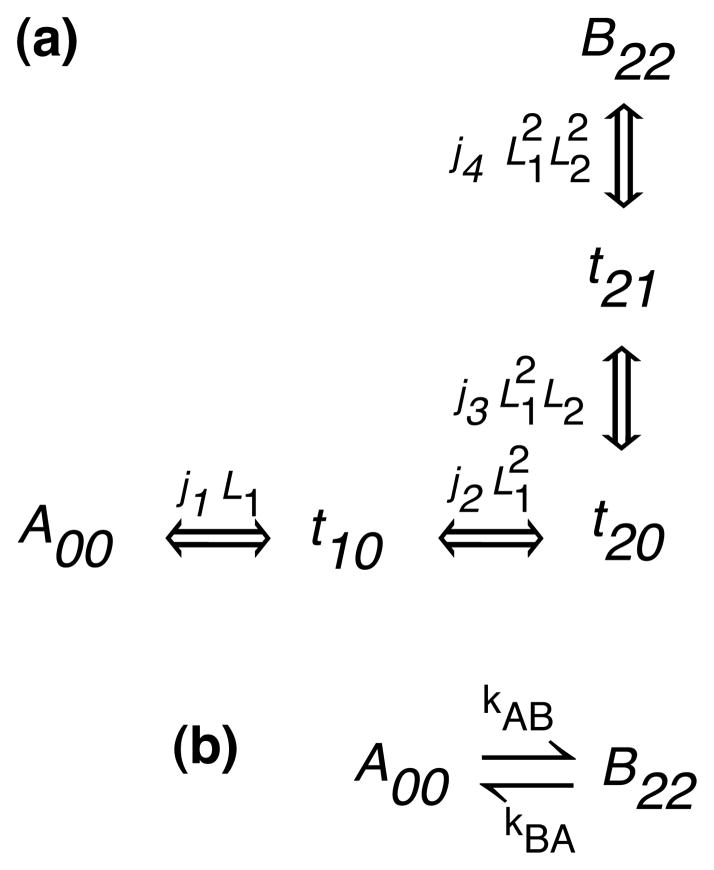
In numerous cases we deal with the Markov chains where the state of the system depends on multiple ligands. In this Appendix we simplify a chain that involves the binding of multiple ligands. The simplification process for such chains is similar to what we have presented for the single ligand case in section “A linear chain”. In Figure B1a we show a chain having total number of 5 states. We wish to simplify this scheme to the one shown in Figure B1b so that the low occupancy states are aggregated into the two high occupancy states. In the first step, the system makes transition from state A₀₀ to t₂₀ by binding two molecules of ligand L₁. In the second step, the system makes transition from state t₂₀ to B₂₂ by binding two molecules of ligand L₂. We will use the electrical circuit analogy to simplify the 5 states chain into 2 states chain (see equation 19).

Figure B1.

Multiple ligand dependent chain. (a) Full scheme with low occupancy states (t₁₀, t₂₀, and t₂₁) included. (a) Simplified scheme after aggregation having only two high occupancy states (A₀₀ and B₂₂). L₁ and L₂ stand for the ligands, and the subscript lm attached to various states represent the l number of ligand L₁ and m number of ligand L₂ bound to the system in the given state.

The effective probability flux from state A₀₀ to B₂₂, J_A00B22, is

$$\frac{1}{J_{A_{00}{B}_{22}}}=\frac{1}{j_1{L}_1}+\frac{1}{j_2{L}_1^2}+\frac{1}{j_3{L}_1^2{L}_2}+\frac{1}{j_4{L}_1^2{L}_2^2}$$ (B.1)

Note that the exponents of ligands L₁ and L₂ in the individual probability fluxes in equation B.1 are equal to the maximum of the number of corresponding ligand molecules bound to the two states involved in the transition.

The probability flux from one state to another is simply the ratio of the occupancy of the initial state and the mean transition time from initial to final state, i.e.

$$J_{A_{00}{B}_{22}}=\frac{\text{Occupancy}\text{of}{A}_{00}}{{\tau }_{AB}}$$ (B.2)

The occupancy of A₀₀ = 1, giving the approximate mean transition time from A₀₀ to B₂₂ is

$${\tau }_{A_{00}{B}_{22}}=\frac{1}{j_1{L}_1}+\frac{1}{j_2{L}_1^2}+\frac{1}{j_3{L}_1^2{L}_2}+\frac{1}{j_4{L}_1^2{L}_2^2}$$ (B.3)

Similarly, the approximate mean transition time from state B₂₂ to A₀₀ is

$${\tau }_{A_{00}{B}_{22}}=K_{B_{22}}L{1}^{2}L{2}^2\left(\frac{1}{j_1{L}_1}+\frac{1}{j_2{L}_1^2}+\frac{1}{j_3{L}_1^2{L}_2}+\frac{1}{j_4{L}_1^2{L}_2^2}\right)$$ (B.4)

Where $K_{B_{22}}{L}_1^2{L}_2^2$ is the occupancy of B₂₂ state. Equations (B.1 – B.4) can be easily generalized for an arbitrary number of states in the chain.

Appendix C

In this Appendix, we simplify the tetrameric MWC model so that the final model is only composed of T₀ and R₄ states. Towards the end of this Appendix, we will discuss the case of x = Λ^1/4 = 10 where state R₃ is not a low-occupancy state. Before writing the matrices W and J used in generator matrix Q (equation 6), we first calculate the unnormalized occupancies of all states in MWC model. Consider the following reaction

$$X_i+L\underset{(i+1)k_r}{\overset{(4-i)k_f}{\rightleftharpoons }}{X}_{i+1},i=0,1,2,3$$ (C.1)

Where X can be either R or T and equilibrium constant $K=\frac{k_r}{k_f}$. The forward rate of the reaction is $\frac{(4-i)k_{r}L}{K}$. At equilibrium the occupancy of X_i+1 state is

$$X_{i+1}=\left(\begin{array}{c}4\\ i\end{array}\right){(L/K)}^{i+1}{X}_i$$ (C.2)

Thus the occupancies of R_i and T_i are given as

$$R_i=\left(\begin{array}{c}4\\ i\end{array}\right)x^i$$ (C.3)

$$T_i=\left(\begin{array}{c}4\\ i\end{array}\right){(xc)}^i\mathrm{\Lambda }$$ (C.4)

Where the occupancies of R₀ and T₀ are 1 and Λ respectively, $x=\frac{L}{K_R},cx=\frac{L}{K_T},c=\frac{K_R}{K_T}$. In MWC language Λ = L and $x=\alpha =\frac{F}{K_R}$.

Thus the diagonal matrix W in equation 6 whose entries are the unnormalized equilibrium occupancies of the all 10 states becomes

$$W=\mathit{diag}(w),$$ (C.5)

where w = (w_R, w_T). Vectors w_R and w_T contain the occupancies of all R and T states respectively.

To write J, we calculate the probability fluxes between various states. Since

$$\text{Probability}\text{flux}=\text{Occupancy}\times \text{Rate}$$ (C.6)

Thus

$$\begin{array}{l}\text{Probability}\text{flux}\text{between}{R}_i\text{and}{R}_{i+1}=\left(\begin{array}{c}4\\ i\end{array}\right){\left(\frac{L}{K_R}\right)}^i\times (4-i)k_R^{f}L\\ =\left(\begin{array}{c}4\\ i\end{array}\right)(4-i)x^{i+1}{k}_R^r\end{array}$$ (C.7)

$$\begin{array}{l}\text{Probability}\text{flux}\text{between}{T}_i\text{and}{T}_{i+1}=\left(\begin{array}{c}4\\ i\end{array}\right){\left(\frac{L}{K_T}\right)}^i\mathrm{\Lambda }\times (4-i)k_T^{f}L\\ =\left(\begin{array}{c}4\\ i\end{array}\right)(4-i){(cx)}^{i+1}\mathrm{\Lambda }{k}_T^r\end{array}$$ (C.8)

If the time for T_i to make the transition to R_i is τ₁ then

$$\text{Probability}\text{flux}\text{between}{R}_i\text{and}{T}_i=\left(\begin{array}{c}4\\ i\end{array}\right)\frac{\mathrm{\Lambda }{c}^i{x}^i}{{\tau }_1}$$ (C.9)

Using the notation $j_{rr}=k_R^r,j_{tt}=k_T^r$, and $j_{rt}=\frac{1}{{\tau }_1}$ for flux parameters, the effective flux matrix, J, in equation 6 becomes

$$J=\left[\begin{array}{cccccccccc}F11& 4j_{rr}x& 0& 0& 0& j_{rt}\mathrm{\Lambda }& 0& 0& 0& 0\\ 4j_{rr}x& F22& 12j_{rr}{x}^2& 0& 0& 0& 4{cj}_{rt}x\mathrm{\Lambda }& 0& 0& 0\\ 0& 12j_{rr}{x}^2& F33& 12j_{rr}{x}^3& 0& 0& 0& 6c^2{j}_{rt}{x}^2\mathrm{\Lambda }& 0& 0\\ 0& 0& 12j_{rr}{x}^3& F44& 4j_{rr}{x}^4& 0& 0& 0& 4c^3{j}_{rt}{x}^3\mathrm{\Lambda }& 0\\ 0& 0& 0& 4j_{rr}{x}^4& F55& 0& 0& 0& 0& c^4{j}_{rt}{x}^4\mathrm{\Lambda }\\ j_{rt}\mathrm{\Lambda }& 0& 0& 0& 0& F66& 4{cj}_{tt}x& 0& 0& 0\\ 0& 4{cj}_{rt}x\mathrm{\Lambda }& 0& 0& 0& 4{cj}_{tt}x& F77& 12c^2{j}_{tt}{x}^2& 0& 0\\ 0& 0& 6c^2{j}_{rt}{x}^2\mathrm{\Lambda }& 0& 0& 0& 12c^2{j}_{tt}{x}^2& F88& 12c^3{j}_{tt}{x}^3& 0\\ 0& 0& 0& 4c^3{j}_{rt}{x}^3\mathrm{\Lambda }& 0& 0& 0& 12c^3{j}_{tt}{x}^3& F99& 4c^4{j}_{tt}{x}^4\\ 0& 0& 0& 0& c^4{j}_{rt}{x}^4\mathrm{\Lambda }& 0& 0& 0& 4c^4{j}_{tt}{x}^4& F1010\end{array}\right]$$ (C.10)

Where

• F11 = −4j_rrx − j_rtΛ

• F22 = −4j_rrx − 12j_rrx² − 4cj_rtxΛ

• F33 = −12j_rrx² − 12j_rrx³ − 6c²j_rtx²Λ

• F44 = −12j_rrx³ − 4j_rrx⁴ − 4c³j_rtx³Λ

• F55 = −4j_rrx⁴ − c⁴j_rtx⁴Λ

• F66 = −4cj_ttx − j_rtΛ

• F77 = −4cj_ttx − 12c²j_ttx² − 4cj_rtxΛ

• F88 = −12c²j_ttx² − 12c³j_ttx³ − 6c²j_rtx²Λ

• F99 = −12c³j_ttx³ − 4c⁴j_ttx⁴ − 4c³j_rtx³Λ

• F1010 = −4c⁴j_ttx⁴ − c⁴j_rtx⁴Λ.

Using equations 6, C.5, and C.10 we can write

$$Q=\left(\begin{array}{cccccccccc}Q11& 4j_{rr}x& 0& 0& 0& j_{rt}\mathrm{\Lambda }& 0& 0& 0& 0\\ j_{rr}& Q22& 3j_{rr}x& 0& 0& 0& {cj}_{rt}\mathrm{\Lambda }& 0& 0& 0\\ 0& 2j_{rr}& Q33& 2j_{rr}x& 0& 0& 0& c^2{j}_{rt}\mathrm{\Lambda }& 0& 0\\ 0& 0& 3j_{rr}& Q44& j_{rr}x& 0& 0& 0& c^3{j}_{rt}\mathrm{\Lambda }& 0\\ 0& 0& 0& 4j_{rr}& Q55& 0& 0& 0& 0& c^4{j}_{rt}\mathrm{\Lambda }\\ j_{rt}& 0& 0& 0& 0& Q66& \frac{4{cj}_{tt}x}{\mathrm{\Lambda }}& 0& 0& 0\\ 0& j_{rt}& 0& 0& 0& \frac{j_{tt}}{\mathrm{\Lambda }}& Q77& \frac{3{cj}_{tt}x}{\mathrm{\Lambda }}& 0& 0\\ 0& 0& j_{rt}& 0& 0& 0& \frac{2j_{tt}}{\mathrm{\Lambda }}& Q88& \frac{2{cj}_{tt}x}{\mathrm{\Lambda }}& 0\\ 0& 0& 0& j_{rt}& 0& 0& 0& \frac{3j_{tt}}{\mathrm{\Lambda }}& Q99& \frac{{cj}_{tt}x}{\mathrm{\Lambda }}\\ 0& 0& 0& 0& j_{rt}& 0& 0& 0& \frac{4j_{tt}}{\mathrm{\Lambda }}& Q1010\end{array}\right)$$ (C.11)

Where

• Q11 = −4j_rrx − j_rtΛ

• Q22 = −j_rr − 3j_rrx − cj_rtΛ

• Q33 = −2j_rr(1 + x) − c²j_rtΛ

• Q44 = −j_rr(3 + x) − c³j_rtΛ

• Q55 = −4j_rr − c⁴j_rtΛ

• $Q66=-j_{rt}-\frac{4{cj}_{tt}x}{\mathrm{\Lambda }}$

• $Q77=-\frac{j_{tt}+3{cj}_{tt}x+j_{rt}\mathrm{\Lambda }}{\mathrm{\Lambda }}$

• $Q88=-\frac{2j_{tt}+2{cj}_{tt}x+j_{rt}\mathrm{\Lambda }}{\mathrm{\Lambda }}$

• $Q99=-\frac{3j_{tt}+{cj}_{tt}x+j_{rt}\mathrm{\Lambda }}{\mathrm{\Lambda }}$

• $Q1010=-j_{rt}-\frac{4j_{tt}}{\mathrm{\Lambda }}$

In analogy with equation (A.8), we can write the exact mean transition time from T₀ to R₄ as

$${\tau }_{T_0{R}_4}^{\mathit{exact}}={\mathrm{\Pi }}_{\mathcal{A}}{(Q^{\mathcal{A}\mathcal{A}})}^{-2}{Q}^{\mathcal{A}{R}_4}{u}_{R_4}$$ (C.12)

Where 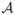represents the aggregate of all states in the MWC model other than R₄ 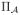is a row matrix of initial probabilities of all states in 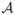(all states in 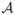except T₀ have 0 initial probability, T₀ has initial probability of 1), 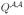is the sub-matrix of Q with entry ij equal to the transition rate between i and j states in 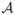, column matrix 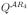is the sub-matrix of Q with entry i equal to the transition rate from i state in , and u_R4 is a unit matrix.

$$Q^{\mathcal{A}\mathcal{A}}=\left(\begin{array}{ccccccccc}Q11& 4j_{rr}x& 0& 0& j_{rt}\mathrm{\Lambda }& 0& 0& 0& 0\\ j_{rr}& Q22& 3j_{rr}x& 0& 0& {cj}_{rt}\mathrm{\Lambda }& 0& 0& 0\\ 0& 2j_{rr}& Q33& 2j_{rr}x& 0& 0& c^2{j}_{rt}\mathrm{\Lambda }& 0& 0\\ 0& 0& 3j_{rr}& Q44& 0& 0& 0& c^3{j}_{rt}\mathrm{\Lambda }& 0\\ j_{rt}& 0& 0& 0& Q66& \frac{4{cj}_{tt}x}{\mathrm{\Lambda }}& 0& 0& 0\\ 0& j_{rt}& 0& 0& \frac{j_{tt}}{\mathrm{\Lambda }}& Q77& \frac{3{cj}_{tt}x}{\mathrm{\Lambda }}& 0& 0\\ 0& 0& j_{rt}& 0& 0& \frac{2j_{tt}}{\mathrm{\Lambda }}& Q88& \frac{2{cj}_{tt}x}{\mathrm{\Lambda }}& 0\\ 0& 0& 0& j_{rt}& 0& 0& \frac{3j_{tt}}{\mathrm{\Lambda }}& Q99& \frac{{cj}_{tt}x}{\mathrm{\Lambda }}\\ 0& 0& 0& 0& 0& 0& 0& \frac{4j_{tt}}{\mathrm{\Lambda }}& Q1010\end{array}\right)$$ (C.13)

$$Q^{\mathcal{A}{R}_4}=\left(\begin{array}{c}0\\ 0\\ 0\\ j_{rr}x\\ 0\\ 0\\ 0\\ 0\\ j_{rt}\end{array}\right)$$ (C.14)

In the limit (Λ → ∞, c → 0, Λc → 0), the mean time to transition from T₀ to R₄, given by equation (C.12) simplifies to

$${\tau }_{T_0{R}_4}=\frac{1}{j_{rt}}+\frac{\mathrm{\Lambda }}{j_{rr}4x}\left(1+\frac{1}{3x}+\frac{1}{3x^2}+\frac{1}{x^3}\right)$$ (C.15)

For the full MWC model, the exact latency (first passage time) distribution for transition from state T₀ to R₄ given by

$$f_{T_0{R}_4}^{\mathit{exact}}={\mathrm{\Pi }}_{\mathcal{A}}{\mathit{exp}}^{(Q_{\mathcal{A}\mathcal{A}}t)}{Q}_{\mathcal{A}{R}_4}{u}_{R_4}$$ (C.16)

For the simplified two state MWC model, the latency distribution becomes

$$f_{T_0{R}_4}={\mathrm{\Pi }}_{T_0}{\mathit{exp}}^{(Q_{T_0{R}_4}t)}{Q}_{T_0{R}_4}{u}_{R_4}$$ (C.17)

Where the initial probability of the system being in T₀ state, Π_T0= 1, and Q_T0R4 = k_T0R4. $k_{T_0{R}_4}=\frac{1}{{\tau }_{T_0{R}_4}}$ is the transition rate from T₀ to R₄ in the simplified 2 state MWC model.

Mean transition time and latency distribution from R₄ to T₀ can be calculated in the same manner.

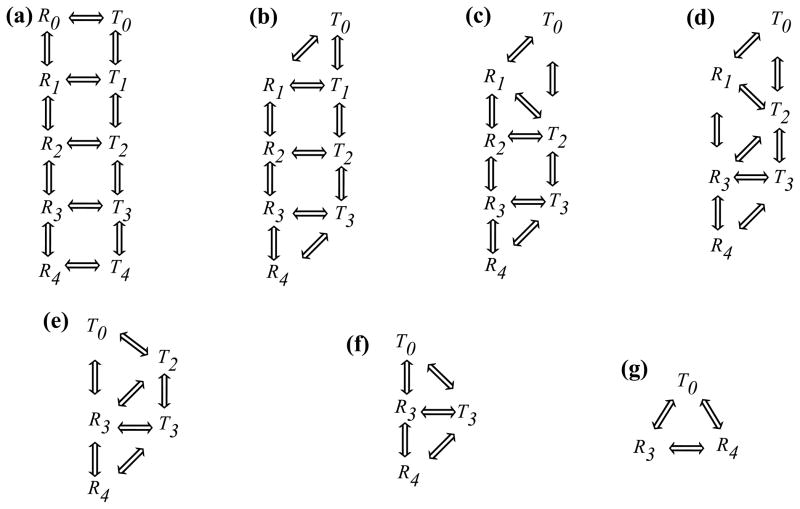
Next we discuss the case where one could keep state R₃ and reduce the MWC model to a “Δ” loop involving T₀, R₃, and R₄ states. We first rewrite the MWC model in terms of probability fluxes (Figure C1a) where the double arrows represent the fluxes between states. The probability fluxes between various states are given by equations C.7 – C.9 and are excluded from Figure C1 for clarity. We use the “Y − Δ” transformation to perform the simplification in the following steps. Step 1: eliminate states R₀ and T₄ from the two linear branches T₀ ⇔ R₀ ⇔ R₁ and T₃ ⇔ T₄ ⇔ R₄ respectively (Figure C1b). The inverse of effective probability flux between T₀ and R₁ is given by the sum of the inverses of fluxes in T₀ ⇔ R₀ and R₀ ⇔ R₁ transitions (see equation 19). Similarly, the effective probability flux between T₃ and R₄ is given by the fluxes involved in T₃ ⇔ T₄ and T₄ ⇔ R₄ transitions. Step 2: eliminate state T₁ using the “Y − Δ” transformation so that states T₀, R₁, and T₂ form a “Δ” loop (Figure C1c). In this and the following steps, the effective probability fluxes between various states in the loop can be calculated by using equation 23. Step 3: follow step 2 to eliminate state R₂ so that R₁, R₃, and T₂ states form a “Δ” loop (Figure C1d). Step 4: convert the “Y” branch composed of states T₀, R₁, R₃, and T₂ to a “Δ” loop involving T₀, R₃, and T₂ to eliminate R₁ (Figure C1e). Step 5: eliminate T₂ from the “Y” chain composed of T₀, T₂, T₃, and R₃ (Figure C1f). Step 6: eliminate T₃ by converting the “Y” branch involving states T₀, R₃, R₄, and T₃ to reach the final “Δ” loop having T₀, R₃, and R₄ states (Figure C1g). One can use this procedure for other complex networks.

Figure C1.

Using Y − Δ transformation to reduce the MWC model to 3 state model in case of x = Λ^1/4 = 10. The reduced model consists of states T₀, R₃, and R₄.

Appendix D

In this Appendix, we calculate the expected number of random numbers required to simulate one transition of the system from state A to B and back to A in the full and reduced models using Gillespie’s Algorithm (Gillespie, 1976). If the system is in state t in the full model, then the probability of transition from t to A, p_A, and t to B, p_B, are given by

$$p_A=\frac{j_{At}/\epsilon }{j_{At}/\epsilon +j_{Bt}L/\epsilon }=\frac{j_{At}}{j_{At}+j_{Bt}L}$$ (D.1)

and p_B = 1 − p_A. Transition from t to either A or B is a Bernoulli process. The probability of making n transitions to A followed by one transition to B is $p_A^n{p}_B$. The expected number of transitions from t to A before reaching B is

$$<N_{tA}>=\sum _n^{\infty }{np}_A^n{p}_B=\frac{p_A{p}_B}{{(1-p_A)}^2}=\frac{p_A}{p_B}$$ (D.2)

The number of transitions from A to t are N_At = N_tA + 1. So <N_At>=<N_tA> +1 = p_A/p_B + 1. The total number of transitions out of t, N_t, is N_t = N_tA + 1 (the final transition is to B). The number of random numbers required to simulate the transition of the system from state A to B through t is

$$\begin{array}{l}{N}_{\mathit{rand}}^{AB}=2N_t+N_{At}\\ =3(N_{tA}+1)\\ =3(p_A/p_B+1)\end{array}$$ (D.3)

Similarly the number of random numbers needed to simulate the transition of the system from state B to A through t is $N_{\mathit{rand}}^{BA}=3(p_B/p_A+1)$. Thus the expected number of random numbers, N_rand, needed to simulate one transition from state A to t to B and state B to t to A in the full model is N_rand = 3(p_A/p_B + p_B/p_A + 2). The number of random numbers needed to simulate one transition from state A to B and B to A in the reduced model is 2. The ratio of the expected number of random numbers needed to simulate one transition of the system from state A to B and back to A using the full and reduced models is 3(p_A/p_B + p_B/p_A + 2)/2, which has a minimum of 6 and an infinite maximum.