Introduction
In order to quantitatively describe the topography of natural surfaces Mandelbrot reintroduced the concept of fractal geometry [1], a non-Euclidean geometry that allows for non-integer dimensions in which fractal objects may exhibit both self-similarity (meaning that multiple features on an the surface of an object appear the same in each of the X, Y and Z axes) and scale invariance (meaning that objects appear the same at all scales of magnification) [2, 3]. Fractal objects are characterized by their fractal dimension, D, and by its fractal dimensional increment, D* [1]. For any given fracture surface, D lies somewhere between a value of 2.0 and 3.0. D* is equal to the non-integer portion of D and lies somewhere between 0 and 1 [4] (Fig. 1). D* represents the degree of tortuosity of the surface outside of the plane [3] and serves as a scaling factor for both the fracture energy and the surface area of the created fracture surface [5].
Figure 1.
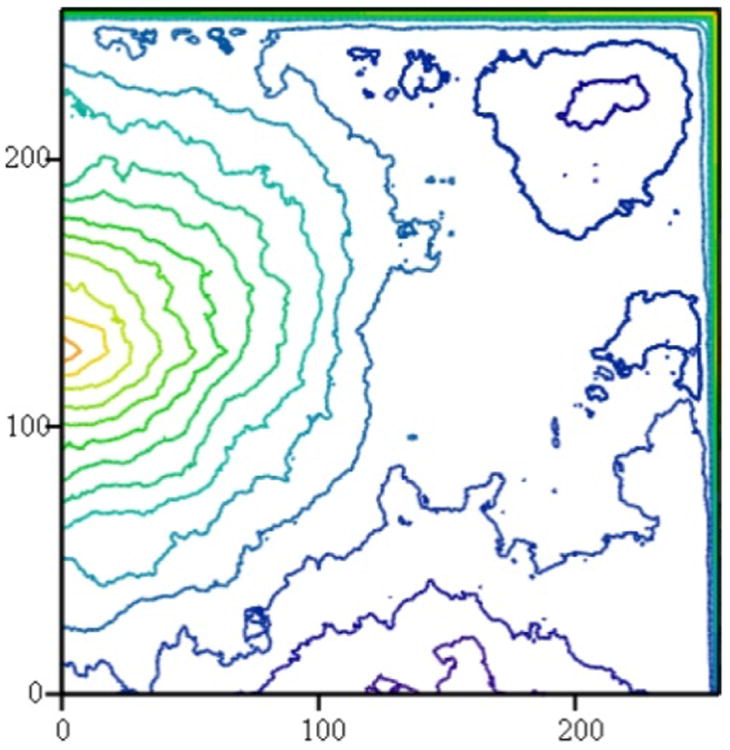
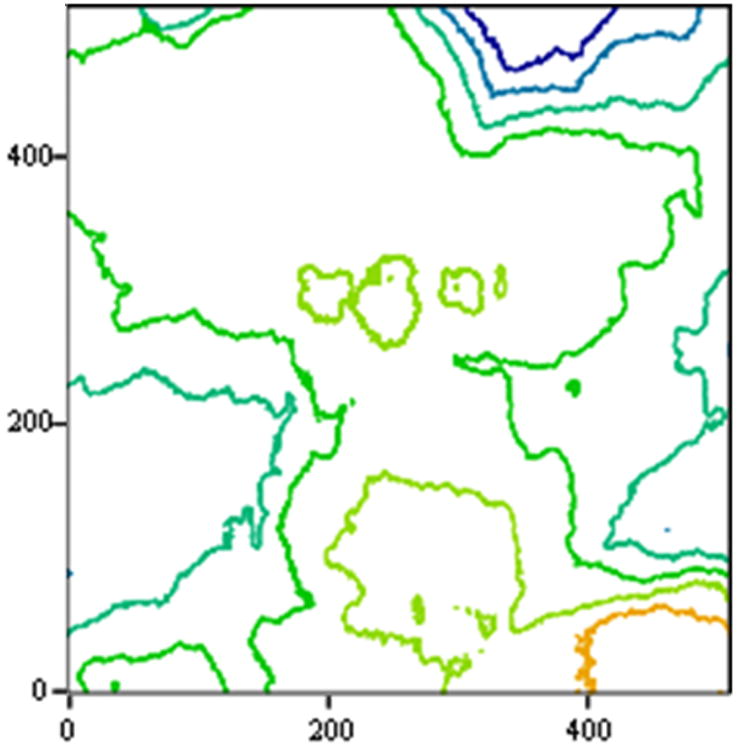
(a) Surface generated via Brownian interpolation with FRACTALS program. (b) Fracture surface of Y-TZP (ZirCAD, Ivoclar Vivadent).
The ability of fractal geometry to simply describe otherwise complex surfaces has led to its application in many fields of chemistry, physics, engineering, computer science and materials science [3, 6]. The brittle fracture of materials has been shown to be a fractal process by numerous experiments [2, 5, 7-12]. The fracture process for brittle materials begins with the separation of primary bonds at the atomic level [5]. Due to the scale invariant nature of fractal geometry, the results of processes can be deduced on the atomic scale by examining specimens on the microscopic scale [2]. Having the ability to determine fracture surface geometry is necessary to gain increased understanding of the toughening mechanisms, fatigue resistance, and role of microstructure in the fracture processes of brittle solids [13]. In addition to describing the tortuosity of a fracture surface [14-17], the fractal dimension of the fracture surface can be used to determine fracture toughness [2, 8, 14, 18-20], impact energy [21], characteristic length [2, 12, 22, 23], and flaw/fracture mirror size ratio [20, 24, 25]. An advantage of fractal analysis is that it offers a method to analyze in vivo failures of dental biomaterials to distinguish whether failure of the prosthesis was due to mechanical overload or the fabrication process [6]. Traditional failure analysis of dental restorations often proves difficult because further damage is created during the clinical retrieval process, and important portions of the fracture surface (i.e. critical flaw/failure origin) are often lost [26]. This may be caused by applied iatrogenic pressure during retrieval of the broken prosthesis or by continued loading following the fracture event. The fractal dimensional increments, D*, of several dental ceramics have previously been investigated [27].
Fractal objects are either self-similar or self-affine. To differentiate, self-similar objects show the same dimensions in the Z direction scale as those in the X and Y; whereas, for self-affine objects the fractal dimension of the vertical direction is different from the lateral directions [24]. This results in a different D* value when measurements are made outside of the horizontal plane [22]. It is commonly accepted that fracture surfaces are self-affine [9, 22, 28].
Many different methods are used for measuring the fractal dimension of a surface. Some can measure an original fracture surface [22, 29-37], while others take a zero-set approach (slicing a cross-section of the original surface) [1, 38-40]. Zero-set methods have been the most commonly used methods for dental materials [23, 24, 27, 41]. The majority of researchers have used a zero-set method called slit-island analysis [3, 4, 23, 42-46] to acquire a horizontal section of a fracture surface followed by the Richardson method [38] to determine the fractal dimension. However, two major obstacles arise when using Slit-Island Richardson (SIR) method [9, 22, 42, 46-52]. First, the SIR method is an extremely tedious and labor intensive technique when human judgment is used to trace a micrograph of the cross-section, and no automated method has been validated [23]. Also, since the D* of a self-affine surface will only match the D* of a zero-set surface when the slicing angle is 0°, a fracture surface can only be analyzed accurately when measured in a plane exactly parallel to the surface, which is difficult to achieve manually [24].
Most methods for measuring fractal dimension have been used only on fracture surfaces of physical specimens [2, 3, 5, 13, 19, 23, 24, 27, 42, 53-55]. Here an obstacle arises because the true D* values of the analyzed surfaces are unknown since there is no standard reference material for the D* of fracture. Therefore, the present study sought to synthetically generate fractal surfaces with known D* values to determine which methods of fractal analysis are the most accurate, precise, and robust. Several other studies have used similar computer-generated surfaces to measure fractal dimension in a systematic way [56-59]. These studies used a limited number of fractal analysis methods to determine the most accurate methods, and none of them considered angle of inclination. While these studies have concentrated on finding the measurement methods with the greatest accuracy [56, 57, 59], one focus of this study is to find a method with the highest precision. Precision is advantageous over accuracy because a correction factor may be applied to compensate for lack of accuracy and hence to achieve an unbiased a result. The objective of this study is to develop a method for determining the fractal dimensional increment (D*) of a surface which is precise, accurate and insensitive to angle of inclination. Such a method would be a valuable tool for failure analysis, production, and development of new dental materials [60].
Materials and Methods
The FRACTALS program provided by Russ [22] was used to generate self-affine fracture surfaces (256×256 pixels) via Brownian interpolation [61] having known D* values of 0.1, 0.2, 0.3, and 0.4. Various methods for generating the fracture surfaces are available, and after conducting a pilot study it was found that surfaces generated by the Fractal Brownian subroutine were representative of the appearance of ceramic fracture surfaces (Fig. 1). Figure 1a was generated using the same parameters used of the current study, and figure 1b was captured via atomic force microscope (Bioscope Catalyst, Veeco Instruments Inc., Plainview, NY) and translated to the FRACTALS software using MathCAD (Parametric Technology Corporation, Needham, MA). An alpha value of 1 minus the desired D* value was entered. For example, to obtain a surface having a known D* value of 0.2 an alpha value of 0.8 was entered. An interpolation rate of 0.5 was used for all generated surfaces. With a D* value of 0.1, the program generates a surface with a D value of 2.1. D* values ranging only from 0.1-0.4 were chosen because this is the range of D* values from ceramic fracture surfaces reported in the previous literature [23]. Ten surfaces that most closely represented real fracture surfaces were generated for each of the D* values for a total of 40 surfaces.
Individual surfaces were loaded into a custom script written using MathCAD. The surfaces were inclined at four angles of 0° (zero tilt), 3°, 5°, and 7° via a rotation matrix. The following Equation was used to rotate the surfaces about the x-axis:
| (1) |
where θ is the desired angle of inclination, variables with a subscript of 1 represent the coordinates of points on the non-rotated surface, and variables with a subscript of 2 represent the inclined surface. In this study, a range of angles between 0° and 7° was used to account for angulation errors expected from mounting a clinically retrieved specimen, as well as those angles that would be considered acceptable to be accurately recorded via a surface imaging method that cannot be tilted more than a few degrees.
Each of the 160 MathCAD-modified surfaces (40 surfaces × 4 angles) was then loaded back into the FRACTALS program and analyzed by various methods to compare the measured D* value versus the actual D* value. These methods included Minkowski Cover (MC) [31], Root Mean Square Roughness vs. Area (RMS) [30], Kolmogorov Box (KB) [40], Hurst Exponent (HE) [29], Slit Island Box (SIB) [1], and Slit Island Richardson (SIR) [38].
The results of each method were appropriately recorded in a Microsoft Excel spreadsheet. The coefficient of variation (CV) and mean error were calculated to identify the methods with the best precision (lowest CV) and the best accuracy (lowest mean error), respectively. Three-way ANOVA followed by Tukey's HSD (α = 0.05) were used to identify significant effects. A least squares linear regression of the actual vs. measured D* was calculated to determine an unbiasing factor for each method.
Results
Figure 2 compares the mean fractal dimension values measured using the different methods at a zero-degree angle of inclination versus the actual fractal dimension of the surface. The dotted black line shows the result that would be obtained using an unbiased measurement method (measured D* equal to actual D*). The KB method showed the least bias at a zero-degree angle of inclination, but the KB method had the largest bias for angled surfaces (Figure 3). All of the other methods had a negative bias (underestimated D*), so it was necessary to develop a bias correction relation for each method. All of the corrections fit well to linear relations (R > 0.99). Table 1 shows the correlation coefficient, slope, and intercept for each correction relation. They may be used to correct for bias, as follows:
Figure 2.
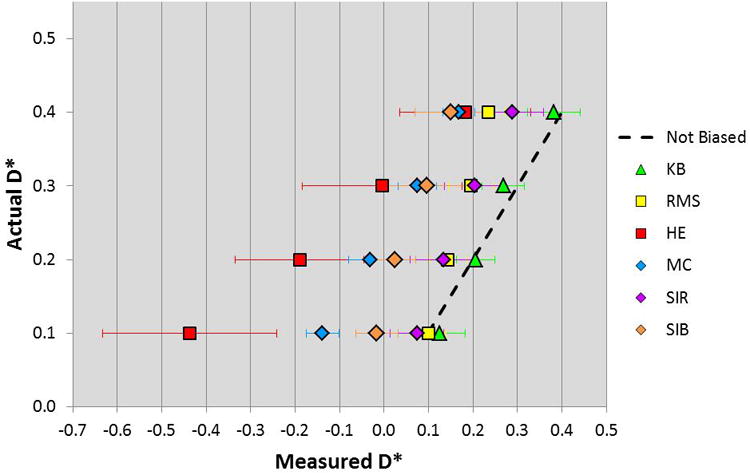
Mean and standard deviations before bias correction of fractal dimensional increment (D*) measured at a zero-degree angle of inclination from Brownian interpolation surfaces with known D* values using different methods, including Kolmogorov Box (KB), root mean square surface roughness versus area (RMS), Hurst exponent (HE), Minkowski cover (MC), slit island Richardson (SIR), and slit island box (SIB).
Figure 3.
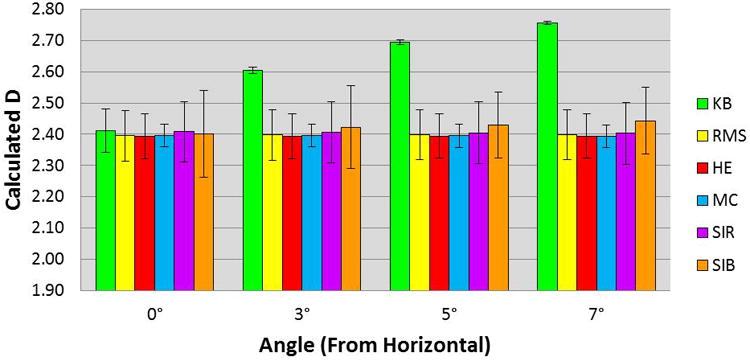
Mean (standard deviation) values after bias correction for the fractal dimension (D) measured on Brownian interpolation surfaces (n=10) using different methods.
Table 1.
The slope (m), intercept (b), and correlation coefficients (R) of correction models for fractal dimensional increment for different methods of determining the fractal dimensions of surfaces.
| Method | R | m | b |
|---|---|---|---|
| KB | 0.9923 | 1.1826 | -0.0406 |
| RMS | 0.9986 | 2.1890 | -0.1193 |
| HE | 0.9973 | 0.4858 | 0.3043 |
| MC | 0.9994 | 0.9756 | 0.2318 |
| SIR | 0.9971 | 1.3917 | 0.0051 |
| SIB | 0.9949 | 1.7361 | 0.1397 |
| (2) |
The coefficient of variation (CV) is defined as the standard deviation divided by the mean. CV after bias correction was used to compare relative levels of precision in estimating fractal dimension, where lower CV corresponds to greater precision. Three-way ANOVA showed that the actual fractal dimension of surfaces significantly affected CV (p = 0.002), but CV did not consistently increase or decrease with increasing fractal dimension. The method of measurement also significantly affected CV (p < 0.001) with the MC method having significantly lower CV than all other methods, and hence the greatest precision. The SIB and SIR methods had significantly higher CV than all other methods and did not significantly differ from each other. The angle of inclination did not significantly affect CV (p = 0.765) across the range of angles studied.
The mean error after bias correction, which is the difference between the actual fractal dimensional increment and the calculated value averaged over 10 surfaces, was used to compare relative levels of accuracy in estimating fractal dimension, where lower mean error corresponds to greater accuracy. Three-way ANOVA showed that the actual fractal dimension, the method of measurement, and the angle of inclination all significantly affected the mean error (p < 0.001), and there was a significant three-way interaction between these factors (p < 0.001). This was primarily associated with the KB method, which was very sensitive to the angle of inclination. The other methods had fairly low mean errors after bias correction across the range of fractal dimension values and angles of inclination studied. The KB method had a low mean error only for a zero-degree angle of inclination, and the error at steeper angles was decreased as the actual fractal dimension increased.
Discussion
The large negative bias shown in Figure 2 for most of the measurement methods emphasizes the importance of validating test methods using surfaces with known properties. It is also important to note that, when a large bias is detected, correction of that bias can alter the precision of estimates. For example, the RMS method had the lowest CV before bias correction but had one of the highest CV values after bias correction. This is because the CV is multiplied by the slope (m) of the bias correction relation (Table 1). Measurement methods with m greater than one decreased in precision, and methods with m less than one increased in precision when the bias was corrected.
One of the objectives of measuring the fractal dimension of a fracture surface is to estimate the fracture toughness of a material. An error in measuring D* corresponds to a larger error in estimating fracture toughness. Hill et al. showed that the fracture toughness values have three different square-root relations to D* values for the three families of ceramics (single crystal, polycrystalline, and glass-ceramic) [23]. Since the relations are not linear, an error in D* corresponds to less error in estimating fracture toughness when D = 2.1 than when D = 2.4. According to the slopes of those relations an error of 0.01 in D* value corresponds to an error of 0.12 MPa·m½ (D = 2.1) to 0.24 MPa·m½ (D = 2.4) in fracture toughness for polycrystalline ceramics or an error of 0.06 to 0.12 MPa·m½ in fracture toughness for glass-ceramics. Compare this to an error of 0.05 in D* value, which represents an error of 0.61 to 1.22 MPa·m½ in fracture toughness for polycrystalline ceramics or an error of 0.30 to 0.59 MPa·m½ in fracture toughness for glass-ceramics. This emphasizes the importance of using the most precise method to measure D*. The square of the ratio of the standard deviation values (Table 2) shows that the least precise method (HE) requires 7 times the sample size as the MC method to obtain the same size of confidence interval when D = 2.1, and the least precise method (SIB) requires 15 times the sample size as the MC method when D = 2.4.
Table 2.
Mean (standard deviation) fractal dimensional increment values after bias correction for different methods of determining the fractal dimensions of surfaces as measured on surfaces (n = 10) generated by Brownian interpolation with known fractal dimensions (D = 2.1 to 2.4).
| Method | D = 2.1 | D = 2.2 | D = 2.3 | D = 2.4 |
|---|---|---|---|---|
| KB | 0.1081 (0.0667) | 0.2035 (0.0508) | 0.2765 (0.0564) | 0.4119 (0.0696) |
| RMS | 0.1010 (0.0845) | 0.1946 (0.0911) | 0.3093 (0.1111) | 0.3952 (0.0811) |
| HE | 0.0918 (0.0951) | 0.2123 (0.0702) | 0.3026 (0.0874) | 0.3933 (0.0716) |
| MC | 0.0970 (0.0359) | 0.2023 (0.0488) | 0.3048 (0.0415) | 0.3958 (0.0355) |
| SIR | 0.1090 (0.0837) | 0.1927 (0.1044) | 0.2905 (0.0950) | 0.4078 (0.0968) |
| SIB | 0.1118 (0.0834) | 0.1817 (0.0809) | 0.3063 (0.1613) | 0.4002 (0.1389) |
A limitation of this study was the use of virtual surfaces as a calibration reference. This was necessary to detect and correct the bias of the measurement methods. However, surfaces generated by Brownian interpolation are expected to be self-similar, whereas real-world fracture surfaces are expected to be self-affine. Zero-set methods, such as the SIR and SIB methods, that use a two-dimensional cross-section of the surface to be analyzed are sensitive to the angle of inclination when the surface is self-affine. In this study, only the KB method showed sensitivity to the angle of inclination, but the other methods may show a greater degree of sensitivity to the angle when used on fracture surfaces.
Conclusion
In this study, a method for analyzing fractal surfaces was identified which met the initial criteria of being precise, and accurate and is insensitive to angle of inclination. MC method was identified as the most promising method of the six tested based on repeatedly having the lowest coefficient of variation across the range of D* values commonly reported for ceramic fracture surfaces. Additionally, a technique was developed to level and import a set of 3D surface coordinates into the FRACTALS program for fractal dimensional analysis, which may serve as a platform for digital data importation and interpretation of actual fracture surfaces.
Acknowledgments
NIH-NIDCR Grant DE013358, NIH-NIDCR Grant DE017991, NIH-NIDCR Bloc Travel Award T14DE017284
The authors would like to thank Dr. Gaurav Joshi for scanning Figure 1b
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Mandelbrot BB. The fractal geometry of nature. 1977 [Google Scholar]
- 2.Mecholsky JJ, Passoja DE, Feinbergringel KS. Quantitative analysis of brittle fracture surfaces using fractal geometry. Journal of the American Ceramic Society. 1989;72:60–65. [Google Scholar]
- 3.Mecholsky JJ, Plaia JR. Fractal analysis on fracture surfaces of glass using replication techniques. Journal of Non-Crystalline Solids. 1992;146:249–255. [Google Scholar]
- 4.Mandelbrot BB, Passoja DE, Paullay AJ. Fractal character of fracture surfaces of metals. Nature. 1984;308:721–722. [Google Scholar]
- 5.Mecholsky JJ, West JK, Passoja DE. Fractal dimension as a characterization of free volume created during fracture in brittle materials. Philosophical Magazine. 2002;82:3163–3176. [Google Scholar]
- 6.Mecholsky JJ., Jr Fractography: determining the sites of fracture initiation. Dental Materials. 1995;11:113–116. doi: 10.1016/0109-5641(95)80045-X. [DOI] [PubMed] [Google Scholar]
- 7.Passoja DE. Fundamental relationships between energy and geometry of fracture. Fractography of Glasses and Ceramics. 1988;22:101–126. [Google Scholar]
- 8.Fahmy Y, Russ JC, Koch CC. Application of fractal geometry measurements to the evaluation of fracture toughness of brittle intermetallics. Journal of Materials Science. 1991;6:1856–1861. [Google Scholar]
- 9.Bouchaud E, Lapasset G, Planès J, Naveos S. Statistics of branched fracture surfaces. Physical Review B. 1993;48:2917–2928. doi: 10.1103/physrevb.48.2917. [DOI] [PubMed] [Google Scholar]
- 10.Poon CY, Sayles RS, Jones TA. Surface measurement and fractal characterization of naturally fractured rocks. Journal of Physics D: Applied Physics. 1992;25:1269. [Google Scholar]
- 11.Neimark AV. Characterization of self-affinity in the global regime. Physical Review B. 1994;50:435. doi: 10.1103/physrevb.50.15435. [DOI] [PubMed] [Google Scholar]
- 12.West JK, Mecholsky JJ, Hench LL. The application of fractal and quantum geometry to brittle fracture. Journal of Non-Crystalline Solids. 1999;260:99–108. [Google Scholar]
- 13.Celli A, Tucci A, Esposito L, Palmonari C. Fractal analysis of cracks in alumina-zirconia composites. Journal of the European Ceramic Society. 2003;23:469–479. [Google Scholar]
- 14.Li JF, Ding CX. Fractal character of circumferences of polishing-induced pull-outs of plasma sprayed Cr3C2-NiCr coatings. Thin Solid Films. 2000;376:179–182. [Google Scholar]
- 15.Avnir D, Farin D, Pfeifer P. Surface geometric irregularity of particulate materials: the fractal approach. Journal of Colloid and Interface Science. 1985;103:112–123. [Google Scholar]
- 16.Amada S, Yamada H. Influence of grit blasting pre-treatment on the adhesion strength of plasma sprayed coatings: fractal analysis of roughness. Surface and Coatings Technology. 1998;102:132–137. [Google Scholar]
- 17.Heimann RB. On the self-affine fractal geometry of plasma-sprayed surfaces. Journal of Thermal Spray Technology. 2011;20:898–908. [Google Scholar]
- 18.Mecholsky JJ. Estimating theoretical strength of brittle materials using fractal geometry. Materials Letters. 2006;60:2485–2488. [Google Scholar]
- 19.Boccaccini AR, Winkler V. Fracture surface roughness and toughness of Al2O3-platelet reinforced glass matrix composites. Composites Part A. 2002;33:125–131. [Google Scholar]
- 20.Mecholsky JJ, Freiman SW. Relationship between fractal geometry and fractography. Journal of the American Ceramic Society. 1991;74:3136–3138. [Google Scholar]
- 21.Ray KK, Mandal G. Study of correlation between fractal dimension and impact energy in a high strength low alloy steel. Acta Metallurgica. 1992;40:463–469. [Google Scholar]
- 22.Russ JC. Fractal surfaces. Springer; New York: 1994. [Google Scholar]
- 23.Hill TJ, Mecholsky JJ, Della Bona A. Establishing a protocol for measurements of fractal dimensions in brittle materials. Journal of Materials Science. 2001;36:2651–2657. [Google Scholar]
- 24.Della Bona A, Hill TJ, Mecholsky JJ. The effect of contour angle on fractal dimension measurements for brittle materials. Journal of Materials Science. 2001;36:2645–2650. [Google Scholar]
- 25.Mecholsky JJ., Jr . Fractography, fracture mechanics and fractal geometry: an integration. In: Varner JP, Frechette VD, Quinn GD, editors. Fractography of Glasses and Ceramics III. The American Ceramic Society; Westerville, OH: 1996. [Google Scholar]
- 26.Scherrer SS, Quinn JB, Quinn DS, Wiskott HW. Fractographic ceramic failure analysis using the replica technique. Dental Materials. 2007;23:1397–1404. doi: 10.1016/j.dental.2006.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Drummond JL, Thompson M, Super BJ. Fracture surface examination of dental ceramics using fractal analysis. Dental Materials. 2005;21:586–589. doi: 10.1016/j.dental.2004.12.002. [DOI] [PubMed] [Google Scholar]
- 28.Bonamy D, Ponson L, Prades S, Bouchaud E, Guillot C. Scaling exponents for fracture surfaces in homogeneous glass and glassy ceramics. Physical Review Letters. 2006;97:135504. doi: 10.1103/PhysRevLett.97.135504. [DOI] [PubMed] [Google Scholar]
- 29.Hurst HE, Black RP. Long term storage: an experimental study. Constable; London: 1965. [Google Scholar]
- 30.Malinverno A. A simple method to estimate the fractal dimension of a self-affine series. Geophysical Research Letters. 1990;17:1953–1956. [Google Scholar]
- 31.Minkowski H. Über die begriffe länge, oberfläche und volumen. Jahresbericht der Deutschen Mathematikervereinigung. 1901;9:115–121. [Google Scholar]
- 32.Nelson JA, Crookes RJ, Simons S. On obtaining the fractal dimension of a 3D cluster from its projection on a plane-application to smoke agglomerate. Journal of Physics D: Applied Physics. 1990;23:465. [Google Scholar]
- 33.Illian J, Penttinen A, Stoyan H, Stoyan D. Statistical analysis and modeling of spatial point pattern. Wiley; Chichester: 2008. [Google Scholar]
- 34.Wong P, Cao QZ. Correlation function and structure factor for a mass fractal bounded by a surface fractal. Physical Review B. 1992;45:7627–7632. doi: 10.1103/physrevb.45.7627. [DOI] [PubMed] [Google Scholar]
- 35.Passoja DE, Amborski DJ. Fractal profile analysis by fourier transform methods. Microstructural Science. 1978;6:143–148. [Google Scholar]
- 36.Mandelbrot BB, Van Ness JW. Fractional brownian motions, fractional noises and applications. SIAM Review. 1968;10:422–437. [Google Scholar]
- 37.Brown CA, Charles PD, Johnsen WA, Chesters S. Fractal analysis of topographic data by patchwork method. Wear. 1993;161:61–67. [Google Scholar]
- 38.Richardson LF. The problem of contiguity: an appendix of statisitics of deadly quarrels. General Systems Yearbook. 1961;6:139–187. [Google Scholar]
- 39.Kaye BH. Sequential mosaic amalgamation as a strategy for evaluating fractal dimensions of a fineparticle profile. Institute for Fineparticle Research, Laurentian University; Sudbury, Ontario: 1978. [Google Scholar]
- 40.Kolmogorov AN. New metric invariant of transitive dynamical systems and endomorphisms of lebesgue spaces. Doklady of Russian Academy Sciences. 1958;119:861–864. [Google Scholar]
- 41.Baran GR, Roque-Carmes C, Wehbi D, DeGrange M. Fractal characteristics of fracture surfaces. Journal of the American Ceramic Society. 1992;75:2687–2691. [Google Scholar]
- 42.Chen Z, Mecholsky JJ, Jr, Joseph T, Beatty CL. Fractal geometry of Si3N4 wear and fracture sufaces. Journal of Materials Science. 1997;32:6317–6323. [Google Scholar]
- 43.Pande CS, Richards LE, Louat N, Dempsey BD, Schwoeble AJ. Fractal characterization of fracture surfaces. Acta Metallurgica. 1987;35:1633–1637. [Google Scholar]
- 44.Pande CS, Richards LE, Smith S. Fractal characteristics of fractured surfaces. Journal of Materials Science Letters. 1987;6:295–297. [Google Scholar]
- 45.Lung CW. Fractals in physics. Amsterdam: Elsevier North-Holland: Science Publishers; 1985. [Google Scholar]
- 46.Lung CW, Mu ZQ. Fractal dimension measured with perimeter-area relation and toughness of materials. Physical Review B. 1988;38:11781. doi: 10.1103/physrevb.38.11781. [DOI] [PubMed] [Google Scholar]
- 47.Richards LE, Dempsey BD. Fractal characterization of fractured surfaces in Ti-4.5 Al-5.0 Mo-1.5 Cr (CORONA 5) Scripta Materialia. 1988;22:687–689. [Google Scholar]
- 48.Huang ZH, Tian JF, Wany ZG. A study of slit island analysis as a method for measuring fractal dimension of fractured surfaces. Scripta Metallurgica et Materialia. 1990;24:967–972. [Google Scholar]
- 49.Imre A. Problems of measuring the fractal dimension by the slit-island method. Scripta Metallurgica et Materialia. 1992;27:1713–1716. [Google Scholar]
- 50.Imre A. Comment on “perimeter-maximum diameter” method for measuring the fractal dimension of a fracture surface. Physical Review B. 1995;51:16470. doi: 10.1103/physrevb.51.16470. [DOI] [PubMed] [Google Scholar]
- 51.Mu ZQ, Lung CW, Kang Y, Long QY. Perimeter-maximum method for measuring the fractal dimension of a fractured surface. Physical Review B. 1993;48:7679–7681. doi: 10.1103/physrevb.48.7679. [DOI] [PubMed] [Google Scholar]
- 52.Lung CW, Zhang SZ. Fractal dimension of the fractured surface of materials. Physica D: Nonlinear Phenomena. 1989;38:242–245. [Google Scholar]
- 53.Ponson L, Bonamy D, Bouchaud E. Two-dimensional scaling properties of experimental fracture surfaces. Physical Review Letters. 2006;96:035506. doi: 10.1103/PhysRevLett.96.035506. [DOI] [PubMed] [Google Scholar]
- 54.Santos SF, Rodrigues JA. Correlation between fracture toughness, work of fracture and fractal dimensions of alumina-mullite-zirconia composites. Materials Research. 2003;6:219–226. [Google Scholar]
- 55.Wasen J, Heier E, Hansson T. Fractal analysis of fracture surfaces in ceramic materials. Scripta Materialia. 1998;38:953–957. [Google Scholar]
- 56.Dubuc B, Quiniou JF, Roque-Carmes C, Tricot C, Zucker SW. Evaluating the fractal dimension of profiles. Physical Review A. 1989;39:1500–1512. doi: 10.1103/physreva.39.1500. [DOI] [PubMed] [Google Scholar]
- 57.Huang SL, Oelfke SM, Speck RC. Applicability of fractal characterization and modeling to rock joint profiles. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1992;29:89–98. [Google Scholar]
- 58.Matsushita M, Ouchi S. On the self-affinity of various curves. Physica D: Nonlinear Phenomena. 1989;38:246–251. [Google Scholar]
- 59.Develi K, Babadagli T. Quantification of natural fracture surfaces using fractal geometry. Mathematical Geology. 1998;30:971–998. [Google Scholar]
- 60.Mecholsky JJ. Fracture mechanics principles. Dental Materials. 1995;11:111–112. doi: 10.1016/0109-5641(95)80044-1. [DOI] [PubMed] [Google Scholar]
- 61.Peitgen HO, Saupe D. The Science of Fractal Images. New York: Springer Verlag; 1988. [Google Scholar]


