Combined linkage disequilibrium and linkage mapping: Bayesian multilocus approach

Abstract

Quantitative trait loci (QTL) affecting the phenotype of interest can be detected using linkage analysis (LA), linkage disequilibrium (LD) mapping or a combination of both (LDLA). The LA approach uses information from recombination events within the observed pedigree and LD mapping from the historical recombinations within the unobserved pedigree. We propose the Bayesian variable selection approach for combined LDLA analysis for single-nucleotide polymorphism (SNP) data. The novel approach uses both sources of information simultaneously as is commonly done in plant and animal genetics, but it makes fewer assumptions about population demography than previous LDLA methods. This differs from approaches in human genetics, where LDLA methods use LA information conditional on LD information or the other way round. We argue that the multilocus LDLA model is more powerful for the detection of phenotype–genotype associations than single-locus LDLA analysis. To illustrate the performance of the Bayesian multilocus LDLA method, we analyzed simulation replicates based on real SNP genotype data from small three-generational CEPH families and compared the results with commonly used quantitative transmission disequilibrium test (QTDT). This paper is intended to be conceptual in the sense that it is not meant to be a practical method for analyzing high-density SNP data, which is more common. Our aim was to test whether this approach can function in principle.

Introduction

There are two main approaches of finding susceptibility genes (quantitative trait loci, QTL) that influence quantitative traits with the aid of molecular markers. One is variance-component-based linkage analysis (LA), where information comes from recombination events occurring between markers within the pedigree (Blangero and Almasy, 1997; Almasy and Blangero, 1998). The other is linkage disequilibrium (LD) mapping, also known as population-based association mapping, which is based on historical recombination events (George and Elston, 1987; Lander and Schork, 1994). In both analyses, one is interested in finding a signal due to close linkage between a marker and a QTL, but they use different sources of information from the data. LA uses the information that exists within families/pedigrees and follows co-segregation of loci, which is broken down by recombination during few generations of the collected pedigree. Association/LD mapping requires a marker allele to be in considerable LD (viz., non-random allelic association) with a QTL allele across the whole population. In this case, the marker and QTL need to be closely linked in the same chromosome in order for LD to persist after several generations.

LA works with known pedigrees and assumes that loci measured at pedigree founders are in linkage equilibrium (i.e., requiring markers to be unlinked). This assumption is often incorrect. LA also needs extended pedigrees and large family size in fine mapping (Darvasi and Soller, 1995). Even if pedigree or family size can be sometimes very large (e.g., in plants), LA-based fine mapping has a low resolution owing to the limited number of recombinants.

In association/LD mapping, the interest is in finding the statistical association between marker loci and trait values. It relies on the assumption that all alleles that affect the trait are inherited from a single or very few common ancestor(s) (Terwilliger and Weiss, 1998). This analysis needs dense markers in order to find the marker that is very closely linked to the QTL. Another drawback of the association analysis is that significant association may be due to population stratification or other confounding factors rather than LD between a considered marker and a near trait locus (Conti and Witte, 2003; Marchini et al., 2004). Combining these two approaches (i.e., LD and LA) into a single analysis, known as LDLA, yields statistically more powerful and robust analysis because linkage information confirms only real association signals (Hernández-Sánchez et al., 2009). In addition, LDLA could improve the mapping resolution (Meuwissen et al., 2002).

Variance-component-based LA uses locus-specific identity-by-descent (IBD) matrix containing sole linkage information (George et al., 2000). This approach has been generalized to LDLA analysis in animal and plant genetics literature. Such variance-component-based LDLA uses a similar model, where linkage and association information are combined in a single IBD matrix (e.g., Meuwissen et al., 2002; Hernández-Sánchez et al., 2009) by assuming that loci measured at pedigree founders can be in LD (i.e., allowing markers to be linked). This is very different from LDLA analyses of human genetics literature, which use mainly quantitative transmission disequilibrium test (QTDT)-based methods (Abecasis et al., 2000a; Ott et al., 2011) testing linkage conditional on LD or the other way round. The overview of previous LDLA and LA methods for quantitative traits has been presented in Table 1. See Ott et al. (2011) for a review of LDLA methods.

Table 1. Overview of previous LA and LDLA methods.

Paper	Model	Data needed	Experimental design	Estimation	1 locus/multilocus	IBD matrix
Meuwissen and Goddard (2004)	LDLA	Haplotypes No. of generations Effective population size	General pedigree	Bayes MCMC	Multilocus	Yes
Lund et al. (2003)	LDLA	Haplotypes	Granddaughter design	Classic ML	1 or 2 locus	Yes
Fulker et al. (1999)	LDLA/TDT	Dense map of diallelic markers Sib-pairs with parental genotypes	Sib-pair	Classic	1 locus	No
George et al. (1999)	TDT	Pedigree	General pedigree	Classic	1 locus	No
Hernández-Sánchez et al. (2009)	LDLA	Genotypes/haplotypes Pedigree No. of generations Effective populationsize	Any population structure	Classic	1 locus	Yes
Pérez-Enciso (2003)	LDLA	Haplotypes Pedigree	General pedigree	Bayes MCMC	1 locus	No
Abecasis et al. (2000b)	TDT	Genotypes	Pedigree	Classic	1 locus	No
Farnir et al. (2002)	LDLA	Haplotypes	Half sib	Classic EM	1 locus	No
Göring and Terwilliger (2000)	LDLA	Genotypes	Any population structure	Classic	1 locus	No
Lee and Van der Werf (2006)	LDLA	Haplotypes	General pedigree	Empirical Bayes/stochastic EM	Multilocus	Yes
Yi and Xu (2000)	LA	Genotypes	General pedigree	Bayes	Multilocus	Yes
George et al. (2000)	LA	Genotypes	General pedigree	Classic	1 locus	Yes
Lange et al. (2013)	LDLA	Pedigree	General pedigree	Classic	1 locus	No

Abbreviations: LDLA, linkage disequilibrium linkage analysis; MCMC, Markov Chain Monte Carlo methods; TDT, transmission disequilibrium test.

Multilocus association analysis is presumably statistically more powerful than single-locus association testing (Zhang et al., 2011) and can reduce the upward bias of effect estimates (Allison et al., 2002). Multiple testing problems can also be avoided when using multilocus models (Kilpikari and Sillanpää, 2003). Note also that Bayesian multilocus association models without a polygenic term have been found to be more robust to the presence of family and population structure than single-locus association models (e.g., Pikkuhookana and Sillanpää, 2009; Kärkkäinen and Sillanpää, 2012).

In addition to the benefits associated with multilocus model, there are several benefits in our LDLA model framework itself. First, our LDLA model yields separate LA and LD signals in addition to combined LDLA signal. In previous variance-component-based LDLA analyses, in order to separate signal sources, one needs to run extra LD and LA analyses. Second, our LDLA model is free of assumptions about parameters of population model such as effective population size, number of generations since base population and known haplotypes for each individual unlike many previous LDLA approaches (e.g., Meuwissen and Goddard, 2001; Meuwissen et al., 2002; Gasbarra et al., 2009; Hernández-Sánchez et al., 2009). For example, supplying strongly incorrect population parameters in LDLA approaches based on the Wright–Fisher model may be detrimental to LDLA (Hernández-Sánchez et al., 2009). Finally, because our Bayesian LDLA model includes additive genotype effects from multilocus association model and additive linkage effects from variance-component-based LA model, most properties of the original models still hold for this new LDLA model. For example, LA-based IBD matrices needed in our LDLA method can be estimated with existing packages, for example, Merlin (Abecasis et al., 2002), SimWalk2 (Sobel and Lange, 1996), Genehunter2 (Kruglyak et al., 1996), LOKI (Heath, 1997; Thompson and Heath, 1999) or SOLAR (Almasy and Blangero, 1998). Moreover, the proposed Bayesian multilocus LDLA model can provide a firm protection against confounding due to family and population structure, because multilocus association model part (see e.g., Kärkkäinen and Sillanpää, 2012) and LA model part (by definition) are both robust to this problem.

Models and methods

We assume that earlier LA or LD studies have already found genetic activity in small chromosomal regions that suggest the presence of QTL (cf. Meuwissen and Goddard, 2004; Cantor et al., 2005). Our LDLA approach is designed to be used as a secondary approach to filter best SNPs (single-nucleotide polymorphisms) as putative QTLs from these regions. In our model, the term QTL is used for the locus, which is associated or linked with actual trait locus, and we consider that QTL exists only in positions where we have genotyped SNP markers. Let us have n individuals from independent families with known pedigrees and from the same population. Let N_M be the number of preselected sets of SNP loci, 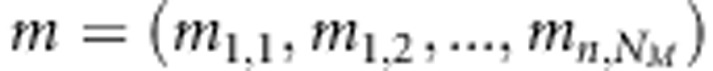SNP genotypes and 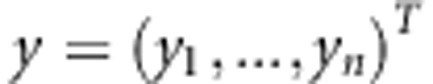the observed continuous phenotypes, where y_i denotes continuous phenotype of the ith individual. We summarize the genotypes as x_i,j=−1, when genotype is AA homozygote, x_i,j=0 for the heterozygote AB and 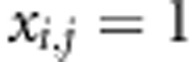for the other homozygote. We follow the notation of Pikkuhookana and Sillanpää (2009) and assume that 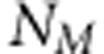is relatively small (a few hundreds at most). A continuous phenotype y_i is explained with genetic factors using the following linear LDLA model

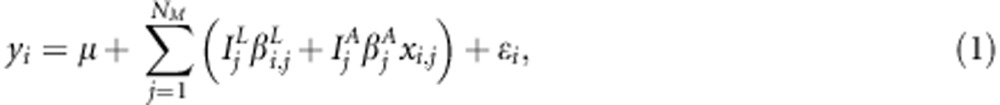where μ is the population intercept and 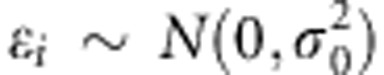is a normally distributed residual term with mean zero and variance 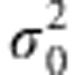. Here, 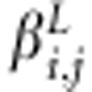is the additive coefficient for the linkage effect of marker j. It is an element in multivariate normally distributed effect vector (over individuals i) with mean 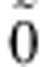(vector of zeroes) and covariance matrix 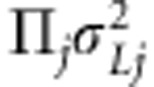, that is, 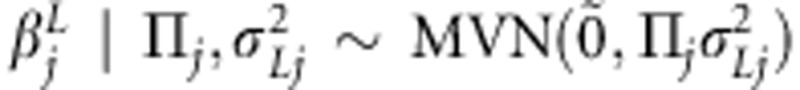. The additive coefficient for the association effect of marker j is 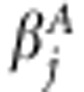. The linkage and association indicators for marker j are 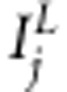and 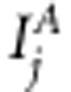, respectively, whose value 1 corresponds to the inclusion, and value 0 to the exclusion of the effect in the model. With restriction 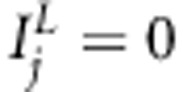for all j, model (1) corresponds to common multilocus association model. In addition, when restricting 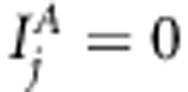for all j, model (1) reduces to a typical multilocus variance component-based LA model. Association indicators can be collected to a vector 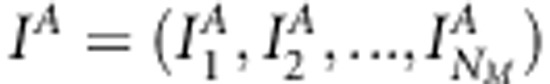and unknown association effects to matrix 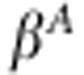whose diagonal elements are 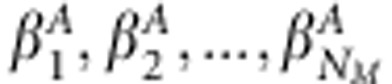and zero elsewhere. Similarly, 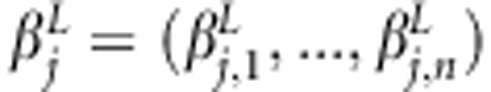, 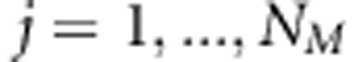is the vector of additive (random) genetic effects due to jth putative QTL with LA covariance 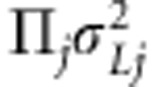. Here, 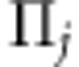is the additive IBD matrix of the putative QTL based on LA information. We use Merlin (Abecasis et al., 2002), which uses information from multiple marker loci simultaneously, to estimate multipoint IBD probabilities (p₀, p₁, p₂) at each SNP position for each pair of individuals. However, one can use any package for estimating IBD probabilities, such as LOKI or SOLAR (for a review of common methods, see Mao and Xu, 2005). We can calculate the expected values of elements of the additive IBD matrix using these probabilities as 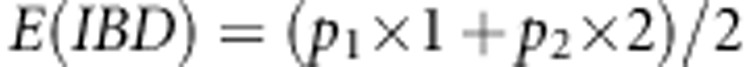, where p₁ is the probability that individuals share one allele IBD and p₂ is the probability that individuals share both alleles IBD. The genotypic data of the jth SNP marker can be written as vector 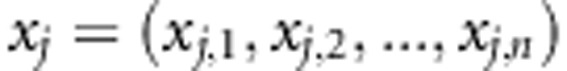, where 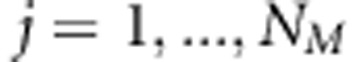, and further as matrix 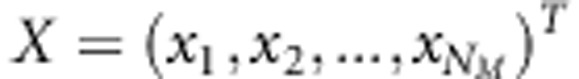. The incidence matrix Z that associates additive linkage effects with phenotypic observations is identified here as an identity matrix Z=I. Matrix Z may also be other than identity matrix for example in cases where there are individuals in pedigree which have no phenotypic values. Now, we can rewrite the linear LDLA-model (1) as

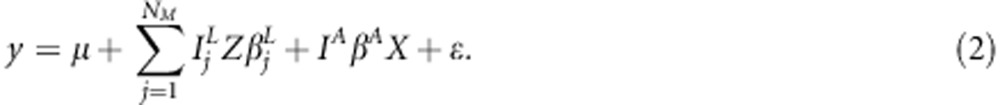To simplify calculations, Mrode and Thompson (1989) and Waldmann et al. (2008) applied transformation for covariance (additive genetic relationship) matrix to obtain prior independence structure for transformed variables. The former standardized variance into 1, whereas the latter restored variance in its original scale. Following the similar principle, we introduced transformation for locus-specific IBD matrices. With transformations 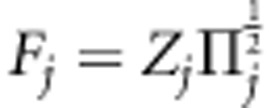and 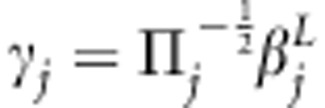, model (2) can be rewritten as

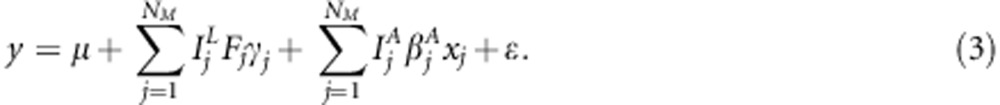With this transformation, we obtai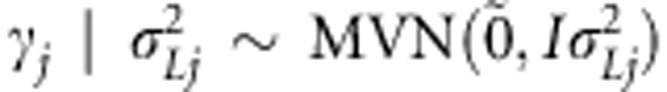n when 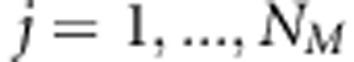. The construction of square-root matrices is shown in Appendix 1.

Hierarchical model

Prior distributions

In Bayesian analysis, one specifies prior distributions for the unknown parameters. For association effects, a prior was assigned as 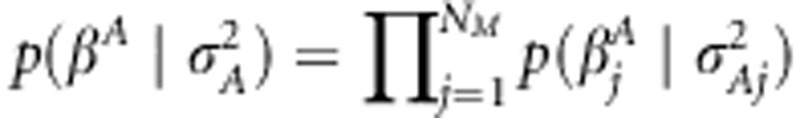. The functional form of 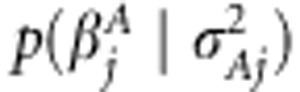is normal density with mean zero and effect-specific variance 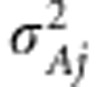. For the effect-specific variances, Jeffreys' prior was assigned as 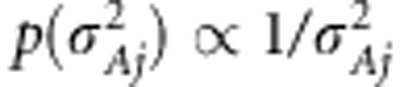. The same shrinkage-based variable selection as described in Pikkuhookana and Sillanpää (2009) is used here to find sparse trait-associated sets of SNPs. This is a double-shrinkage model with two sources of sparseness (indicator-variables and effect shrinkage). Thus, 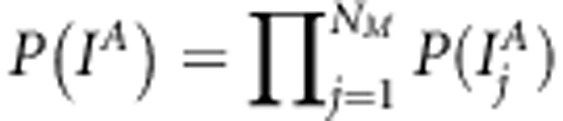and 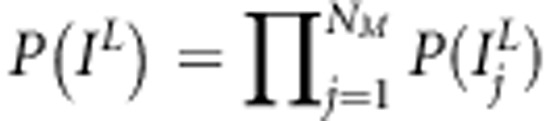. Here, 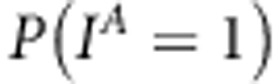represents prior probability of the indicator being one and has been selected to be small. For the effect-specific variances of linkage effects, a Jeffreys' prior was assigned as 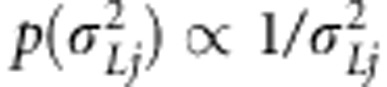. For the transformed linkage effects, a prior was assigned as 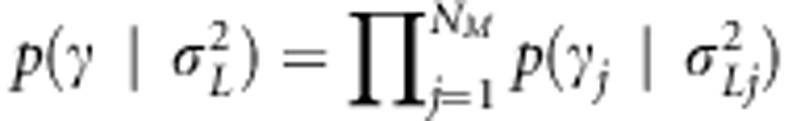, where 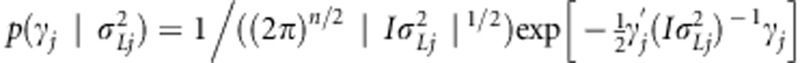. Prior for μ is 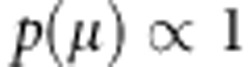and prior density for 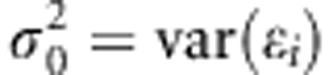is 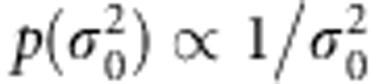. Implementational details are provided in Appendix 1.

Missing data model

In the current simulation study, it is assumed that no phenotypic data are missing. Note that SNP data come to our analysis in two forms: (1) as IBD matrices to the LA model and (2) as coded SNP genotypes to the LD model. Thus, it is natural that in the linkage part of the model the method that is used to estimate multipoint IBD probabilities (e.g., Merlin) also handles in its own way the missing values in genotype data (contributing to the linkage signal). In the association part of the model, missing values are handled as random variables via Bayesian inference following Pikkuhookana and Sillanpää (2009). In this process, the genotypic values of the individuals' parents are accounted for. The joint probability distribution of the marker j over individuals is given by 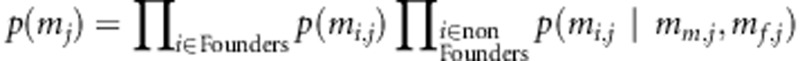, where 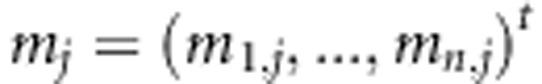is the genotype pattern at marker j. Transmission probabilities follow the Mendelian rules of inheritance. In our genotype data contributing to the association part of the model, we omit the recombination aspect in handling of missing values. However, linkage between markers has been taken into account in estimating IBD probabilities. Thus, the the prior density function of the genetic data is

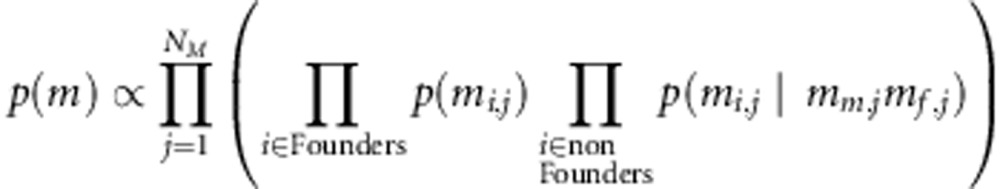More details have been provided in the Appendix 1.

Posterior distributions

Posterior distributions 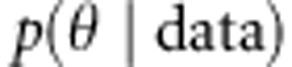for the parameters θ are derived from the likelihood of the data 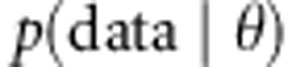and the prior distributions 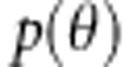(Gelman et al., 2004). From Bayes formula, we obtain the joint posterior density of parameters from likelihood of the data and the prior distributions as 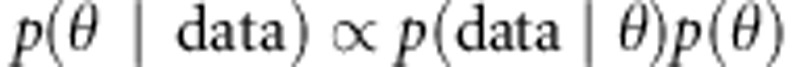. Here, θ represents all unknown parameters and data represents the given data including phenotypes, genotypes and given IBD matrices. The posterior distributions are estimated using Markov Chain Monte Carlo (MCMC) methods.

Examples

Data

We use the same genotype data sample of 15 CEPH families as in our previous study (Pikkuhookana and Sillanpää, 2009). Data were edited to remove 5 individuals with missing genotypes for all markers. This was done to minimize the influence of missing data on the simulation of the phenotype and analysis of the association part of the model. Thus, the number of individuals in our data was 205. Our quality control criteria for choosing markers in the study was Hardy–Weinberg equilibrium, minor allele frequency larger than 5% and only a single missing genotype at a marker. Hardy–Weinberg equilibrium was tested with 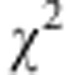-test (Balding, 2006) with a P-value threshold of 0.001. We collected 22 SNP markers that fulfilled all the criteria from chromosome 1 (Table 2). Our selection criteria differ from typical cases of few SNP markers such that we concentrated on markers with few missing genotypes rather than certain small areas. Genotypes that were missing in CEPH database were also missing in our analysis.

Table 2. An overview of selected SNP markers.

SNP locus	NCBI Entrez link	location cM
1	rs594535	4502
2	rs874515	23 752
3	rs726344	33 106
4	rs760594	33 231
QTL	rs1566599	37 481
5	rs905111	37 488
6	rs926830	40 495
7	rs1003323	55 233
8	rs927612	58 007
9	rs556161	61 097
10	rs976574	62 399
11	rs1551331	77 591
12	rs15864	110 094
13	rs930548	112 309
14	rs876694	157 413
15	rs744168	166 361
16-QTL	rs764180	170 067
17	rs725164	170 114
18	rs726427	182 932
19	rs489472	192 344
20	rs1125953	196 235
21	rs1001737	232 484

The name of the SNP on the CEPH database and location on centiMorgans.

Simulated data replicates

To assess average performance of the methods and exclude the influence of sampling variation in the analysis results, we simulated 25 replicated phenotypic data sets conditionally on the genotypic data of selected CEPH families. We used WinBUGS 1.4.3 software to simulate data (Spiegelhalter et al.,1999; Lunn et al., 2000). Simulated QTL positions, with influence on the phenotypic value, were placed on a few such markers that had no missing genotypes. This way, we avoided making any changes on existing linkage patterns in the genotype data that would have an effect on phenotype. Genotypic effects were simulated on the locus between markers 4 and 5 and were (−4, 1, 6) for genotypes (AA, Aa, aa), respectively, and on marker 16 they were (0, 7, 14) for genotypes (BB, Bb, bb), respectively. Simulated QTL between markers 4 and 5 had a smaller effect on phenotype, and that particular marker was removed from the data before the LDLA analysis. Thus, this QTL is expected to be hard to identify with any mapping methods. Simulated heritability of the data replicates varied from 0.418 to 0.584 with a mean value of 0.503. Moreover, the mean QTL heritability of the left QTL was ∼0.064 and that of the right QTL was ∼0.305, while the remainder was due to the polygenes. All replicated data sets were analyzed with both our Bayesian LDLA model and quantitative transmission disequilibrium test (Abecasis et al., 2000a, 2000b).

In addition, we simulated other sets of 25 data replicates. Here, the phenotypic value was simulated using the same QTL positions as in a previous experiment. The stronger genotypic effect (−10, 1, 12) was simulated in the locus between markers 4 and 5 for genotypes (AA, Aa, aa), respectively. Similarly as before, this locus was not included in the data that were used in the analysis. The weaker genotypic effect (0, 3, 6) was simulated on marker 16 for genotypes (BB, Bb, bb), respectively. Thus, the mean QTL heritability of the left QTL was ∼0.308 and that of the right QTL was ∼0.056, whereas overall heritability remained on the same range as in earlier replicated data sets. In the content that follows, we will refer to the above experiments as scenario A (major QTL at position 16) and scenario B (minor QTL at position 16).

Analyses

We analyzed our replicated data sets with the proposed method (Bayesian LDLA) using WinBUGS 1.4.3 for parameter estimation. We used MCMC chain of length 10 000, with burn-in 1000 and thinning of 10; that is, we discarded the first 1000 MCMC samples from the chain and only every 10th MCMC sample was stored and used for estimation. Convergence was assessed by visual inspection of trace plots of different parameters. We summarized our results as the mean posterior occupancy probabilities for SNP j, 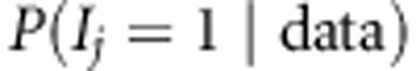, obtained by averaging occupancy probability estimates over 25 replicates. Posterior occupancy probability (or simply QTL-probability) can be calculated as a fraction of MCMC samples where different combinations of linkage and association indicators equal to one. For association 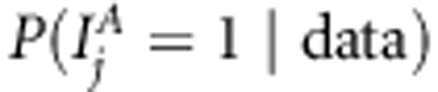, for linkage 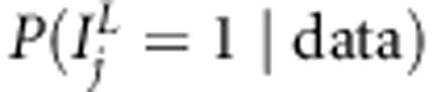, for linkage in presence of association 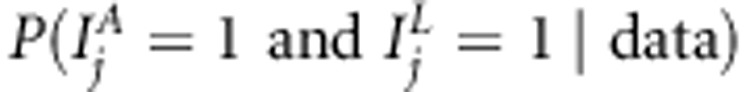and for linkage or association 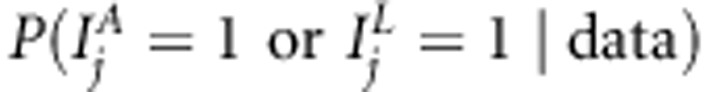. Posterior occupancy probability indicates posterior probability that the corresponding SNP effect is included in the model. Mean posterior occupancy probability provides information about average performance. We also calculated Bayes Factor (BF) of association as

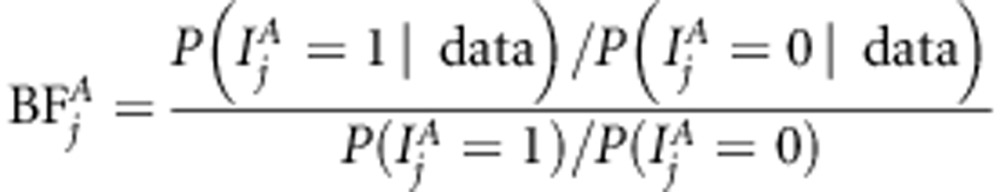for each marker j (see Kass and Raftery, 1995). Bayes factor of linkage, that of linkage and association, as well as BF of linkage or association ( 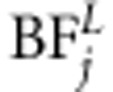, 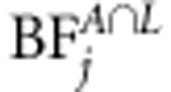and 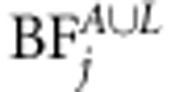) are calculated in a similar principle. Bayes factor is a useful statistic because the Bayes factor scale is independent of prior odds. The following categories have been suggested for Bayes factors according to the strength of evidence provided by data in favor of ‘QTL presence' as opposed to ‘no QTL' (see Jeffreys, 1961). The first class is evidence ‘not worth more than bare mention' when BF is between 1 and 3. The second class is ‘substantial' evidence with BF between 3 and 10. The third class is ‘strong' evidence with BF between 10 and 100. The final class is ‘decisive' evidence with BF above 100. Before MCMC analysis, we first used the Merlin software to estimate IBD matrices for each loci. Three families had one missing founder. As Merlin demands both founders at each family to be present, the missing founder can be created or the existing one removed. We decided to remove the existing founders in these families. Thus, in the linkage part of the model, the number of individuals in the data is three less than that in the association part of the model.

For comparison of the Bayesian LDLA analyses of the current simulated data replicates, we also analyzed the same data with the QTDT program (Abecasis et al., 2000a, 2000b). The QTDT performs LDLA analysis as a joint analysis of means and covariance matrices by using a maximum likelihood and a common association model for pedigree data. The same estimated IBD matrices were used in QTDT as in the Bayesian LDLA analyses with WinBUGS. Three different models analyzed with QTDT included (1) testing the presence of association, (2) testing linkage and (3) testing linkage while simultaneously considering association.

To understand better how our Bayesian LDLA model works, we analyzed the same replicated data sets (scenario A) also with multilocus association model (with restriction 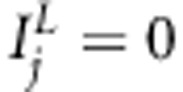for all j in model 1) and with multilocus variance component-based LA model (with restriction 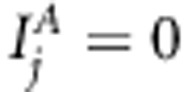for all j in model 1). Details of MCMC estimation and the posterior summaries used were identical as above for Bayesian LDLA analysis.

Results

Bayesian LDLA analysis with replicated data sets

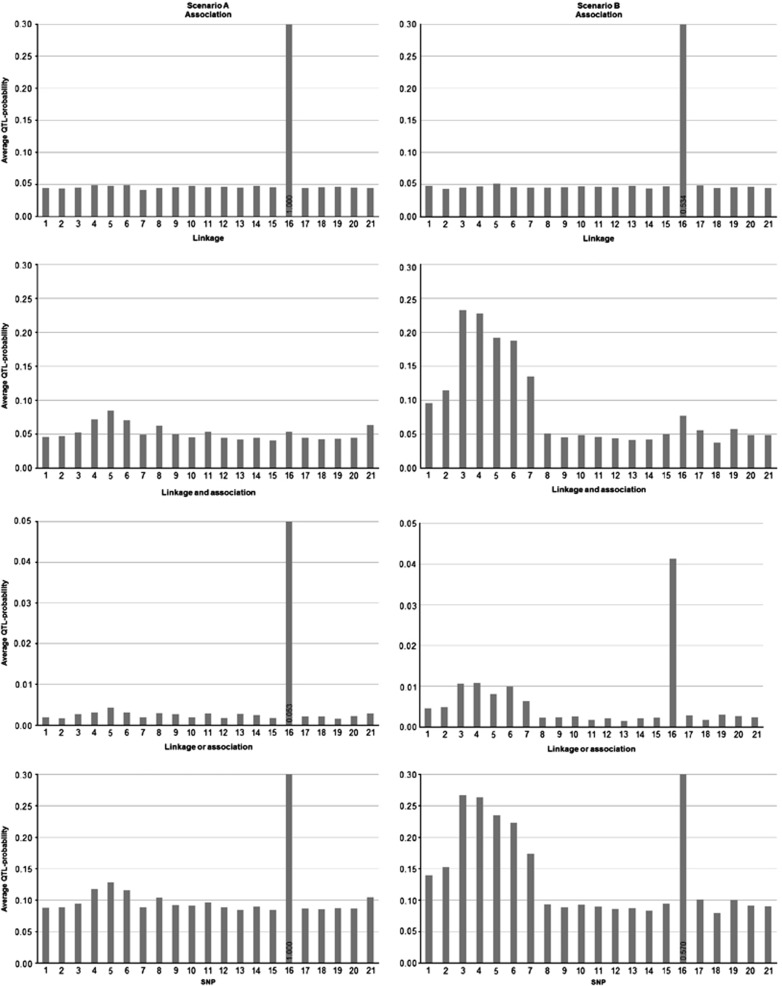
To assess the average performance of the Bayesian LDLA analysis, the results were averaged over 25 replicated data sets (Figure 1).

Figure 1.

Mean posterior occupancy probabilities for SNPs obtained from Bayesian LDLA analysis by averaging QTL-probability estimates over 25 replicated data sets in scenario A (left) and in scenario B (right). Index of SNPs on x-axis and average QTL probabilities on y-axis calculated from indicator variables in the MCMC sample for association (top panel), linkage (second panel), linkage and association (third panel), linkage or association (bottom panel). Note that y-axis scales in panels depend on prior occupancy probabilities. In cases where QTL probability exceeds the upper limit of the y-axis, its value is presented in the bottom of each column of the bar chart.

Scenario A

The LD model of Bayesian LDLA on average detected the simulated stronger QTL at position 16 accurately (top left, Figure 1). In the same analysis, the simulated weaker QTL on the left (QTL between markers 4 and 5) did not show on average almost any association signal at its genomic region. When inspecting the average linkage signal provided by the LA model of Bayesian LDLA (second left, Figure 1), posterior occupancy probabilities were slightly higher in a correct region around the simulated weaker QTL on the left. The average combined linkage or association signal from Bayesian LDLA analysis was very strong at the correct QTL position 16, whereas the simulated weaker QTL on the left, at region between position 4 and 5, showed only a minor peak in this combined analysis (bottom left, Figure 1). Again, the average combined linkage and association signal from Bayesian LDLA analysis was very strong at correct QTL position 16, whereas that of the simulated weaker QTL on the left was only modest (third left, Figure 1).

Scenario B

Here, the LD model of the Bayesian LDLA captured the weaker QTL at position 16 very well (top right, Figure 1). As in scenario A, the left QTL showed no association signal. LA model of Bayesian LDLA found the left QTL region (between markers 4 and 5) quite well (second right, Figure 1). It also showed a small peak at position 16. When inspecting combined signals of linkage or association (bottom right, Figure 1), both QTL regions stand out, even if there are elevated levels of QTL probabilities on every position. The combined signal of linkage and association (third right, Figure 1) shows similar results as the combined signal of linkage or association.

Scenarios A and B

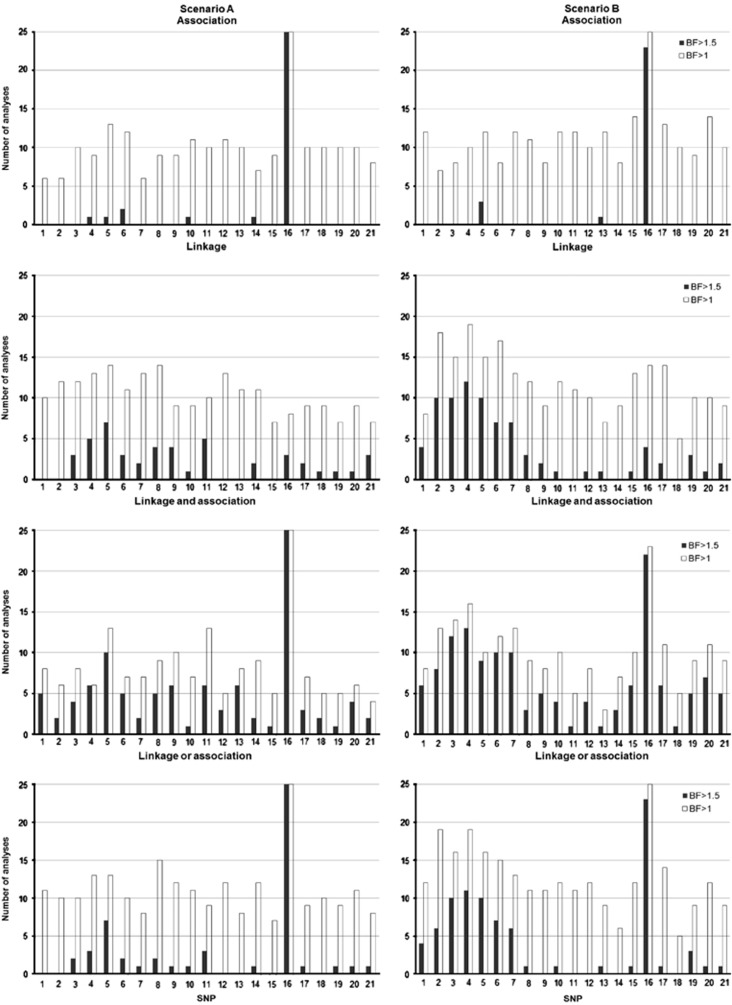
To assess sensitivity of Bayes factor thresholds to judge QTLs, the number of replicated Bayesian LDLA analyses exceeding the given BF threshold by using two hypothetical BF levels 1 and 1.5 was illustrated (Figure 2). Almost none (three or less) of the replicated Bayesian LDLA analyses exceeded the BF threshold of 3 in the vicinity of the weaker QTL on the left (scenario A). Thus, we argue that the BF threshold of substantial evidence 3 is too strict for the weakest QTL in these data. This may be partially due to the fact that indicators act as an additional source of shrinkage and may induce a downward bias on the resulting BFs (Sillanpää et al., 2012). On the other hand, when inspecting Figure 2, the BF threshold of 1.5 seems to protect against false positives while still maintaining real combined LDLA signals around the simulated QTL on the left (especially on panels on bottom, Figure 2). In the figure, BF threshold of 1.0 seems to suffer from false positives, and the QTL evidence is not so clear either.

Figure 2.

Number of Bayesian LDLA analyses where BF exceeds a given threshold. Index of SNPs on the x-axis and the number of analyses where BF exceeds values 1 and 1.5 on the y-axis. Scenario A is shown on the left and scenario B on the right. The first panel shows results from association analysis and the second panel from linkage analysis. The third panel shows results when either linkage or association signal is found in the model, and the case when both association and linkage signals are found simultaneously in the model is in the fourth panel.

QTDT analysis

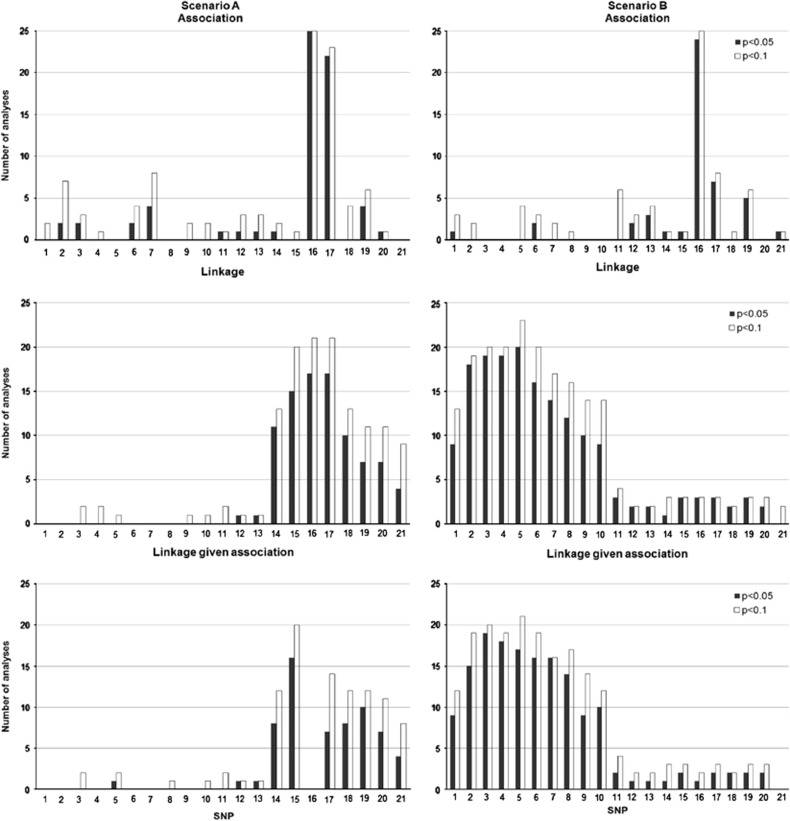
The QTDT program can be used to test the presence of association, linkage or both association and linkage simultaneously. Interpretation of the combined QTDT analysis differs from the Bayesian LDLA analysis presented here. Although the Bayesian combined linkage and association method can separate or combine two sources of signals freely (as was shown in Figure 1), signal detection in QTDT is based on comparing separate analyses of association, linkage and linkage given association (Figure 3). If the QTDT signal of linkage given association seems to disappear (as in bottom left, Figure 3) compared with the signal of the linkage model (middle left, Figure 3) or of the association model (top left, Figure 3), the QTDT signal can be interpreted as the signal of true QTL (Fulker et al., 1999).

Figure 3.

The number of QTDT analyses with significant P-values where P-value exceeds the given values of P-value threshold for significant result of 0.05 and 0.1. Scenario A is shown on the left and scenario B on the right. The panels contain results from sole association analysis (top), sole linkage analysis (middle) and combined association and linkage analysis (bottom).

To assess the sensitivity of P-values to judge QTLs, the number of replicated QTDT analyses exceeding the given threshold of P-values 0.05 and 0.1 was illustrated (Figure 3).

Scenario A

In the analyses of replicated data, the use of the QTDT model on average detected the simulated stronger QTL at position 16 accurately, with averaged P-values varying from 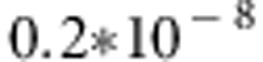to 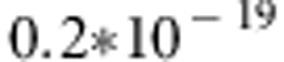. The weaker simulated QTL on the left (in region between markers 4 and 5) was not detected with QTDT too well. Figure 3 clearly illustrates that there is practically no hope to detect the weaker simulated QTL on the left using QTDT. Linkage test found significant P-values only twice in marker 3 (P-values 0.084 and 0.094) and marker 4 (P-values 0.083 and 0.095) and once in marker 5 (P-value 0.067) of the 25 replicated data sets.

Scenario B

QTL at position 16 seems to be found on average correctly by association test in QTDT, even if the QTL heritability at that position is smaller in this scenario. Averaged P-values vary from 0.06 to 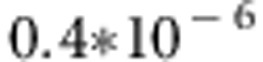. The minor QTL at position 16 was not detected by linkage test or subsequent QTDT test of linkage given association (right, Figure 3). Linkage test in QTDT found on average elevated signals around the correct region of major QTL on the left, although this region is quite wide (from SNP 1 to SNP 10). Because this major QTL region on the left showed no signal in the association test, this QTL cannot be detected by QTDT test of linkage given association either.

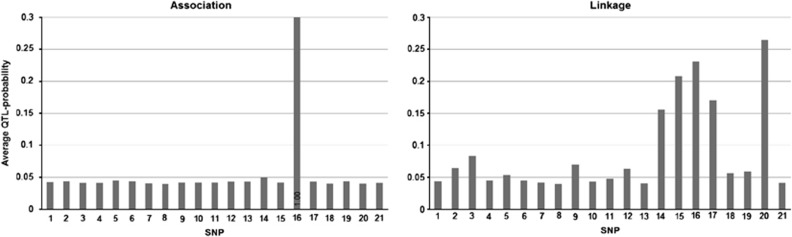
Restricted analyses

Results of the restricted analyses of scenario A data sets are shown in Figure 4. Multilocus association analysis found correct QTL at position 16 (left, Figure 4). No association signal of the weaker QTL between positions 4 and 5 can be found. Unlike LDLA analyses, multilocus variance component-based LA analysis showed linkage signal around position 16 (right, Figure 4). As a drawback, LA analysis suffers from a false positive at position 20, and its signal at the region of the weaker QTL did not seem to be significantly higher than the general signal level.

Figure 4.

Mean posterior occupancy probabilities for SNPs obtained from the restricted analyses of scenario A data. Sole association analysis is on the left and sole linkage analysis on the right. In cases where QTL probability exceeds the upper limit of the y-axis, its value is presented in the bottom of each column of the bar chart.

Discussion

Owing to the limited number of recombination events, LA seems to find QTL regions fine, but it does not separate true QTL from correlated markers. On the other hand, population-based association analysis has a high resolution, but without including LA it tends to give false positives owing to structured data. Thus, we have proposed a conceptual approach of combining LA and LD methods into the Bayesian multilocus LDLA framework. Previous variance component-based LDLA methods developed in plant and animal genetics literature (Table 1) are relying to a certain extent on known haplotypes, which are costly/expensive to collect, and/or they need assumptions about population demography (Hernández-Sánchez et al., 2009). Similar to LDLA approaches of human genetics, our method makes fewer such assumptions than previous methods developed in plant and animal genetics literature (Table 1), and it takes advantage of existing packages on IBD estimation. Combining LA and LD methods together provides more accurate analysis. Combined analysis using QTDT can find true simulated position of QTL, whereas sole association and LA gives less accurate results. The weaker-simulated QTL (scenario A) on the left (in region between markers 4 and 5) was not found at all with QTDT. In addition, Bayesian LDLA had difficulties in finding that QTL, but it showed at least a weak signal. The other simulated QTL was found with Bayesian LDLA with probability one. Poor identification of the smaller effect QTL may be due to the fact that the simulated effect on that QTL was much weaker than the effect of the other QTL. Our Bayesian LDLA outperformed QTDT in replicated simulation analysis of scenario A. It showed better power to identify also the smaller effect QTL. In scenario B, QTDT showed either clear linkage signal or clear association signal for each QTL but not both signals for the same QTL. Thus, QTDT test of linkage given association could not detect the QTLs similarly as Bayesian LDLA analysis. The interesting difference between these two models was that the region showing linkage signal around major QTL (between positions 4 and 5) was few SNP markers wider in QTDT than in Bayesian LDLA analysis.

Restricted analyses of scenario A give hint of the reason why Bayesian LDLA model found no linkage signal at position 16 (second left, Figure 1). It seems that this is a consequence of including various kinds of genetic (LA and LD) effects simultaneously to the model and performing Bayesian variable selection to them jointly. Similar behavior has been seen earlier by Bhattacharjee et al. (2008) and Pikkuhookana and Sillanpää (2009), where SNP marker information and gene expression information were considered jointly in the model, and the stronger information type alone explained most of the variation in the genomic region. In Bayesian LDLA model with scenario A data, the association signal is so strong that it leaves nothing to be explained for linkage signal (second left, Figure 1). The above kind of ‘winner takes it all' phenomenon is suggested by analyzing the same data with Bayesian LDLA model, where association indicators are restricted to zero (with restriction 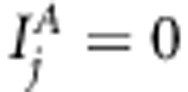for all j). Here, one can see clear elevated levels of linkage signal around QTL position 16 (right panel, Figure 4) as in QTDT.

Our results are in agreement with previous observations that simultaneous modeling of the association and linkage gives more accurate results than modeling them separately. Generally, analyzing data with the LDLA model does not suffer from spurious associations due to population demography and relatedness, which are the main difficulties of the LD model. This is because LA is robust to structured data and gives good control for the LD part of the model (Sillanpää, 2011). Earlier studies (Pikkuhookana and Sillanpää, 2009; Kärkkäinen and Sillanpää, 2012) have shown that the multilocus association model seems to be robust to cryptic relatedness, and thus our Bayesian multilocus LDLA method introduces robustness on each part of the model.

Electronic-database information

CEPH genotype database, http://www.cephb.fr/cephdb/

NCBI GenBank, http://www.ncbi.nlm.nih.gov/Genbank/

Appendix 1

Handling of the missing values of genotypic data in the association part of the model is given here. We assumed Mendelian transmission, uniform allele frequencies and that genotypes are missing at random (Rubin, 1976). Note that assuming missing data mechanism to be random in TDT is known to be a poor choice, as it tends to inflate linkage signals (e.g., Allen et al., 2003; Nicodemus et al., 2007). However, because the new Bayesian LDLA model has been constructed from two separate (LD and LA) models and assuming random missing data mechanism is not a problem in either of them, most properties of the original models still hold for this new LDLA model. In the WinBUGS software, we created two artificial individuals who are parents of all founders. These individuals are heterozygotes in all their markers allowing missing founder genotypes to have all possible allele combinations. Owing to total probability, the genotypes of the founders are dependent on the genotypes of the rest of the pedigree, creating both downward and upward dependencies.

Construction of diagonalizing transformations for the IBD matrices:

Singular value decomposition on symmetric matrix A is 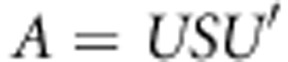, where U is the orthonormal matrix ( 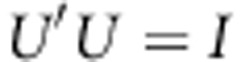and det(U)=1) and S is the diagonal matrix (S =diag(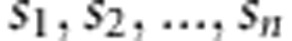)). Required square-root matrix is achieved by equation 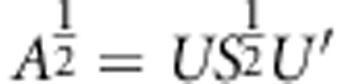and inverse square-root matrix by .

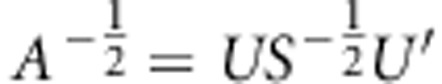Jeffreys' improper prior 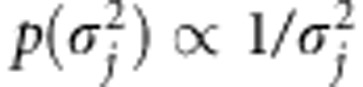is used to induce sparseness into our model (Xu, 2003). Jeffreys' prior equals Inv-Gamma(0,0) prior, which is also improper (Yi and Xu, 2008). Assuming Inv-Gamma(0,0) prior for effect-specific variance components is a special case of scale mixture parameterization of Student's t-distribution, which is assumed marginally for 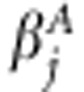(Tipping, 2001). WinBUGS program does not allow the use of improper priors, and thus we approximated the improper prior with a proper one. One solution is to use Inv-Gamma(a,b) prior with a and b close to zero. We have earlier found that this leads to numerical instability producing ‘trap messages' in WinBUGS (Pikkuhookana and Sillanpää, 2009). Let 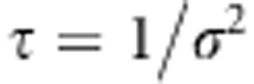be the precision parameter. We used transformation 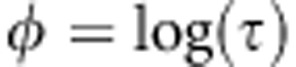for the precision parameters. Prior 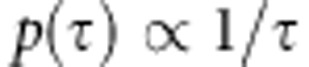leads to flat prior for 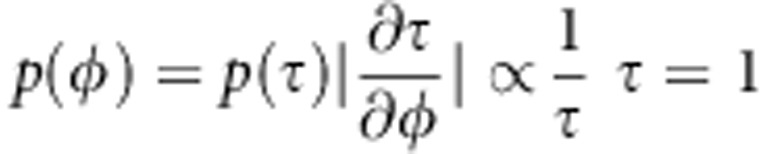(see Gelman et al. 2004, p. 65). Flat prior is also improper, but when we restrict it to some finite range, it will become a proper prior. Flat prior for 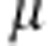is also improper, and we approximate that with flat normal density with zero mean and large variance. With small modifications, our quantitative model can be used for binary phenotype. Logistic regression (see e.g. Hosmer and Lemeshow, 1989) is a good tool for modeling binary traits.

The authors declare no conflict of interest.