Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2013 Oct 23;112(3):255–264. doi: 10.1038/hdy.2013.101

Coestimation of recombination, substitution and molecular adaptation rates by approximate Bayesian computation

J S Lopes 1,2,6,*, M Arenas 3,4,6, D Posada 3, M A Beaumont 1,5
PMCID: PMC3931165  PMID: 24149652

Abstract

The estimation of parameters in molecular evolution may be biased when some processes are not considered. For example, the estimation of selection at the molecular level using codon-substitution models can have an upward bias when recombination is ignored. Here we address the joint estimation of recombination, molecular adaptation and substitution rates from coding sequences using approximate Bayesian computation (ABC). We describe the implementation of a regression-based strategy for choosing subsets of summary statistics for coding data, and show that this approach can accurately infer recombination allowing for intracodon recombination breakpoints, molecular adaptation and codon substitution rates. We demonstrate that our ABC approach can outperform other analytical methods under a variety of evolutionary scenarios. We also show that although the choice of the codon-substitution model is important, our inferences are robust to a moderate degree of model misspecification. In addition, we demonstrate that our approach can accurately choose the evolutionary model that best fits the data, providing an alternative for when the use of full-likelihood methods is impracticable. Finally, we applied our ABC method to co-estimate recombination, substitution and molecular adaptation rates from 24 published human immunodeficiency virus 1 coding data sets.

Keywords: ABC, recombination, molecular adaptation, mutation, dN/dS, HIV-1

Introduction

In nature, different evolutionary processes, such as recombination, substitution and selection, shape the genetic diversity of a population as generations go by. The traces left behind in the gene pool result from the joint action of all the evolutionary processes together, and, ideally, one would want to estimate these parameters simultaneously to avoid potential biases. For instance, ignoring the presence of recombination can bias the estimation of gene trees (Posada and Crandall, 2002) and derived inferences like growth rates (Schierup and Hein, 2000) or molecular adaptation (Anisimova et al., 2003; Scheffler et al., 2006; Arenas and Posada, 2010).

As far as we know, only Wilson and McVean (2006) and Wilson et al. (2009) have proposed methods for the co-estimation of recombination and adaptation rates from coding sequences. The former used an approximation to the coalescent with recombination based on the product of approximating conditionals likelihood and the copying model of Li and Stephens (2003), which was implemented in the package OmegaMap using a Markov chain Monte Carlo framework. The latter introduced an approximate Bayesian computation (ABC) method to jointly infer recombination, adaptation and substitution rates from a particular data set of Campylobacter jejuni, but did not explore further the statistical method. Noticeably, both methods assume that recombination cannot occur within codons, which has been shown to bias the estimation of adaptation rates at individual sites (Anisimova et al., 2003; Arenas and Posada, 2010). On the other hand, the effect of different selective regimes on estimates of the recombination rate has not been evaluated in detail.

Additionally, an accurate choice of the underlining substitution models of evolution also has a significant role in molecular evolution studies (see Sullivan and Joyce, 2005 and references therein). Traditionally, model selection methods require the calculation of likelihood functions; however, for complex models these calculations may become prohibitive. In these cases, the ABC framework can provide a feasible way to choose between complex models (Beaumont, 2008; Cornuet et al., 2008).

In this study we have developed an ABC method for inferring jointly rates of recombination, molecular adaptation and substitution from coding sequences, while accounting for intracodon recombination. We have investigated a large number of summary statistics that are potentially informative about these parameters, and used the mean square error to choose a subset for efficient computation. We have also tested the use of a new ABC approach for model choice and assessed its robustness to model misspecification. In addition, we have compared the performance of our ABC method with that of OmegaMap, PAML (Yang, 2007) and LAMARC (Kuhner, 2006). Finally, we applied our ABC method to analyze 24 published human immunodeficiency virus 1 (HIV-1) data sets.

Materials and methods

ABC approach based on rejection/regression algorithm

The aim of the ABC approach is to summarize typically high-dimensional data by a vector of summary statistics S and then obtain an estimate of the posterior distribution of the parameter vector X in the model of interest:

graphic file with name hdy2013101e1.jpg

where P(X) is the prior distribution, P(S|X) is the likelihood function and P(S) is the marginal likelihood, 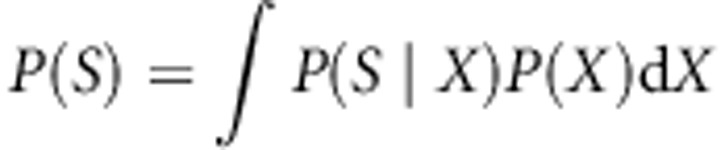Inline graphic. In practice the likelihood function cannot easily be evaluated and the posterior distribution is estimated from simulations.

Recently there has been a great increase in the application of ABC methods for problems in population genetics, and this has largely been driven by the availability of useful software packages (for example, ABCtoolbox package (Wegmann et al., 2009), ABC package (Csillery et al., 2012) or DIY-ABC (Cornuet et al., 2008)). These authors have developed a number of important enhancements to the original rejection and regression algorithms (reviewed in Beaumont (2010)). However, a recent study by Blum et al. (2013) has demonstrated that the original regression approach of Beaumont et al. (2002) typically performs well when compared with more recent developments, and currently there seems to be no ‘best' method across all scenarios. In particular regression adjustment without any selection of summary statistics tends to outperform methods based on partial least squares. In the present study we use a rejection algorithm (Pritchard et al., 1999) and a regression algorithm (Beaumont et al., 2002). Although our method does use a technique for finding an ‘optimal' subset of summary statistics, we demonstrate that this is motivated by its improved performance (as judged by mean square error) over regression adjustment based on all the summary statistics.

In outline, for the rejection algorithm, trial values Xi are simulated from the prior P(X); data are simulated by running the model with Xi; these are summarized by Si and the real data are summarized by S* for some distance metric d(·), the Xi for which d (S, S*)<δ are accepted. These are then regarded as drawn from the posterior distribution. In the regression algorithm the points that are retained by the rejection algorithm are then adjusted as follows. A weighted linear regression—weighted as a function of d(·)—gives an estimate of the posterior mean 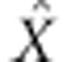Inline graphic as a linear function of S. On the assumption that only the posterior mean changes with S, and no higher moments, then the adjustment 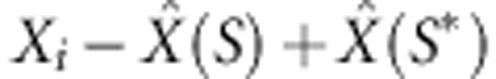Inline graphic should yield samples drawn approximately from the target posterior distribution. Explicit algorithms for these methods are given in Beaumont (2010), but see also Blum et al. (2013). Because our aim is to estimate recombination, adaptation and codon substitution rates from coding sequence alignments, the summary statistics to be used in ABC were chosen according to their correlation with these parameters.

Substitution models and prior distribution considered

The simulated data were obtained using the backwards-in-time coalescent-based program NetRecodon (Arenas and Posada, 2010), which allows recombination breakpoints to occur between and within codons and permits the simulation sequences under a wide range of codon-substitution models and demographic scenarios. Notice that under GY94 substitution codon models, only one nucleotide may change per codon substitution event and, therefore, these models can be crossed with nucleotide models. On the other hand, note that recombination only occurs at the nucleotide level (Arenas and Posada, 2010). Here we simulated data under four codon-substitution models with increasing complexity levels:

Model A: GY94 × K80, where the transition over transversion ratio rate is assumed to be 2.0 (a common value in real data), and the codon frequencies are equally distributed.

Model B: GY94 × GTR+Gnuc with parameter values typical of HIV-1 data sets (following Carvajal-Rodriguez et al. (2006)), particularly, using codon frequencies calculated from the nucleotide frequencies fA=0.35, fC=0.17, fG=0.23 and fT=0.25, transition rates RA–C=3.00, RA–G=5.00, RA–T=0.90, RC–G=1.30, RC–T=5.30 and RG–T=1.00, and alpha shape of the gamma distribution of 0.70.

Model C: GY94 × GTR+Gnuc+Gcodon: model B with an additional gamma distribution for the non-synonymous/synonymous rate ratio (ω) variation per codon. The alpha shape for the latter distribution was obtained from the work of Yang et al. (2000) on HIV-1 (M5 codon model, α=0.557).

Model D: GY94 × GTR3+Gnuc+Gcodon: model C with different GTR substitution rates for each position of the codon calculated from the HIV-1 data set published by Van Rij et al. (2003), and using codon frequencies calculated from the nucleotide frequencies for each position in the codon fA1=0.32, fC1=0.23, fG1=0.31, fT1=0.15, fA2=0.42, fC2=0.18, fG2=0.17, fT2=0.23, fA3=0.50, fC3=0.14, fG3=0.16 and fT3=0.20, changing rates R(A−C)1=2.861, R(A−G)1=4.66, R(A−T)1=0.27, R(C−G)1=0.11, R(C−T)1=4.52, R(G−T)1=1.00, R(A−C)2=195.00, R(A−G)2=4186.73, R(A−T)2=583.60, R(C−G)2=287.81, R(C−T)2=3937.27 and R(G−T)2=1.00, R(A−C)3=1.44, R(A−G)3=6.45, R(A−T)3=1.20, R(C−G)3=1.13, R(C−T)3=9.54 and R(G−T)3=1.00, and alpha shape of the gamma distribution for rate variation among nucleotide sites of 0.028.

Here GY94 × K80 refers to the GY94 codon model (Goldman and Yang, 1994) crossed with the K80 nucleotide model and GY94 × GTR+G refers to that same codon model crossed with the GTR nucleotide model under a gamma distribution for rate variation among nucleotide sites (+Gnuc), or for ω variation among codons (+Gcodon).

The parameters of interest throughout the manuscript were: the scaled recombination rate ρ=4Nrl, where N is the effective (diploid) population size, r is the recombination rate per nucleotide and l is the number of nucleotides in the sequence; the non-synonymous/synonymous rate ratio ω; and the scaled codon substitution rate θ=4NμL, where μ is the substitution rate per codon and L is the number of codons in the sequence. Data were simulated using values of these parameters sampled from different prior distributions. The scaled recombination rate ρ was sampled from a uniform prior distribution between 0 and 50 (note that ρ=50 corresponds to a very high recombination rate with 141 expected recombinant events in the neutral case when considering 15 sequences). In nature, the selective pressure in codon sequences is thought to be mainly purifying (for example, Hughes et al., 2003). Therefore, for ω we choose a lognormal prior distribution with a location parameter of log10 of 0.3 and scale parameter of 0.4. In this way we obtain a prior distribution with only positive values, with a median 0.3 and with small probability of being higher than 1, which we believe represents well our prior beliefs about the distribution of this parameter in real data. The scaled codon substitution rate θ was simulated under a uniform prior distribution between 50 and 300 (nucleotide diversity of between 5 and 20%).

For each of the four scenarios, and using the priors described above, we generated 50 000 samples of n=15 sequences with L=333 codons and an effective population size N=1000. The four simulated data sets were used as reference tables (that is, very large tables of simulations to be reused many times in ABC (Cornuet et al., 2008)). Finally, we generated 1000 data sets for each scenario with values of ρ, ω and θ ranging from the entire extent of the prior, to be used as test data sets (that is, simulated real data for which the true values of the parameters are known).

Definition and choice of summary statistics

We defined an initial pool of 26 summary statistics that were applied at the nucleotide, codon and amino-acid levels (Table 1). Three of the summary statistics consisted of fast statistical tests for detecting recombination: the maximum chi-squared method (χ2, Smith, 1992), the neighbor similarity scope (NSS, Jakobsen and Easteal, 1996) and the pairwise homoplasy index (PHI, Bruen et al., 2006), available in the PhiTest software (Bruen et al., 2006). Other chosen summary statistics were the mean, standard deviation (s.d.), skewness (sk) and kurtosis (ku) of the nucleotide diversity (π), number of segregating sites (S) and heterozygosity (H):

Table 1. Description of the 26 summary statistics used in this work.

Amino-acid level a Codon level a Nucleotide level a
Mean of π (aaπav) Mean of π (cdπav) PHI
s.d. of π (aaπsd) s.d. of π (cdπsd) NSS
sk of π (aaπsk) sk of π (cdπsk) χ2
ku of π (aaπku) ku of π (cdπku) S (nucS)
Mean of H (aaHav) Mean H (cdHav)  
s.d. of H (aaHsd) s.d. of H (cdHsd)  
sk of H (aaHsk) sk of H (cdHsk)  
ku of H (aaHku) ku of H (cdHku)  
S (aaS) S (cdS)  
aaπav/(cdπav–aaπav) (NSRav)  
aaπs.d./(cdπsd–aaπs.d.) (NSRs.d.)  
aaπsk/(cdπsk–aaπsk) (NSRsk)  
aaπku/(cdπku–aaπku) (NSRku)  
Open in a new tab
a

Summary statistics abbreviations are shown in parentheses.

graphic file with name hdy2013101e5.jpg

where ni is the number of total states at site i, m is the number of possible states and fj is the frequency of state j. Finally, we introduced a series of summary statistics, similar to the ω ratio but faster to calculate, that consider information at the codon (cd) and amino-acid (aa) levels jointly (non-synonymous ratio, NSR):

graphic file with name hdy2013101e6.jpg

the use of disequilibrium measures such as pairwise D, D′ or r2 was not considered because they require the comparison of all sites against each other, which would imply heavy computational costs.

The motivation behind using summary statistics is to reduce the dimensionality of the data (D). Ideally one wants to use a set of statistics S=(S1, S2, …, Sn) such that the posterior distribution P(X|S) is similar to the posterior distribution P(X|D). The key consideration is to choose enough summary statistics so that S is close to sufficient for the parameters of the model, while taking into account the increasing inaccuracy of estimation with the number of summary statistics (the so-called curse of dimensionality). The choice of the most suitable summary statistics is still problematic for ABC (Beaumont, 2008). Several attempts to provide a general methodology have been proposed, but there is as yet little consensus on the best approach (Blum et al., 2013). One of the most promising approaches is that of Fearnhead and Prangle (2012), in which, motivated by the need to minimize the expected mean squared error, they prove that the optimal summary statistic for any parameter is the posterior mean for that parameter. Although the posterior mean is unknown it can be estimated in a pilot set of simulations using local regression (as is indeed the aim of the regression adjustment method of Beaumont et al. (2002)). The criterion of Fearnhead and Prangle (2012) does not pertain to the posterior variance, only to the posterior mean. By contrast, our approach aims to minimize the mean integrated squared error (MISE), which is equal to the sum of the mean squared error and the posterior variance. Although it would be desirable in the long term to develop a principled proof-guided method along the lines of Fearnhead and Prangle (2012) we have taken a more empirical approach, following earlier authors (Veeramah et al., 2012), in which the performance of the ABC method for different combinations of summary statistics is evaluated through the use of test data sets in which the true parameter values are known. We aimed to find combinations that minimized the MISE for each parameter over a range of parameter values sampled from the prior:

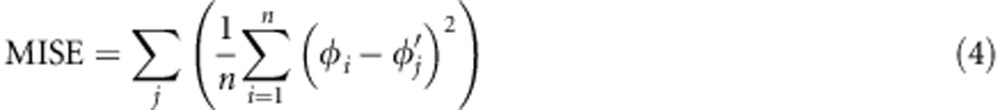graphic file with name hdy2013101e7.jpg

where n is the number of sampled points from the posterior distribution, φi is the ith sampled point from the posterior distribution and φ is the true value of parameter of the jth test data set.

With a pool of 26 summary statistics, the set of all possible combinations is large. In order to reduce this number we chose an initial subset of summary statistics and the order that the remaining summary statistics were added to such subset. This was done by calculating a multiple correlation coefficient between every parameter and different sets of summary statistics with the leaps package (Lumley and Miller, 2004) in R. This way we tested all possible combinations of groups of independent variables (the summary statistics) with respect to a single dependent variable (the parameters) while accounting for ‘over-fit' of the regression model using the Mallow's Cp index:

graphic file with name hdy2013101e8.jpg

where P is the number of predictors, SSEP is the error sum of squares for the model with p predictors, Z2 is the residual mean square after regression on the complete set of predictors and N is the sample size. This procedure provides a ‘best' set of summary statistics for each parameter considered (recombination, substitution rate and molecular adaptation). We then took the union of the ‘best' set of summary statistics of each parameter in order to have one single set that enables us to infer parameters jointly and compare different models.

Optimal tolerance and number of simulations

Following Beaumont et al. (2002) we have chosen the tolerance by setting a proportion of simulations Pδ to be accepted according to d(S, S*). We evaluated the use of different combinations of number of simulations and tolerance intervals by using test data sets. 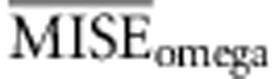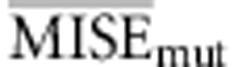For each combination we used 1000 test data sets and calculated their average MISE for the three parameters of interest: rates of recombination, molecular adaptation and substitution (that is, Inline graphic, Inline graphic and Inline graphic). In order to compare the different combinations in use using a single measurement of error, we devised a composite MISE value as:

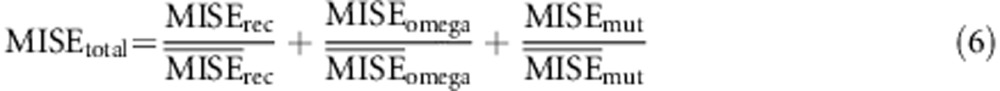graphic file with name hdy2013101e12.jpg

The set of the different conditions to be tested will have an average 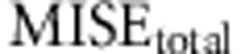Inline graphic equal to the number of parameters to estimate (see for example Figure 2, where the average of the points of each panel is 3). For this reason, the composite value not only helps the comparison between different conditions, but also scales the error values to the number of parameters, allowing for a better comparison of the behavior of the different models.

Results

Experiment I. Selection of the preliminary subsets of summary statistics

The initial experiment focused on choosing the most suitable summary statistics set for estimating recombination, adaptation and substitution rates. The first approach was to select a preliminary subset. Considering the four reference tables and using the Cp index, we obtained the most linearly correlated subsets of 1, 2, …, 6 summary statistics with each parameter for the four models (see Supplementary Tables S1−S4). This information was used to choose a preliminary subset of summary statistics and the order in which the remaining summary statistics were added to that subset. Thus, the preliminary subset was composed of eight summary statistics (PHI, NSS, χ2, aaπav, aaS, cdHav, cdS and nucS) and the order of addition of the remaining summary statistics was cdπav, cdπs.d., aaHav, aaHs.d., cdπsk, NSRav, aaπs.d., cdHs.d., aaπsk, cdHsk, aaHsk, cdHku, aaHku, aaπku, cdπku, NSRs.d., NSRsk and NSRku.

Experiment II. Selection of the final set of summary statistics and accuracy of the ABC method

For the selection of the final set of summary statistics, we applied the developed ABC method to analyze the 1000 test data sets of each model, using the points simulated under the appropriate model, and accepted the closest 0.2% (100 samples). The regression step was performed on each parameter at a time after applying a log transformation to ensure that the regression-adjustment would not project points outside the region of support of the model. The regression-adjusted parameters were then back-transformed. We used each set of summary statistics to perform ABC on the test data sets as follows: taking a model at a time, we analyzed the 1000 test data sets and calculated their median MISE for each parameter (see Supplementary Tables S5−S8); whenever the added summary statistic decreased the MISE, it was added to the preliminary subset of summary statistics. Upon considering the results for the four models, we chose a final subset of 22 summary statistics (PHI, NSS, χ2, aaπav, aaπs.d., aaπsk, aaπku, aaHav, aaHs.d., aaHsk, aaHku, aaS, cdπav, cdπs.d., cdπsk, cdπku, cdHav, cdHs.d., cdHsk, cdHku, cdS, nucS). This subset contains all the suggested summary statistics but the NSRs, which are composite summary statistics calculated as nonlinear functions of aaπ and cdπ.

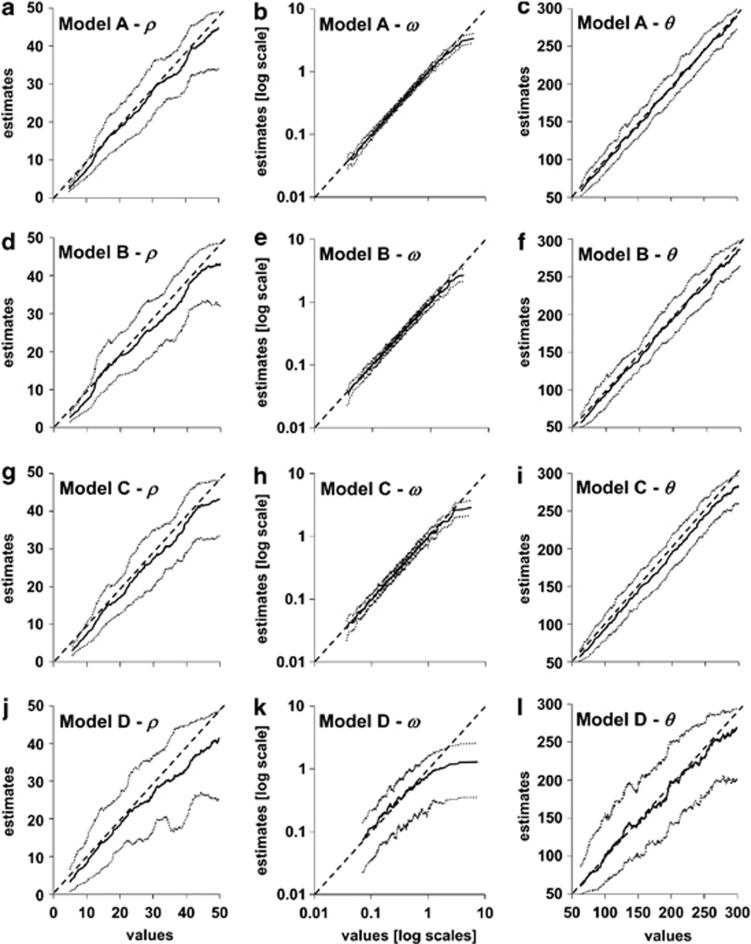
In Figure 1 we present the true values of the parameters that gave rise to the test data sets and their point estimated values (mode of the posterior distribution) using ABC with the final subset of summary statistics. Under the simpler cases (models A, B and C), ABC estimations were accurate, particularly for ω and θ. When considering the most complex scenario (model D), the correlation between the true and estimated values decreased, especially for ω. Under this model each codon can take a different value for ω and each nucleotide position in the codon a different substitution scheme, and thus parameter estimation becomes more difficult. Overall, our results show that the chosen summary statistics can accurately co-estimate recombination, adaptation and substitution rates. As a side study presented in the Supplementary Information, we considered the 1000 test data sets from model A and performed ABC using two different table references with 50 000 simulations each—one table assumed no recombination (ρ=0) and the other no adaptation (ω=1). Results suggest that unaccounted recombination leads to bias in adaptation (Supplementary Figure S1C). Interestingly, contrary to the two sets observed by Scheffler et al. (2006), the trend is for the presence of recombination to lead to an underestimation of global adaptation by using ABC. However, in our case we consider the overall impact of low and high recombination in different values of adaptation. Regarding the impact of ignoring adaptation, this seems to also lead to underestimation of recombination, especially for higher values of recombination (Supplementary Figure S1D).

Figure 1.

Figure 1

Open in a new tab

Accuracy of ABC estimates of ρ, ω and θ rates. The full line indicates the estimated value (y axis) corresponding to each of the 1000 test data sets generated using models A–D under a given true value (x axis). Dotted lines indicate 95% credible intervals. Panels (a) to (l) show results for each parameter of each model as described in the panel's title.

Experiment III. Finding the optimal tolerance and number of simulations

Following the choice of the summary statistics, we studied the optimal tolerance interval and number of simulations. We performed ABC analysis under the same conditions as before and used the set of summary statistics proposed in Experiment II. This time we varied the total number of simulated data used and the tolerance interval. The analyses were performed using the full table references with 50 000 simulations and two subsets of it, 12 500 and 25 000 simulations, while the tolerance intervals were set to 50, 100, 200, 400 and 800 simulated samples, resulting in 15 different simulation scenarios. For each one, we calculated the average MISE for the ABC analysis of the 1000 data sets for each of the three parameters of interest and under models A−D. 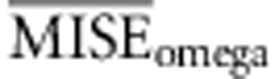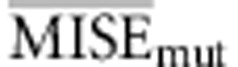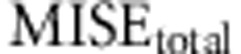In particular, we calculated the average MISE among all the analyses for each parameter separately (that is, Inline graphic, Inline graphic and Inline graphic) and, following equation (6), we calculated Inline graphic.

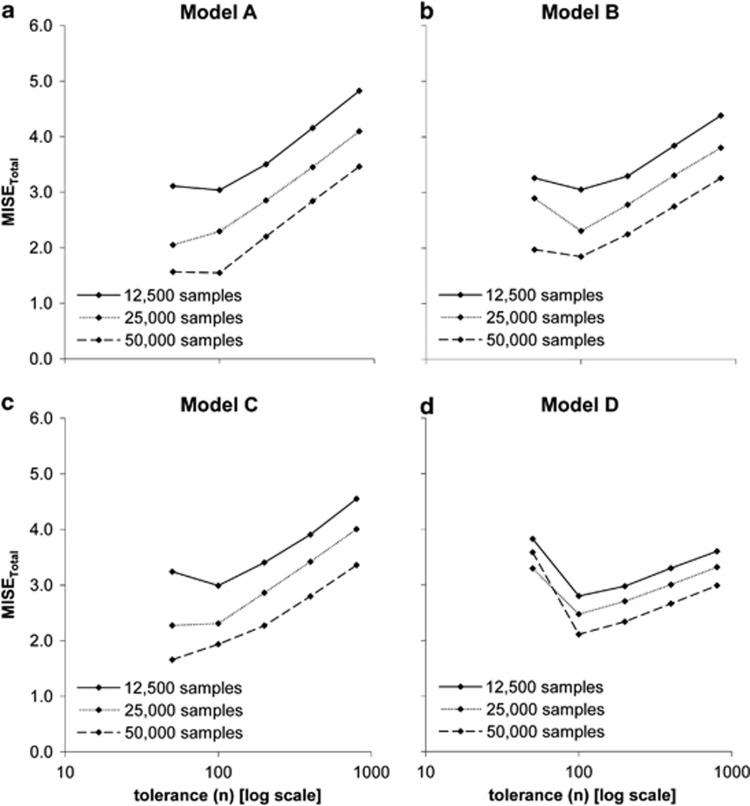
In Figure 2 we show 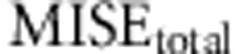Inline graphic as a function of tolerance for models A–D (see Supplementary Figures S2–S4 for results on the MISE of each of the three parameters). Here the MISE values increased considerably when using 25 000 or 12 500 simulations, suggesting that we should not decrease the number of simulated data below 50 000. Likewise, as we moved the tolerance interval down to 100 data sets the MISE decreased consistently, but for lower tolerance intervals the MISE was maintained and even increased. This suggests that a tolerance of 100 data sets (when using either 12 500, 25 000 or 50 000 simulated data) provides a good sample of the posterior distribution.

Figure 2.

Figure 2

Open in a new tab

Effect of number of simulations and tolerance interval on accuracy of ABC using 1000 test data sets generated with models A–D. MISEtotal (y axis) is plotted against different tolerance intervals (x axis) in an analysis with different number of simulated data (12.5k (full line), 25k (dotted line), 50k (dashed line)). (a) Model A. (b) Model B. (c) Model C. (d) Model D.

Experiment IV. Testing ABC robustness to model misspecification

The previous experiments showed that our ABC implementation performs well under the correct model of evolution. As a follow-up, we investigated how robust this method was when the model of molecular evolution is misspecified. As model D is substantially more complex than others, we considered only models A, B and C in this experiment. Thus, we run ABC analyses on three sets (one for each model) of 1000 test data sets. For each set of test data and under the same conditions as in the previous experiments, we performed ABC with the reference tables of the other two models (that is, we used misspecified models for the analyses). When models B and C were misspecified, the results were similar to those obtained under the true model (Supplementary Figures S5 and S6). The analyses using simulated test data from A but assuming any of the other two models, or using simulated test data from B and C and assuming model A, all resulted in high MISEs (Supplementary Figures S5–S7). Indeed, model A is very different from models B and C: the former assumes a K80 nucleotide model, whereas the latter two assume a GTR+G nucleotide model (see MATERIALS AND METHODS). Most importantly, model A assumes that all sites evolve under the same rate, whereas models B and C assume rate variation among nucleotides (B) and both nucleotides and codons (C). The weak impact of misspecification between models B and C suggests that, under this framework, rate variation among codons has a relatively mild effect on parameter estimations. In any case, before using ABC we recommend to test the codon model that best fits the data. The ABC framework also allows for model validation using prior and posterior predictive distributions (Ratmann et al., 2009) and for testing the best-fitting model out of a set of candidate models (Beaumont, 2008). The advantage of using ABC is that we can easily quantify the fit of each suggested model to the data, providing a useful alternative when the likelihood functions are impracticable.

Experiment V. Choosing the appropriate model of evolution using ABC

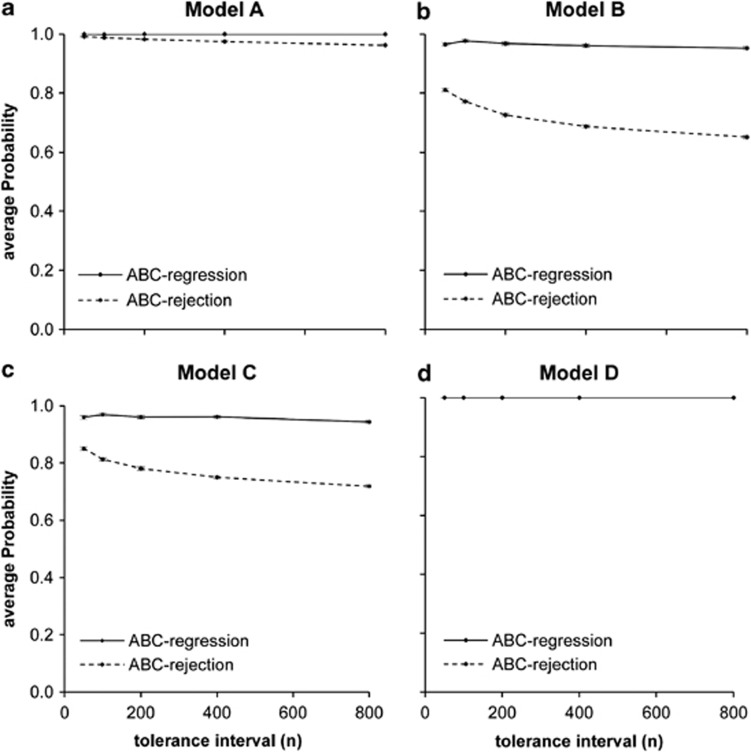
Following the experiment on model misspecification, we evaluated the accuracy of the proposed ABC method on choosing best-fit substitution models. In this experiment we performed model choice on the four sets of 1000 test data sets using a combined reference table of 200 000 simulations (that is, we joined the four reference tables of each model of evolution) with various tolerance intervals and using both ABC-rejection and ABC-logistic-regression methods, as described previously (see Beaumont, 2008; Cornuet et al., 2008). Figure 3 presents the support for the true model as the tolerance intervals decreased. For all models, the regression step increased model selection accuracy considerably, although this advantage decreased at smaller tolerance intervals. An effect that has been observed before in other ABC studies (for example, Guillemaud et al., 2010). For models B and C, when considering the widest tolerance interval (that is, 800 data sets) ABC regression gave around 95% support to the true models, while ABC-rejection algorithm showed a support of about 65% (with the remaining 35% corresponding to model B or C depending on the model used to generate the test data). When considering a tolerance interval of 50 data sets, however, the support for the true model using ABC rejection increased up to 85% (again with the remaining support given to either model B or C). The similarities between models B and C may be responsible for the relative difficulty in being able to distinguish between them. For models A and D, as they are so different from the remaining ones, the method performed very well, identifying them as the correct models, irrespective of the tolerance intervals considered.

Figure 3.

Figure 3

Open in a new tab

Performance of model choice using ABC in 1000 test data sets generated with models A−D. The points (and error bars) correspond to the average (and standard error) of the posterior probabilities of the true model from a choice of the four models in the study (A, B, C and D) using both the rejection (dashed lines) and regression (full lines) algorithms and different tolerance intervals. (a) Model A. (b) Model B. (c) Model C. (d) Model D.

Experiment VI. Comparison of ABC with other methods

In order to evaluate how our approach compares with others, we compared parameter estimates obtained using ABC with estimates calculated by OmegaMap, PAML and LAMARC. Constrained by the extremely large computational time needed to reach convergence in OmegaMap, we simulated 10 replicates of 27 test data sets under model A using as true values every combination of the following settings: ω=0.2, 1.0 and 2.0; ρ=0, 10 and 30; and θ=60, 100 and 200.

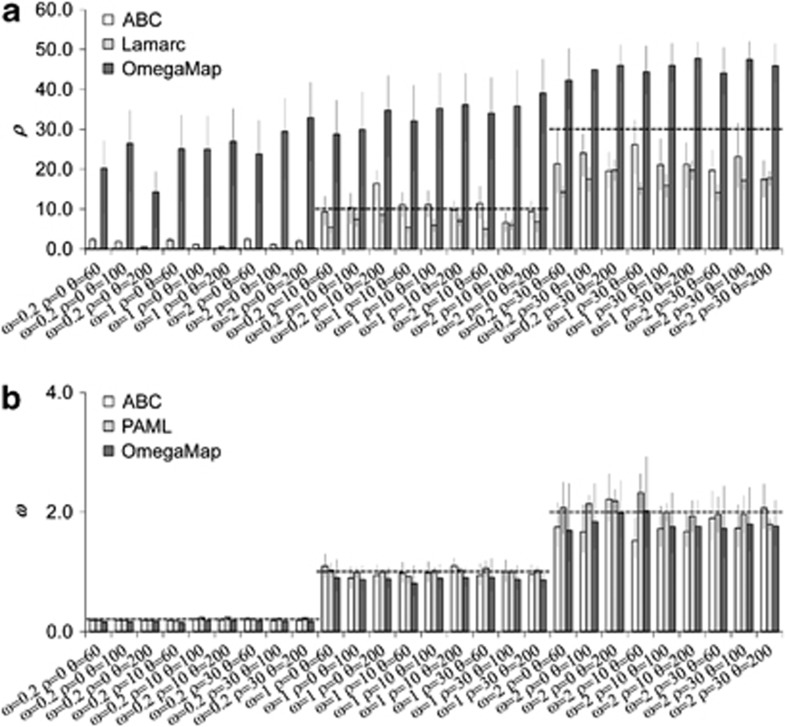
For the ABC estimates we used the reference table generated under model A, as this is the model implemented in OmegaMap. We used the best set of summary statistics, as chosen in Experiment II, and accepted the closest 0.2% (100 samples). As before, we performed the regression step on the log-transformed accepted data and the point estimate was taken as the posterior mode. For OmegaMap we used two sets of priors for ρ: a uniform prior as it was set in ABC, and an exponential with the same mean. The prior for ω was set to be the same as the one used in ABC, and the prior for the synonymous mutation rate was set to the software default, as recommended by the authors. In accordance with the generating model, the transition over transversion ratio rate was set to 2.0. All the other parameters were set as the software default. Note that OmegaMap uses the codon model NY98 (Nielsen and Yang, 1998), equivalent to the model GY94 × K80 used for simulating the test data sets. Estimates were obtained by performing two independent runs for each data set until reaching convergence, the latter being assessed by comparing ω and ρ estimates of the two runs. Note also that NetRecodon enables the user to differentiate between N and r instead of using the scaled parameter ρ. OmegaMap, on the other hand, estimates ρ directly. In order to better compare both approaches, and to remain in line with the results presented in Experiments I−V, we show the results in terms of the scaled parameters. For estimation of ω with PAML, we first reconstructed a maximum likelihood phylogenetic tree using PhyML (Guindon and Gascuel, 2003) and estimated ω with the codeml computer program (included in the PAML package) under the M0 codon model. To estimate ρ with LAMARC, we used the default parameters. In Figure 4 we present a comparison between the recombination and adaptation rates estimates obtained with our ABC method and OmegaMap, PAML and LAMARC. ABC estimates of recombination rate were in general accurate with tight credible intervals, albeit showing some tendency for underestimation of higher values of ρ. These results were expected, as the effect of fitting a prior for ρ with mean 25 was to cause the posterior to underestimate ρ when ρ>25 and potentially to overestimate ρ when ρ<25. This effect, however, was quite mild and decreased as the number of simulations used for ABC increased (results not shown), indicating that there is some space for improvement of the method. By contrast, OmegaMap usually showed overestimations of ρ with credible intervals well off the true value. Even with a more informative exponential prior on ρ the overestimation of recombination rate by OmegaMap still remained (see Supplementary Figure S8). LAMARC was able to accurately infer the absence of recombination and presented a better performance than OmegaMap. However, in the presence of recombination LAMARC underestimated recombination rates (Figure 4). Importantly, the ability of the ABC method to estimate recombination rates was robust to low levels of codon diversity, where the tendency of LAMARC to underestimate recombination rate was increased (see Figure 4a, scenarios with θ=60 and presence of recombination).

Figure 4.

Figure 4

Open in a new tab

Comparison of ABC, OmegaMap, Lamarc and PAML estimates from simulated data. Tweenty-seven evolutionary scenarios were generated under different values of ρ, ω and θ (x axes). The height of the bars correspond to the average values over replicates. Error bars indicate 95% credible intervals and horizontal dashed-lines indicate the true value. (a) Estimates of ρ. (b) Estimates of ω.

On the other hand, all methods were quite accurate in estimating adaptation rates (Figure 4b), where the true value was commonly contained within narrow credible intervals.

Experiment VII. Application of ABC to real data

Here we illustrate the application of our ABC method to 24 sequence alignments of HIV-1. These data were obtained from the PopSet database at the NCBI, and correspond to several genomic regions (for example, partial sequences of genes env, gag, nef, pol, tat and of long terminal repeats) and to different viral types and subtypes (for example, subtypes A, B, C, G)—details and references are shown in Supplementary Table S9. These HIV-1 data sets are particularly interesting to analyze owing to their generally high recombination, adaptation and substitution rates. In all cases, sequences were realigned and missing, ambiguous and stop codons were excluded. The priors were the same as those used in Experiments I–VI, as these were already chosen in order to cover a wide range of empirical scenarios. We used jModelTest (Posada, 2008) to select the best-fit substitution model and Hyphy to calculate the nucleotide frequencies at each codon position. We then considered 500 000 simulated data, from which the closest 0.2% (1000) were retained. This was followed by the regression step on the log-transformed parameters.

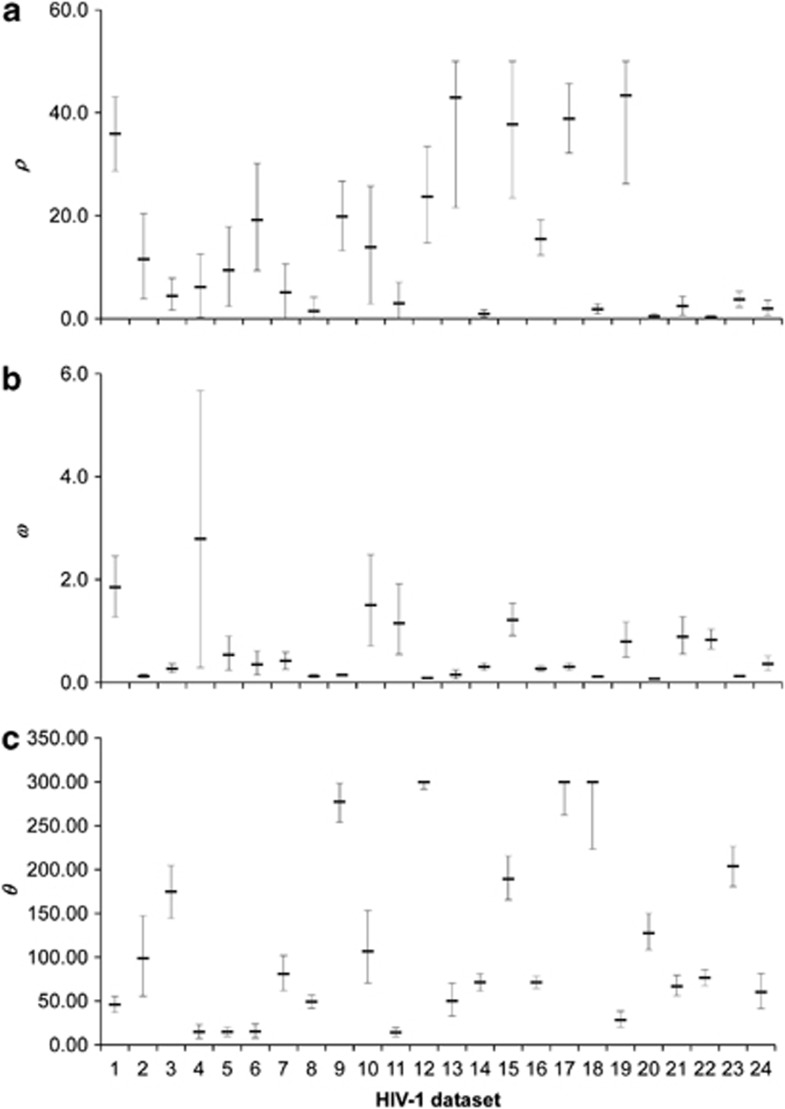
We present the estimates obtained using our ABC method in Figure 5 and Supplementary Table S10. The method seemed to perform well, as the estimates fell well within the prior distributions and the posterior distributions were fairly sharply peaked with narrow credible intervals. Nevertheless there was a trend for credible intervals to become wider when estimated values get higher for all the parameters. This trend was also confirmed in Experiments II and VI. In order to assess the goodness of fit of the models to the data, we performed principal component analysis on the simulated summary statistics and plot the first two components for the accepted simulated data and the observed data (Supplementary Figure S9). Reassuringly, these plots show that the observed data falls consistently within the accepted simulated data.

Figure 5.

Figure 5

Open in a new tab

Estimates of ρ, ω and θ from 24 HIV-1 published data sets. Error bars indicate 95% credible intervals. (a) Estimates of ρ. (b) Estimates of ω. (c) Estimates of θ.

Additionally, we tried to obtain OmegaMap estimates from these same HIV-1 data sets. For a variety of data sets, particularly those with high recombination rates, the program had apparent problems to converge, and even after 20 million Markov chain Monte Carlo iterations (several months running on a cluster) ρ estimates from the two independent runs still differ by more than five units of ρ. Nevertheless, the comparison of molecular adaptation estimates obtained using ABC and those obtained with OmegaMap showed an encouraging agreement (Supplementary Figure S10).

Discussion

We present a novel approach that allows one to assume a codon-substitution model, while considering recombination at the nucleotide level. We show that this method provides accurate estimates of recombination, molecular adaptation and substitution rates from alignments of coding sequences under different conditions. Thus, for the relatively simple models explored (A, B and C), all the three parameters were accurately estimated, except in the high recombination scenario, which seems to be more challenging. For more complex models, with both substitution and adaptation rates differing per site (case D), the precision of ABC decreased, as might be expected.

The efficacy of ABC depends to a great extent on the choice of summary statistics that extract and summarize maximal information from data, while allowing simulated data sets to be easily compared with the real data set under investigation. The strategy for choosing summary statistics in the ABC study of Wilson et al. (2009) was to use previously developed method-of-moments estimators (a similar approach is justified theoretically in Fearnhead and Prangle (2012)). Note that Wilson et al. (2009) developed their ABC to analyze a single data set, and could afford for summary statistics that require a noticeable computation time. By contrast, we present a general method for choosing a subset of summary statistics based on the calculation of the Cp index. We used test data to perform informed trial-and-error tests that suggest that a set of 22 summary statistics, chosen to be rapidly computable, is adequate to provide accurate estimates of the parameters studied.

ABC has been shown to be an efficient alternative to full-likelihood methods when the likelihood function is intractable. This approximate method has also the advantage of being potentially faster than the correspondent full-likelihood approach. Nevertheless, ABC can still be highly computational intensive if the simulation step is complex. For this reason it is important to refine the method in order to find an optimal number of simulations both in terms of accuracy and speed. We showed that in a range of simple to complex models of molecular evolution a sample size of 100 points provided sufficient information to construct reliable posterior summaries. Given this number, at least 50 000 simulated points in total are needed to successfully perform ABC in the scenarios proposed. Under these conditions we obtained very good estimates, reaching correlations between the true and the estimated values approaching 1. Note, however, that we have worked with moderately small samples size (15 sequences with 333 codons). Larger data would require more computation time for each simulation, but might need fewer simulations to reach the same accuracy. An illustrative list of running times for NetRecodon is shown in the Supplementary Table S11, and as expected longer sequences and higher sample sizes require longer computational times. We also observe that the prior distribution of the parameters can affect the required simulation time, indeed a higher recombination rate requires more computation time. Importantly, NetRecodon simulations can be run in parallel, reducing the simulation time, which is the ABC step with the highest computational cost. Finally, the estimation part of ABC requires only a few minutes and does not depend on the simulation settings.

We also examined the problem of misspecification of the model of evolution. In cases where the model used for the ABC approach and the model used to generate the data differed on the assumption of rate variation among sites, the estimation of the parameters was poor. Fortunately, rate variation among sites is easily detected using model selection techniques, and our results show that ABC is robust to slight model misspecification, in particular regarding different relative substitution matrices (see Supplementary Figures S5–S7). As noted by Ratmann et al. (2009), it is relatively straightforward to investigate model misspecification under an ABC framework through comparison of observed summary statistics with those generated under predictive distributions. ABC model choice enables different models to be compared, although such tests do not assure that the most supported model is correct. Recently, attention has been drawn to the potential sensitivity of ABC model choice to sufficiency of the summary statistics (Robert et al., 2011). These studies recommend the use of simulation testing to evaluate performance of model choice procedures. We have carried out extensive simulations, and showed that ABC can easily distinguish between distant models. In the comparisons between evolutionary models that were similar its efficiency was slightly reduced, but we still obtained a high support for the true model (see Figure 3).

We compared estimates of recombination and adaptation rates made by our ABC method, OmegaMap, PAML and LAMARC on simulated test data sets. An important difference between these approaches is that only the ABC method considers intracodon recombination. Nevertheless, according to previous studies, our expectation was that the estimations of alignment-wise adaptation rates (ω) would not be much affected by ignoring intracodon recombination (Arenas and Posada, 2010). Reassuringly, this was the case, and the similar estimates obtained by the different methods reinforce our beliefs about the validity of the ABC method proposed here (Figure 4b). More interesting, though, was the observation that overall recombination rates were most accurately estimated by ABC, OmegaMap showed a clear tendency for overestimation (Figure 4a). In fact, some authors have shown that there is an upward bias on product of approximating conditionals-likelihood estimations of ρ even on data without intracodon recombination (Li and Stephens, 2003; Wilson and McVean, 2006), although this can be corrected as suggested by Li and Stephens (2003). LAMARC performed well in the absence of recombination but for higher recombination rates tended to underestimate the rate. Interestingly, although such an underestimation was increased in scenarios with lower levels of codon diversity, ABC was quite robust to these scenarios. Additional advantages of the ABC approach are its speed and the possibility to analyze data sets with a vast variety of codon models, as implemented in NetRecodon or in other simulator, in contrast with the single codon model implemented in OmegaMap. This can be particularly beneficial when there is a need to consider substitution models that best-fit the data (see Yang et al., 2000; Arbiza et al., 2011).

We collected 24 HIV-1 data sets with which we challenged our developed ABC method. In this case our ABC approach exhibited good behavior, in that estimates using different tolerance intervals and either the regression or the rejection algorithms showed considerable agreement, and as the tolerance interval decreased, the credible intervals got tighter (results not shown). Furthermore, the tests to assess the goodness of fit of the models show that the models explain the data reasonably well (Supplementary Figure S9). In accordance with previous studies, our results suggest that overall the analyzed HIV-1 data sets exhibit large recombination rates, and that, considering the whole sequences, selection pressure has been mostly purifying (Scheffler et al., 2006). Nevertheless, there is space for improvement. First, we have assumed a uniform recombination rate along sequences, although some studies revealed the presence of hotspots in HIV-1 (for example, Zhuang et al., 2002). Second, we have estimated molecular adaptation for the whole sequence, although estimating adaptation at local (codon) level is possible (for example, by using the Bayesian hierarchical model developed by Bazin et al., 2010). In any case, we argue that the ABC approach can be an ideal framework to incorporate more relaxed model assumptions.

In this study we assumed a model that only considers molecular adaptation by the non-synonymous/synonymous ratio. Although this ratio is widely used as an indicator of molecular adaptation (for example, Nielsen and Yang, 1998; Wilson and McVean, 2006; Wilson et al., 2009), this methodology is not free from some controversy. One of the main criticisms is its use in single-population samples, where the close ancestry of the sequences may break the relation of this ratio to the adaptation coefficient (Kryazhimskiy and Plotkin, 2008). However, for populations with high substitution rate, non-synonymous/synonymous ratio approaches have been shown to perform well (for example, virus and bacteria). Nonetheless, this assumption should be considered when applying the methodology we present here.

To summarize, our approach provides a novel ABC method to estimate jointly codon substitution, adaptation and recombination rates under realistic substitution models from coding data. This new method can also accurately choose the substitution model that best fits the data between a series of candidate models. In addition, further increase of model complexity is relatively straightforward, requiring only the introduction of new features to the simulation software. Such alterations may require testing different summary statistics and optimizing the number of simulations and the tolerance interval, a procedure that we believe can be easily attained by following the steps we have proposed here.

Data archiving

There were no data to deposit.

Acknowledgments

We thank Maria Anisimova, Nicolas Galtier and one anonymous reviewer for thoughtful comments, which improved the quality of the original manuscript. This work was supported by the Spanish Ministry of Science (grants BIO2007-61411 and BFU2009-08611 to DP and FPI fellowship BES-2005-9151 to MA). JSL and MAB were supported by EPSRC (grant H3043900). JSL was also supported by Fundacao Ciencia Tecnologia (grant SFRH/BD/43588/2008).

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Information
Click here for additional data file. (4.5MB, doc)

References

  1. Anisimova M, Nielsen R, Yang Z. Effect of recombination on the accuracy of the likelihood method for detecting positive selection at amino acid sites. Genetics. 2003;164:1229–1236. doi: 10.1093/genetics/164.3.1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Arbiza L, Patricio M, Dopazo H, Posada D. Genome-wide heterogeneity of nucleotide substitution model fit. Genome Biol Evol. 2011;3:896–908. doi: 10.1093/gbe/evr080. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Arenas M, Posada D. Coalescent simulation of intracodon recombination. Genetics. 2010;184:429–437. doi: 10.1534/genetics.109.109736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bazin E, Dawson KJ, Beaumont MA. Likelihood-free inference of population structure and local adaptation in a Bayesian hierarchical model. Genetics. 2010;185:587–602. doi: 10.1534/genetics.109.112391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Beaumont M.2008Joint determination of topology, divergence time, and immigration in population treesIn: Matsumura S, Forster P, Renfrew C (eds)Simulations, Genetics, and Human Prehistory McDonald Institute for Archaeological Research: Cambridge; 135–154. [Google Scholar]
  6. Beaumont MA. Approximate Bayesian computation in evolution and ecology. Annu Rev Ecol Evol Syst. 2010;41:379–405. [Google Scholar]
  7. Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162:2025–2035. doi: 10.1093/genetics/162.4.2025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Blum MGB, Nunes MA, Prangle D, Sisson SA. A comparative review of dimension reduction methods in approximate Bayesian computation. Stat Sci. 2013;28:189–208. [Google Scholar]
  9. Bruen TC, Philippe H, Bryant D. A simple and robust statistical test for detecting the presence of recombination. Genetics. 2006;172:2665–2681. doi: 10.1534/genetics.105.048975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Carvajal-Rodriguez A, Crandall KA, Posada D. Recombination estimation under complex evolutionary models with the coalescent composite-likelihood method. Mol Biol Evol. 2006;23:817–827. doi: 10.1093/molbev/msj102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cornuet JM, Santos F, Beaumont MA, Robert CP, Marin JM, Balding DJ, et al. Inferring population history with DIY ABC: a user-friendly approach to approximate Bayesian computation. Bioinformatics. 2008;24:2713–2719. doi: 10.1093/bioinformatics/btn514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Csillery K, Francois O, Blum MGB. abc: an R package for approximate Bayesian computation (ABC) Methods Ecol Evol. 2012;3:475–479. [Google Scholar]
  13. Fearnhead P, Prangle D. Constructing ABC summary statistics: semi-automatic ABC. J R Statist Soc B. 2012;74:1–28. [Google Scholar]
  14. Goldman N, Yang Z. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol Biol Evol. 1994;11:725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
  15. Guillemaud T, Beaumont MA, Ciosi M, Cornuet JM, Estoup A. Inferring introduction routes of invasive species using approximate Bayesian computation on microsatellite data. Heredity. 2010;104:88–99. doi: 10.1038/hdy.2009.92. [DOI] [PubMed] [Google Scholar]
  16. Guindon S, Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol. 2003;52:696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
  17. Hughes AL, Packer B, Welch R, Bergen AW, Chanock SJ, Yeager M. Widespread purifying selection at polymorphic sites in human protein-coding loci. Proc Natl Acad Sci USA. 2003;100:15754–15757. doi: 10.1073/pnas.2536718100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Jakobsen IB, Easteal S. A program for calculating and displaying compatibility matrices as an aid to determining reticulate evolution in molecular sequences. Comput Appl Biosci. 1996;12:291–295. doi: 10.1093/bioinformatics/12.4.291. [DOI] [PubMed] [Google Scholar]
  19. Kryazhimskiy S, Plotkin JB. The population genetics of dN/dS. PLoS Genet. 2008;4:e1000304. doi: 10.1371/journal.pgen.1000304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kuhner MK. LAMARC 2.0: maximum likelihood and Bayesian estimation of population parameters. Bioinformatics. 2006;22:768–770. doi: 10.1093/bioinformatics/btk051. [DOI] [PubMed] [Google Scholar]
  21. Li N, Stephens M. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics. 2003;165:2213–2233. doi: 10.1093/genetics/165.4.2213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lumley T, Miller A.2004. Leaps: Regression Subset Selection, R package version 2.7. Available at, http://CRAN.R-project.org/web/packages/leaps .
  23. Nielsen R, Yang Z. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics. 1998;148:929–936. doi: 10.1093/genetics/148.3.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Posada D. jModelTest: phylogenetic model averaging. Mol Biol Evol. 2008;25:1253–1256. doi: 10.1093/molbev/msn083. [DOI] [PubMed] [Google Scholar]
  25. Posada D, Crandall KA. The effect of recombination on the accuracy of phylogeny estimation. J Mol Evol. 2002;54:396–402. doi: 10.1007/s00239-001-0034-9. [DOI] [PubMed] [Google Scholar]
  26. Pritchard JK, Seielstad MT, Perez-Lezaun A, Feldman MW. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Mol Biol Evol. 1999;16:1791–1798. doi: 10.1093/oxfordjournals.molbev.a026091. [DOI] [PubMed] [Google Scholar]
  27. Ratmann O, Andrieu C, Wiuf C, Richardson S. Model criticism based on likelihood-free inference, with an application to protein network evolution. Proc Natl Acad Sci USA. 2009;106:10576–10581. doi: 10.1073/pnas.0807882106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Robert CP, Cornuet JM, Marin JM, Pillai N. Lack of confidence in approximate Bayesian computation model choice. Proc Natl Acad Sci USA. 2011;108:15112–15117. doi: 10.1073/pnas.1102900108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Scheffler K, Martin DP, Seoighe C. Robust inference of positive selection from recombining coding sequences. Bioinformatics. 2006;22:2493–2499. doi: 10.1093/bioinformatics/btl427. [DOI] [PubMed] [Google Scholar]
  30. Schierup MH, Hein J. Consequences of recombination on traditional phylogenetic analysis. Genetics. 2000;156:879–891. doi: 10.1093/genetics/156.2.879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Smith JM. Analyzing the mosaic structure of genes. J Mol Evol. 1992;34:126–129. doi: 10.1007/BF00182389. [DOI] [PubMed] [Google Scholar]
  32. Sullivan J, Joyce P. Model selection in phylogenetics. Annu Rev Ecol Evol Syst. 2005;36:445–466. [Google Scholar]
  33. van Rij RP, Worobey M, Visser JA, Schuitemaker H. Evolution of R5 and X4 human immunodeficiency virus type 1 gag sequences in vivo: evidence for recombination. Virology. 2003;314:451–459. doi: 10.1016/s0042-6822(03)00454-9. [DOI] [PubMed] [Google Scholar]
  34. Veeramah KR, Wegmann D, Woerner A, Mendez FL, Watkins JC, Destro-Bisol G, et al. An early divergence of KhoeSan ancestors from those of other modern humans is supported by an ABC-based analysis of autosomal resequencing data. Mol Biol Evol. 2012;29:617–630. doi: 10.1093/molbev/msr212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wegmann D, Leuenberger C, Excoffier L. Efficient approximate bayesian computation coupled with markov chain monte carlo without likelihood. Genetics. 2009;182:1207–1218. doi: 10.1534/genetics.109.102509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wilson DJ, Gabriel E, Leatherbarrow AJ, Cheesbrough J, Gee S, Bolton E, et al. Rapid evolution and the importance of recombination to the gastroenteric pathogen Campylobacter jejuni. Mol Biol Evol. 2009;26:385–397. doi: 10.1093/molbev/msn264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Wilson DJ, McVean G. Estimating diversifying selection and functional constraint in the presence of recombination. Genetics. 2006;172:1411–1425. doi: 10.1534/genetics.105.044917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yang Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol Biol Evol. 2007;24:1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
  39. Yang Z, Nielsen R, Goldman N, Pedersen A-MK. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics. 2000;155:431–449. doi: 10.1093/genetics/155.1.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Zhuang J, Jetzt AE, Sun G, Yu H, Klarmann G, Ron Y, et al. Human immunodeficiency virus type 1 recombination: rate, fidelity, and putative hot spots. J Virol. 2002;76:11273–11282. doi: 10.1128/JVI.76.22.11273-11282.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (4.5MB, doc)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES