Lensfree holographic imaging for on-chip cytometry and diagnostics

Abstract

We experimentally illustrate a lensfree holographic imaging platform to perform on-chip cytometry. By controlling the spatial coherence of the illumination source, we record a 2D holographic diffraction pattern of each cell or micro-particle on a chip using a high resolution sensor array that has ~2 µm pixel size. The recorded holographic image is then processed by using a custom developed decision algorithm for matching the detected hologram texture to existing library images for on-chip characterization and counting of a heterogeneous solution of interest. The holographic diffraction signature of any microscopic object is significantly different from the classical diffraction pattern of the same object. It improves the signal to noise ratio and the signature uniformity of the cell patterns; and also exhibits much better sensitivity for on-chip imaging of weakly scattering phase objects such as small bacteria or cells. We verify significantly improved performance of this holographic on-chip cytometry approach by automatically characterizing heterogeneous solutions of red blood cells, yeast cells, E. coli and various sized micro-particles without the use of any lenses or microscope objectives. This lensless on-chip holography platform will especially be useful for point-of-care cytometry and diagnostics applications involving e.g., infectious diseases such as HIV or malaria.

Introduction

Flow cytometry is a powerful technology that enables counting, characterization and sorting of cells flowing through a hydro-dynamically concentrated channel. By collecting fluorescence and scattered light from the cells as a function of time, this technology can provide various sources of information such as the count, type or surface morphology variation of the cells, which are all very important in clinical diagnostics.¹ Most flow cytometers use rather bulky and expensive equipment such as photomultiplier tubes (PMTs) and avalanche photodiodes, which limit their application at the point-of-care especially in resource limited settings.^2,3 To address this issue, there have been a variety of studies to miniaturize conventional bench-top flow cytometers into portable micro flow systems. For instance, to miniaturize the source and detection in micro flow cytometry, researchers adopted commercial waveguides that are integrated with micro-fluidic channels.^4–7 Cleaved ends of these waveguides are aligned to the micro-channel to illuminate and detect the scattered or fluorescence light from the cells. To address another significant challenge in miniaturized system design (i.e., to provide reliable and rapid flow of cells on a chip) electrokinetic focusing in micro-fabricated channel structures has also been widely used to achieve 2D and even 3D hydrodynamic focusing.^8–13 All of these efforts and many others^14–19 are still based on the fundamental principles of conventional flow cytometry and analyze cells one at a time (i.e., on-chip detection is achieved serially).

In this article we introduce a lensless holographic imaging platform that can provide a versatile solution to on-chip cytometry and diagnostics. In this scheme, by use of a variable pinhole, we control the spatial coherence of the illumination source to enable lensfree recording of the holographic diffraction pattern of each cell on the chip using a high-resolution optoelectronic sensor array that has ~2 µm pixel size (see Fig. 1). After recording of this holographic lensfree image, a custom developed decision algorithm is utilized to process the 2D texture of acquired holograms to rapidly recognize and characterize the type and 3D location of each cell/micro-object located within a heterogeneous solution of interest. Since this holographic approach does not rely on conventional optical components such as lenses, mirrors, beam splitters, etc., it offers a flexible, compact and cost-effective alternative for many on-chip diagnostics applications such as whole blood analysis.

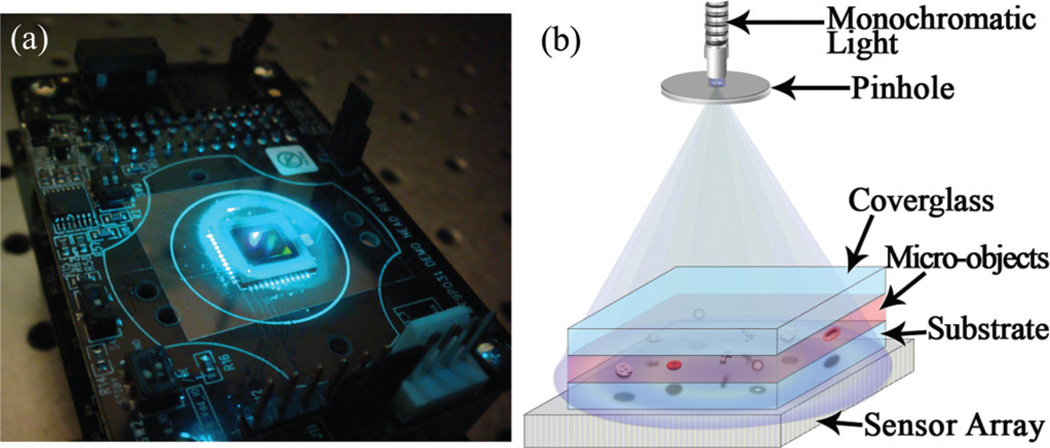
Fig. 1.

(a) Experimental apparatus (under blue light illumination) and (b) schematic diagram of the Holographic-LUCAS platform are shown.

The holographic diffraction pattern of each cell/micro-object is created by the interference of the scattered light from the cell/ micro-object with the un-scattered light directly emanating from the source. This holographic diffraction pattern should not be confused with the classical diffraction signature of the same micro-object. When recorded with a high-resolution sensor array, the holographic diffraction signature exhibits several advantages compared to the classical diffraction pattern of the same micro-object. These advantages will be further explored in the Discussions section and in the Appendix.

Since there exist several different forms of on-chip cytometry, lensless imaging or holographic imaging systems, let us briefly outline the key differences between some of the existing systems and the approach of this article:

1. When compared to miniaturized flow cytometers, the proposed approach does not involve any fluid flow and captures the holographic diffraction information of the cells on the chip all in parallel within less than 0.3 seconds. Quite different from flow-cytometry, our approach relies on digital processing of the holographic diffraction signatures of different cell types to rapidly characterize a heterogeneous cell solution on a chip.

2. When compared to existing digital in-line holographic microscopy (DIHM) systems^20–23 our approach differs in several significant ways such as much simpler digital processing, simpler optical design, and elimination of the use of lenses. We should also emphasize that unlike DIHM we do not claim high resolution microscopy, and therefore the two approaches should be classified in different categories. However, for the general audience, in the Discussions section we will further expand on these key technical differences between DIHM and our approach.

3. There exist various other non-holographic lensless imaging and microscopy approaches in the literature.^24–27 Several of these approaches are not designed for cytometry, but rather aim to achieve high resolution imaging of e.g., C. elegans within a micro-fluidic channel. For instance, the ingenious concept of opto-fluidic microscopy (OFM)^24–26 can achieve a high spatial resolution of ~0.5 µm on a chip using a slanted array of holes that capture a transformed image of the micro-object of interest as it moves through a micro-fluidic channel at a constant speed. Our lensless on-chip cytometry approach makes use of digital holography to identify different cell types on a chip, and in this sense is quite different from these on-chip microscopy systems. Furthermore, our approach does not utilize any fluidic motion unlike OFM and therefore can monitor a larger field of view much faster, increasing the throughput of cell characterization.

4. Finally we would like to discuss the major differences of our new holographic cytometry approach with respect to some of the existing on-chip imaging work that our group has recently demonstrated.^28–30 To realize high-throughput cell counting and characterization within a compact and cost-effective platform, we have recently reported a lensfree on-chip imaging platform termed LUCAS (Lensfree Ultra-wide-field Cell monitoring Array platform based on Shadow imaging).²⁸ In this initial proof-of-concept, using spatially incoherent broadband white-light illumination we recorded the classical diffraction pattern (not the holographic diffraction) of a homogenous solution of cells using a low-resolution sensor array that had ~9 µm pixel size. In this primitive LUCAS platform, the volume of the sample solution that could be monitored within a second was limited to <0.1 ml.²⁸ Relatively recently, we have improved this original LUCAS platform of our group by using a narrowband (i.e., monochromatic) tunable wavelength illumination together with a custom-developed pattern recognition algorithm.^29,30 These improvements enabled label-free characterization of a heterogeneous cell population on a chip over a field of view of ~10 cm² and a depth of field of >4 mm, corresponding to a solution volume of >4 ml—refer to Fig. S1–S3.^†

Holographic on-chip cytometry approach of this manuscript is significantly different from the existing LUCAS based techniques.^28–30 LUCAS utilizes spatially incoherent light which implies that the detected quantity is simply the classical diffraction pattern of each cell/microparticle, whereas the proposed approach of this manuscript uses spatially coherent illumination to record the holographic diffraction of each cell/micro-object on the chip. This important difference brings several advantages to our new approach when compared to existing LUCAS systems. First, since classical diffraction fringes are due to self-interference of the scattered light from the cell with itself, they are much weaker in signal strength when compared to holographic diffraction patterns. In other words, this improved signal to noise ratio (SNR) is due to the heterodyne nature of holographic interference, whereas classical diffraction can be modeled as a homodyne system. This SNR improvement is especially more pronounced for small cells or bacteria that act as weak scatterers. This point will be experimentally verified in the Results section and is further discussed in the Appendix. Second, holographic diffraction exhibits improved signature uniformity for a given cell type, i.e., the digital similarity among different holographic signatures of the same micro-object type is significantly improved. This is especially quite relevant to enable automated pattern recognition of the target cell type within a heterogeneous solution using a decision algorithm. Third, with holographic diffraction, the signature differences among different cell types become more evident. We will quantify the statistical performance of this improvement in the Results section, however, intuitionally this improvement is due to the fact that with self-interference most phase related information of the cell/micro-object is lost, whereas by recording a hologram with respect to a reference beam (the un-scattered direct light) this phase information is now encoded into amplitude oscillations, which enriches the 2D information content of the detected cell signature on the chip. A more rigorous discussion of this claim will be provided in the Theory section of the Appendix.

Another major difference between the presented technique and our previous LUCAS work^28–30 is that here we use a much higher resolution sensor array that has more than 4 fold smaller pixel size (i.e., 2.2 µm vs. 9.0 µm). The significance of this higher resolution sensor array will be further quantified in the Results section.

These significant improvements of the holographic cytometry approach permit improved performance for automated characterization of different cell types within a heterogeneous cell solution based on 2D texture analysis of the detected holograms. Apart from these noteworthy differences and advances, conceptually, the on-chip lensfree imaging idea of our holographic technique can be considered as a significant improvement of the existing LUCAS approach, and therefore to help us establish this link, we will refer to this new on-chip cytometry approach as Holographic-LUCAS.

In summary, Holographic-LUCAS exhibits several advantages within a novel lensfree imaging and digital processing scheme to provide a flexible, compact and cost-effective alternative to existing approaches for point-of-care cytometry and diagnostics applications such a monitoring of HIV patients in resource scarce settings.

Experimental methods

Set-up

Fig. 1 shows the experimental configuration of our Holographic-LUCAS imaging set-up. The results that are presented in this article are acquired using two different sensor arrays: (1) a charged couple device (CCD, KAI-10002, Kodak) and complementary metal-oxide-semiconductor (CMOS, MT9P031, Micron) image sensor which have pixel sizes of 9.0 µm (CCD) and 2.2 µm (CMOS), respectively. As illustrated in the schematic diagram of Fig. 1(b), using these two opto-electronic sensor arrays we recorded the holographic diffraction signatures of various micro-objects such as red blood cells, yeast cells (S. pombe), polystyrene microbeads of various diameters (D = 3, 5, 10 and 20 µm, Duke Scientific) and Escherichia Coli (E. Coli) samples. The same optical set-up can also record the classical diffraction fringes of the cells/micro-objects by removing the pinhole or enlarging its diameter. The micro-objects to be imaged are diluted with either 1 × PBS or buffered blood bank saline (Fisherbrand, Blood Bank Saline, Fisher Scientific), and a total solution volume of 10–100 µl is dropped on a microscope slide using a micro-pipette and gently sandwiched by another identical cover glass. Then, the sample is positioned using a vacuum pen (NT57–636, Edmund Optics) onto the active region of the sensor array. To be able to illuminate the sample volume with tunable monochromatic light (scanning a wavelength range of λ ~ 350– 1000 nm), we used a digital monochromator (Oriel Cornerstone™ 260–1/4m, Newport) along with a standard grade fused silica fiber which consists of a bundle of 250µm diameter fibers (77564, Newport). For Holographic-LUCAS experiments, we used a pinhole diameter of ~100 µm placed ~5 cm above the sensor array. As will be discussed later on, this configuration implies no fringe magnification (close to unity) for the detected holograms.

Image quality metrics and decision algorithm

To provide quantitative comparison for the improvement in the quality of Holographic-LUCAS images, we utilized three image metrics: (1) digital signal-to-noise ratio (SNR), (2) spot/shadow radius (R_rms), and (3) correlation index, all of which will be mathematically defined below.

Digital SNR of our images is calculated using SNR = |(max(I) − µ_b)/σ_b|, where I is the light intensity on the sensor array, and µ_b and σ_b are the mean and variance of the background noise region. For R_rmscalculations, we used the concept of root-mean-square (RMS) width which is defined as

$$R_{\text{rms}}=\sqrt{\raisebox{1ex}{$\sum _{x=1}^W{(x-\overline{x})}^2{|f(x,y=y_0|}^2$}\!\left/ \!\raisebox{-1ex}{$\sum _{x=1}^W{|f(x,y=y_0)|}^2$}\right.}$$

where W is the maximum number of pixels in the region of interest, and

$$\overline{x}=\left(\raisebox{1ex}{$\sum _{x=1}^{W}x{|f(x,y=y_0)|}^2$}\!\left/ \!\raisebox{-1ex}{$\sum _{x=1}^W{|f(x,y=y_0)|}^2$}\right.\right)$$

In these equations, (x,y) and f(x,y = y₀) denote the index of the image pixel and the detected intensity profile of a line represented by y = y₀, respectively.³¹

To better quantify the digital similarity between different holograms of the same cell/object type, we introduced the concept of “correlation index” which simply calculates the numerical deviation of a given cell image compared to a mean library image of the same cell type. For each cell/micro-object type a mean library image, L(x,y), was formed by averaging >20 arbitrarily chosen samples within a homogenous solution that are imaged under the same conditions (e.g., the same wavelength, the same depth of field etc.). Each individual holographic (or classical) diffraction pattern of an unknown particle (i.e.,f(x,y)) was first compared to the library image of a known particle type to calculate its “deviation” given by

$$\text{Dev}=\sum _{(x,y)\in \text{ROI}}|f(x,y)-L(x,y)|$$

The region of interest (ROI) for each calculation occupies an equal amount of area as that of the library image. After this step, the correlation of the unknown particle image f(x,y) to the average library image L(x,y) is calculated using:

$$\text{Corr}=1-\frac{\text{Dev}-{\text{Dev}}_{\text{MIN}}}{{\text{Dev}}_{\text{MAX}}-{\text{Dev}}_{\text{MIN}}}$$

where Dev_MAX and Dev_MIN refer to the maximum and minimum of the deviation values of f(x,y) calculated using the individual library images forming L(x,y). Therefore, a target image f(x,y) that has the maximum deviation from all the library images will have a correlation index of “0”, and a correlation index of “1” will be assigned to an image with minimal deviation from the same set of library images.

To characterize the acquired Holographic-LUCAS images, a 2D correlation map is calculated for each one of the existing cell/particle image libraries. The user can select which target cell libraries to be used, or otherwise, all the existing image libraries are used. To generate the 2D correlation map for each library image, first a 2D deviation profile is calculated:

$$\text{Dev}(x,y)=\sum _{(x\prime ,y\prime )\in D_{\mathrm{L}}}|f(x\prime +x,y\prime +y)-L(x\prime ,y\prime )|$$

where D_L represents the domain of the library image. Then the 2D deviation map is converted into a 2D correlation map using:

$$\text{Corr}(x,y)=1-\frac{\text{Dev}(x,y)-{\text{Dev}}_{\text{MIN}}}{{\text{Dev}}_{\text{MAX}}-{\text{Dev}}_{\text{MIN}}}$$

After the creation of this 2D correlation map, potential candidates showing a large correlation peak (that is above a certain threshold value) are further investigated using R_rms and/ or SNR criterion to make a characterization and counting decision. We should note here that a similar decision making process is also utilized in existing LUCAS based incoherent systems.^29,30 As far as the decision algorithm is concerned, the most important difference between Holographic-LUCAS and our previous approaches^29,30 is that the cell signatures (together with their image libraries) now exhibit a richer source of texture information, together with better uniformity and SNR, which then translate into improved characterization performance, as will be quantified in the discussions to follow.

Results

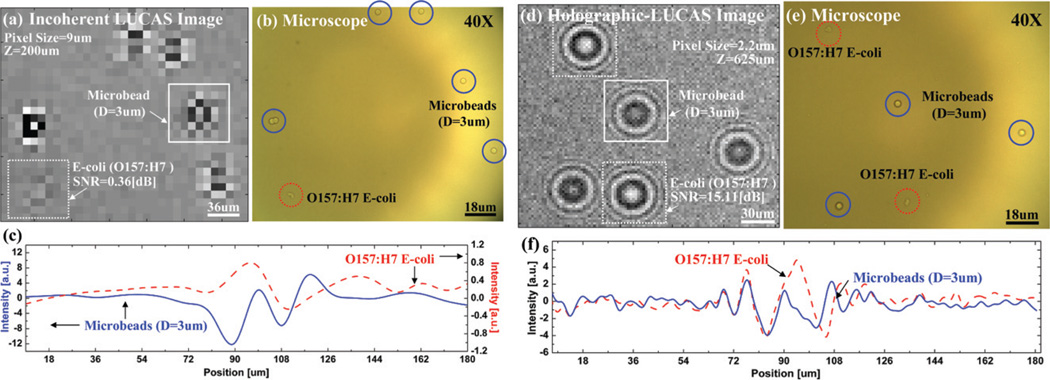
To illustrate the performance of the Holographic-LUCAS platform with a high-resolution sensor array, we initially imaged a mixture of polystyrene microbeads (3 µm diameter) and E. Coli samples. To provide a direct comparison, Fig. 2(a) shows the classical diffraction image of this mixture that is acquired with a conventional incoherent LUCAS system as described in the literature,^28–30i.e., a pixel size of 9.0 µm, under λ = 400 nm and at Z = 200 µm, where λ and Z are the illumination wavelength and the distance from the sample to the sensor plane, respectively. In this figure, conventional diffraction patterns of five 3 µm beads and one E. Coli sample are shown. The same region of interest is also imaged using a 40 × objective-lens as shown in Fig. 2(b) to verify the LUCAS results. As illustrated in Fig. 2(a), because this mixture contains small particles (3 µm) and weakly scattering phase objects (E. coli), the conventional LUCAS system has serious issues with signature non-uniformity and low SNR. To demonstrate the improvement of the Holographic-LUCAS platform with the high-resolution sensor array, in Fig. 2(d) we show the holographic diffraction pattern of the same solution sampled with a pixel size of 2.2 µm. In contrast to the poor SNR and signature non-uniformity of the conventional LUCAS system (Fig. 2(a)), Fig. 2(d) now clearly shows the details of the holographic diffraction signatures of three 3 µm beads and two E. coli samples, which were again verified by acquiring a high resolution (40×) microscope image of the same region of interest as shown in Fig. 2(e). In particular, this experimental comparison illustrates significantly improved performance of the Holographic-LUCAS platform for on-chip imaging of phase objects such as E. Coli samples that are quite difficult to see even under a 40× objective lens. For instance, the E. Coli diffraction pattern which was very close to the background noise level in Fig. 2(a) is significantly improved in Fig. 2(d) with over 40 times SNR improvement even at a larger sample-to-sensor distance of Z = 625 µm. Furthermore, the signature uniformity of the micro-particles is now much better (see Fig. 2(d)) with the use of the high-resolution holographic set-up.

Fig. 2.

(a) Conventional incoherent LUCAS image for a mixture of polystyrene microbeads (D = 3 µm) and E. Coli samples imaged with a 9 µm pixel size sensor array. (b) For comparison purposes, a microscope image of the same field of view that is acquired with a 40× objective-lens is also shown. (c) The cross sectional intensity profile (taken from (a)) of the classical diffraction pattern of a microbead and an E. coli sample is illustrated. (d) Holographic-LUCAS image of the same heterogeneous solution now exhibits much better signature uniformity. Furthermore, the weak diffraction pattern of the E. coli samples is now significantly improved with over 40 times SNR improvement. (e) For comparison purposes, a microscope image of the same field of view that is acquired with a 40× objective-lens is also shown. (f) The cross sectional intensity profile (taken from (d)) of the holographic diffraction pattern of a microbead and an E. Coli sample is illustrated. Notice that the signal scale is different for the E. coli signature when compared to (c), which illustrates the improved performance of the Holographic-LUCAS platform for imaging weakly scattering phase objects such as small bacteria.

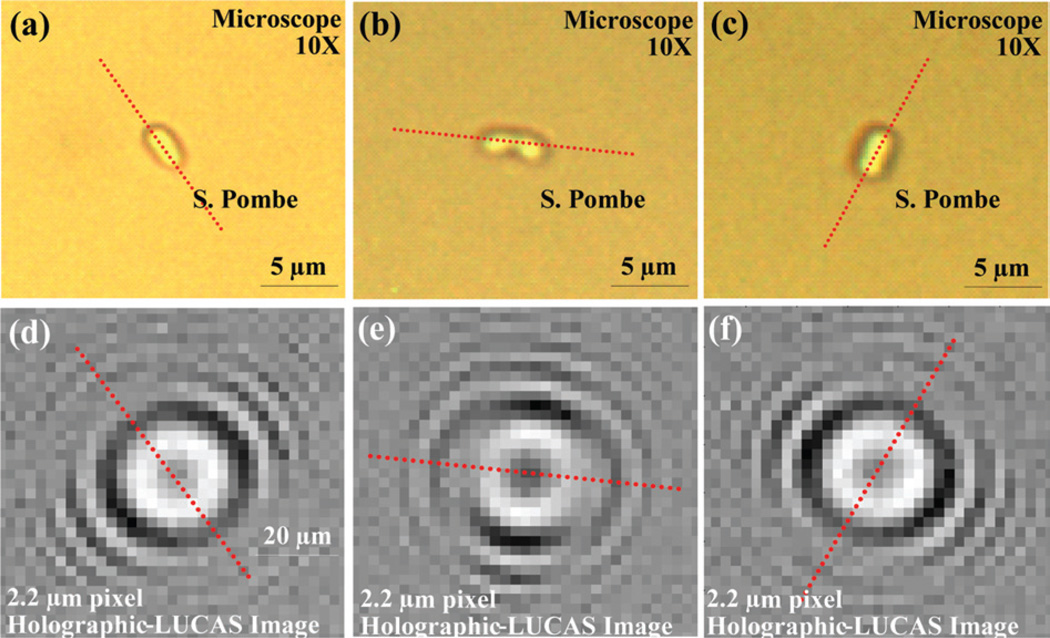
Another advantage of using the high-resolution Holographic-LUCAS platform is the on-chip detection of 2D orientation of asymmetric cells with a finer accuracy. One example is illustrated in Fig. 3 for yeast cells (S. Pombe), where the broken symmetry of the hologram uniquely determines the 2D orientation of each yeast cell on the chip. This performance would be greatly degraded with a coarser pixel size of e.g., ~9 µm since the fine details of the holographic pattern would mostly be smeared out.

Fig. 3.

Detection of 2D orientation of asymmetric cells using Holographic-LUCAS is illustrated. (a), (b), and (c) are the microscope images of S. Pombe yeast cells imaged under 10× objective-lens. (d), (e), and (f) show the corresponding Holographic-LUCAS images of the same field of view as in (a), (b), and (c), respectively. The orientation of each yeast cell can be uniquely determined by the broken symmetry as shown in the holographic-LUCAS images.

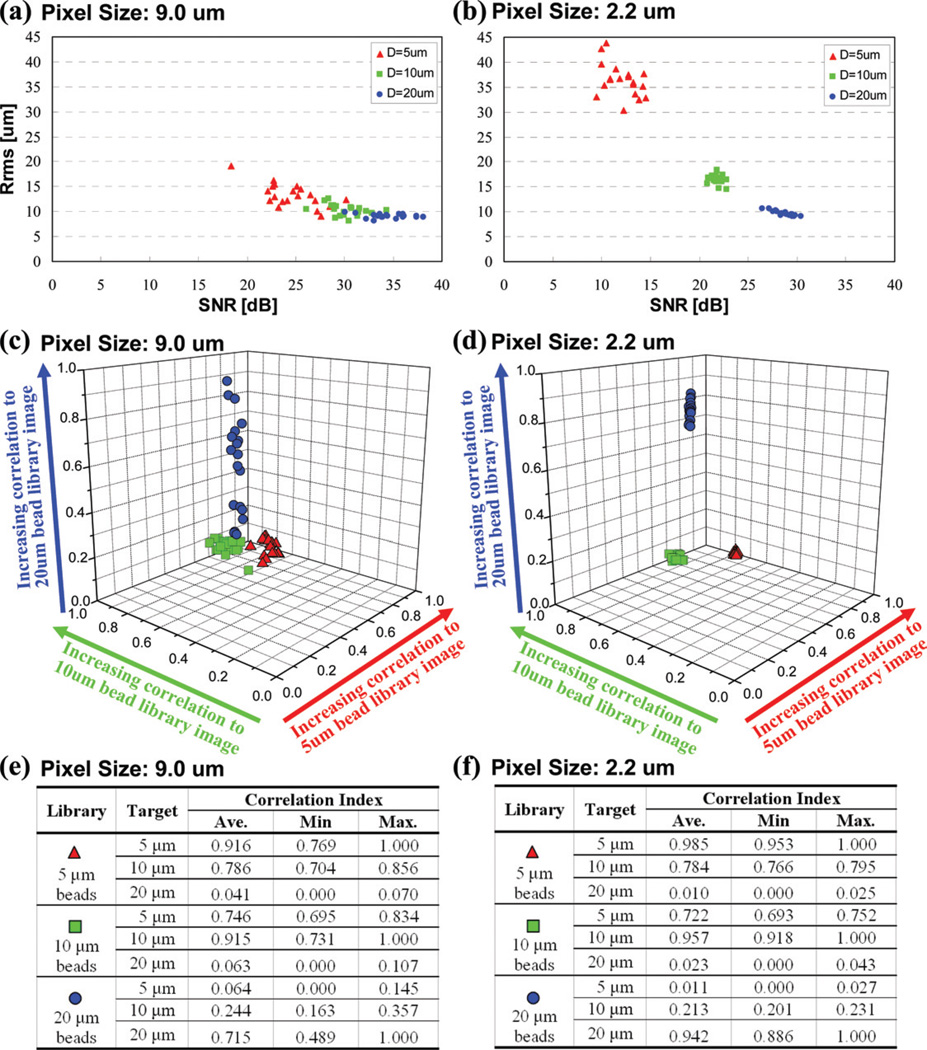
To better quantify the performance improvement of the high-resolution sensor array, we performed a series of characterization experiments with homogenous solutions containing 5, 10 and 20 µm polystyrene beads. Statistical distribution of three major image parameters, i.e. SNR, R_rms and correlation index, are calculated for each particle type using 20 different samples. Fig. 4 shows the performance summary of a large pixel size sensor (9.0 µm) compared to a small pixel size sensor (2.2 µm) for these three image metrics. In Fig. 4(a–b), SNR and R_rms distribution of three different sized particles, i.e.,D = 5, 10 and 20 µm is shown with red triangles, green squares and blue circles, respectively. The performance of the large pixel size sensor array (Fig. 4(a)) reveals that there is significant overlap among the SNR and R_rms signatures of different sized particles, which may translate into possible characterization errors. Furthermore, Fig. 4(c) also plots the correlation index of these 3 different types of particles to their corresponding mean library images. Even though the correlation results of Fig. 4(c) reveal, as expected, three different groups that can be used for characterization decisions, the variation in the correlation index of the same particle type is relatively large, resulting in a large group size. On the other hand, the performance of the high-resolution sensor-array platform, as summarized in Fig. 4(b) and 4(d), shows significant improvement for characterization decisions. Both of these figures illustrate that the high-resolution sensor array can do a much better job to pick up the fine differences of the diffraction patterns corresponding to different particle types. As a result of this improved performance, the signature uniformity of each particle type is now much improved, yielding more reliable characterization decisions with distinct statistical groups for each image metric as shown in Fig. 4(b) and 4(d).

Fig. 4.

The effects of the pixel size of the sensor array on the statistical distribution of various image metrics calculated for three different microbead types are shown. (a) 9 µm pixel size performance: SNR and R_rms map for 20 samples from each micro-particle type is shown. (b) Same as (a) except for 2.2 µm pixel size sensor array. (c) 9 µm pixel size performance: The 3D correlation index map that is calculated using 20 samples from each micro-particle type is shown. (d) Same as (c) except for 2.2 µm pixel size sensor array. The tables in (e) and (f) briefly summarize the statistics of the correlation index results of (c) and (d), respectively. These results illustrate that the diffraction signature uniformity of each particle type is significantly improved using a high-resolution sensor array, yielding more reliable characterization decisions with distinct statistical groups for each one of the image metrics.

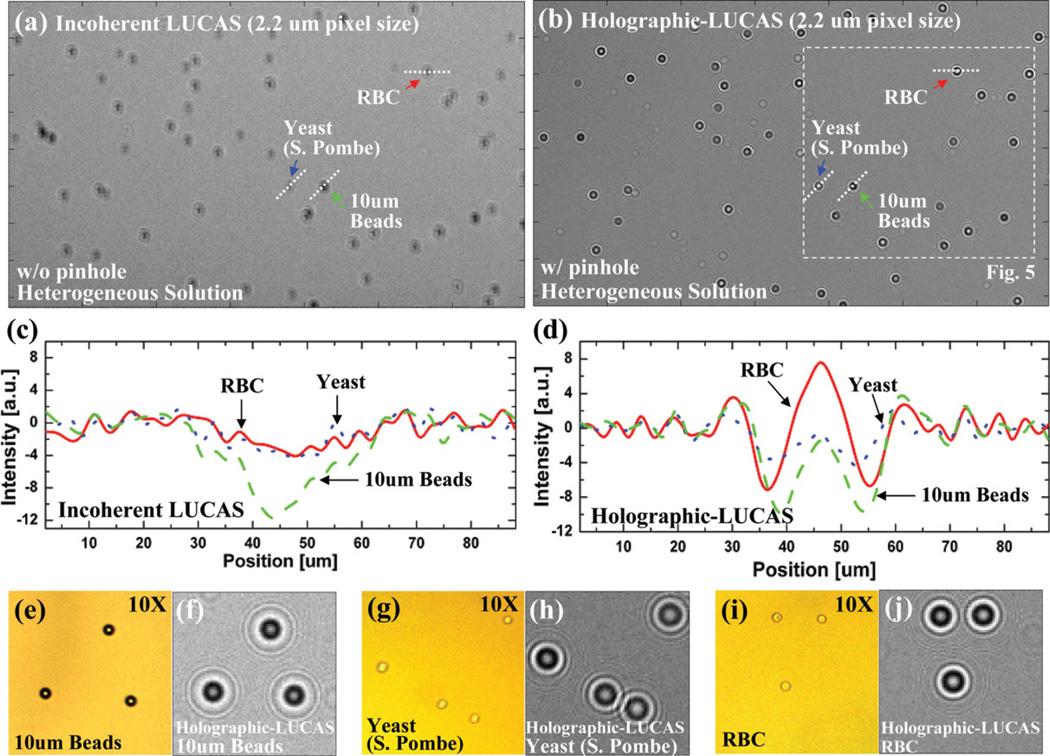
Next we evaluated the performance improvement of the holographic on-chip system over the classical LUCAS platform using the same high-resolution sensor array. For this purpose, we imaged without using any lenses a heterogeneous solution that contained red blood cells (RBCs), yeast cells (S. Pombe), and 10 µm polystyrene microbeads, with and without a 100 µm pinhole to control the spatial coherence properties of the source. Fig. 5 illustrates the significant differences between the holographic detection (Fig. 5(b)) vs. the conventional incoherent detection (Fig. 5(a)), both of which utilized the high-resolution sensor-array. As discussed earlier, with the pinhole, due to increased spatial coherence, the holographic diffraction pattern of each micro-object type exhibits much richer texture information with unique oscillating features containing the phase information of each cell/micro-particle. This phase information is normally lost during incoherent illumination as discussed in the theory section of the article in the Appendix. Fig. 5(c) and 5(d) also illustrate the cross-sectional profiles of the diffraction pattern of different objects under incoherent and coherent illuminations cases, respectively. These results, together with Fig. 5(e–j) clearly demonstrate that the holographic diffraction pattern of different cells/micro-particles are quite rich in 2D texture providing significant advantages when compared to conventional LUCAS systems^28–30 for lensless characterization and counting of a heterogeneous cell solution on a chip.

Fig. 5.

(a) and (b) illustrate the performance differences between conventional LUCAS vs. Holographic-LUCAS. In each image a high-resolution CMOS sensor array (2.2 µm pixel size) was used. (c) and (d) show the cross sectional intensity profiles (taken from (a) and (b)) of various micro-objects imaged using conventional LUCAS and Holographic-LUCAS, respectively. Due to increased spatial coherence, the holographic diffraction pattern of each micro-object type exhibits much richer texture information with unique oscillating features containing phase information of the cell/micro-particle. This phase information is normally lost during incoherent illumination as discussed in the Appendix. (f,h,j) show zoomed images of the holographic diffraction signatures of 10 µm beads, yeast cells (S. Pombe) and RBCs, respectively. For comparison purposes, a microscope image of the same field of view that is acquired with a 10 × objective-lens is also shown in (e,g,i).

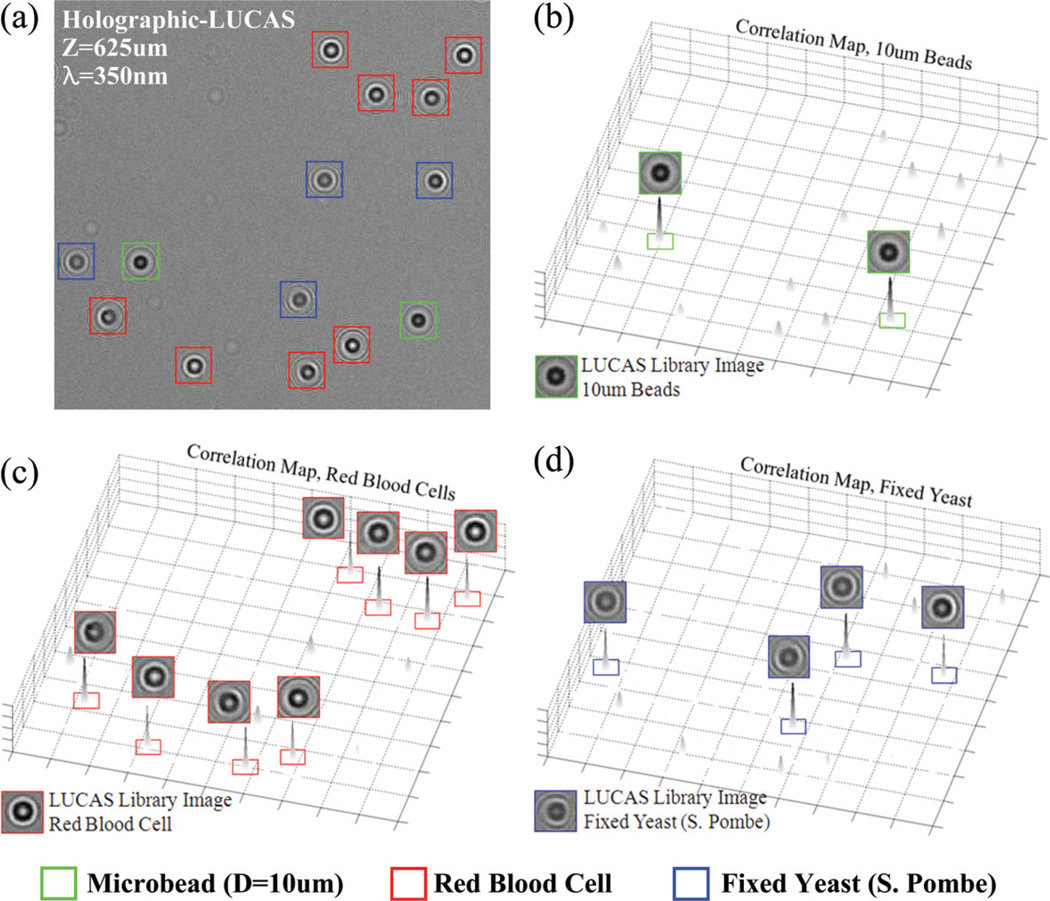
To experimentally illustrate this last claim, Fig. 6 shows an example of automatic characterization of a heterogeneous solution containing RBCs, fixed yeast cells (S. Pombe) and 10 µm beads. These three types of micro-objects were individually identified within the acquired Holographic-LUCAS image by calculating their correlation to the mean library images of each type. The calculated 2D correlation maps (see the Experimental methods section) are illustrated in Fig. 6(b–d) for each one of the mean library images, exhibiting sharp correlation peaks for target cell/object types. In Fig. 6(a) which is taken from the white frame of Fig. 5(b), two 10 mm beads, eight RBCs, and four yeast cells were successfully identified by the decision algorithm based on the 2D correlation maps shown in Fig. 6(b–d). These results demonstrate the proof-of-concept for on-chip characterization of a heterogeneous cell solution based on pattern recognition of the holographic diffraction pattern of each object type.

Fig. 6.

(a) Automatic characterization of a heterogeneous solution of RBCs, yeasts (S. Pombe) and 10 µm beads is illustrated using Holographic-LUCAS (λ = 350 nm). 2D correlation maps corresponding to each library image are also illustrated in (b–d), exhibiting sharp correlation peaks for the target cells/objects.

Discussions

As briefly outlined in the Introduction section, the Holographic-LUCAS platform of this article exhibits several key differences when compared to exisiting DIHM systems.^20–23First, since spatial resolution is not directly relevant to our on-chip cytometry approach, there is no 3D reconstruction involved in our technique. With existing DIHM systems, the aim is high-resolution numerical reconstruction of the 3D volume of the sample solution, which requires extensive numerical processing of the acquired 2D hologram. In our approach, there is no such digital reconstruction, and the detected holographic lensfree image is simply analyzed by a pattern recognition algorithm to classify different cell types on the chip. Note that this pattern recognition step is common to any other imaging based cytometry approach (including DIHM) once the image is captured or reconstructed, and therefore, it does not add an extra source of complexity and computation time to our technique. Therefore, numerically and computationally our approach is much simpler and faster since high spatial resolution is not of interest for this work.

Second, DIHM systems need to over-sample the diffraction pattern of the cells to achieve a reliable reconstruction. This necessitates the use of physical magnification of the fringes of the cell signatures (typically by 20–30 ×). On the other hand, with our approach there is no fringe magnification (i.e. close to unity), which also implies that the recorded holograms in our case are under-sampled or critically-sampled. The advantage of under-sampling is that the limited number of pixels on the sensor array is now utilized more efficiently, which helps us to increase the characterization throughput. In other words, fewer pixels of the sensor array can now represent the type and the 3D location of a target cell within a heterogeneous solution.

Third, DIHM systems rely on near-perfect spatial coherence of the illumination source together with a large zero-order emission cone from the pinhole to achieve a high spatial resolution. That is the reason why in most DIHM systems a pinhole diameter of <2–3 µm is used. With our approach, these requirements are more relaxed since even with partially coherent illumination, the signature of different cells/micro-particles can exhibit uniquely different features enabling automated characterization of a cell solution using a pinhole diameter of ~ 100 µm (see the Results section). This significantly larger diameter of the pinhole is quite important to increase the light throughput for illumination. For instance, in DIHM systems, usually a high magnification objective lens is utilized right in front of the pinhole to increase its transmission, which in our set-up is redundant, making it highly suitable for lensless on-chip miniaturization. This is especially significant to reduce the cost and the space requirement of a point-of-care on-chip cytometry system.

With our illumination scheme, for a pinhole diameter of 0.1 mm, using the van Cittert–Zernike Theorem,³² we can estimate the diameter of near-perfect spatial coherence circle at the sensor-array plane as: D_coherence ≈ 160λ. However, since Holographic-LUCAS is only concerned with the 2D texture of the cell holograms, it essentially also works for partially coherent illumination. This implies that the diameter within which we have a partial hologram of the cell is effectively larger than D_coherence ≈ 160λ. We should note that one can utilize a smaller pinhole size to increase the diameter of this coherence circle at the detection plane. However, a smaller pinhole size will also increase the interference among neighboring cell holograms, which might reduce the pattern matching accuracy due to spatial overlap of the cell patterns. Therefore, a relatively large aperture size such as 0.05–0.1 mm does not only improve the light transmission efficiency without the use of any focusing optics, but also improves the accuracy of Holographic-LUCAS, especially at high cell concentrations.

To better understand the relationship between the cell density and the counting accuracy of Holographic-LUCAS, we can analytically calculate the percentage of cells that statistically overlap with each other at the hologram plane as:

$$\text{Overlap}\_\text{Ratio}=1-\text{exp}(-\pi D^{2}HC)$$

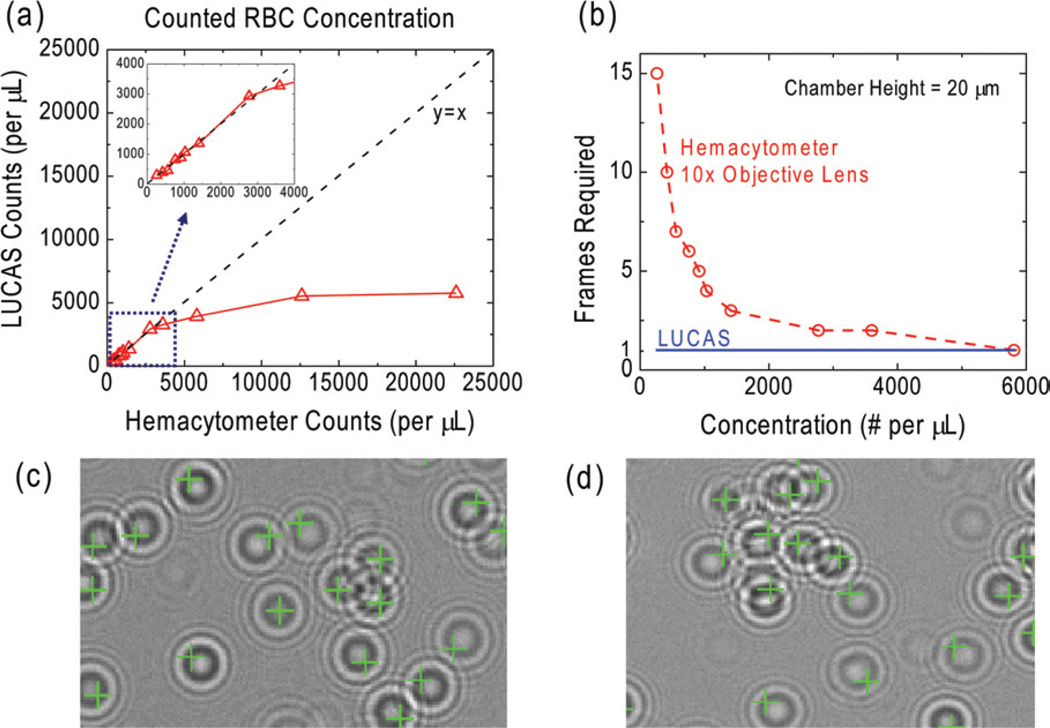
where D is the effective diameter of the cell hologram, H is the channel height and C is the concentration of the cell solution.²⁸ This implies that, for a channel height of ~20 µm and a cell hologram diamater (RMS) of ~50 µm, to achieve less than 10% overlap among cell holograms, we need a cell density of C < 671 cells µL⁻¹. As a matter of fact, for a certain fraction of those 10% of the cells that do overlap with each other at the detector plane, the pattern matching decision algorithm of Holographic-LUCAS can still enable correct counting results, to further improve its accuracy for a cell concentration level of >671 cells µL⁻¹. To illustrate this fact, in Fig. 7, we show the counting results for various concentration levels of RBCs. Dilution of the blood sample was achieved by using buffered blood bank saline (Fisherbrand, Blood Bank Saline, Fisher Scientific). For each sample solution, Holographic-LUCAS automatically counted the cells using pattern matching to an RBC library image (Fig. 7(c–d)). To verify the counting accuracy of Holographic-LUCAS, we also used a hemacytometer (H = 20 µm, CELL-VU CBC DRM-70, Millennium Sciences) to analyze the same sample solution using manual counting through a 10× objective lens. As illustrated in Fig. 7(a), Holographic-LUCAS maintained its accuracy upto an RBC concentration of ~3000 cells µL⁻¹. Beyond this concentration level, the statistical overlap of the cell holograms reaches upto ≥37%, which increases the counting errors made by Holographic-LUCAS. However, we should emphasize that for a cell density of ~3000 cells µL⁻¹, Holographic-LUCAS can still monitor >100 000 cells, all in parallel, due to its ultra-large field of view.

Fig. 7.

The quantified comparison between Holographic-LUCAS (λ = 500 nm) and a Hemacytometer for counting of RBCs as a function of the cell concentration is given in (a–b). For Holographic-LUCAS measurements, the RBC concentration for each sample is measured by automated processing of the acquired lensfree images, whereas for Hemacytometer measurements manual counting of several 10 × microscope images was used. The inserted figure in (a) zooms into the linear region (y = x) illustrating that Holographic-LUCAS can achieve a reliable performance for a cell density of up to ~3000 cells µL⁻¹. In (b) the minimum number of captured frames/images that is required for counting of ≥50 cells is shown for a Hemacytometer vs. Holographic-LUCAS. For a cell density range of <800 cells µL⁻¹, LUCAS always required the capture of a single frame, whereas a Hemacytometer, through a 10× microscope objective lens, required >10 different frames, corresponding to different field of views. (c–d) A zoomed field of view for automated characterization of an RBC solution is illustrated using Holographic LUCAS, where even partially overlapping cell signatures can be detected. The faint pattern in (c), which is not identified as an RBC is simply a dust particle at the surface of the sample.

Another important distinction between hemacytometer and Holographic-LUCAS is also highlighted in Fig. 7(b): for a cell concentration level of <800 cells µL⁻¹, more than 10 different frames (corresponding to different field of views) are captured with a regular 10 × objective lens to enable a statistically significant count of at least 50 cells using the hemacytometer. On the other hand, Holographic-LUCAS requires just a single image to be captured since it can immediately monitor a much larger sample volume.

Since the Holographic-LUCAS approach does not rely on conventional optical components such as lenses, mirrors, beam splitters, etc., it offers a flexible, compact and cost-effective alternative for many on-chip diagnostics applications including whole blood analysis. To specifically point to its flexible design, before we conclude, we will briefly discuss one possible scenario to directly merge capillary tubes with the Holographic-LUCAS platform. For diagnostics applications, capillary tubes offer great flexibility for handling and testing of bodily fluids or other heterogeneous cell solutions. For example, blood samples of a patient can be very easily collected using a capillary tube from e.g., the finger tip of the patient. Towards this end, the lensfree and compact platform of Holographic-LUCAS can be directly combined with such capillary tubes. This capillary based on-chip imaging approach can be quite convenient for especially blood tests as it may offer measurement of the cell count with inexpensive disposable capillaries avoiding any extra sample handling steps. To illustrate the initial proof-of-concept, we used a special capillary tube (from Polymicro Technologies) that had an air–core diameter of 20 µm, with a total outer diameter of ~ 130 µm to directly image RBCs within the capillary tube as shown in Fig. S4.^† To train our decision algorithm for recognition of the specific holographic diffraction pattern of each cell type through the capillary walls, new image libraries need be formed for each cell type of interest. Since holographic cell patterns are now significantly changed (Fig. S4^†), the decision algorithm will also be modified to utilize the asymmetry with respect to the capillary length.

Conclusions

We experimentally demonstrated the proof-of-concept of a lensfree holographic imaging platform for on-chip cytometry and diagnostics applications. We term this new on-chip platform as Holographic-LUCAS. By controlling the spatial coherence of the illumination source, we record 2D holographic diffraction pattern of each cell/microparticle on the chip using a high resolution sensor array. The recorded hologram is then processed by using a custom developed decision algorithm for matching the detected hologram texture to existing mean library images for on-chip characterization and counting of a heterogeneous solution of interest. When compared to existing on-chip systems, we verified significantly improved performance of our approach by automatically characterizing heterogeneous solutions of red blood cells, yeast cells, E. coli and various sized micro-particles without the use of any lenses or microscope objectives. This Holographic-LUCAS platform may especially be quite useful for point-of-care cytometry and diagnostics applications including infectious diseases such as HIV or malaria.

Appendix

Theory behind Holographic-LUCAS

To theoretically model the behavior of the Holographic-LUCAS platform, for simplicity let us assume that the illumination is achieved through an ideal coherent source emitting waves given by the complex function i(x,y,z), where (x,y,z) represents the 3D coordinate system. Let us also assume that the cell/micro-object of interest acts as a local scatterer with a complex emission function of s(x,y,z). Then one can write the complex field right in front of the sensor plane (located at z = z₀) as: i(x,y,z =z₀) + s(x,y,z =z₀). Therefore the field intensity that is sampled by the sensor array can be written as:

$${|i(x,y,z=z_0)|}^2+{|s(x,y,z=z_0)|}^2+2\mathrm{R}\mathrm{e}\{i(x,y,z=z_0)\times s^{*}(x,y,z=z_0)\}$$

where “*” denotes the complex conjugate operation. In this formula, the sampling grid of the sensor array has been left out as a topic that will be discussed later on.

This above equation summarizes the entire operation of the Holographic-LUCAS platform. The first term above, |i(x,y,z = z₀)|² corresponds to the background illumination and does not contain any useful information regarding the cell/micro-object. To digitally increase the signal to noise ratio and to eliminate dead pixels of the sensor array, a useful method that we utilize is to capture a background image without the cell solution of interest and perform a digital subtraction of the background term, |i(x,y,z =z₀)|² from the recorded hologram.

The second term above, |s(x,y,z = z₀)|² represents the classical diffraction pattern of the micro-object. The physical origin of this term is self-interference of the scattered fields from the cell body, and therefore it is not affected much by the spatial coherence properties of the illumination source as long as the scattering volume of the cell is small. As a matter of fact, our previous approach, LUCAS,^28–30 depends on the detection of this term for high-throughput cell characterization. Note that as the size of the cell/micro-object gets smaller, the relative amplitude of this term becomes also smaller, making it rather difficult to detect with existing incoherent LUCAS systems. The same issue also exists for phase objects like an E. coli sample that act as a weak scatterer making the detection of their classical diffraction pattern rather difficult. As illustrated in the Results section, Holographic-LUCAS is especially suitable for on-chip monitoring and characterization of these weakly scattering phase objects such as small bacteria.

The third term above, 2Re{i(x,y,z =z₀) × s*(x,y,z =z₀)} represents the holographic diffraction pattern, and has several significant advantages for on-chip cytometry when compared to the classical diffraction term. First, since |s(x,y,z=z₀)|≪|i(x,y,z =z₀)|, the signal strength of holographic diffraction is much stronger than the classical diffraction term due to heterodyne nature of holography. We should note that for strongly scattering samples (which have a large refractive index contrast or a large size), |s(x,y,z = z₀)|≪|i(x,y,z =z₀)| is no longer valid, and for such objects SNR improvement of the holographic diffraction pattern will be smaller.

Second, unlike |s(x,y,z = z₀)|² term, the hologram now has the phase information of the complex scattered field encoded in the amplitude oscillations of 2Re {i(x,y,z =z₀) × s*(x,y,z =z₀)}. This brings an important source of additional texture to the cell hologram pattern that improves the differences between different cell types for automated identification and classification. Furthermore, it also helps to improve the visibility of phase objects such as E. coli samples (refer to the Results section for an experimental verification—Fig. 2).

Note that conventional DIHM systems normally use 2Re{i(x,y,z =z₀) × s*(x,y,z =z₀)} term for solving the inverse wave problem to enable a high resolution volume map of the solution of interest. Holographic-LUCAS on the other hand, does not aim for numerical reconstruction of a high-resolution image, but instead utilizes the texture of the hologram to identify the cell type and location. This step involves straightforward pattern recognition algorithms, and therefore is numerically much simpler and faster than the solution of the inverse wave problem. Furthermore, from a cell characterization point of view, a reduction in spatial coherence of the source or an interference of the classical diffraction pattern, |s(x,y,z = z₀)|², with the recorded hologram does not affect our characterization results. The main reason for this improved resistance to such undesired effects is that Holographic-LUCAS works with mean library images of a target cell type, and therefore, all such nonideal terms are taken into account while building the mean library image to be used as the target pattern. Therefore, in Holographic-LUCAS the secondary effect of the classical diffraction pattern is also included in our characterization results.

Before we conclude the description of the theory behind Holographic-LUCAS, we would like to briefly comment on the sampling of the field intensity by the sensor array. In conventional DIHM systems, this sampling issue is so important for the reconstruction that a fringe magnification of >20 times is typically used. With Holographic-LUCAS this is not needed as our aim is pattern recognition based on hologram texture. Furthermore, as the cell-sensor distance in our experimental setup is much smaller than the pinhole-sensor distance, we effectively have unity fringe magnification. This implies that the hologram or the diffraction pattern that we sample is highly undersampled. This pauses no restrictions for our characterization results, as an under-sampled diffraction pattern can still uniquely represent a cell type based on a statistical image library (see the Results section for more discussion on this). A significant advantage of using under-sampling in Holographic-LUCAS is actually to use the total number of available pixels efficiently. In other words, by under-sampling the holographic pattern, we can actually use fewer pixels to represent a cell type, which increases the total throughput without the need for extensive numerical reconstruction.