Using the Plasmon Linewidth to Calculate the Time and Efficiency of Electron Transfer between Gold Nanorods and Graphene

Abstract

We present a quantitative analysis of the electron transfer between single gold nanorods and monolayer graphene under no electrical bias. Using single particle dark-field scattering and photoluminescence spectroscopy to access the homogenous linewidth, we observe broadening of the surface plasmon resonance for gold nanorods on graphene compared to nanorods on a quartz substrate. Because of the absence of spectral plasmon shifts, dielectric interactions between the gold nanorods and graphene are not important and we instead assign the plasmon damping to charge transfer between plasmon-generated hot electrons and the graphene that acts as an efficient acceptor. Analysis of the plasmon linewidth yields an average electron transfer time of 160 ± 30 fs, which is otherwise difficult to measure directly in the time domain with single particle sensitivity. In comparison to intrinsic hot electron decay and radiative relaxation, we furthermore calculate from the plasmon linewidth that charge transfer between the gold nanorods and the graphene support occurs with an efficiency of ~ 10%. Our results are important for future applications of light harvesting with metal nanoparticle plasmons and efficient hot electron acceptors as well as for understanding hot electron transfer in plasmon-assisted chemical reactions.

The nonradiative decay of surface plasmons supported by metal nanoparticles involves the generation of excited (‘hot’) electrons, which can induce photochemical reactions of adsorbate molecules on the nanoparticle surface.^1–2 The light assisted growth of silver nanoparticles has been demonstrated to involve the reduction of metal ions after plasmon-generated hot electron transfer.^3–4 Redox reactions of molecules at the surface of metallic nanoparticles have also been detected using tip-enhanced Raman spectroscopy (TERS),⁵ and the breaking of chemical bonds has been identified through the formation of HD from a mixture H₂ and D₂ using mass spectrometry.⁶ The mechanism for dissociation of H₂ and D₂ was assigned to plasmon-generated hot electron injection from the gold nanoparticles into the molecular antibonding orbitals.⁶ In addition to charge transfer to molecular adsorbates, excitation of surface plasmons can promote electrons across the Schottky barrier formed at the interface between metal nanoparticles and semiconductor materials.^7–10 In particular, such photo-induced metal nanoparticle - semiconductor charge transfer has been exploited for water splitting involving a multistep reduction - oxidation cycle.^11–12 A central question that still remains and is critical for the further improvement in plasmon-assisted photo-catalytic processes is how charge transfer from the metal nanoparticle can effectively compete with the intrinsic ultrafast energy relaxation in the metal.^13–16

In order to maximize charge separation of hot electrons from the nanoparticle surface, the nanoparticles must be coupled not only with an efficient electron acceptor, but also combined with a material that has a high electron mobility. Graphene is an attractive material to address these issues because it exhibits exceptional charge transport properties with an intrinsic electron mobility limit of 2 × 10⁵ cm² V⁻¹ s⁻¹.¹⁷ Strong coupling through charge transfer and local electric fields have indeed been reported for gold nanoparticles interacting with graphene.^18–22 Pristine graphene also possesses unique properties emerging from its electronic structure, the Dirac cone.^23–25 The Fermi-level of pristine graphene furthermore lies only 0.6 eV above the level of gold^26–27, making graphene an excellent candidate for harvesting hot electrons produced via plasmon excitation over a large wavelength range. Gold nanoparticle - graphene hybrids have therefore been fabricated to create photodetectors and photovoltaic devices that operate based on hot electron transfer upon illumination at plasmon resonant wavelengths.^28–30

The observed charge transfer process must, however, be further optimized if gold nanoparticle - graphene hybrids are to perform in the efficiency regime necessary for practical light harvesting applications. Measuring the current produced for a bulk device based on gold nanoparticle - graphene hybrids is insufficient for quantifying plasmon-generated hot electron transfer because differences in electron transport properties in the graphene and at the interfaces between the graphene and the electrodes can drastically influence the detected photo-current. Therefore it is important to isolate the parameters that determine the hot electron transfer time and efficiency from gold nanoparticles to graphene without an applied electrical bias. Although this electron transfer process has been implied based on the observed photo-current generation,^28–29 the electron transfer time in gold nanoparticle - graphene hybrids remains unexplored to date.

Determination of the time scales for hot electron transfer between chemically prepared gold nanoparticles and monolayer graphene, as well as the factors governing it, is impeded by two central challenges: nanoparticle size and shape inhomogeneity and the expected ultrafast (i.e. femtosecond) charge transfer. Chemical synthesis of metal nanoparticles often yields broad distributions of sizes and shapes, leading to inhomogeneous broadening of the surface plasmon resonance in ensemble spectroscopy. This issue of sample inhomogeneity can be overcome by using single particle spectroscopy.^31–36 The second difficulty arises from the fact that the electron transfer time is expected to be very fast based on previous ensemble studies for gold nanoparticles interacting with TiO₂ nanoparticles, for which electron transfer was reported to be less than 100 fs.³⁷ Although ultrafast pump-probe transient absorption spectroscopy can routinely be used to access such time scales in ensemble measurements, achieving similar time resolutions with single particles is very demanding because of the pulse broadening in a microscope objective.

In this study, we employed single particle dark-field scattering (DFS) and photoluminescence (PL) spectroscopy to investigate the electron transfer between gold nanorods and monolayer graphene without an applied bias in the frequency domain. Single particle spectroscopy enables the determination of the homogenous plasmon linewidth, which can be used as a measure for the time scale of the energy relaxation after photo-excitation. By comparing the linewidths obtained from individual gold nanorods on quartz and graphene substrates, we determined the time scale and efficiency for electron transfer between gold nanorods and graphene. Simulations using a quasi-static model and the finite difference time domain (FDTD) method support our conclusions.

RESULTS AND DISCUSSION

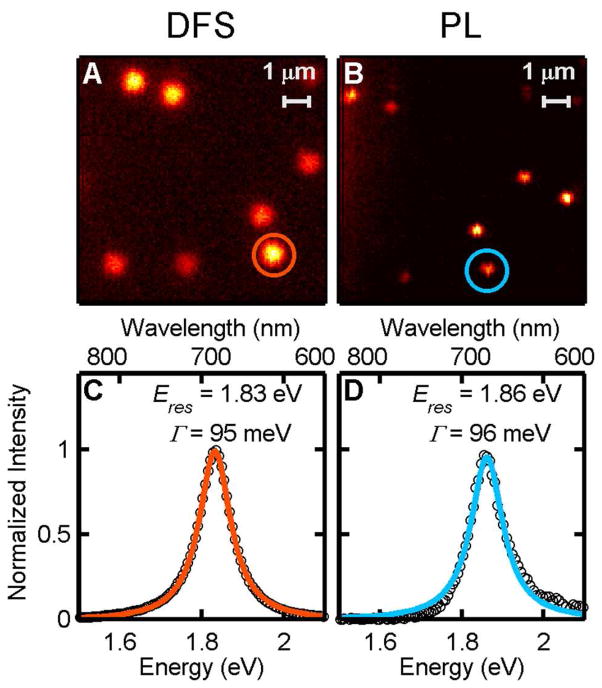
The resonance energy, intensity, and linewidth of the longitudinal surface plasmon mode were determined for DFS and PL spectra from 100 single nanorods on bare quartz substrates. Individual nanorods with an average size of 27 × 70 nm (Figure S1) were easily identified using both their DFS and PL, as shown in the images in Figure 1A and 1B, respectively. Figure 1C and 1D show representative DFS and PL spectra collected from the nanorod indicated in the corresponding images. A 532 nm laser was used as the excitation source for the one-photon PL of the nanorods, and the PL spectrum closely followed the DFS spectrum, as observed previously in other one-photon PL single particle studies.³⁸ In order to obtain the plasmon linewidth, Γ, each single nanorod spectrum was fitted to a Lorenztian function (solid lines in Figure 1C and 1D). Correlated scanning electron microscopy (SEM) and DFS images for selected areas confirmed that single nanorods were investigated (Figure S3), and verified the high density of single particles present across the sample. Outside of correlated areas, single particles were identified based on the Lorenztian nature of their DFS and PL spectra. Non-Lorenztian spectra likely caused by nanorod aggregates were excluded from the analysis.

Figure 1.

A, B) Normalized DFS (A), and PL (B), images of single gold nanorods on bare quartz. C, D) Normalized DFS (C) and PL (D) spectra of a representative single nanorod as indicated by the circles in the images. The homogeneous linewidth (Γ) and resonance energy (E_res) were determined from a Lorenztian fit, which is displayed as the orange and blue lines.

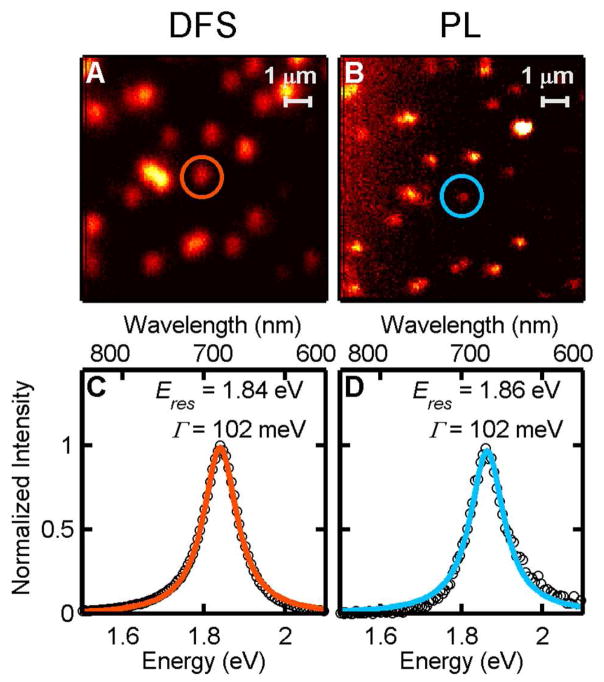
Single particle spectra of 95 nanorods deposited on graphene were acquired and analyzed in the same manner. Graphene was transferred to a quartz slide prior to gold nanorod deposition, and Raman spectroscopy and SEM confirmed the presence of monolayer graphene (Figure S4). Figure 2A and 2B show DFS and PL images of single nanorods on graphene. Corresponding spectra of the longitudinal surface plasmon resonance are given in Figure 2C and 2D. These unpolarized single particle spectra are again well described by a Lorenztian lineshape (solid lines).

Figure 2.

A, B) Normalized DFS (A), and PL (B) images of single gold nanorods on graphene. C, D) Normalized DFS (C) and PL (D) spectra of a representative single nanorod as indicated by the circles in the images. The homogeneous linewidth (Γ) and resonance energy (E_res) were determined from a Lorenztian fit, which is displayed as the orange and blue lines.

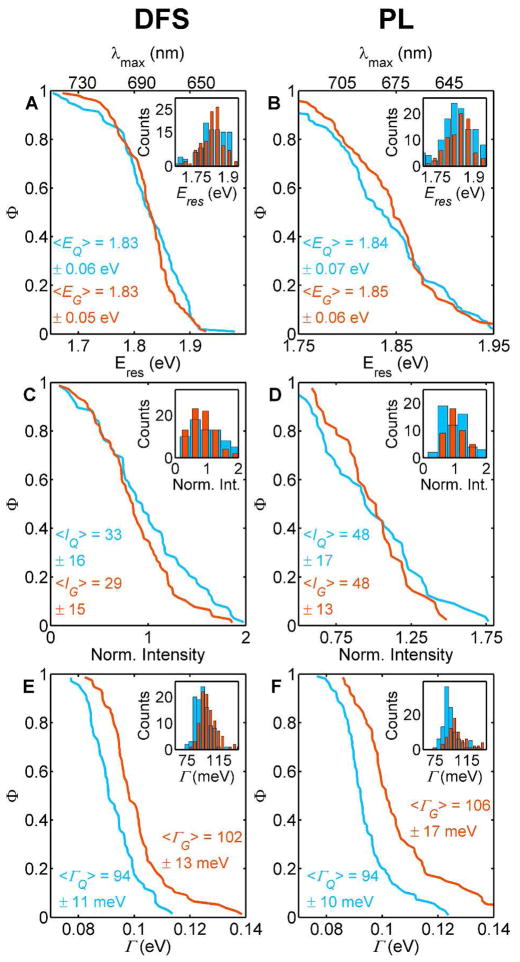
Based on the data in Figures 1 and 2, a comparison of the longitudinal plasmon linewidth for nanorods on quartz and graphene suggests that the plasmon resonance is damped due to interaction with the graphene layer. However, to draw such a conclusion a statistical analysis of all single particle spectra is necessary. Figure 3 shows complementary cumulative distribution functions (CCDFs) obtained from the single particle DFS (left column) and PL (right column) spectra. CCDFs are opposite to cumulative distribution functions (CDFs), illustrating the fraction of nanorods, Φ, with a value higher than the one indicated on the x-axis. Two important properties of the CCDFs are easily visualized in Figure 3: first, the average value corresponds to Φ = 0.5; and second, the slope of CCDFs corresponds to the standard deviation (smaller slope equals larger standard deviation). Regular histograms have been added as insets in each panel of Figure 3.

Figure 3.

Summary of the spectral parameters extracted from 100 nanorods measured on bare quartz (blue) and 95 nanorods measured on graphene (orange). The results for DFS are shown in the left column as complementary cumulative distributions, while the corresponding PL data is compiled in the right column: resonance energy E_res (A and B), intensity (C and D), and linewidth Γ (E and F). The same data is also displayed in form of a standard histogram as an inset, and the mean values and standard deviations are listed in each panel. The intensity values were normalized by the respective means of each distribution for better comparison.

The DFS and PL resonance energy of the longitudinal surface plasmon did not change when the nanorods were placed on graphene. Figure 3A and 3B show that the CCDFs for the plasmon resonance energy are almost identical when the nanorods were placed on quartz (blue) vs. graphene (orange), consistent with the overlapping histograms pictured in the insets. The lack of a shift in resonance energy suggests that the dielectric function of the material surrounding the nanorods did not change, and therefore, the underlying graphene layer did not modify the refractive index of the gold nanoparticles. Even though considerable plasmon resonance redshifts have been reported for gold nanoparticles on graphene,^{18–19, 39} similar shifts were not observed here most likely because of the small interfacial area and the absence of an applied bias. In addition, because the graphene in this study consisted of only an atomic monolayer and the nanorods were surrounded by an organic capping agent, it is reasonable that dielectric effects were very small. Small plasmon resonance shifts beyond the sensitivity of our single particle measurements can, however, not be completely ruled out.

The chemical environment of a metal nanoparticle can, however, influence the surface plasmon resonance in other ways than through changes in the refractive index, as has been demonstrated in many early ensemble studies of metal nanoparticles interacting with different molecular adsorbates such as Cl⁻¹, CN⁻¹, and SH⁻¹.^40–43 The adsorption of these species on metal nanoparticles causes damping of the plasmon resonance as evidenced by a decrease in peak intensity and increase in linewidth. This change in the plasmon resonance was labeled interface damping and was assigned to a charge transfer process between the photo-excited metal nanoparticles and the molecular adsorbates, leading to a faster dephasing of the plasmon and hence a broader linewidth.^41–43 A decrease of peak intensity was not observed for the DFS of the gold nanorods on graphene compared to quartz (Figure 2C). However, small intensity changes can be difficult to monitor by single particle spectroscopy as it has been observed for single gold nanospheres that the DFS intensities vary dramatically from particle to particle despite minor differences in the nanoparticle size.³⁶ Such fluctuations could obscure an intensity decrease due to plasmon damping by the graphene for our samples. The PL intensity also did not change when changing the substrate from quartz to graphene (Figure 2D) and will be discussed below in more detail.

In contrast to the indistinguishable intensity and resonance energy of the longitudinal surface plasmon for both substrates, graphene broadened the linewidth of the DFS and PL spectra. The difference in linewidth is illustrated in Figure 3E and 3F by the clear separation between the CCDFs for nanorods on quartz vs. graphene and the shift in the corresponding histograms (insets). The average increase in plasmon linewidth of 10 meV confirms the presence of an additional damping pathway for nanorods on graphene.⁴³ We assign this change in plasmon linewidth to the charge interaction between gold nanorods and the graphene, similar to interface damping described above. The small magnitude of the linewidth increase is consistent with the absence of an intensity decrease, as the latter appears to be harder to quantify by single particles vs. ensemble spectroscopy. However, only single particle studies can determine the homogenous plasmon linewidth,^{31–35, 44–46} which can be quantitatively linked to different plasmon dephasing mechanisms including interface damping as shown next. The plasmon linewidth measured by ensemble UV-vis spectroscopy is 214 meV in comparison to the average value of 94 meV for nanorods on quartz (Figure S2).

The total linewidth, Γ, describes the overall decay of the plasmon oscillation and is due to contributions from intrinsic electron scattering in the metal, γ_b, and radiation damping, Γ_rad, expressed according to Γ= γ_b + Γ_rad.^{31–35, 44–46} Electron surface scattering in small nanoparticles leads to further damping. ^{31–35, 44–46} However, for nanorods with widths greater than 10 nm, as is the case here, electron surface scattering is negligible. ^{31–35, 44–46} The bulk damping term γ_b is related to the dielectric function of the metal and therefore depends on the resonance energy of the surface plasmon. ^{31–35, 44–46} The distributions of linewidth values as shown in Figure 3 are hence not sufficient enough to quantify the different contributions to plasmon damping, and Figure 4A plots the measured linewidth for gold nanorods on quartz Γ_Q as a function of the corresponding surface plasmon resonance maximum. As is clearly seen in Figure 4A, the plasmon linewidth for nanorods increased for higher resonance energies, consistent with previous studies, which assigned this trend to an increased nonradiative damping due to generation of electron-hole pairs for smaller aspect ratio nanorods with resonances approaching the interband transition threshold.^{31–35, 44–46} The variation in linewidths for the same resonance energy, on the other hand, was likely due to the experimental size dispersion of the nanorods (Figure S1) and not an experimental error. For easier comparison, the linewidth values for single nanorods were averaged in bins of 0.03 eV (Γ_{Q bin}).

Figure 4.

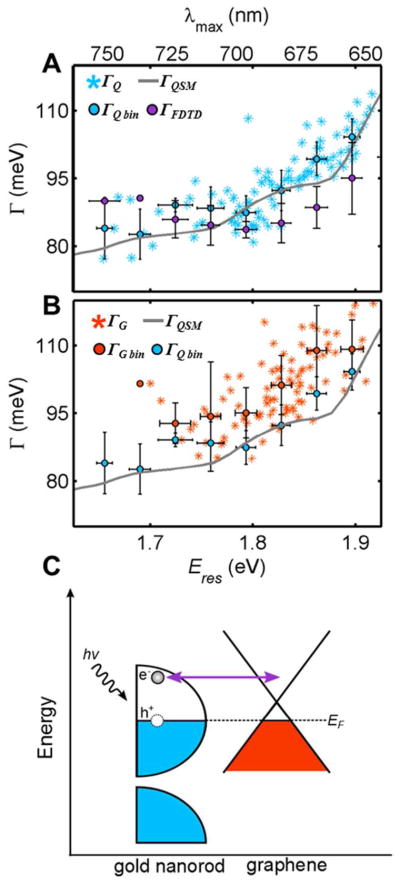
Linewidth, Γ, as a function of resonance energy, E_res, for the longitudinal surface plasmon resonance of single gold nanorods. A) Experimental linewidths for all single gold nanorods on quartz (Γ_Q, blue stars) and binned in 0.03 eV intervals (Γ_{Q bin}, blue circles) are compared to the linewidths calculated using a quasi-static model (Γ_QSM, gray line) and FDTD simulations (Γ_FDTD, purple circles). A total of 60 spectra were calculated by FDTD simulations for nanorods with dimensions based on the experimental size distribution, and the resulting data was binned in 0.03 eV intervals. See text and supporting information for more details. B) Experimental linewidths for all single gold nanorods on graphene (Γ_G, orange stars) and binned in 0.03 eV intervals (Γ_{G bin}, orange circles) are juxtaposed to Γ_{Q bin} and Γ_QSM. The error bars for all binned data correspond to one standard deviation in the linewidth and resonance energy. Note that several nanorods on quartz had resonance energies below 1.7 eV, while all nanorods on graphene had larger resonance energies (compare panels A and B). While we cannot exclude a small resonance shift on the graphene substrates due to steady state charging or dielectric effects, the sample size for this spectral range is too small to draw statistically significant conclusions and it is also possible that slightly different distributions of particle sizes were measured on each substrate. C) A schematic energy diagram illustrating charge transfer between a gold nanorod (left) and graphene (right) following plasmon induced hot electron generation.

The experimental linewidth for gold nanorods on quartz, Γ_Q, can be fully described by a quasi-static model of nanorods in a homogeneous environment, implying that the quartz substrate had a negligible effect on plasmon damping (Figure 4A). In this model, the bulk damping term, γ_b, was accounted for with a quasi-static model according to the procedure published by Sönnichsen et al (see SI).³⁵ The radiation damping term, Γ_rad, was calculated using the equation Γ_rad = 2ħκV, where κ is the radiation damping coefficient, and V is the particle volume.⁴⁴ We assumed κ to be 4.0 × 10⁻⁷ fs⁻¹ nm⁻³,³⁵ and a linear approximation of nanorod volume as a function of resonance energy was used to account for the nanorod size dispersity (Figure S8). Apart from the measured dielectric function of gold⁴⁷, an effective medium refractive index of 1.25, and κ, no adjustable parameters entered into our calculation. The excellent agreement between the experimental data for nanorods on quartz and the linewidth values of the simple quasi-static model, Γ_QSM, suggests that no other damping mechanisms contributed to the total plasmon linewidth in this case. In particular, the quartz substrate could be accounted for through the dielectric constant of the environment without additional charge transfer interactions.

More detailed FDTD calculations confirmed that the quartz substrate did not induce significant changes to the plasmon linewidth (Figure 4A). FDTD calculations allowed us to model the actual nanorod geometry (Figure S6). The nanorods were modeled with a hemispherical end cap geometry, surrounded by a 2 nm thick cetyl trimethylammonium bromide (CTAB) layer,⁴⁸ and resting on a quartz substrate. The nanorod sizes were varied according to the experimental size distribution (Figure S1), and the resulting spectra were fit to Lorenztian functions to extract the linewidth (Figure S7). By using the actual nanorod dimensions, the FDTD simulations implicitly accounted for both bulk and radiation damping. Averaged linewidths for 0.03 eV bins obtained from these FDTD simulations, Γ_FDTD, are also included in Figure 4A and are in very good agreement with the experimental data and the quasi-static model. The small deviation of the linewidth by the FDTD simulations could be due to the multitude of geometric and dielectric parameters that were included, and none of them were optimized from the literature values. For example, just the end cap geometry of nanorods has been shown to have drastic effects on the plasmon resonance energy and linewidth.⁴⁹ Because the FDTD calculated linewidths are close to the experimental values for nanorods on quartz, interface damping due to charge interaction between the gold nanorods and quartz is ruled out as an additional contribution to the plasmon linewidth, in agreement with the results from the quasi-static model.

Because the linewidth for gold nanorods on graphene, Γ_G, was found to be broadened beyond intrinsic bulk damping and radiation damping (Figure 4B), we assign the additional plasmon damping to charge transfer interactions with the graphene monolayer. In the absence of a spectral shift for the plasmon resonance energy (Figure 3A), neither the quasi-static model nor the FDTD simulations can account for the increased linewidth through changes in the graphene refractive index. While graphene could in principle be modeled by a complex dielectric function¹⁸, we instead adopt here the model of interface damping and introduce the additional plasmon relaxation pathway in the following phenomenological way: Assuming that charge transfer introduces another plasmon relaxation channel, the overall linewidth for nanorods on graphene can be written as Γ= γ_b + Γ_rad + Γ_ET, where Γ_ET represents damping due to electron transfer. Γ_ET can now be related to an electron transfer time. Plasmon dephasing is characterized by the time constant, T₂, which is related to the inelastic population decay time constant, T₁, through the equation $T_2^{-1}=T_1^{-1}/2+T^{\ast -1}$, where T*describes elastic dephasing processes.³⁵ The equation is simplified to $T_2^{-1}=T_1^{-1}/2$ for gold nanorods because pure dephasing does not contribute to the overall linewidth.³⁵ Γ_ET can then be converted into an electron transfer time via T_2,i = 2ħ/Γ_i,^{35, 46} yielding a T_2,ET of 160 ± 30 fs for gold nanorods on graphene. Energy transfer instead of electron transfer would similarly lead to plasmon broadening and could be treated equivalently. While we cannot distinguish between electron and energy transfer in this study, electron transfer between gold nanoparticles and graphene has been demonstrated before. For instance, electron transfer occurs between gold nanostructures and graphene in photodetectors.^28–29

Furthermore, the efficiency, η, of electron transfer can be calculated from $\eta =T_{1,ET}^{-1}/T_1^{-1}=T_{1,ET}^{-1}/(T_{1,r}^{-1}+T_{1,nr}^{-1}+T_{1,ET}^{-1})$ where the subscripts r, nr, and ET indicate radiative, nonradiative, and electron transfer, respectively. We obtained an average electron transfer efficiency of ~10%. The relatively slow electron transfer time and the associated low electron transfer efficiency to graphene, compared to electron transfer to TiO₂ nanoparticles for example,³⁷ could be enhanced by covering all nanorod surfaces completely with graphene. Furthermore, eliminating the CTAB capping layer should dramatically increase electron transfer times that crucially depend on the separation between electron donors and acceptors.⁵⁰

The schematic illustration in Figure 4C summarizes the suggested charge interaction between gold nanorods and graphene following plasmon-generated hot electron production. The gold nanorod first absorbs resonant photons, forming through plasmon decay energetic electrons, which can be transferred to nearby unoccupied energy states in graphene. The hot electrons have a maximum energy above the gold Fermi level equal to the excitation energy supplied by the incident photons. The gold nanorod and graphene are considered to be in equilibrium, and the Fermi level of graphene is shifted below the Dirac point because graphene is easily p-doped by gold.²⁷ Because the Fermi energies are equivalent, electron transfer from nanorods to graphene occurs only in the excited state. The simple mechanism in Figure 4C is similar to photo-induced charge transfer in molecular donor-acceptor complexes, for which Marcus theory quantitatively describes the rate of electron transfer with a driving force that depends on the energy difference of the molecular orbitals involved in the electron transfer process.⁵⁰ Although in the current gold nanoparticle - graphene hybrid system electronic bands instead of distinct orbitals must be considered, future studies will address the question if the hot electron transfer time and efficiency measured through the plasmon linewidth in these single particle studies can be tuned by changing the plasmon resonance energy through the nanorods aspect ratio and by tuning of the graphene Fermi level via doping.

Important conclusions can also be drawn from the results obtained from the PL measurements. The PL mimics the trends observed for DFS on quartz and graphene in every aspect (see Figure 3 as well as Figures S9 – S12). Particularly interesting is the fact that the PL intensity did not decrease for nanorods on graphene despite the charge interaction established through the plasmon linewidth broadening. One-photon PL in gold nanorods, excited at higher energies than the longitudinal plasmon resonance, has been assigned to plasmon emission, involving a hot electron intermediate that is created by the initial photo-excitation and converts back into a plasmon.^{38, 51} It has also been suggested though that the PL originates from local emitters such as a surface defect or molecular adsorbate, which radiate with the nanorod acting as an antenna⁵² and hence yielding a far-field spectrum that resembles the surface plasmon resonance. This latter mechanism of an amplification of extrinsic local emitters seems, however, very unlikely given that we do not observe any detectable PL quenching in Figure 3D despite the fact that graphene is an excellent electron acceptor for small molecules over a wide range of energies.^53–55 For the one-photon PL mechanism of plasmon emission after interconversion between hot electrons and plasmon, the lack of intensity loss is not inconsistent and implies that back electron transfer from the graphene to the gold must be very fast as well, as indicated by the doubled arrow in Figure 4C. This fast back electron transfer also ensures that the nanorods do not become permanently charged,² consistent with the absence of a plasmon resonance shift, although charge induced effects could be offset by dielectric changes. Another important observation is that similar linewidth broadening occurs in the nanorod PL spectra, confirming our conclusions based on the DFS, and excluding possible experimental issues such as local background correction or inaccurate peak fits.

CONCLUSIONS

In conclusion, we have compared single particle spectra of the longitudinal surface plasmon resonance of gold nanorods on quartz and graphene substrates, and observed a linewidth broadening for gold nanorods on graphene indicative of an additional plasmon damping channel. Measuring the homogeneous plasmon linewidth by single particle spectroscopy allowed for the detection and quantification of this decay channel as the small change in resonance peak width of 10 meV would be obscured in ensemble studies. We attribute the additional relaxation pathway to hot electron transfer between gold nanorods and graphene, consistent with substantial evidence of charge transfer reported in similar hybrid systems. Our frequency domain measurements, yielding an electron transfer time of 160 ± 30 fs, circumvent difficulties involved both in nanoparticle inhomogeneities and the time resolution achieved for typical ultrafast pump-probe transient absorption spectroscopy measurements of single particles. The same approach introduced here can also be applied to study other redox reactions at metal nanoparticle surfaces and hence has broad impacts on the developing field of plasmon-assisted photochemistry. We furthermore determined the electron transfer efficiency to be ~ 10%. We expect that this value can, however, be significantly improved by removing the CTAB layer covering the nanorods or completely wrapping the gold nanorods with graphene.

METHODS

Gold nanorods were purchased from Nanopartz (part # A12-25-750) and characterized by transmission electron microscopy (TEM) using a JEOL 1230 TEM, and UV-vis extinction spectroscopy using an Ocean Optics S1024DWX spectrometer. The gold nanorod dimensions determined via TEM are given in Figure S1, which also shows a typical TEM image. For gold nanorods on quartz substrates, the gold nanorods were spin-coated onto a cleaned quartz slide at a concentration optimized to yield a coverage appropriate for single particle spectroscopy. Quartz slides were used as substrates instead of glass because they yielded a lower background signal for the PL measurements. A gold identification pattern was then evaporated onto the sample with an electron-beam evaporator using a copper TEM grid as a mask.^56–57 Scanning electron microscopy (SEM) for correlation with single particle spectroscopy was performed on an FEI Quanta 400 ESEM.

High-quality large-area graphene was grown on copper foil by chemical vapor deposition (CVD) with CH₄ as the carbon source and Ar/H₂ as the carrier gas.⁵⁸ First, the copper foil was loaded into the CVD furnace, and annealed at 1,000 °C for 20 min in a 1 Torr Ar/H₂ gas flow (15 vol% H₂ balanced by 85 vol% Ar). Simultaneously, 4 s.c.c.m. CH₄ was introduced for ~10 min to grow monolayer graphene, as confirmed by Raman spectroscopy (Figure S4). The as-grown graphene on Cu foils was spin-coated with PMMA (poly(methyl methacrylate)), then the copper substrates were etched away using a 0.05 M aqueous (NH₄)₂S₂O₈ solution. The remaining free-standing graphene/PMMA layer was transferred onto quartz slides. Subsequently, the PMMA layer were removed by acetone and rinsed with DI water. After the graphene transfer, gold nanorod samples on graphene were prepared for single particle spectroscopy in an identical method to those on quartz only.

The set-up of the single particle spectrometer is shown in Figure S5. A home-built DFS and fluorescence instrument based on an inverted microscope (Zeiss) was used for all measurements. Transmission DFS spectroscopy was conducted with halogen lamp illumination through an oil-immersion condenser (NA = 1.4). The DFS signal was collected by a 50x (NA = 0.8) air-spaced objective. A 50 μm confocal pinhole was placed in the detection path to allow only the scattering from the region of interest to be detected. DFS images were recorded using a scanning piezo stage (Physik Instrumente) and avalanche photodiode (APD, Perkin-Elmer) to locate the positions of individual nanorods. Single nanorod spectra were collected by first moving the scanning stage so that only the scattered light from the desired gold nanorod passed through the pinhole, and then switching detection from the APD to a spectrometer equipped with a CCD camera (Jobin Yovin). For PL measurements, a 532 nm diode pumped continuous wave laser (Coherent) was used as the excitation source in an epi-fluorescence geometry. Dichoric, notch, and long-pass filters inserted in the detection path ensured that all laser light was removed from the PL signal. Typical excitation powers for the PL measurements were 200 μW at the sample. All spectra were background corrected and adjusted for the wavelength sensitivity of the detection system using either a white light standard (Labsphere) for the DFS or a calibrated lamp (Ocean Optics) for the PL measurements.