Medical decision support using machine learning for early detection of late-onset neonatal sepsis

Abstract

Objective

The objective was to develop non-invasive predictive models for late-onset neonatal sepsis from off-the-shelf medical data and electronic medical records (EMR).

Design

The data used in this study are from 299 infants admitted to the neonatal intensive care unit in the Monroe Carell Jr. Children’s Hospital at Vanderbilt and evaluated for late-onset sepsis. Gold standard diagnostic labels (sepsis negative, culture positive sepsis, culture negative/clinical sepsis) were assigned based on all the laboratory, clinical and microbiology data available in EMR. Only data that were available up to 12 h after phlebotomy for blood culture testing were used to build predictive models using machine learning (ML) algorithms.

Measurement

We compared sensitivity, specificity, positive predictive value and negative predictive value of sepsis treatment of physicians with the predictions of models generated by ML algorithms.

Results

The treatment sensitivity of all the nine ML algorithms and specificity of eight out of the nine ML algorithms tested exceeded that of the physician when culture-negative sepsis was included. When culture-negative sepsis was excluded both sensitivity and specificity exceeded that of the physician for all the ML algorithms. The top three predictive variables were the hematocrit or packed cell volume, chorioamnionitis and respiratory rate.

Conclusions

Predictive models developed from off-the-shelf and EMR data using ML algorithms exceeded the treatment sensitivity and treatment specificity of clinicians. A prospective study is warranted to assess the clinical utility of the ML algorithms in improving the accuracy of antibiotic use in the management of neonatal sepsis.

Introduction

Machine learning (ML) is a subfield of artificial intelligence, which focuses on building new predictive models from data by performing an extensive search over a large number of models and parameters followed by validation. Earlier work demonstrated the feasibility of building predictive models with clinical potential.^1–8 The challenge we face moving forward is to identify compelling clinical problem areas, build powerful models from quality data and validate them carefully. Ideally, one wishes to be able to build such models from data routinely collected in electronic medical records (EMR). In the present work our objective was to generate novel continuous risk-assessment tools for neonatal sepsis from data using ML methods leading to earlier diagnosis and improved disease management. In addition, we emphasize that we use and demonstrate the value of applying data mining techniques to routinely collected data as opposed to data specifically gathered for a hypothesis-driven research protocol.

Neonatal sepsis causes significant morbidity and mortality in neonatal intensive care unit (NICU) patients.⁹ The incidence of sepsis among infants of under 1500 g birth weight is approximately 20% or 200-fold higher compared to term infants.⁹ Sepsis in these infants has been classified as early onset (≤72 h after birth) and late onset (>72 h after birth). Late-onset sepsis is over 10 times more common than early-onset sepsis in NICU patients and is frequently healthcare associated. Because of its frequency and high risk of morbidity and mortality, ‘rule out sepsis’ accounts for more than half of admission diagnoses made in the NICU.¹⁰ In addition, the large Kaiser Permanente Medical Care Program reported that 49% of admission diagnoses in their special care nursery were labeled ‘rule-out sepsis’.¹¹ When sepsis is suspected blood is drawn for blood culture and the infant is started on antibiotics. On average for every culture-positive sepsis result an additional 11–23 infants receive antibiotic treatment contributing to antibiotic resistance in the community and increased healthcare costs.^{10 12} Forty-seven per cent of very low birth weight infants in the National Institute of Child Health and Human Development Neonatal Research Network population received continuing antibiotic therapy for five or more days, despite negative blood culture results for 98% of patients.¹³ On the other hand, a serious infection may remain unrecognized too long in infants who die in the NICU.¹⁴ A positive blood culture remains the gold standard, although its sensitivity has been challenged by an 18% false-negative rate for bacterial sepsis documented by autopsy.¹⁵ In addition, volume obtained for blood culture is often too low to detect bacteria.^{16 17} When blood culture results are not available, the decision to continue or stop antibiotics is made based on laboratory test results and the clinical profile of the infant. Although clinical algorithms have been suggested,¹⁸ currently, no uniform guidelines exist on how to interpret these data.^{19 20} New sepsis prediction tests typically include additional blood tests, which not only contribute to anemia resulting in blood transfusions²¹ but also to the short and long-term sequelae associated with painful procedures in preterm infants.²²

Here we present non-invasive (no additional invasive tests such as an additional blood draw are proposed in our predictive modeling framework) and NICU population-based predictive models for late-onset neonatal sepsis from EMR to provide decision support tools for healthcare providers to optimize antibiotic administration when sepsis is suspected. Once their clinical utility is confirmed in the future in prospective studies, these models may contribute to the discontinuation of antibiotics in sepsis-negative cases before blood culture results become available. The end result could be reduced antibiotic use with its associated benefits for the patient and for healthcare utilization. Likewise, it might be possible to intitiate early and prompt treatment of sepsis-positive infants before blood culture results are available and for whom clinical suspicion is below the physician's threshold for initiating antibiotic threapy.

Methods

Dataset

The data used in this study is from infants admitted to the NICU in the Monroe Carell Jr. Children’s Hospital at Vanderbilt University over a period of 18 months starting from 1 January 2006. Out of the 1826 total admissions during this period our study sample consisted of 299 infants evaluated for late-onset sepsis. We defined late-onset sepsis as neonatal sepsis occurring over 72 h after birth. The datasets used in this work were acquired from the Vanderbilt NICU database with manually entered predefined data elements utilized for quality improvement and outcome research and the hospital EMR. We created a data repository by merging records from the antibiotics, microbiology, laboratory and NICU nursing documentation datasets. Additional details about the four datasets and the process of study dataset creation are illustrated in figure 1. The Vanderbilt institutional review board approved the creation of a data repository and its subsequent analysis.

Figure 1.

Study dataset generation (MRN, medical record number). All the datasets provided structured data.

Antibiotics, microbiology tests, and laboratory datasets were used to assign sepsis diagnosis labels. A sepsis diagnosis label was assigned for each unique patient who had at least one microbiology test and laboratory dataset record. The information in the laboratory, microbiology, antibiotics and the NICU datasets were merged to create a single dataset for performing ML to predict the sepsis diagnosis labels.

We generated temporal variables from the time-stamped measurements in the laboratory dataset for a period of 60 h (starting 48 h before and finishing 12 h after the first blood culture test) with 6 h increments. The time of withdrawal of blood for blood culture test was denoted by t(0). Note that t(0) represents a point in time and not a 6 h time interval while t(−48), t(−42), …, t(−6), t(6), t(12) represent successive 6 h time slots. For example, t(−48) denotes the 6 h duration starting from 48 h before t(0) and ending at 42 h before t(0). Likewise, if t(0) is 12 noon, t(−6) will be the time interval 6 a.m.–12 noon and t(6) will be the time interval 12 noon–6 p.m. A subset of the NICU variables considered to be relevant to sepsis was selected for model building. This variable selection was done by a neonatologist (JHW) involved in the study based on literature evidence and clinical expertise. All selected NICU variables were available within 12 h after the first blood test at time t(0). The objective of sepsis classification was to predict whether an infant had sepsis within 12 h of phlebotomy for the microbiology test. We used a cut-off of 12 h after blood draw to utilize blood count results that are typically available within a few hours of blood draw. This provided 10 6 h slots for the t(−48) to t(12) time interval plus t(0). Seven hundred and eighty-one (71×11) temporal variables from the laboratory dataset and 30 non-temporal variables (demographics, birth weight, gestational age, Apgar scores, mode of delivery etc.) from the NICU dataset were selected that met the relevance and time line criteria.

Because we use EMR data that were collected as part of routine care, the dataset contains many missing values particularly in the temporal variables. Variables such as heart rate and respiratory rate had values for many of the 6 h time slots while others such as oxygen saturation and blood counts had values for only one or two time slots. To address this limitation, temporal variables were converted to non-temporal scalar variables by taking the last non-missing entry for a temporal variable. This last observation carry forward (LOCF) approach has been validated previously.^23–25 This conversion procedure decreased the missing values for the temporal variables from 91% to 64%. The dataset consisted of 299 instances and 101 variables. The histogram showing the number of variables for different missing value ratios indicates that only 30 variables in the dataset have less than 10% missing values (figure 2). Eight variables with more than 90% missing values were removed from the dataset. As discussed later, single imputation is incorporated in the algorithm for the missing data problem. The 93 variables included in the study dataset with their descriptions are listed in supplementary appendix 1 (available online only).

Figure 2.

Histogram showing the number of variables for different missing value percentage intervals.

Sepsis diagnostic algorithm

We assigned gold standard diagnostic labels to the infants as sepsis-positive and sepsis-negative using all available variables. Sepsis-positive infants were further categorized into culture-positive sepsis and culture-negative (clinical) sepsis. These label assignments (classifications) were considered gold standard diagnostic labels for our study purposes. The sepsis label assignment algorithm was based on published data²⁶ and the current best practice in Monroe Carell Jr. Children's Hospital at Vanderbilt University (figure 3). Two datasets were created for analysis: dataset 1, which included culture-negative sepsis (n=299) and dataset 2, which excluded culture-negative sepsis (n=185). A listing of the blood culture bacteria type specification is provided in supplementary appendix 2 (available online only).

Figure 3.

Sepsis diagnostic algorithm (modified from Gladstone et al).²⁶

Algorithmic methods

A representative set of classification algorithms was selected for the sepsis prediction (classification) task from the dataset. These algorithms were the support vector machine (SVM),²⁷ the naive Bayes (NB) classifier²⁸ and variants (tree augmented naive Bayes (TAN)²⁹ and averaged one dependence estimators (AODE)),³⁰ a sample-based classifier (K-nearest neighbor),³¹ the decision tree classifiers classification and regression trees (CART)³² and random forests (RF),³³ logistic regression (LR) and lazy Bayesian rules (LBR).³⁴

As most of the classification algorithms and variable selection methods are not applicable for data with missing values, we used a single imputation approach to impute the missing values. For each continuous variable, we imputed the missing values assuming a Gaussian distribution. For each missing value in this variable, we generated a random number based on the same Gaussian distribution with the mean and SD estimated from the observed variables. For discrete variables, imputation was done by randomly selecting one from all discrete values weighted by its proportion.

In order to increase classification performance given the small sample size relative to the number of variables in our data, we used feature selection algorithms that select a subset of the features (independent variables) that are highly predictive of the class (outcome or dependent variable). In this work, six feature selection algorithms were used. These are SVM-BW, SVM-FW, SVM-FBW, SVM-RFE,³⁵ HITON-MB and HITON-PC algorithms (FW, forward; BW, backward; FBW, forward and backward; RFE, recursive feature elimination; MB, Markov blanket and PC, parents and children).^36–38 The general schema for predictive model building, evaluation and clinical validation is shown in figure 4.

Figure 4.

Schema for predictive model building, evaluation and clinical validation. NICU, neonatal intensive care unit.

For finding the optimal classifier and feature selection algorithm combination for the problem, a nested cross-validation (CV) procedure³⁹ was employed. In the nested CV procedure, the parameters of the classifiers were optimized in the inner CV loop, and the outer CV loop was used to evaluate the performance of the models. The nested CV procedure is illustrated in figure 5. The nested CV design fully penalizes for feature selection. The maximum cardinality of the conditioning set for the HITON algorithms was set to three and the threshold values were selected to be 0.01 and 0.05. The SVM classifier was run with a polynomial kernel with the cost parameter C ranging from 0.01 to 100 with a multiplicative step of 10 and kernel degrees from 1 to 5. The number of the CV folds K was set to 5. The performances of the decision tree (CART) and NB classifier and its variants were also optimized using various feature selection algorithms with a different set of parameters in the nested CV procedure. Area under the receiver operator characteristics curve (AUC) was selected as a general performance measure because it provides an efficient measure independent of the class sizes and the classification threshold⁴⁰ even though we are unable to ascertain the AUC for the physician. The AUC of the optimized model among all five folds is presented. A 95% CI of this AUC value was constructed by bootstrapping the patients in the test set corresponding to the optimized model AUC value. The lower bound of the 95% CI is then compared to 0.5 (random guess). The nested CV procedure was implemented in Matlab. For the SVM classifiers, LibSVM⁴¹ was called from Matlab. The WEKA⁴² implementations of NB, TAN, AODE and LBR algorithms were executed using Matlab scripts. The Matlab implementation of CART was used. RF was run using the implementation in R, and LR was run using the liblinear package.⁴³ HITON-MB and HITON-PC feature selection algorithms were called from Causal Explorer.⁴⁴

Figure 5.

Nested cross-validation procedure for performance estimation in the outer loop and parameter optimization in the inner loop.

In order to compare the treatment matrix (classification/misclassification 2×2 tables) of the physician with that of the classification algorithms we used five-fold CV. To assess the potential clinical impact of the ML approach we compared the sensitivity and specificity of the physician and the ML algorithms as follows. The performance comparison is over the whole sample. In the CV framework the test partitions are mutually exclusive and collectively exhaustive and therefore the whole sample becomes the test set for the ML algorithms. We first defined treatment sensitivity and treatment specificity for purposes of this comparison based on antibiotic treatment.

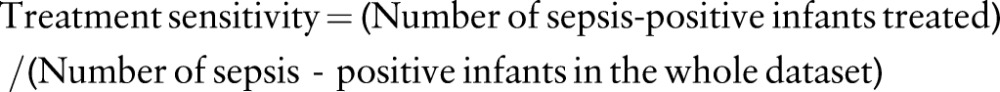For the calculation of treatment sensitivity, an infant was considered treated if the physician started an antibiotic treatment between t(−48) and t(12). Note that the goal here is to predict sepsis before blood culture results become available. For the calculation of treatment specificity an infant was considered not treated if no antibiotics were given to the infant between t(12) and t(120). Note that antibiotic treatment may be started after blood culture results become available. The required data for the antibiotics treatment were acquired by processing the start and end time of the antibiotics treatments in the antibiotics dataset. Using the sepsis labels and antibiotics treatment information, the physician antibiotic treatment matrix was created by assigning each of the 299 infants to the appropriate cell in the 2×2 matrix. Table 1 shows the physician treatment matrices for the study samples. The performance measures for the ML algorithms shown in tables 2 and 3 were generated as explained below. To compare the ML algorithm performance to the physician using dataset 1 (table 2), first the ML algorithm measures were generated such that their specificities are the same as that of the physician. This allowed us to infer whether the ML algorithms perform better or worse than the physician with respect to the treatment sensitivity if they have the same treatment specificity of the physician. Second, the performance measures for the ML algorithms were generated such that their treatment sensitivities are the same as that of the physician. Then their treatment specificities were compared to the treatment specificity of the physician. A similar comparison was performed after excluding the infants belonging to the culture-negative sepsis group using dataset 2 (table 3).

Table 1.

Physician treatment matrix for both dataset 1 (n=299 and includes culture negative sepsis) and dataset 2 (n=185 and excludes culture negative sepsis)

Physician versus gold standard	Dataset 1 (n=299)		Dataset 2 (n=185)
	Non-treated	Treated	Non-treated	Treated
Not septic	16	74	16	74
Septic (culture +ve)	26	69	26	69
Septic (culture −ve)	27	87	0	0
Septic (total)	53	156	26	69
Physician sensitivity	0.75		0.73
Physician specificity	0.18		0.18
Physician PPV	0.68		0.48
Physician NPV	0.23		0.38

Table 2.

Algorithm performance compared with physician based on dataset 1 which includes culture negative sepsis (n=299)

Algo	AUC	AUC 95% CI	Sens.	Diff.	Sensitivity 95% CI	p Value	PPV	Diff.	PPV 95% CI	p Value	NPV	Diff.	NPV 95% CI	p Value
(A) n=299, fixed specificity (0.18)
Phy	NA		0.75				0.68				0.23
NB	0.64	0.7864 to 0.5141	0.83	0.08	(0.0000 to 0.1635)	0.048	0.70	0.02	(−0.0120 to 0.0564)	0.199	0.3077	0.08	(−0.0591 to 0.2130)	0.263
RF	0.57	0.7315 to 0.5040	0.82	0.08	(−0.0049 to 0.1569)	0.062	0.70	0.02	(−0.0151 to 0.0565)	0.243	0.3019	0.07	(−0.0730 to 0.2124)	0.321
SVM	0.61	0.7566 to 0.5065	0.79	0.05	(−0.0355 to 0.1336)	0.24	0.69	0.01	(−0.0223 to 0.0511)	0.47	0.2712	0.04	(−0.0917 to 0.1750)	0.56
KNN	0.54	0.6973 to 0.5026	0.83	0.08	(0.0103 to 0.1614)	0.026	0.70	0.02	(−0.0129 to 0.0586)	0.214	0.3156	0.08	(−0.0583 to 0.2225)	0.247
CART	0.65	0.7708 to 0.5250	0.75	0.01	(−0.0750 to 0.0869)	0.898	0.68	0.00	(−0.0372 to 0.0391)	0.948	0.2355	0.00	(−0.1265 to 0.1316)	0.957
LR	0.61	0.7638 to 0.5076	0.86	0.11	(0.0324 to 0.1881)	0.004	0.71	0.03	(−0.0061 to 0.0650)	0.11	0.3478	0.12	(−0.0404 to 0.2688)	0.147
LBR	0.62	0.7798 to 0.5068	0.86	0.11	(0.0367 to 0.1937)	0.003	0.71	0.03	(−0.0043 to 0.0653)	0.081	0.3556	0.12	(−0.0278 to 0.2779)	0.11
AODE	0.61	0.7519 to 0.5066	0.88	0.13	(0.0519 to 0.2067)	<0.001	0.71	0.03	(−0.0020 to 0.0703)	0.064	0.381	0.15	(−0.0140 to 0.3178)	0.076
TAN	0.59	0.7218 to 0.5053	0.84	0.09	(0.0102 to 0.1682)	0.023	0.70	0.02	(−0.0131 to 0.0622)	0.199	0.32	0.09	(−0.0680 to 0.2416)	0.278
	AUC	AUC 95% CI	Spec.	Diff.	Specificity 95% CI	p Value	PPV	Diff.	PPV 95% CI	p Value	NPV	Diff.	NPV 95% CI	p Value
(B) N=299 to fixed sensitivity (0.75)
Phy	NA		0.18				0.68				0.23
NB	0.64	0.7864 to 0.5141	0.32	0.14	(0.0312 to 0.2553)	0.011	0.72	0.04	(0.0005 to 0.0793)	0.048	0.35	0.12	(0.0033 to 0.2353)	0.045
RF	0.57	0.7315 to 0.5040	0.23	0.06	(−0.0595 to 0.1728)	0.302	0.69	0.02	(−0.0268 to 0.0560)	0.473	0.28	0.05	(−0.0786 to 0.1812)	0.431
SVM	0.61	0.7566 to 0.5065	0.20	0.02	(−0.0849 to 0.1277)	0.605	0.68	0.01	(−0.0323 to 0.0444)	0.753	0.25	0.02	(−0.1000 to 0.1446)	0.716
KNN	0.54	0.6973 to 0.5026	0.25	0.08	(−0.0510 to 0.2006)	0.243	0.70	0.02	(−0.0212 to 0.0627)	0.334	0.30	0.07	(−0.0638 to 0.1995)	0.313
CART	0.65	0.7708 to 0.5250	0.18	−0.0021	(−0.1150 to 0.1115)	0.969	0.68	−0.0005	(−0.0394 to 0.0372)	0.976	0.23	−0.0023	(−0.1314 to 0.1240)	0.978
LR	0.61	0.7638 to 0.5076	0.33	0.16	(0.0411 to 0.2697)	0.006	0.72	0.04	(0.0036 to 0.0856)	0.03	0.36	0.13	(0.0120 to 0.2464)	0.031
LBR	0.62	0.7798 to 0.5068	0.33	0.16	(0.0333 to 0.2809)	0.01	0.72	0.04	(0.0005 to 0.0874)	0.046	0.36	0.13	(0.0035 to 0.2546)	0.045
AODE	0.61	0.7519 to 0.5066	0.36	0.18	(0.0556 to 0.2976)	0.003	0.73	0.05	(0.0079 to 0.0942)	0.021	0.38	0.14	(0.0214 to 0.2680)	0.023
TAN	0.59	0.7218 to 0.5053	0.32	0.14	(0.0128 to 0.2697)	0.02	0.72	0.04	(−0.0022 to 0.0832)	0.066	0.35	0.12	(−0.0048 to 0.2451)	0.058

The performance measures are generated by fixing specificity at 0.18 (A) and by fixing sensitivity at 0.75 (B).

Significant p values are in bold.

AODE, averaged one dependence estimators; AUC, area under the curve for the optimized model; CART, classification and regression trees; Diff., difference between algorithm and physician; LBR, lazy Bayesian rules; LR, logistic regression; NA, not available; NB, naive Bayes; NPV, negative predictive value; Phy., physician; PPV, positive predictive value; RF, random forests; Sens., sensitivity; Spec., specificity, SVM, support vector machine, TAN, tree augmented naive.

Table 3.

Algorithm performance compared with physician based on Dataset 2 which excludes culture negative sepsis infants (n=185)

Algo	AUC	AUC 95% CI	Sens.	Diff.	Sensitivity 95% CI	p Value	PPV	Diff.	PPV 95% CI	p Value	NPV	Diff.	NPV 95% CI	p Value
(A) n=185, fixed specificity (0.18)
Phy	NA		0.73				0.48				0.38
NB	0.78	0.9230 to 0.6111	0.95	0.22	(0.1209 to 0.3247)	<0.001	0.55	0.07	(0.0197 to 0.1153)	0.004	0.76	0.38	(0.1501 to 0.6000)	0.002
RF	0.65	0.8263 to 0.5091	0.94	0.21	(0.1047 to 0.3158)	<0.001	0.55	0.06	(0.0174 to 0.1119)	0.01	0.73	0.35	(0.1198 to 0.5692)	0.004
SVM	0.68	0.8663 to 0.5176	0.88	0.16	(0.0370 to 0.2796)	0.008	0.53	0.05	(−0.0042 to 0.1022)	0.073	0.59	0.21	(−0.0258 to 0.4386)	0.081
KNN	0.62	0.7588 to 0.5059	0.86	0.14	(0.0245 to 0.2472)	0.018	0.53	0.04	(−0.0057 to 0.0934)	0.088	0.55	0.17	(−0.0396 to 0.3847)	0.113
CART	0.77	0.9126 to 0.6096	0.81	0.08	(−0.0330 to 0.2020)	0.133	0.51	0.03	(−0.0251 to 0.0797)	0.29	0.47	0.09	(−0.1188 to 0.2950)	0.374
LR	0.61	0.7897 to 0.5059	0.87	0.15	(0.0323 to 0.2626)	0.007	0.53	0.05	(−0.0018 to 0.0958)	0.061	0.57	0.19	(−0.0250 to 0.4056)	0.078
LBR	0.58	0.7697 to 0.5058	0.85	0.12	(0.0060 to 0.2367)	0.041	0.52	0.04	(−0.0112 to 0.0888)	0.126	0.52	0.14	(−0.0631 to 0.3490)	0.167
AODE	0.53	0.7018 to 0.5030	0.85	0.13	(0.0141 to 0.2457)	0.026	0.52	0.04	(−0.0111 to 0.0941)	0.127	0.54	0.16	(−0.0629 to 0.3785)	0.165
TAN	0.53	0.6982 to 0.5029	0.84	0.12	(−0.0078 to 0.2448)	0.068	0.52	0.04	(−0.0161 to 0.0919)	0.168	0.52	0.14	(−0.0813 to 0.3552)	0.209
	AUC	AUC 95% CI	Spec.	Diff.	Specificity 95% CI	p Value	PPV	Diff.	PPV 95% CI	p Value	NPV	Diff.	NPV 95% CI	p Value
(B) n=185 to fixed sensitivity (0.73)
Phy	NA		0.18				0.48				0.38
NB	0.78	0.9230 to 0.6111	0.47	0.29	(0.1667 to 0.4074)	<0.001	0.59	0.11	(0.0408 to 0.1737)	0.001	0.62	0.24	(0.0775 to 0.3944)	0.003
RF	0.65	0.8263 to 0.5091	0.47	0.29	(0.1591 to 0.4157)	<0.001	0.59	0.11	(0.0405 to 0.1771)	0.002	0.62	0.24	(0.0719 to 0.3982)	0.007
SVM	0.68	0.8663 to 0.5176	0.26	0.08	(−0.0500 to 0.2083)	0.21	0.51	0.02	(−0.0374 to 0.0864)	0.43	0.47	0.09	(−0.1053 to 0.2790)	0.358
KNN	0.62	0.7588 to 0.5059	0.29	0.11	(−0.0092 to 0.2372)	0.071	0.52	0.04	(−0.0191 to 0.0949)	0.205	0.50	0.12	(−0.0490 to 0.2946)	0.166
CART	0.77	0.9126 to 0.6096	0.30	0.12	(0.0016 to 0.2436)	0.048	0.52	0.04	(−0.0203 to 0.1013)	0.191	0.51	0.13	(−0.0489 to 0.3042)	0.15
LR	0.61	0.7897 to 0.5059	0.30	0.12	(0.0000 to 0.2474)	0.047	0.52	0.04	(−0.0185 to 0.1012)	0.185	0.51	0.13	(−0.0453 to 0.3033)	0.147
LBR	0.58	0.7697 to 0.5058	0.30	0.12	(0.0000 to 0.2449)	0.045	0.52	0.04	(−0.0206 to 0.1025)	0.178	0.51	0.13	(−0.0513 to 0.3116)	0.143
AODE	0.53	0.7018 to 0.5030	0.28	0.10	(−0.0161 to 0.2178)	0.093	0.52	0.03	(−0.0268 to 0.0934)	0.283	0.49	0.11	(−0.0708 to 0.2876)	0.236
TAN	0.53	0.6982 to 0.5029	0.23	0.06	(−0.0625 to 0.1720)	0.309	0.50	0.02	(−0.0435 to 0.0783)	0.553	0.45	0.07	(−0.1198 to 0.2543)	0.477

The performance measures are generated by fixing specificity at 0.18 (A) and by fixing sensitivity at 0.73 (B).

Significant p values are in bold.

AODE, averaged one dependence estimators; AUC, area under the curve for the optimized model; CART, classification and regression trees; Diff., difference between algorithm and physician; LBR, lazy Bayesian rules; LR, logistic regression; NA, not available; NB, naive Bayes; NPV, negative predictive value; Phy., physician; PPV, positive predictive value; RF, random forests; Sens., sensitivity; Spec., specificity; SVM, support vector machine; TAN, tree augmented naïve.

As physicians provided binary decisions and ML methods yielded a probabilistic risk of sepsis (a value ranging between 0 and 1), to compare the performance between ML methods and physicians’ judgment, we calculated their difference in sensitivity by choosing the threshold values so that the ML methods would have the same specificity as the physicians. Note that the physicians were not asked to provide such binary decisions. The decisions of the physicians were inferred from their clinical decisions (whether they started antibiotics within 12 h of blood draw for sensitivity and whether any antibiotics were administered beyond 12 h of blood draw for specificity, as explained earlier). We also repeated this process to compare the specificity with the threshold values chosen so that the methods would have the same sensitivity level. The corresponding positive predictive values (PPV) and negative predictive values (NPV) were also compared under these two circumstances. For ML methods, when there were ties at the selected threshold values, we randomly assigned the ties to the two classes to achieve the targeted specificity/sensitivity and repeat the random assignment 1000 times. The corresponding difference in sensitivity/specificity, PPV and NPV were calculated as the average of the 1000 repetitions. For the results shown in tables 2 and 3, 95% CI of sensitivity, specificity, PPV and NPV were obtained using 10 000 bootstrap samples. The bootstrap was done for the combined test set from the k-fold partition. This is because the five test sets of the fivefold CV are mutually exclusive and collectively exhaustive. The following methodology^{45 46} was adopted: (1) we calculated the predicted sepsis risk for the patients in each test set based on the model developed in the corresponding train set; (2) we chose a cut-off point for the combined predicted risks of the whole samples so that the achieved overall specificity is same as the specificity of the physician; (3) we calculated the target statistics as the sensitivity difference between the ML method and physician; (4) we bootstrapped the whole samples 10 000 times and repeated steps (1)–(3) within each bootstrap sample to construct the 95% CI of the target statistics using the 2.5% and 97.5% quantiles of the sample statistics. Similarly, we constructed the 95% CI for the specificity difference between the ML method and physician. McNemar's test was used for ascertaining whether the results of the ML algorithms are statistically significantly different from the physician's decisions.

Results

In this section we first report the predictive performance of the various ML algorithms and then present evaluation results based on comparison with physician performance.

Predictive performance of the ML algorithms

Table 4 shows the demographics of the infants in the study dataset. The maximum, minimum and mean number of features selected by different feature selection algorithms for the various classifiers over the five outer cross-validation folds are summarized in supplementary tables S5A and S5B (available online only). In most cases, the features were selected using SVM-based feature selection algorithms.

Table 4.

Demographics of the study population and neonatal sepsis

	Whole sample
No of infants	299
Birth weight (g): median (25,75) percentiles	1400 (865, 2424)
Gestational age (weeks): median (25,75) percentiles	30 (27, 36)
Male n (%)	166 (56%)
Race (white) n (%)	227 (76%)
Ethnicity (Hispanic) n (%)	31 (10%)
(non-Hispanic) n (%)	268 (90%)
Sepsis (positive) n (%)	209 (70%)
Culture-positive sepsis n (%)	95 (32%)
Culture-negative sepsis n (%)	114 (38%)
Sepsis negative n (%)	90 (30%)

Table 1 provides performance measures of the physician versus the gold standard. The mean AUC scores and other performance statistics for the various classification algorithms based on fivefold CV using the study datasets 1 and 2 are shown in tables 2 and 3, respectively. The receiver operator characteristics curve for the NB model from dataset 2 is shown in figure 6.

Figure 6.

Receiver operator characteristic (ROC) curve for naive Bayes with area under the ROC curve 0.78 (n=185). The curve in the middle is the actual ROC curve; the upper and lower curves show the upper error bound and lower error bound for the ROC curve, respectively.

Evaluation of ML algorithms by comparison with physician

With the treatment specificity set at the level of the physician, the treatment sensitivity level of all the nine ML algorithms exceeded that of the physician with dataset 1 and dataset 2. AODE had the best sensitivity (88%) with dataset 1 and NB and RF had 95% and 94% sensitivity with dataset 2. Compared to the physician AODE advised prompt treatment of an additional 27 infants who developed sepsis based on dataset 1 and NB and RF recommended prompt treatment of an additional 21 and 20 infants, respectively, who developed sepsis based on dataset 2. When the treatment sensitivity was at the level of the physician, the treatment specificity of all the ML algorithms except CART was higher compared to the physician with dataset 1 and the treatment specificity of all the nine ML algorithms were higher with dataset 2. AODE had the best specificity (36%) with dataset 1 and NB and RF had 47% specificity with dataset 2. Compared to the physician, AODE (based on dataset (1), NB and RF (based on dataset (2) would have prevented most likely unnecessary treatment of 16, 26 and 26, respectively, out of 90 infants not having sepsis. These results suggest that models based on these ML algorithms should not only be clinically evaluated for their potential in reducing unnecessary antibiotic therapy but also for their value in detecting potentially fatal bacteremia earlier in the NICU.

Based on McNemar's test six algorithms (NB, KNN, LR, LBR, AODE and TAN) had statistically significant better performance with fixed treatment specificity (table 2A) and five algorithms (NB, LR, LBR, AODE and TAN) had statistically significant better performance with fixed treatment sensitivity with dataset 1 (table 2B). All the algorithms except CART and TAN had statistically significant better performance with fixed treatment specificity (table 1A) and five algorithms (NB, RF, CART, LR and LBR) had statistically significant better performance with fixed treatment sensitivity with dataset 2 (table 1B).

Supplementary tables S5A and S5B (available online only) provide the number and range of features selected by the various ML algorithms during the fivefold CV.

Supplementary table S6 (available online only) provides the list of the top 10 predictive variables based on our modeling over all the algorithms and cross-validation folds for both of the datasets.

Discussion

The results indicate that ML algorithms should be evaluated prospectively in their clinical use of providing decision support for predicting sepsis in most neonates within 12 h of phlebotomy for blood culture. Early prediction with targeted antibiotic therapy could be effective in reducing neonatal mortality, bringing down healthcare costs and is likely to lower the rates of bacterial resistance to antibiotics in the community. Although the study focuses on neonatal intensive care, the methodology (not the models per se) can be generalized to different acute care clinical settings such as medical and surgical intensive care units and emergency departments.

We used a representative set of ML algorithms to build our models. SVM are considered state-of the-art ML algorithms for classification.³⁸ The NB and decision tree classifiers have been used in many applications for clinical decision making.^{47 48} Moreover, models generated by decision trees are human understandable in general given that the models are not too complex. Based on our results from both dataset 1 and dataset 2 the ML algorithms NB, CART, AODE and RF show promise as candidates for a prospective clinical evaluation.

The Gaussian imputation method that we used in our study is superior to a simple mean, median, or mode value imputation because it introduces less bias.⁴⁹ The single imputation procedure used can be improved with multiple imputation. However, this will result in a substantial increase in computational costs and analytic complexity. The end results of our current approach should be unbiased although with underestimated SE and there is scope for further improvement with enhanced imputation techniques. Note that missing values in future patients can be imputed using the values from the available (classified with gold standard labels) dataset.

The study that is closest to ours reported in the literature is a prospective study for sepsis prediction using heart rate characteristics, in the complex NICU patient.⁵⁰ Griffin et al⁵⁰ reported an AUC of 0.82 for sepsis prediction using multivariable LR based on a comparison between cases and controls. In contrast, our study population consisted of infants for whom a blood culture test had been ordered for suspected sepsis. Predicting sepsis from a study group consisting of infants with clinical suspicion of sepsis alone is more challenging because the control (comparison) group consists of infants with a clinical picture that calls for a sepsis work-up. In other words the previously published case–control design suffers from spectrum bias because the sample consists of more extreme cases than our cohort of infants receiving sepsis evaluation. The receiver operating characteristic curve in figure 6 supports the utility of this novel decision support system for early detection (starting treatment within 12 h of blood draw) of late-onset neonatal sepsis. Given the sample size limitation and the retrospective nature of our study additional evaluation of the methodology is needed before the results can be put to clinical use.

Our study has several limitations. The LOCF method that we used to convert temporal variables to non-temporal scalar variables can introduce bias. Basically, LOCF assumes that a value that was missing would be found to be identical to the previous value, with no error.⁵¹ In future we will consider using a multiple imputation approach⁵² to improve the prediction model. We did consider clinical sepsis with negative blood culture results in this study. Given the presumed limited sensitivity of blood cultures in the NICU setting, many of the infants in our study sample assigned a culture-negative sepsis label would have been truly infected. The larger dataset (dataset 1 with n=299) that also includes culture-negative sepsis somewhat mitigates this problem. However, there is also an element of uncertainty in the assignment of culture-negative sepsis based on clinical and laboratory criteria and antibiotic treatment history. All variables available within 12 h of blood draw for culture were available to the ML algorithms. Interestingly, however, despite including clinical and laboratory parameters as input to the ML algorithm, only one predictor (absolute neutrophil count) overlapped with supplementary table S6 (available online only). None of other variables listed in supplementary table S6 (available online only) were included in the diagnostic label set we applied to define culture-negative sepsis and we were indeed surprised to find previously unrecognized variables (eg, low hematocrit, maternal age) to be strong predictors for neonatal sepsis. Although we show for the first time that ML algorithms based on already obtained clinical and laboratory parameters can predict neonatal sepsis within 12 h of blood draw for blood culture testing more accurately than physicians, sensitivity and specificity need to be improved further. For example, the receiver operating characteristic curve shown in figure 6 shows only a specificity of 38% for obtaining a sensitivity of 95%. Further refinement and analysis of the predictive models will be necessary to optimize performance.

The top 10 predictors determined by ML algorithms for neonatal sepsis include established risk factors such as chorioamnionitis⁵³ and clinical signs of infection such as an abnormal neutrophil count.⁵⁴ Chorioamnionitis is typically associated with early-onset sepsis if defined as sepsis occurring within the first 7 days post partum. Here we defined late-onset sepsis as sepsis occurring after 72 h post partum. This may explain why chorioamnionitis was a strong predictor of culture-positive sepsis in this study. The strong predictive value of the blood hematocrit (PCV) for neonatal sepsis is unexpected. We can only speculate about the possible reasons. Although the hematocrit is not a recognized sepsis marker in the NICU, the association between sepsis and anemia is well established.⁵⁵ The pathophysiology probably involves suppression of erythropoietin by proinflammatory cytokines.⁵⁶ Premature infants exhibit relative decreased erythropoietin levels (anemia of prematurity) and a further suppression by sepsis-associated inflammation may suppress the hematocrit even further. Alternatively, a low PCV could be an indirect marker for blood transfusions and increasing hemoglobin levels could promote bacterial proliferation.^57–59 We were surprised to find chorioamnionitis, maternal age and resuscitation at birth to be strong predictive factors for late-onset sepsis given that they are traditionally associated with risk factors for early-onset sepsis.^{13 60} Interestingly, early-onset sepsis reportedly decreases the risk of late-onset sepsis.⁶¹ Our data seem to suggest, however, that similar risk factors apply for early and late-onset sepsis.

Twelve infants were identified as sepsis positive from dataset 2 by the ML algorithms but were not treated within 12 h after the blood culture was obtained. We performed a detailed chart review for these cases and found that treatment was missed either due to patient transfer, a negative sepsis screen (reassuring complete blood count, differential and C-reactive protein) or the fact that the initial culture grew coagulase-negative Staphylococcus and was considered a contaminant until confirmed by a second positive blood culture. Therefore, in addition to earlier detection of culture-positive sepsis and earlier discontinuation of antibiotics when there is no infection, another potential clinical application for the ML algorithm to be tested in future studies could be the differentiation between positive blood cultures with a contaminant and a true pathogen.

Our study suggests that ML methods can be used to identify predictors of late-onset sepsis within the large and complex database about NICU patients. In addition, ML algorithms may identify truly infected newborns before the availability of blood culture data and therefore contribute to earlier treatment. The improvement in sensitivity (earlier treatment) for the algorithms is not at the cost of specificity (over-treatment). The specificity of the algorithms was fixed at the level of the physician's specificity while calculating the sensitivity and vice versa. The ML algorithm model described here has the significant strengths of being real time, non-invasive, and could be used as an early warning system to alert physicians that sepsis may be present or developing. However, like heart rate characteristic monitoring proposed by Griffin et al⁵⁰ and clinically evaluated by Moorman et al⁶² and Griffin et al⁶³ these ML models should be used as screening and decision support tools and not as stand-alone decision-making expert systems. While our model may not be directly applicable to other NICU datasets, we think that our study supports the potential for ML algorithms in assisting NICU care givers in the management of late-onset neonatal sepsis. The current models have to be tested in prospective settings and also using data from other institutions (in future studies). In our opinion the NICU setting with its highly vulnerable patient population, rich database and poor sensitivity of blood cultures is the ideal environment for evaluating computational methods for medical decision support.

It may be possible, although we did not test this here, that the model plus humans will do better than either one alone (see the fundamental theorem of biomedical informatics, which states that humans partnering with information resources will perform better than those working without such resources).⁶⁴

Conclusion

Predictive models developed from off-the-shelf and EMR data using ML algorithms exceeded the sensitivity and specificity of clinicians, and a prospective study is warranted to test clinical utility in improving the accuracy of antibiotic use in the management of neonatal sepsis. Further optimization of the ML models could provide a decision support aid that can be tested in a randomized clinical trial.