Diagnosis code assignment: models and evaluation metrics

Abstract

Background and objective

The volume of healthcare data is growing rapidly with the adoption of health information technology. We focus on automated ICD9 code assignment from discharge summary content and methods for evaluating such assignments.

Methods

We study ICD9 diagnosis codes and discharge summaries from the publicly available Multiparameter Intelligent Monitoring in Intensive Care II (MIMIC II) repository. We experiment with two coding approaches: one that treats each ICD9 code independently of each other (flat classifier), and one that leverages the hierarchical nature of ICD9 codes into its modeling (hierarchy-based classifier). We propose novel evaluation metrics, which reflect the distances among gold-standard and predicted codes and their locations in the ICD9 tree. Experimental setup, code for modeling, and evaluation scripts are made available to the research community.

Results

The hierarchy-based classifier outperforms the flat classifier with F-measures of 39.5% and 27.6%, respectively, when trained on 20 533 documents and tested on 2282 documents. While recall is improved at the expense of precision, our novel evaluation metrics show a more refined assessment: for instance, the hierarchy-based classifier identifies the correct sub-tree of gold-standard codes more often than the flat classifier. Error analysis reveals that gold-standard codes are not perfect, and as such the recall and precision are likely underestimated.

Conclusions

Hierarchy-based classification yields better ICD9 coding than flat classification for MIMIC patients. Automated ICD9 coding is an example of a task for which data and tools can be shared and for which the research community can work together to build on shared models and advance the state of the art.

Introduction

With three out of every four physicians reporting to use electronic health records (EHRs),^{1 2} the volume of data available is growing rapidly. Besides the benefits of health information technology for patient care, much promise is held by the secondary analysis of these data. Diagnosis codes, for instance, are used in the EHR as a billing mechanism. But these codes have also been shown crucial in phenotyping efforts and predictive modeling of patient state.^3–6 Our goal in this paper is to build community-shared, baseline models and experimental setups for automated ICD9 coding. As such, this work has three key contributions: (i) Modeling of ICD9 coding: while this task has been investigated in the past, we tackle discharge summary coding, without any constraint on the search space for codes. We cast the task as a multi-label classification with a very large number of classes (over 15 000 codes). (ii) Evaluation metrics specific to ICD9 coding: to enable informative assessment and comparison across models, we propose novel evaluation metrics, which reflect the distances among gold-standard and predicted codes and their locations in the ICD9 tree. (iii) Community sharing of experimental setup and code. One of the critical ways in which data-driven informatics research can advance is through sharing of data and reproducible experiments. Our models are trained and tested on a large publicly available dataset, and all code for the models and the evaluation metrics is provided to the research community.

Background and significance

ICD9-CM codes are a taxonomy of diagnostic codes.^{7 8} Codes are organized in a rooted tree structure, with edges representing is-a relationships between parents and children. They have been primarily used for administrative purposes. Trained medical coders review the information in the patient record for a clinical episode and assign a set of appropriate ICD9 codes. Manual coding can be noisy: human coders sometimes disagree,⁹ tend to be more specific than sensitive in their assignments,¹⁰ and sometimes make mistakes.^{11 12} Nevertheless, the large set of narratives and their associated ICD9 codes, especially when taken in aggregate, represents a valuable dataset to learn from.¹³

Automated ICD9 coding has been investigated in the informatics community. In fact, the task of ICD9 coding for radiology reports was one of the first informatics community challenges⁹: nearly 1000 radiology reports for training and 1000 for testing, labeled over 94 unique ICD9 codes. Methods ranged from manual rules to online learning.^14–17 There, manual rules, along with basic text processing, and decision trees were the most successful. Other work had leveraged larger datasets and experimented with K-nearest neighbor, naive Bayes, support vector machines (SVMs), Bayesian ridge regression, as well as simple keyword mappings, all with promising results.^18–22 Comparison of these methods is difficult, however, because they all leverage different datasets and/or methods.

Here, we experiment with ICD9 coding on a large scale with complex documents (discharge summaries) and a large set of possible ICD9 codes (approx. 5000). We provide a benchmark for the community based on a hierarchically structured set of SVMs similar to that reported in Zhang's work.²³ This work differs, however, as Zhang experimented with curated ICD9 codes from the radiology notes and a much smaller set of 45 ICD9 codes.^{9 23} This particular method was chosen because of the effectiveness of linear SVMs for text classification problems with few examples and high dimensionality.²⁴ This is important because a large number of individual SVMs compose the overall classifier, where each individual SVM may be trained on relatively few examples.

Review of classification systems (to ICD9 codes or other categories like smoking status) from the clinical narrative shows that existing approaches report one or more of the following standard evaluation metrics: recall, precision, specificity, and accuracy.^{25 26} For ICD9 coding, however, additional evaluation metrics have been proposed in the literature. Researchers argue that recall might be the metric to optimize for, as the goal is to present coders with a set of potential codes which includes the right codes, rather than an incomplete list.^{18 20} Thus, Recall at K was proposed to compute the micro-averaged recall at K=10, 15, and 20 (with the assumption that coders will not look at more than 20 predicted codes, and that most documents get assigned no more than 20 codes). In the 2007 challenge, a cost-sensitive accuracy metric was considered. The intuition behind this metric is to penalize predictions for over-coding (which could result in fraud) and under-coding (which could result in a loss of revenue).^{9 27} Finally, because of the high-granularity of ICD9 codes, researchers have also suggested differentiating between full-code predictions and category-level predictions.¹⁸ The task of ICD9 coding is by nature complex to evaluate, as it consists of a multi-label classification over a tree structure, where both the distance and locations in the tree of two given nodes has varying meaning. In this paper, we propose a new set of evaluation metrics to capture the different aspects of a prediction, such as over/under-predicting in terms of granularity, and comparison of paths within the ICD9 tree for predicted and gold-standard codes.

To ensure reproducibility of our work, we train and test our methods on a publicly available dataset, and make our code and experimental setup public (data preparation and scripts for evaluation metrics). Our goal is to enable researchers interested in designing novel algorithms for clinical data processing to compare their results on the same data with the same metrics, and thus advance the state of the art.

Materials and methods

Datasets

The corpus of discharge summaries and associated ICD9 codes was extracted from the Multiparameter Intelligent Monitoring in Intensive Care II (MIMIC II) clinical database,²⁸ a publicly available repository of records for patients in the intensive care unit. Out of the 22 815 non-empty discharge summaries in the repository, the first 90% (20 533 based on MIMIC subject id) were used for training and the remaining 10% (2282) for testing. Because the MIMIC repository is fully de-identified, the ordering of patients is unknown to us, but most likely random with respect to time.

Discharge summaries were tokenized. A vocabulary was defined as the top 10 000 tokens ranked by their tf-idf score computed across the whole MIMIC dataset. Thus, the words in the vocabulary are a mix of neither too-frequent nor too-rare tokens and with a manageable, yet large enough number of dimensions (10 000) to represent documents. Documents are represented as bags of words (ie, all other tokens not in the vocabulary were filtered out).

The hierarchy of ICD9 codes was downloaded from the NCBO BioPortal.²⁹ No pre-processing was carried out on the hierarchy. The ICD9 tree, excluding procedures, contains 16 626 codes. It has eight levels (counting root as the first level). At each level, nodes have a varying number of children ranging from 0.12 (for level 7) to 18 for level 2. The mean leaf depth is 6.46 (median=7, SD=0.81, min=4, max=8).

Prediction models

We describe two prediction models for automated ICD9 code assignment. Both models utilize SVMs. Standard implementations of SVMs are binary classifiers. Our task is a multi-label classification task, where one or more labels can be assigned to a given document. One way to construct such a classifier is to combine the predictions of many binary classifiers, one per label. This approach defines our baseline classification, which we refer to as flat SVM. Because it considers each prediction independently, this baseline ignores the information provided by the inherent structure of ICD9 codes. Our second approach, called hierarchy-based SVM, leverages the hierarchy in constructing the training data and constructs the overall classifier as a set of dependent SVMs.

Flat SVM

The flat SVM considers each label as an independent binary decision. There exists one linear SVM classifier for each possible ICD9 code, excluding the root, which is always considered positive. All documents in the training set labeled with that ICD9 code are considered positive, and all others are considered negative.

Parents and children in the ICD9 tree have is-a relationships. Therefore, ancestors of an assigned ICD9 code must also be positive. Conversely, descendants of a negative ICD9 code must also be negative. We take this into consideration only during testing, where single predictions are augmented to include all ancestors and the root is always assumed positive.

Hierarchy-based SVM

The hierarchy-based SVM takes into consideration the hierarchical nature of the ICD9 code tree during training and testing.²³ During training, we leverage the hierarchy to create an augmented label set for each document and train many SVM classifiers—one for each code, excluding the root.

The classifier associated with a given code in the hierarchy is applied only if its parent code has been classified as positive. Therefore, only documents where a parent code is positive are included in the training data for the child classifier. Whereas in the flat SVM, each classifier has the same amount of training data, in the hierarchy-based SVM, some classifiers could have many fewer training documents. We hypothesize that because the documents are all relevant to the parent's given code, they will be more informative than all the documents from the flat setting.

For held-out data, the classifiers are applied from the root downward until a child node is classified as negative. Afterwards, there is no need to apply further classifiers to respect the constraints of the is-a hierarchy. This procedure is repeated for all paths from the root to all possible leaves. The result is a positive subtree of multi-label predictions for a given document. Unlike in the flat SVM, it is not necessary to augment the predictions with their ancestors since all ancestors are already positive.

Baseline evaluation statistics

We report recall and precision as the baseline evaluation statistics for the two classifiers. Because there were gold-standard assignments that had descendants (61 in our dataset, probably because of the different ICD9 revisions through time), true positives were defined as predicted codes that were ancestors of, descendants of, or identical to a gold-standard code. False positives were defined as predicted codes that are not true positives. False negatives were defined as gold-standard codes where the code itself or a descendant was not predicted.

Multi-label hierarchical evaluation statistics

There are several challenges in evaluating ICD9 code predictions. First, the prediction task is a multi-label classification—for each document, there are several gold-standard nodes and several predicted nodes over the ICD9 tree. Second, the label space is large. Lastly, the hierarchical structure of the codes impacts the way mispredictions can be interpreted. For instance, it is less of a misprediction if a predicted code is the child of a gold-standard code than if it is a remote ancestor, or worse a node in a distant subtree. We present novel evaluation metrics, which highlight the various aspects of prediction performance. In particular, the metrics help with error analysis of a prediction model in highlighting the distance between gold-standard and predicted codes and the degree of predicting at a too coarse or too granular level for a given gold-standard code.

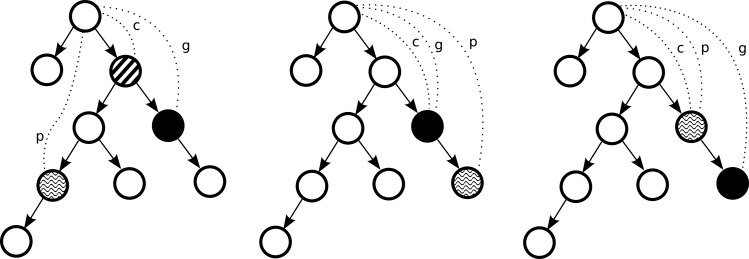
Given n gold-standard labels and m predicted labels we compute five types of metrics based on the quantities (figure 1):

• g: the depth in the ICD9 tree of a gold-standard code;

• p: the depth in the ICD9 tree of a predicted code;

• c: the depth in the ICD9 tree of the deepest common ancestor between a gold-standard and a predicted code.³⁰

Figure 1.

Quantities used in novel evaluation metrics for evaluation of automated ICD9 coding for different cases (left: prediction path diverges from the gold-standard path; middle: prediction is on the correct path but is too granular; and right: prediction is on the correct path, but is not granular enough).

The deepest-common ancestor between a gold-standard and a predicted code is determined depending on whether the focus is on the gold-standard codes or the predicted codes. When the focus is on gold-standard codes, c represents the deepest common ancestor between a particular gold-standard code and the nearest predicted code (of the m predicted codes). Whereas when the focus is on predicted codes, c represents the deepest common ancestor between a particular predicted code and the nearest gold-standard code (of all n gold-standard codes in the tree). Given these quantities, we propose the following evaluation metrics to assess the quality of prediction.

• Shared path (c) represents the depth in the ICD9 tree of the deepest common ancestor between a gold-standard code and a predicted code. It characterizes how deep in the tree the prediction went before diverging towards a wrong prediction code and is a raw count. Reporting such raw information over a test set can inform the error analysis as to the granularity of mistakes. This value is calculated as an average of deepest common ancestor depths over all gold-standard codes.

• Divergent path to gold standard (g−c) represents the distance from the deepest common ancestor to the gold standard. While the shared path characterizes the overlap of the paths in the ICD9 tree to gold standard and to the predicted nodes, the divergent path to gold standard characterizes how far the deepest common ancestor is from the gold standard, that is, by how many levels the gold-standard code was missed. This value is calculated as an average of distances over all gold-standard codes.

• Normalized divergent path to gold standard ((g−c)/g) represents the normalized version of the divergent path to gold standard. It ranges between 0, when the gold-standard node is indeed the deepest common ancestor and 1, when there is no overlap between the paths to predicted and gold-standard nodes in the ICD9 tree. When this measure is 0, the predicted node is either the gold standard (ie, correct prediction), or a descendant of the gold standard (ie, too granular prediction). This value is calculated as an average of normalized distances over all gold-standard codes.

• Divergent path to predicted (p−c) represents the distance from the deepest common ancestor to the predicted node. This measure reflects how far the predicted path has diverged from the path of the gold-standard node in the tree. It is similar to divergent path to gold standard, but from the standpoint of predicted. This value is calculated as an average of distances over all predicted.

• Normalized divergent path to predicted ((p−c)/p) represents the normalized version of the divergent path to predicted. It ranges between 0, when the predicted node is indeed the deepest common ancestor and 1, when there is no overlap between the paths to predicted and gold-standard nodes in the ICD9 tree. When this measure is 0, the predicted node is either the gold standard (ie, correct prediction), or an ancestor of the gold standard (ie, too course prediction). This value is calculated as an average of normalized distances over all predicted.

Experimental setup and public repository

Both the flat SVM and the hierarchy-based SVM were implemented with SVM^light with default parameters.³¹ Training and testing sets, scripts for all evaluation metrics, and source code for the classifiers are available as part of a PhysioNet project “ICD9 coding of discharge summaries” at https://physionet.org/works/ICD9CodingofDischargeSummaries. Furthermore, future models of ICD9 coding can be trained and tested on the same dataset and evaluated according to the same metrics described in this paper, thus allowing for a useful comparison of future algorithms.

The MIMIC discharge summaries and associated codes were extracted from the MIMIC II clinical database V.2.6.

Results

Data

The MIMIC repository contained 22 815 discharge summaries and 215 826 ICD9 codes (5030 distinct codes). Augmenting these nodes with their ancestors in the ICD9 hierarchy to keep a tree structure resulted in a tree of 7042 ICD9 codes. This tree is the basis for our prediction models.

Across the whole MIMIC repository, the mean number of codes per discharge summary was 9.45 (median=9, SD=4.7, min=1, max=39). Furthermore, discharge summaries with 9 assigned codes were 3.5 times more frequent than summaries with 8 codes (the next most frequent) and 11 times more frequent than those with 10 codes.

The discharge summaries in the MIMIC repository had a mean length of 1083 words (median=1000, SD=629, min=40, max=6054).

Prediction models

We report evaluation of the two prediction models: flat SVM and hierarchy-based SVM.

Precision, recall, and F-measure

On the test set, the flat SVM yielded 27.6% F-measure, 86.7% precision, and 16.4% recall. On average, it predicted 1.66 codes per document (SD=1.59). When we consider as true positives only the gold-standard codes, flat SVM yielded 21.1% F-measure, 56.2% precision, and 13.0% recall.

The hierarchy-based SVM yielded 39.5% F-measure, 57.7% precision, and 30.0% recall. On average, it predicted 6.31 codes per document (SD=3.47). When considering as true positives only the gold-standard codes, hierarchy-based SVM yielded 29.3% f1-measure, 39.4% precision, and 23.3% recall.

Shared path

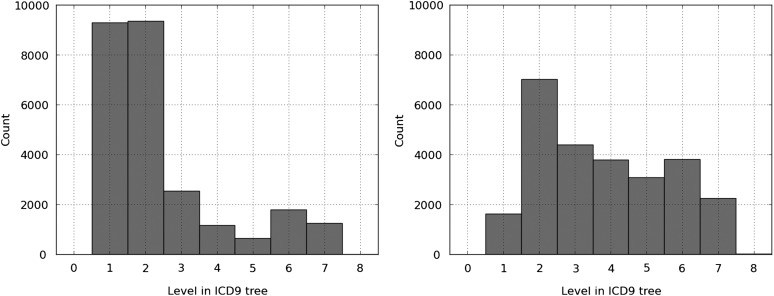
The gold-standard codes in the test set were most common in the ICD9 tree at a depth of 6 (with 7 as the next most common depth). In comparison, in the hierarchy-based SVM, predicted codes also had a most common depth of 6 (6080 codes). The second and third most common depths were 7 (3936 codes) and 5 (2363 codes). The predictions of the flat SVM classifier were bimodal. For many documents, no codes were predicted aside from the default prediction of the root code. Therefore, the most common depth was also 6 (2155 codes), but the second and third most common were 7 (1474 codes) and 1 (696 codes).

Figure 2 shows the histograms for flat SVM and hierarchy-based SVM for the shared path metric. The hierarchy-based SVM is able to predict further along the correct path to the gold-standard codes than the flat SVM, where depths 1 and 2 share the majority of the predictions.

Figure 2.

Histogram of shared path for flat support vector machine (SVM) (left) and hierarchy-based SVM (right) predictions.

Divergent path to gold standard

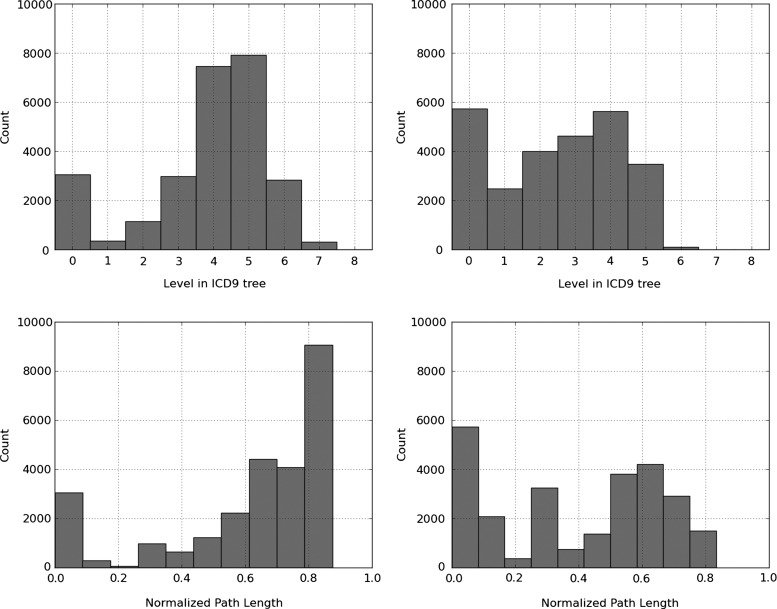
Figure 3 shows the histogram of the divergent path to gold standard and its normalized version for flat SVM and the hierarchy-based SVM. For the hierarchy-based SVM, zero is the most common deviation length, but there is a bimodal distribution. For the flat SVM, there is also a bimodal distribution, but the gold-standard path diverges from the prediction path by 5 or 6 levels by a large margin. As can be seen in the normalized version, this constitutes approximately 80% of the gold-standard path.

Figure 3.

Histogram of the divergent path to gold standard for flat support vector machine (SVM) (top left) and hierarchy-based SVM (top right) predictions, and of the normalized divergent path to gold standard for flat SVM (bottom left) and hierarchy-based SVM (bottom right).

Divergent path to predicted

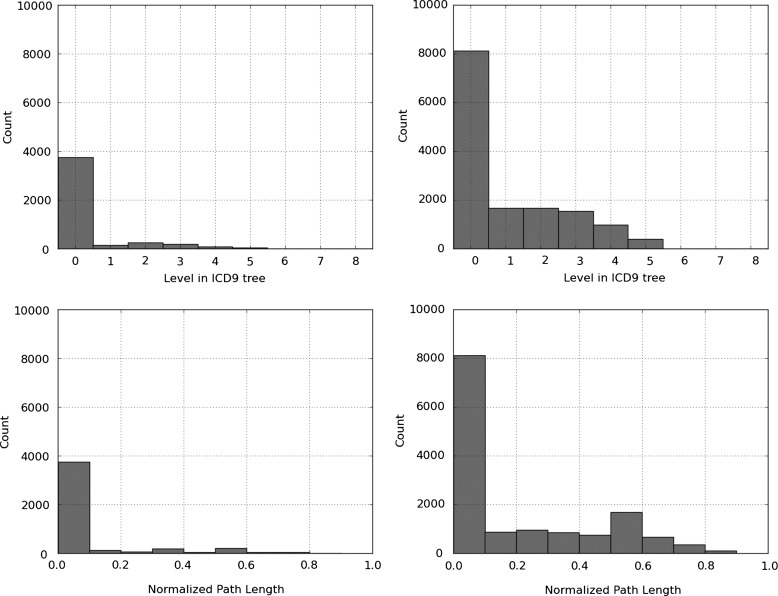
Figure 4 shows the histogram of the divergent path to predicted and its normalized version for flat SVM and the hierarchy-based SVM. For both classifiers, the most common divergence is zero. This indicates that most commonly, the predictions made by both flat SVM and hierarchy-based SVM are part of the gold-standard subtree. However, this information in combination with results in figure 3 suggests that the hierarchy-based SVM predictions cover a significantly larger proportion of the gold-standard subtrees.

Figure 4.

Histogram of the divergent path to predicted for flat support vector machine (SVM) (top left) and hierarchy-based SVM (top right) predictions, and of the normalized divergent path to predicted for flat SVM (bottom left) and hierarchy-based SVM (bottom right).

Also, the second most likely divergence for the hierarchy-based SVM is one. This indicates that when this classifier is incorrect, it is most often very close to the gold-standard prediction.

Discussion

Our results indicate that the hierarchy-based SVM predicts ICD9 coding with a much higher F-measure than the flat SVM (39.5% vs 27.6%), with an improved recall (30.0% vs 16.4%) at the expense of precision (57.7% vs 86.7%). The novel metrics help us get a better sense of the usefulness of the hierarchical approach, however. The shared path metric shows that even with a reduced precision compared to the flat SVM, the hierarchy-based SVM can guide manual coders closer to the ICD9 subtree of interest. This feature would prove useful in a support tool for ICD9 coders.

For a given input document, the hierarchy-based SVM requires fewer classifiers than the flat SVM. Since the search space of codes is large, this makes the hierarchy-based SVM a more attractive model in a use case where near-real-time coding is needed.

The results differ from a previous comparison between flat and hierarchical SVMs by Zhang.²³ There, no significant difference was observed between the two approaches. However, Zhang's dataset was on a limited domain of radiology with 45 ICD9 codes to classify against, and with curation of the ICD9 assignments.⁹ We hypothesize that a hierarchical approach has less opportunity to be leveraged when only 45 codes are considered, whereas in our case, 5030 codes out of the entire ICD9 tree have examples of documents.

To understand the cases where the test documents are misclassified, we analyzed: (i) the predictions in more depth, focusing on a particular diagnosis, ischemic stroke; and (ii) the effect of ICD9 code prevalence on predictive performance.

Error analysis for ischemic stroke

An error analysis for the predictions of the hierarchy-based SVM was conducted. We examined the documents for which there was either a gold standard or a prediction for ischemic stroke. Ischemic stroke was chosen as a representative diagnosis with relatively high prevalence. We identified these documents by the existence of an ICD9 code that is a descendant of code 434—“occlusion of cerebral arteries”. In this analysis, a medical expert evaluated the documents for which the gold standard and the prediction did not agree. Of the 2282 test documents, this included 47 true positives, 20 false positives, and 41 false negatives.

Of the false positives, there were nine with occlusions of cerebral arteries, five cases with precerebral occlusions, two with subacute stenosis of cerebral arteries, two with chronic microvascular changes, one with subarachnoid hemorrhage, and one with idiopathic stroke-like symptoms. Of the false negatives, there were a total of 17 cases without mention of ischemic stroke: 10 with no mention of a cerebrovascular event, three with hemorrhagic strokes, two with small vessel disease, one with a non-occlusive hypoxic event, and one with non-symptomatic septic emboli. The rest of the false negatives did have evidence for stroke, but for many it was sparingly documented.

Under the assumption that the documented ICD9 codes are correct, the hierarchy-based SVM had 53.4% recall and 70.1% precision. However, taking into consideration the above corrections to the gold standard, the hierarchy-based SVM reached 70.0% recall and 83.6% precision for cerebral artery occlusions.

Impact of ICD9 code prevalence in training set on performance

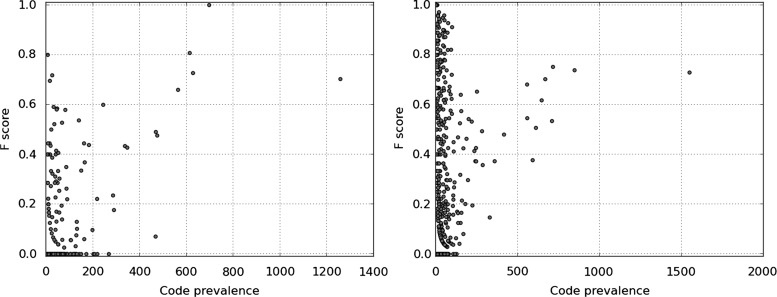
Figure 5 shows a scatter plot of the F-measure for the prediction against the prevalence of ICD9 codes in the training set and provides additional insight into the mispredictions for both models.

Figure 5.

F-measure performance versus ICD9 code prevalence in the training set for flat support vector machine (SVM) (left) and hierarchy-based SVM (right).

These figures suggest there is a slight relationship between ICD9 code prevalence in the training data and out-of-sample performance. The Spearman rank correlation coefficient indicates a significant correlation at 0.45 (two-sided p value of <0.001) for the hierarchy-based SVM and 0.30 (two-sided p value of <0.001) for the flat SVM.

Limitations

Considering our goal of shared resources and models, we report experiments on a single dataset. Furthermore, the MIMIC repository is for patients in intensive care, and we do not know the generalizability of our methods to other types of patients.

Conclusions

Predicting ICD9 codes based on discharge summary content is an example of large-scale modeling applied to a routine healthcare task. We show that when the hierarchical nature of ICD9 codes is leveraged, modeling is improved. Because ICD9 coding is a multi-label classification over a very large tree of codes, we present novel evaluation metrics, which provide a refined view of mispredictions. Detailed evaluation reveals that the predictions of the hierarchy-based SVM are precise, but can lack in recall. A similar but probabilistic classifier such as relevance vector machines would allow for the fine-tuning of the balance between precision and recall. Finally, detailed error analyses reveal that ICD9 code prevalence is correlated with predictive performance and that ICD9 codes as assigned by medical coders are sometimes an imperfect gold standard.

There is a need for benchmark datasets for research to progress and for the community to assess the value of different approaches reliably. Furthermore, there is a need for task-specific evaluation metrics that can inform error analysis and deepen understanding of task characteristics. Towards this end, we have trained and tested our methods on publicly available data and have made the materials for this work available to the research community.

In future work, we will compare more complex models such as hierarchically supervised latent dirichlet allocation (HSLDA) with the methods presented here.¹³ Currently, hierarchy-based SVM performs better than HSLDA, and we suspect this is because HSLDA does not handle negative instances, but unobserved instances instead (and as such avoids a prohibitive performance penalty).