Abstract
In many applications the graph structure in a network arises from two sources: intrinsic connections and connections due to external effects. We introduce a sparse estimation procedure for graphical models that is capable of isolating the intrinsic connections by removing the external effects. Technically, this is formulated as a conditional graphical model, in which the external effects are modeled as predictors, and the graph is determined by the conditional precision matrix. We introduce two sparse estimators of this matrix using the reproduced kernel Hilbert space combined with lasso and adaptive lasso. We establish the sparsity, variable selection consistency, oracle property, and the asymptotic distributions of the proposed estimators. We also develop their convergence rate when the dimension of the conditional precision matrix goes to infinity. The methods are compared with sparse estimators for unconditional graphical models, and with the constrained maximum likelihood estimate that assumes a known graph structure. The methods are applied to a genetic data set to construct a gene network conditioning on single-nucleotide polymorphisms.
Keywords: Conditional random field, Gaussian graphical models, Lasso and adaptive lasso, Oracle property, Reproducing kernel Hilbert space, Sparsity, Sparsistency, von Mises expansion
1. INTRODUCTION
Sparse estimation of the Gaussian graphical models has undergone intense development during the recent years, partly due to their wide applications in such fields as information retrieval and genomics, and partly due to the increasing maturity of statistical theories and techniques surrounding sparse estimation. See, for example, Meinshausen and Buhlmann (2006), Yuan and Lin (2007), Bickel and Levina (2008), Peng et al. (2009), Guo et al. (2009), and Lam and Fan (2009). The precursor of this line of work is the Gaussian graphical model in which the graph structure is assumed to be known; see Dempster (1972) and Lauritzen (1996).
Let Y = (Y1, …, Yp)⊤ be a random vector, Γ = {1, …, p}, and E ⊆ Γ × Γ. Let
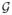 = (Γ, E) be the graph with its vertices in Γ and edges in E. We say that Y follows a Gaussian graphical model (GGM) with respect to
= (Γ, E) be the graph with its vertices in Γ and edges in E. We say that Y follows a Gaussian graphical model (GGM) with respect to
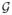 (Lauritzen 1996) if Y has a multivariate normal distribution and
(Lauritzen 1996) if Y has a multivariate normal distribution and
| (1) |
where A ⫫ B|C means A and B are independent given C, and Y−(i,j) denotes the set {Y1, …, Yp}\{Yi, Yj}. Let ωij be the (i, j)th entry of [var(Y)]−1. Then, Yi ⫫ Yj|Y−(i,j) if and only if ωij = 0. Thus, estimating E is equivalent to estimating the set {(i, j) ∈ Γ × Γ: ωij = 0}. Conventional Gaussian graphical models focus on maximum likelihood estimation of ωij given the knowledge of E. In sparse estimation of graphical models, however, E is itself estimated by sparse regularization, such as lasso and adaptive lasso (Tibshirani 1996; Zou 2006).
The conditional graphical model, with which we are concerned, is motivated by the analysis of gene networks and the regulating effects of DNA markers. Let X1, …, Xq represent the genetic markers at q locations in a genome, and let Y1, …, Yp represent the expression levels of p genes. The objective is to infer how the q genetic markers affect the expression levels of the p genes and how these p genes affect each other. Since some markers may have regulating effects on more than one gene, the connections among the genes are of two kinds: the connections due to shared regulation by the same marker, and the innate connections among the genes aside from their shared regulators. In this setting, we are interested in identifying the network of genes after removing the effects from shared regulations by the markers.
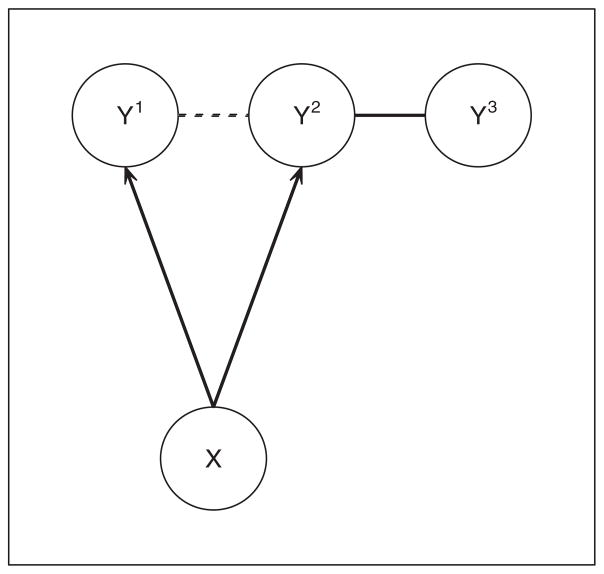
The situation is illustrated by Figure 1, in which X represents a single marker, and Y1, Y2, Y3 represent the expressions of three genes. If we consider the marginal distribution of the random vector (Y1, Y2, Y3), then there are two (undirected) edges in the unconditional graphical model: 1 ↔ 2 and 2 ↔ 3, as represented by the solid and the dotted line segments. However, if we condition on the marker and consider the conditional distribution of Y1, Y2, Y3|X, then there is only one (undirected) edge, 2 ↔ 3, in the conditional graphical model, as represented by the solid line segment.
Figure 1.
Unconditional and conditional graphical models.
In mathematical terms, a conditional graphical model can be represented by
| (2) |
where X = (X1, …, Xq)⊤. Compared with the unconditional graphical model, here we have an additional random vector X, whose effects we would like to remove when constructing the network for Y1, …, Yp. The conditional graphical model (2) was introduced by Lafferty, McCallum, and Pereira (2001) under the name “conditional random field.” However, in that article, the graph
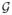 = (Γ, E) was assumed known and maximum likelihood was used to estimate the relevant parameters.
= (Γ, E) was assumed known and maximum likelihood was used to estimate the relevant parameters.
Our strategy for estimating the conditional graphical model (2) is as follows. In the first step, we propose a class of flexible and easy-to-implement initial (nonsparse) estimators for the conditional variance matrix Σ = var(Y | X), based on a conditional variance operator between the reproducing kernel Hilbert spaces (RKHS) of X and Y. In the second step, we incorporate the nonsparse estimators with two types of sparse penalties, the lasso and the adaptive lasso, to obtain sparse estimators of the conditional precision matrix Σ−1.
We have chosen RKHS as our method to estimate Σ for several reasons. First, it does not require a rigid regression model for Y versus X. Second, the dimension of X only appears through a kernel function, so that the dimension of the largest matrix we need to invert is the sample size n, regardless of the dimension of X. This feature is particularly attractive when we deal with a large number of predictors. Finally, RKHS provides a natural mechanism to impose regularization on regression. Here, it is important to realize that our problem involves two kinds of regularization: one for the components of var(Y | X) and the other for the regression of Y on X. Considering the nature of our problem, the former must be sparse, but the latter need not be. Indeed, since estimating the regression parameter is not our purpose, it seems more natural to introduce the regularization for regression through RKHS than to try to parameterize the regression and then regularize the parameters.
The rest of the article is organized as follows. In Section 2, we introduce a conditional variance operator in RKHS and describe its relation with the conditional gaussian graphical model. In Section 3, we derive two RKHS-based estimators of conditional variance Σ. In Section 4, we subject the RKHS estimators to sparse penalties to estimate the conditional precision matrix Θ = Σ−1. In Sections 5, 6, and 7, we establish the asymptotic properties of the sparse estimators for a fixed dimension p. In Section 8, we derive the convergence rate of the sparse estimators when p goes to infinity with the sample size. In Section 9, we discuss some issues involved in implementation. In Sections 10 and 11, we investigate and explore the performance of the proposed methods through simulation and data analysis.
2. CONDITIONAL VARIANCE OPERATOR IN RKHS
We begin with a formal definition of the conditional Gaussian graphical model. Throughout this article, we use
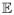 to denote expectation to avoid confusion with the edge set E. We use ℙ to denote probability measures.
to denote expectation to avoid confusion with the edge set E. We use ℙ to denote probability measures.
Definition 1
We say that (X, Y) follows a conditional Gaussian graphical model (CGGM) with respect to a graph
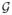 = (Γ, E) if
= (Γ, E) if
relation (2) holds;
Y | X ~ N(
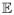 (Y | X), Σ) for some nonrandom, positive-definite matrix Σ.
(Y | X), Σ) for some nonrandom, positive-definite matrix Σ.
Note that we do not assume a regression model for Y versus X. However, we do require that Y | X is multivariate normal with a constant conditional variance, which is satisfied if Y = f (X) + ε, ε ⫫ X, and ε ~ N(0, Σ) for an arbitrary f.
Let ΩX ⊆ ℝq and ΩY ⊆ ℝp be the support of X and Y. Let κX: ΩX × ΩX → ℝ, κY: ΩY × ΩY → ℝ be positive-definite kernels and
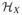 and
and
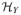 be their corresponding RKHS’s. For further information about RKHS and the choices of kernels, see Aronszajn (1950) and Vapnik (1998). For two Hilbert spaces
be their corresponding RKHS’s. For further information about RKHS and the choices of kernels, see Aronszajn (1950) and Vapnik (1998). For two Hilbert spaces
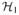 and
and
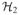 , and a bounded bilinear form b:
, and a bounded bilinear form b:
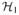 ×
×
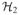 → ℝ, there uniquely exist bounded linear operators A:
→ ℝ, there uniquely exist bounded linear operators A:
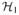 →
→
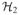 and B:
and B:
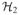 →
→
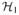 such that 〈f, Bg〉
such that 〈f, Bg〉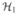 = 〈Af, g〉
= 〈Af, g〉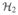 = b(f, g) for any f ∈
= b(f, g) for any f ∈
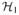 and g ∈
and g ∈
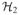 . Applying this fact to the bounded bilinear forms
. Applying this fact to the bounded bilinear forms
we obtain three bounded linear operators
| (3) |
Furthermore, ΣXY can be factorized as
, where RXY:
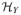 →
→
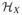 is a uniquely defined bounded linear operator. The conditional variance operator of Y, given X, is then defined as the bounded operator from
is a uniquely defined bounded linear operator. The conditional variance operator of Y, given X, is then defined as the bounded operator from
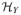 to
to
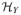 :
:
This construction is due to Fukumizu, Bach, and Jordan (2009).
Let L2(ℙX) denote the class of functions of X that are squared integrable with respect to ℙX,
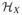 + ℝ denote the set of functions {h + c: h ∈
+ ℝ denote the set of functions {h + c: h ∈
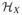 , c ∈ ℝ}, and cl(·) denote the closure of a set in L2(ℙX). The next theorem describes how the conditional operator ΣYY
|
X uniquely determines the CGGM, and suggests a way to estimate Σ.
, c ∈ ℝ}, and cl(·) denote the closure of a set in L2(ℙX). The next theorem describes how the conditional operator ΣYY
|
X uniquely determines the CGGM, and suggests a way to estimate Σ.
Theorem 1
Suppose
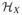 ⊆ L2(ℙX) and, for each i = 1, …, p,
⊆ L2(ℙX) and, for each i = 1, …, p,
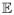 (Yi|X) ∈ cl(
(Yi|X) ∈ cl(
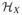 + ℝ);
+ ℝ);κY is the linear kernel: κY (a, b) = 1 + a⊤b, where a, b ∈ ℝp.
Then,
| (4) |
The assumption
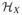 ⊆ L2(ℙX) is satisfied if the function κX(x, x) belongs to L2(ℙX), which is a mild requirement.
⊆ L2(ℙX) is satisfied if the function κX(x, x) belongs to L2(ℙX), which is a mild requirement.
Proof
By assumption 2, any member of
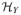 can be written as α⊤y for some α ∈ ℝp. Hence, by Proposition 2 of Fukumizu et al. (2009),
can be written as α⊤y for some α ∈ ℝp. Hence, by Proposition 2 of Fukumizu et al. (2009),
By assumption 1, for any ε > 0, there is an f ∈
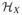 + ℝ such that var{
+ ℝ such that var{
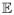 [(α⊤Y | X) − f (X)]} < ε. So, the second term on the right-hand side above is 0, and we have
[(α⊤Y | X) − f (X)]} < ε. So, the second term on the right-hand side above is 0, and we have
| (5) |
In the meantime, we note that
Applying Equation (5) to the left-hand sides of the above equations, we obtain
as desired.
Condition 1 in the theorem can be replaced by the stronger assumption that
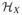 + ℝ is a dense subset of L2(PX), which is satisfied by some well known kernels, such as the Gaussian radial kernel. See Fukumizu et al. (2009).
+ ℝ is a dense subset of L2(PX), which is satisfied by some well known kernels, such as the Gaussian radial kernel. See Fukumizu et al. (2009).
3. TWO RKHS ESTIMATORS OF CONDITIONAL COVARIANCE
To construct a sample estimate of Equation (4), we need to represent operators as matrices in a finite-dimensional space. To this end, we first introduce a coordinate notation system, adopted from Horn and Johnson (1985, p. 31) with slight modifications. Let
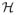 be a finite-dimensional Hilbert space and
be a finite-dimensional Hilbert space and
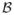 = {b1, …, bm}⊆
= {b1, …, bm}⊆
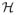 be a set of functions that span
be a set of functions that span
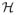 but may not be linearly independent. We refer to
but may not be linearly independent. We refer to
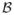 as a spanning system (as opposed to a basis). Any f ∈
as a spanning system (as opposed to a basis). Any f ∈
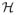 can be written as α1b1 + ··· + αmbm for some α = (α1, …, αm)⊤ ∈ ℝm. This vector is denoted by [f]
can be written as α1b1 + ··· + αmbm for some α = (α1, …, αm)⊤ ∈ ℝm. This vector is denoted by [f]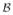 , and is called a
, and is called a
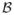 -coordinate of f. Note that [f]
-coordinate of f. Note that [f]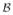 is not unique unless b1, …, bm are linearly independent. However, this does not matter because
unique regardless of the form of [f]
is not unique unless b1, …, bm are linearly independent. However, this does not matter because
unique regardless of the form of [f]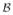 . The same reasoning also applies to the nonuniqueness of coordinates below.
. The same reasoning also applies to the nonuniqueness of coordinates below.
Let
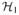 and
and
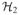 be finite-dimensional Hilbert spaces with spanning systems
be finite-dimensional Hilbert spaces with spanning systems
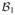 = {b11, …, b1m1}and
= {b11, …, b1m1}and
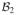 = {b21, …, b2m2}. Let T :
= {b21, …, b2m2}. Let T :
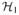 →
→
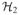 be a linear operator. The (
be a linear operator. The (
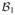 ,
,
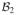 )-representation of T, denoted by
)-representation of T, denoted by 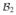 [T]
[T]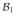 , is the m2 × m1 matrix
, is the m2 × m1 matrix
Then, (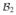 [T]
[T] 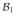 )[f]
)[f] 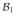 is a
is a
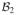 -coordinate of Tf. We write this relation as
-coordinate of Tf. We write this relation as
| (6) |
Let
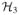 be another finite-dimensional Hilbert space with a spanning system
be another finite-dimensional Hilbert space with a spanning system
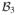 . Let T1:
. Let T1:
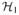 →
→
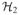 and T2 :
and T2 :
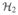 →
→
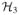 be linear operators. Then,
be linear operators. Then,
| (7) |
The equality means the right-hand side is a (
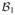 ,
,
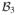 )-representation of T2T1. Finally, if
)-representation of T2T1. Finally, if
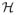 is a finite-dimensional Hilbert space with a spanning system
is a finite-dimensional Hilbert space with a spanning system
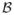 and T :
and T :
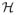 →
→
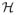 is a self-adjoint and positive-semidefinite linear operator, then, for any c > 0,
is a self-adjoint and positive-semidefinite linear operator, then, for any c > 0,
| (8) |
Let (X1, Y1), …, (Xn, Yn) be independent copies of (X, Y), ℙn be the empirical measure based on this sample, and
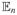 be the integral with respect to ℙn. Let
be the integral with respect to ℙn. Let
| (9) |
where, for example,
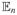 κX(·, X) stands for the function x ↦
κX(·, X) stands for the function x ↦
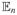 κX(x, X). We center the functions κX(·, Xi) because constants do not play a role in our development. Let Σ̂XX, Σ̂YY, and Σ̂XY be as defined in the last section but with
κX(x, X). We center the functions κX(·, Xi) because constants do not play a role in our development. Let Σ̂XX, Σ̂YY, and Σ̂XY be as defined in the last section but with
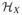 ,
,
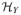 replaced by
replaced by
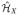 ,
,
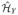 , and cov replaced by the sample covariance. Let
, and cov replaced by the sample covariance. Let
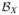 and
and
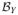 denote the spanning systems in Equation (9). Let KX and KY represent the n × n kernel matrices {κX(Xi, Xj)} and {κY (Yi, Yj)}. For a symmetric matrix, A, let A† represent its Moore-Penrose inverse. Let Qn = In − n
−1Jn, In is the n × n identity matrix, and Jn be the n × n matrix whose entries are 1. To simplify notation, we abbreviate Qn by Q throughout the rest of the article. The following lemma crystallizes some known results, which can be proved by coordinate manipulation via formulas (6), (7), and (8).
denote the spanning systems in Equation (9). Let KX and KY represent the n × n kernel matrices {κX(Xi, Xj)} and {κY (Yi, Yj)}. For a symmetric matrix, A, let A† represent its Moore-Penrose inverse. Let Qn = In − n
−1Jn, In is the n × n identity matrix, and Jn be the n × n matrix whose entries are 1. To simplify notation, we abbreviate Qn by Q throughout the rest of the article. The following lemma crystallizes some known results, which can be proved by coordinate manipulation via formulas (6), (7), and (8).
Lemma 1
The following relations hold:
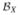 [Σ̂ XX]
[Σ̂ XX] 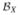 = n−1QKXQ,
= n−1QKXQ, 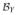 [Σ̂YY]
[Σ̂YY]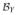 = n−1QKYQ;
= n−1QKYQ;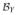 [Σ̂YX]
[Σ̂YX]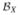 = n−1QKXQ,
= n−1QKXQ, 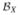 [Σ̂XY]
[Σ̂XY]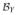 = n−1QKY
Q;
= n−1QKY
Q;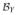 [Σ̂YY
|
X]
[Σ̂YY
|
X]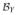 = n−1[QKY
Q − (QKXQ)(QKXQ)† (QKY
Q)].
= n−1[QKY
Q − (QKXQ)(QKXQ)† (QKY
Q)].
When the dimension q of X is large relative to n, it is beneficial to use regularized version of (QKXQ)†. Here, we employ two types of regularization: the principal-component (PC) regularization and the ridge-regression (RR) regularization. Let A be a positive-semidefinite matrix with eigenvalues λ1, …, λ n and eigen-vectors v1, …, vn. Let ε ≥0. We call the matrix the PC-inverse of A. Note that . We call the matrix the RR-inverse of A. The following result can be verified by simple calculation.
Lemma 2
For any f1, f2 ∈
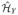 , we have 〈 f1, f2〉
, we have 〈 f1, f2〉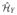 = ([f1]
= ([f1]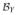 )⊤QKY
Q[f2]
)⊤QKY
Q[f2]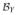 .
.
We now derive the sample estimate of the conditional covariance matrix Σ= var(Y | X). Let DY denote the matrix (Y1, …, Yn)⊤.
Theorem 2
Let Σ̂YY
|
X:
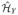 →
→
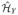 be defined by the coordinate representation
be defined by the coordinate representation
| (10) |
where * can be either † or ‡, KY is the linear kernel matrix, and {εn} is a sequence of nonnegative numbers. Then
| (11) |
Despite its appearance, the matrix
is actually a symmetric matrix. One can also show that Equation (11) is a positive-semidefinite matrix. We denote the matrix (11) as Σ̂PC(εn) if * = †, and as Σ̂RR(εn) if * = ‡. In the following, ei represents a p-dimensional vector whose ith entry is 1 and other entries are 0. For an expression that represents a vector, such as [f]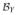 , let ([f]
, let ([f]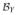 )i denote its ith entry.
)i denote its ith entry.
Proof of Theorem 1
Note that, for an f ∈
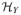 , [f]
, [f]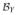 is any vector a ∈ ℝp such that f (y) = a⊤QDY
y. Because
, we have
is any vector a ∈ ℝp such that f (y) = a⊤QDY
y. Because
, we have
Then, by Lemma 2,
When κY is the linear kernel, . Hence, the right-hand side reduces to
Now substitute Equation (10) into the above expression to complete the proof.
4. INTRODUCING SPARSE PENALTY
Let Σ̂ denote either of the RKHS estimators given by Equation (11). We are interested in the sparse estimation of Θ= Σ−1. Let
| (12) |
This objective function has the same form as that used in unconditional Gaussian graphical models, such as those considered by Lauritzen (1996), Yuan and Lin (2007), and Friedman, Hastie, and Tibshirani (2008), except that the sample covariance matrix therein is replaced by the RKHS estimate of conditional covariance matrix.
To achieve sparsity in Θ, we introduce two types of penalized versions of the objective function (12):
| (13) |
| (14) |
where, in Equation (14), γ is a positive number and {θ̃ij} is a -consistent, nonsparse estimate of Θ. For more details about the development of these two types of penalty functions; see Tibshirani (1996), Zou (2006), Zhao and Yu (2006), and Zou and Li (2008). Yuan and Lin (2007) used lasso and nonnegative garrote (Breiman 1995) penalty functions for the unconditional graphical model, the latter of which is similar to adaptive lasso with γ = 1. In the following, we will write
5. VON MISES EXPANSIONS OF THE RKHS ESTIMATORS
The sparse and oracle properties of the estimators introduced in Section 4 depend heavily on the asymptotic properties of the RKHS estimators Σ̂PC(εn) and Σ̂RR(εn). In this section, we derive their von Mises expansions (von Mises 1947). For simplicity, we base our asymptotic development on the polynomial kernel. That is, we let
| (15) |
For a matrix A and an integer k ≥ 2, let A⊗k be the k-fold Kronecker product A ⊗ ··· ⊗ A. For k = 1, we adopt the convention A⊗1 = A. For a k-dimensional array B = {bi1…ik : i1, …, ik = 1, …, q}, we define the “vec half” operator as
This is a generalization of the vech operator for matrices introduced by Henderson and Searle (1979). It can be shown that there exists a matrix Gk,q, of full column rank, such that vec(B) = Gk,q vech(B). The specific form of Gk,q is not important to us. For k = 1, we adopt the convention vech(B) = B, G1,q = Iq. Let
The estimators Σ̂PC(εn) and Σ̂RR(εn) involve n × n matrices QKXQ and , which are difficult to handle asymptotically because their dimensions grow with n. We now give an asymptotically equivalent expression which only involves matrices of fixed dimensions. Let
| (16) |
Lemma 3
Suppose κX is the polynomial kernel (15) and var(U) is positive definite.
If εn = o(n), then, with probability tending to 1, Σ̂PC(εn) = Σ̃;
If , then .
It is interesting to note that different choices of inversion requires different convergence rates for εn.
Proof
By simple computation, we find
Hence, where . So,
| (17) |
Let s be the dimension of U. Then, rank(QKXQ) = s. Let λ1 ≥ ··· ≥ λs > 0 be the nonzero eigenvalues and v1, …, vs be the corresponding vectors of this matrix. Since λ1,…, λs are also eigenvalues of , which converges in probability to the positive-definite matrix , we have λs = nc + oP(n) for some c > 0. This, together with εn = o(n), implies with probability tending to 1. Consequently, with probability tending to 1,
| (18) |
Now it is easy to verify that if B ∈ ℝs×t is a matrix of full column rank and A ∈ ℝt×t is a positive-definite matrix, then
| (19) |
Thus, the right-hand side of Equation (18) is Σ̃, which proves part 1. To prove part 2, we first note that
| (20) |
Since the function −εn/(εn + λ) is increasing for λ> 0, we have
Hence,
| (21) |
By Equation (19),
Hence, the right-hand side of Equation (21) is of the order . In other words,
Here, we evoke Equation (19) again to complete the proof.
Note that when r = 1 and p < n, and εn = 0, Σ̂PC(εn) reduces to
where varn(·) and covn(·, ·) denote the sample variance and covariance matrices. This is exactly the sample estimate of the residual variance for linear regression.
Lemma 3 allows us to derive the asymptotic expansions of Σ̂PC(εn) and Σ̂RR(εn) from that of Σ̃, which is a (matrix-valued) function of sample moments. Let
 be a convex family of probability measures defined on ΩXY that contains all the empirical distributions ℙn and the true distribution ℙ0 of (X, Y). Let T :
be a convex family of probability measures defined on ΩXY that contains all the empirical distributions ℙn and the true distribution ℙ0 of (X, Y). Let T :
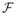 → ℝp×p be the following statistical functional:
→ ℝp×p be the following statistical functional:
| (22) |
In this notation, Σ̃ = T (ℙn). In the following, we use var and cov to denote the variance and covariance under ℙ0. For the polynomial kernel (15), the evaluation T (ℙ0) has a special meaning, as described in the next lemma. Its proof is standard, and is omitted.
Lemma 4
Suppose:
Entries of
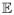 (Y | X) are polynomials in X1, …, Xq of degrees no more than r;
(Y | X) are polynomials in X1, …, Xq of degrees no more than r;Y | X ~ N(
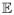 (Y | X), Σ), where Σ is a nonrandom matrix.
(Y | X), Σ), where Σ is a nonrandom matrix.
Then, T (ℙP0) = Σ.
Let ℙα = (1 − α)ℙ0 + αℙn, where α ∈ [0, 1]. Let Dα denote the differential operator ∂/∂α, and let Dα=0 denote the operation of taking derivative with respect to α and then evaluating the derivative at α = 0. It is well known that if T is Hadamard differentiable with respect to the norm || · ||∞ in
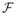 , then
, then
| (23) |
Since the functional T in our case is a smooth function of sample moments, it is Hadamard differentiable under very general conditions. See, for example, Reeds (1976), Fernholz (1983), Bickel et al. (1993), and Ren and Sen (1991). The next lemma can be verified by straightforward computation.
Lemma 5
Let V1 and V2 be square-integrable random vectors. Then,
where q(V1, V2) = (V1 −
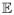 V1)(V2 −
V1)(V2 −
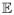 V2)⊤.
V2)⊤.
We will adopt the following notational system:
The next theorem gives the first-order von-Mises expansion of Σ̃.
Theorem 3
Suppose the functional in Equation (22) is Hadamard differentiable, and the conditions in Lemma 4 hold. Then,
| (24) |
where M = M0 −
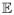 M0 and
M0 and
Proof
We have
We now apply Lemma 5 to obtain
By the chain rule for differentiation and Lemma 5,
Hence,
This can be rewritten as
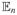 M0 −
M0 −
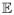 M0, where M0 is the matrix in the theorem.
M0, where M0 is the matrix in the theorem.
Using this expansion, we can write down the asymptotic distribution of Σ̃.
Corollary 1
Suppose the functional in Equation (22) is Hadamard differentiable. Then,
| (25) |
where
By Lemma 3, Theorem 3, and Slutsky’s theorem, we arrive at the following von Mises expansions for the two RKHS estimators Σ̂PC(εn) and Σ̂RR(εn) of the conditional variance Σ.
Corollary 2
Suppose the functional in Equation (22) is Hadamard differentiable, and the conditions in Lemma 4 hold.
Although in this article we have only studied the asymptotic distribution for the polynomial kernel, the basic formulation and analysis could potentially be extended to other kernels under some regularity conditions. We leave this to future research.
6. SPARSITY AND ASYMPTOTIC DISTRIBUTION: THE LASSO
In this section, we study the asymptotic properties of the sparse estimator based on the objective function ϒn(Θ) in Equation (13). Let
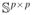 denote the class of all p × p symmetric matrices. For a matrix A ∈
denote the class of all p × p symmetric matrices. For a matrix A ∈
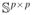 , let σi (A) be the ith eigenvalue of A. Note that, for any integer r, we have
, let σi (A) be the ith eigenvalue of A. Note that, for any integer r, we have
| (26) |
Let En be the sample estimate of E; that is, En = {(i, j): θ̂ij ≠ 0}, where Θ̂ = {θ̂ij}is the minimizer of Equation (13). Following Lauritzen (1996), for a matrix A = {aij} and a graph
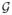 = (Γ, E), let A(
= (Γ, E), let A(
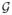 ) denote the matrix that sets aij to 0 whenever (i, j) ∉ E. Let
) denote the matrix that sets aij to 0 whenever (i, j) ∉ E. Let
We define a bivariate sign function as follows. For any numbers a, b, let
The following lemma will prove useful. Its proof is omitted.
Lemma 6
The bivariate sign function sign(a, b) has the following properties:
For any c1 > 0, c2 > 0, sign(c1a, c2b) = sign(a, b);
For sufficiently small |b|, |a + b| − |a| = sign(a, b)b.
The next theorem generalizes Theorem 1 of Yuan and Lin (2007). It applies to any random matrix Σ̂ with expansion (24), including Σ̂PC(εn) and Σ̂RR(εn).
Theorem 4
Suppose (X, Y) follows CGGM with respect to a graph (Γ, E). Let Θ̂ be the minimizer of Equation (13), where and Σ̂ having the expansion (24). Let W ∈ ℝp×p be a random matrix such that vec(W) is distributed as N[0, var(vec(M))]. Then, the following assertions hold.
0 < limn →∞ ℙ(En = E) < 1;
For any ε > 0, there is a λ0 > 0 such that limn →∞ ℙ(En = E) > 1 − ε;
- , where
The inequality limn→∞ ℙ(En = E) > 0 implies that, as n → ∞, there is a positive probability to estimate a parameter as 0 when it is 0. A stronger property is that this probability tends to 1. For clarity, we refer to the former property as sparsity, and the latter as sparsistency (see Fan and Li 2001; Lam and Fan 2009). According to this definition, the two inequalities in part 1 mean that lasso is sparse but not sparsistent. Note that the unconstrained maximum likelihood estimate—and indeed any regular estimate—is not sparse. Part 2 means that, even though lasso is not sparsistent, we can make it as close to sparsistent as we wish by choosing a sufficiently large λ0. Part 3 gives the asymptotic distribution of . It is not the same as that of the maximum likelihood estimate under the constraint θij = 0 for (i, j) ∈ Ec. That is, it does not have the oracle property. The proof of part 3 is similar to that of Theorem 1 in Yuan and Lin (2007) in the context of GGM. However, to our knowledge there were no previous results parallel to parts 1 and 2 for GGM. Knight and Fu (2000) contains some basic ideas for the asymptotics for lassotype estimators.
Proof of Theorem 2
We prove the three assertions in the order 3, 1, 2.
3. Let Θ0 be the true value of Θ, and let
By an argument similar to Yuan and Lin (2007, Theorem 1), it can be shown that
Since , we have
Both Φn(Δ) and Φ(Δ, W) are strictly convex with probability 1. Applying Theorem 4.4 of Geyer (1994) we see that
However, by construction, if Δ̂ is the (almost surely unique) minimizer of Φn(Δ), then Δ̂ = n1/2(Θ̂ − Θ0). This proves part 3.
1. For a generic function f(t) defined on t ∈ ℝs, let
and
be the left and right partial derivatives with respect to the ith component of t. When f is differentiable with respect to ti, we write
. Note that En = E if and only if Φ(Δ, W) is minimized within
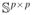 (
(
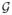 ). This happens if and only if
). This happens if and only if
| (27) |
Here, we only consider the cases i ≥ j because Δ is a symmetric matrix. Let
Then, ∂L(Δ, W)/∂Δ = ΣΔΣ + W. For (i, j) ∈ E, P (Δ, W) is differentiable with respect to δij and ∂δij P(Δ, W) = λ0sign(θ0,ij). For (i, j) ∈ Ec, P (Δ, W) is not differentiable with respect to δij, but has left and right derivatives, given by and . Condition (27) now reduces to
| (28) |
where Δ ∈
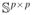 (
(
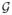 ), sij = λ0sign(θ0,ij) if (i, j) ∈ E and i ≠ j and sij = 0 if i = j.
), sij = λ0sign(θ0,ij) if (i, j) ∈ E and i ≠ j and sij = 0 if i = j.
Now consider the event
We need to show that ℙ(G) > 1. Since Δ belongs to
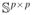 (
(
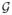 ), it has as many free parameters as there are equations in the first line of Equation (28). Since Σ is a nonsingular matrix, for any {wij: i ≥ j, (i, j) ∈ E}, there exists a unique Δ that satisfies the first line of Equation (28) and it is a linear function of {wij: (i, j) ∈ E, i ≥ j}. Writing this function as Δ({wij : (i, j) ∈ E, i ≥ j}), we see that Equation (28) is satisfied if and only if
), it has as many free parameters as there are equations in the first line of Equation (28). Since Σ is a nonsingular matrix, for any {wij: i ≥ j, (i, j) ∈ E}, there exists a unique Δ that satisfies the first line of Equation (28) and it is a linear function of {wij: (i, j) ∈ E, i ≥ j}. Writing this function as Δ({wij : (i, j) ∈ E, i ≥ j}), we see that Equation (28) is satisfied if and only if
Since the mapping
from ℝp(p+1) to ℝcard(Ec)/2 is continuous, the set τ−1[(−λ0, λ0)card(Ec)/2] is open in ℝp(p+1)/2. Furthermore, this open set is nonempty because if we let
then τ ({wij : i ≥ j}) = 0. Because {wij : i ≥ j} has a multivariate normal distribution with a nonsingular covariance matrix, any nonempty open set in ℝp(p+1)/2 has positive probability. This proves limn→∞ ℙ(En = E) > 0.
Similarly, the set τ−1[(λ0, 3λ0)card(Ec)/2] is open in ℝp(p+1)/2, and if we let
then τ({wij: i ≥ j}) = (2λ0, …, 2λ0)⊤ ∈ (λ0, 3λ0)card(Ec)/2. Hence, the W-probability of τ−1[(λ0, 3λ0)card(Ec)/2] is positive, implying limn→∞ ℙ(En = E) < 1.
2. For each (i, j) ∈ Ec, i ≥ j, Let Uij = [ΣΔ ({wμν : (μ, ν) ∈ E, μ ≥ ν}) Σ]ij + wij. Then, for any η > 0, there is a such that . Let , i ≥ j}. Then, ℙ(Uij ∈ [−λ0, λ0]) > 1 − η. Hence,
This proves part 2 because η can be arbitrarily small.
7. SPARSISTENCY AND ORACLE PROPERTY: THE ADAPTIVE LASSO
We now turn to the adaptive lasso based on Equation (14). We still use Θ̂ = {θ̂ij} to denote the minimizer of Equation (14). For a matrix Δ = {δij} ∈
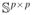 , and a set C ∈ Γ × Γ, let δC = {δij : (i, j) ∈ C, i ≥ j}, which is to be interpreted as a vector where index i moves first, followed by index j.
, and a set C ∈ Γ × Γ, let δC = {δij : (i, j) ∈ C, i ≥ j}, which is to be interpreted as a vector where index i moves first, followed by index j.
Theorem 5
Suppose that (X, Y) follows CGGM with respect to a graph (Γ, E). Let Θ̂ be the minimizer of Equation (14), where Σ̂ has expansion (24), and
Suppose Θ̃ in Equation (14) is a -consistent estimate of Θ0 with ℙ(θ̃ij ≠ 0) = 1 for (i, j) ∈ Ec. Then,
limn→∞ ℙ(En = E) = 1;
.
Part 1 asserts that the adaptive lasso is sparsistent; part 2 asserts that it is asymptotically equivalent to the minimizer of L(Δ, G) when E is known. In this sense Θ̂ is oracle. The condition P (θ̃ij ≠ 0) = 1 means that θ̃ij is not sparse, which guarantees that |θ̃ij |−γ is well defined. For example, we can use the inverse of one of the RKHS estimates as Θ̃.
Proof
Let Δ ∈
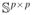 and Ψn(Δ) = n[Λn(Θ0 + n−1/2Δ) − Λn(Θ0)]. Consider the difference
and Ψn(Δ) = n[Λn(Θ0 + n−1/2Δ) − Λn(Θ0)]. Consider the difference
By Lemma 6, for large enough n, the right-hand side can be rewritten as
| (29) |
If (i, j) ∈ E, then |θ̃ij |−γ = OP(1). Because n1/2 λn → 0, the summand for such (i, j) converges to 0 in probability. Hence, Equation (29) reduces to
| (30) |
If (i, j) ∉ E, then θ̃ij = OP(n−1/2), and hence
From this, we see that Equation (30) converges in probability to ∞ unless δEc = 0, in which case it converges in probability to 0. In other words,
This implies that
Since both Ψn(Δ) and Ψ(Δ, G) are convex and Ψ(Δ, G) has a unique minimum, by the epi-convergence results of Geyer (1994), we have
This proves part 2 because the right-hand side is, in fact, argmin{L(Δ, G) : Δ ∈
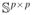 (
(
 )}, and the left-hand side is
.
)}, and the left-hand side is
.
The function Ψ(Δ, W) is always minimized in a region of Δ in which it is not ∞. As a consequence, if Δ minimizes Ψ(Δ, W) over
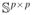 , then δEc = 0. Hence, ℙ(En ⊇ E) → 1. In the meantime, since
, we have
. If (i, j) ∈ E, then θ0,ij ≠ 0. Thus, we see that ℙ(En ⊆ E) → 1. This proves part 1.
, then δEc = 0. Hence, ℙ(En ⊇ E) → 1. In the meantime, since
, we have
. If (i, j) ∈ E, then θ0,ij ≠ 0. Thus, we see that ℙ(En ⊆ E) → 1. This proves part 1.
We now derive the explicit expression of the asymptotic distribution of Θ̂. Let G be the unique matrix in ℝp2×[card(E)+p]/2 such that for any Δ ∈
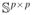 (
(
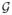 ), vec(Δ) = GδE. For example, if p = 3 and E = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (1, 3), (3, 1)}, then δE = (δ11, δ21, δ31, δ22, δ33)⊤, and G is defined by
), vec(Δ) = GδE. For example, if p = 3 and E = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (1, 3), (3, 1)}, then δE = (δ11, δ21, δ31, δ22, δ33)⊤, and G is defined by
Corollary 3
Under the assumptions of Theorem 5,
where
| (31) |
Proof
Note that
Hence,
This is a quadratic function minimized by δE = −[G⊤(Σ2 ⊗ Ip)G]−1G⊤vec(W). In terms of Δ, the minimizer is vec(Δ) = −G[G⊤(Σ2 ⊗ Ip)G]−1G⊤vec(W). The corollary now follows from Theorem 5.
The asymptotic variance of can be estimated by replacing the moments in Equation (25) and (31) by their sample estimates.
8. CONVERGENCE RATE FOR HIGH-DIMENSIONAL GRAPH
In the last two sections, we have studied the asymptotic properties of our sparse CGGM estimators with the number of nodes p in the graph
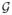 held fixed. We now investigate the case where p = pn tends to infinity. Due to the limited space, we shall focus on the lasso-penalized RKHS estimator with PC regularization. That is, the minimizer of ϒn(Θ) with Σ̂ in Equation (12) is taken to be the RKHS estimator Σ̂PC(εn) based on κX(a, b) = (1 + a⊤b)r. Throughout this section, Θ̂ denotes this estimator. The large-pn convergence rate for the lasso estimator of the (unconditional) GGM has been studied by Rothman et al. (2008).
held fixed. We now investigate the case where p = pn tends to infinity. Due to the limited space, we shall focus on the lasso-penalized RKHS estimator with PC regularization. That is, the minimizer of ϒn(Θ) with Σ̂ in Equation (12) is taken to be the RKHS estimator Σ̂PC(εn) based on κX(a, b) = (1 + a⊤b)r. Throughout this section, Θ̂ denotes this estimator. The large-pn convergence rate for the lasso estimator of the (unconditional) GGM has been studied by Rothman et al. (2008).
In this case, Σ, Θ, and Y should in principle be written as Σ(n), Θ(n), and Y(n) because they now depend on n. However, to avoid complicated notation, we still use Σ, Θ, and Y, keeping in mind their dependence on n. Following Rothman et al. (2008), we develop the convergence rate in Frobenius norm. Let ||·||1, ||·||F, and ||·||∞ be the L1-norm, Frobenius norm, and the L∞-norm of a matrix A ∈ ℝd1×d2:
where aij denotes the (i, j)th entry of A. Let ρ(A) denote the number of nonzero entries of A. For easy reference, we list some properties of these matrix functions in the following proposition.
Proposition 1
Let A ∈ ℝd1×d2, B ∈ ℝd2×d3. Then,
The first inequality follows from the definition of ||·||∞; the second from Hölder’s inequality; the third from the Cauchy-Schwarz inequality. The last two inequalities were used in Rothman et al. (2008). Let ℕ = {1, 2, …}. Consider the array of random matrices: { , n ∈ ℕ}, where A(n) ∈ ℝpn×q, pn may depend on n but q is fixed. Let (A(n))rs denote the (r, s)th entry of A(n).
Lemma 7
Let { , n ∈ ℕ} be an array of random matrices in ℝpn×q, each of whose rows is an iid sample of a random matrix A(n). Suppose that the moment generating functions of (A(n))st, say φnst, are finite on an interval (−δ, δ), and their second derivatives are uniformly bounded over this interval for all s = 1,…, pn, t = 1,…, q, n ∈ ℕ. If pn → ∞, then .
Proof
Let μnst =
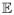 (A(n))st. Since
, there is C > 0 such that |μnst| ≤ C for all s, t, n. Let (B(n))st = (A(n))st − μnst, and ψnst be the moment generating function of (B(n))st. Then, ψnst (τ) = e−μnstτφnst (τ). For any a > 0,
(A(n))st. Since
, there is C > 0 such that |μnst| ≤ C for all s, t, n. Let (B(n))st = (A(n))st − μnst, and ψnst be the moment generating function of (B(n))st. Then, ψnst (τ) = e−μnstτφnst (τ). For any a > 0,
By Taylor’s theorem and noticing that , we have
for some 0 ≤ ξnst ≤ n−1/2. By assumption, there is C1 > 0 such that lim supn→∞ φ″ (ξnst) ≤ C1 for all s = 1,…, pn and t = 1,…, q. Hence,
Thus, we have . By the same argument, we can show that . Therefore,
It follows that
In particular,
which implies the desired result.
In the following, we call any array of random matrices satisfying the conditions in Lemma 7 a standard array. We now establish the convergence rate of ||Θ̂ −Θ0||F. Let sn denote the number of nonzero off-diagonal entries of Θ0. Let Z = Y − μY − E(Y | X). Let Xt and Ys denote the components of X and Y. Their powers are denoted by (Xt)r and (Ys)r. For a symmetric matrix A, let σmax(A) and σmin(A) denote the maximum and minimum eigenvalues of A.
Theorem 6
Let Θ̂ be the sparse estimator defined in the first paragraph of this section with λn ~ (log pn/n)1/2, εn = o(n), and κ(a, b) = (1 + a⊤b)r. Suppose that (X, Y) follows a CGGM, and satisfies the following additional assumptions:
Y, YU⊤, and ZU⊤ are standard arrays of random matrices;
for all n ∈ ℕ, σmax(Σ) < ∞ and σmin(Σ) > 0;
pn → ∞ and pn (pn + sn)1/2(log pn)5/2 = o(n3/2);
the fixed-dimensional matrix VU = var(U) is nonsingular;
each component of
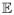 (Y | X = x) is a polynomial in x1,…, xq of at most rth order.
(Y | X = x) is a polynomial in x1,…, xq of at most rth order.
Then, ||Θ̂ − Θ0||F = OP ([(pn + sn) log pn/n]1/2).
Note that we can allow pn(pn + sn)1/2 to get arbitrarily close to n3/2. This condition is slightly stronger than the corresponding condition in Rothman et al. (2008) for the unconditional case, which requires (pn + sn) log pn = o(n1/2). Also note that ||Θ̂ − Θ0||F is the sum, instead of average, of elements (roughly pn + sn nonzero elements). With this in mind, the convergence rate [(pn + sn) log pn/n]1/2 is quite fast. This is the same rate as that given in Rothman et al. (2008) for the unconditional GGM.
Proof of Theorem 3
Let rn = [(pn + sn) log pn/n]1/2, and
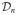 = {Δ ∈
= {Δ ∈
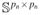 : ||Δ||2 = Mrn} for some M > 0. Let,
: ||Δ||2 = Mrn} for some M > 0. Let,
where
| (32) |
Then, Θ̂ minimizes L(Θ) if and only if Δ̂ = Θ̂ − Θ0 minimizes Gn(Δ). As argued by Rothman et al. (2008), since Gn(Δ) is convex in Δ and Gn(Δ̂) ≤ 0, the minimizer Δ̂ resides within the sphere
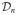 if Gn(Δ) is positive and bounded away from 0 on this sphere. That is, it suffices to show
if Gn(Δ) is positive and bounded away from 0 on this sphere. That is, it suffices to show
The proof of Lemma 3 shows, in the context of fixed p, that with probability tending to 1 if εn = o(n). This result still holds here because the dimension q of X remains fixed. Consequently ℙ(Σ̂PC(εn) = Σ̃) → 1, where Σ̃ is as defined in Equation (16) but now its dimension increases with n. Thus, we can replace the Σ̂PC(εn) in Equation (32) by Σ̃. Let
Let , and . Then,
The term μY|U − μ̂Y|U can be further decomposed as ZI + ZII + ZIII, where
The function Gn(Δ) can now be rewritten as
where . Since Z ~ N(0, Σ), we can use the same argument in the proof of Theorem 1 in Rothman et al. (2008) to show that
Thus, our theorem will be proved if we can show that
for A being any one of the following eight random matrices
| (33) |
By Proposition 1, inequalities (2) and (3), we have, for Δ ∈
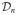 ,
,
Thus, it suffices to show that,
| (34) |
Since ||
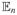 (A)||∞ = ||
(A)||∞ = ||
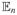 (A⊤)||∞, we only need to consider the following A:
(A⊤)||∞, we only need to consider the following A:
From the definitions of Z and ZI, we have
| (35) |
where μ̂Z =
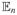 (Z). By the first inequality of Proposition 1,
(Z). By the first inequality of Proposition 1,
| (36) |
Since Z ⫫ X, we have E[Z(U − μU)⊤] = 0. Hence, by Lemma 7,
| (37) |
Similarly,
| (38) |
Since μ̂U − μU has a fixed-dimension finite-variance matrix, by the central limit theorem,
| (39) |
By definition,
By Proposition 1, first inequality,
Substituting Equations (38) and (39) into the above inequality, we find
| (40) |
Since Z is multivariate normal whose components have means 0 and bounded variance, it is a standard array. Hence,
| (41) |
Since the dimension of V̂U is fixed, its entries have finite variances, and VU is nonsingular, we have, by the central limit theorem,
| (42) |
Substituting Equations (37), (39), (40), (41), and (42) into Equation (36), we find that
which, by condition (3), satisfies Equation (34).
The order of magnitudes of the rest of the three terms can be derived similarly. We present the results below, omitting the details:
By condition (3), all of these terms satisfy the relation in Equation (34).
9. IMPLEMENTATION
In this section, we address two issues in implementation: the choice of the tuning parameter and the minimization of the objective functions (13) and (14). For the choice of the tuning parameter, we use a BIC-type criterion (Schwarz 1978) similar to that used in Yuan and Lin (2007). Let Θ̂(λ) = {θ̂ij(λ) : i, j ∈ Γ} be the lasso or the adaptive lasso estimate of Θ0 in the conditional graphical model for a specific choice of λ of the tuning parameter. Let En(λ) = {(i, j) : θ̂ij(λ) ≠ 0}, and
The tuning parameter is then chosen to be
Practically, we evaluate this criterion on a grid of points in (0, ∞) and choose the minimizer among these points.
For the minimization of Equations (13) and (14), we follow the graphical lasso procedure proposed by Friedman et al. (2008), but with the sample covariance matrix therein replaced by the RKHS estimates, Σ̂PC(εn) or Σ̂RR(εn), of the conditional covariance matrix Σ. The graphical lasso (glasso) procedure is available as a package in the R language.
10. SIMULATION STUDIES
In this section, we compare the sparse estimators for the CGGM with the sparse estimators of the GGM, with the maximum likelihood estimators of the CGGM, and with two naive estimators. We also explore several reproducing kernels and investigate their performances for estimating the CGGM.
10.1 Comparison With Estimators for GGM
We use three criteria for this comparison:
- False positive rate at λ̂BIC. This is defined as the percentage of edges identified as belonging to E when they are not; that is,
- False negative rate at λ̂BIC. This is defined as the percentage of edges identified as belonging to Ec when they are not; that is,
Rate of correct paths. The above two criteria are both specific to the tuning method (in our case, BIC). To assess the potential capability of an estimator of E, independently of the tuning methods used, we use the percentage of cases where E belongs to the path {En(λ) : λ ∈ (0, ∞)}, where En(λ) is an estimator of E for a fixed λ. We write this criterion as PATH.
Example 1
This is the example, illustrated in Figure 1, in which p = 3, q = 1, and (X, Y) satisfies CGGM with E = {(1, 1), (2, 2), (3, 3), (2, 3), (3, 2)}. The conditional distribution of Y | X is specified by
| (43) |
where β = (β1, β2, 0)⊤, X ~ N(0, 1), and ε ~ N(0, Σ), X ⫫ ε, and
For each simulated sample, β1 and β2 are generated, independently, from the uniform distribution defined on the set (−6, −3) ∪ (3, 6). We use two sample sizes n = 50, 100. The linear kernel κX(a, b) = 1 + a⊤b is used for the initial RKHS estimate. The results are presented in the first three rows of Table 1. Entries in the table are the means calculated across 200 simulated samples.
Table 1.
Comparison of graph estimation accuracy among the lasso and the adaptive lasso estimators of GGM and CGGM for Example 1, Example 2 (including three scenarios), and Example 3. “ALASSO” means adaptive lasso
| Example/scenario | Criteria |
n = 50
|
n = 100
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| LASSO
|
ALASSO
|
LASSO
|
ALASSO
|
||||||
| GGM | CGGM | GGM | CGGM | GGM | CGGM | GGM | CGGM | ||
| EX1 | FP | 1 | 0.51 | 1 | 0.15 | 1 | 0.40 | 1 | 0.05 |
| FN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| PATH | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | |
| EX2-SC1 | FP | 0.84 | 0.02 | 0.54 | 0.06 | 0.93 | 0.01 | 0.67 | 0.02 |
| FN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| PATH | 0 | 1 | 0.01 | 0.63 | 0 | 1 | 0.98 | 1 | |
| EX2-SC2 | FP | 0.98 | 0.55 | 0.96 | 0.31 | 1 | 0.51 | 1 | 0.22 |
| FN | 0.06 | 0.01 | 0.15 | 0.02 | 0.02 | 0 | 0.08 | 0 | |
| PATH | 0 | 0.57 | 0 | 0.71 | 0 | 0.79 | 0 | 0.98 | |
| EX2-SC3 | FP | 0.71 | 0.68 | 0.18 | 0.19 | 0.75 | 0.77 | 0.10 | 0.11 |
| FN | 0 | 0 | 0.01 | 0.02 | 0 | 0 | 0 | 0 | |
| PATH | 0 | 0.43 | 0.80 | 0.52 | 0 | 0.56 | 1 | 0.87 | |
| EX3 | FP | 0.79 | 0.23 | 0.41 | 0.09 | 0.83 | 0.16 | 0.59 | 0.03 |
| FN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| PATH | 0 | 0.94 | 0.95 | 0.99 | 0 | 1 | 1 | 1 | |
The table indicates that the unconditional sparse estimators have much higher false positive rate than false negative rate. This is because they tend to pick up connections among the components of Y that are due to X. In comparison, the conditional sparse estimators (both lasso and adaptive lasso) can successfully remove the edges effected by X, resulting in more accurate identification of the graph.
Example 2
In this example, we consider three scenarios in which the effect of an external source on the network varies in degree, resulting in different amounts of gain achievable by a conditional graphical model.
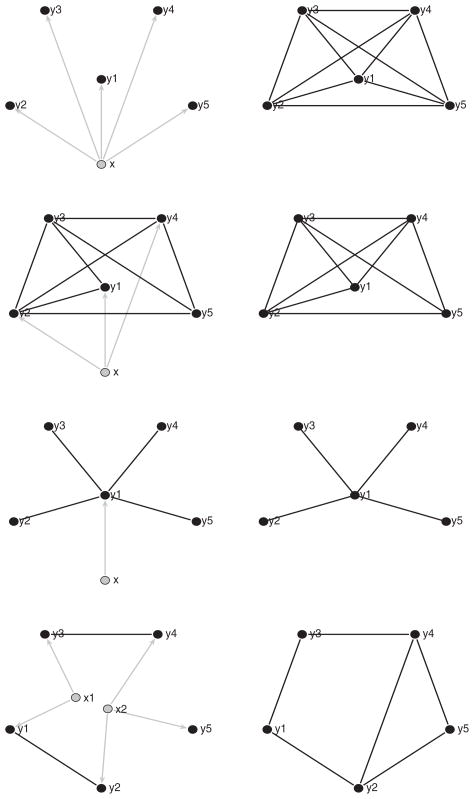
We still assume the linear regression model (43), but with p = 5. The first scenario is shown in the top two panels in Figure 2, where all the components of β are nonzero and Σ diagonal. In this case, the conditional graph is totally disconnected (left panel); whereas the unconditional graph is a complete graph (right panel). Specifically, the parameters are
Figure 2.
Conditional and unconditional graphical models in Examples 2 and 3. Left panels: the conditional graphical models. Right panels: the corresponding unconditional graphical models. Black nodes indicate response variables; gray nodes are the predictors. Edges in the conditional and unconditional graphs are indicated by black lines; regression of Y on X is indicated by directed gray lines with arrows. (The online version of this figure is in color.)
The panels in the third row of Figure 2 represent the other extreme, where only Y1 is related to X, and each Yi for i ≠ 1 shares an edge with Y1 but has no other edges. In this case, the conditional and unconditional graphs are identical. The parameters are specified as follows. The first row (and first column) of Θ is (6.020, −0.827, −1.443, −1.186, −0.922); the remaining 4 × 4 block is I4. The first entry of β is 0.656, and rest entries are 0. Between these two extremes is scenario 2 (second row in Figure 2), where the conditional and unconditional graphs differ only by one edge: 1 ↔ 4. The parameters are
For each scenario, we generate 200 samples of sizes n = 50, 100 and compute the three criteria across the 200 samples. The results are presented row 4 through row 12 of Table 1. We see significant improvements of the rates of correct identification of the graphical structure by the sparse estimator of CGGM whenever the conditional graph differs from the unconditional graph. Also note that, for scenario 3, where the two graphs are the same, the adaptive lasso estimator for GGM performs better than the adaptive lasso estimator for CGGM. This is because the latter needs to estimate more parameters.
Example 3
In this example, we investigate a situation where the edges in the unconditional graphical model have two external sources. We use model (43) with p = 5, q = 2, X ~ N(0, I2),
The results are summarized in the last three rows of Table 1, from which we can see similar improvements by the sparse CGGM estimators.
10.2 Comparison With Maximum Likelihood Estimates of CGGM
In Section 7, we showed that the adaptive lasso estimate for the CGGM possesses oracle property; that is, its asymptotic variance reaches the lower bound among regular estimators when the graph
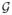 is assumed known. Hence, it makes sense to compare adaptive lasso estimate with the maximum likelihood estimate of Θ under the constraints θij = 0, (i, j) ∉ E, which is known to be optimal among regular estimates. In this section, we make such a comparison, using all three examples in Section 10.1. As a benchmark, we also compare these two estimates with the maximum likelihood estimate under the full model, which for the linear kernel is [Σ̂PC(0)]†. For this comparison we use the squared Frobenius norm
, which characterizes the closeness of two precision matrices rather than that of graphs.
is assumed known. Hence, it makes sense to compare adaptive lasso estimate with the maximum likelihood estimate of Θ under the constraints θij = 0, (i, j) ∉ E, which is known to be optimal among regular estimates. In this section, we make such a comparison, using all three examples in Section 10.1. As a benchmark, we also compare these two estimates with the maximum likelihood estimate under the full model, which for the linear kernel is [Σ̂PC(0)]†. For this comparison we use the squared Frobenius norm
, which characterizes the closeness of two precision matrices rather than that of graphs.
Table 2 shows that the adaptive lasso estimator is rather close to the constrained MLE, with the unconstrained MLE trailing noticeably behind. In three out of five cases, the constrained MLE performs better than the adaptive lasso, which is not surprising because, although the two estimators are equivalent asymptotically, the former employs the true graphical structure unavailable for adaptive lasso, making it more accurate for the finite sample. When the errors of adaptive lasso are lower than the constrained MLE, the differences are within the margins of error.
Table 2.
Comparison of parameter estimation accuracy among adaptive lasso, and unconstrained and constrained MLE for CGGM. Entries are of the form a ± b, where a is the mean, and b the standard deviation, of criterion computed from 200 simulated samples
| Example/scenario | ALASSO | MLE
|
|
|---|---|---|---|
| Unconstrained | Constrained | ||
| EX1 | 1.458 ± 0.125 | 2.256 ± 0.171 | 1.575 ± 0.155 |
| EX2-SC1 | 0.142 ± 0.008 | 0.400 ± 0.018 | 0.122 ± 0.007 |
| EX2-SC2 | 1.858 ± 0.120 | 2.294 ± 0.148 | 1.663 ± 0.116 |
| EX2-SC3 | 1.147 ± 0.071 | 2.139 ± 0.186 | 0.969 ± 0.081 |
| EX3 | 0.303 ± 0.016 | 0.773 ± 0.555 | 0.327 ± 0.275 |
10.3 Exploring Different Reproducing Kernels
In this section, we explore three types of kernels for RKHS
| (44) |
and investigate their performances as initial estimates for lasso and adaptive lasso. These kernels are widely used for RKHS (Genton 2001). For the CGGM, we use a nonlinear regression model with four combinations of dimensions: q = 10, 20, p = 50, 100. The nonlinear regression model is specified by
| (45) |
where β1 and β2 are q-dimensional vectors
The distribution of (ε1, …, εp)⊤ is multivariate normal with mean 0 and precision matrix
where each Γ is the precision matrix in Example 3.
The following specifications apply throughout the rest of Section 10: γ = 1/(9q) for RB, c = 200 for RQ, and r = 2 for PN (because the predictors in Equation (45) are quadratic polynomials); the RKHS estimator Σ̂PC(εn) is used as the initial estimator for lasso and adaptive lasso, where εn are chosen so that the first 70 eigenvectors of QKXQ are retained. Ideally, the kernel parameters γ, c, and εn should be chosen by data-driven methods such as cross-validation. However, this is beyond the scope of the present article and will be further developed in a future study. Our choices are based on trial and error in pilot runs. Our experience indicates that the sparse estimators perform well and are reasonably stable when εn is chosen so that 10% ~ 30% of the eigenvectors of QKXQ are included. The sample size is n = 100 and the simulation is based on 200 samples. To save computing time we use the BIC to optimize λn for the first sample and use it for the rest 199 samples.
In Table 3, we compare the sparse estimators lasso and adaptive lasso, whose initial estimates are derived from kernels in Equation (44), with the full and constrained MLEs. The full MLE is computed using the knowledge that the predictor is a quadratic polynomial of x1, …, xp. The constrained MLE uses, in addition, the knowledge of the conditional graph
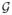 ; that is, the positions of the zero entries of the true conditional precision matrix.
; that is, the positions of the zero entries of the true conditional precision matrix.
Table 3.
Exploration of different reproducing kernels. Entries are averaged over 200 simulation samples
| p | q | LASSO
|
ALASSO
|
MLE
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| PN | RB | RQ | PN | RB | RQ | Full | Constrained | ||
| 50 | 10 | 1.84 | 6.88 | 8.14 | 1.84 | 2.31 | 2.71 | 29.41 | 3.82 |
| 20 | 11.03 | 11.03 | 11.03 | 17.15 | 17.14 | 17.14 | 299.28 | 94.18 | |
| 100 | 10 | 5.96 | 20.07 | 24.06 | 3.35 | 4.33 | 5.17 | 171.32 | 7.73 |
| 20 | 20.06 | 20.05 | 20.05 | 29.10 | 28.30 | 28.31 | 1787.32 | 186.39 | |
Table 3 shows that in all cases the sparse estimators perform substantially better than the full MLEs. For q = 10, the adaptive lasso estimates based on all three kernels also perform better than both the full and constrained MLEs; whereas the accuracy of most of the lasso estimates are between the full and the constrained MLEs. For q = 20, all sparse estimators perform substantially better than both the full and the constrained MLEs. From these results, we can see the effects of two types of regularization: the sparse regularization of the conditional precision matrix and the kernel-PCA regularization for the predictor. The first regularization counteracts the increase in the number of parameters in the conditional precision matrix as p increases, and the second counteracts the increase in the number of terms in a quadratic polynomial as q increases, both resulting in substantially reduced estimation error.
10.4 Comparisons With Two Naive Estimators
We now compare our sparse RKHS estimators for the CGGM with two simple methods: the linear regression and the simple thresholding.
10.4.1 Naive Linear Regression
A simple estimate of CGGM is to first apply multivariate linear regression of Y versus X, regardless of the true regression relation, and then apply a sparse penalty to the residual variance matrix. To make a fair comparison with linear regression, we consider the following class of regression models:
| (46) |
This is a convex combination of a linear model and a quadratic model: it is linear when a = 1, quadratic when a = 0, and a mixture of both when 0 < a < 1. The distribution of ε is as specified in Section 10.3. The fraction 1/4 in the quadratic term in Equation (46) is introduced so that the linear and quadratic terms have the similar signal-to-noise ratios. In Table 4, we compare the estimation error of the CGGM based on Equation (46) by sparse linear regression and by sparse RKHS estimator using the adaptive lasso as penalty. We take q = 10, p = 50, and n = 500. The Gauss radial basis is used for the kernel method, with tuning parameters γ and εn being the same as specified in Section 10.3.
Table 4.
Comparison with linear regression. Entries are averaged over 200 samples
| a | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| Linear | 10.49 | 10.48 | 10.48 | 10.42 | 10.10 | 0.75 |
| Kernel | 1.56 | 2.13 | 1.77 | 1.72 | 1.67 | 1.56 |
We see that the sparse RKHS estimate performs substantially better in all cases except a = 1, where Equation (46) is exactly a linear model. This suggests that linear-regression sparse estimate of CGGM is rather sensitive to nonlinearity: a slight proportion of nonlinearity in the mixture would make the kernel method favorable. In comparison, the sparse RKHS estimate is stable and accurate for different types of regression relations.
10.4.2 Simple Thresholding
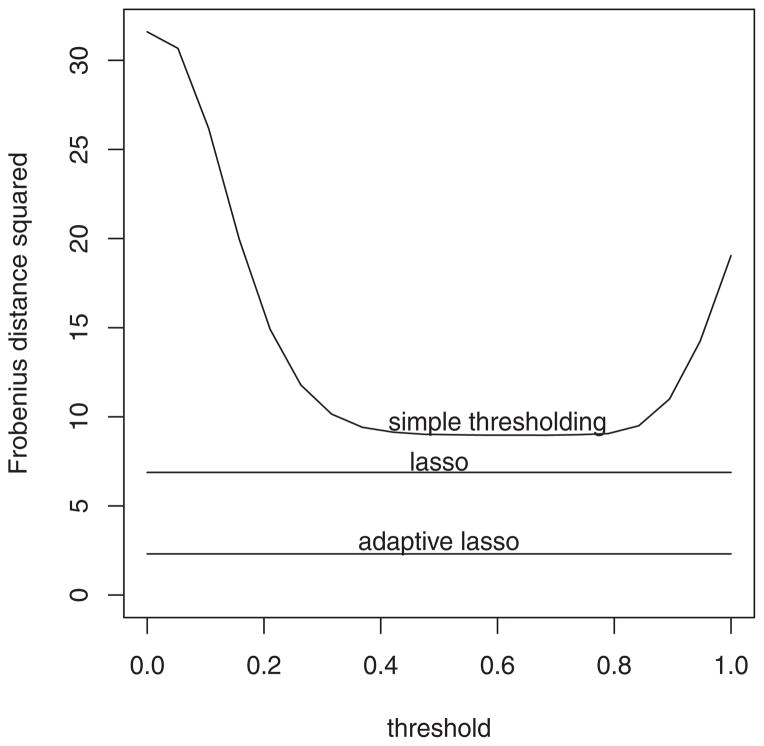
A naive approach to sparsity is by dropping small entries of a matrix. For example, we can estimate Θ by setting to zero the entries of whose absolute values are smaller than some τ > 0. Let Θ̃(τ) denote this estimator. Using the example in Section 10.3 with p = 50, q = 10, n = 500, we now compare the sparse RKHS estimators with Θ̃(τ). The curve in Figure 3 is the error versus τ ∈ [0, 1]. Each point in the curve is the error over 200 simulated samples. The estimate Σ̂PC is based on the gauss radial basis, whose tuning parameters γ and εn are as given in Section 10.3. The two horizontal lines in Figure 3 represent the errors for the lasso and the adaptive lasso estimators based on Σ̂PC, which are read off from Table 3.
Figure 3.
Comparison of lasso, adaptive lasso, and simple thresholding.
The figure shows that the simple thresholding estimate, even for the best threshold, does not perform as well as either of our sparse estimates. Note that in practice Θ0 is unknown, and the optimal τ cannot be obtained by minimizing the curve in Figure 3. With this in mind, we expect the actual gap between the thresholding estimate and the sparse estimates to be even greater than that shown in the figure.
11. NETWORK INFERENCE FROM eQTL DATA
In this section, we apply our CGGM sparse estimators to two datasets to infer gene networks from expression quantitative trait loci (eQTL) data. The dataset is collected from an F2 intercross between inbred lines C3H/HeJ and C57BL/6J (Ghazalpour et al. 2006). It contains 3,421 transcripts and 1,065 markers from the liver tissues of 135 female mice (n = 135). The purpose of our analysis is to identify direct gene interactions by fitting the CGGM to the eQTL dataset. Although a gene network can be inferred from expression data alone, such a network would contain edges due to confounders such as shared genetic causal variants. The available marker data in the eQTL dataset allow us to isolate the confounded edges by conditioning on the genomic information.
We restrict our attention to subsets of genes, partly to accommodate the small sample size. In the eQTL analysis tradition, subsets of genes can be identified by two methods: co mapping and co expression. For co-mapping, each gene expression trait is mapped to markers, and the transcripts that are mapped to the same locus are grouped together. For co-expression, the highly correlated gene expressions are grouped together.
We first consider the subset of genes identified by co-mapping. It has been reported (Neto, Keller, Attie, and Yandell 2010) that 14 transcripts are mapped to a marker on chromosome 2 (at 55.95 cM). As this locus is linked to many transcripts, it is called a hot-spot locus. It is evident that this marker should be included as a covariate for CGGM. In addition, we include a marker on chromosome 15 (at 76.65 cM) as a covariate, because it is significantly linked to gene Apbb1ip (permutation p-value < 0.005), conditioning on the effect of the marker on chromosome 2. The transcript mapping is performed using the qtl package in R (Broman, Wu, Sen, and Churchill 2003).
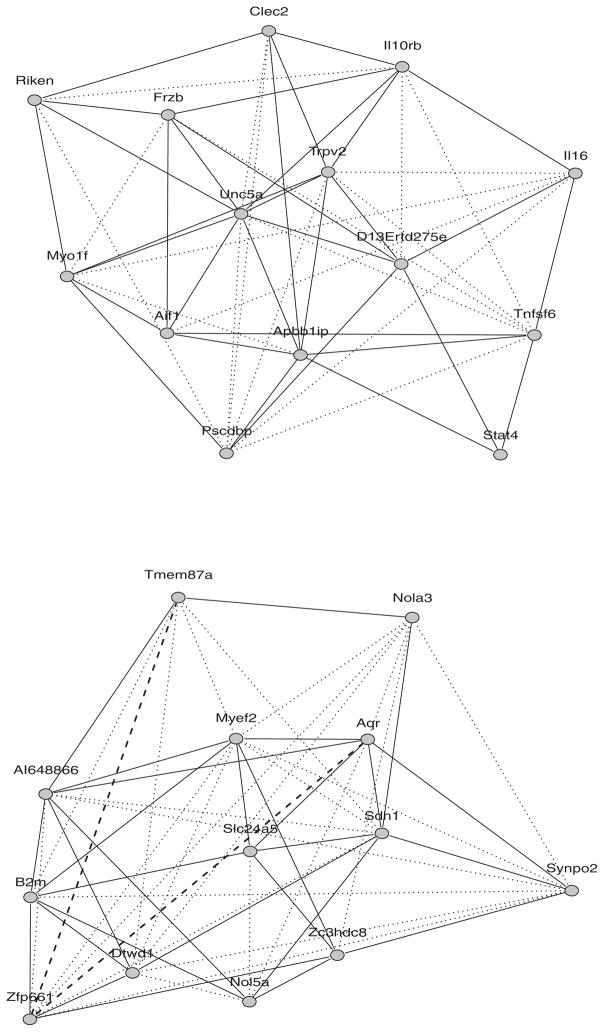
The GGM detects 52 edges; the CGGM detects 34 edges, all in the set detected by the GGM. The two graphs are presented in the upper panel of Figure 4, where edges detected by both GGM and CGGM are represented by black solid lines, and edges detected by GGM alone are represented by blue dotted lines. In the left panel of Table 5, we compare the connectivity of genes of each graph. Among the 14 transcripts, Pscdbp contains the hot spot locus within the ±100 kb boundaries of its location. Interestingly, in CGGM, this cis transcript has the lowest connectivity among the 14 genes, but one of the genes with which it is associated (Apbb1ip) is a hub gene, connected with seven other genes. In sharp contrast, GGM shows high connectivity of Pscdbp itself.
Figure 4.
Gene networks based on GGM and CGGM. Upper panel: data based on co mapping selection. Lower panel: data based on coexpression selection. An edge from both GGM and CGGM is represented by a solid line; an edge from the GGM alone is represented by a dotted line; an edge from CGGM alone is represented by a broken line. (The online version of this figure is in color.)
Table 5.
Connectivity of genes in the conditional and unconditional graphical models. The cis-regulated transcripts are indicated with boldface
| Co-mapping
|
Co-expression
|
||||||
|---|---|---|---|---|---|---|---|
| Gene | GGM | CGGM | Diff. | Gene | GGM | CGGM | Diff. |
| Il16 | 7 | 3 | 4 | Aqr | 7 | 6 | 1 |
| Frzb | 7 | 5 | 2 | Nola3 | 8 | 2 | 6 |
| Apbb1ip | 8 | 7 | 1 | AI648866 | 9 | 6 | 3 |
| Clec2 | 6 | 4 | 2 | Zfp661 | 8 | 5 | 3 |
| Riken | 6 | 4 | 2 | Myef2 | 11 | 5 | 6 |
| Il10rb | 8 | 5 | 3 | Synpo2 | 9 | 3 | 6 |
| Myo1f | 8 | 5 | 3 | Slc24a5 | 6 | 5 | 1 |
| Aif1 | 6 | 5 | 1 | Nol5a | 7 | 4 | 3 |
| Unc5a | 11 | 8 | 3 | Sdh1 | 10 | 6 | 4 |
| Trpv2 | 9 | 6 | 3 | Dtwd1 | 9 | 4 | 5 |
| Tnfsf6 | 9 | 4 | 5 | B2m | 8 | 6 | 2 |
| Stat4 | 3 | 3 | 0 | Tmem87a | 6 | 3 | 3 |
| Pscdbp | 9 | 3 | 6 | Zc3hdc8 | 6 | 5 | 1 |
| D13Ertd275e | 7 | 6 | 1 | ||||
We next study the subset identified by co-expression. We use a hierarchical clustering approach in conjunction with the average agglomeration procedure to partition the transcripts into 10 groups. The relevant dissimilarity measure is 1 − |ρij|, where ρij is the Pearson correlation between transcripts i and j. Among the 10 groups, we choose a group that contains 15 transcripts with the mean absolute correlation equal to 0.78. Thirteen of the 15 transcripts have annotations, and they are used in our analysis. Using the qtl package in R, each transcript is mapped to markers, and seven markers on chromosome 2 are significantly linked to transcripts (permutation p-value 0.005). Among those, we drop two markers that are identical to the adjacent markers. We thus use five markers (Chr2@100.18, Chr2@112.75, Chr2@115.95, Chr2@120.72, Chr2@124.12) as covariates.
The GGM identifies 52 edges and the CGGM identifies 30 edges. Among these edges, 28 are shared by both methods. The two graphs are presented in the lower panel of Figure 4, where edges detected by both GGM and CGGM are represented by black solid lines, edges detected by GGM alone are represented by blue dotted lines, and edges detected by CGGM alone are represented by red broken lines. Among the 13 transcripts, Dtwd1 is the closest to all markers (distances < 300 kbp). The connectivity of each method is shown in the right panel of Table 5. The number of genes that are connected to Dtwd1 is reduced by 5 by CGGM. Unlike in the co-mapping network, in the co-expression network, CGGM detects two edges (Aqr–Zfp661, Zfp661–Tmem87a) that are not detected by GGM. These additional edges could be caused by the error in regression estimation. For example, if the regression coefficients for some of markers are 0, but are estimated to be nonzero, then spurious correlations arise among residuals. This indicates that the accurate identification of the correct covariates is more important in the co-expression network.
As a summary, in the network inference from the transcripts identified by co-mapping, we see that after conditioning on the markers, the cis-regulated transcripts (Pscdbp) are connected to relatively few genes of high connectivity. However, without conditioning on the markers, they appear to have high connectivity themselves. In other words, without conditioning on markers, these cis-regulated transcripts might be misinterpreted as hub-genes themselves. In the network inference from the transcripts identified by co expression, we see that after conditioning on the markers, a few edges are additionally detected, which may result from inaccurate identification of covariates for an individual transcript. Thus, including the correct set of markers for an individual transcript can be important.
Acknowledgments
Bing Li’s research was supported in part by NSF grants DMS-0704621, DMS-0806058, and DMS-1106815.
Hyonho Chun’s research was supported in part by NSF grant DMS-1107025.
Hongyu Zhao’s research was supported in part by NSF grants DMS-0714817 and DMS-1106738 and NIH grants R01 GM59507 and P30 DA018343.
We would like to thank three referees and an Associate Editor for their many excellent suggestions, which lead to substantial improvement on an earlier draft. Especially, the asymptotic development in Section 8 is inspired by two reviewers’ comments.
Contributor Information
Bing Li, Email: bing@stat.psu.edu, Professor of Statistics, The Pennsylvania State University, 326 Thomas Building, University Park, PA 16802.
Hyonho Chuns, Email: chunh@purdue.edu, Assistant Professor of Statistics, Purdue University, 250 N. University Street, West Lafayette, IN 47907.
Hongyu Zhao, Email: hongyu.zhao@yale.edu, Professor of Biostatistics, Yale University, Suite 503, 300 George Street, New Haven, CT 06510.
References
- Aronszajn N. Theory of Reproducing Kernels. Transactions of the American Mathematical Society. 1950;68:337–404. [Google Scholar]
- Bickel PJ, Levina E. Covariance Regularization by Thresholding. The Annals of Statistics. 2008;36:2577–2604. [Google Scholar]
- Bickel PJ, Ritov Y, Klaassenn CAJ, Wellner JA. Efficient and Adaptive Estimation for Semiparametric Models. Baltimore, MD: The Johns Hopkins University Press; 1993. [Google Scholar]
- Breiman L. Better Subset Regression Using the Nonnegative Garrote. Technometrics. 1995;37:373–384. [Google Scholar]
- Broman KW, Wu H, Sen S, Churchill GA. R/qtl: QTLMapping in Experimental Crosses. Bioinformatics. 2003;19:889–890. doi: 10.1093/bioinformatics/btg112. [DOI] [PubMed] [Google Scholar]
- Dempster AP. Covariance Selection. Biometrika. 1972;32:95–108. [Google Scholar]
- Fan J, Li R. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. Journal of American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- Fernholz LT. Lecture Notes in Statistics. Vol. 19. New York: Springer; 1983. Von Mises Calculus for Statistical Functionals. [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Sparse Inverse Covariance Estimation with the Graphical Lasso. Biostatistics. 2008;9:432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukumizu K, Bach FR, Jordan MI. Kernel Dimension Reduction in Regression. The Annals of Statistics. 2009;4:1871–1905. [Google Scholar]
- Genton MG. Classes of Kernels for Machine Learning: A Statistics Perspective. Journal of Machine Learning Research. 2001;2:299–312. [Google Scholar]
- Geyer CJ. On the Asymptotics of Constrained M-estimation. The Annals of Statistics. 1994;22:1998–2010. [Google Scholar]
- Ghazalpour A, Doss S, Zhang B, Wang S, Plaisier C, Castellanos R, Brozell A, Shadt EE, Drake TA, Lusis AJ, Horvath S. Integrating Genetic and Network Analysis to Characterize Gene Related to Mouse Weight. PLoS Genetics. 2006;2:e130. doi: 10.1371/journal.pgen.0020130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo J, Levina E, Michailidis G, Zhu J. Joint Estimation of Multiple Graphical Models. 2009 doi: 10.1093/biomet/asq060. unpublished manuscript available at http://www.stat.lsa.umich.edu/gmichail/manuscript-jasa-09.pdf[152] [DOI] [PMC free article] [PubMed]
- Henderson HV, Searle SR. Vec and Vech Operators for Matrices, with Some Uses in Jacobians and Multivariate Statistics. Canadian Journal of Statistics. 1979;7:65–81. [Google Scholar]
- Horn RA, Johnson CR. Matrix Analysis. New York: Cambridge University Press; 1985. [Google Scholar]
- Knight K, Fu W. Asymptotics for Lasso-Type Estimators. The Annals of Statistics. 2000;28:1356–1378. [Google Scholar]
- Lafferty J, McCallum A, Pereira F. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. Proceedings of the Eighteenth International Conference on Machine Learning (ICML 2001); 2001. pp. 282–289. [Google Scholar]
- Lam C, Fan J. Sparsistency and Rates of Convergence in Large Covariance Matrix Estimation. The Annals of Statistics. 2009;37:4254–4278. doi: 10.1214/09-AOS720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauritzen SL. Graphical Models. Oxford: Clarendon Press; 1996. [Google Scholar]
- Meinshausen N, Bühlmann P. High-Dimensional Graphs with the Lasso. The Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
- Mises Rv. On the Asymptotic Distribution of Differentiable Statistical Functions. The Annals of Mathematical Statistics. 1947;18:309–348. [Google Scholar]
- Neto EC, Keller MP, Attie AD, Yandell BS. Causal Graphical Models in Systems Genetics: A Unified Framework for Joint Inference of Causal Network and Genetic Architecture for Correlated Phenotypes. The Annals of Applied Statistics. 2010;4:320–339. doi: 10.1214/09-aoas288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J, Wang P, Zhou N, Zhu J. Partial Correlation Estimation by Joint Sparse Regression Models. Journal of American Statistical Association. 2009;104:735–746. doi: 10.1198/jasa.2009.0126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reeds JA. PhD dissertation. Harvard University; 1976. On the Definition of Von Mises Functionals. [Google Scholar]
- Ren J, Sen PK. On Hadamard Differentiability of Extended Statistical Functional. Journal of Multivariate Analysis. 1991;39:30–43. [Google Scholar]
- Rothman AJ, Bickel P, Levina E, Zhu J. Sparse Permutation Invariant Covariance Estimation. Electronic Journal of Statistics. 2008;2:494–515. [Google Scholar]
- Schwarz GE. Estimating the Dimension of a Model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Tibshirani R. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society, Series B. 1996;58:267–288. [Google Scholar]
- Vapnik NV. Statistical Learning Theory. New York: Wiley; 1998. [Google Scholar]
- Yuan M, Lin Y. Model Selection and Estimation in the Gaussian Graphical Model. Biometrika. 2007;94:19–35. [Google Scholar]
- Zhao P, Yu B. On Model Selection Consistency of Lasso. Journal of Machine Learning Research. 2006;7:2541–2563. [Google Scholar]
- Zou H. The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
- Zou H, Li R. One-Step Sparse Estimates in Nonconcave Penalized Likelihood Models (with discussion) The Annals of Statistics. 2008;36:1509–1533. doi: 10.1214/009053607000000802. [DOI] [PMC free article] [PubMed] [Google Scholar]