Task-based evaluation of segmentation algorithms for diffusion-weighted MRI without using a gold standard

Abstract

In many studies, the estimation of the apparent diffusion coefficient (ADC) of lesions in visceral organs in diffusion-weighted (DW) magnetic resonance images requires an accurate lesion-segmentation algorithm. To evaluate these lesion-segmentation algorithms, region-overlap measures are used currently. However, the end task from the DW images is accurate ADC estimation, and the region-overlap measures do not evaluate the segmentation algorithms on this task. Moreover, these measures rely on the existence of gold-standard segmentation of the lesion, which is typically unavailable. In this paper, we study the problem of task-based evaluation of segmentation algorithms in DW imaging in the absence of a gold standard. We first show that using manual segmentations instead of gold-standard segmentations for this task-based evaluation is unreliable. We then propose a method to compare the segmentation algorithms that does not require gold-standard or manual segmentation results. The no-gold-standard method estimates the bias and the variance of the error between the true ADC values and the ADC values estimated using the automated segmentation algorithm. The method can be used to rank the segmentation algorithms on the basis of both accuracy and precision. We also propose consistency checks for this evaluation technique.

1. Introduction

Diffusion can be described as the thermally-induced behavior of molecules moving in a microscopic random pattern in a field. Diffusion-weighted magnetic resonance imaging (DWMRI) is sensitive to this microscopic motion [1, 2] and, therefore, measures the mobility of water in tissues. This mobility is quantified using the apparent diffusion coefficient (ADC) parameter. Generally, cellular structures restrict water movement, so a decrease in lesion size in response to therapy typically results in a change in the ADC value [3]. In previous studies, the ADC value has been shown to be a positive indicator to tumor response to therapy, both pre-clinically and clinically [4–8]. However, for DWMRI to function as an imaging biomarker, the ADC must be estimated accurately. Accurate ADC estimation is a challenge due to noise corruption of the diffusion-weighted (DW) image, contamination due to flow artifacts and ghosting, and other random phenomena. In visceral organs such as the liver, pancreas, and spleen, this task is even more complicated due to movement of the lesion across different scans [6–8]. To circumvent the issues due to movement of the lesion, in many studies, the ADC value of the lesion in visceral organs is computed by segmenting the lesion and subsequently determining its mean signal intensity at the different b values [6–11]. The lesion mean signal intensity is invariant to organ movement. Using this mean signal intensity, the ADC value of the lesion is determined. However, for this scheme to work, the first-required step is accurate lesion segmentation. Segmenting the lesion manually is a time-consuming and error-prone task [12–14], so automated segmentation algorithms are required. There is ongoing research and published literature on developing automated segmentation techniques for DW images [12–18]. To compare the performance of various automated segmentation algorithms in order to choose the best one, appropriate evaluation methods are required.

In the field of medical image segmentation, characterizing the performance of segmentation algorithms is an important research problem. Evaluation of segmentation algorithms is a complicated task due to multiple reasons [19]. The first reason is the absence of a gold standard; typically the only standards available for comparison are segmentations produced by expert observers, but even they suffer from observer bias and intra- and inter-expert variability [20–25]. Moreover, the precision of manual segmentations depends on the crispness of the boundaries, the window-level settings for image display, the computer monitor and its settings and the operator’s vision characteristics [22]. The other difficulty in comparing segmentation algorithms is defining a metric to compare the computer-generated segmentation results to the ones produced by expert observers. There is also a lack of standardized statistical protocols for summarizing the results and making conclusions about algorithm performance. Finally, the evaluation study with expert-defined segmentations is tedious, time-consuming and expensive to carry out.

Currently, in the field of image segmentation evaluation, a widely-employed technique is to compare the automated segmentations from these algorithms to manual segmentation generated by a single expert [22,26,27]. Metrics based on spatial distance are used when the delineation of the boundary is critical in the segmentation [28]. Also, in many evaluation studies [12, 17, 18, 29], the manual and automated segmentations are compared using a measure of region overlap [30], such as the Dice coefficient [31] and the Jaccard index [32]. Segmentation results are also evaluated by using manual segmentations obtained from multiple experts, using algorithms such as the simultaneous truth and performance level estimation (STAPLE) [20,26,33] algorithm.

In DWMRI, to evaluate the segmentation algorithms, the most widely-employed technique is to compare the automated segmentation with a manual segmentation using a region-overlap approach [12, 14, 17, 18]. However, this approach suffers from various issues, apart from the general issues with image segmentation evaluation mentioned earlier. The manual segmentations are potentially error-prone due to the low signal-to-noise ratio (SNR) of DW images, ghosting artifacts and fuzzy lesion boundaries [12–14]. Also, the process of acquiring segmentation results from experts is time-consuming, expensive and tedious in DWMRI as well. Often, we have poor or, even worse, no manual segmentation results at all. In fact, in many cases, the radiologists do not perform manual segmentation on the DW images, but rather on a separate set of T1-weighted images that are acquired along with them. Therefore, the inaccuracy of the manual segmentation, or its absence, is a major issue in the evaluation of segmentation algorithms in DWMRI.

More significantly, in DWMRI, the images are acquired for a specific task, which is to compute the ADC value of the lesion. Lesion segmentation or any other intermediate image analysis algorithm is merely a step towards the end task of determining this ADC value. Therefore, an objective approach to evaluate the segmentation algorithms should also decide which algorithm aids the best in this task. The region-overlap methods do not evaluate the segmentation results based on this criterion. These methods are more suited for the task of determining whether the set of pixels that represent the object in manual segmentation also describe that object in the automated segmentation. While this criterion is important, and the segmentation algorithms should be evaluated based on this criterion, it is also important that they be evaluated based on the criterion of ADC estimation since that is the end task from these images. It was of interest for us to study if we could evaluate the segmentation algorithms in DWMRI on this task-based measure. This paper is an outcome of that study. The motivation for the study came from the work done in Barrett et al. [34–36], where the authors emphasize that an objective approach to image quality assessment must determine quantitatively how well the task required of the image can be performed from it. The purpose of this paper is to suggest a framework for task-based evaluation of segmentation algorithms in DWMRI in the absence of gold-standard segmentation.

Task-based evaluation of imaging systems or algorithms in the absence of a gold standard has been a technically challenging but important research problem. A major breakthrough for evaluating systems performing classification tasks in the absence of a gold standard was achieved by Henkelman et al. [37], who were able to perform receiver operating characteristic (ROC) analysis without knowing the true diagnosis. They demonstrated that the ROC parameters can be estimated by using two or more diagnostic tests, neither of which is accepted as the gold standard. A method to compare imaging systems for estimation tasks in the absence of a gold standard was developed by Hoppin et al. [38] and Kupinski et al. [39]. The method was experimentally validated [40] and used to compare ejection-fraction-estimation algorithms in the absence of a gold standard [41]. In this paper, we build upon the basic framework proposed in Hoppin et al. [38] and Kupinski et al. [39], to design a no-gold-standard technique to evaluate segmentation algorithms on the task-based measure of ADC estimation.

The basic idea of task-based evaluation of segmentation algorithms in DWMRI was proposed by us in Jha et al. [42]. In this paper, we carry out a significantly more rigorous study of the idea and the methods for its implementation. In the process, we suggest extensions to the original no-gold-standard approach so that it can be used more generally. The proposed technique compares the segmentation algorithms on the basis of both accuracy and precision. We also suggest a consistency check to verify whether the results obtained using the no-gold-standard approach are consistent with measured data.

2. Theory

2.1. ADC computation

Let us denote the b values at which the scan is performed by b_i, where i denotes the b value index. Assume we have P lesions each of which are imaged at two b values, b₁ and b₂, to give us P sets of images. In the p^th set of images, the lesion is manually segmented to define the region of lesion pixels. Using the manual segmentation results for the p^th set of images, the mean signal intensity of the lesion is calculated at both b values. Denote the mean signal intensities of the p^th lesion at b values b₁ and b₂ by $s_{p1}^{\text{m}}$ and $s_{p2}^{\text{m}}$, respectively, where the superscript m denotes manual segmentation. Also, denote the ADC of the p^th lesion computed using the manual segmentation by $a_p^{\text{m}}$. The equation to compute $a_p^{\text{m}}$ is given by [6]

$$a_p^{\text{m}}=\frac{-1}{b_1-b_2}ln\left(\frac{s_{p1}^{\text{m}}}{s_{p2}^{\text{m}}}\right).$$ (1)

Let the true ADC value of the p^th lesion be a_p. Let there be K automated segmentation algorithms that we have to compare on the task-based measure of ADC estimation. Using the k^th segmentation algorithm, we segment the lesion in the p^th set of images. From the segmentation result, we obtain the mean signal intensity of the lesion at b values b₁ and b₂. Let us denote these mean signal intensities at the two b values by $s_{p1}^k$ and $s_{p2}^k$, respectively. Using these mean signal intensities, we calculate the ADC of the lesion for the p^th set, which we denote by $a_p^k$, as

$$a_p^k=\frac{-1}{b_1-b_2}ln\left(\frac{s_{p1}^k}{s_{p2}^k}\right).$$ (2)

We refer to the ADC value estimated using manual and automated segmentations as “manual” and “automated” ADCs, respectively and denote them by the random variables A_m and A_k respectively. The true ADC value is denoted by the random variable A.

2.2. Use of manual segmentations for task-based evaluation

The end task from DW images is ADC estimation, so the metric that ranks the segmentation algorithms on this task should quantify the error between the true and automated ADC values. To quantify this error for an estimation task, the most commonly used metric is the ensemble mean square error (EMSE) [42–44]. The EMSE quantifies the error between the automated and true ADC, averaged over the whole dataset of lesions, i.e. over different possible lesion variations and noise realizations. Therefore, the EMSE is considered as a comprehensive test statistic. For the k^th automated segmentation algorithm, the EMSE, denoted by EMSE_k, is given by

$${\text{EMSE}}_k=E\{{(A_k-A)}^2\},$$ (3)

where E{ } denotes the expected value of the quantity inside the parentheses. A segmentation algorithm is considered more accurate if it has a lower value of EMSE_k [45]. The issue is that in the absence of a gold standard segmentation, we do not know the true ADC values, so that EMSE_k cannot be computed. However, we do know the manual ADC values. Our objective is to examine whether the EMSE between the manual and automated ADC values, which we denote by d(A_k, A_m), can serve as an indicator of the performance of the different segmentation algorithms. The expression d(A_k, A_m) is mathematically defined as

$$d(A_k,A_{\text{m}})=\text{E}\{{(A_k-A_{\text{m}})}^2\}.$$ (4)

The expression can be rewritten by adding and subtracting the true ADC A inside the modulus sign, which yields

$$d(A_k,A_{\text{m}})=\text{E}\{{(A_k-A)}^2\}+\text{E}\{{(A-A_{\text{m}})}^2\}+2\text{E}\{(A_k-A)(A-A_{\text{m}})\}.$$ (5)

We denote E{(A − A_m)²}, which is the EMSE between the true and manual ADC values, by EMSE_man. Using Eq. (3), the expression for d(A_k, A_m) can be rewritten as

$$d(A_k,A_{\text{m}})={\text{EMSE}}_k+{\text{EMSE}}_{\text{man}}+2\text{E}\{A_k(A-A_{\text{m}})\}-2\text{E}\{A(A-A_{\text{m}})\}$$ (6)

The rankings obtained using d(A_k, A_m) and EMSE_k will be the same if the expression for d(A_k, A_m) is just the sum of EMSE_k and terms that are independent of the k^th segmentation algorithm. From the above expression, it is evident that this will occur only when the term E{A_k(A − A_m)} vanishes. However, if there exists a systematic bias between the true and manual ADC value, then it can be easily shown that this term will not become zero. The manual segmentations themselves typically suffer from bias [19,20,33,46], which can easily lead to a bias between the true and manual ADC values. To study the existence of bias, we performed experiments with manual segmentations on simulated lesions with known ADC values. We detail on these experiments in the results section. The ADC values estimated from these manual segmentations provide further evidence of this bias. In light of these experimental observations and due to the documented presence of systematic bias between true and manual lesion segmentations, the assumption of absence of bias between true and manual ADC is very debatable. Therefore, we cannot assume that the term E{A_k(A − A_m)} will vanish, and thus, we cannot be sure if the ranking determined using d(A_k, A_m) and EMSE_k will be the same. As a result, using manual segmentations for evaluation of segmentation algorithms on this task-based measure and d(A_k, A_m) as the figure of merit is not reliable.

2.3. The no-gold-standard approach

In this section, we propose the no-gold-standard approach to compare the automated segmentation algorithms in the absence of any manual segmentation results. As with manual segmentation, there could be bias between the true segmentation and the segmentation performed with any automated segmentation algorithm. Due to this bias, the automated ADC value will deviate from the true ADC value. We hypothesize that the relation between the true and automated ADC value should consist of a deterministic and a stochastic part. We model the deterministic part as a polynomial relationship between the true and automated ADC values. The motivation behind using a polynomial expression is that it can model any kind of relationship between the true and automated ADC values. The stochastic part is assumed to be a zero-mean normally-distributed noise term. The reason for considering a zero-mean noise term is that if the noise is not zero-mean, then the deterministic part of the relationship will account for that using the bias term. We consider a normally-distributed noise term since it is the most commonly-used model for representing such errors. To further study the nature of this relationship, we performed a set of experiments, which we detail in the results section. From these experiments, we infer that a bias and a zero-mean normally distributed noise term are sufficient to relate the true and automated ADC values. Therefore, for the p^th lesion, the relation between the true ADC value and the ADC value estimated using the k^th segmentation algorithm can be described through a bias term v_k and a noise term ${\epsilon }_p^k~\mathcal{N}(0,{\sigma }_k^2)$, as below:

$$a_p^k=a_p+v_k+{\epsilon }_p^k.$$ (7)

We assume that the parameters v_k and σ_k are characteristic of the k^th segmentation algorithm and independent of the lesion. We would like to mention that although we are assuming the above linear relationship between the true and automated ADC values, our approach can be easily generalized to any general-polynomial relationship between these parameters.

The true ADC values are from different lesions and thus we assume that they have been sampled from a certain distribution. We choose this distribution to lie in the family of beta distributions since it is known that a beta distribution is flexible in modeling probabilistic data [47] and can adapt itself to different probability distributions that the true ADC distribution can take. The beta distribution has the ability to model non-symmetric data, negatively-skewed data as well as uni-modal, strictly-increasing, strictly-decreasing, concave, convex and uniform distributions, and therefore, is used in a wide range of applications [48]. Moreover, the beta distribution is the conjugate prior to a binomial distribution and has a potential for Bayesian extensions [49]. The standard beta distribution returns values only between 0 and 1, but the true ADC value, a_p, has a different range of values, say (l, u), so that 0 ≤ l ≤ a_p ≤ u. However, this can easily be accommodated for by sampling the true ADC values from a four-parameter generalized beta distribution (GBD) [48,50–52] instead of a standard beta distribution. The four-parameter GBD, in addition to the two shape parameters (α > 0 and β > 0), has parameters for the lower and upper limits of the distribution. It can be obtained by transforming the standard beta distribution using a recentering-rescaling transform [50]. The probability density function of the four-parameter GBD of the true ADC values is

$$pr(a_p\mid \alpha ,\beta ,g,l)=\frac{{(a_p-l)}^{(\alpha -1)}{(g-a_p)}^{(\beta -1)}}{B(\alpha ,\beta ){(g-l)}^{(\alpha +\beta -1)}},$$ (8)

where pr( ) denotes the probability density function of the quantity inside the parenthesis. Note that we do not know the values of {α, β, g, l}, since we do not know the true ADC values or their prior distribution.

Our objective is to estimate the linear model parameters v_k and σ_k in Eq. (7) for each of the K segmentation algorithms, given only the automated ADC values $a_p^k$ for the P lesions, and with no knowledge of the corresponding true ADC values a_p. This problem is thus equivalent to fitting the regression line without the x axis. To solve this problem, we take a maximum-likelihood (ML) approach [43]. Let the set of K noise terms, { ${\epsilon }_p^1,{\epsilon }_p^2,\dots {\epsilon }_p^K$}, for the K segmentation algorithms and the p^th lesion be denoted by{ ${\epsilon }_p^k$}. We assume that these noise terms are statistically independent, since they are due to different segmentations. Since we have modeled these noise terms to be normally distributed with zero-mean and standard deviation σ_k, with the above assumption of independence, we can write the joint probability density function of the noise terms {ε_pk} for the p^th lesion as

$$pr(\{{\epsilon }_p^k\})=\prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}exp\left(\frac{-{\epsilon }_p^{k^2}}{2{{\sigma }_k}^2}\right).$$ (9)

Using Eq. (7), we can rewrite the above equation as

$$pr\left(\{a_p^k\}\mid \{v_k,{\sigma }_k\},a_p\right)=\prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}exp\left[\frac{-{\left(a_p^k-a_p-v_k\right)}^2}{2{{\sigma }_k}^2}\right],$$ (10)

where { $a_p^k$} denotes the set of K ADC values estimated for the p^th lesion using the K segmentation algorithms and {v_k, σ_k} denotes the set of linear model parameters in Eq. (7) for all the K segmentation algorithms. Using Bayes theorem and marginalizing Eq. (10) over a_p using Eq. (8), we get

$$pr\left(\{a_p^k\}\mid \{v_k,{\sigma }_k\},\{\alpha ,\beta ,g,l\}\right)=\int {\text{d}a}_{p}pr(a_p\mid \alpha ,\beta ,g,l)\prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}exp\left[\frac{-{\left(a_p^k-a_p-v_k\right)}^2}{2{{\sigma }_k}^2}\right].$$ (11)

Since the different true ADC values are from different lesions, therefore we assume that the true ADC value a_p is statistically independent from one lesion to another. Using this assumption, the probability of all the observed automated ADC values, which we denote by the likelihood function L, can be written as

$$L=\prod _{p=1}^{P}pr\left(\{a_p^k\}\mid \{v_k,{\sigma }_k\},\{\alpha ,\beta ,g,l\}\right).$$ (12)

Taking the logarithm of both sides and using Eq. (11), we get the log-likelihood function

$$\lambda =log(L)=Plog\left(\prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}\right)+\sum _{p=1}^{P}log\int {\text{d}a}_{p}pr(a_p\mid \alpha ,\beta ,g,l)\sum _{k=1}^{K}exp\left[\frac{-{(a_{pk}-a_p-v_k)}^2}{2{{\sigma }_k}^2}\right].$$ (13)

Based on the philosophy of ML approach, we estimate the values {{v_k, σ_k}, {α, β, g, l}} for k = 1, …, K that maximize the probability of the observed data, or alternatively, the log-likelihood function λ given by Eq. (13). We denote the ML estimates of these parameters as {{v̂_k, σ̂_k}, {α̂, β̂, ĝ, l̂}}.

We use a quasi-Newton optimization technique [53] in Matlab software to determine the values {{v̂_k, σ̂_k}, {α̂, β̂, ĝ, l̂}} for which the maximum of the likelihood is obtained. We constrain this optimization to search between reasonable values of the parameters. To determine the search space for the beta distribution parameters, we assume that the automated and true ADC values would have similar distributions. Setting v_k = 0 and assuming no noise term in Eq. (7), we can get an approximate estimate of the true ADC distribution from the distribution of automated ADC values. To use the distribution of automated ADCs from the different segmentation algorithms, we first scale the histogram of automated ADC values so that all the automated ADC values lie between 0 and 1. For the k^th segmentation algorithm, we determine the ML estimates of the beta distribution parameters {α̂_k, β̂_k} that would fit these histograms, using the method mentioned in Hahn et al. [54]. The search space for the beta-distribution parameters α and β is restricted to lie between the minimum and maximum of the computed individual α̂_k and β̂_k values. The search space for l and g is considered to be [0.5, 1.5] and [2.0, 3.0] respectively, in units of mm²/10³s to encompass the typical range of ADC values encountered in our experiments. The search space for {v_k, σ_k} is kept as [−0.5,0.5] and [0.1,1.0], respectively, again in units of mm²/10³s, to span a reasonably wide range of the bias and the standard deviation due to the noise term. The optimization routine is tuned to minimize the possibility of getting caught in a local minimum. To account for the possibility that the actual {α̂, β̂} values might lie outside the specified search space for the beta parameters, we iterate the optimization routine. In each iteration of the routine, the search space for {α, β} parameters is increased. The iteration is repeated until the estimated parameters or the likelihood function converges. Using the optimization routine, we estimate the values of {v̂_k, σ̂_k}, i.e. the bias and variance in the automated ADC values, for each segmentation algorithm.

The bias and variance parameters estimated using the no-gold-standard approach can be used to rank the different segmentation algorithms on the basis of both accuracy and precision. As we mentioned earlier, to compare the segmentation algorithms on the basis of accuracy, it would be ideal to use the EMSE parameter (Eq. (3)), but this parameter cannot be used since the true ADC is not known. However, with our assumption regarding the model relating the true ADC values to the automated ADC values (Eq. (7)), we can derive an expression for the estimate of the EMSE between the true and automated ADC values. We denote this estimated EMSE for the k^th segmentation algorithm by ${\widehat{\text{EMSE}}}_k$. Using Eq. (3) and (7), we can derive the expression for ${\widehat{\text{EMSE}}}_k$ to be

$${\widehat{\text{EMSE}}}_k={\widehat{v}}_k^2+{\widehat{\sigma }}_k^2$$ (14)

where we use the fact that ε_k is a zero-mean noise term. Using the estimated values of v_k and σ_k, ${\widehat{\text{EMSE}}}_k$ can be computed for the k^th segmentation algorithm. A more accurate algorithm will have a lower value of ${\widehat{\text{EMSE}}}_k$, and thus the algorithms can be ranked on the basis of accuracy using this parameter.

To rank the algorithms on the basis of precision, we realize that the variance in the error of the automated ADC values is given by ${\sigma }_k^2$. This variance is inversely proportional to the precision of the ADC values obtained using a particular segmentation algorithm [41]. Therefore, the noise variance, or alternatively, the noise standard deviation value can be used to compare the segmentation algorithms on the basis of precision. The segmentation algorithm for which the value of the estimated noise standard deviation σ̂_k is the minimum is ranked as the most precise segmentation algorithm with respect to the task of ADC estimation using the no-gold-standard approach.

2.4. Consistency check

Using the suggested no-gold-standard approach, given the automated ADC values, we can rank the segmentation algorithms, but we cannot validate the computed rankings since we do not know the true ADC values. However, we can check whether the parameters obtained using the no-gold-standard approach are consistent with the estimated ADC values. Such consistency-checks have been used to verify no-gold-standard approaches [41]. In this section, we suggest consistency checks for our proposed evaluation technique.

The consistency checks we suggest use the fact that if the parameters obtained using the no-gold-standard approach are consistent with the estimated ADCs, then the histogram of the estimated ADCs $a_p^k$ should match the theoretically-estimated distribution of $a_p^k$ obtained using Eq. (7) for all the k segmentation algorithms. To plot the theoretically-estimated distribution for $a_p^k$, we first generate a four-parameter GBD using the estimated beta distribution parameters {α̂, β̂, ĝ, l̂} and the estimated bias term v̂_k. We then convolve it with the normal distribution for the noise term with standard deviation σ̂_k. The histogram of the automated ADC values $a_p^k$ is then compared with this estimated distribution to check whether the two are similar. In order to evaluate the similarity of the two distributions, a quantile-quantile (Q-Q) plot [55] is displayed. The Q-Q plot is a probability plot used for comparing probability distributions by plotting their quantiles against one-another. If most of the values on this plot lie along the 45° line, then this indicates that the two distributions are similar, or equivalently, that the no-gold-standard output is consistent with measured data. To quantitatively evaluate how well the points lie along the 45° line, we compute the correlation coefficient between the quantiles of the two probability distributions. A correlation coefficient close to one indicates that the two distributions are similar. We also perform Pearson’s chi-squared test [56] to compare the similarity of the theoretically-estimated distribution and the distribution of estimated ADCs. The X² test-statistic is determined, and the p-value of this test-statistic is computed. Based on the computed p-value, we can infer whether the two distributions are similar. We should mention that if these consistency checks pass, then that does not guarantee that the no-gold-standard technique has worked correctly, but its failure clearly indicates otherwise.

3. Materials and methods

3.1. In-vivo imaging

In the study being carried out at the Arizona Cancer Center, DWMRI is being used to monitor the therapeutic response in breast cancer patients with metastases to the liver [7]. Conventional T1 and T2-weighted imaging is performed at 1.5 T, along with DW single-shot echo-planar imaging (DW-SSEPI) using magnetic diffusion gradient values (b values) of 0 and 450 s/mm². Image parameters for the DW-SSEPI images are as follows: TE = 91.6 ms, 128 × 128 image matrix, FOV = 38 cm, TR = 6 s, BW = 250 kHz and 6 mm slice thickness. DWMRI image pairs at b=0 and 450 s/mm² are collected within a 24 s single breath-hold. Each patient is imaged at day 0, 4, 11 and 39 following the commencement of cytotoxic therapy. From the in-vivo study, we obtain a set of DW images for each lesion imaged. The lesions in the acquired images at different b values are segmented using a manual or automated segmentation algorithm. From the segmented lesion data, the mean signal intensity of the lesion at the different b values is computed, and using this data, the ADC value of the lesion is determined.

To verify our evaluation technique, it is ideal to use the real in-vivo DW images of the liver containing the lesion. However, to determine the true ranking of the segmentation algorithms, we need to know the true ADC of the lesions, which we do not know in the real DW images. The next ideal approach is to develop bio-phantoms containing lesion-like structures having known ADC values and image them in a scanner. Although there has been research on designing phantoms with different ADC values [57], for this study we would require biophantoms with lesion-like structures that could be segmented with the different segmentation algorithms. Some recent works in this direction [58,59], where the authors develop a bio phantom containing tumor cells, are encouraging. However, the ADC values of these tumor cells are not known a priori, so again we do not know the true ADC value. Thus, we instead take the next-best strategy to verify our evaluation technique, which is using real DW images that contain simulated lesions with known ADC values. We now describe our approach to generate the simulated lesions for real DW images.

3.2. Lesion simulation

From our dataset of real patient images, we select seven sets of real images as templates for the background, where a set comprises of corresponding image slices at b values of 0 and 450 s/mm². Our next objective is to simulate lesions with known ADC value and insert them into the real DW images.

To simulate the lesion, we study the lesion images in the dataset. We select seven lesion images, all imaged at b value 0 s/mm², from our dataset. Each lesion is sufficiently different from the other in terms of size, intensity and other parameters. We observe that the shape of the lesions is approximately elliptical. The parameters of the ellipse are computed by determining two values: the area of the lesion and the width-height ratio of the lesion. We also observe that the lesion intensity is almost constant, with some variability that we attribute to the presence of noise. This noise in MR images is Rician. However, in high-SNR regions, this noise can be approximated as Gaussian [60]. We thus simulate the lesion as a constant-intensity ellipse corrupted by zero-mean Gaussian noise. The constant intensity parameter and the standard deviation of the Gaussian noise for each lesion are assigned values equal to the mean signal intensity and the standard deviation of intensities of the corresponding real lesion. Using these parameters, we are able to simulate lesions at b value 0 s/mm².

For each lesion simulated at b value 0, we randomly select an ADC value from a normal distribution with mean 1.5 mm²/(10³s) and standard deviation of 0.3 mm²/(10³s). We choose this distribution to be a normal, and not beta distribution, since we want to validate if our method works even when the distribution of true ADC values is not a beta distribution. The mean and standard deviation of this normal distribution have been chosen based on the typical ADC values that we have observed in our study. Using this ADC value, the simulated lesion at b value 0 s/mm², and the standard ADC equation, we simulate the lesion at b value 450 s/mm². For each lesion, we repeat this process ten times, each time having a different true ADC value and a different noise realization in the image. The lesions simulated at b value 0 s/mm² and 450 s/mm² are inserted into the real DW images at b value 0 s/mm² and 450 s/mm², respectively. We compared the simulated images with the real DW images, and they were found to be very similar. At the end of this exercise, we have a dataset of seventy simulated DW images containing lesions with known ADC values. We generate two such datasets, which we denote by dataset 1 and dataset 2, respectively.

To study the performance of the method when the true ADC values are sampled from a beta distribution, we repeat the above procedure with the difference being that the true ADC value is sampled from a four-parameter GBD with α = 5, β = 5, l = 1.0 mm²/10³s, and g = 1.0 mm²/10³s. These values for the parameters of this four-parameter GBD have again been chosen based on the typical ADC values that we observed in our study. Using the above procedure, we generate two more simulated lesion datasets, that we denote as dataset 3 and dataset 4, respectively. Finally, we also generate another dataset of simulated lesions, in which the true ADC value is sampled from a normal distribution with mean 1.5 mm²/(10³s) and a standard deviation of 0.6 mm²/(10³s). The simulated-lesion dataset generated through this process is denoted as dataset 5.

3.3. Method to validate the no-gold-standard approach

The simulated lesion in the DW images is segmented manually and using three automated segmentation methods: a maximum-likelihood estimation (MLE) algorithm for segmenting lesions in digital mammograms [61], a clustering algorithm [62], and an expectation-maximization (EM) algorithm [63]. The segmentation algorithms are modified to perform segmentation only on a bounding box marked around the lesion as opposed to the entire image. From the segmentation results, we obtain the mean signal intensity of each lesion and thus compute the ADC of the lesion using Eq. (2) for each segmentation algorithm. This process is repeated for all the lesions in the two datasets.

The automated ADC values using the three segmentation algorithms for all the lesions are input to the no-gold-standard technique. The technique outputs {v̂_k, σ̂_k} for the K segmentation algorithms. To determine the true ranking of the algorithms on the basis of accuracy, we use the actual EMSE (Eq. (3)) as the figure of merit. We can compute the actual EMSE since we do know the true ADC values in our simulation. To obtain the ranking using the no-gold-standard approach, as we mentioned earlier, we use $\widehat{\text{EMSE}}$ given by Eq. (14). If the rankings obtained using the two parameters are the same, and the parameters are reasonably close to each other, it confirms that for our dataset, the no-gold-standard method is able to correctly rank the algorithms based on accuracy.

To determine the true ranking of the algorithms on the basis of precision, we use the residual sum of squares (RSS) as the figure of merit [56]. The RSS is the measure of variance of the measured ADC values since the no-gold-standard approach is based on a linear-regression model. We evaluate the RSS by performing a least-squares (LS) fit of the true and automated ADC values, with the model as mentioned in Eq. (7). From the LS fit, the value for the bias parameter for the k^th segmentation algorithm, v̂_k,ls is obtained. The RSS for the k^th segmentation algorithm is then given by

$${\text{RSS}}_k=\sqrt{\frac{1}{P}\sum _{p=1}^P{\left(a_p-a_p^k-{\widehat{v}}_{k,\text{ls}}\right)}^2}.$$ (15)

The ranking for the no-gold-standard method is obtained using the noise variance σ̂_k estimated for each segmentation algorithm. We compare the two rankings and if they are similar, and to a certain degree, if the parameters RSS_k and σ_k are close, that helps to show that the no-gold-standard approach has successfully ranked the algorithms on the basis of precision for our simulated dataset.

4. Results

4.1. Validating the relationship between the true and estimated ADC values

On the simulated lesion datasets 1 and 2, we use manual and different automated segmentation algorithms to compute the manual and automated ADC values. Our first set of experiments studies the relationship between the true ADC value and the measured ADC value estimated using the different segmentation techniques, including the manual segmentation technique.

Our first objective is to check for the existence of bias between the true and manual ADCs, A and A_m respectively. To verify this, we perform the Student t-test [56] on the error between true and manual ADC value, i.e. A − A_m, assuming that the error follows a normal distribution. The null hypothesis is that the mean of this distribution is zero, i.e. there is no bias. On performing the test, we find that this hypothesis can be rejected, as the p-value is less than 0.0001 for both the simulated lesion datasets. Due to the presence of bias in manual ADC values, as we have demonstrated earlier, the parameter d(A_k, A_m) cannot be used to rank the segmentation algorithms. We also perform the Student t-test for the difference between the true and automated ADC values, and the p-values obtained point to the existence of a bias between these ADC values also.

The next objective is to determine the polynomial order of the relationship between the true and measured ADC values. To determine this relationship, we first perform a LS fit between the true and estimated ADC values from each segmentation technique, for different polynomial orders. The different polynomial orders are the zeroth-order polynomial, a first-order polynomial with just the bias term, a first-order polynomial with bias and slope terms, and second and third-order polynomials. The LS curve fit is performed since in our model, the noise terms are normally distributed, and therefore, the polynomial coefficients determined by the LS method are the maximum-likelihood estimates of the coefficients [43]. Next, to determine the polynomial relationship that best models the relation between true and automated ADC values, we use Akaike’s information criterion (AIC) [64]. The AIC measures the relative goodness of fit of a statistical model by measuring the amount of information loss that occurs when a model is used to describe some measured data. Since we have a finite amount of data, we use the AIC with the second-order correction term, denoted by AIC_c. The AIC_c for least-squares (LS) estimation with normally distributed error is given by

$${\text{AIC}}_{\text{c}}=Plog({\delta }^2)+2Q+\frac{2Q(Q+1)}{P-Q-1},$$ (16)

where Q is the number of parameters to be estimated, P is the number of lesions in the dataset and δ² is the residual sum of squares (RSS) in the LS-fitted model. Using Eq. (16), we determine the value of AIC_i with different order polynomials, where the subscript i denotes the index for the polynomial. We then determine the minimum AIC_i, which we denote by AIC_min. Subsequently, we rescale AIC_i by computing the term Δ_i given by [64]

$${\mathrm{\Delta }}_i={\text{AIC}}_i-{\text{AIC}}_{min}$$ (17)

This transformation causes the best model to have Δ_i = 0, while the rest of the models have positive values. We determine the set Δ_i for all the segmentation algorithms and also for the manual ADC values. This process is repeated for the second lesion dataset too. In Table 1, the Δ_i values for the different segmentation algorithms with different polynomial orders for both the lesion-datasets are presented. We observe that in most scenarios, the Δ_i value is equal to zero when the polynomial is 1^st order, with only the bias-term. Even when not zero, Δ_i is quite small when the polynomial is 1^st order with only bias term, with its highest value being 2.1. As mentioned in Burhman et al. [64], a model that has Δ_i ≤ 2 has substantial support in modeling the data. Based on the values obtained for Δ_i for the simulated dataset and the different segmentation algorithms, the 1^st order polynomial with no bias term is the most suitable for modeling the relation between the true and automated ADC values. This experiment helps to show that the model described using Eq. (7) is appropriate for the relation between true and automated ADC values.

Table 1.

The Δ_i values for different polynomial orders, with different segmentation algorithms and with the two lesion-datasets.

	Segm. Alg.	Polynomial order
		0th order	1st order, only bias	1st order	2nd order	3rd order
Dataset 1	Manual	13.31	0	1.82	3.69	5.02
	Clustering	7.92	1.08	0	2.16	2.31
	MLE	0	2.10	4.30	6.56	8.52
	EM	13.61	0	2.05	4.24	6.23
Dataset 2	Manual	16.89	0	2.14	3.64	4.98
	Clustering	5.88	0	1.67	2.97	4.75
	MLE	0.81	0.42	0	2.07	3.37
	EM	1.79	0	2.08	3.90	5.61

4.2. Validating the no-gold-standard approach and consistency check

For all the simulated lesions in each simulated-lesion dataset, the automated ADC values using the three segmentation algorithms are computed, in units of mm²/10³s. These automated ADC values are input to the no-gold-standard method, which then estimates the bias and noise variance parameters for each of the three segmentation algorithms. Using the bias and noise variance parameters, the algorithms are ranked on the basis of accuracy and precision. The rankings using the no-gold-standard approach are then compared with the true rankings. Following this, the suggested consistency checks are performed, and it is determined whether the consistency check output correctly predicts the success or failure of the no-gold-standard approach. The experiment is performed for all five simulated lesion datasets. We now present the results for the individual datasets.

4.2.1. Datasets 1 and 2

Using the output obtained from the no-gold-standard method for datasets 1 and 2, the three automated-segmentation algorithms are ranked on the basis of accuracy, as shown in Table 2. As is evident from the observations, the rankings obtained using the true and estimated EMSE parameters are the same. The rank of the algorithms on the basis of precision is summarized in Table 3. The no-gold-standard rankings obtained using the noise variance are the same as the true rankings obtained using the RSS parameter for both the simulated-lesion datasets.

Table 2.

True and estimated EMSE for the three segmentation algorithms.

Segm. Alg.	Dataset 1		Dataset 2
	True EMSE	Estimated EMSE	True EMSE	Estimated EMSE
Clustering	0.117	0.075	0.140	0.255
EM	0.469	0.361	0.769	0.870
MLE	0.646	0.744	0.474	0.458

Table 3.

RSS and noise standard deviation for the three segmentation algorithms.

Segm. Alg.	Dataset 1		Dataset 2
	RSS	Noise std. dev.	RSS	Noise std. dev.
Clustering	0.315	0.246	0.357	0.289
EM	0.625	0.599	0.858	0.787
MLE	0.809	0.826	0.662	0.661

On the basis of both accuracy and precision, the two simulated-lesion datasets yield different rankings for the three algorithms. This indicates a difference in performance of the algorithms on the different datasets. However, in spite of this, the no-gold-standard method predicts the same rankings as the true rankings for the two datasets, thus showing its efficacy.

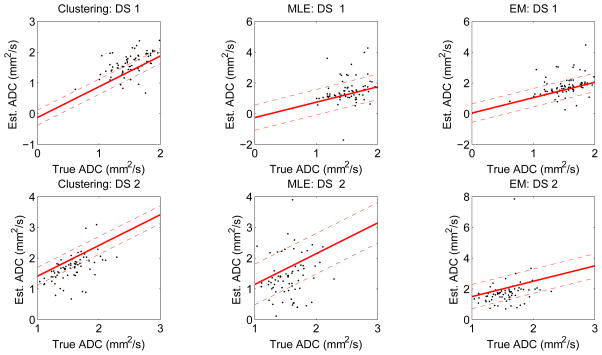
Fig. 1 shows the regression lines obtained using the estimated bias and variance parameters using the no-gold-standard approach, for the three segmentation algorithms for datasets 1 and 2, respectively. The true vs. measured ADC values are also overlaid as a scatter-plot for visual comparison. We note that although we have plotted the true ADC value on the x axis, this information was not used to compute the regression-line parameters, which were computed entirely using the automated ADC values.

Figure 1.

The regression lines estimated using the no-gold-standard method for the three segmentation algorithms and for the two simulated lesion datasets: DS1 and DS2. In these two datasets, the true ADC values were sampled from a normal distribution. The solid line is generated using the estimated linear model parameters, and the dashed line denotes the estimated standard deviation. The scatter plots show the computed ADC values vs. the true ADC value. ADC values are in units of mm²/10³s. Note that although we have plotted the true ADC value on the x axis of the graph, this information was not used in computing the linear model parameters.

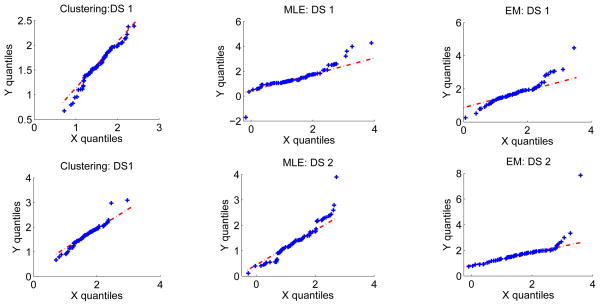
We then perform the suggested consistency checks. The Q-Q plot is plotted and is shown in Fig. 2. The correlation between the quantiles of the two distributions is also computed and is close to one in all the cases. Pearson’s chi-squared test is performed to compare the theoretical and estimated distributions and in all the cases, the determined X² test statistic has a p-value close to 1, indicating that the distributions are very similar. Thus, the consistency-check output indicates that the no-gold-standard method has not failed, which is in accordance with the observation that the no-gold-standard method predicts the correct ranking of the segmentation algorithms.

Figure 2.

Consistency check: The Q-Q plot comparing the histogram of automated ADC values to the theoretically-estimated distribution for the clustering, MLE and EM-based segmentation algorithms and for the two simulated lesion datasets: DS1 and DS2. The quantiles of the theoretically-estimated distribution and the measured ADC distribution are plotted along the x and y axis, respectively. The 45° line is also plotted for visual convenience. We observe that the Q-Q plot lies approximately along the 45° line in all the scenarios, thus confirming that the measured and estimated distributions are consistent with each other.

4.2.2. Datasets 3 and 4

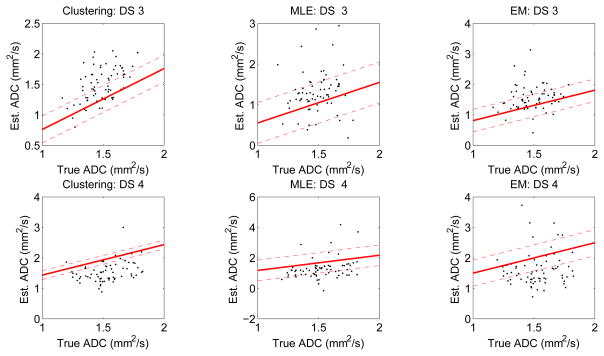
The experiments are repeated for datasets 3 and 4. In these two datasets, as mentioned earlier, the true ADC values have been sampled from a four-parameter GBD. The algorithms are ranked on the basis of accuracy and precision, and as the results in Tables 4 and 5 show, the no-gold-standard approach ranks the algorithms correctly. Fig. 3 shows the regression lines obtained using the estimated bias and variance parameters for the three segmentation algorithms for these two datasets.

Table 4.

True and estimated EMSE for datasets 3 and 4

Segm. Alg.	Dataset 3		Dataset 4
	True EMSE	Estimated EMSE	True EMSE	Estimated EMSE
Clustering	0.056	0.106	0.101	0.211
EM	0.175	0.173	0.317	0.435
MLE	0.299	0.457	0.466	0.486

Table 5.

RSS and noise standard deviation for datasets 3 and 4

Segm. Alg.	Dataset 3		Dataset 4
	RSS	Noise std. dev.	RSS	Noise std. dev.
Clustering	0.238	0.221	0.315	0.146
EM	0.408	0.371	0.547	0.430
MLE	0.506	0.505	0.645	0.675

Figure 3.

The regression lines estimated using the no-gold-standard method for the three segmentation algorithms and for the two simulated lesion datasets: DS3 and DS4. The solid line is generated using the estimated linear model parameters, and the dashed line denotes the estimated standard deviation. The scatter plots show the computed ADC values vs. the true ADC value. ADC values are in units of mm²/10³s.

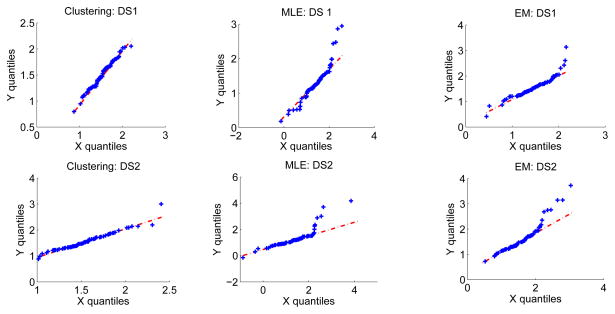
We next perform the suggested consistency checks. The Q-Q plot shown in Fig. 4, the correlations between the quantiles of the two distributions, which is close to one in all the cases, and Pearson’s chi-squared test, all indicate that the no-gold-standard approach has not failed. This is again in accordance with the observation that the no-gold-standard method predicts the ranking of the segmentation algorithms correctly.

Figure 4.

Consistency check: The Q-Q plot comparing the histogram of automated ADC values to the theoretically-estimated distribution for the clustering, MLE and EM-based segmentation algorithms and for the two simulated lesion datasets: DS3 and DS4.

4.2.3. Dataset 5

On performing the experiment with dataset 5, the no-gold-standard approach does not rank the algorithms correctly. This is evident from the results shown in Table 6, where we observe that the rankings from the no-gold-standard approach do not match the true rankings, for both accuracy and precision. On performing the consistency checks, while the output using the Q-Q plot appears to be consistent with estimated ADC values, Pearson’s chi-square test outputs a X² test statistic with a p-value close to 0 for two of the automated segmentation algorithms. These p-values are shown in the last column of Table 6, and indicate that the no-gold-standard output is inconsistent with estimated ADC values. Thus, Pearson’s chi-square consistency check is able to correctly predict the failure of the no-gold-standard approach for this dataset.

Table 6.

No-gold-standard and consistency check result for dataset 5

Segm. Alg.	True EMSE	Estimated EMSE	RSS	Noise std. dev.	p-value of X2 statistic
Clustering	0.419	0.169	0.546	0.295	1
EM	0.702	0.395	0.796	0.573	0
MLE	0.500	0.648	0.578	0.720	0

5. Discussion

In this paper, we have explored the idea of quantifying image analysis algorithms, especially image segmentation algorithms, based on how well they aid in achieving the end task from the image. In many image analysis tasks, the analyzed images are acquired for a certain purpose. This is especially true in medical imaging. Therefore, evaluating the image analysis algorithms on a task-based measure is important. Another idea explored in this paper is evaluating the segmentation algorithms in the absence of gold-standard or manual segmentation results. In most general images, and especially in medical images, achieving perfect manual segmentation is almost impossible due to reasons discussed earlier. This paper recognizes this issue and proposes an evaluation method for DW images that accounts for this.

The desired task from DW images is accurate lesion-ADC estimation. We have shown using theoretical and experimental study that using manual instead of gold-standard segmentations to evaluate the automated-segmentation algorithms is not reliable. We have then suggested a generalized-no-gold-standard approach to compare the automated segmentation algorithms. The no-gold standard approach does not require either manual or perfect segmentation results and can rank the algorithms on the basis of both accuracy and precision. We have also suggested consistency checks to validate the output obtained from the no-gold-standard technique.

From experiments on our simulated lesion dataset, we observed that even the manual ADC values are related to the true ADC values through the model described by Eq. (7). Therefore, the proposed no-gold-standard approach can also be used to rank multiple human experts performing manual segmentation, on the basis of both accuracy and precision. The bias and variance of the experts can be estimated. We can also compare the manual segmentation obtained by an expert to the outputs obtained using a set of automated segmentation algorithms, and therefore, decide which one is the best. Another advantage of our no-gold-standard approach is that it estimates the bias in the ADC values estimated using a segmentation algorithm. Therefore, using this bias value, the estimated ADC values can be corrected. Similarly, instead of segmentation algorithms, if human experts are performing the manual segmentation task, there may be a systematic bias in the segmentation performed by them [33]. The no-gold-standard approach can be used to estimate and compensate for this bias. Apart from this, the no-gold-standard method also estimates the true distribution of the parameter of interest, i.e. the ADC value. This can provide information about the true distribution of the ADC values for the population being studied.

The original no-gold-standard approach [38, 39] requires the parameter of interest to lie between 0 and 1. However, using the four-parameter GBD for the parameter of interest, we have extended the no-gold-standard approach to account for any range of the parameter of interest. Therefore, the scheme can be used in many other scenarios. For example, the segmentation algorithms to delineate tissue in single photon emission computed tomography (SPECT) images to determine the radioactive activity within the tissue [65] can be evaluated using the proposed method. Similarly, algorithms to segment the lesion in MR images of multiple sclerosis to compute its signal intensity [66] can also be compared using the suggested no-gold-standard approach. However, in these applications, the model that relates the parameter of interest to the estimated value of the parameter should be carefully determined.

To determine the relation between the true- and automated-ADC values, we use simulated-lesion datasets. It would be ideal if this study could be done on bio-phantoms that have lesions with known ADC values. Based on some recent studies [58], we predict that such a study could be possible in the near future. Also, it may be the case that, with a real-lesion dataset, the relation between true and estimated ADCs is more complicated than our model assumption. However, the suggested no-gold-standard method can be very easily adapted for that case, by just changing the polynomial-order of the relationship. We would then have to estimate more coefficients of the model, than just the bias term. Also, the parameters based on which we rank the algorithms for accuracy and precision will change.

In this paper, we have focused on the performance of the suggested task-based technique, and not compared it with other conventional techniques like Dice’s coefficient, Jaccard index, and STAPLE [20]. These evaluation techniques rank the segmentation algorithms based on region-overlap. Thus, comparing our evaluation scheme, which ranks the algorithms based on how well they aid in the ADC estimation task, with the region-overlap based schemes is inappropriate. In fact, the two approaches can yield different rankings, in which case, the diffusion-analyst should decide the measure that is more critical for further study. In our opinion, measuring region overlap is also important to evaluate the efficacy of the segmentation algorithm, and thus, while evaluating segmentation algorithms, both the approaches should be used.

A requirement of the the suggested no-gold-standard technique, and in fact of most other evaluation techniques, is the requirement of many lesion images. A large number of lesion images are required in the no-gold-standard technique since the number of parameters to be estimated is high. To compare three segmentation algorithms, we have to solve for ten parameters, i.e. {{v_k, σ_k}, {α, β, g, l}} for k = 1, 2, 3. It is appropriate if the dataset size is at least three times the number of parameters to be estimated. Generally the datasets available are this large, so this is not a very difficult requirement to satisfy.

The effect of outliers on the sensitivity of the no-gold-standard method is important to discuss. As we observe in the scatter plot shown in Fig. 1 and Fig. 3, some of the automated ADC values in our dataset are outliers. While few automated ADC values are negative, others are significantly greater than 3 mm²/10³s, which is the upper range of ADC values typically observed in our DWMRI study. The input to the no-gold-standard algorithm consists of all the automated ADC values, i.e. the outlier ADC values are not filtered from the dataset. Filtering the outlier automated values from the dataset will lead to unfair comparison between the segmentation algorithms, since if a segmentation algorithm outputs an outlier ADC value when the other algorithms do not, then such an output should negatively affect the rank of the particular segmentation algorithm. The no-gold-standard approach is able to rank the algorithms correctly in spite of the presence of these outlier ADC values for our dataset. The method is able to perform satisfactorily in the presence of some outlier values. However, since it is a linear-regression technique, it will be sensitive to the presence of many outliers. Moreover, if a segmentation algorithm produces many outliers, then the assumption of a linear relationship between the true and automated ADC values can be violated. Therefore, if a segmentation algorithm consistently outputs poor segmentations or outlier ADC values, then it is not appropriate to use the no-gold-standard approach for its evaluation. In that case, it may perhaps be more useful to use a quantile-regression technique, which is less sensitive to the presence of outliers [67].

Another important discussion topic is the validation of the output obtained using the no-gold-standard approach. The no-gold-standard method is essentially a ML estimation technique, and therefore, there can be error in the various parameters that are estimated using this technique. For example, we observe that the values of the estimated EMSE in the different experiments are not exactly the same as the true EMSE values. This error can affect the rankings that are determined using these estimated parameters, as we observe in dataset 5. In our experiments, we have not observed many cases where the error in parameter estimation has affected the rankings, but this possibility cannot be ignored. Therefore, the consistency checks that we have suggested are important and should be performed.

We would like to add that in our ADC-estimation procedure, we considered only a mono-exponential model for signal decay. However, in liver imaging, bi-exponential behavior has been observed over the range of b values used for clinical imaging [68]. Also, the b values taken in this study can be subject to uncertainty due to tolerances in scanner gradient switching characteristics and timing limitations, but are assumed to be accurate, as is common in this type of analysis [69]. A more robust approach to ADC estimation could take care of these issues as well. However, this will not have any effect on our no-gold-standard approach, as long as the true ADC values are related to the automated ADC values by just a bias and noise term. We do not expect that a small change in the ADC estimation technique would lead to any significant alteration of this relationship.

The rankings determined using the suggested no-gold-standard approach aid in the choice of the best segmentation algorithm for DW images of visceral organs. This segmentation algorithm can then be used in studies where lesion segmentation is required in the clinical DW images to determine the ADC value of the lesion. The computed ADC value can then be used to study the therapeutic response of a patient over a period of time, as is being done in various clinical studies [6–8]. This can help in the growth of DWMRI as an accurate biomarker to predict anti-cancer therapy response, and lead to improved patient healthcare.

In this paper, we have dealt exclusively with the task of quantifying segmentation algorithms in DW images. However, there are other intermediate tasks that are performed to compute the ADC value from data acquired using DWMRI, such as image reconstruction [70] and ADC estimation [10,71]. The algorithms for these intermediate steps can also be evaluated based on the no-gold-standard approach. More generally, there are many intermediate tasks that are performed to get the parameter of interest from an image, for which various algorithms can be developed. To compare these algorithms, task-based assessment can be used.