Response times from ensembles of accumulators

Significance

The delay of responding to stimuli, known as response time (RT), is randomly variable. Psychologists explain this variability through models in which RT is dictated by the termination of a single random accumulation process. Neurophysiologists explain this variability through the dynamics of neurons sampled from very large networks. This paper explains how these radically different scales of explanation can both be correct.

Abstract

Decision-making is explained by psychologists through stochastic accumulator models and by neurophysiologists through the activity of neurons believed to instantiate these models. We investigated an overlooked scaling problem: How does a response time (RT) that can be explained by a single model accumulator arise from numerous, redundant accumulator neurons, each of which individually appears to explain the variability of RT? We explored this scaling problem by developing a unique ensemble model of RT, called e pluribus unum, which embodies the well-known dictum “out of many, one.” We used the e pluribus unum model to analyze the RTs produced by ensembles of redundant, idiosyncratic stochastic accumulators under various termination mechanisms and accumulation rate correlations in computer simulations of ensembles of varying size. We found that predicted RT distributions are largely invariant to ensemble size if the accumulators share at least modestly correlated accumulation rates and RT is not governed by the most extreme accumulators. Under these regimes the termination times of individual accumulators was predictive of ensemble RT. We also found that the threshold measured on individual accumulators, corresponding to the firing rate of neurons measured at RT, can be invariant with RT but is equivalent to the specified model threshold only when the rate correlation is very high.

Response time (RT) is a core measure of human decision-making in experimental psychology (1). The random variation of RT across otherwise identical trials has been a puzzle since the mid-19th century. Since the 1960s, this variation of RT—measured in a wide range of perceptual, cognitive, and economic tasks (1–5)—has been explained through stochastic accumulator models. These models assume that a response is generated when evidence accumulates at a certain rate (v) over time to a threshold (θ) and that the stochastic variation of RTs arises primarily from random fluctuations in accumulation rates (Fig. 1A). Historically, these models were formulated and tested before data on the underlying neural processes were available.

Fig. 1.

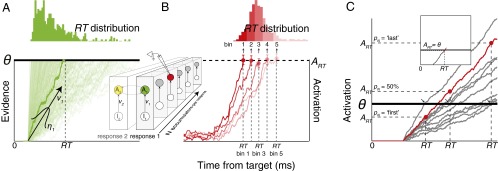
Response times predicted by ensembles of redundant stochastic accumulators. (A) Stochastic accumulator models describe RT in terms of an accumulation process (one trajectory per trial) that proceeds at a certain rate (v) to reach a fixed threshold (θ). Stochastic variation of RT arises from fluctuations of v between (η) and within trials (ξ). It is common to consider one accumulator associated with each of multiple responses; we considered instead the case of multiple accumulators associated with the same response (Inset). (B) RT can also be described by the time at which the evolving spike rates of certain neurons, averaged across bins of trials with common RTs (one trajectory per RT bin, replotted from ref. 49), reach an activation level that is invariant with RT (A_RT). These neurons have been argued to instantiate the process described by stochastic accumulator models. (C) Unless accumulators are perfectly correlated (Inset), it is unclear (i) how an ensemble of accumulators makes the transition from evidence accumulation to response execution, (ii) under what termination rules (p_N) and accumulation rate correlations (r_v) the dynamics of one accumulator (highlighted red) predicts RT distributions and the invariant relationship between A_RT and RT, as observed empirically, and (iii) how A_RT relates to the unobserved threshold of an accumulator (θ).

Subsequently, neurons exhibiting accumulating discharge rates in various RT tasks have been found in sensory, sensorimotor, and motor brain structures; in premotor circuits for limb and eye movements it is known that the neurons with accumulating activity are necessary and sufficient for initiating movements (6, 7). Movements are initiated when the trial-averaged accumulating spike rate of these neurons reaches a fixed activation level (6) (A_RT) like a threshold, and the distribution of RTs is accounted for by the stochastic variability in the rate of growth of neural activity toward A_RT (Fig. 1B). This discovery inspired the conjecture that individual neurons instantiate the evidence accumulation process described by stochastic accumulator models (6). This conjecture has stimulated extensive research replicating the original observation and equating accumulator model parameters with measures of neural dynamics assessed by spike rates (8–17), EEG (18, 19), magnetoencephalography (MEG) (20), and functional MRI (21–23) and simulated with neural network models (24–28).

However, this productive line of research has overlooked a fundamental scaling problem. On the one hand, the behavior of specific single neurons seems sufficient to account for the RT of the whole brain. On the other hand, we know that ensembles of tens of thousands of neurons are necessary to produce any action (SI Text, How Many Neurons Produce a Movement?). Hence, how can each individual accumulator neuron, recorded in isolation, seem sufficient to initiate a movement by crossing a unique threshold when no single accumulator neuron is necessary for a movement to occur? In other words, how is the accumulating activity of numerous redundant and idiosyncratic neurons in a large ensemble coordinated and combined to produce variable RTs that can be predicted by a model consisting of just a single stochastic accumulator? This question has not been addressed previously (SI Text, Extension of Previous Work).

This question is challenging to investigate empirically because the limited number of spikes emitted by individual neurons precludes reliable assessment of single-trial dynamics, and simultaneous measurement of numerous functionally homogeneous neurons is not possible with current technology. Therefore, we performed computer simulations of ensembles of stochastic accumulators.

We address four major issues. First, we investigate how RT distributions can be explained both by a single accumulator model and by the ensemble activity of many accumulators. Second, we explore how RT distributions scale with the accumulator ensemble size. Third, we investigate how the A_RT measured across trials from an individual accumulator can be invariant with RT even though RT is produced by a large ensemble of accumulators with different growth rates. Fourth, we explore how the measured A_RT from an individual accumulator relates to the actual threshold of that accumulator (θ).

To address these issues, we developed a unique ensemble model of RT, called e pluribus unum (EPU), which embodies the well-known dictum “out of many, one.” Stochastic accumulator models are typically designed to explain both RT and accuracy obtained in choice tasks. However, our questions are specifically centered on the basic variability of RT that is observed in responses in any task. Thus, this model does not address accuracy, although we envision natural extensions of this approach to racing or competing ensembles of accumulators embodied by simple differential equations or in more complex spiking network models.

In single-accumulator models, RT critically depends on two key parameters: the accumulation rate (v) and the threshold (θ). Extrapolating these parameters to the ensemble case is not trivial (Fig. 1C).

First, how are accumulation rates coordinated across the ensemble? At one extreme, if all accumulators share identical dynamics, then the ensemble reduces to one accumulator (Fig. 1C, Inset), yet perfect correlation is implausible (29). At the other extreme, if all accumulators have uncorrelated dynamics, then unrealistic RT variability would occur. Moreover, uncorrelated dynamics would also be implausible from a biological perspective, given that ensembles receive common inputs, have recurrent connections, and are modulated by common neurotransmitter systems. We investigated this question by sampling correlated accumulation rates, with rate correlation (r_v) varying between 0.0 and 1.0. Though the range of rate correlations we simulated exceeds the noise correlation found among neighboring neurons (30, 31), they can arise naturally from redundancy in common inputs, recurrent connectivity, and modulation by a common source (32–34).

Second, how is ensemble activity combined to produce one RT? At one extreme, if RT is specified by the time when the fastest accumulator reaches threshold, the RT distribution will shrink with ensemble size. At the other extreme, if RT is specified by the time when the slowest accumulator reaches threshold, the RT distribution will expand with ensemble size. How large is the region between these two extremes where the RT distribution remains stable with ensemble size? We investigated these questions by assuming that each accumulator projects to a unit that either tallies the proportion of accumulators having crossed a threshold activation (a “polling” mechanism akin to quorum sensing) (35) or monitors the average firing rate of the ensemble (a “pooling” mechanism akin to the vector averaging that guides movement dynamics in final common neural circuits that initiate movements) (36, 37). When this unit tallies a critical proportion of units hitting threshold (p_N, polling) or reaches a threshold of average activity (θ_trigger, pooling), an overt response is triggered that is measured as RT.

We determined how RT distributions and the dynamics of individual accumulators were influenced by three ensemble properties: the number of accumulators (1 ≤ n ≤ 1,000), the correlation of accumulation rates across accumulators (0.0 ≤ r_v ≤ 1.0), and the termination rule of the accumulation process (polling: 0% < p_N ≤ 100%; and pooling: Σ A_i(t)/N ≥ θ_trigger). We explored two influential types of stochastic accumulator models, one assuming within-trial as well as between-trial variability in accumulation (diffusion model) (38) and one assuming only between-trial variability (linear ballistic accumulator model) (39), as well as four variants making additional assumptions. Conclusions based on simulation of these models agreed, so we present the simple linear ballistic accumulator model here and the diffusion model and other more complex models in SI Text, Robustness of Findings.

Results

RT Distributions from One and Many Accumulators.

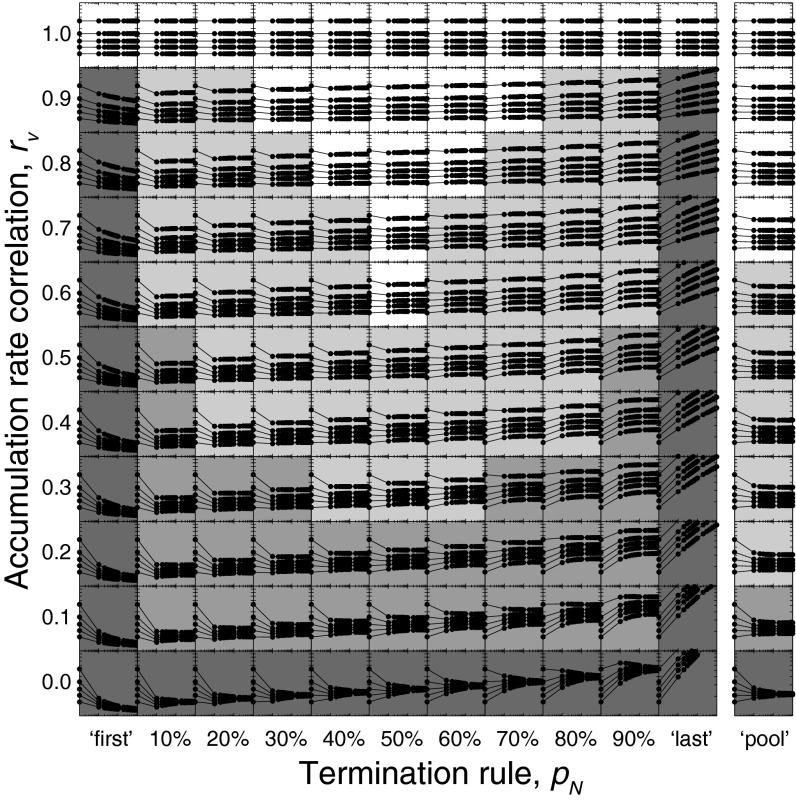
We began by identifying the conditions under which an individual accumulator model (n = 1) and a large-ensemble accumulator model (n = 1,000) predict RT distributions with similar shapes, defined as overlapping 95% confidence intervals over all five RT quintiles (0.1, 0.3, 0.5, 0.7, 0.9). We observed that an individual accumulator model and a large ensemble accumulator model predict RT distributions with virtually indistinguishable shapes if accumulation rates are at least moderately correlated (r_v ≥ 0.6) with intermediate termination rules. Much higher rate correlations (r_v ≥ 0.9) are necessary under extreme termination rules (Fig. 2). Similar results were obtained under a pooling mechanism (Fig. 2, rightmost column). Thus, RT distributions can be explained both by an individual model accumulator and by accumulating activity of large neuronal ensembles only if their activation dynamics are moderately correlated and RT is not governed by extremely fast or slow accumulators.

Fig. 2.

Predicted RT distributions as a function of ensemble size (N), termination rule (p_N), and accumulation rate correlation (r_v). Each panel shows the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles on a log-log scale (the x axis ranges from 10⁰ to 10³; the y axis ranges from 10² to 10³) as a function of N, p_N, and r_v vary across columns and rows, respectively. We identified conditions (p_N and r_v) under which RT distributions were (i) invariant over the entire interval of N (i.e., 1,1,000; white panels], (ii) invariant with N over the interval (10,1,000; light gray panels), (iii) invariant with N over the interval (100,1,000; medium gray panels), and (iv) not invariant with N (dark gray panels).

RT Distributions Over a Range of Accumulator Ensemble Sizes.

We also investigated the invariance of RT distributions over a range of ensemble sizes to determine whether RTs may be invariant once some critical ensemble size is reached. Knowing that the same RT distributions are predicted whether an ensemble has 10 accumulators or 1,000 accumulators or more provides important insights into the properties of ensemble dynamics. It may be that ensembles need to be “large enough” but that the precise size of the ensemble has little effect on the RT that the ensemble generates.

Extending the analysis above, we investigated how RT distributions scale with accumulator ensemble size. We identified conditions under which a small-ensemble model (n = 10) and an intermediate-ensemble model (n = 100) predict RT distributions with similar shapes as a large-ensemble model (n = 1,000). RT distributions were invariant across ensembles with at least 10 accumulators if accumulation rates were at least modestly correlated (r_v ≥ 0.3) and termination rules avoided the extremes (10% ≤ p_N ≤ 90%). RT distributions were invariant across larger ensembles (n ≥ 100) with even lower rate correlations (r_v ≥ 0.1). Only if accumulation rates were uncorrelated (r_v = 0.0) or termination rules were extreme (p_N = first and p_N = last) did RT distributions vary dramatically in scale and shape with ensemble size (Fig. 2). Similar findings were observed when RT was determined by the pooling termination mechanism (Fig. 2, rightmost column) and with other accumulator model variants we investigated (SI Text, Robustness of Findings).

Variability in RT remains remarkably constant across different ensemble sizes over a large proportion of parameter space. Only for uncorrelated accumulators and extreme termination rules (p_N = first or p_N = last) does ensemble size affect RT variability, a lack of invariance anticipated by extreme value statistics. By analogy to the central limit theorem, we can perhaps anticipate why median RT remains invariant with ensemble size. However, there is no single mathematical property that might allow us to anticipate why variability in RT is invariant with ensemble size across correlated samples and intermediate termination rules, so we need to rely on simulation. To begin with, we know that for p_N = first, variability decreases with ensemble size, and for p_N = last, variability increases with ensemble size. So at some point in the range of termination rules we might expect an invariance of variability with ensemble size. What is striking is that this invariance is observed across all of the intermediate termination rules we investigated, not just a single value of termination rule. Also, for small ensemble sizes, variability is largely dominated by sampling variability across those few accumulators, and low correlations between accumulator rates may have only a small influence on the predicted variability from trial to trial. By contrast, for large ensemble sizes, variability is largely dominated by the between-trial variability introduced by the correlation between accumulator rates. These counteracting effects of ensemble size and correlation largely cancel each other out, producing invariance in RT distributions over a range of model parameters and model architectures (SI Text, Robustness of Findings) that we did not anticipate.

Invariance of A_RT with RT.

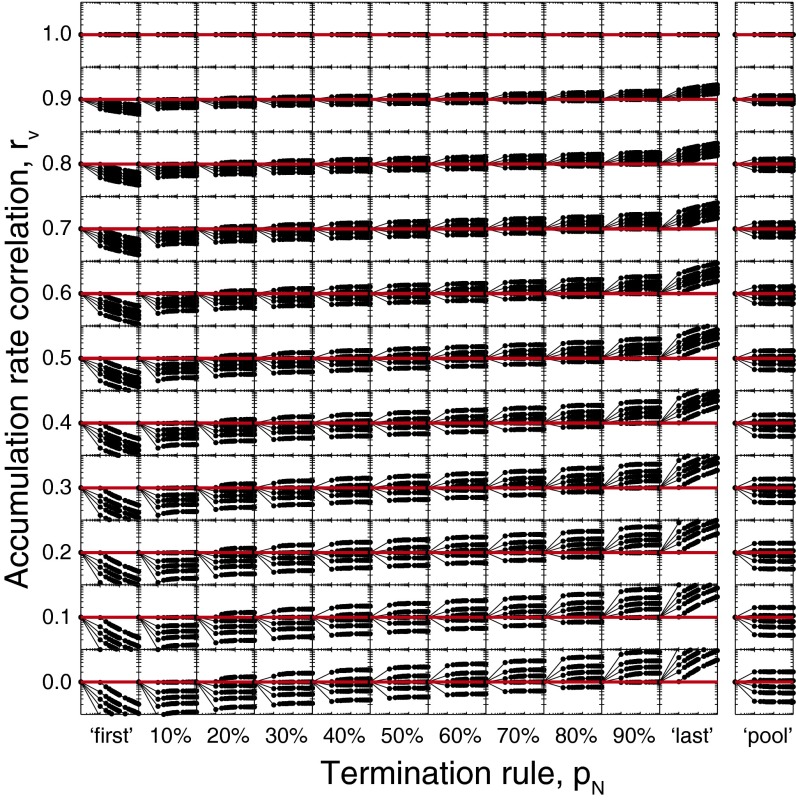
We then investigated how the trial-averaged A_RT from an individual accumulator can be invariant with RT even though RT is produced by a large ensemble of accumulators. Most accumulator models are based on thresholds that are invariant across RT (40–42), and multiple laboratories have observed invariant thresholds of neural discharge rate (6–17). However, the A_RT of an individual accumulator participating in the ensemble is not guaranteed to reach the same value on each trial because of the stochastic nature of its accumulation process—on some trials it has reached θ and contributes to the measured RT, but on other trials it has not yet reached θ and so does not contribute (Fig. 1C). Though it is trivially true for a single accumulator that A_RT will be invariant with RT, it is unknown whether large ensembles of accumulators with intermediate termination rules and accumulation rate correlations reproduce the invariance of A_RT with RT that is regularly measured in neurophysiology.

Just like a neurophysiology experiment would randomly sample one neuron in some brain region, we randomly selected one accumulator in the ensemble and measured A_RT for that accumulator on each simulated trial. We then quantified how the slope of the linear regression of A_RT over RT varied for ensembles of 10, 100, and 1,000 accumulators (Fig. 3), mimicking the approach used in neurophysiological analyses. For small ensembles (n = 10), A_RT was invariant over RT under intermediate termination rules (10% ≤ p_N ≤ 90%) and moderate rate correlations (r_v ≥ 0.4). With many accumulators (n = 1,000), the invariance of A_RT with RT was only violated for the earliest termination rule (p_N = first) and low accumulation rate correlations (r_v ≤ 0.3). Under a pooling mechanism, the invariance of A_RT with RT was never violated. Thus, the invariance of A_RT with RT emerges from the dynamics of individual accumulators operating in large ensembles, even though the dynamics of no single accumulator uniquely determine RT.

Fig. 3.

Relationship between A_RT and RT as a function of ensemble size (N), termination rule (p_N), and accumulation rate correlation (r_v). Each panel shows the linear regression slope of A_RT on RT, expressed as colored pixels, for three ensemble sizes (Left, n = 10; Center, n = 100; Right, n = 1,000) and all combinations of termination rules and accumulation rate correlations. Hatched pixels indicate parameter combinations for which A_RT varied systematically with RT. Thus, beige, nonhatched pixels represent parameter combinations for which the slope of the linear relationship between A_RT and RT was zero and nonsignificant.

Relationship Between A_RT and θ.

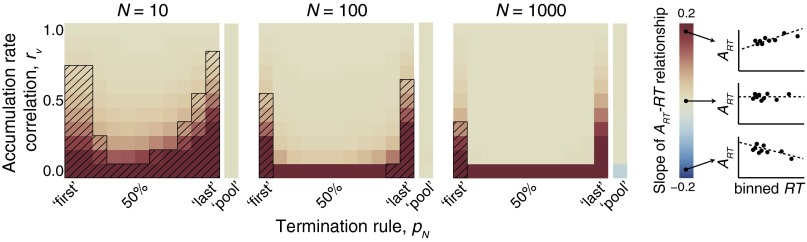
Finally, we explored how the A_RT measured from an individual accumulator relates to the actual threshold of that accumulator (θ). In the neurophysiology literature, it is commonly assumed that the A_RT of an individual neuron represents a threshold like that in stochastic accumulator models. However, because A_RT is a trial-averaged measure and the true threshold of a neuron (θ) is unknown, we do not know how closely the value of A_RT approximates the value of θ.

As expected, with n = 1, A_RT was constant with RT and identical across trials, and the measured A_RT equaled the model parameter θ. However, in ensembles operating under intermediate termination rules (10% < p_N < 90%) A_RT varied significantly between trials (Fig. 4). Thus, individual accumulators acting in ensembles do not reach the same activation level at RT on each trial, meaning that measured A_RT is not necessarily equivalent to the threshold specified by the model (θ) for any given accumulator. Analogous nonequivalence was observed for pooling mechanisms. We further observed that the termination rule determined how closely A_RT approximated θ. Under early termination rules (p_N < 50%), average A_RT was less than θ. Under late termination rules (p_N > 50%), average A_RT was greater than θ. Under the median termination rule (p_N = 50%), average A_RT equaled θ; this entails that the relationship between A_RT and θ cannot be determined without knowledge of the termination rule. The accumulation rate correlation determined the magnitude of variability in A_RT. The more homogeneous the accumulators, the smaller the variability in A_RT and the closer the agreement with θ, which implies that the degree of stochastic variation in A_RT is indicative of the homogeneity of the accumulation process in the ensemble. Together, though these findings demonstrate unanticipated complexity in the relationship between A_RT measured in an individual accumulator and the true θ that defines its dynamics, in conditions under which one accumulator resembles many, the average A_RT measured from neurons is a fair proxy of the relation of θ to RT.

Fig. 4.

Distribution of measured activation level around RT (A_RT) between trials in a randomly selected accumulator as a function ensemble size (N), termination rule (p_N), and accumulation rate correlation (r_v). The x axis ranges from 10⁰ to 10³, and the y axis ranges from 10² to 10³. Other conventions as in Fig. 2. Individual threshold (θ, red line) was identical across accumulators. Thus, correspondence between A_RT and θ is indicated by overlap of distributions (black lines) and threshold (red line).

Discussion

Before carrying out these simulations, we thought that different combinations of ensemble size, accumulation rate correlation, and termination rule might produce markedly different qualitative behavior. Instead, we observed that the RT distributions predicted by large ensembles of redundant accumulators were invariant with ensemble size, except in the conditions of extreme termination rules and low accumulation rate correlations. These results did not depend on the particular form of the accumulator, variation in parameters such as leakage or within-trial noise magnitude, and consistency of v and θ across accumulators (SI Text, Robustness of Findings).

These findings complement previous models of decision-making by incorporating stochastic variability across multiple redundant accumulators and specifying constraints on the degree of consensus necessary for robust performance across variation in ensemble size. The rate correlations we found exceed the noise correlation found among neighboring neurons (30, 31) but can arise naturally from redundancy in common inputs, recurrent connectivity, and modulation by a common source (32–34, 43). Consensus through correlation of accumulation rates also prevents extreme neural activity from governing behavior.

These findings also provide clarification and caution about the conjecture that the activation level reached by particular neurons before RT (A_RT) corresponds conceptually and quantitatively to the threshold parameter of accumulator models (θ_trigger). This linking proposition cannot be taken for granted (44), and the current demonstration that mapping model parameters onto measures of individual accumulators depends on unobserved statistical properties of the ensemble in which these accumulators operate. However, the EPU model demonstrates the necessity of obtaining multielectrode recordings to assess correlations in neural accumulation rates. These recordings should be made from homogeneous ensembles of neurons at different sensorimotor levels, but most importantly in neurons projecting to brainstem and spinal circuits that innervate motor neurons; this can provide key insights into termination rules and variability of A_RT across trials. These observations are crucial to validating the mapping of model parameters onto neural measures. However, the robustness of the relationships between RT distributions and ensemble size may reveal how measurements at different scales (single neurons, multiunit activity, local field potentials, EEG, MEG, fMRI) can appear to relate so well to the parameters of accumulator models.

To summarize, the random variation of RT has been explained through models of a stochastic accumulation process and through measures from individual neurons that appear to correspond to that process. This juxtaposition entails a previously unaddressed scaling problem—how can the activity of a multitude of redundant neurons map onto a single model accumulator? We now show how coordinated stochastic accumulation among many redundant accumulators can produce realistic RT distributions and accumulator dynamics regardless of the number of accumulators over a wide range of ensemble parameters, requiring only modest accumulation rate correlations and prohibiting the fastest or slowest accumulators from governing performance. Under this design principle, the dynamics of individual accumulators predict the behavior of the ensemble. In future work, these scaling properties can be explored in two complementary approaches. First, the EPU model can be extended to more complex models explaining performance in choice and stopping tasks (SI Text, Future Model Extensions). Second, as technologies develop to map the activity of large ensembles of neurons in the brain (45), it will become more tractable to monitor the activity of ensembles of neurons in circuits instantiating accumulation and threshold mechanisms (SI Text, Neural Threshold Mechanisms), providing an opportunity to verify the predictions of our simulations.

Materials and Methods

EPU Model.

Embodying the well-known dictum “out of many, one,” we simulated ensembles of N stochastic accumulators (2) to understand how one RT is produced from that ensemble. With bold letters used to represent N-dimensional vectors, the ensemble of accumulators is governed by the following stochastic differential equation

Eq. 1 implies that the change in activation dA at every time step dt depends on the accumulation rate v driving the accumulators toward threshold θ, the leakage constant k pushing activation back to baseline as it becomes larger, and Gaussian random noise ξ. The linear ballistic accumulator model presented in Results assumed no leakage and no within-trial Gaussian random noise, but we do consider models with these characteristics in SI Text, Robustness of Findings.

We sampled v from an N-dimensional multivariate lognormal distribution, 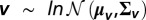, where μ_v is a vector of identical location parameters (μ_v) and Σ_v is the covariance matrix. This covariance matrix was computed as

where r_v is the accumulation rate correlation matrix with off-diagonal elements equal to r_v, and σ_v is the scale parameter of the lognormal distribution.

We sampled v from a multivariate log-normal distribution for three reasons. First, the lognormal distribution takes positive values only and is therefore a natural choice for modeling accumulation rates of movement neurons that increase firing rate before a movement (46). Second, log-normal race models with similar parameter values (see below) can account for the shape of RT distributions (47). Third, the multivariate log-normal and multivariate normal are the only distributions for sampling correlated random variables with simple analytic solutions. In additional simulations, we demonstrate that the type of sampling distribution does not change findings qualitatively (SI Text, Robustness of Findings).

We assumed identical accumulation distributions (mean = 1 and SD = 1) and thresholds (θ = 100 units) across accumulators; this seems to contrast with the idiosyncrasy of neurons, but much of this idiosyncrasy is eliminated in the analysis of neurophysiological data through normalization of spike density functions. Moreover, additional simulations demonstrate that varying accumulation rate distributions and thresholds across accumulators did not alter our findings qualitatively (SI Text, Robustness of Findings).

Following the stochastic accumulator literature (1, 3), RT was modeled as the sum of the duration of three processing stages: (i) a stimulus-encoding stage with fixed duration (T_E = 100 ms), during which activation level of all N accumulators was equal to zero, A(0) = 0; (ii) an accumulation stage with variable duration (T_A), during which A increased with rate v toward θ until the termination rule was met (see Introduction); and (iii) a response-execution stage with fixed duration (T_R = 15 ms), during which A continued to increase. T_E and T_R were set in accordance with values measured empirically (48) and used in previous neurally constrained stochastic accumulator models (49). If the accumulation process had not met the termination rule within 100 s, it was aborted and no RT was logged. This cutoff time was chosen so that an RT was obtained in >90% of all simulated trials under all combinations of ensemble size, accumulation rate correlation, and termination rule.

Monte Carlo Simulations.

Simulations were performed in MATLAB (MathWorks Inc., version 7.13), running in parallel on the high-performance computer cluster at the Vanderbilt Advanced Center for Computing for Research and Education.

We manipulated three key parameters: ensemble size (N), accumulation rate correlation (r_v), and termination rule (p_N). We varied the ensemble size across 20 levels (1 ≤ n ≤ 1,000, in increments of 10 between 10 and 100 accumulators and in increments of 100 between 100 and 1,000 accumulators), the accumulation rate correlation across 11 levels (0.0 ≤ r_v ≤ 1.0 in increments of 0.1), and the termination rule across 12 levels (polling mechanism, 0% < p_N ≤ 100%, in 10% increments; pooling mechanism, Σ A_i(t)/N ≥ θ_trigger), yielding a total of 2,640 RT models. Although neuronal ensembles constitute many more accumulators, we did not go beyond 1,000 due to limitations of computational time and resources. In some versions of the models we investigated ensemble sizes of 5,000–10,000 and found the same results. Moreover, previous work has demonstrated that intrinsic noise correlations among neurons entail upper limits on pool size (50).

For each combination of those three key parameters, a simulation consisted of 1,000 Monte Carlo repetitions of 500 trials. On each trial, we simulated N correlated, redundant accumulation processes. When a critical proportion of these accumulators reached threshold (p_N, polling mechanism) or when the average activity across all accumulators reached threshold (Σ A_i(t)/N ≥ θ_trigger, pooling mechanism), a response was made that was measured as RT. Analogous to a neurophysiology experiment, we measured A_RT as the mean activation level 10–20 ms before RT in a single accumulator that was randomly selected from the ensemble once per session.

For each set of 500 trials, we computed a number of descriptive statistics. To characterize the distributions of RT and A_RT, we computed five quantiles (0.1, 0.3, 0.5, 0.7, and 0.9). To describe the relationship between A_RT and RT, we sorted trials by RT, binned them into groups of 10, and computed the linear regression slope of the relationship between A_RT and RT. The 1,000 Monte Carlo repetitions enabled us to compute 95% confidence intervals on the descriptive statistics by estimating the 2.5th and 97.5th percentile of the distribution across the 1,000 repetitions.

To determine the conditions under which RT distributions can be explained by 1 and 1,000 accumulators, we identified accumulation rate correlations and termination rules producing overlapping confidence intervals for each RT quintile. To determine how RT distributions scale with ensemble size, we repeated the same analysis for the n = 10 vs. n = 1,000 and n = 100 vs. n = 1,000 comparisons. To determine conditions under which A_RT was invariant with RT, we identified accumulation rate correlations and termination rules that produce regression slope confidence intervals including zero, separately for n = 10, n = 100, and n = 1,000.